2. 中国船舶重工集团有限公司,北京 100097
2. China Shipbuilding Industry Corporation Ltd., Beijing 100097, China
自主式水下航行器(AUV)是新一代水下航行器,具有活动范围大、机动性好等优点,在民用领域,可用于海底考察、海底施工,水下设备维护与维修等任务;在军用领域可用于侦察、扫雷、援潜和救生等任务。要使AUV完成预定的任务,离不开水下导航技术,水下导航与空中导航相比,具有工作时间长、信息源少、隐蔽性高等特点,它是决定AUV技术发展与应用的瓶颈问题[1 – 2]。
由加速计和陀螺仪构成的捷联式惯性导航系统(SINS)是AUV定位导航的传统传感器,它可以在短时间提供精确的定位信息。由于惯性器件的固有误差,惯性测量装置(IMU)的误差会随着时间累积增大,这种累积会带来定位误差的发散,因此需要多个导航传感器提供外信息对SINS误差进行补偿[3]。目前,用于AUV的组合导航系统主要有SINS/DVL,INS/GPS,SINS/GPS/DVL等。
GPS是一种具有全方位、全天候、全时段、高精度的卫星导航系统,能为全球用户提供低成本、高精度的三维位置、速度和精确定时等导航信息,但是它只能在陆地、水面和空中使用[4]。若采用GPS进行水下导航则仅限于浅水航行,AUV必须定期浮出水面才能利用GPS更新其定位信息。因此,必须设计一种适合AUV水下航行的新型导航方法。若没有外信息输入,SINS和DVL组合也很难提供高精确的导航信息。声学定位系统无累积误差,但存在高频误差,且更新率很低。由于地形辅助导航系统能够克服水下声学定位中存在的缺陷,本文研究了包含捷联式惯性导航系统(SINS)、多普勒计程仪(DVL)和磁罗经(MCP)与地形辅助导航系统(TAN)的组合导航系统。
卡尔曼滤波(KF)技术是目前组合导航系统中应用最广泛的,并且它也是一直有效的最佳估计算法。在噪声干扰下,经典的KF会发散,无法满足AUV的导航精度。神经网络具有结构简单、可操作性强、模拟输入输出随机非线性关系等特点,在非线性系统中有着广泛的应用[5]。因此,近年来,KF与神经网络相结合的方法得到了广泛研究,本文提出了一种基于神经网络自适应滤波的组合导航方法。
1 组合系统的结构配置本文提出的SINS/DVL/MCP/TAN组合导航系统是一种较好的解决方案,可以提供比传统导航系统性能优越的导航系统。SINS通过测量加速度和角速度计算AUV的姿态、位置和速度。DVL和MCP分别提供高精度的AUV相对海底的绝对速度信息和航向信息。在高精度的测深仪和地图匹配算法配合下,安装在AUV上的TAN能够间歇地提供定位信息。
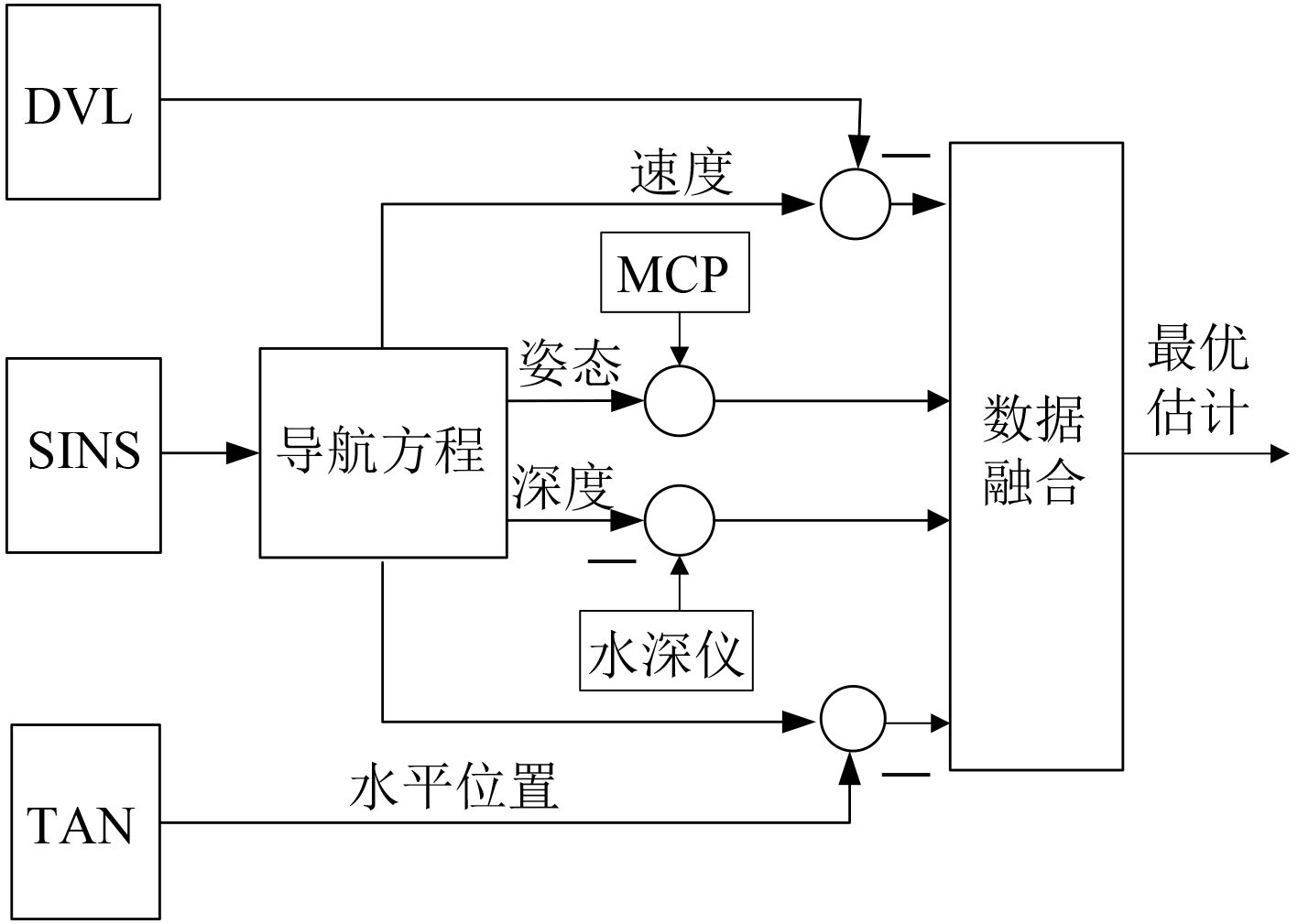
|
图 1 AUV组合导航系统框图 Fig. 1 Block diagram of AUV integrated navigation system |
SINS没有实质性的平台,陀螺仪和加速计都是直接安装在AUV载体上。
SINS的姿态角误差方程可以表示为:
| ${\dot \phi ^n} = \delta \omega _{ie}^n + \delta \omega _{en}^n - (\omega _{ie}^n + \omega _{en}^n) \times {\phi ^n} + {\varepsilon ^p}\text{,}$ | (1) |
速度误差方程可以表示为:
| $\delta {\dot V^n} \!=\! {f^n} \times {\phi ^n}\! -\! (2\delta {\omega _{ie}} \!+\! \delta \omega {}_{en}) \times {V^n} \!-\! (2{\omega _{ie}} \!+\! {\omega _{en}}) \times \delta {{ }}{V^n} \!+\! {\nabla ^p}\text{。}$ | (2) |
纬度、经度和高度的误差方程可以表示为:
| $\left\{ {\begin{array}{*{20}{l}} {\delta \dot L = \displaystyle\frac{{\delta {V_N}}}{{Rn + h}} - \displaystyle\frac{{{V_N}}}{{{{(Rn + h)}^2}}}\delta h}\text{,} \\ {\delta \dot \lambda \!=\! \displaystyle\frac{{\delta {V_E}}}{{{Re} \! +\! h}}\sec L \!+\! \displaystyle\frac{{{V_E}}}{{{Re} \!+\! h}}\sec L\tan L\delta L \!-\! \displaystyle\frac{{{V_E}}}{{{{({Re} + h)}^2}}}\sec L\delta h}\text{,} \\ {\delta \dot h = \delta {V_U}} \text{。}\end{array}\begin{array}{*{20}{c}}\end{array}} \right.$ | (3) |
式中:
多普勒计程仪是一种高精度测量系统,它可以通过四波束法获取速度。四波束如图2所示。
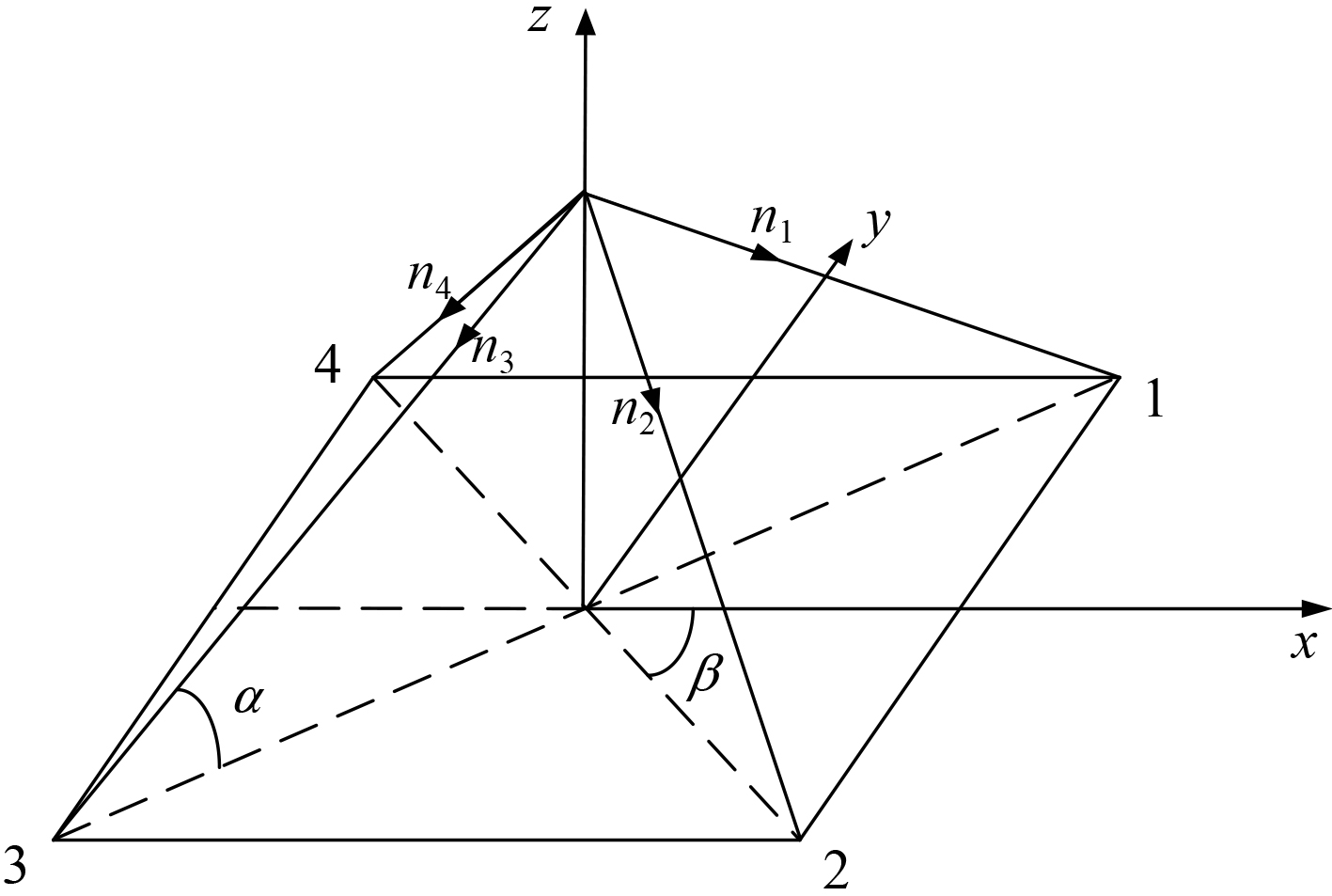
|
图 2 四波束示意图 Fig. 2 The four-beam system |
四波束在方向上对称分布,水平角为
| $V = {V_x}i + {V_y}j + {V_z}k\text{,}$ | (4) |
| $\left\{ {\begin{array}{*{20}{l}} {{n_1} = \cos \alpha \cos \beta i + \cos \alpha \sin \beta j - \sin \alpha k}\text{,} \\ {{n_2} = \cos \alpha \cos \beta i - \cos \alpha \sin \beta j - \sin \alpha k}\text{,} \\ {{n_3} = - \cos \alpha \cos \beta i - \cos \alpha \sin \beta j - \sin \alpha k}\text{,} \\ {{n_4} = - \cos \alpha \cos \beta i + \cos \alpha \sin \beta j - \sin \alpha k}\text{,} \end{array}} \right.$ | (5) |
| $\!\left\{ {\begin{array}{*{20}{l}} \! \!\!\!\!{{V_1} \!\!=\!\! V \!\cdot\! {n_1} \!\!=\!\! {V_x}\cos \alpha \cos \beta \!+\! {V_y}\cos \alpha \sin \beta \!-\! {V_z}\sin \alpha }\text{,} \!\!\!\\ \!\!\!\!\!{{V_2} \!\!=\!\! V \!\cdot\! {n_2} \!\!=\!\! {V_x}\cos \alpha \cos \beta \!-\! {V_y}\cos \alpha \sin \beta \!-\! {V_z}\sin \alpha }\text{,} \!\!\!\\ \!\!\!\!\!{{V_3} \!\!=\!\! V \!\cdot\! {n_3} \!\!=\!\! \! -\! {V_x}\cos \alpha \cos \beta - {V_y}\cos \alpha \sin \beta \!-\! {V_z}\sin \alpha }\text{,} \!\!\!\\ \!\!\!\!\! {{V_4} \!\!=\!\! V \!\cdot\! {n_4} \!\!=\!\! \!-\! {V_x}\cos \alpha \cos \beta \!+\! {V_y}\cos \alpha \sin \beta \!-\! {V_z}\sin \alpha } \text{。}\!\!\!\end{array}} \right.$ | (6) |
| $\left\{ {\begin{aligned} & {{f_{d1}} \!=\! \displaystyle\frac{{2{f_0}}}{c}\left( {{V_x}\cos \alpha \cos \beta \!+\! {V_y}\cos \alpha \sin \beta \!-\! {V_z}\sin \alpha } \right)}\text{,} \\ & {{f_{d2}} \!=\! \displaystyle\frac{{2{f_0}}}{c}\left( {{V_x}\cos \alpha \cos \beta \!-\! {V_y}\cos \alpha \sin \beta \!-\! {V_z}\sin \alpha } \right)}\text{,} \\ & {{f_{d3}} \!=\! \displaystyle\frac{{2{f_0}}}{c}\left( { - {V_x}\cos \alpha \cos \beta \!-\! {V_y}\cos \alpha \sin \beta \!-\! {V_z}\sin \alpha } \right)}\text{,} \\ & {{f_{d4}} \!=\! \displaystyle\frac{{2{f_0}}}{c}\left( { - {V_x}\cos \alpha \cos \beta \!+\! {V_y}\cos \alpha \sin \beta \!-\! {V_z}\sin \alpha } \right)}\text{。} \end{aligned}} \right.$ | (7) |
| $\left\{ {\begin{aligned}& {{V_x} = \displaystyle\frac{c}{{4{f_0}\cos \alpha \cos \beta }}\left( {{f_{d2}} - {f_{d3}}} \right)} \text{,}\\ & {{V_y} = \displaystyle\frac{c}{{4{f_0}\cos \alpha \cos \beta }}\left( {{f_{d1}} - {f_{d2}}} \right)} \text{,}\\ & {{V_z} = - \displaystyle\frac{c}{{4{f_0}\sin \alpha }}\left( {{f_{d2}} + {f_{d4}}} \right)} \text{。}\end{aligned}} \right.$ | (8) |
磁罗经由三维磁阻传感器、角度传感器和单片机组成,利用磁装置获取地球磁场方向,给出AUV的磁航向角[6]。这里,地球磁场矢量可以用正交分量X、Y、Z来描述。地球磁场水平分量可以表示为:
| $\left\{ {\begin{array}{*{20}{l}} {{X_h} = X\cos \phi + Y\sin \theta \sin \phi - Z\cos \theta \sin \phi }\text{,} \\ {{Y_h} = Y\cos \theta + Z\sin \theta } \text{。}\end{array}} \right.$ | (9) |
磁航向角可表述为:
| $H = \left\{\!\!\!\! {\begin{array}{*{20}{l}} {{{180}^ \circ } - \arctan ({Y_h}/{X_h})}\text{,} \!\!\!\\ {\arctan ({Y_h}/{X_h})}\text{,} \!\!\!\\ {{{360}^ \circ } - \arctan ({Y_h}/{X_h})}\text{,}\!\!\! \\ {{{90}^ \circ }}\text{,} \!\!\!\\ {{{270}^ \circ }}\text{,} \!\!\!\end{array}} \right.\begin{array}{*{20}{l}} {\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!} \\ {\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!} \\ {\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!} \\ {\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!} \\ {\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!} \end{array}\begin{array}{*{20}{l}} {{X_h} < 0} \text{,}\\ {{X_h} > 0} \text{,}\\ {{X_h} > 0} \text{,}\\ {{X_h} = 0} \text{,}\\ {{X_h} = 0} \text{,}\end{array}\begin{array}{*{20}{l}} {\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!} \\ {\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!} \\ {\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!} \\ {\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!} \\ {\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!} \end{array}\begin{array}{*{20}{l}} {} \\ {{Y_h} < 0}\text{,} \!\!\!\!\!\!\!\!\\ {{Y_h} < 0}\text{,}\!\!\!\!\!\!\!\! \\ {{Y_h} > 0}\text{,}\!\!\!\!\!\!\!\! \\ {{Y_h} > 0} \text{。}\!\!\!\!\!\!\!\!\end{array}$ | (10) |
|
|
表 1 仪器误差模型 Tab.1 Bathometer error model |
地形辅助导航的原理是通过AUV实际测量的水深值与已配置的数字地图进行匹配,对AUV进行的定位,定位精度与匹配区域的导航信息和地形匹配算法有关。地形匹配算法是地形辅助导航系统研究的核心技术。迭代最近点(ICP)算法是基于相关分析的大多数地形匹配方法的研究热点[7]。
通过计算机对算法进行仿真。仿真的三维水下地形如图3所示。地形图存储格式为90 m×90 m的方形网格。水深仪的测量误差设置见表1。ICP算法的初始条件和模型参数如下:导航速度为10 m/s,行进方向角为45°,导航深度为100 m,仿真时间为1 h。ICP算法的经纬度曲线误差如图4所示,匹配误差控制在0.3″以内。
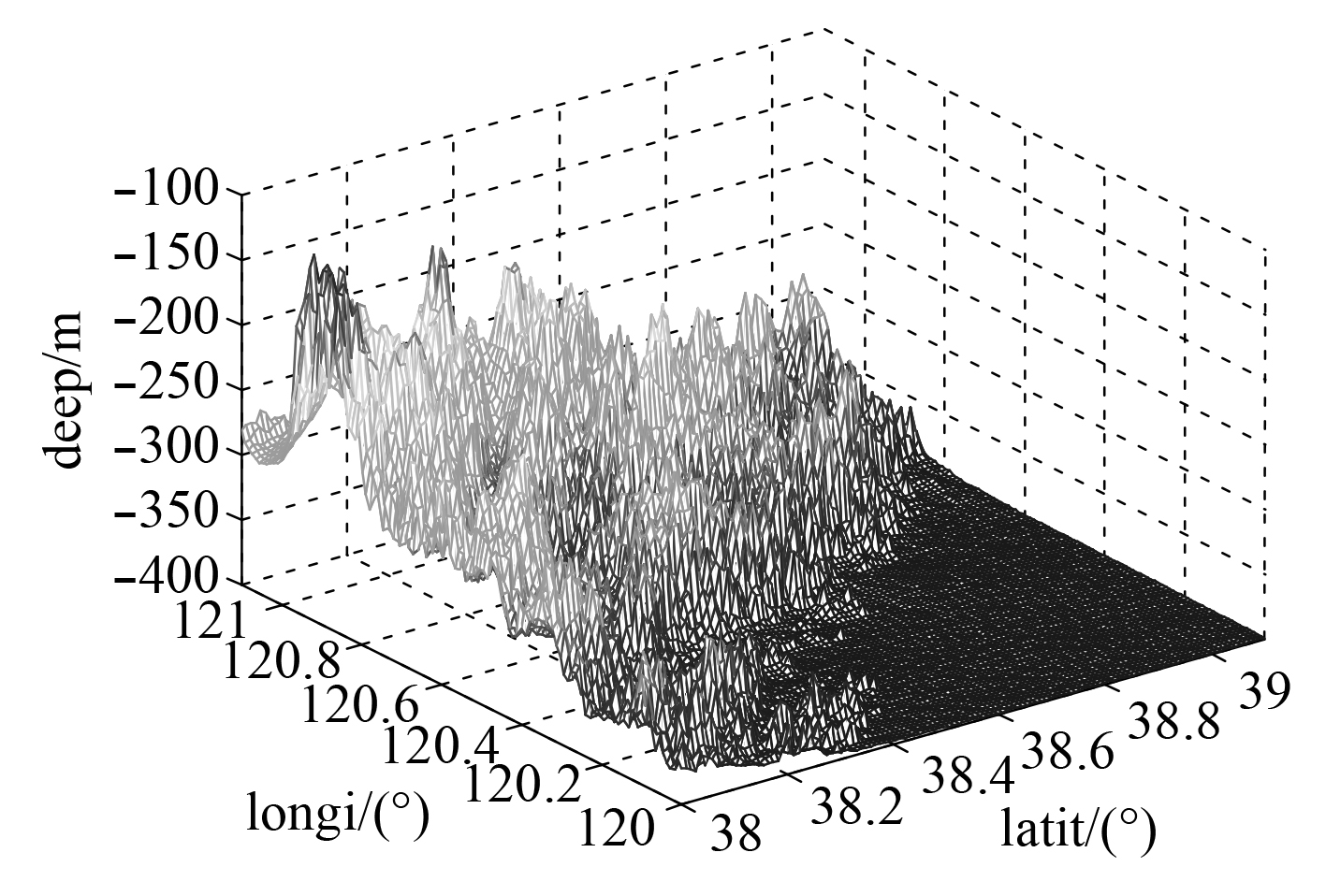
|
图 3 地图三维图像 Fig. 3 The 3-D Image of the map |
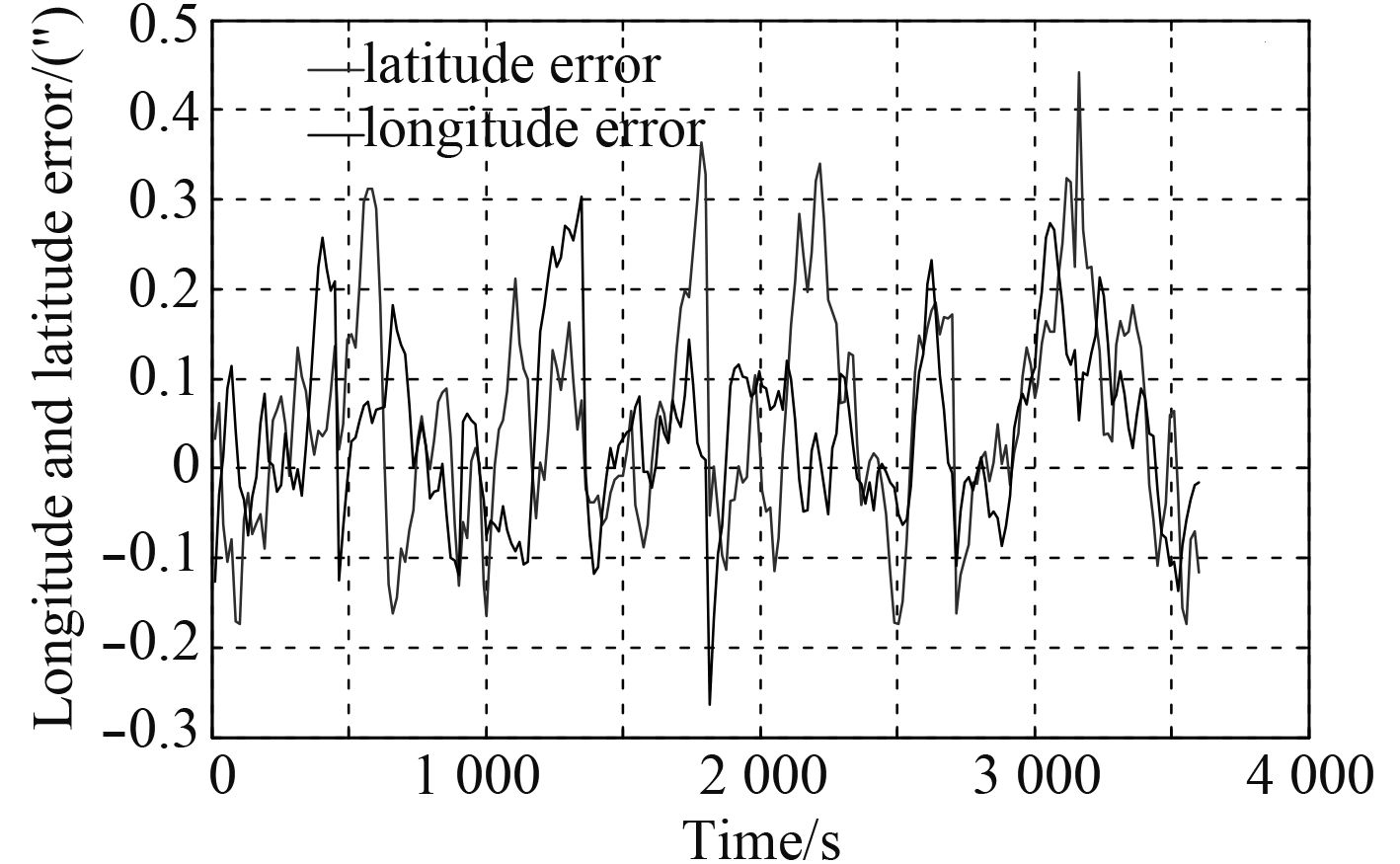
|
图 4 经纬度误差图 Fig. 4 The longitude and latitude error figure |
导航坐标系定义为东-北-天地理坐标系,SINS误差模型为:
| $\begin{aligned} {X_{SINS}} = & \ \; [\delta {V_E} \ \;\delta {V_N} \ \;\delta {V_U} \ \;{\varphi _E} \ \;{\varphi _N} \ \;{\varphi _U} \ \;\delta L \ \;\delta \lambda \ \;\\ & \delta h \ \;{\nabla _{bx}} \ \;{\nabla _{by}} \ \;\nabla _{bz}^{} \ \;{\varepsilon _{bx}} \ \;{\varepsilon _{by}} \ \;{\varepsilon _{bz}}]\text{。}\end{aligned}$ |
其中:
系统的状态方程为:
AUV的真实位置为
| $\left\{ {\begin{array}{*{20}{c}} {{L_I} = {L_r} + \delta L}\text{,} \\ {{\lambda _I} = {\lambda _r} + \delta \lambda }\text{,} \\ {{h_I} = {h_r} + \delta h} \text{,}\end{array}} \right.$ | (12) |
TAN测得的位置信息为
| $\left\{ {\begin{aligned}& {{L_T} = {L_r} - \displaystyle\frac{{{N_N}}}{{{R_m} + h}}} \text{,}\\ & {{\lambda _T} = {\lambda _r} - \displaystyle\frac{{{N_E}}}{{\left( {{R_n} + h} \right)\cos L}}} \text{,}\\ & {{h_T} = {h_r} - N_h} \text{。}\end{aligned}} \right.$ | (13) |
式中:
位置量测方程为:
| ${Z_P} \!\!=\!\! \left[\!\!\!\!\! {\begin{array}{*{20}{c}} {\left( {{L_I} \!-\! {L_T}} \right)\left( {{R_m} \!+\! h} \right)} \\ {\left( {{\lambda _I} \!-\! {\lambda _T}} \right)\left( {{R_n} \!+\! h} \right)\cos L} \\ {{h_I} \!-\! {h_T}} \end{array}}\!\!\!\!\! \right] \!\!=\!\! \left[\!\!\!\!\! {\begin{array}{*{20}{c}} {\left( {{R_m} \!+\! h} \right)\delta L \!+\! {N_N}} \\ {\left( {{R_n} \!+\! h} \right)\cos L\delta \lambda \!+\! {N_E}} \\ {\delta h \!+\! {N_h}} \end{array}}\!\!\!\!\! \right]\text{。}$ | (14) |
设AUV的真实速度为
| $\left\{ {\begin{array}{*{20}{c}} {{V_{IE}} = {V_{rE}} + \delta {V_E}} \text{,}\\ {{V_{IN}} = {V_{rN}} + \delta {V_N}} \text{,}\\ {{V_{IU}} = {V_{rU}} + \delta {V_U}} \text{。}\end{array}} \right.$ | (15) |
DVL测得的速度为:
| $\left\{ {\begin{array}{*{20}{c}} {{V_{DE}} = {V_{rE}} + \delta {V_{DE}}} \text{,}\\ {{V_{DN}} = {V_{rN}} + \delta {V_{DN}}} \text{,}\\ {{V_{DU}} = {V_{rU}} + \delta {V_{DU}}}\text{。} \end{array}} \right.$ | (16) |
| $\left\{ {\begin{aligned}\begin{array}{l}\delta {V_{DE}} = {\varphi _U}{V_{rN}} - {\varphi _N}{V_{rU}} + C_b^n(1,1)\delta {V_{Dx}} + C_b^n(1,2)\delta {V_{Dy}} + \\ C_b^n(1,3)\delta {V_{Dz}} + C_b^n(1,1){V_{rE}}\delta {K_{Dx}} + \\ C_b^n(1,2){V_{rN}}\delta {K_{Dy}} + C_b^n(1,3){V_{rU}}\delta {K_{Dz}} + {\eta _E}\text{,}\end{array}\\\begin{array}{l}\delta {V_{DE}} = {\varphi _E}{V_{rU}} - {\varphi _U}{V_{rE}} + C_b^n(2,1)\delta {V_{Dx}} + C_b^n(2,2)\delta {V_{Dy}} +\\ C_b^n(2,3)\delta {V_{Dz}} + C_b^n(2,1){V_{rE}}\delta {K_{Dx}}+ \\ C_b^n(2,2){V_{rN}}\delta {K_{Dy}} + C_b^n(2,3){V_{rU}}\delta {K_{Dz}} + {\eta _N}\text{,}\end{array}\\\begin{array}{l}\delta {V_{DE}} = {\varphi _N}{V_{rE}} - {\varphi _E}{V_{rN}} + C_b^n(3,1)\delta {V_{Dx}} + C_b^n(3,2)\delta {V_{Dy}}+ \\ C_b^n(3,3)\delta {V_{Dz}} + C_b^n(3,1){V_{rE}}\delta {K_{Dx}}+ \\ C_b^n(3,2){V_{rN}}\delta {K_{Dy}} + C_b^n(3,3){V_{rU}}\delta {K_{Dz}} + {\eta _U}\text{。}\end{array}\end{aligned}} \right.$ | (17) |
其中,ηE,ηN,ηU分别为DVL沿北-东方向的测量白噪声。
速度量测方程为:
| ${Z_V} = \left[ {\begin{array}{*{20}{c}} {{V_{IE}} - {V_{DE}}} \\ {{V_{IN}} - {V_{DN}}} \\ {{V_{IU}} - {V_{DU}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\delta {V_E} - \delta {V_{DE}}} \\ {\delta {V_N} - \delta {V_{DN}}} \\ {\delta {V_U} - \delta {V_{DU}}} \end{array}} \right]\text{。}$ | (18) |
假设AUV的真实航向为
| ${\phi _I} = {\phi _r} + \delta {\phi _I}, \; {\phi _C} = {\phi _r} - \delta {\phi _C}\text{,}$ | (19) |
| $\begin{split}\delta {\phi _I} = & - \frac{{C_n^b(2,1) \cdot C_n^b(2,3)}}{{{{\left[ {C_n^b(2,1)} \right]}^2} + {{\left[ {C_n^b(2,2)} \right]}^2}}}{\varphi _E} - \\ &\frac{{C_n^b(2,2) \cdot C_n^b(2,3)}}{{{{\left[ {C_n^b(2,1)} \right]}^2} + {{\left[ {C_n^b(2,2)} \right]}^2}}}{\varphi _{_N}} + {\varphi _U}\text{。}\end{split}$ | (20) |
航向的量测方程为:
| ${Z_\phi } = {\phi _I} - {\phi _C} = \delta {\phi _I} + \delta {\phi _C} + {\eta _{MU}} = {H_{MCP}}X + {\eta _{MU}}\text{。}$ | (21) |
系统的量测方程为:
对系统的数学模型离散化,其形式如下:
| $\left\{ {\begin{aligned}& {{X_k} = {\varPhi _{k,k - 1}}{X_{k - 1}} + {\Gamma _{k - 1}}{W_{k - 1}}}\text{,} \\ & {{Z_k} = {H_k}{X_k} + {V_k}}\text{。} \end{aligned}} \right.$ | (22) |
当
每一子滤波器方程的算法如下:
| $\begin{aligned}{\hat X_{k,k - 1}} =& {\varPhi _{k,k - 1}}{\hat X_{k - 1}}, \; {P_{k,k - 1}}\\ = & {\varPhi _{k,k - 1}}{P_{k - 1}}\varPhi _{k,k - 1}^{\rm T} + {\Gamma _{k - 1}}{Q_{k - 1}}\Gamma _{k - 1}^{\rm T}\text{,}\end{aligned}$ | (23) |
| $\begin{aligned}{K_{k - 1}} = & {P_{k,k - 1}}H_k^{\rm T}{\left( {{H_k}{P_{k,k - 1}}H_k^{\rm T} + {R_k}} \right)^{\rm T}}, \\\; {\hat X_k} = & {\hat X_{k,k - 1}} + {K_k}\left( {{Z_k} - {H_k}{{\hat X}_{k,k - 1}}} \right), \\\; {P_k} =& \left( {I - {K_k}{H_k}} \right){P_{k,k - 1}}\text{。}\end{aligned}$ | (24) |
针对由噪声模式带来的不确定性,联合滤波器具有极强的可逆性。联合滤波器信息分布算法如下:
| ${P_i} = \beta _i^{ - 1}{P_g}, \; {{ Q}_i} = \beta _i^{ - 1}{{ Q}_g}{\text{。}}$ | (25) |
当
| ${\beta _1} + {\beta _2} + \cdots + {\beta _n} + {\beta _m} = 1{\text{。}}$ | (26) |
其中,n=3。
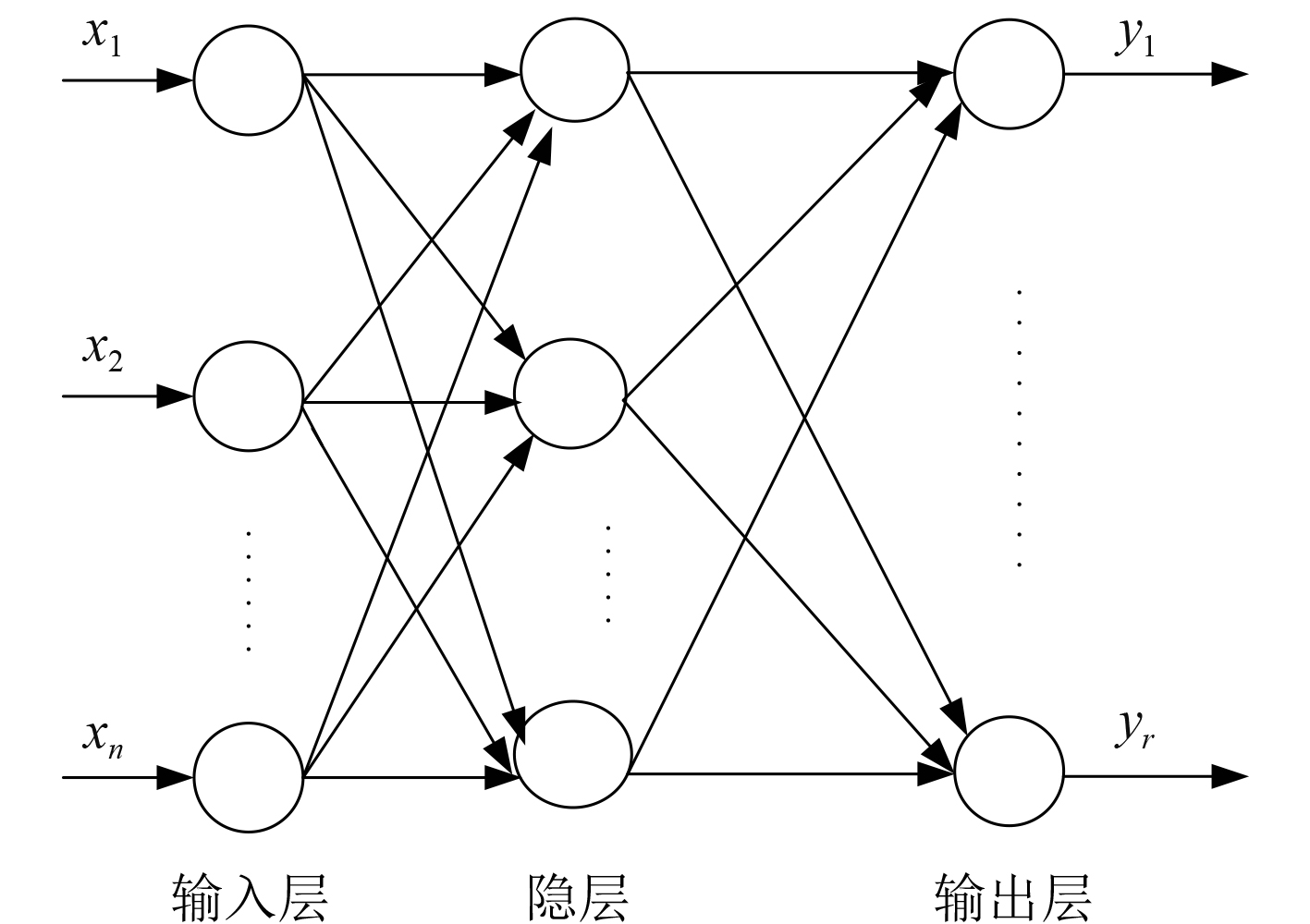
3 BP神经网络模型 3.1 BP神经网络架构BP神经网络是一个多层网络,是一种按误差反向传播训练的多层前馈网络,如图5所示。它有3层或更多层,含输入层、隐层和输出层。BP算法是一种监督式的学习算法,通过输入学习样本,使用反向传播算法对网络的权值和偏差进行反复的调整训练,使输出的向量与期望向量尽可能地接近,当网络输出层的误差平方和小于指定的误差时训练完成,保存网络的权值和偏差[6]。
|
图 5 BP神经网络模型 Fig. 5 BP neural networks model |
在BP神经网络中,假设输入向量为
| $E = \frac{1}{2}\sum\limits_i {{{(y_{pi}^d - {y_{pi}})}^2} = \sum\limits_p {{E_p}} } {\text{。}}$ |
误差的反向传播采用梯度下降法调整各层间的连接权值,使目标函数达到最小。
通过计算梯度下降后的
| $\Delta {w_{ji}} \propto - \frac{{\partial {E_p}}}{{\partial {w_{ji}}}}, \; \Delta {w_{ji}} = \eta {\delta _{pj}}{y_{pj}} \text{,} \eta > 0\text{。}$ |
这里
在BP算法中,权值校正所需的误差按正常网络传播方向反向进行,从输出层向输入层的神经元传播[10]。采用迭代算法直到目标函数小于设定值
采用联合卡尔曼滤波对组合导航系统进行状态估计的方法对系统的模型要求严格,若由于复杂环境所引起的对干扰统计特性无法准确获得时,得到的状态估计值就很难满足定位精度的要求,因此本文采用基于BP神经网络的自适应滤波算法,实现组合导航系统的状态估计。
针对AUV水下组合导航系统,提出了基于BP神经网络的自适应滤波方案。基于BP神经网络的自适应滤波方案见图6。在反馈回路,将BP网络输出的修正加入到滤波算法不准确的状态向量估计中,提高了系统的导航性能。

|
图 6 基于BP神经网络的自适应滤波方案 Fig. 6 Principle diagram of BP neural network aided kalman filter |
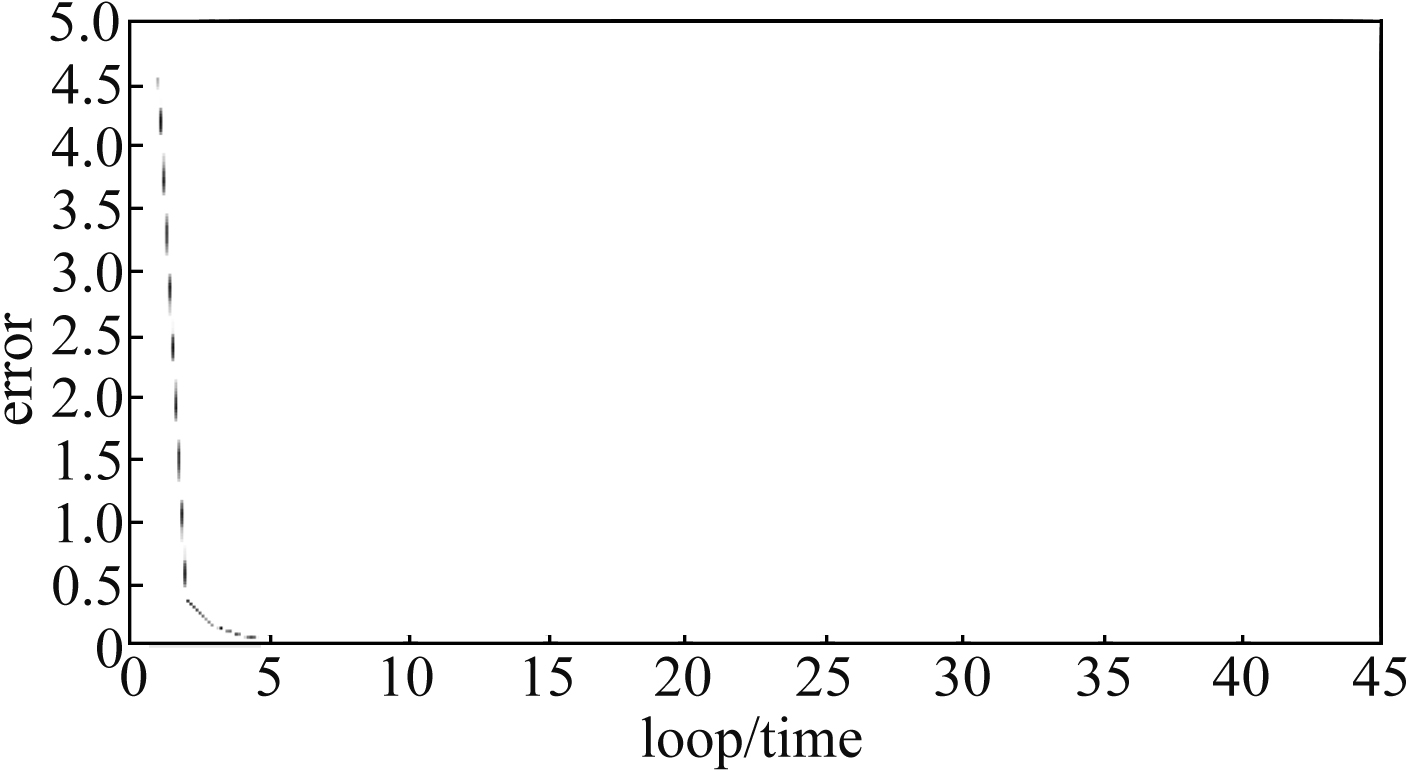
本文为AUV组合导航系统设计了基于BP神经网络的自适应滤波算法。采用离线训练的BP网络对实际动态环境下系统模型的不准确性进行校正,使其具有足够的精度。该方案以减小导航误差为目标,选取对误差有直接影响的参数作为BP网络的输入,选择观测向量与一步预测测量向量之差
|
图 7 BP神经网络训练结果 Fig. 7 Training result of BP neural network |
假设AUV在一个平面上,以一定的深度航行,系统仿真时间为5 h。根据AUV的使用环境,系统仿真条件如下:AUV速度为4 kn,初始姿态角均为0,初始航向角为45°,初始位置为165°E,32°N。组合导航系统的传感器误差模型如表2所示。
|
|
表 2 组合导航系统的传感器误差模型 Tab.2 Sensor model in the integrated navigation system |
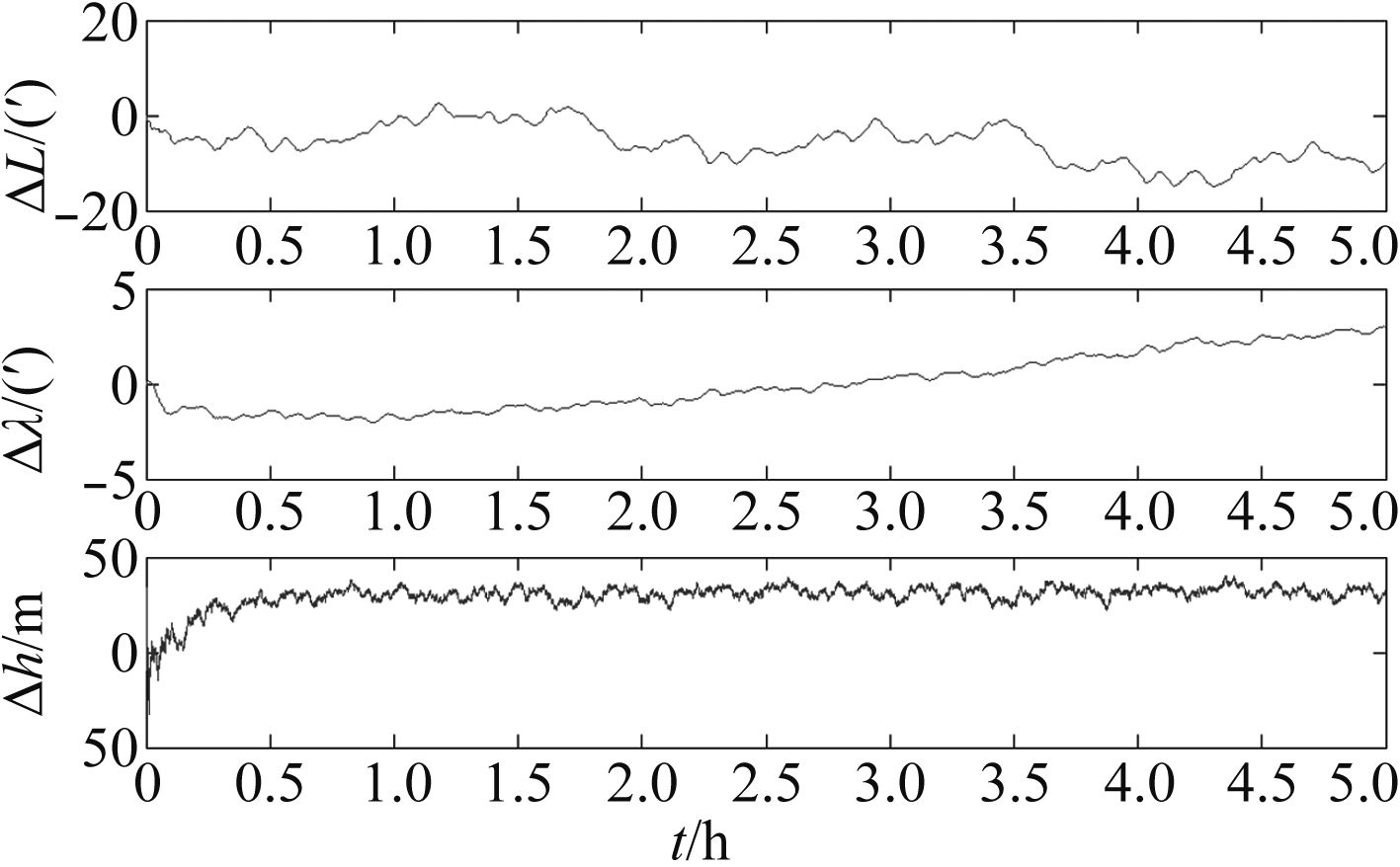
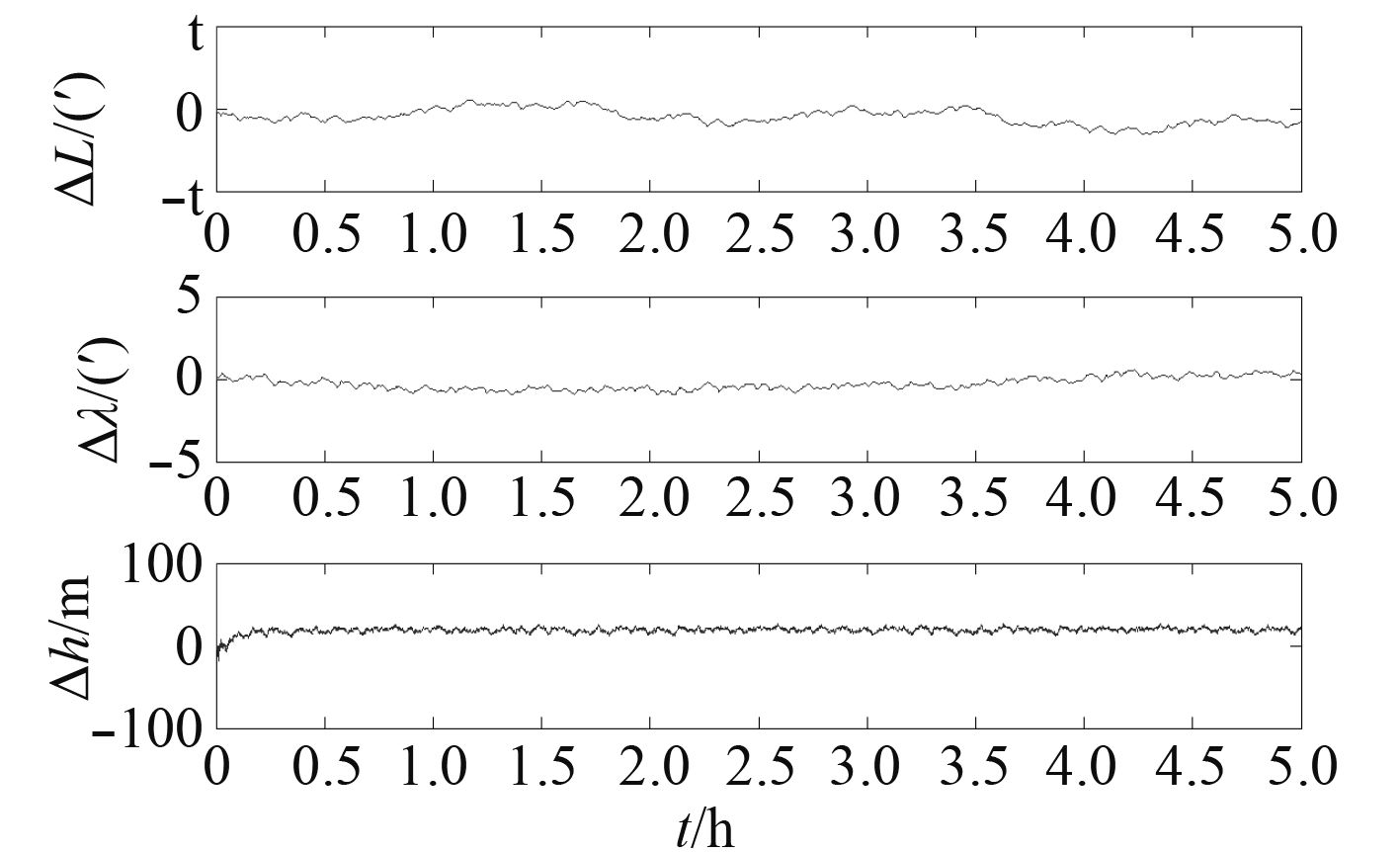
为了比较本文提出的方法效果,在相同的初始条件下,对经典卡尔曼滤波器和基于BP自适应滤波器进行仿真实验,仿真结果见图8和图9。仿真实验结果表明:基于BP神经网络的自适应滤波算法通过 BP神经网络对卡尔曼滤波输出修正,提高了卡尔曼滤波器的估计精度,使组合导航系统定位精度均有所提高。
|
图 8 经典联合滤波器的位置误差 Fig. 8 Position error of classical federated filter |
|
图 9 BPNN联合滤波器的位置误差 Fig. 9 Position error of federated filter with BPNN |
本文提出了一种新的地形组合导航系统,能够满足AUV长期保持高稳定和高精度导航的需求。基于神经网络辅助的联合卡尔曼滤波器比经典联合卡尔曼滤波器具有更好的导航性能。该方法利用离线训练的BP神经网络对经典联邦卡尔曼滤波估计中的误差进行校正。AUV定位误差大大减小,水下导航精度大大提高。
| [1] |
张涛, 石宏飞, 陈立平, 等. 基于UKF的SINS/LBL水下AUV紧组合定位技术[J]. 中国惯性技术学报, 2016, 24(10): 639–642.
ZHANG Tao, SHI Hong-fei, CHEN Li-pin, et al. An underwater positioning technology based on tightly coupled SINS/LBL for AUV[J]. Journal of Chinese Inertial Technology, 2016, 24(10): 639–642. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zggxjsxb201504015 |
| [2] | TITTERTON D H, WESTON J L. Strapdown inertial navigation technology[Z]. London, U. K.: Peter Pegerinus, 1997: 19–56, 259–320, and 385–392. |
| [3] |
周保军, 刘硕. 水下导航技术研究[J]. 现代导航, 2012, 2(1): 19–23.
ZHOU Bao-jun, LIU Shuo. Research of underwater navigation technology[J]. Modern Navigation, 2012, 2(1): 19–23. http://www.docin.com/p-743148286.html |
| [4] | ALCOCER A, OLIVEIRA P, PASCOAL A. Study and implementation of an EKF GIB-based underwater positioning system, in Proc[Z]. IFAC Conf. Control Appl. Mar. Syst. (CAMS), Ancona, Italy. 2004. |
| [5] | HOLTZHAUSEN S, MATSEBE O, TLALE N S, et al. Autonomous underwater vehicle motion tracking using a Kalman filter for sensor fusion[J]. 15th International conference on Mechatronics and Machine Vision in Practice, 2008: 103–108. |
| [6] |
葛锡云, 申高展, 潘琼文, 等. 基于惯性导航/地磁的水下潜器组合导航定位方法[J]. 舰船科学技术, 2014, 36(11): 120–123.
GE Xi-yun, SHEN Gao-zhan, PAN Qiong-wen , et al. The underwater integrated navigation method of underwater vehicle based on INS / geomagnetic[J]. Ship Science and Technology, 2014, 36(11): 120–123. |
| [7] |
徐遵义, 晏磊, 刘光军, 等. 海底地形辅助导航全面仿真技术研究[J]. 舰船科学技术, 2007, 29(1): 123–128.
XUN Zun-yi, YAN Lei, LIU Guang-jun, et al. Study on comprehensive simulation technology for seabed terrain-aided navigation[J]. Ship Science and Technology, 2007, 29(1): 123–128. http://d.wanfangdata.com.cn/Periodical_jckxjs200701034.aspx |
| [8] |
郭俊. 神经网络与非线性滤波在景象匹配辅助导航中的应用研究[D]. 南京: 南京航空航天大学, 2009: 15–21, 33–37.
GUO Jun. Application of BP neural network and nonlinear filtering in scene matching aided navigation. [D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2009: 15–21, 33–37. |
| [9] |
徐晓苏, 周峰, 张涛, 等. 遗传算法优化的神经网络在SINS/GPS中的应用[J]. 中国惯性技术学报, 2015, 23(3): 322–327.
XU Xiao-su, ZHOU Feng, ZHANG Tao, et al. Application of neural network by genetic algorithm optimization in SINS/GPS [J]. Journal of Chinese Inertial Technology, 2016, 24(10): 639–642. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zggxjsxb201503008 |
| [10] | HECHT-NIELEN R. Theory of the back propagation neural network[J]. International Joint Conference on Neural Networks, 2015: 322–327. |
 2018, Vol. 40
2018, Vol. 40
