采用单矢量水听器角度谱可以获得接收点处声能流的方向性。早在20世纪50年代,美国已在空投声呐浮标中使用二维矢量水听器对水下目标进行测向。文献[1]采用Wilcoxon出产的单矢量水听器进行湖试,对26 m远发出的146.7 dB单频信号进行方位估计,观测到多径效应对来波方位的影响。文献[2]采用平均声强器和复声强器方法对海上远场舰船噪声和宽带声源进行方位估计。文献[3]对湖试采用时域波束形成(time domain beamforming,TDBF)和频域波束形成(frequency domain beamforming,FDBF)进行方位估计。文献[4]采用2个矢量水听器进行近场源定位。文献[5]研究了弹性球壳声散射对矢量传感器测向精度的影响。然而,上述方法均是在某一个窄带上分析或是整个宽带上对方位角进行统计的结果,缺乏展现宽带信号角度特征的手段。文献[6]采用矢量水听器的角度谱分析海洋环境噪声声能流的水平方向性和垂直方向性,通过研究1978–1994年的外场实验,在200 Hz以下频带观察到远处舰船产生的能流,在200 Hz以上频带观察到从海面向海底传播的能流,其方向来自接近海面风速方向。
在一次海上试验中发现,对于吊放在锚泊舰船尾部水深10 m处的矢量水听器水平阵,单个阵元测得的噪声水平方向性在不同频率上指向锚泊舰船的不同位置,不同阵元在同一频率处所测得的噪声水平方向性不同。基于简正波理论,对锚泊舰船噪声进行建模,找出这一现象产生的原因,得出和试验结果规律一致的噪声水平方向性。
文献[6]研究海洋环境噪声的方向性时仅定义方向随频率的变化为角度谱。由于锚泊舰船船首方向会随海流变化而变化,因此对于运动的宽带信号来说,定义角度谱随时间的变化是必要的。通过矢量水听器角度谱分析噪声的水平方向性,分析了海上试验收到的噪声信号是否来自近场舰船,展现了近场锚泊舰船的宽带信号特征,探索了声压阵波束形成方法受近场锚泊舰船干扰的原因,对海上试验数据分析及装备研发有重大意义。
1 多个点声源相互作用时声能流的水平方向性水平方位角
| $\varphi (f,t) = \arctan \frac{{{W_{Ry}}(f,t)}}{{{W_{Rx}}(f,t)}}, $ | (1) |
其中,声功率流本征矢量
| ${W_{Rx}}(f,t) = \frac{1}{2}\operatorname{Re} \left( {p(f,t)v_x^*(f,t)} \right){\text{。}}$ | (2) |
声功率流本征矢量
根据声波叠加原理和小振幅声波运动方程[8],N列波叠加时质点合成振速矢量v为
| $v = - \frac{1}{\rho }\int {gradp} {\rm d}t = \sum\limits_{j = 1}^N {{{{v}}_j}} = \sum\limits_{j = 1}^N {\left( {{v_{jx}}{{i}}{\rm{ + }}{v_{jy}}{{j}} + {v_{jz}}{{k}}} \right)}{\text{。}} $ | (3) |
根据简正波理论[9]及式(1)~式(3),N个点声源在接收深度z=z1、时刻t、频率f处的叠加的水平方位角谱为
| $\varphi (f,t) = \arctan \frac{{\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{k_{rm}}{k_{rn}}} } {{\left. {{{{B}}_m}{{B}}_n^*} \right|}_{z = {z_1}}}\sum\limits_{s = 1,s \ne j}^N {\sum\limits_{j = 1}^N {\frac{{\cos ({k_{rm}}{r_s}(t) - {k_{rn}}{r_j}(t))\sin {\varphi _{0j}}(t)}}{{\sqrt {{r_s}(t){r_j}(t)} }}} } }}{{\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{k_{rm}}{k_{rn}}} } {{\left. {{{{B}}_m}{{B}}_n^*} \right|}_{z = {z_1}}}\sum\limits_{s = 1,s \ne j}^N {\sum\limits_{j = 1}^N {\frac{{\cos ({k_{rm}}{r_s}(t) - {k_{rn}}{r_j}(t))\cos {\varphi _{0j}}(t)}}{{\sqrt {{r_s}(t){r_j}(t)} }}} } }}, $ | (4) |
其中,
当N=1时,即只有一个点声源时,
2014年9月在黄海海域某区域进行海上试验,海深50~55 m,海况1级,舰船锚泊,发动机停机。在接收船尾吊放矢量水听器刚性阵如图1所示。图1(a)中,同振式矢量水平阵用3根缆绳吊放,2号和5号矢量水听器相距2.25 m。图1(b)中,矢量水听器阵入水深度10 m,海浪拍打船体产生浪花。

|
图 1 海试布放矢量水听器阵 Fig. 1 The vector hydrophone array is dipped into the sea |
矢量水听器阵和锚泊舰船相对位置如图2(a)所示,矢量水听器阵位于舰船尾部一侧。以2号矢量水听器中心为原点,矢量水听器振速通道x轴、y轴在水平面上,z轴指向天空。矢量水听器阵列放置在y轴上,对2号和5号水听器进行分析,如实心圆所示。根据姿态测量装置实测结果,采用地理坐标系,锚泊舰船船首方向与时间的关系如图2(b)所示,锚泊舰船8 min内船首方向主要在344º±5º。

|
图 2 锚泊舰船的船艏的方向 Fig. 2 The direction of the mooring ship |
采用N个点声源的声能流相互作用对近场舰船噪声建模,分别对多个点声源位置不变和点声源位置扰动建立模型。假设:声源深度3 m。海水深度50 m,密度1 020 kg/m3。沉积层厚度10 m,密度1 790 kg/m3,声速1 600 m/s,衰减系数0.9 dB/λ。岩石层厚度10 m,密度2 200 kg/m3,声速1 800 m/s。
2.2.1 多个点声源位置不变近场舰船噪声由多个点声源声能流相互作用而成,点声源如图3空心圆所示,假设船长100 m,宽8 m。
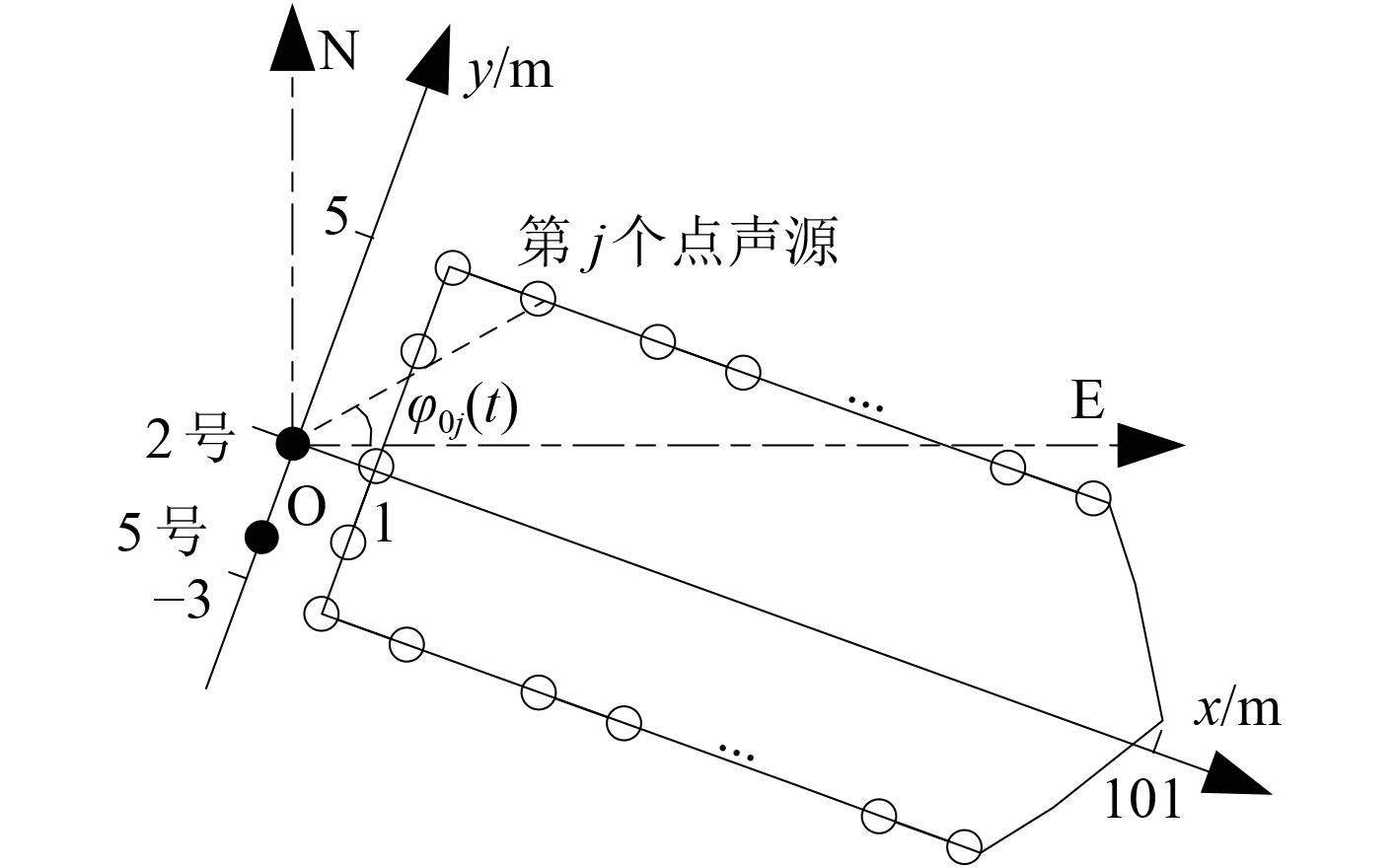
|
图 3 近场舰船噪声的声源模型示意图 Fig. 3 The diagram of noise model of near-field ship |
根据表达式(12)~式(13)对105个点声源进行叠加,得到接收点处近场舰船噪声的合成声压和合成振速,代入式(4)得接收点处近场舰船噪声的水平方位角谱,如图4所示。

|
图 4 多个点声源位置不变时的水平方位角谱仿真 Fig. 4 The horizontal azimuth spectrum in the simulation of multiple sound sources with permanent position |
图4(a)和图4(b)均是由深浅相间条纹组成,表示声能流的方向主要来自300º~360º(呈现浅色)和0~60º(呈现深色),由图2(a)可知,该方向指向近场锚泊舰船。水平方位角基本不随时间变化,是因为图2(b)所示锚泊舰船8 min内船首方向变化不大。
图4(a)中2号水听器水平方位角主要呈现浅色,表示近场舰船噪声来自340º方向,而图4(b)5号水听器水平方位角以深色为主,表示近场舰船噪声来自0º~30º方向。说明了不同接收点处的近场舰船噪声声能流方向性并不相同。
2.2.2 多个点声源位置随机扰动海浪拍打船体的位置不可能始终在同一点,假设点声源沿船体水平方向随机扰动,即在2 m间隔处叠加一个均值为0 m,方差为0.3 m的正态分布随机数,精度取0.1 m,作为点声源位置,则此时水平方位角谱如图5所示。
|
图 5 近场舰船的点声源位置随机扰动时的水平方位角谱仿真 Fig. 5 The horizontal azimuth spectrum in the simulation of multiple sound sources with random disturbance position |
与2.2.1节多个点声源位置不变的水平方位角谱仿真结果相比,图5在保持图4水平方位角分布特性的基础上,多个点声源位置随机扰动使得水平方位角谱分布随机变化。
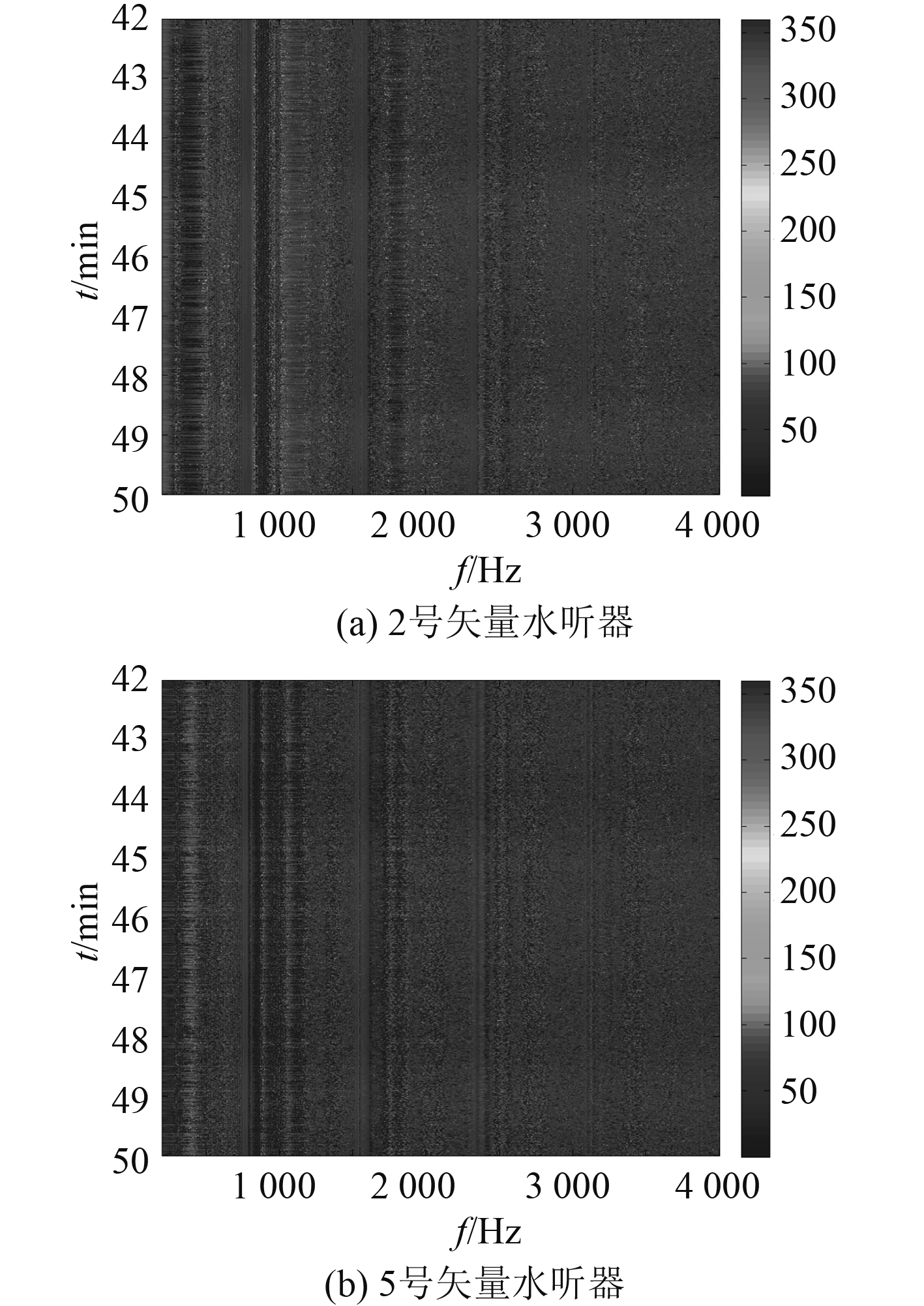
2.3 海上实验根据式(1),2号和5号矢量水听器持续8 min接收的声强流水平方向性如图6所示,为水平方位角的时间-频率分布,色带代表水平方位角,单位为(°)。
|
图 6 海上试验的水平方位角谱 Fig. 6 The horizontal azimuth spectrum in the sea trial |
图6(a)和图6(b)均由深浅相间条纹构成,且水平方位角随频率变化,与仿真结果图5的规律基本一致,说明了仿真模型的合理性。由于所建立的模型是理想条件下单个水平面中的点声源产生的声能流相互作用,与实际海洋中的海浪拍打舷侧钢板的噪声产生机制并不相同,且海上实验中的舷侧钢板是大型的不规则障板,仿真模型结果无法与海上实验结果完全一致。但是这并不影响采用2.2.2节的多个点声源位置随机扰动模型合理解释图6的海上实验结果。假若采用单个点声源对近场舰船进行建模,虽然能够说明2号和5号水听器的声能流水平方向性不同,但是根据式(4),N=1时,
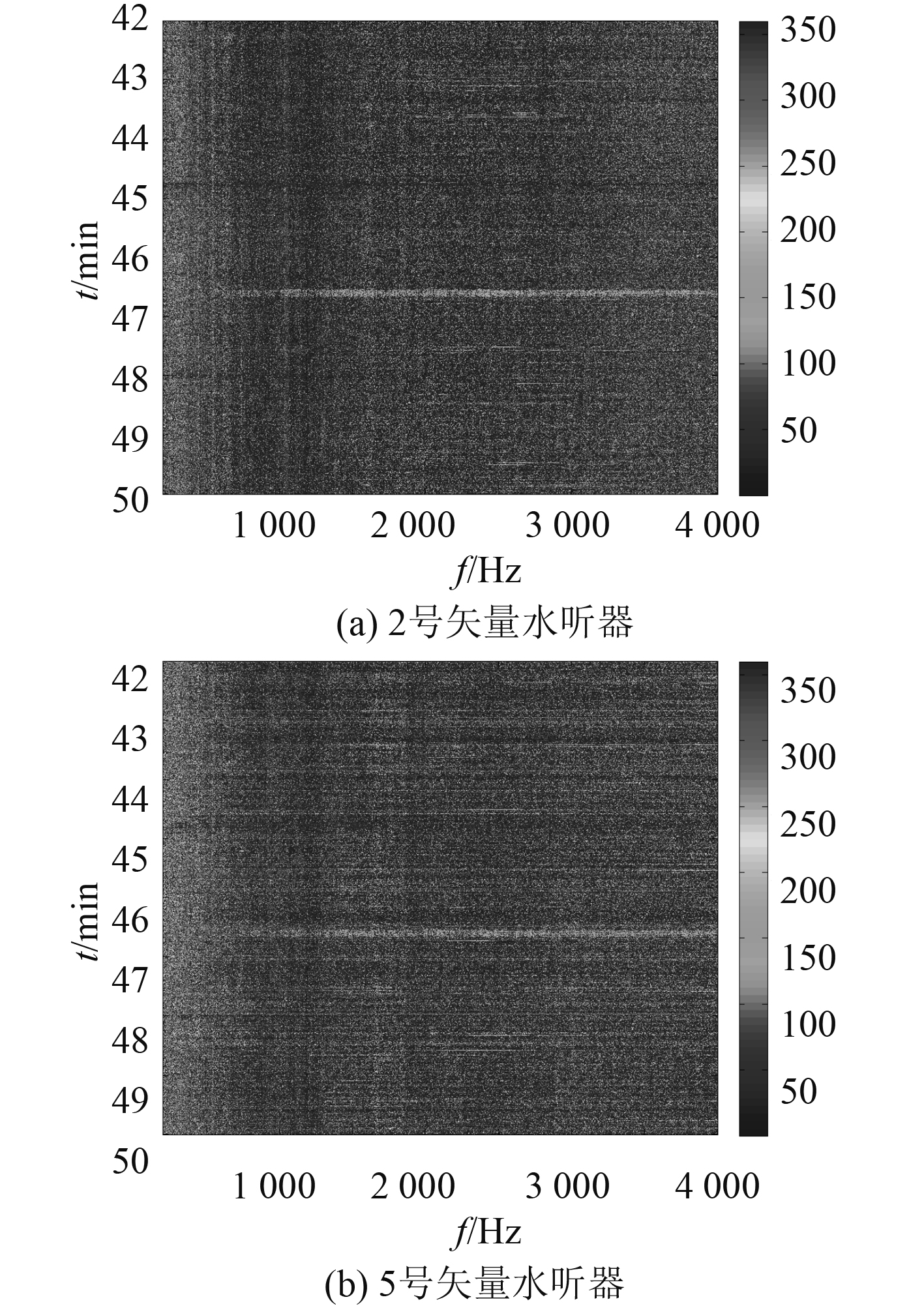
对图4~图6中8 min数据进行统计得到每个频点上的概率密度频数,2号和5号水听器FRAZ FRAZ(Frequency-Azimuth)[11]图分别如图7~图9所示。
|
图 7 多个点声源位置不变时的多个点声源FRAZ图仿真 Fig. 7 FRAZ display in the simulation of multiple sound sources with permanent position |
|
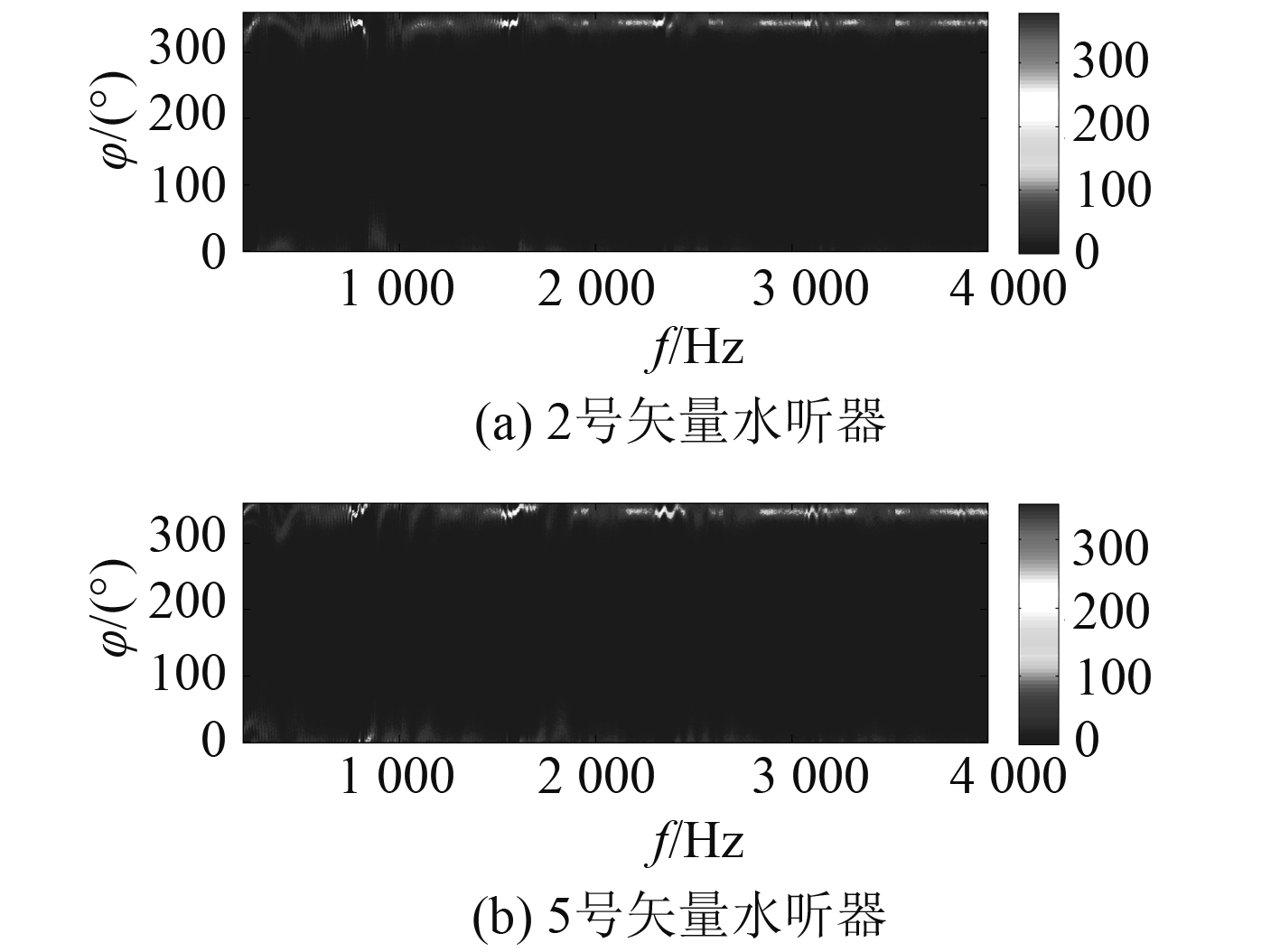
图 8 近场舰船的点声源位置随机扰动时的FRAZ图仿真 Fig. 8 FRAZ display in the simulation of multiple sound sources with random disturbance position |

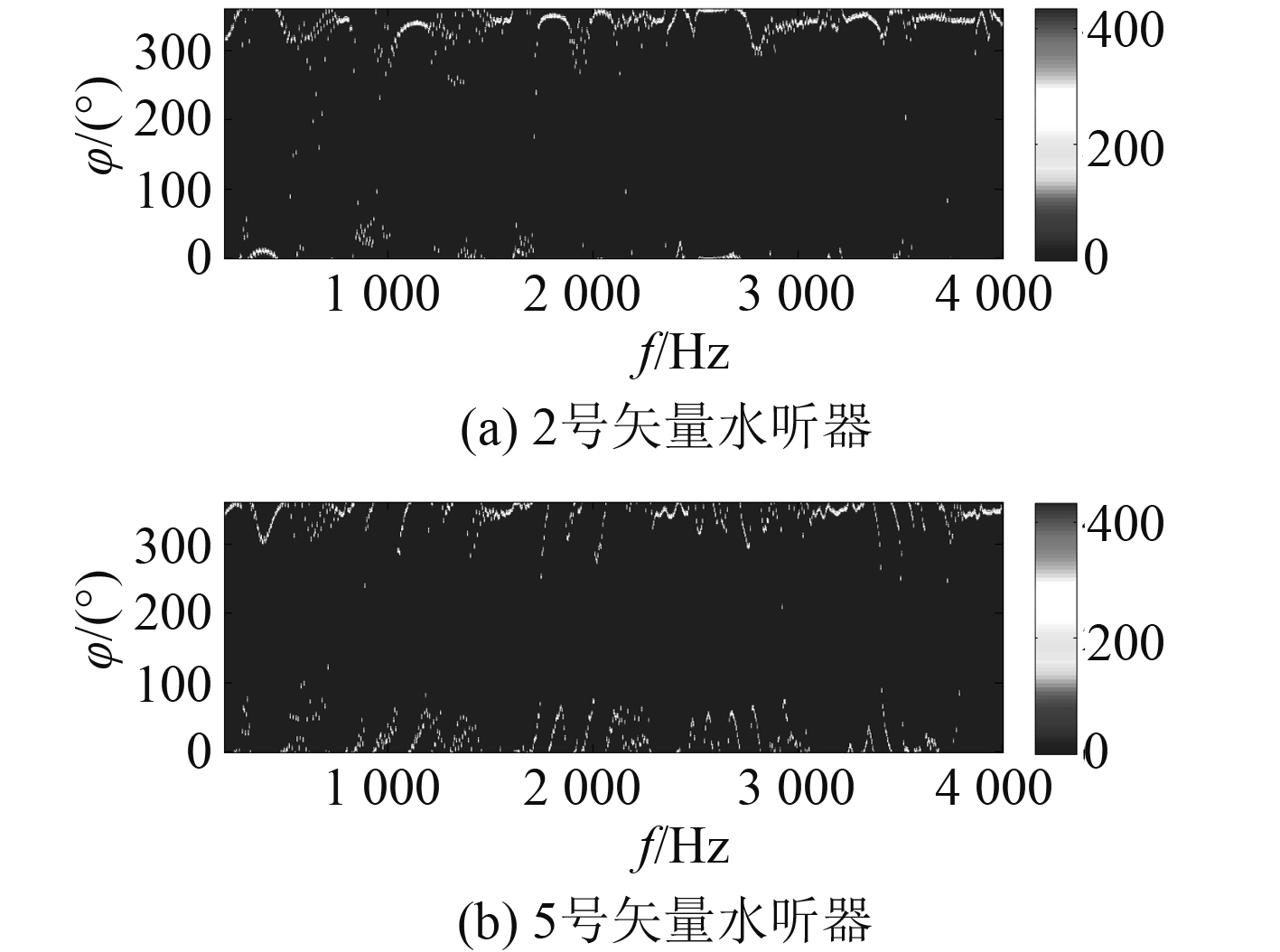
|
图 9 海上试验的FRAZ图 Fig. 9 FRAZ display in sea trial |
图7~图9中,2号和5号水听器的水平方位角随频率变化情况并不相同,这一点在图9中海上实验结果尤为明显。图8和图9在500 Hz以下的统计结果相似,从另一个角度说明2.2.2的多个点声源位置随机扰动的仿真模型更贴近海上实验结果。
4 结 语基于简正波的矢量场理论,采用多个点声源声能流的相互作用对近场舰船噪声进行建模,探明近场锚泊舰船的噪声形成机制,主要得到以下结论:1)基于矢量水听器的水平方位角谱,近场平台为锚泊舰船时水听器接收到的声能流主要来自于锚泊舰船。2)在浅海中,基于简正波矢量场,采用多个点声源声能流相互作用建立的噪声模型合理解释了海上试验锚泊舰船的噪声水平方向性。多个点声源位置随机扰动的模型比位置不变的模型更加贴近海上实际情况。3)锚泊舰船近场区域内,相距2.25 m的不同接收点处声场方向特性完全不同,这种差异极大影响了近场区域使用水平声压阵波束形成方法进行方位估计的性能。
| [1] | SILVIA M T, RICHARDS R T. A theoretical and experimental investigation of low-frequency acoustic vecter sensors[C]// In Proc. of the OCEANS’02 Conf. Mts/ IEEE, 2002(3): 1886–1897. |
| [2] | FELISBERTO P, SANTOS P, JESUS S M. Tracking source azimuth using a single vector sensor[C]// 2010 Fourth International Conference on Sensor Technologies and Applications, 2010: 416–421. |
| [3] | BEREKETLI A, GULDOGAN M B, TANER K, et al. Experimental results for direction of arrival estimation with a single acoustic vector sensor in shallow water[J]. Journal of sensors, 2015: 1–10. |
| [4] | WU Y I, WONG K T. Acoustic near-field source-localization by two passive anchor-nodes[J]. IEEE Trans. on aerospace and electronic systems, 2012, 48(1): 159–169. |
| [5] | 梁国龙, 庞福滨, 庞秀珍, 等. 弹性球壳声散射对矢量传感器测向精度的影响[J]. 振动与冲击, 2014, 33(3): 46–50. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGZC200508002051.htm |
| [6] | 休罗夫(著), 贾志富(译). 海洋矢量声学[M]. 北京: 国防工业出版社, 2011. |
| [7] | GORDIENKO V A (著), 贾志富(译). 声矢量——相位技术[M]. 北京: 国防工业出版社, 2014. |
| [8] | 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 南京: 南京大学出版社, 2001. |
| [9] | REN Q Y, HERMAND J P. Acoustic interferometry for geoacoustic characterization in a soft-layered sediment environment[J]. Journal of the Acoustical Society of America, 2013, 133(1): 82–93 |
| [10] | 林旺生, 梁国龙, 付进, 等. 浅海矢量声场干涉结构形成机理及试验研究[J]. 物理学报, 2013, 62(14): 144301. |
| [11] | SILVIA M T, RICHARDS R T. A theoretical and experimental investigation of low-frequency acoustic vecter sensors[C]// in Proc. of the OCEANS’02 Conf. Mts/IEEE, 2002(3): 1886–1897. |
 2018, Vol. 40
2018, Vol. 40
