0 引　言

舰船低频线谱噪声在水中可远距离传播，是敌声呐探测、跟踪、识别的重要信息源。随着舰船噪声测量、海底声学参数反演等工程实践的发展，对浅海近距离声场传播的研究也愈发重要。当前的声传播计算方法主要包括简正波法、波数积分法、抛物方程法、有限元法。其中，简正波方法^[1]是研究比较多而且应用比较广的一种方法。其基本原理是把积分拓展到复平面，应用柯西原理通过计算围道内的留数来计算原积分，一般在处理时忽略分支线积分，所以简正波理论在较近距离上存在较大误差。抛物方程法^[2]存在近距离时有效计算角度受限问题，有限元方法^[3]存在较远距离时超大计算量问题，都不能很好的同时兼顾近程和远程的传播损失计算。波数积分法^[4]是对水平分层介质的积分变换的数值实现方法，声场解的形式是深度分离波动方程解的谱积分，其采用的是直接数值求积分的方法，因而其对较大距离范围内的声场计算更为准确。

在浅海中，声传播不仅受到海水声速剖面的制约，同时海底地形及底质特性也对其有重要影响。李整林^[5]利用实轴积分法和快速傅里叶变换法研究了浅海中沉积层有横波参数后对低频点源声传播波形的影响；马黎黎^[6]进一步考虑了浅海中沉积层为孔隙底质时对指向性脉冲源声传播波形的影响；朱业^[7]利用波束位移射线简正波模型研究了理想负跃层浅海中脉冲波形的传播；潘长明^[8]利用抛物方程法研究了浅海温跃层对水声传播损失的影响。本文将着重利用波数积分法研究浅海声速剖面和沉积层对低频声传播损失的影响。

1 波数积分理论

浅海分层海洋环境下的声场可以通过如下方法进行描述。声源在均匀分层环境中沿垂直轴分布时，采用柱坐标系 $(r,\varphi ,z)$ ，并让z轴通过声源，则声场将与方位角 $\varphi $ 无关。对于各项同性介质，含有声源的第m层中具有时间关系 $\exp ( - iwt)$ 的声场可以用标量位移势 ${\psi _m}(r,z)$ 表示，位移势满足以下Helmoltz方程

${\rm{[}}{\nabla ^{\rm{2}}} + k_m^2(z)]{\psi _m}(r,z) = {f_s}(z,\omega )\frac{{\delta (r)}}{{2\pi r}}{\text{，}}$

(1)

式中， ${k_m}(z)$ 是第m层的介质波数。

类似的，对于不含声源的层，声场必须满足齐次Helmoltz方程，即式（1）中 ${f_s}(z,\omega ) = 0$ 。将式（1）利用正向Bessel变换

$f({k_r},z) = \int\nolimits_0^\infty {f(r,z){J_0}} ({k_r}r)r{\rm d}r{\text{，}}$

(2)

得到深度分离的波动方程

${\rm{\{ }}\frac{{{{\rm{d}}^2}}}{{{\rm d}{z^2}}} - {\rm{[}}k_r^2 - k_m^2\left( z \right){\rm{]\} }}{\psi _{\rm{m}}}({k_r},z) = \frac{{{f_s}(z)}}{{2\pi }}{\text{。}}$

(3)

该方程的解是方程（3）的特解 $\hat \psi _{\rm{m}}^{}({k_r},z)$ 与齐次方程的2个独立解 $\psi _{\rm{m}}^ + ({k_r},z)$ 与 $\psi _{\rm{m}}^{\rm{ - }}({k_r},z)$ 的任何线性组合之和。

因此，与深度有关的格林函数为

$\begin{split}{\psi _{\rm{m}}}({k_r},z) = {\hat \psi _m}({k_r},z) + A_m^ + ({k_r})&\psi _m^ + ({k_r},z)+ \\ A_m^ - ({k_r})\psi _m^ - ({k_r},z)\text{，}\end{split}$

(4)

式中： $A_m^ + ({k_r})$ 和 $A_m^{\rm{ - }}({k_r})$ 是任意系数，由分层界面上的边界条件确定。方程（3）的特解可以非常方便的选择为声源在无边界空间产生的声场。

为确定距离为r深度为z的某一特定接收器处的声压，必须对深度分离波动方程的声压解 $g({k_r},z)$ 的逆Bessel变换进行数值计算。

$g(r,z) = \int\nolimits_0^\infty {g({k_r},z){J_0}} ({k_r}r){k_r}{\rm d}{k_r}{\text{。}}$

(5)

由于式（5）的积分区间为半无穷区间，且水平波数在复数平面上存在极点，加之Bessel函数具有复杂的性质，所以很难对上式直接求积分。可先利用汉克尔函数表示Bessel函数

$g(r,z) = \frac{{\rm{1}}}{{\rm{2}}}\int\nolimits_0^\infty {g({k_r},z){\rm{[H}}_0^1({k_r}r) + H_0^2({k_r}r]} {k_r}{\rm d}{k_r}\text{，}$

(6)

式中， $H_0^2$ 项对应进入波，仅在很短距离上的驻波场时才重要，可以忽略。将 $H_0^{\rm{1}}$ 项换成它的渐进式，从而得到

$g(r,z) = \sqrt {\frac{{\rm{1}}}{{{\rm{2}}\pi {\rm{r}}}}} {e^{ - i\frac{\pi }{4}}}\int\nolimits_0^\infty {g({k_r},z)\sqrt {{k_r}} } {e^{i{k_r}r}}{\rm d}{k_r}{\text{。}}$

(7)

在声波的传播过程中，声压振幅随距离不断衰减，当 ${k_r} > {k_{\max }}$ 时，对整个声场的贡献可以忽略，所以将积分区间截断为（0， ${k_{\max }}$ ）。

接下来对波数区间和距离区间进行采样：

${k_l} = {k_{\min }} + l\Delta {k_r},\Delta {k_r} = \frac{{{k_{\max }} - {k_{\min }}}}{{M - 1}}{r_j} = {r_{\min }} + j\Delta r\text{，}$

(8)

其中l=0，1，2…M-1，j=0，1，2…M-1，且距离间隔和波数间隔满足 $\Delta {r}\Delta {k_r} = \frac{{2\pi }}{M}$ ，M为2的整数次幂。由此得到式（7）的离散近似式

$g({r_j},z)\! \approx \!\frac{{\Delta {k_r}}}{{\sqrt {2\pi {r_j}} }}{e^{ - i[{k_{\min }}{r_j} - \pi /4]}}\!\sum\limits_{l = 0}^{M - 1} \!{[g({k_l},z){e^{ - i{r_{\min }}l\Delta {k_r}}}\!\!\!\sqrt {{k_l}} ]{e^{ - i\frac{{2\pi lj}}{M}}}}\!\text{。}\! $

(9)

式中的求和可用FFT完成。

由于离散傅里叶具有周期性，在变换过程中如果采样率不足，距离区间之外的声压值将叠加到所求区间的声压值上面去，从而使结果产生误差，解决的办法是：将距离区间的左端尽量取小，通常取为0，同时要求当时r>R= ${{M}}\Delta {{r}}$ 。

利用式（7）求解声场时，由于对格林函数尖峰的欠抽样，容易引入较大的误差。但是由柯西积分定理，可以对波数人为的引入一个衰减因子 $\varepsilon $ （ $\varepsilon < < {k_{\max }} - $ k_min)，使 $\tilde k = {k_r} - i\varepsilon $ ，通常 $\varepsilon $ 取 $\frac{3}{{2\pi (M - 1)\log e}}({k_{\max }} - {k_{\min }})$ 就可消除由格林函数尖峰欠抽样时造成的混叠问题。

2 浅海中低频声传播损失计算 2.1 浅海声速剖面对低频声传播损失的影响

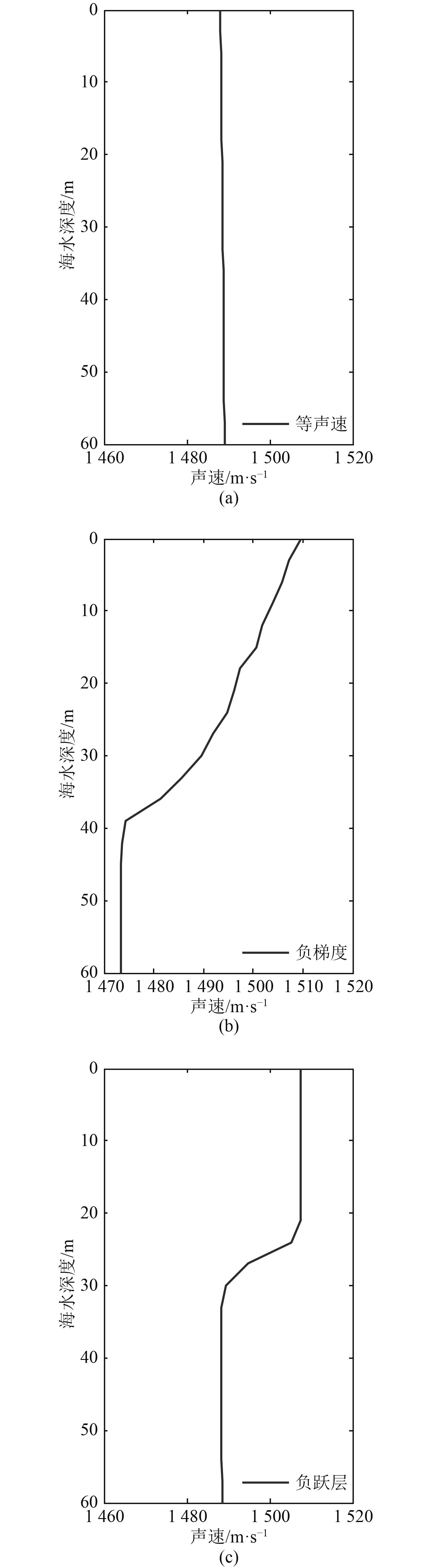
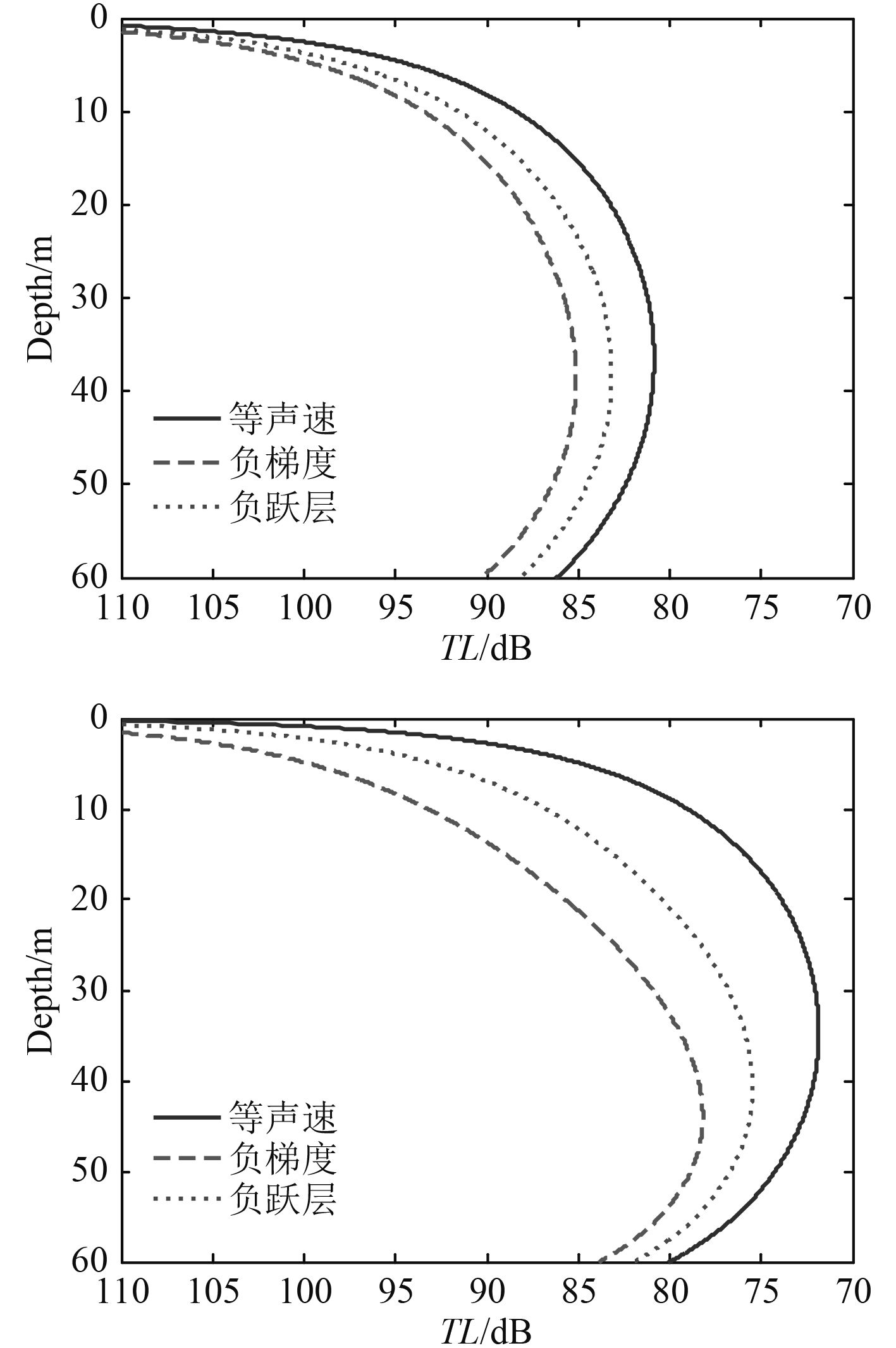
一般来说，在近岸浅海及大陆架区域，声速剖面有比较明显的季节特征，冬季典型的声速剖面是等声速，夏季则为负跃层，冬季过渡至夏季则为表面负梯度。图1给出了浅海3种典型的声速分布。海深60 m，海底为细砂，声学参数见表1，声源深度水下25 m。利用快速场算法，图2给出了3种声速剖面下接收位于25 m时40 Hz、63 Hz时的水平传播损失，可以看出，在500 m以内的近距离上，声速剖面对水平传播损失影响很小，随着距离的增加，声速负梯度、负跃层声速分布的水平传播损失明显高于等声速分布的传播损失，这是由于在负梯度和负跃层条件下，声线偏向海底，声波与海底的接触次数增多，横波的传播和声吸收导致传播损失增大。图3和图4分别为3种声速剖面下距离声源50 m和10 km时的垂直传播损失，可以看出，近距离上，声速剖面对垂直传播损失没有显著影响，远距离上，声速负梯度、负跃层声速分布的垂直传播损失也明显高于等声速分布的传播损失，这同样由上述原因引起。

2.2 浅海沉积层对低频声传播损失的影响

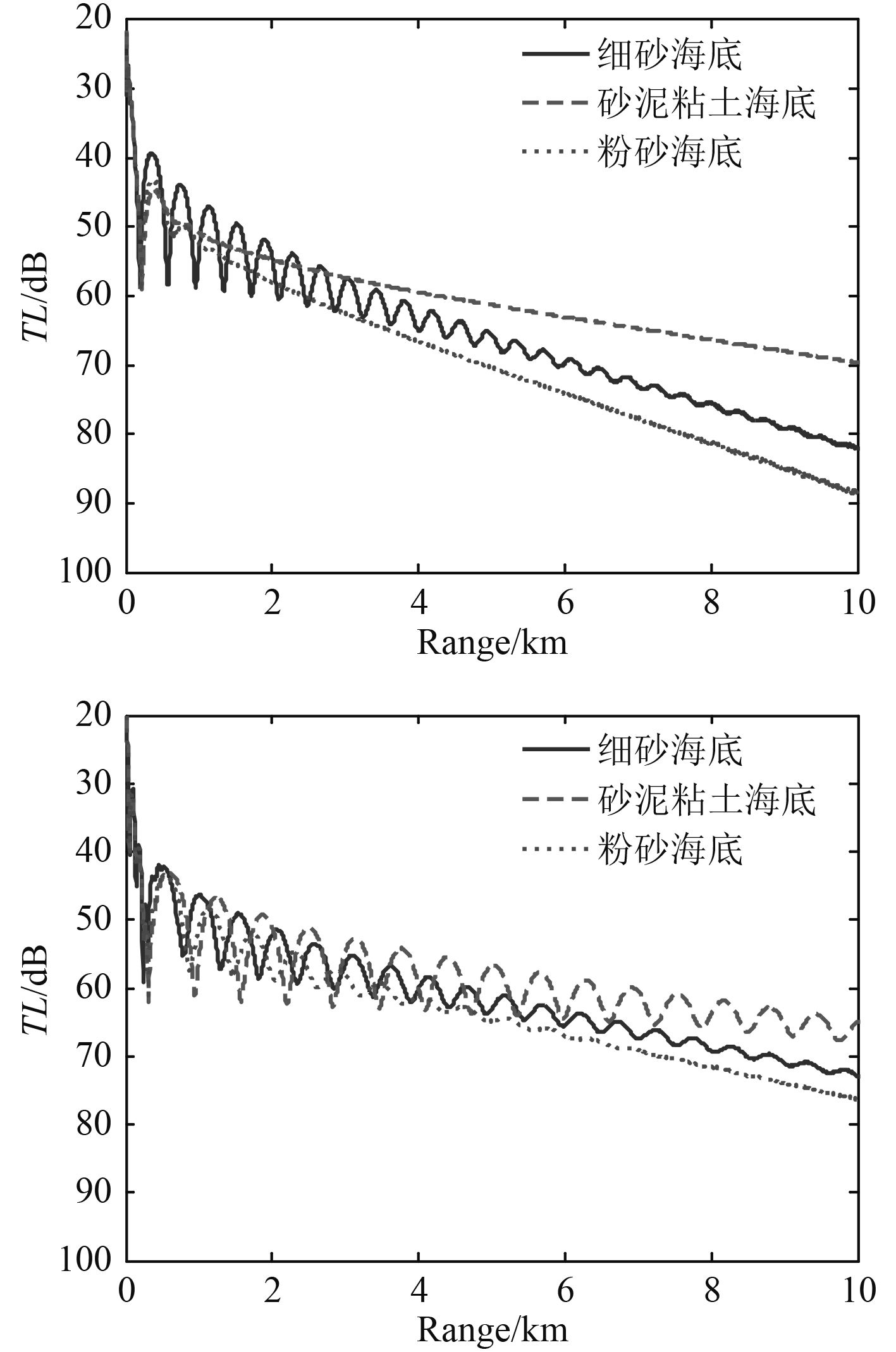
在浅海海域，海底地形及沉积层特性成为限制水下声传播的重要因素。不同的沉积层对声波的反射和吸收不同，表1给出了浅海常见的3种沉积层的地声参数。当海深60 m，声速剖面为等声速，声源深度水下25 m时，图5给出3种沉积层接收位于25 m时40 Hz，63 Hz时的水平传播损失，图6给出63 Hz时不同沉积层在平面上的传播损失。可以看出，在500以内的近距离，不同的沉积层对传播损失仍有较大影响，在远距离处，砂-泥-粘土层的传播损失最小，细砂层次之，粉砂层的传播损失最大。这主要是由于不同沉积层对声波的衰减系数不同，同一频率声波在不同沉积层浅海的传播距离以及能量强度也不同，其传播损失随距离的变化存在明显的差异。

3 结　语

本文利用波数积分法研究浅海声速剖面和沉积层对低频声传播损失的影响，得到如下结论：

1）近距离上，声速剖面对水平传播损失和垂直传播损失没有显著影响；远距离上，声速负梯度、负跃层声速分布的水平传播损失明显高于等声速分布的传播损失，声速负梯度、负跃层声速分布的垂直传播损失也明显高于等声速分布的传播损失。主要是由于在负梯度和负跃层条件下，声线偏向海底，声波与海底的接触次数较多，横波的传播和声吸收导致传播损失增大。

2）由于不同沉积层对声波的衰减系数不同，同一频率声波在不同底质的浅海海域的传播距离以及能量强度也不同，其传播损失随距离的变化存在明显的差异。在远距离处，在远距离处，砂-泥-粘土层的传播损失最小，细砂层次之，粉砂层的传播损失最大。