2. 中国船舶重工集团公司第七一四研究所,北京 100101
2. The 714 Research Institute of CSIC, Beijing 100101, China
近年来,基于同步式测距的水声定位系统引起了学界的关注,可在水下航行器不主动暴露且正常航行状态下实现对自身惯导累积误差的修正,但是信标与水下航行器时间同步的难题限制了其实际应用[1 – 3]。
时间同步是水下传感器网络组网的前提,国内外学者已经进行了广泛研究。文献[4]提出的高延迟网络时间同步协议(Time Synchronization for High Latency networks,TSHL)是第1个考虑了高的传输时延会导致同步过程时钟漂移率影响不可忽视的同步算法,但是TSHL算法及其改进算法基于多次单程传输过程中节点位置固定和传播时延固定的假设,不适用于移动节点间的同步问题。针对移动场景下的时间同步问题,相关学者提出了MU-Sync[5],Mobi-Sync[6],D-Sync[7]和E2DTS等算法[8]。但是这些算法在对时钟漂移相位进行估计时要求待同步节点主动向外发送信号,无法用于对静默要求高的水下平台的定位与同步。
文献[9]提出一种沉默定位机制,被定位节点通过侦听不同信标之间的应答实现时钟同步和定位的定位体制,虽然被定位节点可以全程保持静默,但是这种算法要求有4个锚节点,无法应用于单信标测距定位系统。
洪泛时间同步协议[10](Flooding Time Synchronization Protocol,FTSP)是基于发送者的单程同步算法,用对同步消息在传输路径上所有时延的估计来实现节点间的时钟同步。文献[11]将FTSP协议应用于水下传感器网络时间同步,提出一种使用锚节点泛洪的水下机器人自定位协议。但是FTSP假设消息的传播是近似瞬间完成的,只能用于传播时延可以忽略的场景。
目前尚未见解决水下单个信标与移动静默节点间时间同步问题的报道,本文在总结相关研究基础上,结合水下航行器在运动状态下进行单信标测距定位的实际应用场景,提出移动联合沉默定位与时钟同步算法(Mobile-Joint silent time synchronization and localization,Mobi-JSSL)和改进的MM-sync算法(Improved MM-sync,IMM-sync)以解决航行器移动静默状态下时间同步的难题,并对2种算法的性能进行仿真。仿真结果表明,2种算法均可以在存在测距误差的情况下有效减小时间同步误差,IMM-sync算法的性能优于Mobi-JSSL算法。
1 固定单信标测距定位模型
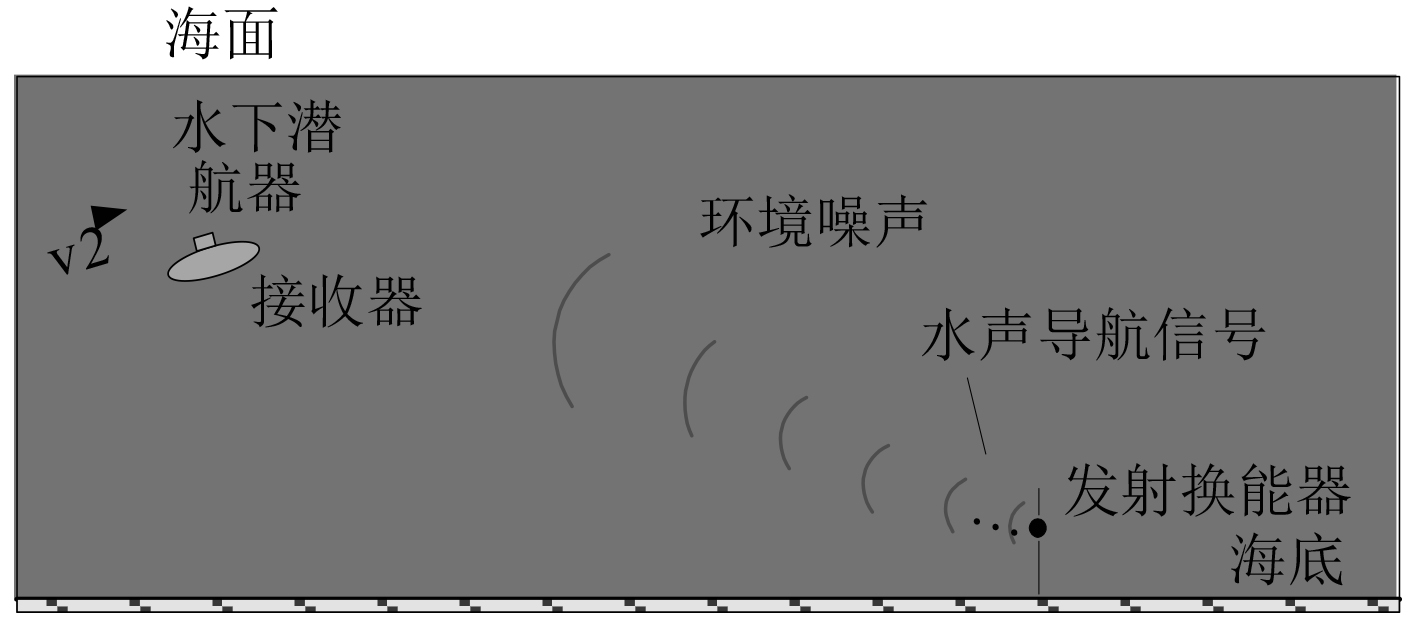
|
图 1 水下单信标测距定位示意图 Fig. 1 Schematic diagram of underwater single beacon distance measurement |
单信标测距定位系统的应用场景如图1所示,信标锚系固定在海底,通过水声通信的方式以固定频率等时间间隔
| $OWTT = {t_{{\text{抵达}}}} - {t_{{\text{发射}}}}{\text{。}}$ | (1) |
需要注意的是,t发射由信标时钟确定,t抵达由水下航行器时钟确定,两者之间会存在时钟同步误差。水下航行器基于单程传播时延求得到信标的距离,结合自身航迹推算实现对自身的定位。
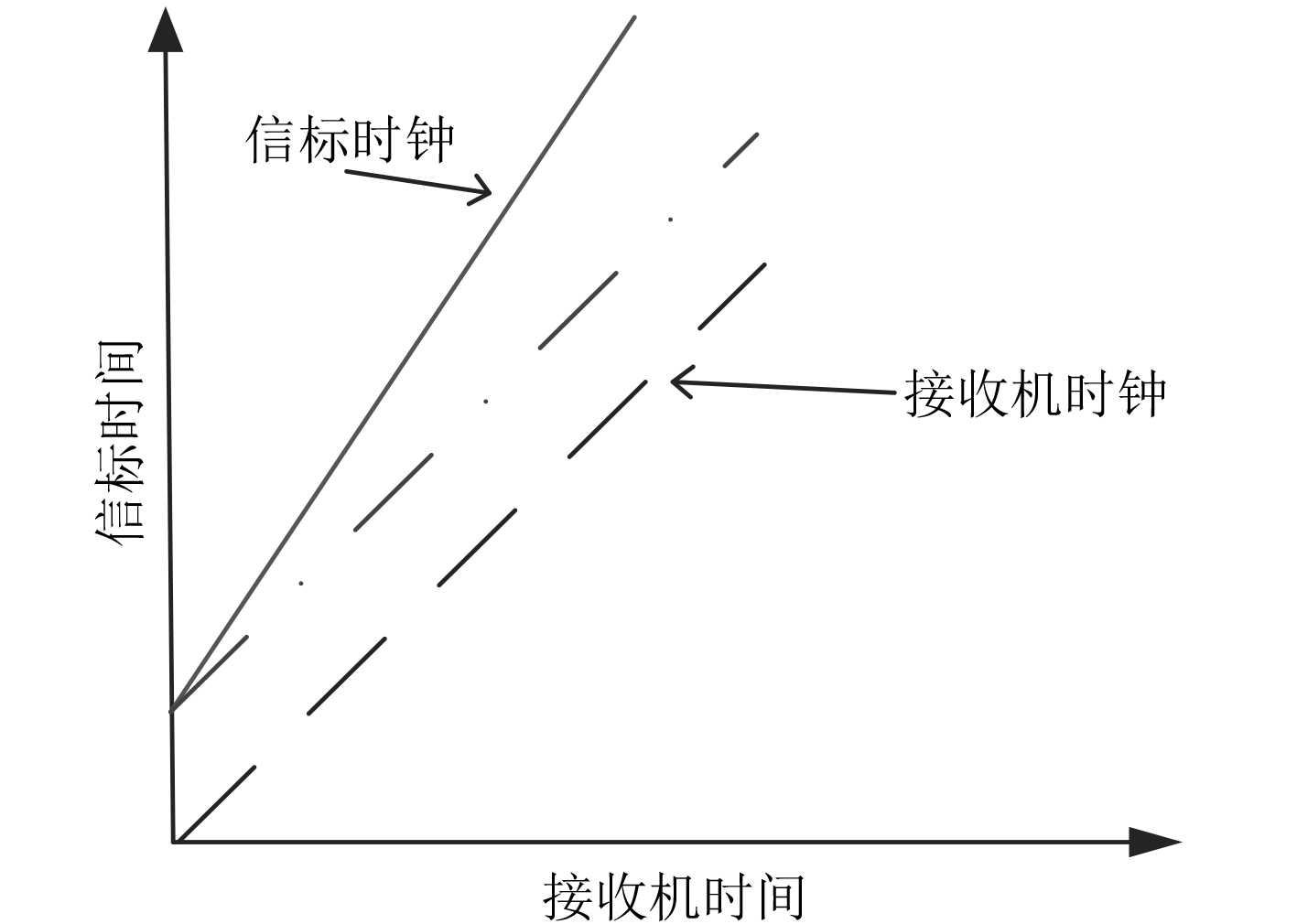
|
图 2 时钟同步误差模型图 Fig. 2 Clock synchronization error model |
时钟同步误差模型如图2所示。若水下航行器和信标之间不存在时间同步误差,则信标时钟将如图2中虚线所示,而实际情况中信标时钟与水下航行器时钟之间的关系如图2中实线所示,既存在初始相位偏差,也存在时钟频率偏差。
假设水下航行器的时钟为真实时间,以其为基准建立信标的本地时钟模型:
| ${T_B}(t) = \int {a(t){\rm d}t} + b{\text{。}}$ | (2) |
式中:
| ${T_B} = at + b{\text{。}}$ | (3) |
文献[12]提出一种为水下沉默节点提供定位与时钟同步的联合沉默定位与时钟同步方法,但是其需要至少4个固定节点,并且没有考虑传播时延变化的情况,也不适用于单信标系统的时间同步。本文对其进行改进,提出适用于单信标测距定位系统的移动联合沉默定位与时钟同步算法(Mobi-JSPS)。
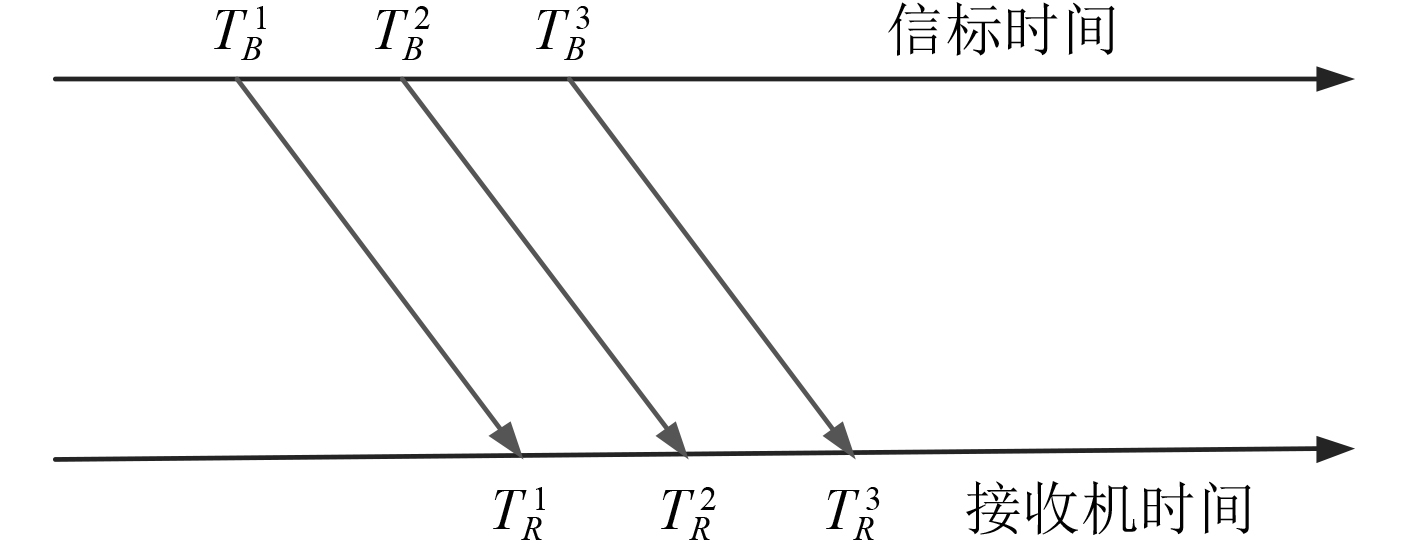
|
图 3 水下单信标测距定位示意图 Fig. 3 Schematic diagram of underwater single beacon distance measurement |
本文算法模型如图3所示,信标在本地时钟
信标时钟同步误差模型如式所示,则在时间同步过程中
| $(T_B^i - b)/a + D{T_i} = T_R^i\text{,}$ | (4) |
式中,
| $\begin{aligned}& T_R^1 - T_B^1 = (\frac{1}{a} - 1)T_B^1 - \frac{b}{a} + D{T_1}\text{,}\\& T_R^2 - T_B^2 = (\frac{1}{a} - 1)T_B^2 - \frac{b}{a} + D{T_2}\text{,}\\& ...\\& T_R^N - T_B^N = (\frac{1}{a} - 1)T_B^N - \frac{b}{a} + D{T_N}\text{。}\end{aligned}$ | (5) |
将式(5)中每一行减去第1行,得到
| ${{{T}}_{1}} = (\frac{1}{a} - 1){{{T}}_{2}} + {{DT}}{\text{。}}$ | (6) |
式中:
| ${{{T}}_{1}} = \left( \begin{array}{c}(T_R^2 - T_R^1) - (T_B^2 - T_B^1)\\ \vdots \\(T_R^N - T_R^1) - (T_B^N - T_B^1)\end{array} \right)\text{,}$ |
| ${{{T}}_{2}} = \left( \begin{gathered} T_B^2 - T_B^1 \\ \vdots \\ T_B^N - T_B^1 \\ \end{gathered} \right)\text{,}$ |
| ${{DT}}{\text{ = }}\left( \begin{gathered} D{T_2} - D{T_1} \\ \vdots \\ D{T_N} - D{T_1} \\ \end{gathered} \right)\text{。}$ |
对于静止节点间的时钟同步而言,忽略水声信道的时变特性,每一次的传播时延可以视为相同的;对于移动的水下水下航行器而言,虽然信标等时间间隔
文献[13]提出的单信标分阶段时钟同步算法中利用节点移动的运动要素来表征传播时延的变化。本文借鉴其思路,用
| $D{T_i} - D{T_1} = \frac{{{S_i} - {S_{i - 1}}}}{c} = \frac{{v(T_B^i - T_B^1)}}{{ac}}\text{,}$ | (7) |
则式(7)变为
| ${{{T}}_{1}} = (\frac{1}{a} - 1){{{T}}_{2}} + \frac{v}{{ac}}{{{T}}_{2}}{\text{。}}$ | (8) |
由于发射接收时间的确定并非完全准确没有误差,因此式(8)需要用最小二乘法进行求解
| $a = \frac{{c + v}}{{c{{\left( {{{T}}_2^{\rm T}{{{T}}_2}} \right)}^{{\rm{ - }}1}}{{T}}_2^{\rm T} \cdot {{{T}}_3}}}{\text{。}}$ | (9) |
式中:
| ${{{T}}_3} = {{{T}}_1} + {{{T}}_2} = \left( \begin{array}{c}(T_R^2 - T_R^1)\\ \vdots \\(T_R^N - T_R^1)\end{array} \right)\text{。}$ | (10) |
至此,实现了对时钟漂移率的估计,接下来需要对时钟漂移相位进行估计。传统的时钟漂移相位估计方法是利用至少一次收发应答过程对时钟漂移相位进行估计,文献[12]提出的JSPS算法需要接收至少4个信标发送的信号才可以实现对时钟漂移相位的估计。在JSPS算法各个信标的时钟是同步的,同一个时刻接收到的不同信标的时钟与水下航行器之间只存在一个相同的时钟相位偏差。若将这种思路应用到单信标定位系统中,只能采用虚拟长基线[14]的方法。此时,不同时刻接收到的信标发射时间与接收时间之间的时钟偏差不同,不仅有固定的初始相位偏差,还有随时间变化的频率偏差带来的额外相位偏差。因此,必须首先利用第1步估计出来的时钟频率偏差对不同时刻的相位偏差进行重新建模。
由式(4)得
| $D{T_i} = T_R^i - (T_B^i - b)/a\text{,}$ | (11) |
伪距
| ${S_i} = D{T_i} \cdot c{\text{ = }}\sqrt {{{({x_{{B_i}}} - {x_R})}^2} + {{({y_{{B_i}}} - {y_R})}^2} + {{({z_{{B_i}}} - {z_R})}^2}}\text{。} $ | (12) |
式中:
Mobi-JSPS算法的实质是用水下航行器的位移近似表征声传播路径的变化,通过这种近似在时钟漂移率估计时将传播时延的变化考虑进去,从而提高估计的精确度。但是这种近似与信标和水下航行器的相对态势有关,传播路径长度的变化在水下航行器正横经过信标附近时最小,信标位于水下航行器首尾方向时变化最大,而水下航行器匀速直线航行时,单位时间内的位移大小是固定的,因此这种方法采用的近似只能在某一段航程上取得较高的精度。为了提高时间同步精度,在Mobi-JSPS算法框架基础上提出了IMM-sync算法。
3 IMM-sync算法文献[16]在建立节点移动模型的基础上提出一种能应用于水下高时延网络的时间同步算法 MM-sync,该方法采用单向通信,可以使被定位的水下航行器保持静默。

|
图 4 水下航行器匀速直线运动模型 Fig. 4 Underwater vehicle uniform linear motion model |
假设水下航行器保持匀速直线运动,移动模型如图4所示。设
| ${{{S}}_{{R_i}}} = (T_R^i - T_B^1){{v}} = [T_R^i-(T_B^1-b)/a]{{v}}{\text{。}}$ | (13) |
传播时延
| $D{T_i} = \frac{{{S_i}}}{c} = \frac{{\sqrt {{{[(T_R^i-(T_B^1-b)/a){{v}} + {{S}}]}^2}} }}{c}\text{,}$ | (14) |
由此可以建立如下模型:
| $\frac{{{{[(T_R^i-(T_B^1-b)/a){{v}} + {{S}}]}^2}}}{{{c^2}}}{\text{ = [}}T_R^i-(T_B^i-b)/a{]^2}\text{。}$ | (15) |
式中含有未知数
IMM-sync算法建立了更加精细的运动模型,理论上对时间同步误差模型表征得最精确,但是该算法求解困难,高次方程必须进行线性化,从而会带来舍入误差。
4 仿真分析

|
图 5 水下航行器直线航迹模型 Fig. 5 Underwater vehicle linear path model |
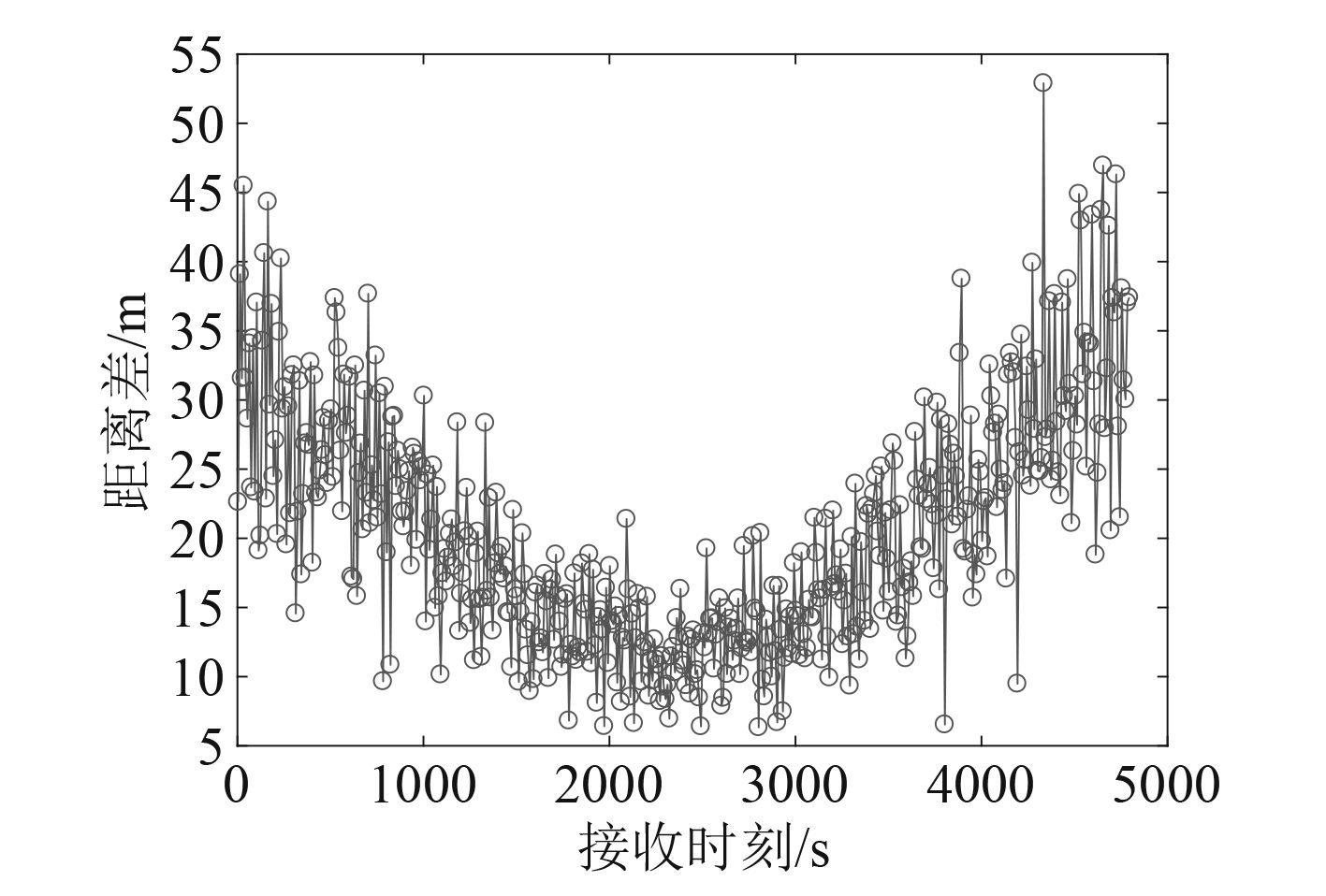
|
图 6 测距误差 Fig. 6 Ranging error |
仿真算例:布放的单只信标位置坐标为(0,0),水下航行器直线航迹如图5所示,以2 m/s的前向航速定深匀速运动,水下航行器掌握的平均声速为1 500 m/s,信标相对水下航行器时钟漂移相位为50 ms,时钟漂移率为10 ppm,仿真时间5 000 s。分别仿真了真实声速误差服从均值为0,10,20,方差为5的3种高斯分布条件下(均值为10,方差为5声速误差带来的测距误差如图6所示)Mobi-JSPS算法和IMM-sync算法的性能,进行1 000次蒙特卡罗仿真,航程结束前100个接收时刻的时间同步误差取平均,得到的仿真结果如表1所示,其中时间同步误差的单位为ms。
|
|
表 1 不同声速误差下时间同步算法性能 Tab.1 Performance of time synchronization algorithm under different speed errors |
从表1可以看出,2种算法在3种条件下都对时间同步误差进行了约束;声速误差越大,时间同步算法的性能越差;整体而言,IMM-sync算法的性能优于Mobi-JSSL算法。
5 结 语本文提出2种水下航行器在移动静默状态下同单信标进行时间同步的算法,仿真结果表明:2种算法均能有效减小时间同步误差;IMM-sync算法的性能优于Mobi-JSSL算法;算法的性能受限于测距精度,后续可将测距修正手段同时间同步算法结合在一起,提升算法性能。
| [1] |
孙大军, 郑翠娥. 水声导航、定位技术发展趋势探讨[J]. 海洋技术学报, 2015, 34(3): 64–68.
SUN Da-jun, ZHENG Cui-e. Study on the development trend of underwater acoustic navigation and posi-tioning technologies[J]. Journal of Ocean Technolo-gy, 2015, 34(3): 64–68. http://www.docin.com/p-1571435783.html |
| [2] |
殷冬梅, 惠俊英, 孙圣和, 等. 无线遥控、浮标式水下目标跟踪定位系统[J]. 系统工程与电子技术, 2004, 26(9): 1246–1249.
YIN Dong-mei, HUI Jun-ying, SUN Sheng-he, et al. Design of wireless acoustic buoy array multi-targets tracking and positioning system[J]. Systems Engineering and Electronics, 2004, 26(9): 1246–1249. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xtgcydzjs200409026 |
| [3] | SARAH E, WEBSTER CEXUS J C. Decentralized single beacon acoustic navigation: communication and navi-gation for underwater vehicles[D]. The Johns Hopkins University, 2010, 6–22. |
| [4] | SYED A A, HEIDEMANN J. Time synchronization for high latency acoustic networks[C]// INFOCOM 2006. IEEE International Conference on Computer Communications. Proceedings. IEEE, 2006: 1–12. |
| [5] | CHIRDCHOO N, SOH W S, CHUA K C. MU-Sync: a time synchronization protocol for underwater mobile net-works[C]// The Workshop on Underwater Networks. DBLP, 2008: 35–42. |
| [6] | LIU J, ZHOU Z, PENG Z, et al. Mobi-sync: efficient time synchronization for mobile underwater sensor networks[C]// Global Telecommunications Conference. IEEE, 2011: 1–5. |
| [7] | LU F, MIRZA D, SCHURGERS C. D-sync: Doppler-based time synchronization for mobile underwater sensor networks[C]// ACM International Workshop on Un-derwater Networks. ACM, 2010: 1–8. |
| [8] |
李正宝. 具有时空多变性的水下传感器网络基础协议研究[D]. 青岛: 中国海洋大学, 2011.
LI Zheng-bao. Research of basic protocols in spa-tial-temporal varying underwater acoustic sensor net-works[D]. Qingdao: Ocean University of China, 2011. |
| [9] | XIUZHEN C, RAINING S, QILIAN L, et al. Silent positioning in underwater acoustic sensor networks[C]//IEEE Transactions on Vehicular Technolo-gy. 2008, 57(3): 1756–1766. |
| [10] | MAR, TI M, KUSY B, et al. The flooding time synchro-nization protocol[J]. Proc. acm Conf. embedded Net-worked Sensor Systems, 2004: 39–49. |
| [11] | YUECHENG Z, LIANG C. A distributed protocol for multi-hop underwater robot positioning[C]//In: Robotics and Biomimetics, 2004. ROBIO 2004. IEEE Interna-tional Conference on: 2004. 480–484. |
| [12] |
张弓, 齐望东, 刘鹏, 等. 水下侦察网络中的联合沉默定位与时钟同步[J]. 解放军理工大学学报: 自然科学版, 2014, 15(2): 113–120.
ZHANG Gong, QI Wang-dong, LIU Peng, et al. Joint silent positioning and synchronization in underwater surveillance networks[J]. Journal of PLA University of Science and Technology: Natural Science Edition, 2014, 15(2): 113–120. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jfjlgdxxb201402003 |
| [13] |
邢芙宁. 水下传感器网络时钟同步算法的研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
XING Fu-ning. Research on time synchronization algorithm in underwater acoustic sensor network [D]. Harbin: Harbin Engineering University, 2013. |
| [14] | LARSEN M B. Synthetic long baseline navigation of underwater vehicles[C]//OCEANS 2000 MTS/IEEE Conference and Exhibition, Providence, RI, USA, IEEE, 2000, 2043–2050. |
| [15] |
曹俊, 郑翠娥, 孙大军, 等. AUV直线航迹下的单信标测距定位[J]. 哈尔滨工程大学学报, 2017, 38(5): 733–738.
CAO Jun, ZHENG Cui-e, SUN Da-jun, et al. AUV positioning based on single-beacon ranging in straight-line trajectory[J]. Journal of Harbin Engineering University, 2017, 38(5): 733–738. http://www.doc88.com/p-7496381685407.html |
| [16] |
王慧强, 温秀秀, 林俊宇, 等. 基于移动模型的水下传感器网络时间同步算法[J]. 通信学报, 2016, 37(1): 1–9.
WANG Hui-qiang, WEN Xiu-xiu, LIN Jun-yu, et al. Time synchronization algorithm based on mobility model for underwater sensor networks[J]. Journal on Com-munications, 2016, 37(1): 1–9. |
| [17] |
刘明雍, 张加全, 张立川. 洋流影响下基于运动矢径的AUV协同定位方法[J]. 控制与决策, 2011, 26(11): 1632–1636.
LIU Ming-yong, ZHANG Jia-quan, ZHANG Li-chuan. AUV cooperative localization method based on motion radius vector in the presence of unknown currents[J]. Control and Decision, 2011, 26(11): 1632–1636. http://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201111007.htm |
 2018, Vol. 40
2018, Vol. 40
