2. 海军工程大学 船舶振动噪声重点实验室,湖北 武汉 430033
2. State Key Laboratory of Ship Vibration and Noise, Naval University of Engineering, Wuhan 430033, China
直驱式电液伺服系统是近年来随着材料技术、电力电子技术和控制技术的发展而研究产生的一种新型电液伺服系统[1]。相比传统电液伺服系统,由于取消了流量伺服控制阀,利用伺服电机的变速和变向实现流量大小和方向调节,所以直驱式电液伺服系统具有结构简单、可靠性高以及效率高等优点[2 – 5]。直驱式电液伺服系统的非线性不确定负载主要包含摩擦力和外界随机干扰,是影响直驱式电液伺服系统低速稳定性[6, 7]和准确性[8-9]的关键因素之一。由于自身高度非线性以及受系统参数时变等非线性因素交叉耦合影响[10],导致非线性不确定负载的数学模型无法准确描述。因此,使用常规PID控制算法往往达不到补偿效果。
滑模变结构控制具有响应快、对参数变化及扰动不灵敏、物理实现简单等优点[11 – 14],但是要求被控对象的不确定性满足匹配条件,而直驱式电液伺服系统是非匹配的,且为高阶系统[15]。此外,滑模变结构控制需要来回地作逻辑切换,容易引起抖振现象[16 – 18]。
因此,针对直驱式电液伺服系统的非线性不确定负载,本文结合神经网络的自学习功能以及对非线性系统的强大映射能力[19 – 21],提出一种多滑模神经网络自适应控制策略,实现对非线性不确定负载有效补偿,提高直驱式电液伺服系统的控制精度和动态特性。
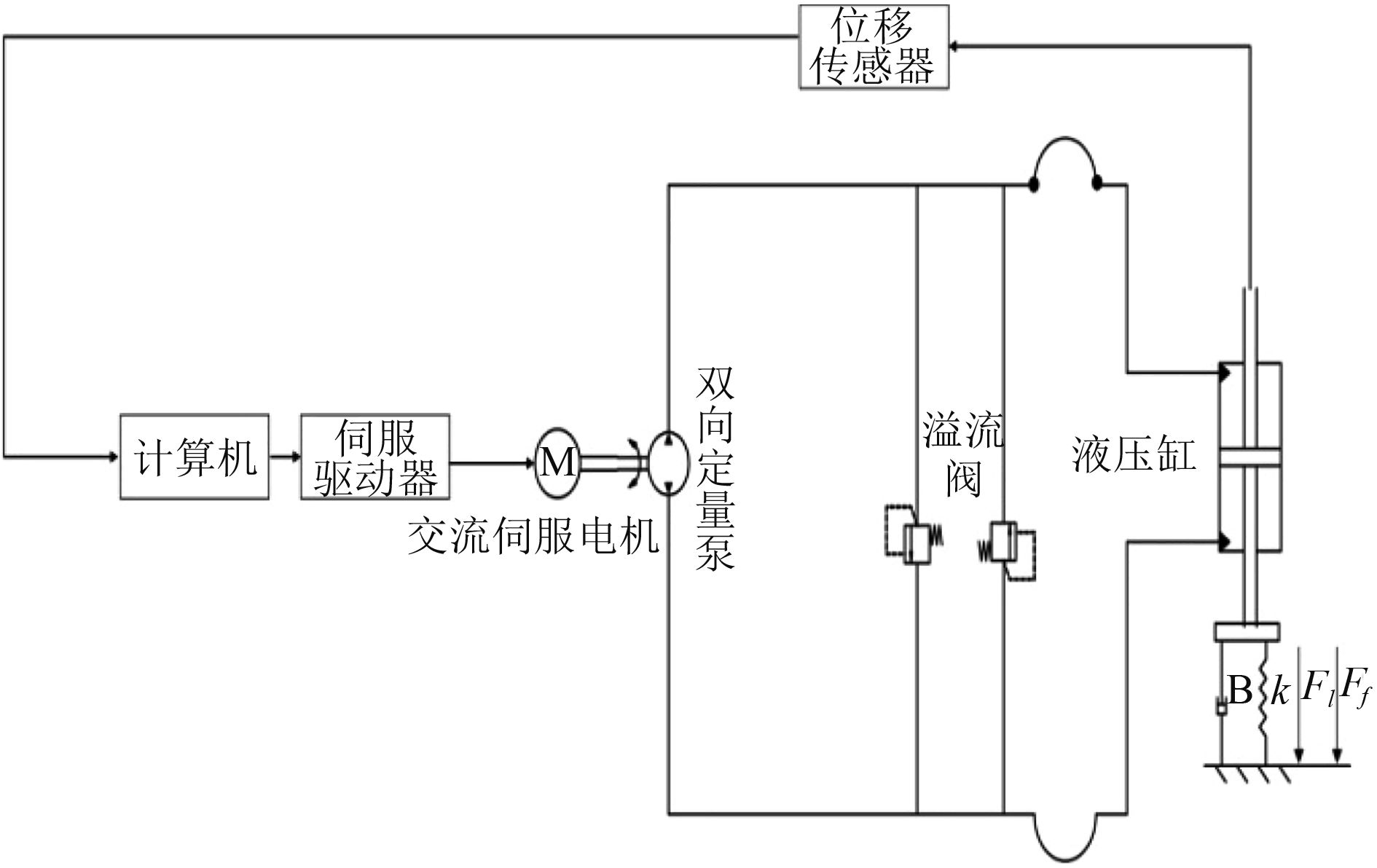
1 数学模型图1为直驱式电液伺服系统原理图,其主要工作原理是:伺服电机驱动器根据计算机的输入指令信号,控制伺服电机以特定转速和扭矩驱动双向定量泵输出一定的流量和压力直接推动液压缸运动,同时计算机根据传感器组的反馈信号不断调节伺服电机的转速和扭矩输出,实现速度和位置控制目的。整个系统的数学模型描述如图1所示。
|
图 1 直驱式电液伺服系统原理图 Fig. 1 Schematic diagram of direct drive electro-hydraulic servo system |
1)液压泵流量连续性方程。对于液压泵的出油口,根据实际输出流量等于理论计算流量与内外泄漏流量之差,可得:
| ${q_{_1}} = n{V_p} - {C_{ep}}{p_{_1}} - {C_{ip}}({p_{_1}} - {p_{_4}}), $ | (1) |
式中:q1为液压泵的输出流量;n为电机转速;Vp为液压泵排量;p1为液压泵出油口压力;p4为液压泵吸油口压力;Cep为液压泵外泄漏系数;Cip为液压泵内泄漏系数。相比液压泵出油口p1,液压泵吸油口压力p4大小以及变化可忽略,设为0。
2)液压缸流量连续性方程。由于直驱式电液伺服系统通常采用集成设计,其管路很短,因此管路动态特性可忽略。对于液压缸进油腔,根据进入进油腔的实际流量等于流体压缩流量、液压缸泄漏流量与活塞运动所需流量之和,可得
| ${q_{_1}} = \frac{V}{\beta }\frac{{{\rm{d}}{p_{_1}}}}{{{\rm{d}}t}} + A\frac{{{\rm{d}}y}}{{{\rm{d}}t}} + {C_{tm}}{p_{_1}}, $ | (2) |
式中:A为液压缸的作用面积;V为受控腔体积;
3)液压缸力平衡方程。根据液压缸输出力等于负载惯性力、粘性力、弹性力与非线性不确定负载之和,可得
| $({p_{_1}} - {p_{_4}})A = m\frac{{{\rm{d}}{y^2}}}{{{\rm{d}}{t^2}}} + ky + {F_f} + {F_l}, $ | (3) |
式中:m为液压缸的活塞杆和负载总质量;k为弹性负载刚度;Ff为液压缸与外界负载的总摩擦力;Fl为外界随机干扰。
令
| $\begin{gathered} {{\dot x}_1} = {x_2}, \hfill \\ {{\dot x}_2} = \frac{A}{m}{x_3} - \frac{k}{m}{x_1} - \frac{{{F_f} + {F_l}}}{m}, \hfill \\ {{\dot x}_3} = \frac{\beta }{V}(n{V_p} - {C_t}{x_3} - A{x_2})\text{。}\end{gathered} $ | (4) |
式中:
摩擦力Ff服从Stribeck摩擦曲线分布[22],其表达式为
| ${F_f} = \sigma \dot y + sign(\dot y)\left[ {{F_{c0}} + {F_{s0}}\exp ( - \frac{{\left| {\dot y} \right|}}{{{c_s}}})} \right], $ | (5) |
式中:
由式(5)可知,摩擦力本身是非线性的,同时式中的相关系数随着系统工作状态变化(如温度)而变化,具有慢时变特征,无法准确确定。因此,无法基于式(5)对摩擦力进行补偿。
外界随机干扰Fl由于具有不确定性,无法描述其确定的数学模型。用一个函数进行描述,表达式如下:
| ${F_l} = d({x_1},{x_2},{x_3},t),\text{其中}\left| {d({x_1},{x_2},{x_3},t)} \right| \leqslant D{\text{。}}$ | (6) |
式中:D为外界随机干扰的上界。
将非线性不确定负载视为一个非线性光滑函数f(x1,x2,x3),采用RBF神经网络对其进行辨识建模,由万能逼近定理可得:
| $f({x_1},{x_2},{x_3}) = \frac{{{F_f} + {F_l}}}{m} = {W^ * }^{\rm T}\varPhi ({x_1},{x_2},{x_3}) + {\varepsilon _0}, $ | (7) |
式中:
| $\begin{split}& {\phi _i}({x_1},{x_2},{x_3}) = \exp ( - \frac{{{{({x_{^1}} - {c_{1i}})}^2} + {{({x_2} - {c_{2i}})}^2} + {{({x_3} - {c_{3i}})}^2}}}{{2b_i^2}}), \\& i = 1,2, \cdots ,l{\text{。}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\ \ (8)\end{split} $ |
式中:
由式(4)~式(6)可知,直驱式电液伺服系统是一个非线性耦合高阶系统。因此,本文定义3个滑模面
1)定义第1个Lyapunov函数
| ${V_1} = \frac{1}{2}{s_1}^2, $ | (9) |
则
| ${\dot V_1} = {s_1}{\dot s_1}, $ | (10) |
对位置滑模面
| ${\dot s_1} = {\dot x_1} - {\dot y_d} = {x_2} - {\dot y_d}, $ | (11) |
结合
| ${\dot s_1} = {s_2} + {x_{2d}} - {\dot y_d}, $ | (12) |
取速度输出期望值
| ${\dot V_1} = - {k_1}{s_1}^2 + {s_1}{s_2}, $ | (13) |
显然,当
2)定义第2个Lyapunov函数
| ${V_2} = {V_1} + \frac{1}{2}{s_2}^2 + \frac{1}{2}\gamma {\tilde W^{\rm T}}\tilde W, $ | (14) |
式中,
对
| ${{\dot{V}}_{2}}={{\dot{V}}_{1}}+{{s}_{2}}{{\dot{s}}_{2}}-\gamma {{\tilde{W}}^{\text{T}}}\dot{\hat{W}},$ | (15) |
结合式(4)、式(7)以及
| ${\dot s_2} = \frac{A}{m}{s_3} + \frac{A}{m}{x_{3d}} - f({x_1},{x_2},{x_3}) - {\dot x_{2d}}, $ | (16) |
取压力期望值
| ${x_{3d}} = \frac{m}{A}(\hat f({x_1},{x_2},{x_3}) + {\dot x_{2d}} - {k_2}{s_2} - {\varepsilon _N}h({s_2})), $ | (17) |
其中
| $\left| s \right| - sh(s) \leqslant \eta ,\eta \text{为任意小正数}\text{。} $ | (18) |
证明:
| $\begin{aligned}\left| s \right| - sh(s) = & \left| s \right| - \frac{{\left| s \right|}}{{\sqrt {1 + \frac{\delta }{{{s^2}}}} }} \leqslant \left| s \right| - \frac{{\left| s \right|}}{{1 + \sqrt {\frac{\delta }{{{s^2}}}} }} = \\ & \frac{{\sqrt \delta }}{{1 + \sqrt {\frac{\delta }{{{s^2}}}} }} \leqslant \sqrt \delta = \eta ,\end{aligned}$ |
将式(13)、式(16)和式(17)代入式(15)得:
| $\begin{split} {{\dot V}_2} = & - {k_1}{s_1}^2 - {k_2}{s_2}^2 + {s_1}{s_2} + \frac{A}{m}{s_2}{s_3} + \\ & {{\tilde W}^{\rm{T}}}({s_2}\Phi ({x_1},{x_2},{x_3}) - \gamma \dot {\hat W}) - ({\varepsilon _N}h({s_2}) - \varepsilon ){s_2}, \end{split} $ | (19) |
则在该步中,初步取估计权值自适应控制律为
| ${\dot {\hat W}} = \frac{1}{\gamma }{s_2}\varPhi ({x_1},{x_2},{x_3}), $ | (20) |
将式(20)代入式(19),并结合式(18)可得:
| ${{\dot V}_2} \leqslant - {k_1}{s_1}^2 - {k_2}{s_2}^2 + {s_1}{s_2} + \frac{A}{m}{s_2}{s_3} - {\delta _1}, $ | (21) |
式中:
显然,当
3)定义第3个Lyapunov函数
| ${V_3} = {V_2} + \frac{1}{2}{s_3}^2\text{,}$ | (22) |
对式(22)求导,并将式(19)代入,可得
| $\begin{split} & {{\dot V}_3} = - {k_1}{s_1}^2 - {k_2}{s_2}^2 + {s_1}{s_2} + \frac{A}{m}{s_2}{s_3} + \\ & {{\tilde W}^{\rm{T}}}({s_2}\varPhi ({x_1},{x_2},{x_3}) - \gamma \dot {\hat W}) - ({\varepsilon _N}h({s_2}) - \varepsilon ){s_2} + {s_3}{{\dot s}_3}\text{。} \end{split} $ | (23) |
结合式(4),对压力滑模面求导可得:
| ${\dot s_3} = \frac{\beta }{V}(n{V_p} - {C_t}{x_3} - A{x_2}) - {\dot x_{3d}}\text{。} $ | (24) |
式(4)和式(17)可得压力期望值的导数为
| $\begin{split} &{{\dot x}_{3d}} = \frac{{\partial {x_{3d}}}}{{\partial {x_1}}}{{\dot x}_1} + \frac{{\partial {x_{3d}}}}{{\partial {x_2}}}{{\dot x}_2} + \frac{{\partial {x_{3d}}}}{{\partial {x_3}}}{{\dot x}_3} + \sum\limits_{i = 1}^3 {\frac{{\partial {x_{3d}}}}{{\partial {y_d}^{(i - 1)}}}} {y_d}^{(i)} + \\ &\frac{{\partial {x_{3d}}}}{{\partial \hat W}}{\dot {\hat W}} = \frac{{\partial {x_{3d}}}}{{\partial {x_1}}}x2 + \frac{{\partial {x_{3d}}}}{{\partial {x_2}}}(\frac{A}{m}x3 - {{\hat W}^{\rm{T}}}\varPhi ) + \\ &\frac{{\partial {x_{3d}}}}{{\partial {x_3}}}(\frac{\beta }{V}(n{V_p} - {C_t}{x_3} - A{x_2})) + \sum\limits_{i = 1}^3 {\frac{{\partial {x_{3d}}}}{{\partial {y_d}^{(i - 1)}}}} {y_d}^{(i)} + \\ &\frac{{\partial {x_{3d}}}}{{\partial {\hat W}}}{\dot {\hat W}} - \frac{{\partial {x_{3d}}}}{{\partial {x_2}}}(\tilde W\varPhi + \varepsilon ) = {{\dot {\hat x}}_{3d}} - \frac{{\partial {x_{3d}}}}{{\partial {x_2}}}({{\tilde W}^{\rm T}}\varPhi + \varepsilon ){\text{。}}\end{split}$ | (25) |
结合式(24)和式(25),取转速控制值
| $n = \frac{V}{{\beta {V_p}}}({C_t}{x_3} + A{x_2} + {{\dot {\hat x}}_{3d}} - {k_3}{s_3} - {\varepsilon _N}\sqrt {{{(\frac{{\partial {x_{3d}}}}{{\partial {x_2}}})}^2} + {\delta _2}} h({s_3})), $ | (26) |
式中,
将式(26)、式(24)代入式(23)可得
| $\begin{split}{{\dot V}_3} = & - {k_1}{s_1}^2 - {k_2}{s_2}^2 - {k_3}{s_3}^2 + {s_1}{s_2} + \frac{A}{m}{s_2}{s_3} + \\ &{{\tilde W}^{\rm{T}}}({s_2}\varPhi - \frac{{\partial {x_{3d}}}}{{\partial {x_2}}}\varPhi {s_3} - \gamma {\dot {\hat W}}) - ({\varepsilon _N}h({s_2}) - \varepsilon ){s_2} - \\ &\left( {{\varepsilon _N}\sqrt {{{(\frac{{\partial {x_{3d}}}}{{\partial {x_2}}})}^2} + {\delta _2}} h({s_3}) - \frac{{\partial {x_{3d}}}}{{\partial {x_2}}}\varepsilon } \right){s_3},\end{split}$ | (27) |
取权值最终自适应控制律为
| ${\dot {\hat W}} = \frac{1}{\gamma }(\varPhi {s_2} - \frac{{\partial {x_{3d}}}}{{\partial {x_2}}}\varPhi {s_3}), $ | (28) |
将式(28)代入式(27)可得
| $\begin{split}{{\dot V}_3} = & - {k_1}{s_1}^2 - {k_2}{s_2}^2 - {k_3}{s_3}^2 + {s_1}{s_2} + \\ &\frac{A}{m}{s_2}{s_3} - ({\varepsilon _N}h({s_2}) - \varepsilon ){s_2} - \\ &\left( {{\varepsilon _N}\sqrt {{{(\frac{{\partial {x_{3d}}}}{{\partial {x_2}}})}^2} + {\delta _2}} h({s_3}) - \frac{{\partial {x_{3d}}}}{{\partial {x_2}}}\varepsilon } \right){s_3} = \\ & - {s^{\rm T}}{ Q}s - ({\varepsilon _N}h({s_2}) - \varepsilon ){s_2} - \\ &\left( {{\varepsilon _N}\sqrt {{{(\frac{{\partial {x_{3d}}}}{{\partial {x_2}}})}^2} + {\delta _2}} h({s_3}) - \frac{{\partial {x_{3d}}}}{{\partial {x_2}}}\varepsilon } \right){s_3},\end{split}$ | (29) |
式中,
定理1:对于直驱式电液伺服系统(4),控制器(26)以及自适应律(28)构成的闭环控制系统,选取合适的
证明 由式(18)可知
| $\begin{split}({\varepsilon _N}h({s_2}) - & \varepsilon ){s_2}{\rm{ - }}{\varepsilon _N}{\eta _2}{\rm{ = - }}{\delta _4}\\ &\left( {{\varepsilon _N}\sqrt {{{(\frac{{\partial {x_{3d}}}}{{\partial {x_2}}})}^2} + {\delta _2}} h({s_3}) - \frac{{\partial {x_{3d}}}}{{\partial {x_2}}}\varepsilon } \right){s_3} \geqslant \\ &\left( {{\varepsilon _N}\left| {\frac{{\partial {x_{3d}}}}{{\partial {x_2}}}} \right|h({s_3}) - \frac{{\partial {x_{3d}}}}{{\partial {x_2}}}\varepsilon } \right){s_3} \geqslant \\ &{\rm{ - }}{\varepsilon _N}\left| {\frac{{\partial {x_{3d}}}}{{\partial {x_2}}}} \right|{\eta _3}{\rm{ = - }}{\delta _6}{\text{。}}\end{split}$ | (30) |
其中,
由于矩阵Q正定,将式(30)代入式(29)可得:
| ${\dot V_3} \leqslant - {s^{\rm T}}{ Q}s + {\delta _4} + {\delta _5} = - s{'^{\rm T}}{ Q}s' \leqslant 0, $ | (31) |
其中,
令
| $\begin{split}\int\nolimits_0^t {W(t)} {\rm d}t=& {V_3}({s_1}'(0),{s_2}'(0),{s_3}'(0)) - \\&{V_3}({s_1}'(t),{s_2}'(t),{s_3}'(t))\text{。}\end{split}$ | (32) |
因为
| $\mathop {\lim }\limits_{t \to \infty } \int\nolimits_0^t {W(t)}{\rm d}t < \infty {\text{。}}$ | (33) |
由Barbalat引理可知,当
使用本文提出的控制算法,在Matlab软件中编程对直驱式电液伺服系统进行仿真研究。主要仿真参数如表1所示。
|
|
表 1 主要仿真参数表 Tab.1 Major simulation parameters |
控制算法中采用结构3-11-1的RBF神经网络,输入矢量为系统状态量(x1,x2,x3),隐藏层神经元的中心均匀分布在空间[–0.1,0.1]×[–0.03,0.03]×[–107,107]上,直驱式电液伺服控制系统的初始参数值取为:
|
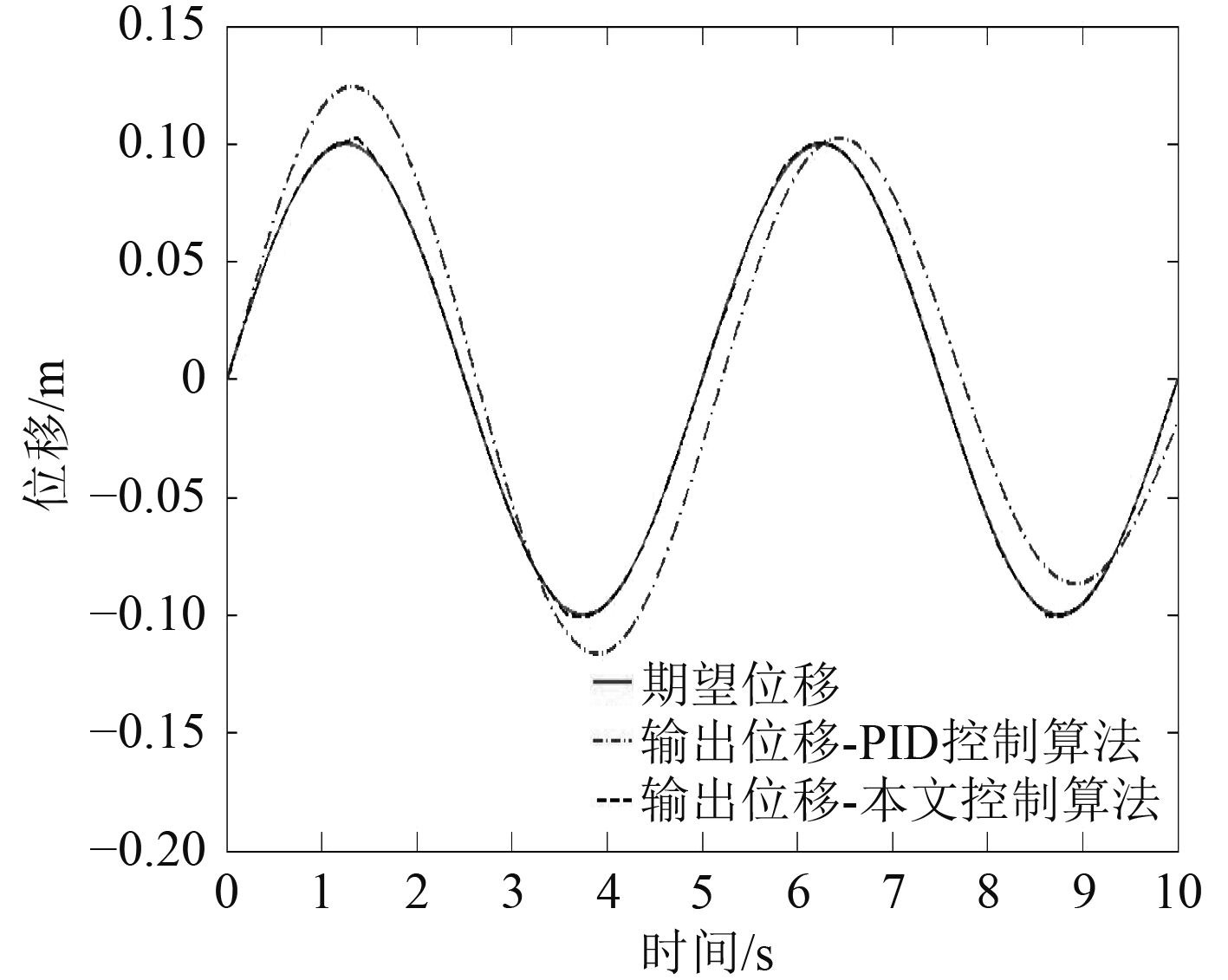
图 2 位移输出仿真结果 Fig. 2 Simulation result of the output displacement |
|
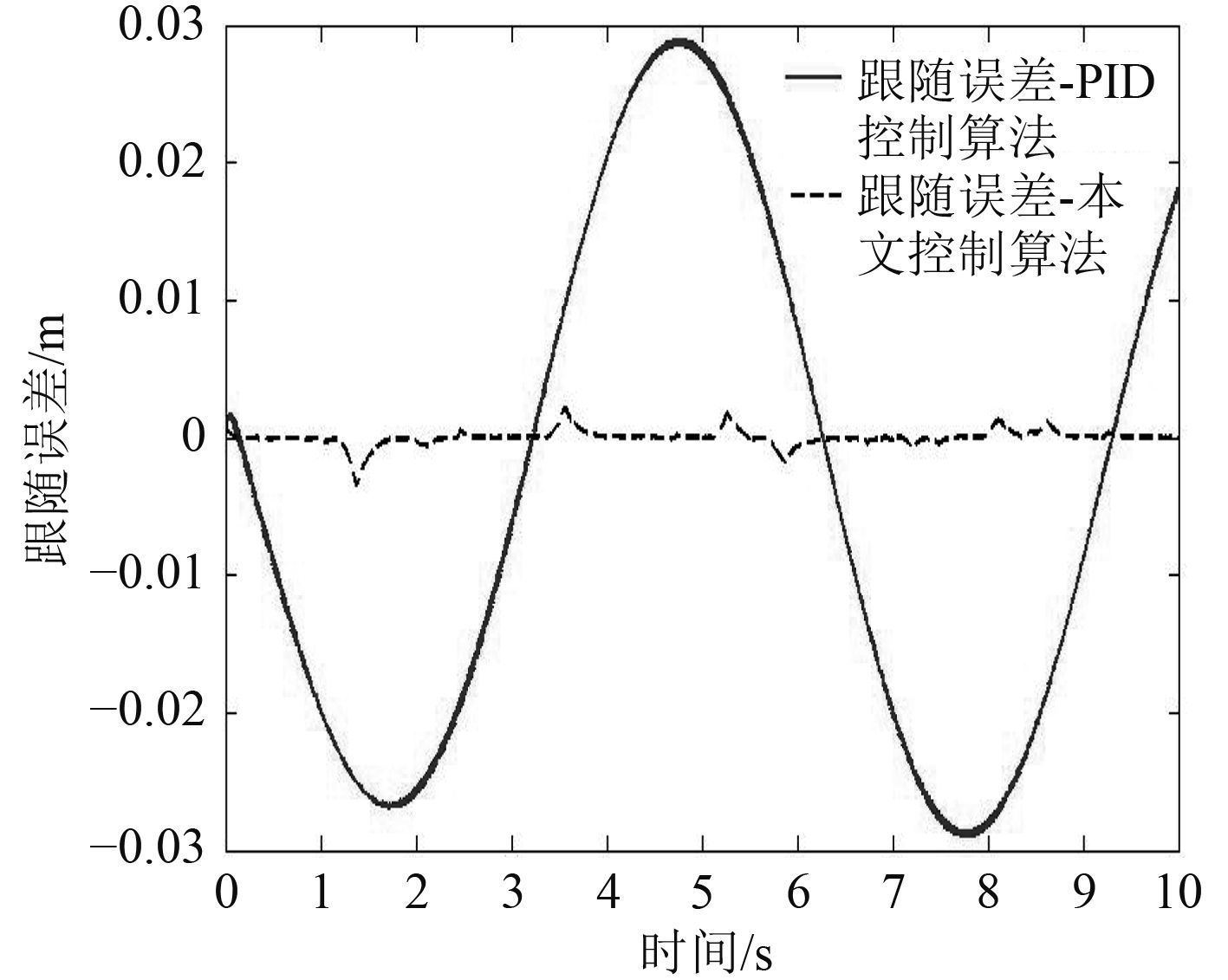
图 3 跟随误差仿真结果 Fig. 3 Simulation result of the following error |
|
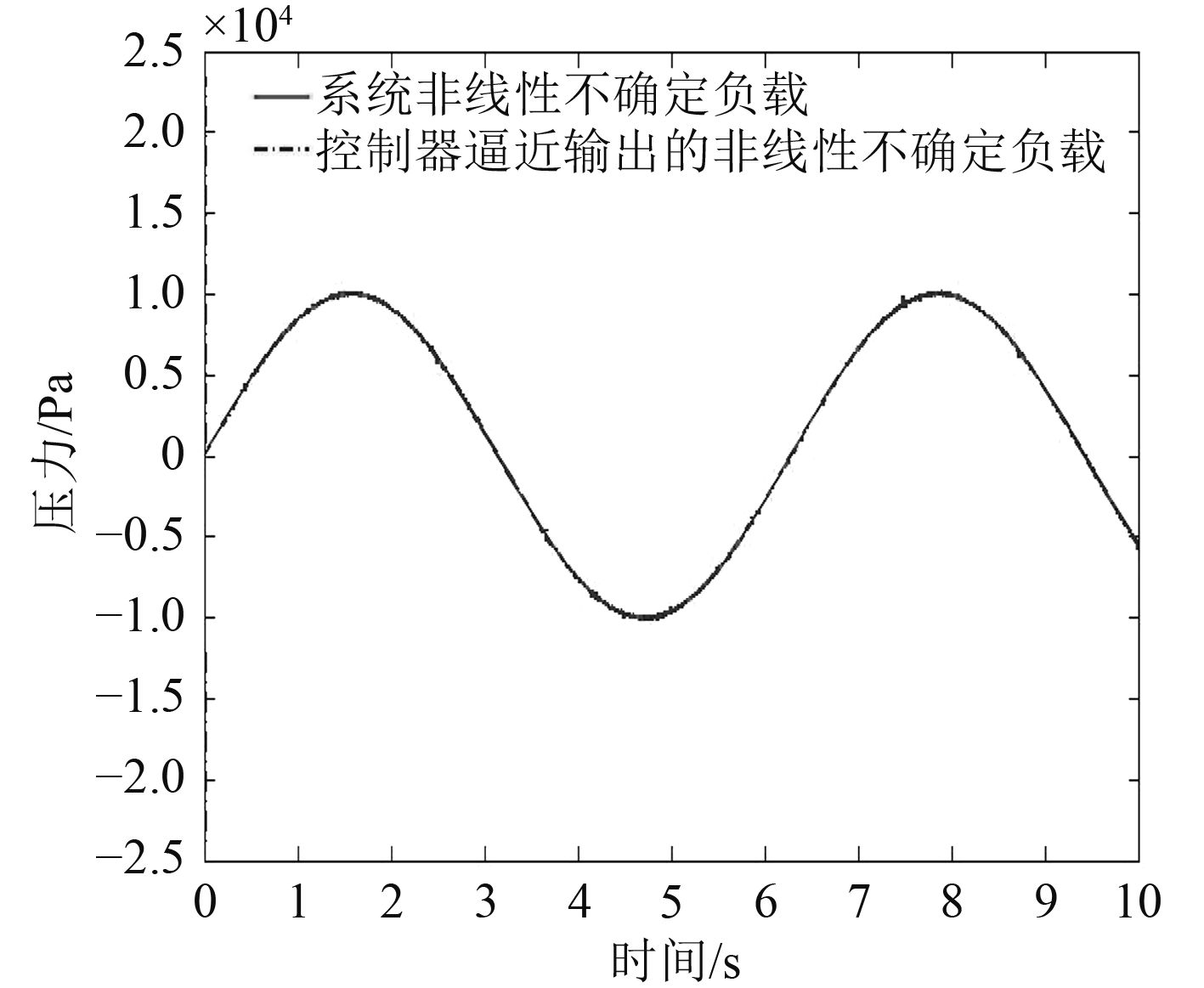
图 4 非线性不确定负载逼近仿真结果 Fig. 4 Simulation result of the uncertain nonlinear load |
由仿真结果,可得:
1)使用本文提出的控制算法,直驱式电液伺服系统的输出有界,控制系统稳定;
2)由于使用连续函数h(s)替代传统的非连续切换函数,有效消除了控制系统抖振现象;
3)控制算法中的RBF神经网络在自适应控制律下可以有效逼近直驱式电液伺服控制系统的非线性不确定负载,相比传统PID控制算法,本文的控制算法跟随误差较小,跟随特性更优。
5 结 语本文针对直驱式电液伺服系统的非线性不确定负载以及系统状态参数耦合特点,结合滑模控制的强抗干扰性及神经网络万能逼近特性,提出了一种多滑模神经网络自适应控制策略。控制算法不仅可以有效克服非线性不确定负载对系统跟随精度影响,而且能够避免传统滑模控制的抖振现象。通过理论分析与仿真验证,本文提出的控制算法稳定有效,对直驱式电液伺服系统的控制品质提高有一定的理论与实践价值。
| [1] | 王晓成. 直驱式电液伺服装置的改进及控制系统设计[D]. 哈尔滨: 哈尔滨工业大学, 2010. |
| [2] | ITO M, HIROSE N, SHIMIZU E. Main engine revolution control for ship with direct drive volume control system[C]//ISME. Tokyo, 2000. |
| [3] | ITO, SATO H, MAEDA Y. Direct drive volume control of hydraulic system and its application to the steering system of ship[C]//FLUCOME. Tokyo, 1997: 445–450. |
| [4] | MIN G, SUNG H, JONG S, et al. Modeling and control and electro hydrostatic actuator systems[C]//International Joint Conference, Japan, 2009: 3003–3008. |
| [5] |
姜继海, 涂婉丽, 曹健. 火箭舵机用直驱式容积控制电液伺服系统的研究[J]. 流体传动与控制, 2005, (1): 13–15.
JIANG Jihai, TU Wanli, CAO Jian. Study of direct drive volume control electro-hydraulic servo for a rocket rudder [J]. Fluid Power Transmission and Control, 2005, (1): 13–15. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ltcdykz200501005 |
| [6] |
陈娟, 乔彦峰. 伺服系统低速摩擦力矩特性及补偿研究概况[J]. 光机电信息, 2002, (11): 30–34.
CHEN Juan, QIAO Yan-feng. Review of low speed friction torsion and its compensation in servo systems [J]. Optics, Mechanics & Electronics Information, 2002, (11): 30–34. |
| [7] |
王旭永, 刘庆和. 电液马达位置伺服系统低速特性的机理研究[J]. 哈尔滨工业大学学报, 1993, 25(2): 60–68.
WANG Xu-yong, LIU Qin-he. Investigation into mechanism of low speed in electrohydraulic position servomotor system [J]. Journal of Harbin Institute of Technology, 1993, 25(2): 60–68. http://www.cnki.com.cn/Article/CJFDTOTAL-ZHJC408.004.htm |
| [8] | ZIAEI K, SEPEH RI N. Design of a nonlinear adaptive controller for an electrohydraulic actuator[J]. ASME Journal of Dynamic Systems, Measurement, and Control, 2003, 123(9): 449–456. |
| [9] | MORCL G, IAGNEMMA K, DUBOWSKY S. The precise control of manipulators with high joint-friction using base force torque sensing [J]. Automatic, 2000, 36: 931–941. |
| [10] |
陈刚, 柴毅, 丁宝苍, 等. 电液位置伺服系统的多滑模神经网络控制[J]. 控制与决策, 2009, 24(2): 221–225.
CHEN Gang, CHAI Yi, DING Bao-cang, etc. Multiple sliding mode neural network control of electro-hydraulic position servo system [J]. Control and Decision, 2009, 24(2): 221–225. http://www.oalib.com/paper/4220855 |
| [11] | 刘金琨. 滑模变结构控制Matlab仿真[M]. 北京: 清华大学出版社, 2005. |
| [12] |
晁红敏, 胡跃明. 动态滑模控制及其在移动机器人输出跟踪中的应用[J]. 控制与决策, 2001, 16(5): 565–568.
CHAO Hong-min, HU Yue-ming. Dynamical sliding mode control and its applications to output tracking of mobile robots [J]. Control and Decision, 2001, 16(5): 565–568. http://www.oalib.com/paper/4224317 |
| [13] | HEDRICK J K, YIP P P. Multiple sliding surface control: theory and application[J]. Journal of Dynamic Systems, Measurement, and Control, 2000, 122(4): 586–593. |
| [14] | DA F P. Decentralized sliding mode adaptive controller design based on fuzzy neural networks for interconnected uncertain nonlinear systems[J]. IEEE Trans on Neural Networks, 2000, 11(6): 1471–1480. |
| [15] |
管成, 朱善安. 基于Backstepping的电液伺服系统多级自适应滑模控制[J]. 仪器仪表学报, 2005, 26(6): 569–573.
GUAN Cheng, ZHU Shan-an. Backstepping-based multiple cascade adaptive sliding mode control of an electro-hydraulic servo system [J]. Chinese Journal of Scientific Instrument, 2005, 26(6): 569–573. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yqyb200506005 |
| [16] | KACHROO P, TOMIZUKA M. Chattering reduction and error convergence in the sliding-mode control of a class of nonlinear systems[J]. IEEE Trans on Automatic Control, 1996, 41(7): 1063–1068. |
| [17] | EDWARDS C. A practical method for the design of sliding mode controllers using linear matrix inequalities[J]. Automatica, 2004, 40(10): 1761–1769. |
| [18] | SLOTINE J J, SASTRY S S. Tracking control of nonlinear systems using sliding surfaces with application to robot manipulator[J]. Int J Control, 1983, 38(2): 465–492. |
| [19] |
焦宗夏, 华清. 电液负载模拟器的R B F 神经网络控制[J]. 机械工程学报, 2003, 39(1): 10–14.
JIAO Zong-xia, HUA Qing. RBF neural network control on electro-hydraulic load simulator [J]. Chinese Journal of Mechanical Engineering, 2003, 39(1): 10–14. |
| [20] |
高宁, 张建中. MATLAB 在RBF 神经网络模型中的应用[J]. 农业网络信息, 2: 110–116.
GAO Ning, ZHANG Jian-zhong. Application of RBF neural network model based on MATLAB [J]. Agriculture Network Information, 2: 110–116. http://www.cnki.com.cn/Article/CJFDTotal-JSSG201303052.htm |
| [21] | KNOHL T, UNBEHAUEN H. Adaptive position control of eletrohydraulic servo systems using ANN [J]. Mechatronics, 2000, 10(1): 127–143. https://www.sciencedirect.com/science/article/pii/S0957415899000549 |
| [22] |
顾凯, 李长春, 刘晓东. 电液伺服系统摩擦力分析及补偿研究[J]. 液压与气动, 2010, 5: 43–45.
GU Kai, LI Chang-chun, LIU Xiao-dong. Analysis and compensation for the friction in electro-hydraulic servo systems [J]. Chinese Hydraulics and Pneumatics, 2010, 5: 43–45. http://d.wanfangdata.com.cn/Periodical_yyyqd201005017.aspx |
 2018, Vol. 40
2018, Vol. 40
