直接转矩控制(DTC)自20世纪80年代提出以来,因其控制思想新颖、结构简单、鲁棒性强一直受到国内外学者的关注。但是它同时也存在定子磁链和转矩的脉动较大、逆变器开关频率不固定、系统低速运行时控制效果差等问题。针对这些问题,国内外相关研究人员做了大量的改进工作,并在直接转矩控制系统中融入智能控制算法,大大提高了这种控制方法的性能。
由于在传统的直接转矩控制系统中使用滞环控制器,虽然可以在一定的范围内限制转矩和磁链的误差,但是却导致了逆变器开关频率不固定,大大增加了开关器件的损耗和噪声。这个问题可以利用空间矢量调制技术来解决,通过合成的电压矢量来减缓定子磁链的增减速度,从而固定逆变器的开关频率。
在船舶电力推进系统实际运行的时候,电机由于受到定子电流频率变化和定子绕组温升等不确定因素的影响,定子电阻不断变化,这种变化在电机高速运行对定子磁链观测的影响不大,但是在低速时就容易造成定子磁链观测不准确。针对这个问题,采用的最普遍的方法是在DTC系统中加入定子电阻辨识模块,利用模糊控制技术、神经网络、模型参考自适应等方法在线辨识定子电阻。虽然这种方法可以在一定程度上解决低速时定子磁链观测不准确的问题,但是却使直接转矩控制结构变得复杂,因此引入滑模控制技术来解决这个问题。利用滑模控制技术对系统内部参数变化和外部干扰鲁棒性强的特点,构造出了一个不受定子电阻变化影响的定子磁链观测器,并且结构简单容易实现。
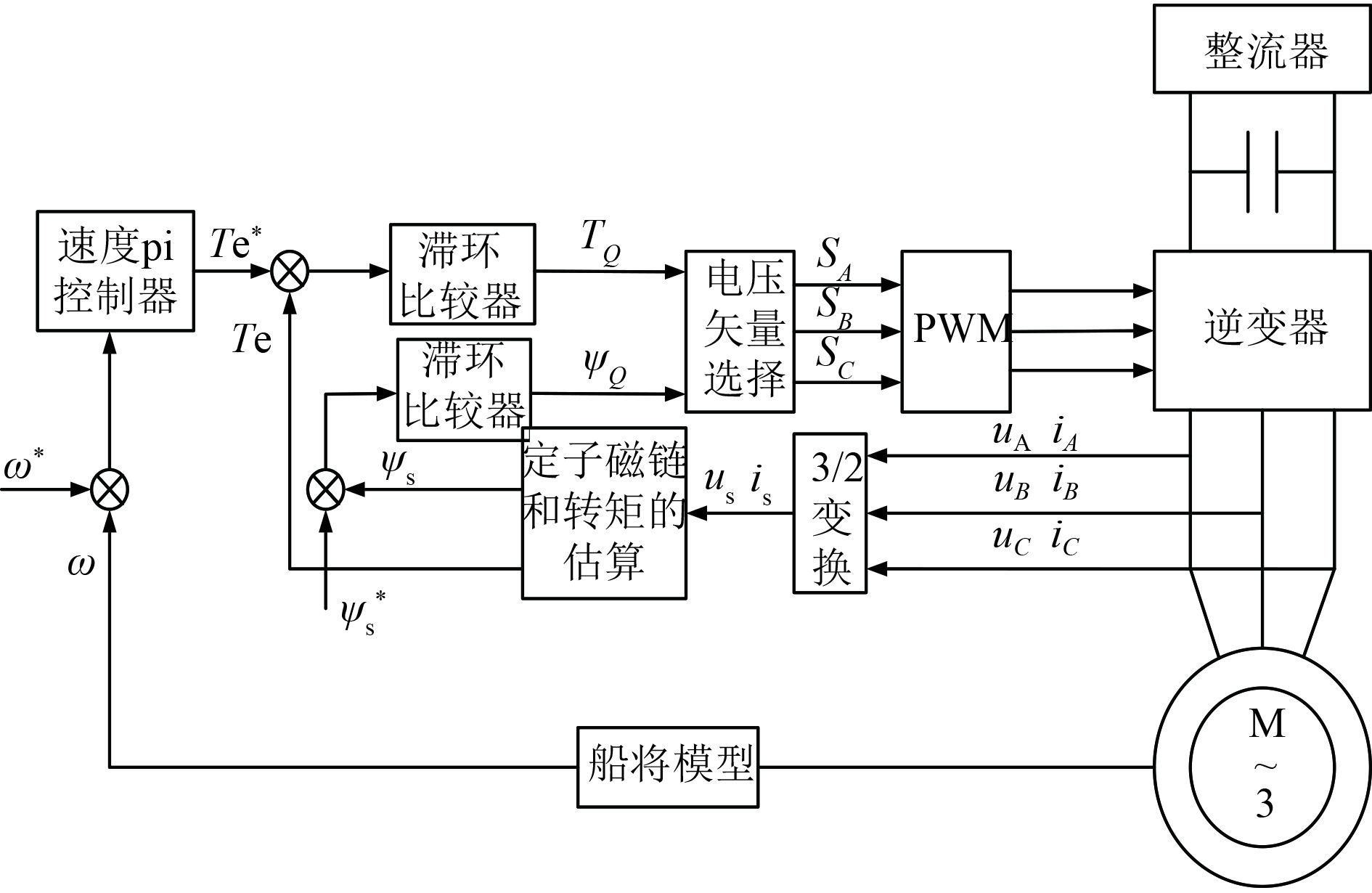
1 直接转矩控制(DTC) 1.1 传统直接转矩控制传统直接转矩控制系统框图如图1所示,其基本思想为利用采样得到的电流值与母线电压值估算出定子磁链值和转矩值,再将定子磁链估算值与转矩估算值分别与给定值进行滞环比较,利用得到的值选择出一个合适的电压矢量决定逆变器的开关状态,实现对电机的最佳控制。
|
图 1 DTC系统结构框图 Fig. 1 The control theory diagram of traditional DTC |
与传统直接转矩控制在1个控制周期内只选择8个电压矢量中1个电压矢量参与磁链与转矩的调节不同的是,电压空间矢量调制技术(space vector modulation,SVM)利用2个相邻的有效工作矢量和零电压矢量合成出所期望的电压矢量,理论上这种方法可以合成出任意多的电压矢量供选择,从而有效的减小转矩脉动,使控制效果得到明显的改善。
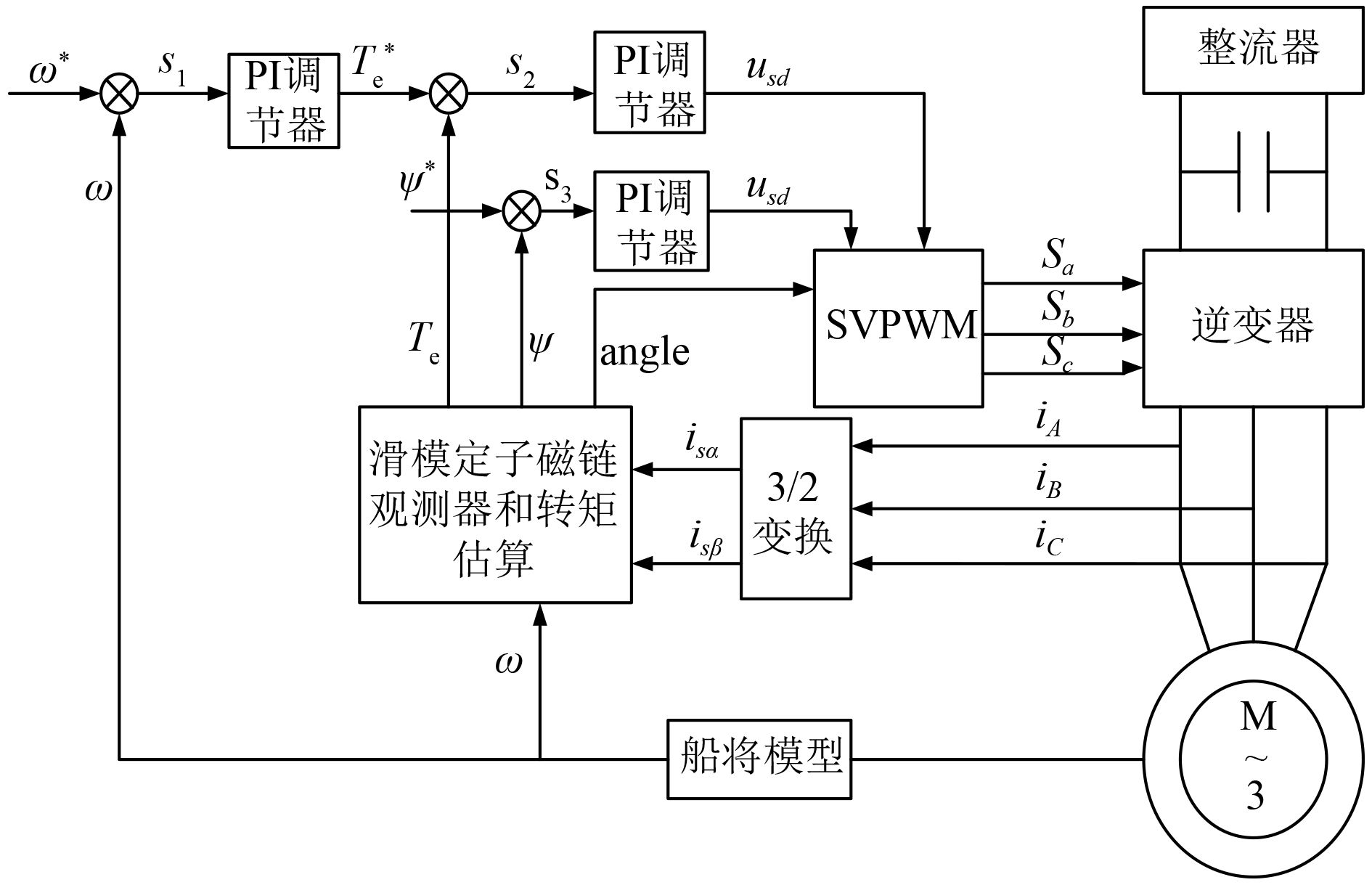
基于空间矢量调制的直接转矩控制系统框图如图2所示,与传统直接转矩控制一样,都需要利用定子磁链估算值与给定值、转矩估算值与给定值做比较,不同的是基于空间矢量调制技术的直接转矩控制用比较的结果经过PI调节器来产生参考电压矢量
|
图 2 DTC-SVM系统框图 Fig. 2 The control theory diagram of DTC-SVM |
在以电机角速度旋转的参考坐标系下,感应电机可以用下面的公式来表示。
磁链矩阵方程为:
| $\left[ \begin{array}{l}\psi _{s\alpha} \\\psi _{s\beta} \\\psi _{r\alpha} \\\psi _{r\beta} \end{array} \right] = \left[ {\begin{array}{*{20}{c}}{L_S}&0&{L_m}&0\\0&{L_S}&0&{L_m}\\{L_m}&0&{L_r}&0\\0&{L_m}&0&{L_r}\end{array}} \right]\left[ \begin{array}{l}i_{s\alpha} \\i_{s\beta} \\i_{r\alpha} \\i_{r\beta} \end{array} \right]\text{,}$ | (1) |
电压矩阵方程为:
| $\begin{split} \left[ \begin{array}{l}u_{s\alpha} \\u_{s\beta} \\u_{r\alpha} \\u_{r\beta} \end{array} \right] = & \left[ {\begin{array}{*{20}{c}}{R_s}&0&0&0\\0&{R_s}&0&0\\0&0&{R_r}&0\\0&0&0&{R_r}\end{array}} \right]\left[ \begin{array}{l}i_{s\alpha} \\i_{s\beta} \\i_{r\alpha} \\i_{r\beta} \end{array} \right] + \\ & p\left[ \begin{array}{l}\psi _{s\alpha} \\\psi _{s\beta} \\\psi _{r\alpha} \\\psi _{r\beta} \end{array} \right] + \left[ \begin{array}{l}0\\0\\\omega _r\psi _{r\beta} \\ - \omega _r\psi _{r\alpha} \end{array} \right]\text{,}\end{split}$ | (2) |
由上述2式可得:
| $ \left[ {\begin{array}{*{20}{c}}\!\!\! {u_{s\alpha} } \!\!\! \\\!\!\! {u_{s\beta} } \!\!\! \\\!\!\! {u_{r\alpha} } \!\!\! \\\!\!\! {u_{r\beta} } \!\!\! \end{array}} \right] = \left[ {\begin{array}{*{20}{c}}\!\!\! {R_s + L_{sp}}&0&{L_{mp}}&0 \!\!\! \\\!\!\! 0&{R_s + L_{sp}}&0&{L_{mP}} \!\!\! \\\!\!\! {L_{mp}}&{\omega _rL_m}&{R_r + L_{rp}}&{\omega _rL_r} \!\!\! \\\!\!\! { - \omega _rL_m}&{L_{mp}}&{ - \omega _r}&{L_r} \!\!\! \end{array}} \right] \left[ {\begin{array}{*{20}{c}}\!\!\! {i_{s\alpha} } \!\!\! \\\!\!\! {i_{s\beta} } \!\!\! \\\!\!\! {i_{r\alpha} } \!\!\! \\\!\!\! {i_{r\beta} } \!\!\! \end{array}} \right]\text{。}$ | (3) |
由式(1)~式(3)可以推导整理出定子电流的状态方程,表达式如下:
| $\begin{split}& p\left[ {\begin{array}{*{20}{c}}{i_s{\alpha} }\\{i_s{\beta} }\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{ - \displaystyle\frac{{R_sL_r + R_rL_s}}{{\sigma L_sL_r}}}&{ - \omega _r}\\{\omega _r}&{ - \displaystyle\frac{{R_sL_r + R_rL_s}}{{\sigma L_sT_r}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{i_{s\alpha} }\\{i_{s\beta} }\end{array}} \right]+\\ & \left[ {\begin{array}{*{20}{c}}{\displaystyle\frac{1}{{\sigma L_sT_r}}}&{\displaystyle\frac{{\omega _r}}{{\sigma L_s}}}\\{ - \displaystyle\frac{{\omega _r}}{{\sigma L_s}}}&{\displaystyle\frac{1}{{\sigma L_sT_r}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{\psi _{s\alpha} }\\{\psi _{s\beta} }\end{array}} \right] + \displaystyle\frac{1}{{\sigma L_S}}\left[ {\begin{array}{*{20}{c}}{u_{s\alpha} }\\{u_{s\beta} }\end{array}} \right]\text{。}\quad\quad\quad\;\;(4)\end{split}$ |
其中:
可以将式(4)改写成下面的形式:
| $\begin{split}p_{is\alpha} = & \frac{1}{{\sigma L_s}}(u_{s\alpha} - R_{sis\alpha} ) - \frac{{R_r}}{{\sigma L_r}}i_{s\alpha} - \\& \omega _ri_{s\alpha} + \frac{{R_r}}{{\sigma L_sL_r}}\psi _{s\alpha} + \frac{{\omega _r}}{{\sigma L_s}}\psi _{s\beta} \text{,}\end{split}$ | (5) |
| $\begin{split}p_{is\beta} = & \frac{1}{{\sigma L_s}}(u_{s\beta} - R_si_{s\beta} ) + \omega _ri_{s\alpha} - \\& \frac{{R_r}}{{\sigma L_r}}i_{s\beta} + \frac{{\omega _r}}{{\sigma L_s}}\psi _{s\alpha} + \frac{{R_r}}{{\sigma L_sL_r}}\psi _{s\beta} \text{,}\end{split}$ | (6) |
利用电流误差构造滑模面如下:
| $s = \left\{ \begin{aligned}& \widehat {i_{s\alpha} } - i_{s\alpha} = 0\text{,}\\& \widehat {i_{s\beta} } - i_{s\beta} = 0\text{,}\end{aligned} \right.$ | (7) |
利用滑模函数
| $\begin{split}p\widehat {_{is\alpha} } =& - \frac{{R_r}}{{\sigma L_r}}\widehat {i_{s\alpha} } - \omega _r\widehat {i_{s\alpha} } + \frac{{R_r}}{{\sigma L_sL_r}}\widehat {\psi _{s\alpha} } + \\& \frac{{\omega _r}}{{\sigma L_s}}\widehat {\psi _{s\beta} } + u_0{\mathop{\rm sgn}} (\widehat {i_{s\alpha} } - i_{s\alpha} )\text{,}\end{split}$ | (8) |
| $\begin{split}p\widehat {_{is\beta} } = & \omega _r\widehat {i_{s\alpha} } - \frac{{R_r}}{{\sigma L_s}}\widehat {i_{s\beta} } + \frac{{\omega _r}}{{\sigma L_s}}\widehat {\psi _{s\alpha} } + \\& \frac{{R_r}}{{\sigma L_sL_r}}\widehat {\psi _{s\beta} } + u_0{\mathop{\rm sgn}} (\widehat {i_{s\beta} } - i_{s\beta} )\text{。}\end{split}$ | (9) |
其中:
由式(9)–式(6)、式(8)–式(5)可以得到下面2个等式:
| $\begin{split}p(\widehat {i_{s\alpha} } - i_{s\alpha} ) = & \frac{1}{{\sigma L_s}}(u_{s\alpha} - R_si_{s\alpha} )\frac{{R_r}}{{\sigma L_r}}(\widehat {i_{s\alpha} } - i_{s\alpha} ) - \\ & \omega _r(\widehat {i_{s\beta} } - i_{s\beta} ) + \frac{{R_r}}{{\sigma L_sL_r}}(\widehat {\psi _{s\alpha} } - \psi _{s\alpha} ) + \\ & \frac{{\omega _r}}{{\sigma L_s}}(\widehat {\psi _{s\beta} } - \psi _{s\beta} ) - u_0sign(\widehat {i_{s\alpha} } - i_{s\alpha} )\text{,}\end{split}$ | (10) |
| $\begin{split}p(\widehat {i_{s\beta} } - i_{s\beta} ) = & \frac{1}{{\sigma L_s}}(u_{s\beta} - R_si_{s\beta} )\frac{{R_r}}{{\sigma L_r}}(\widehat {i_{s\beta} } - i_{s\beta} ) - \\ & \omega _r(\widehat {i_{s\alpha} } - i_{s\alpha} ) + \frac{{R_r}}{{\sigma L_sL_r}}(\widehat {\psi _{s\beta} } - \psi _{s\beta} ) + \\ & \frac{{\omega _r}}{{\sigma L_s}}(\widehat {\psi _{s\alpha} } - \psi _{s\alpha} ) - u_0sign(\widehat {i_{s\beta} } - i_{s\beta} )\text{。}\end{split}$ | (11) |
根据滑模控制理论可知,当系统进入滑动模态时:
| $\begin{split}& s = \left\{ \begin{array}{l}\widehat {i_{s\alpha} } - i_{s\alpha} = 0\\\widehat {i_{s\beta} } - i_{s\beta} = 0\end{array} \right.\text{,}{\text{并且有}}\widehat {\psi _{s\alpha} } - \psi _{s\alpha} = 0,\\& \widehat {\psi _{s\beta} } - \psi _{s\beta} = 0\text{。}\end{split}$ |
此时根据式(10)和式(11)可以得到下面2个等式:
| $u_{s\alpha} - R_si_{s\alpha} = \sigma L_su_0{\mathop {\rm sgn}} (\widehat {i_{s\alpha} } - i_{s\alpha} )\text{,}$ | (12) |
| $u_{s\beta} - R_si_{s\beta} = \sigma L_su_0{\mathop {\rm sgn}} (\widehat {i_{s\beta} } - i_{s\beta} )\text{,}$ | (13) |
根据下式即可求得定子磁链:
| $\psi _{s\alpha} = \int {\sigma L_su_0{\mathop {\rm sgn}} (\widehat {i_{s\alpha} } - i_{s\alpha} ){\rm d}t} \text{,}$ | (14) |
| $\psi _{s\beta} = \int {\sigma L_su_0{\mathop {\rm sgn}} (\widehat {i_{s\beta} } - i_{s\beta} ){\rm d}t}\text{。} $ | (15) |
由于系统受到固有惯性以及状态观测误差等的影响,系统在滑模面切换时并不是像理想要求的那样滑动而是在滑模面上来回穿行,因此产生高频抖动。本文用如下连续函数取代原来的开关函数,以此来减小系统的抖动。
| ${\mathop {\rm sgn}} (s) = \left\{ {\begin{aligned}& 1\text{,}&{s > \varepsilon }\text{,}\\& {s/\varepsilon }\text{,}&{s = \varepsilon }\text{,}\\& { - 1}\text{,}&{s < \varepsilon }\text{。}\end{aligned}} \right.$ | (16) |
式中的ε为正常数,这个常数的确定需要在实验过程中不断调整,选择出合适的值。
2.4 观测器稳定性分析选取李雅普诺夫函数:
| $\begin{split}p(S_\alpha ) = & \frac{1}{{\sigma L_s}}(u_{s\alpha} - R_si_{s\alpha} )\frac{{R_r}}{{\sigma L_r}}(S_\alpha ) - \\ &\omega _r(S_\beta ) + \frac{{R_r}}{{\sigma L_sL_r}}(\widehat {\psi _{s\alpha} } - \psi _{s\alpha} ) + \\ &\frac{{\omega _r}}{{\sigma L_s}}(\widehat {\psi _{s\beta} } - \psi _{s\beta} ) - u_0{\rm sign}(S_\alpha )\end{split}\text{,}$ | (17) |
| $\begin{split}p(S_\beta ) = & \frac{1}{{\sigma L_s}}(u_{s\beta} - R_si_{s\beta} )\frac{{R_r}}{{\sigma L_r}}(S_\beta ) - \\ &\omega _r(S_\alpha ) + \frac{{R_r}}{{\sigma L_sL_r}}(\widehat {\psi _{s\beta} } - \psi _{s\beta} ) + \\ &\frac{{\omega _r}}{{\sigma L_s}}(\widehat {\psi _{s\alpha} } - \psi _{s\alpha} ) - u_0{\rm sign}(S_\beta )\end{split}\text{。}$ | (18) |
根据滑模控制器的稳定性定理,当
本文分别在不考虑船舶电力推进系统电机参数变化和考虑电机参数变化情况下对2种方法进行仿真验证与结果分析。仿真中选用的异步电机参数如下:额定功率50 kW,额定电压
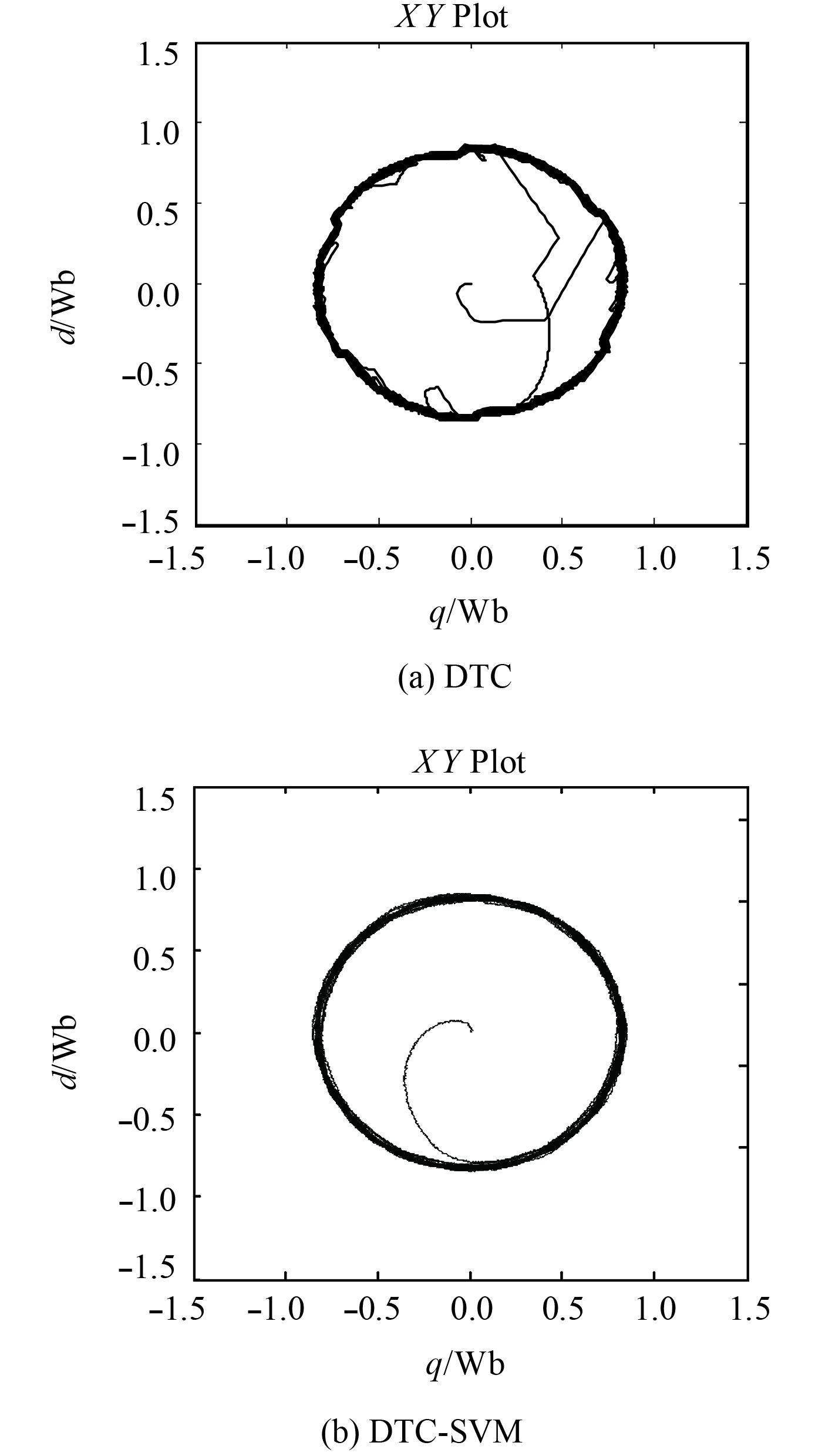
图3为传统DTC的磁链轨迹和本文使用方法的对比图。从图中可以看出,这2种控制方法的定子磁链轨迹都近似为圆形,也都能稳定的保持在给定0.83 Wb左右,但是传统方法在切换到低速时,定子磁链轨迹会因磁链内陷而导致畸变,而本文所使用方法的圆形轨迹更为光滑、磁链幅值脉动范围更小。2图的对比表明,改进后的磁链控制更加准确。
|
图 3 定子磁链仿真波形 Fig. 3 The simulation waveform of stator flux track |
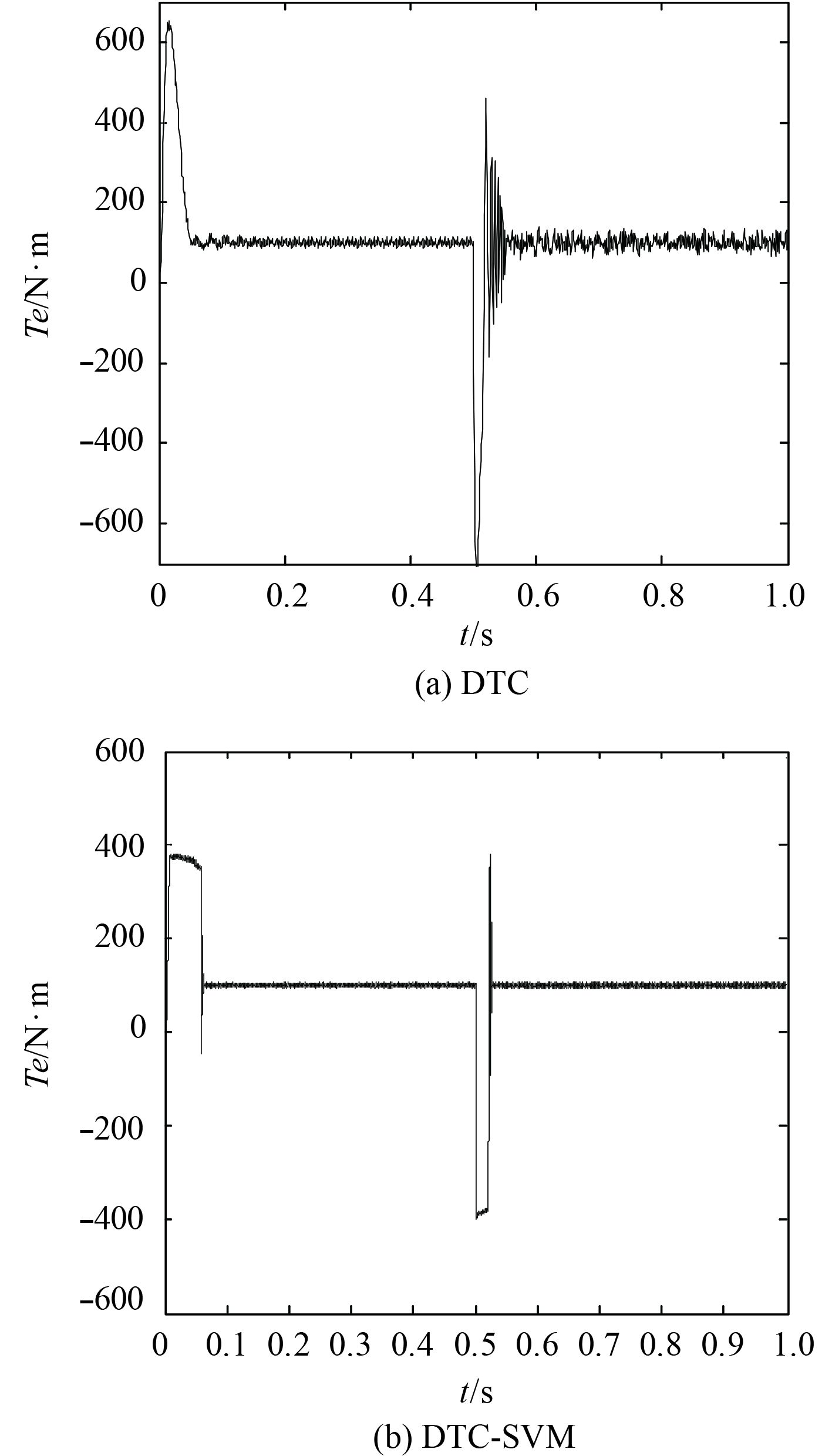
图4为2种方法转矩波形的对比图。从图中明显可以看出传统方法在电机低速运行时转矩脉动明显比高速运行时要大,在低速时波动范围大致为(70,130)
|
图 4 转矩仿真波形对比 Fig. 4 The simulation waveform of the torque |
由于电机在实际运行时定子电阻阻值会随着电机温度、定子电流频率的变化而变化到原有阻值的0.75~1.7倍。本文在做仿真时只考虑了电阻的变化问题,并没有考虑电机运行时实际如何变化。图5是本文做仿真时给定的参数变化曲线图,定子电阻变化曲线由原来的0.28 Ω增加到0.5 Ω。转子电阻变化曲线由0.816 Ω增大为原来的1.5倍。由于定子磁链滑模观测器计算模型中没有用到定子电阻而是用到了转子电阻,所以不需要考虑定子电阻对它的影响。
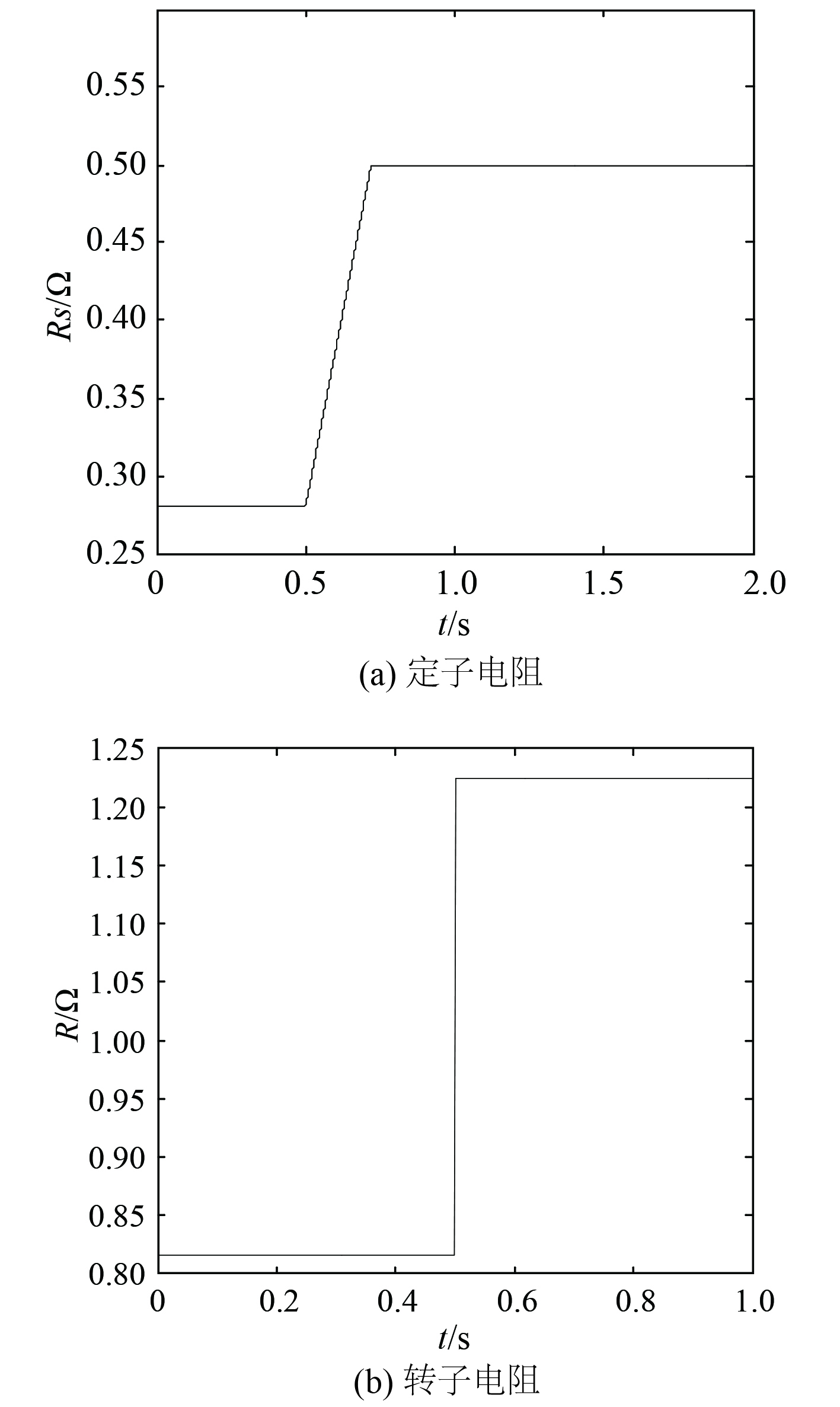
|
图 5 定子电阻和转子电阻变化轨迹 Fig. 5 Stator resistance and rotor resistance change trajectory |
图6是当电机定子电阻和转子电阻变化时2种方法的磁链对比图。传统DTC当定子电阻变化后磁链无法维持圆形轨迹。在电机实际运行中内部参数的变化是不可避免的,所以如何减小或者避免电机参数变化对电机精确控制带来的影响极其重要,它不仅关系到电机动态性能的好坏,甚至还有可能造成控制失败。而采用滑模变结构控制的控制策略中参数变化带来的影响则很小,说明本文所采用的方法能很好地避免因系统参数变化对系统控制性能的影响。
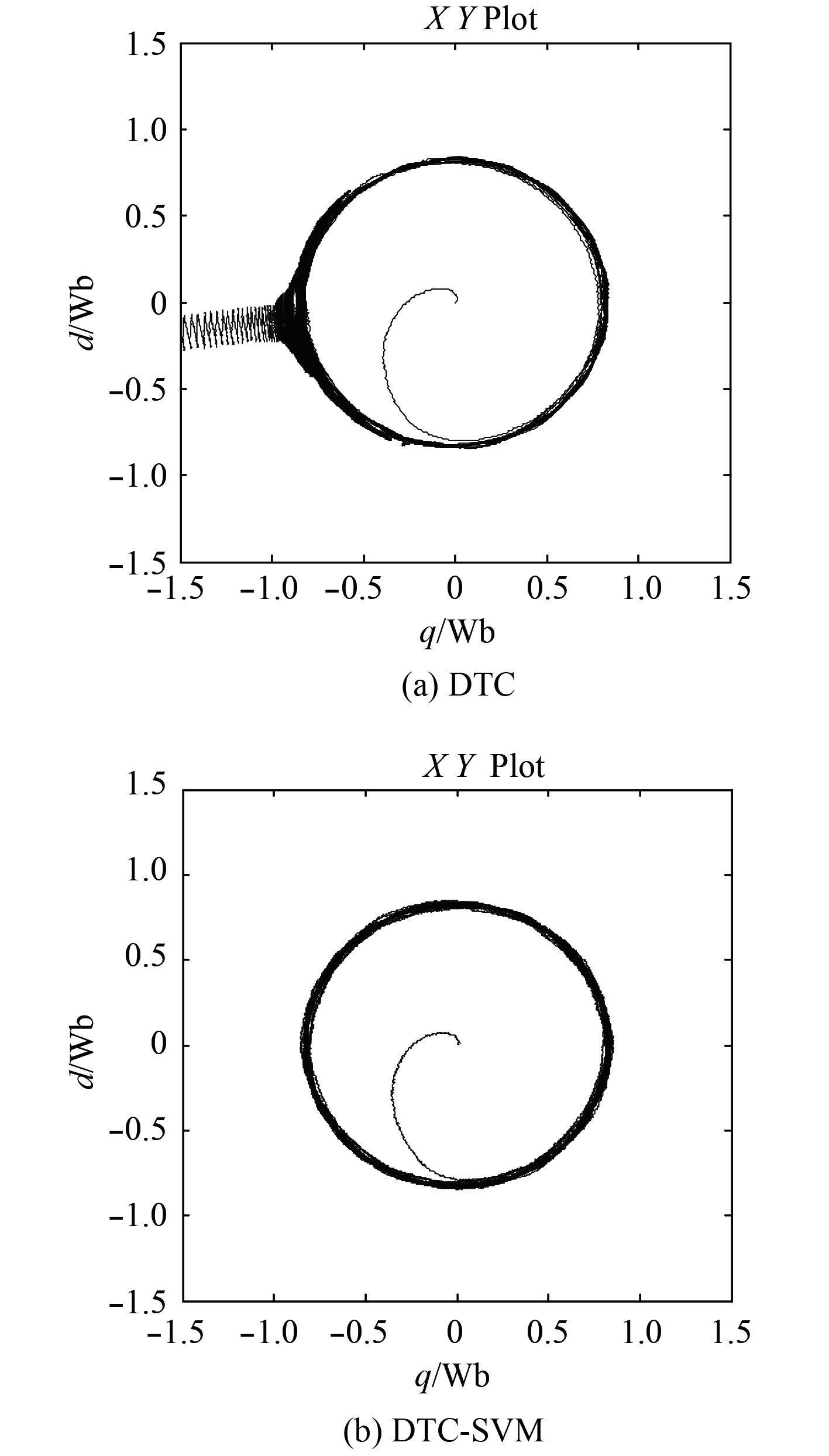
|
图 6 定子磁链轨迹对比图 Fig. 6 The simulation waveform of stator flux track |
由于转矩值是由定子磁链值得到的,所以磁链的误差对转矩脉动的影响非常大。图7中的转矩脉动可以看出定子电阻变化时引起的转矩脉动太大,这对我们实现精确电机控制来说是致命的缺点。而采用滑模控制技术的方法中的转矩脉动受系统参数变化的影响则比较小,依然能够达到预期值。综合磁链轨迹和转矩波形的对比图不难看出,采用定子磁链滑模观测器的直接转矩控制对电机参数变化的鲁棒性极强,可以很好地解决由于参数变化而导致的系统不稳定等问题。
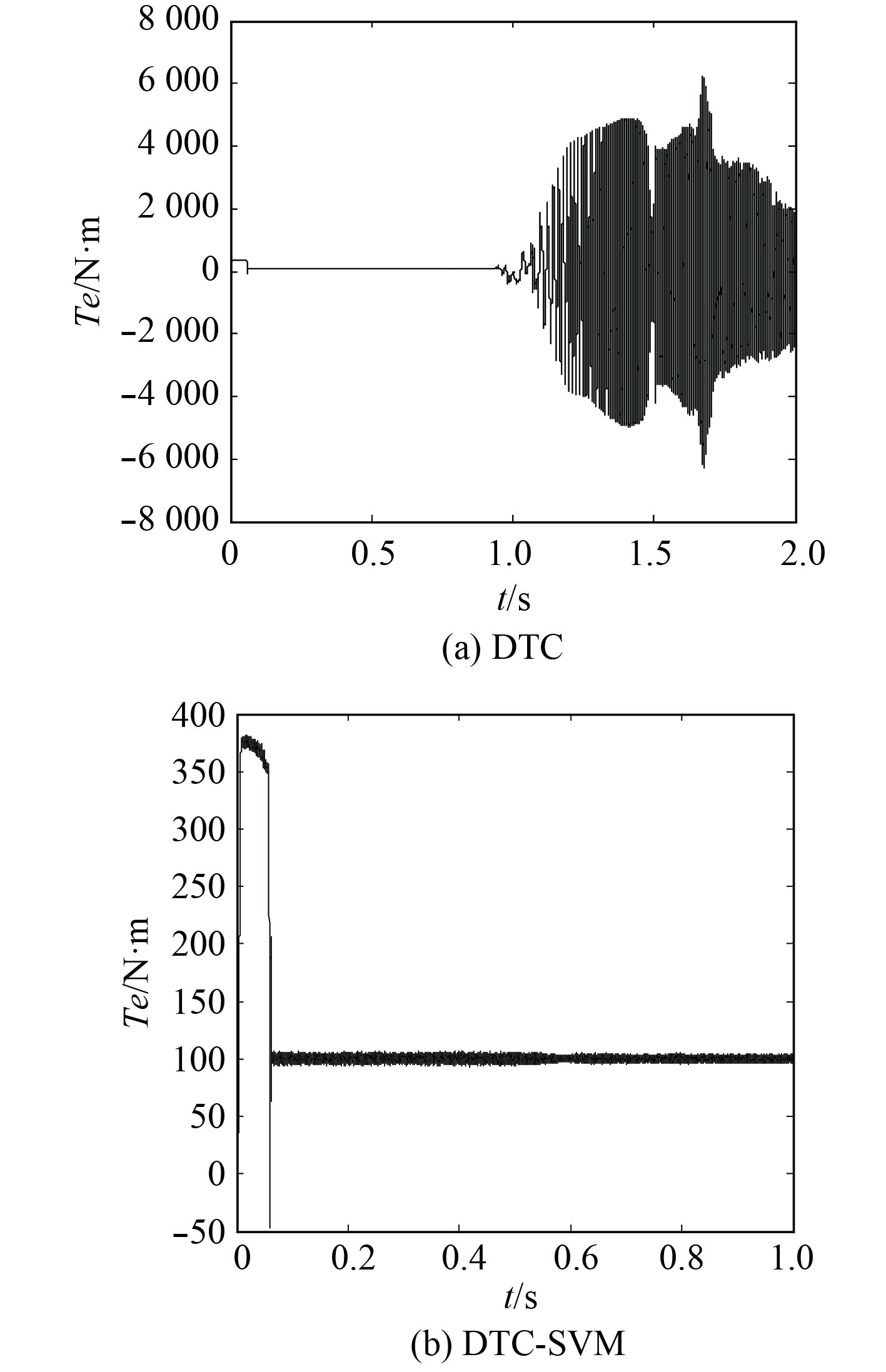
|
图 7 转矩波形对比图 Fig. 7 The simulation waveform of the torque |
仿真结果的分析与对比表明,本文采用的基于定子磁链滑模观测器的空间矢量调制直接转矩控制方法,对于船舶电力推进系统内部参数的变化有极强的鲁棒性,而且可以在保证逆变器的开关频率恒定的同时准确地观测定子磁链与减小转矩脉动,提高了电机在低速运行时的性能。
| [1] | 王丰尧. 滑模变结构控制[M]. 北京: 机械工业出版社, 1995: 315–330. |
| [2] | 高为炳. 变结构控制的理论及设计方法[M]. 北京: 科学出版社, 1996: 140–210. |
| [3] | 阮毅, 陈伯时. 电力拖动自动控制系统: 运动控制系统[M]. 北京: 机械工业出社, 2011: 115–199. |
| [4] |
王磊, 王京, 张勇军. 基于滑模变结构的异步电机直接转矩控制研究[J]. 电力电子技术, 2010, 44(1): 44–51.
WANG Lei, WANG Jing, ZHANG Yong-jun. Research on the asynchronous motor direct torque control based on the sliding mode variable structure [J]. Power Electronics, 2010, 44(1): 44–51. http://tjz.docin.com/p-265929883.html |
| [5] |
李春杰, 李旭春. 一种改进的直接转矩控制系统的定子磁链观测方法[J]. 电机与控制应用, 2006, 33(6): 32–35.
LI Chun-jie, LI Xu-chun. A modified stator flux observer of DTC control system[J]. Electric Machines & Control Application, 2006, 33(6): 32–35. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zxxdj200606007 |
| [6] |
李彦, 唐智星. 船舶电力推进DTC系统低速性能的改善研究[J]. 科学技术与工程, 2013, 07(6): 1773–1778.
LI Yan, TANG Zhi-xing. The improvement study of low speed performance in ship electric propulsion DTC system[J]. Science Technology and Engineering, 2013, 07(6): 1773–1778. http://doi.wanfangdata.com.cn/10.3969/j.issn.1671-1815.2013.07.013 |
| [7] |
吴晓新, 顾菊平, 易龙芳. 直接转矩控制系统中定子磁链观测器研究[J]. 微电机, 2010, 43(9): 48–51.
WU Xiao-xin, GU Ju-ping, YI Long-fang. Study of stator flux observer in direct torque control[J]. Micromotors, 2010, 43(9): 48–51. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=wdj201009014 |
| [8] |
王威, 刘惠康, 杨永利, 等. 基于直接转矩控制的异步电动机定子磁链自适应控制系统的仿真研究(J). 矿山机械, 2016, 44(1): 27–31.
WANG Wei, LIU Hui-kang, YANG Yong-li, et al. Simulation and research on stator flux adaptive control system of asynchronous motor based on DTC(J). Mining & Processing Equipment, 2016, 44(1): 27–31. http://www.cnki.com.cn/Article/CJFDTotal-KSJX201601008.htm |
| [9] |
张华强, 王新生, 魏鹏飞. 基于空间矢量调制的直接转矩控制算法研究[J]. 电机与控制学报, 2012, 6(6): 13–18.
ZHANG Hua-qiang, WANG Xin-sheng, WEI Peng-fei. Study on direct torque control algorithm based on apsce vector modulation[J]. Electric Machines and Control, 2012, 6(6): 13–18. http://www.cnki.com.cn/Article/CJFDTOTAL-DJKZ201206004.htm |
| [10] |
王剑平, 程樊, 张果. 基于滑模变结构的异步电机直接转矩控制系统研究[J]. 机械科学与技术, 2015, 34(12): 1896–1902.
WANG Jian-ping, CHEN Fan, ZHANG Guo. Research on asynchronous motor direct torque control system based on sliding mode variable structure[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(12): 1896–1902. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dldzjs201001017 |
| [11] |
黄志武, 阳同光. 基于滑模观测器定子磁链观测研究(J). 电气传动, 2008, 38(9): 43–46.
HUANG Zhi-wu, YANG Tong-guang. Observation of stator flux observer based on sliding mode [J]. Electric Drive, 2008, 38 (9): 43–46. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dqcd200809011 |
 2018, Vol. 40
2018, Vol. 40
