随着现代电力船舶技术的发展,电力推进已成为主流的推进方式,因此对动力装置的要求也越来越高。随之而来的是电力推进船舶用电量的增加导致船舶电网的管理也变得愈加复杂。相比陆地上的电网系统来说,船舶电站的电网容量较小,由于在海上航行,船上的各种电气设备面临着更恶劣的工作环境,因此造成的耗损也将更大。能量管理系统在保证船舶供电可靠性及稳定性的基础上,实现船舶最小燃油消耗,减少电气设备耗损,提高船舶经济性,从发电到用电之间实现能量的优化配置管理[1]。因此,能量管理系统结合其他控制系统相互控制,使船舶电站在发生故障时,例如发电机组跳闸,保证船舶的稳定运行,使船舶的性能可以得到最大程度的发挥。陆地上电力系统的减载策略已趋于成熟,文献[2 – 6]详细叙述了陆地电网低频减载策略及优化算法。本文借鉴陆地上电力系统的减载策略,在分析发电机组响应特性的基础上,针对发电机组跳闸的情况,分析了不同降低负载控制方法的优劣性,根据不同的瞬态负载选择合适的减载量,在提出的优化减载量的基础上,结合船舶失电快速性的特点,提出一种在系统频率变化未知时频率检测的方法,通过2次不同电压的采样值,在船舶发生电网故障时,能有效快速地检测电网频率的变化,为减载系统及时提供控制信号以进行减载控制。
1 发电机响应特性发电机发生跳闸故障,必须在很短时间内使电力系统重新达到正常状态。受制于失电的快速性,系统需要在短时内做出反应,保证电力系统的正常运行。
由于发电机组本身是一个惯性系统,且在网机组的数量也影响着减载系统的可用时间,因此根据牛顿运动力学第二规律,将发电机转子作用与发电机轴转矩关系表述如下[7]:
| $\frac{{2H}}{\omega }\frac{{{\rm d}\omega }}{{{\rm d}t}} = {T_{au}}{\text{。}} $ | (1) |
式中:
将式(1)进行简化,在标幺值的情况下,采用经典的同步发电机模型,当角速度
| $\frac{{2H}}{\omega }\frac{{{\rm d}\omega }}{{{\rm d}t}} \cong {P_{au}}{\text{。}}$ | (2) |
根据式(2),由1台发电机跳闸引起在网发电机频率降低,定义安全时间为频率下降到最低允许值的时间:
| ${t_{SL}} = \Delta \omega \frac{{2H}}{{P_{tran}^{\max } - 100\% }}{\text{。}} $ | (3) |
式中:
现定义发电机出现跳闸故障时,在网机组的瞬态阶跃负载如下:
| $\Delta {P_{tran}}(k,{N_f}) = \sum\limits_{f = 1}^{{N_f}} {{P_{gi}}(k,{N_f})}{\text{。}} $ | (4) |
式中:
每台发电机组提供的功率与它的惯性时间常数
| $\Delta {P_{tran,gi}}(k,{N_f}) = \frac{{{H_i}{P_{r,gi}}(k)}}{{\sum\limits_{i = 1}^{k - {N_f}} {{H_i}{P_{r,gi}}} }}\Delta {P_{tran}}(k,{N_f}){\text{。}} $ | (5) |
式中:
现定义每台发电机负载与瞬态阶跃负载之和为瞬态负载:
| ${P_{tran,gi}}(k,{N_f}) = {P_{gi}} + \Delta {P_{tran,gi}}(k,{N_f}){\text{。}}$ | (6) |
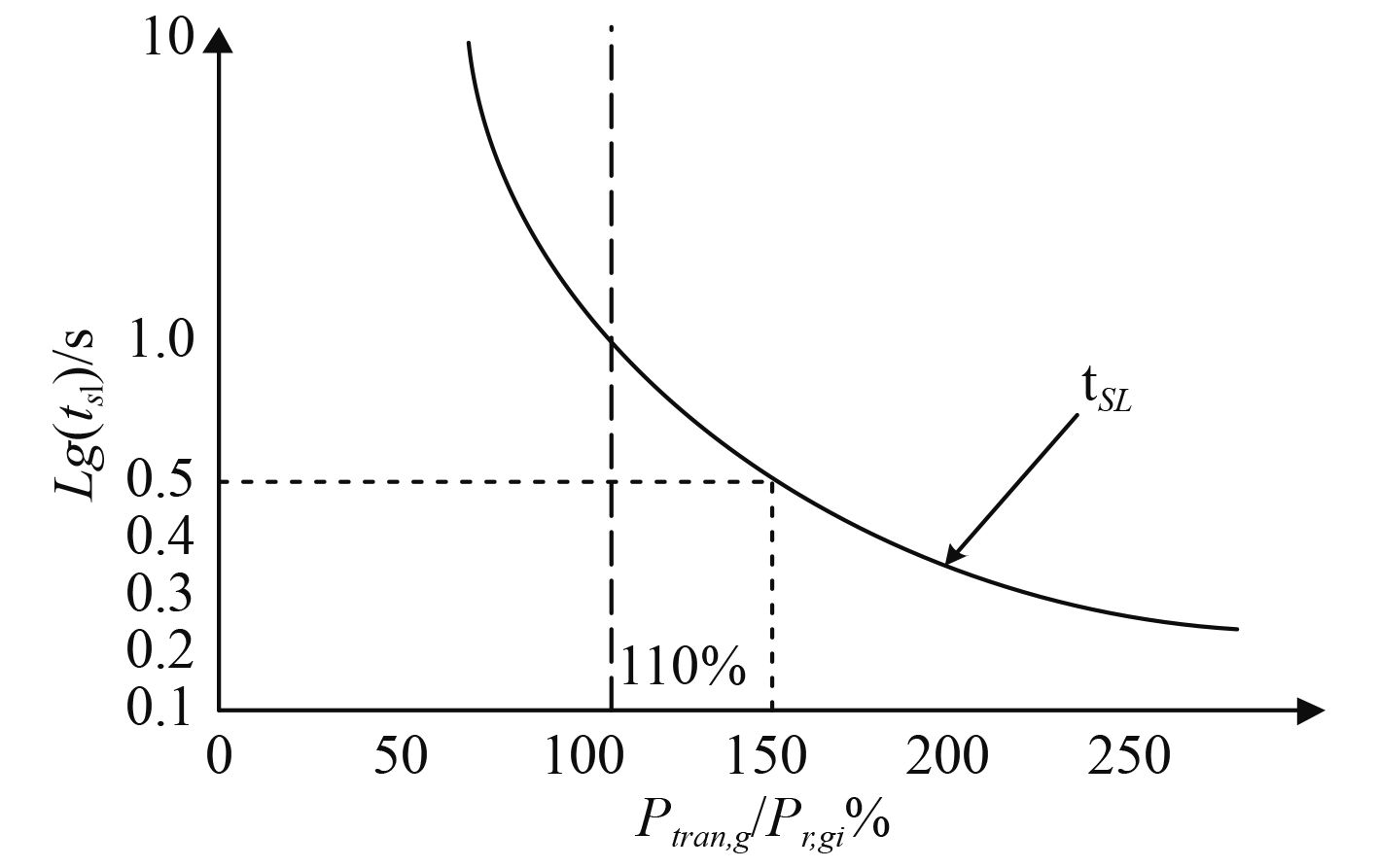
|
图 1 负载控制反应时间 Fig. 1 Load control the reaction time |
从图1可以看出,图中区域以安全时间为分界线,在曲线左下方区域为发电机组可承受的最大瞬态负载量,右上方区域为发生失电故障危险的瞬态负载量。对于不同的控制方法而言,都会造成其安全时间值也不同,允许的最大瞬态负载量也不相同。根据图1所示,当最大瞬态负载达到160%时,减载控制的响应时间在500 ms之内。
根据式(3)可知,当减载量较低时,则加载的时间限制将延长。快速减载系统(FLR)的减载取决于最大瞬态负载,现定义减载系统瞬态负载变化量如下:
| $\begin{aligned}\Delta {P_{FLR,gi}} =& {P_{tran,gi}}(k,{N_f}) - {P_{gi}} - \min ({a_{\max }}{P_{r,gi}} - {P_{gi}},\Delta {P_{gi}})\\\;\;\;\;\;\;\;\;\;\;\; = &\Delta {P_{tran,gi}}(k,{N_f}) - \min ({a_{\max }}{P_{r,gi}} - {P_{gi}},\Delta {P_{gi}}){\text{。}}\end{aligned}$ | (7) |
式中:最大瞬态负载
船级社规定发电机组最大频率降限值
| $\Delta {\omega _{FLR,gi}} = \Delta \omega _{gi}^{\max } - \Delta {\omega _{en,gi}}(\Delta {P_{gi}}){\text{。}}$ | (8) |
当在网机组原本就少而发生1台机组跳闸的情况,则会呈现出在网机组负载波动达到140%~160%的现象,危及到整个船舶电力系统。因此,能量管理系统必须尽快减少负载来降低其他机组的负载以防止发生连环效应。对于各船舶柴油机发电机,根据船级社要求,发电机必须在0.5~1 s内减去多余的负载以保证船舶运行的安全性。
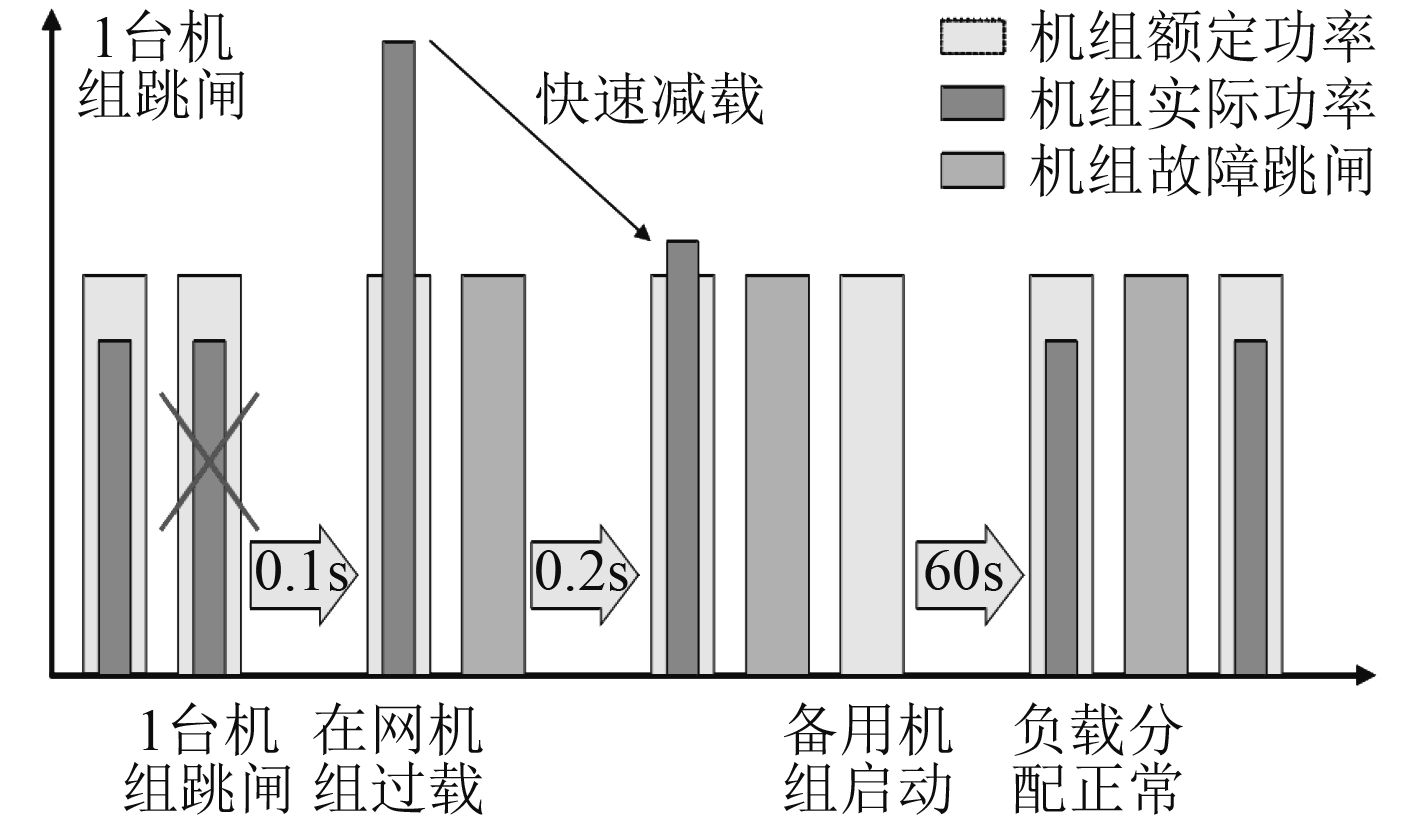
|
图 2 能量管理系统的控制步骤 Fig. 2 Power management system control steps |
图2描述的是能量管理系统控制减载步骤。系统监测到在网机组由于跳闸机组引起的高瞬态负载,在安全时间内通过减去其多余的加载在在网机组上的负载,保证负载分配正常,起到保护安全的作用。经研究,已有如下几种比较成熟的减载方法运用在海洋船舶上:
1)基于可用功率的卸载方式:根据有功功率进行减负载,通过各层节点分阶段断开不重要的耗载件;
2)基于频率的卸载方式:当频率低于临界值时发挥作用,通过全波傅里叶测频算法检测电网的频率,实现实时监测;
3)基于事件的减载方式:根据减载件的不同重要性进行有选择的减载;
4)基于频率的相反馈减载方式:以频率下降为基础系统保护措施将故障区直接隔断。
3 减载数量 3.1 过量瞬态阶跃负载减载柴油机的惯性和柴油机对阶跃负载的反应能力决定了剩余在网机组能承担阶跃负载的时间。当快速减载系统被设计成减去超过柴油机最大承受量上限的负载时,则
| $\begin{aligned}& \Delta {P_{FLR,gi}} = \Delta {P_{FLR,gi}}(k,{N_f}) - \Delta P_{gi}^{\max },\\& \Delta {\omega _{FLR,gi}} = \Delta \omega _{gi}^{\max } - \Delta \omega _{en,gi}^{\max }{\text{。}}\end{aligned}$ | (9) |
通常根据柴油机的特性有如下限制;
| $\begin{aligned}& 0.25{P_{rgi}} \text{≤} \Delta P_{gi}^{\max }({P_{gi}}) \text{≤} 0.33{P_{rgi}},\\& 0.03\Delta {\omega _{0,gi}} \text{≤} \Delta {\omega _{en,gi}}(0.25{P_{r,gi}}) \text{≤} 0.06\Delta {\omega _{0,gi}},\\& \Delta \omega _{gi}^{\max } = 0.1{\omega _{0,gi}}{\text{。}}\end{aligned}$ | (10) |
式中:
| $\begin{aligned}{t_{SL,i}} =& (\Delta \omega _{gi}^{\max } - \Delta {\omega _{en,gi}}) \times \\&\frac{{2{H_i}}}{{\Delta {P_{tran,gi}}(k,{N_f}) - \min ({a_{\max ,g}}{P_{r,gi}} - {P_{gi}},\Delta {P_{gi}})}}{P_{r,gi}}{\text{。}}\end{aligned}$ | (11) |
达到频率下限时间
快速减载系统的执行时间可能的范围:
| $\begin{split}{P_{tran,gi}} = & (\Delta \omega _{gi}^{\max } - \Delta \omega _{en,gi}^{\max })\frac{{2{H_i}}}{{{t_{FLR,i}}}}{P_{r,gi}} + {P_{gi}}+ \\ & \min ({a_{\max ,g}}{P_{r,gi}} - {P_{gi}},\Delta {P_{gi}}){\text{。}}\end{split}$ | (12) |
从式中可以看出,最大瞬态负载与柴油机初始承担的负载
如果要求减掉所有故障后的负载,则
| $\begin{split}& \Delta {P_{FLR,gi}} = \Delta {P_{tran,gi}}(k,{N_f}),\\&\Delta {\omega _{FLR,gi}} = \Delta \omega _{gi}^{\max }{\text{。}}\end{split}$ | (13) |
全瞬态阶跃负载减载所需时间和柴油机不承担故障后的阶跃负载的计算如下:
| ${t_{SL,i}} = (\Delta \omega _{gi}^{\max })\frac{{2{H_i}}}{{\Delta {P_{tran,gi}}(k,{N_f})}}{P_{r,gi}}{\text{。}}$ | (14) |
当
| ${P_{tran,gi}} = (\Delta \omega _{gi}^{\max })\frac{{2{H_i}}}{{{t_{FLR,i}}}}{P_{r,gi}} + {P_{gi}}{\text{。}}$ | (15) |
本文将上述2种不同的控制策略进行优化组合,以达到降低减载所需的时间。当发生故障前运行的负载不同时,其可承受的阶跃负载能力也不同,而按照船级社的规范,定义的柴油机的最大允许负载阶跃,其线性方程表示如下:
| $\frac{{\Delta P_g^{\max }({P_g})}}{{{P_{rg}}}} = \left\{ \!\!\!\begin{array}{l}0.33 - 0.303{P_g},\;0 \leqslant {P_g} < 0.33;\\0.3 - 0.217{P_g},\;0.33 \leqslant {P_g} < 0.56;\\ - 0.068 + 0.444{P_g},\;0.56 \leqslant {P_g} < 0.74;\\1 - {P_g},\;0.74 \leqslant {P_g} < 1{\text{。}}\end{array} \right.\!\!\!\!\!$ | (16) |
柴油机接近最优的负载阶跃响应如图3所示。
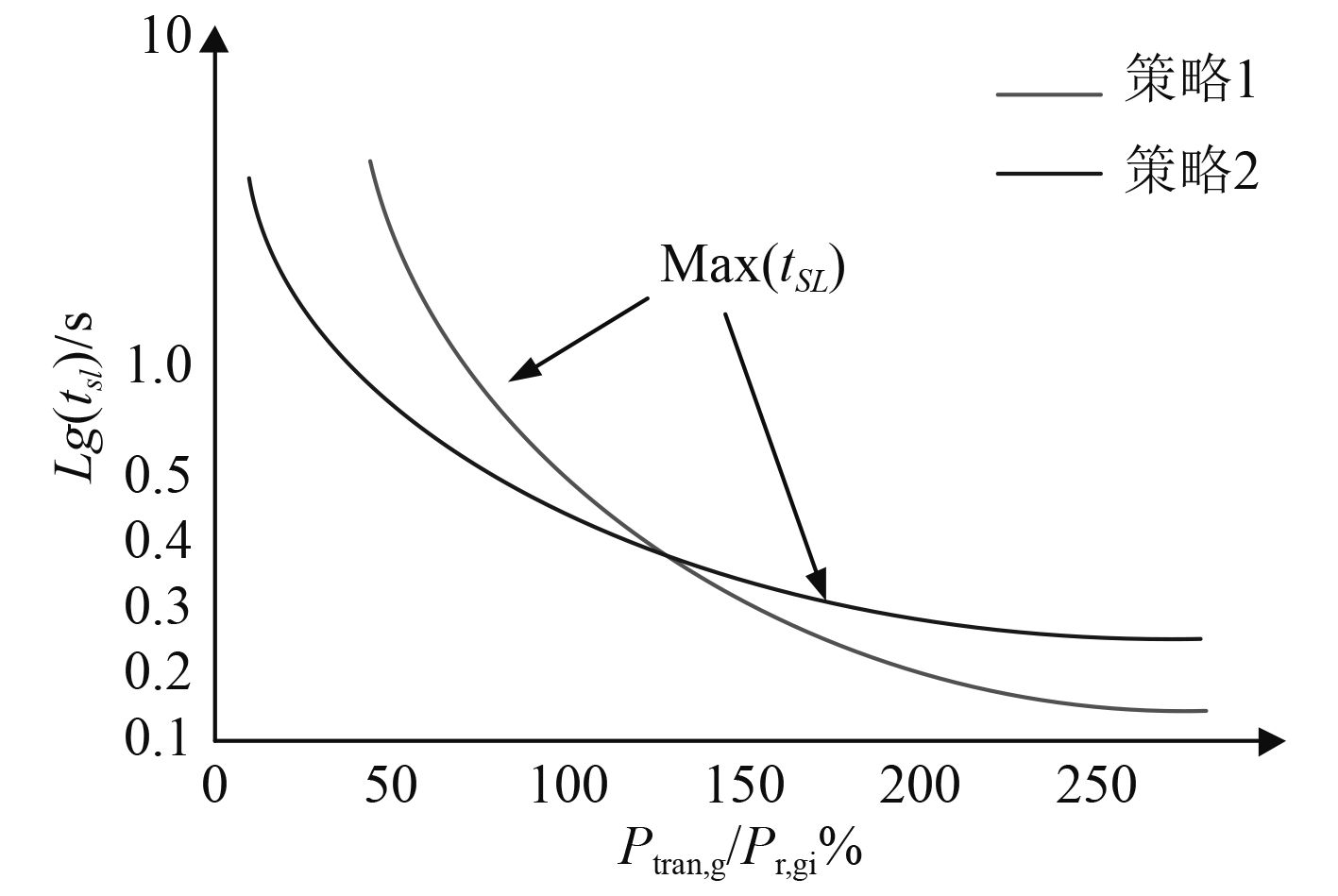
|
图 3 策略1和策略2的减载时间关系 Fig. 3 Strategy 1 and 2 of the lightening time relationship |
为了找到柴油机最优阶跃响应,本文将目标函数设定如下:
| $\begin{array}{l}\max ({t_{SL,i}}) =\\\; \mathop {\max }\limits_{\Delta {P_{gi}}} \left\{ {(\Delta \omega _{gi}^{\max } - \Delta {\omega _{en,gi}}(\Delta {P_{gi}}))\displaystyle\frac{{2{H_i}}}{{\Delta {P_{tran,gi}}(k,{N_f}) - \Delta {P_{r,gi}}}}} \right\},\\\Delta {P_{gi}} = \left\{ \begin{array}{l}\Delta P_{gi}^*\\0\end{array} \right.\\\Delta {\omega _{en,gi}}(\Delta {P_{gi}}) = \left\{ \begin{array}{l}\Delta \omega _{en,gi}^*(\Delta {P_{gi}}),\\0{\text{。}}\end{array} \right. \quad\quad\quad\quad\quad\quad\quad\,\;\; (17)\end{array}$ |
基于本文提出的优化后的瞬态阶跃负载的减载量,本文结合陆地上电网频率检测以及船舶失电的快速性,提出一种在系统频率变化趋势未知时频率检测的方法。首先,通过滤波器对母线三相电压进行采样得到基频分量。三相电压各自的余弦表达式为:
| ${u_A}(t) = {U_m}\cos (\omega t), $ | (18) |
| ${u_B}(t) = {U_m}\cos (\omega t - \frac{2}{3}\pi ){\text{,}}$ | (19) |
| ${u_C}(t) = {U_m}\cos (\omega t + \frac{2}{3}\pi ){\text{。}}$ | (20) |
由式(18)~式(20)容易得出,A相电压对应的正弦表达式为:
| $u{'_A}(t) = {U_m}\sin (\omega t) = \frac{{{u_B}(t) - {u_C}(t)}}{{\sqrt 3 }}{\text{。}}$ | (21) |
由式(18)和式(21)可以得出实时测量的电压幅值
| ${U_m} = \sqrt {({u_A}{{(t)}^2}) + {{(\frac{1}{\omega }\frac{{{\rm d}{u_A}(t)}}{{{\rm d}t}})}^2}}{\text{。}} $ | (22) |
取2次不同的采样值,例如取
| $\begin{aligned}& \displaystyle\frac{{{u_A}(k){u_A}(k - 1) - u{'_A}(k)u{'_A}(k - 1)}}{{{U_m}^2}}=\\& \cos (k\omega {T_s})\cos [(k - 1)\omega {T_s}] - \sin (k\omega {T_s})\sin [(k - 1)\omega {T_s}]=\\& \cos [(2k - 1)\omega {T_s}],\end{aligned}$ | (23) |
因此,由式(23)可得
| $f = \frac{{{\rm arc}(\displaystyle\frac{{{u_A}(k){u_A}(k - 1) - u{'_A}(k)u{'_A}(k - 1)}}{{{U_m}^2}})}}{{2\pi (2k - 1){T_s}}}, $ | (24) |
其中
快速减负载系统原理框图如图4所示。
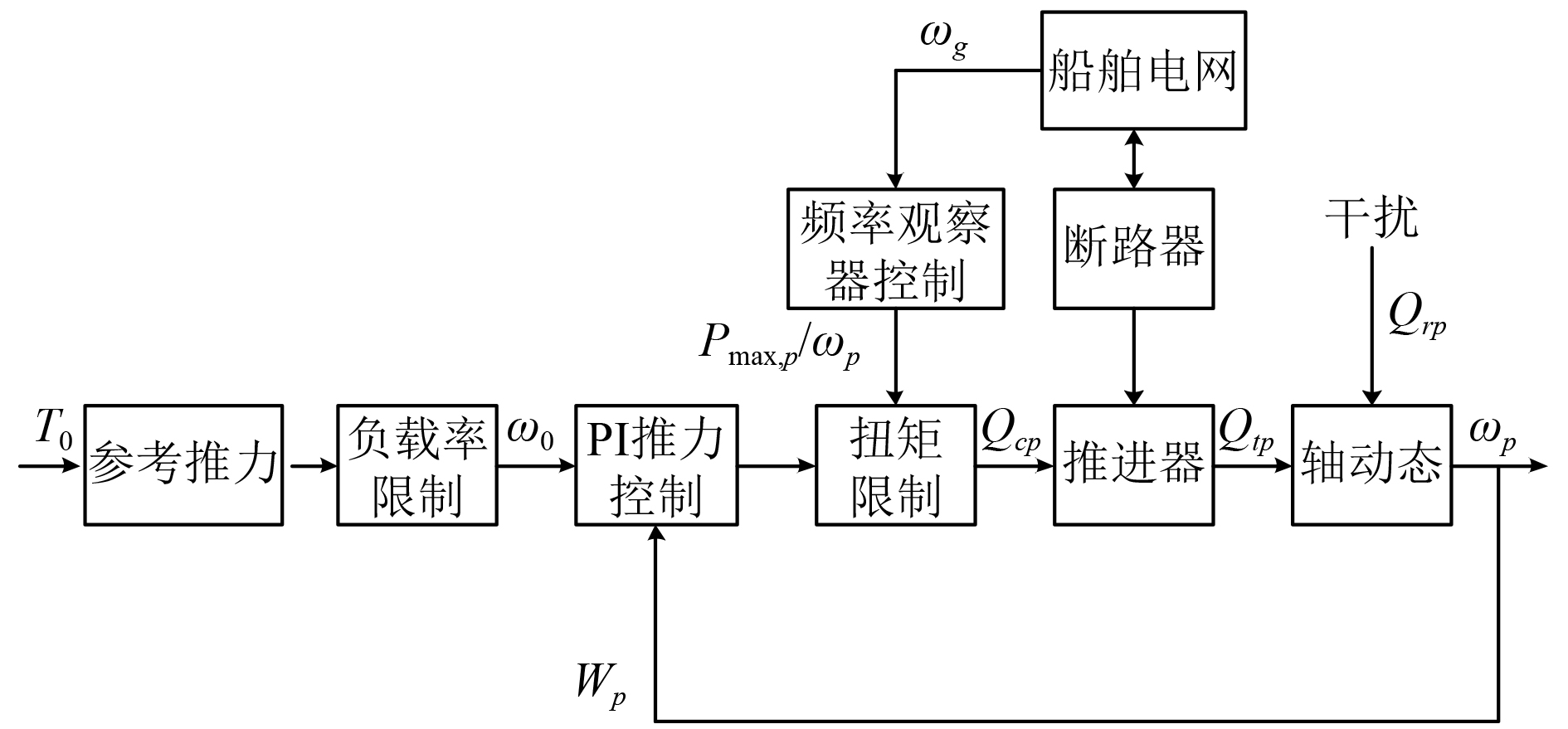
|
图 4 快速减负载系统 Fig. 4 Rapid during the load system |
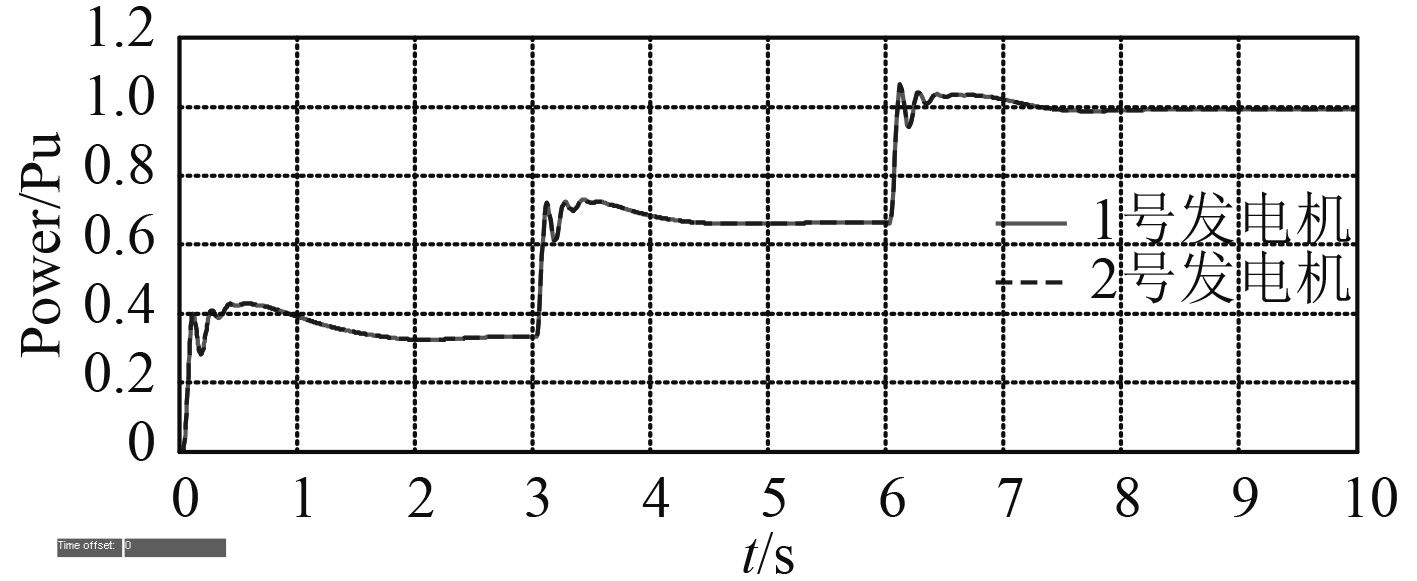
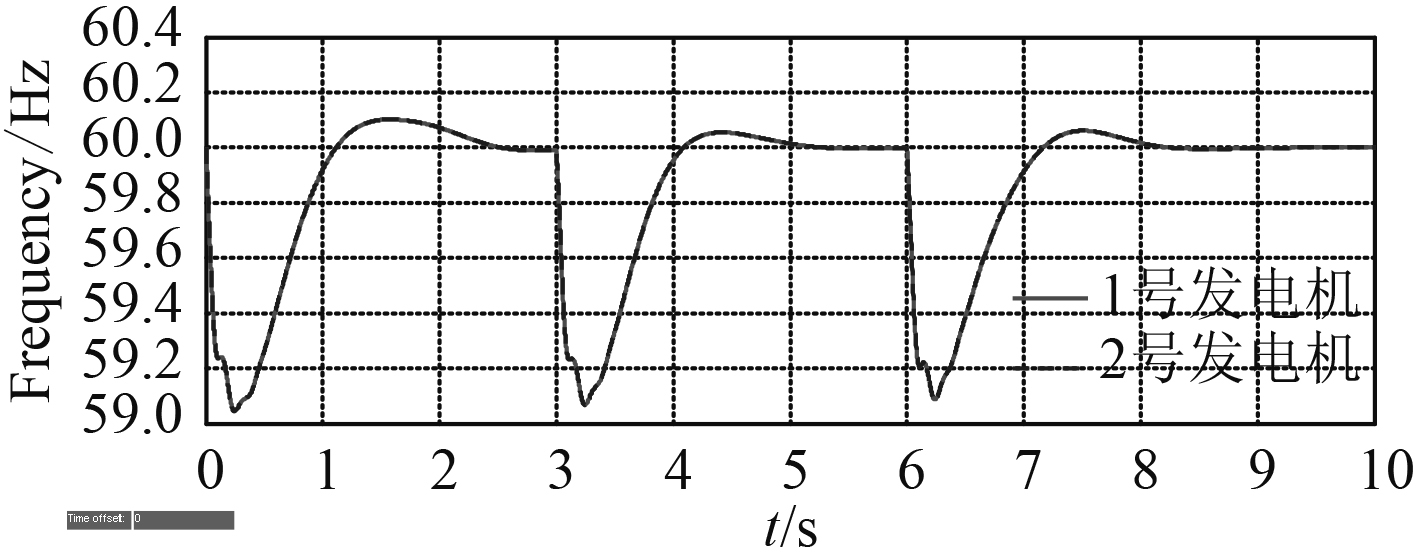
通过对发电机组加载、减载,简单模拟发电机输出功率的变化,验证发电机输出功率的稳定性和可靠性。图5和图6显示了对2台发电机在网进行加载仿真。
|
图 5 发电机在网加载功率变化 Fig. 5 Generator load changes in power network |
|
图 6 发电机在网加载频率变化 Fig. 6 Generator in network load frequency change |
0 s时加载到33%,3 s时加载到66%,6 s时加载到100%,这是一般柴油机的加载过程。从图5和图6中可以看出2台发电机的功率有明显的阶跃反应,并最终达到稳住状态。电网频率也出现了明显的下降,其偏差在1 Hz以内,小于2%。。
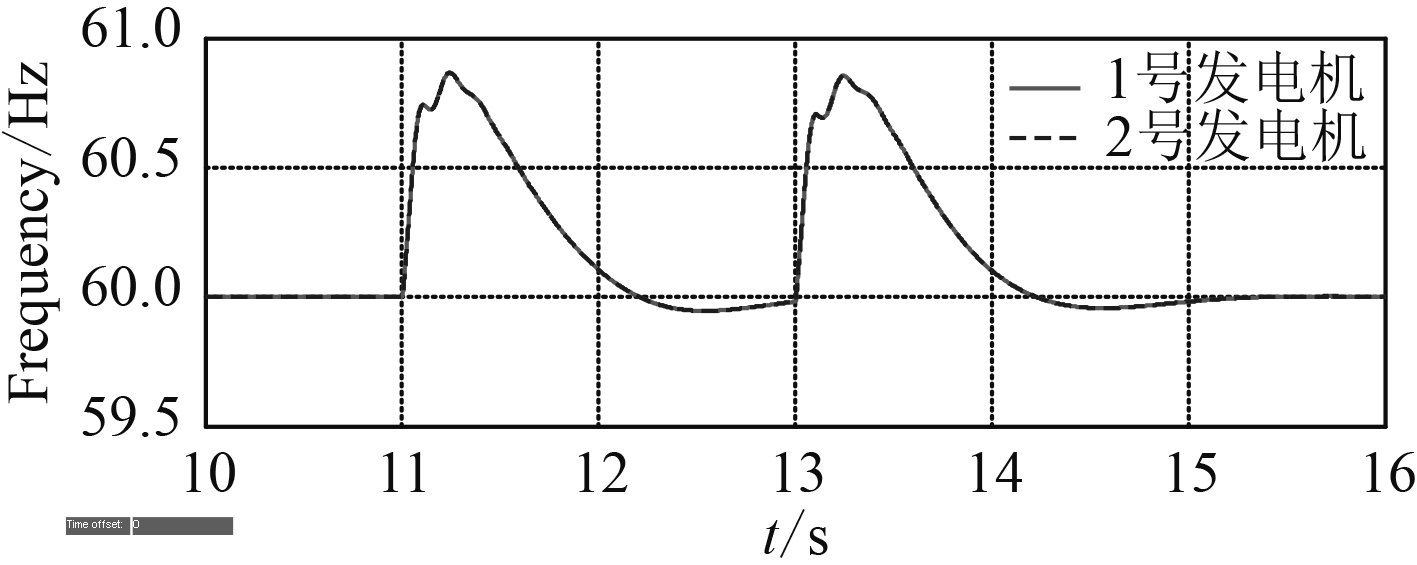
仿真实验模拟了发电机组减载过程,图7和图8显示了发电机组减载仿真特性。

|
图 7 发电机在网减载功率变化 Fig. 7 Generator lightening power changes in the network |
|
图 8 发电机在网减载频率变化 Fig. 8 Generator in network load shedding frequency change |
发电机组从额定负载情况下进行减载操作,首先减去40%的负载,从图7和图8中可以看出,整个柴油机的功率出现快速的下降,同时会有一定的回升,主要是防止频率下降时,使整个电网频率过低,从而引起发电机组主开关跳闸,最终导致失电事故的发生。电网频率也有一定的上升现象,并最终回到额定频率,其频率偏差在1 Hz以内。用过以上仿真验证柴油发电机功率输出的稳定性,为接下来的仿真实验提供基础。
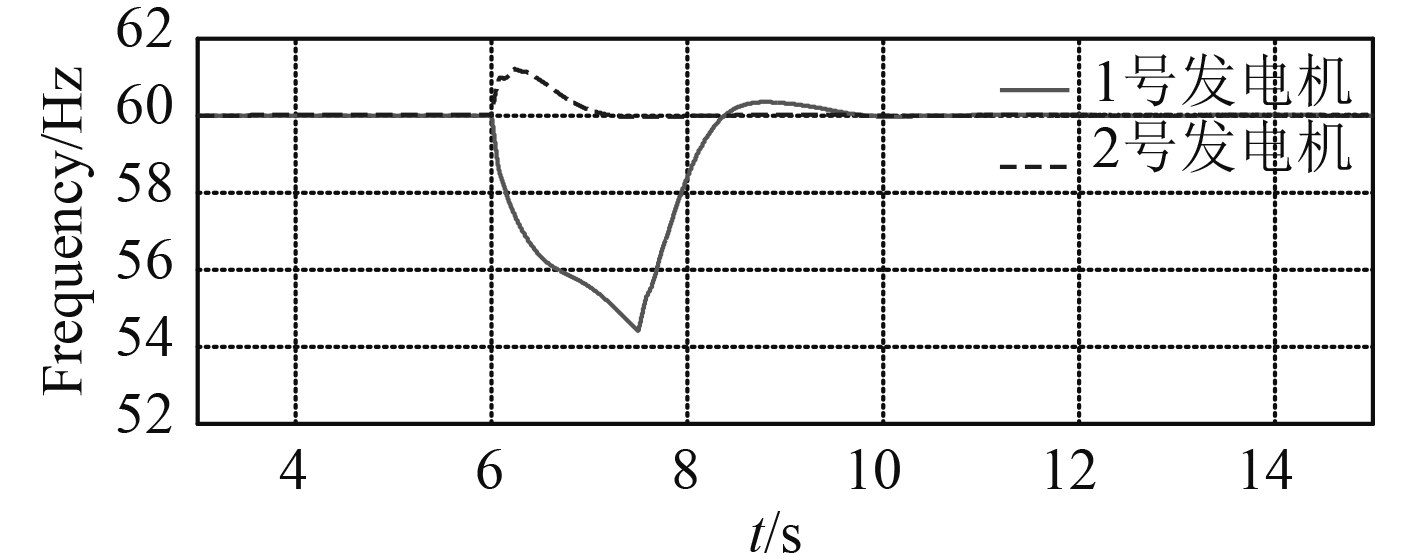
6.2 分析比较实验模拟2台发电机组在网情况下,1台发电机组跳闸时,在网发电机组的特性以及减载特性进行仿真研究。
|
图 9 传统减载方法下发电机跳闸频率变化 Fig. 9 Conventional method of lightening issued by motor tripping frequency change |

|
图 10 改进减载方法下发电机跳闸频率变化 Fig. 10 Improved method of reducing load generator tripping frequency change |
图9和图10显示了2台发电机的仿真结果,其中H1=H2=2 s,故障前的状态为:1号发电机和2号发电机进行正常的运作。在第6 s 2号发电机跳闸,从图9中可以看出,在传统方法的减载系统中,在发生跳闸后的1.9 s时,减载系统对不重要的负载进行减载,所需时间较长,电网频率回升速度也较慢;从图10中可以看出,本文所提出的改进减载方法,在发生跳闸0.4 s进行多余负载减载,电网频率回升速度也较快。
7 结 语从改进后的减载方法策略与传统的减载方法策略的比较可以得出以下规律:
1)传统的减载方法由于在电网频率检测上缺乏快速性,导致减载所需的时间较长,对实际功率缺额的计算也不够准确,导致在减载量具有一定的偏差,同时导致电网频率回升速度较慢。
2)改进后的减载方法,由于采用了2次不定时采样,当电网频率变化未知时也能精确测量频率的变化,因此减载速度要快于传统的减载方法。同时,结合本文所提出的优化的减载量整定策略,较精确地控制所需切削的负载,因此,负载切削后电网的频率回升速度也比较快。
综上所述,本文所提出来的减载量整定方法与频率检测方案相结合,在柴油机发生跳闸时,对电网的恢复具有快速性,效果好于传统的减载方法。
| [1] | 潘志强. 电力推进船舶能量管理系统控制策略研究[D]. 武汉: 武汉理工大学, 2014. |
| [2] |
蔡国伟, 孙正龙, 王雨薇, 等. 基于改进频率响应模型的低频减载方案优化[J]. 电网技术, 2013, 11: 3131–3136.
CAI Guo-wei, SUN Zheng-long, WANG Yu-wei, et al. Based on the improved model of frequency response of low frequency load shedding scheme optimization [J]. Journal of Grid Technology, 2013, 11: 3131–3136. http://www.cnki.com.cn/Article/CJFDTOTAL-DWJS201311022.htm |
| [3] | 和敬涵, 柏丹丹, 王小君, 等. 低频减载综合代价最优化算法[J]. 电网技术, 2013, 12: 3461–3466. http://www.oalib.com/references/17565555 |
| [4] | 杜奇壮. 电力系统低频减载研究[D]. 北京: 华北电力大学, 2007. |
| [5] |
常喜强, 何恒靖, 解大, 等. 计及频率差变化率的低频减载方案的研究[J]. 电力系统保护与控制, 2010, 04: 68–73.
CHANG Xi-qiang, HE Hen-jing, XIE Da, et al. Meter and frequency difference rate of change of low frequency load shedding scheme research [J]. Power System Protection and Control, 2010, 68: 68–73. http://www.cqvip.com/qk/90494a/201004/33047089.html |
| [6] | 刘少华, 王超, 安军, 等. 计及频率静特性的低频减载方案的研究[J]. 电力系统保护与控制, 2011, 9: 140–144. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_jdq201109026 |
| [7] | RADAN, DAMIR, SØRENSEN, et al. Reducing power load fluctuations on ships using power redistribution control[J]. Marine Technology and SNAME News, 2008, 453 . https://www.itk.ntnu.no/ansatte/Johansen_Tor.Arne/s5.pdf |
 2018, Vol. 40
2018, Vol. 40
