2. 高新船舶与深海开发装备协同创新中心(船海协创中心),上海 200240;
3. 上海交通大学 船舶海洋与建筑工程学院,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, China;
3. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China
根据国家海事组织(IMO)和各大船级社的定义,动力定位(DP)船舶是指利用推进器来将其位置和首向保持在固定的位置或预设的轨迹上的船舶[1]。一般来说,动力定位系统由位置测量、控制、推力三大系统组成,控制系统是动力定位系统的最核心组成部分[2]。
浮托安装法适用于大型平台的安装作业,具有精准的对接能力和较大的载荷空间,在近年来被广泛关注研究。Xia等[3]用数值模拟方法研究了小型平台浮托安装的运动响应,并在此基础上进行了物理模型试验。Hu[4]对浮托安装过程中的非线性动力和环境载荷进行了研究。
进船过程是动力定位浮托安装过程最重要的过程之一。进船过程中,为保护驳船和导管架结构,一般会在导管架桩腿上安装护舷靠垫,护舷靠垫对动力定位驳船的影响很明显,在研究动力定位系统中具有重要意义。对动力定位系统的研究自20世纪末以来引起了很多学者的重视。Balchen[5]最先提出了基于多元最优控制和卡尔曼滤波理论的控制方法。Sørensen[6]提出了针对小水线面海洋结构物的动力定位方法。Serraris[7]对1艘动力定位单体钻井船进行了时域模拟研究,并与模型试验结果进行对比。
本文通过建立时域模拟程序对考虑护舷靠垫影响的进船安装过程进行数值模拟,并将结果与模型试验结果进行比较,为动力定位浮托安装系统设计和实地操作提供参考。
1 动力定位系统数学模型 1.1 波浪载荷平台的低频运动是关注的焦点,在计算平台低频运动时,风力和流力均设为定常值,通过模型试验结果决定,剩余需要重点关注的对象是2阶波浪力。2阶波浪力通常可以视为由低频波浪力(差频)、高频波浪力(和频)及平均漂移力组成,2阶波浪力的幅值与入射波幅值的平方呈正比例关系。用2次传递函数(QTF)来表示只考虑低频部分的二阶波浪力[8]:
| $\begin{split}{{\bf{\tau }}_{wave2}} = & 2\sum\limits_{i = 1}^N {\sum\limits_{j > i}^N {{\zeta _i}{\zeta _j}} } {P_{ij}}\cos \left\{ {({\omega _i} - {\omega _j})t + ({\varepsilon _i} - {\varepsilon _j})} \right\} + \\ &2\sum\limits_{i = 1}^N {\sum\limits_{j > i}^N {{\zeta _i}{\zeta _j}} {Q_{ij}}\sin \left\{ {({\omega _i} - {\omega _j})t + ({\varepsilon _i} - {\varepsilon _j})} \right\}} \text{。}\end{split}$ | (1) |
式中:
本文动力定位系统时域模拟程序的控制方法采用PID控制,控制方法如下式所示:
| ${{\bf{\tau }}_c} = {K_p}{\bf{\eta }} + {K_d}{\bf{\dot \eta }} + {K_i}\int\nolimits_0^t {{\bf{\eta }}(\tau ){\rm d}\tau } \text{。}$ | (2) |
在推力系统中,控制系统所需要的推力将被分配到不同的推进器上,本文推力系统分配策略如式(3)所示,其解的最小值问题即代表推力分配策略的输出结果 [9]:
| $\begin{split}\sum\limits_{{{i = 1}}}^{{n}} {{{{T}}_{{i}}}^{\rm{2}}} + &{{{C}}_{{x}}}{\left( {{{{F}}_{{x}}}{\rm{ - }}\!\sum\limits_{{{i = 1}}}^{{n}} {{{{T}}_{{i}}}\cos {\alpha _{{i}}}} } \right)^{\rm{2}}}\!\! + \!\!{{{C}}_{{y}}}{\left( {{{{F}}_{{y}}}\!\! - \!\!\!\sum\limits_{{{i = 1}}}^{{n}} {{{{T}}_{{i}}}\sin {\alpha _{{i}}}} } \right)^{{2}}}{{ + }}\\ &{{{C}}_\psi }{\left( {{{{N}}_\psi }{\rm{ - }}\sum\limits_{{{i = 1}}}^{{n}} {{{{T}}_{{i}}}\sin {\alpha _{{i}}}{{{x}}_{{i}}}} {\rm{ + }}\sum\limits_{{i = {\rm 1}}}^{{n}} {{{{T}}_{{i}}}\cos {\alpha _{{i}}}{{{y}}_{{i}}}} } \right)^{\rm{2}}}\text{,}\end{split}$ | (3) |
式中:Ti为第i个推进器输出的力;n为推力器的数目;C为权重系数;αi为第i个推进器的方向;xi和yi分别为推进器相对于船舶重心的横向和纵向位置。可以通过设置αi的取值范围以考虑禁止角的问题,用意是避免推进器之间的干扰问题。分配策略得出各推进器的推力后,可通过下式计算推进器的功率:
| $P = \frac{{2\pi {K_Q}}}{{K_T^{3/2}{\rho ^{1/2}}D}}{T^{\frac{3}{2}}}\text{。}$ | (4) |
式中:KQ为转矩系数;KT为推力系数;D为螺旋桨的直径。
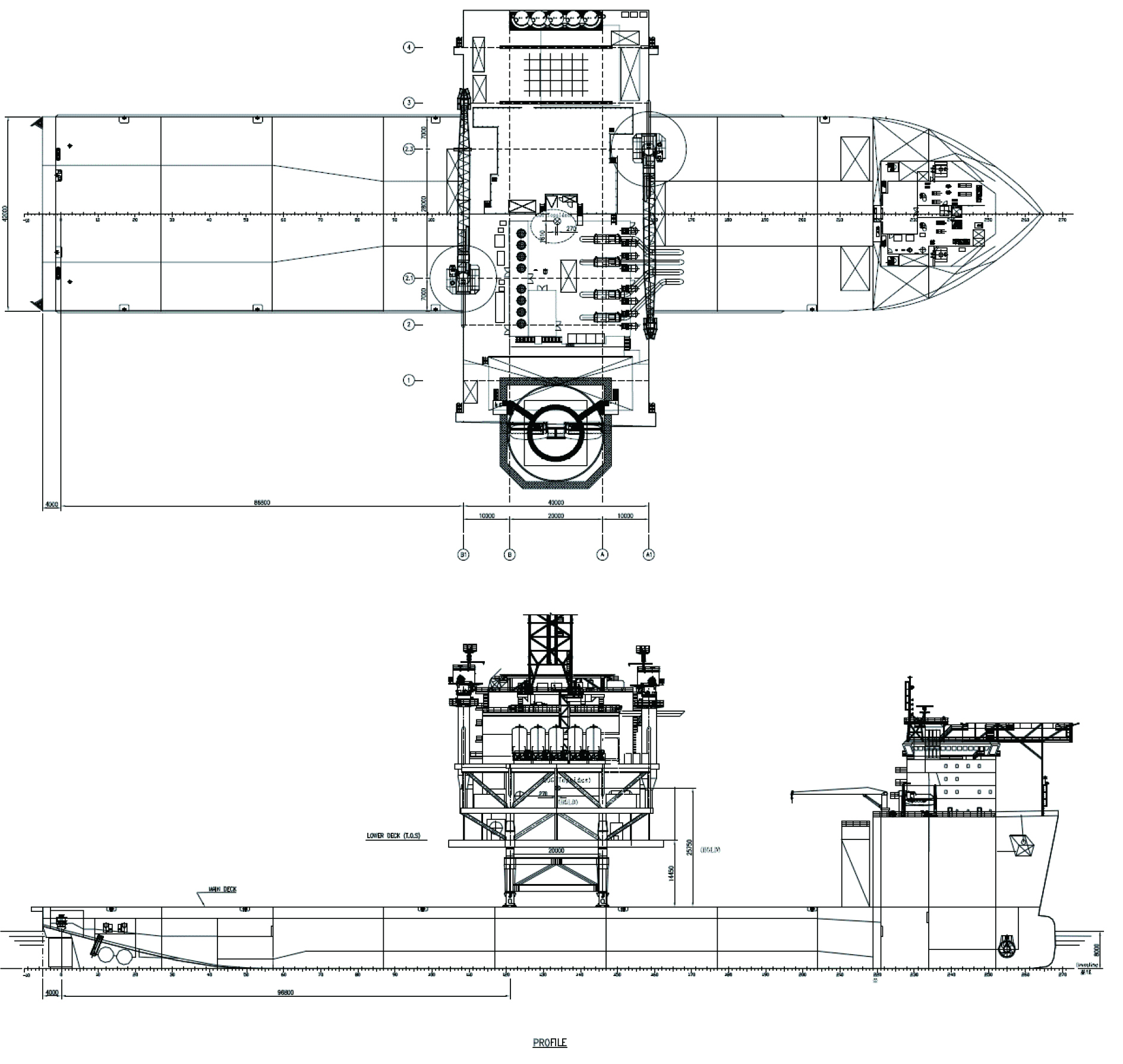
2 数值模拟算例 2.1 模拟对象及环境参数 2.1.1 驳船尺度参数本文的研究对象为装备有动力定位系统的某驳船,该驳船将被用于某油田中心平台上部模块的运输和浮托安装作业。该驳船在进船工况下的主要参数如表1所示,驳船的总布置图及型线图如图1所示。
|
|
表 1 进船工况驳船主尺度 Tab.1 Main dimension of barge during docking operation |
|
图 1 某驳船总布置图 Fig. 1 General arrangement of the barge |
该驳船与导管架之间存在护舷靠垫,护舷靠垫被布置在导管架上,已知护舷靠垫的刚度曲线如图2所示,横轴表示护舷靠垫的压缩变形量,纵轴左边表示应力,纵轴右侧表示压缩能,压缩变形量为72%时,护舷靠垫力达最大允许值。

|
图 2 护舷靠垫刚度 Fig. 2 Stiffness of fenders |
本文中,导管架上共有8只靠垫,其中横向4只,纵向2只,护舷靠垫与驳船间隙值为0.1 m,位置布置如图3所示,方框表示导管架的范围,圆圈表示护舷靠垫所在位置,其中2/3/5/8号护舷靠垫位于上方,其下方对应护舷靠垫力为1/4/6/7号。

|
图 3 护舷靠垫位置布置 Fig. 3 Position arrangement of fenders |
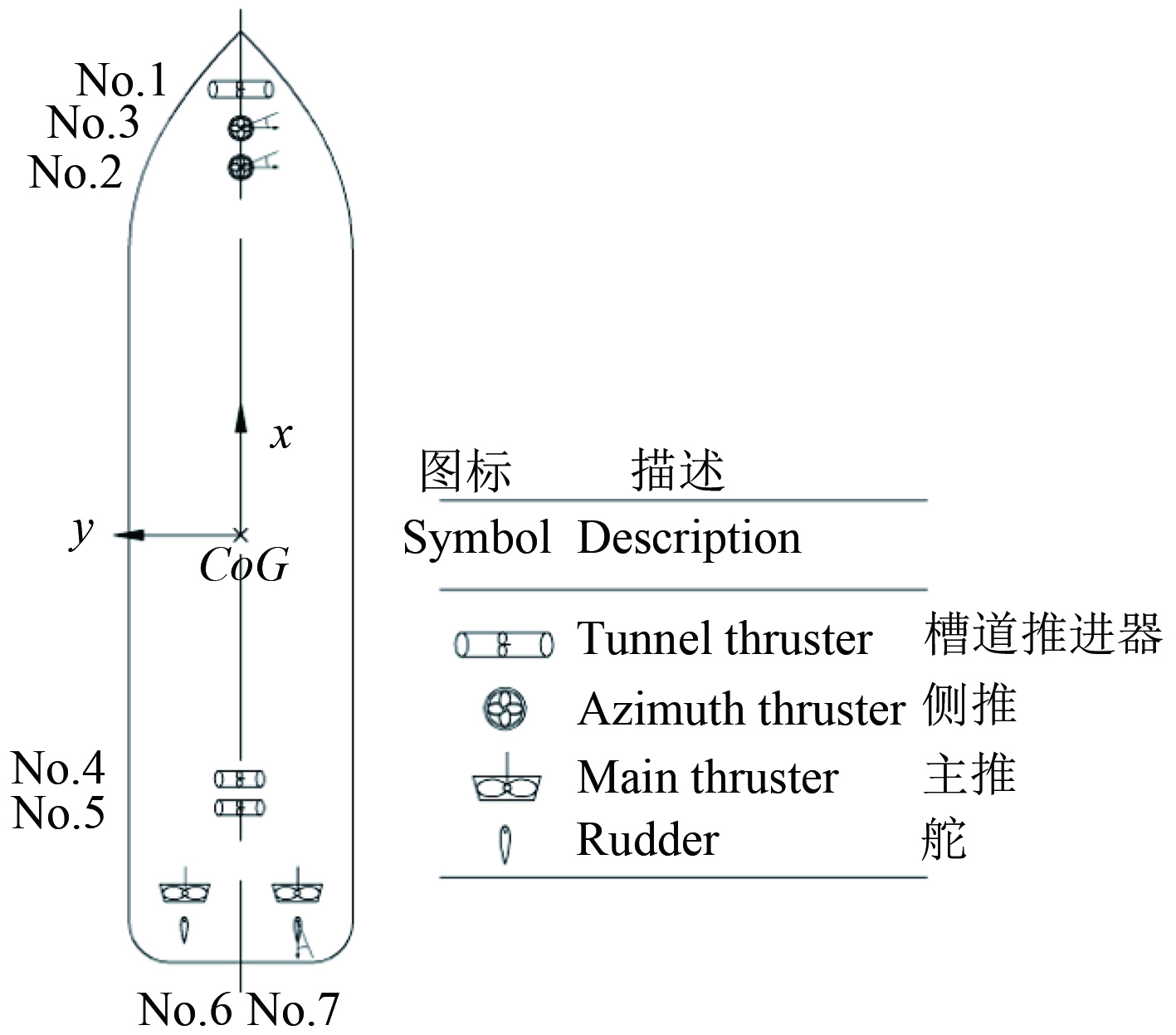
本文研究对象驳船共配备7套推进器,其中2套主推进器、3套槽道推进器、2套全回转推进器。各推进器的位置分布如图4所示,主要性能以及具体位置参数如表2所示。
|
|
表 2 实船上的推进器各主要性能与相对重心处的水平位置 Tab.2 Main performances and horizontal positions of thrusters on real ship |
|
图 4 推进器位置布置图 Fig. 4 Position arrangement of thrusters |
本文时域模拟中的环境条件考虑了风力、波浪力、流力同时作用,波浪选用ISSC谱,风速和流速均采用定常值。本文模拟了90°/180°方向环境载荷下的浮托安装进船过程,具体环境载荷参数如表3所示。
|
|
表 3 环境载荷参数 Tab.3 Parameters of environment conditions |
通过在Matlab/Simulink环境下编写动力定位时域模拟程序,考虑护舷靠垫力对驳船影响,对动力定位浮托安装进船过程进行数值模拟,时域模拟程序计算求解流程如图5所示。

|
图 5 时域模拟程序计算求解流程 Fig. 5 Calculation process of time domain simulation program |
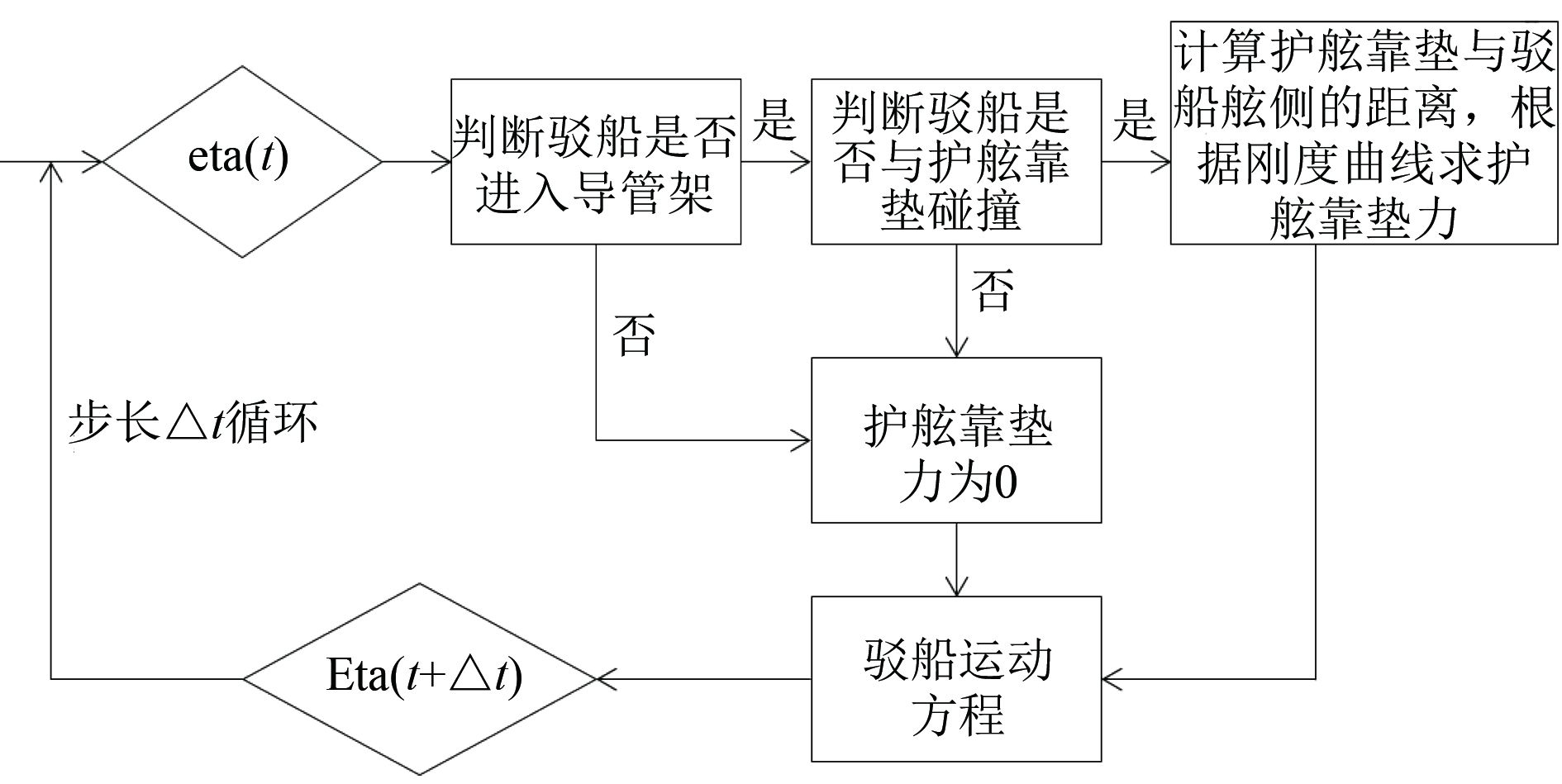
在时域模拟程序中,本文对护舷靠垫进行模拟。许鑫[10]在对浮托安装系统耦合响应研究中提出一种计算护舷靠垫与驳船相互作用的方法,将驳船与护舷靠垫接触的两侧看成一个接触点与一个接触面,通过点到面的距离来判断靠垫作用力。本文考虑的工况中,将护舷靠垫简化为4个位置固定的点,通过驳船的位置信息计算护舷靠垫与驳船舷侧的距离,进而对护舷靠垫力进行计算。护舷靠垫力计算流程如图6所示。本文中护舷靠垫与驳船舷侧的间隔为0.1 m,护舷靠垫的厚度为1.2 m,最大压缩值为0.864 m,此时压力达到最大值328 t。
|
图 6 护舷靠垫力计算流程 Fig. 6 Calculation process of fender force |
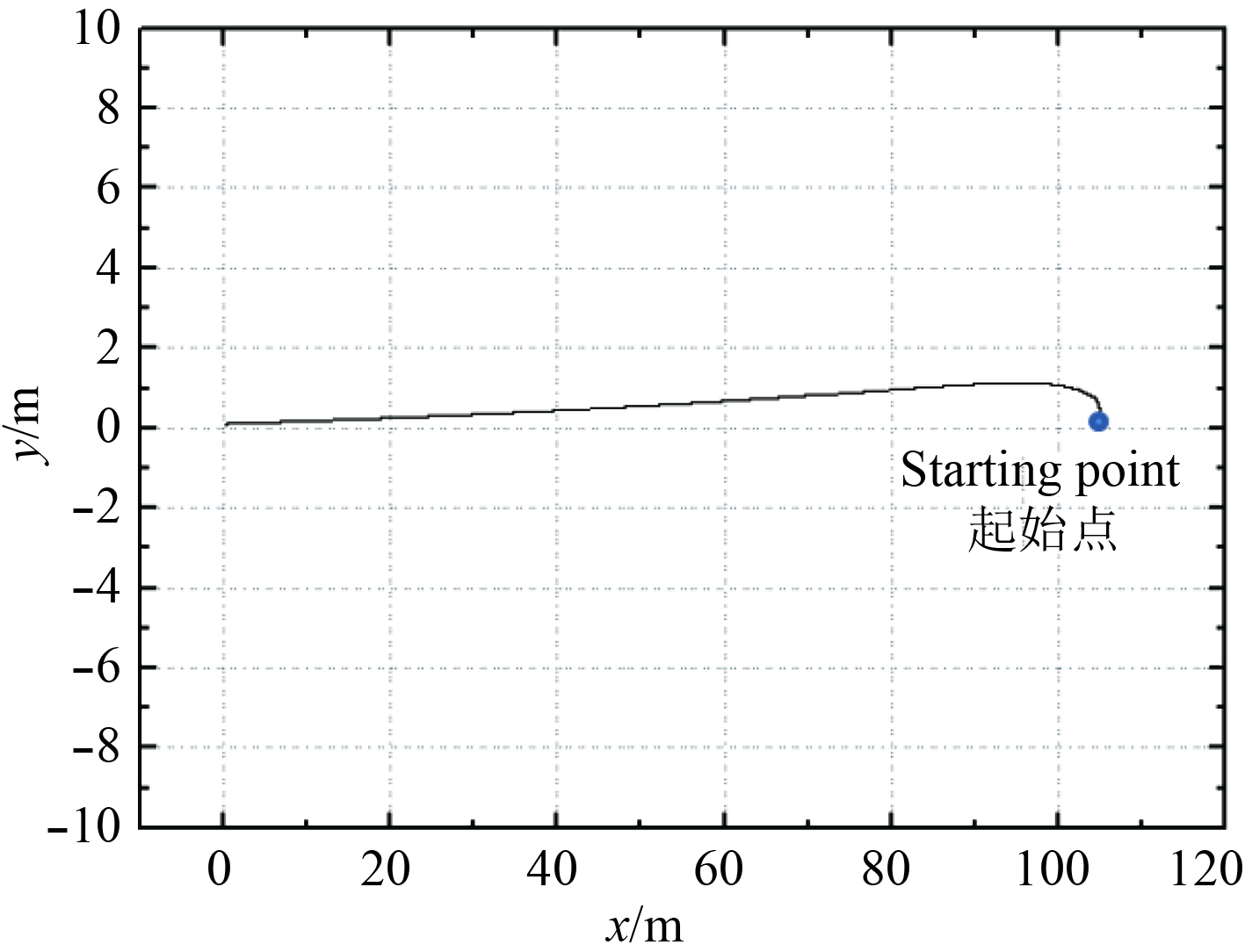
90°浪向角下驳船横向运动受外界影响较大,本文根据模拟结果得到其运动轨迹、首摇角以及护舷靠垫力如图7~图9所示,原点为定位目标点。
|
图 7 90°浪向角驳船运动轨迹 Fig. 7 Trail of barge movement (90° wave angle) |
|
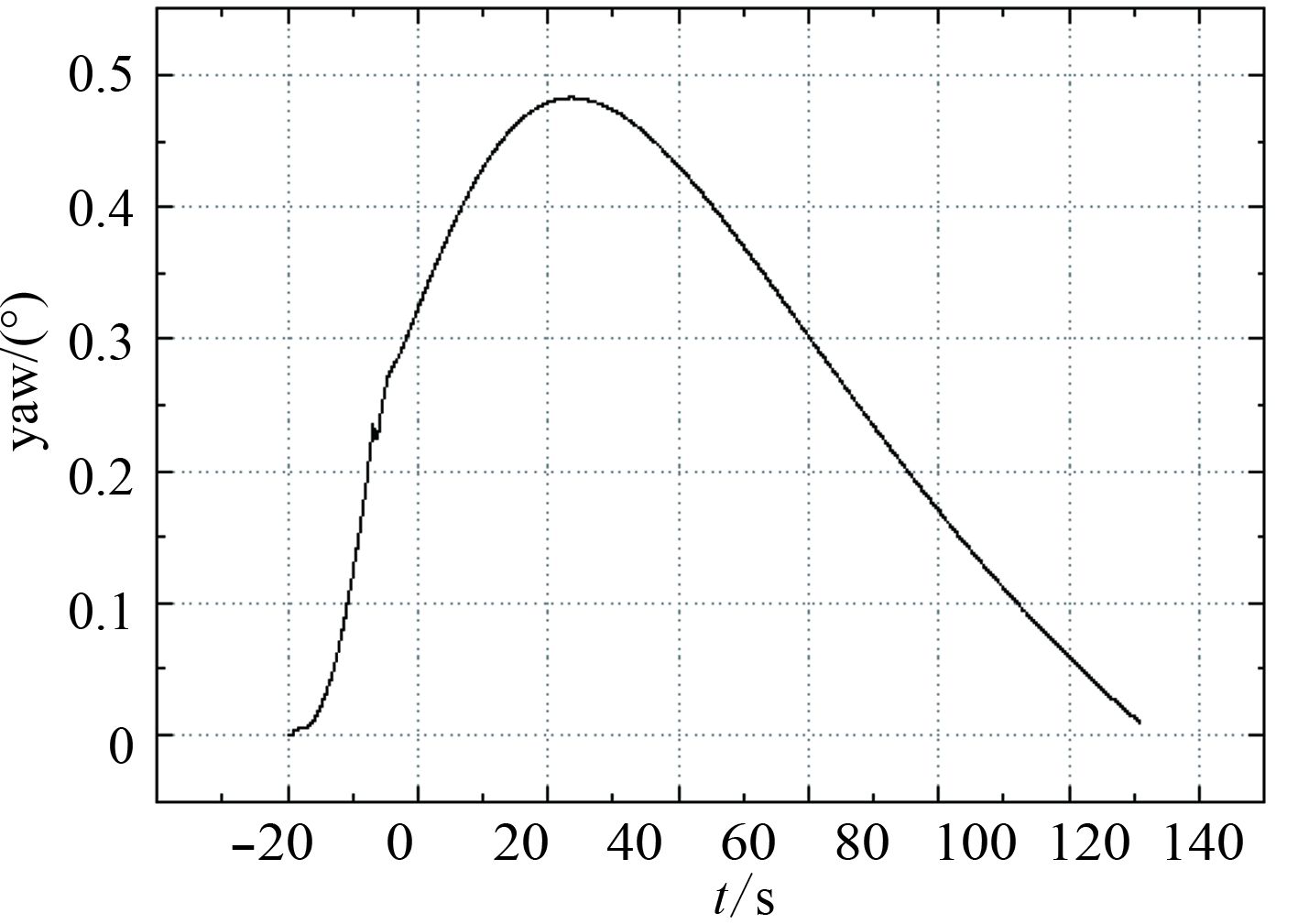
图 8 90°浪向角驳船首摇角 Fig. 8 Angle of yaw (90° wave angle) |

|
图 9 90°浪向角护舷靠垫力 Fig. 9 Fender forces (90° wave angle) |
90°浪向角下,驳船受到横向的环境力扰动较大,因此驳船的横向位置偏移较大。模拟程序设定驳船与中心位置偏移量超过0.964 m时,护舷靠垫力将取最大值,在此情况下,驳船刚进入导管架中间时,偏离平衡位置较远,故护舷靠垫力会呈现一段时间的最大值。
2.3.2 180°浪向角模拟结果本文给出180°浪向角下驳船运动轨迹、首摇角以及护舷靠垫力如图10~图12所示,原点为定位目标点。

|
图 10 180°浪向角驳船运动轨迹 Fig. 10 Trail of barge movement (180° wave angle) |
|
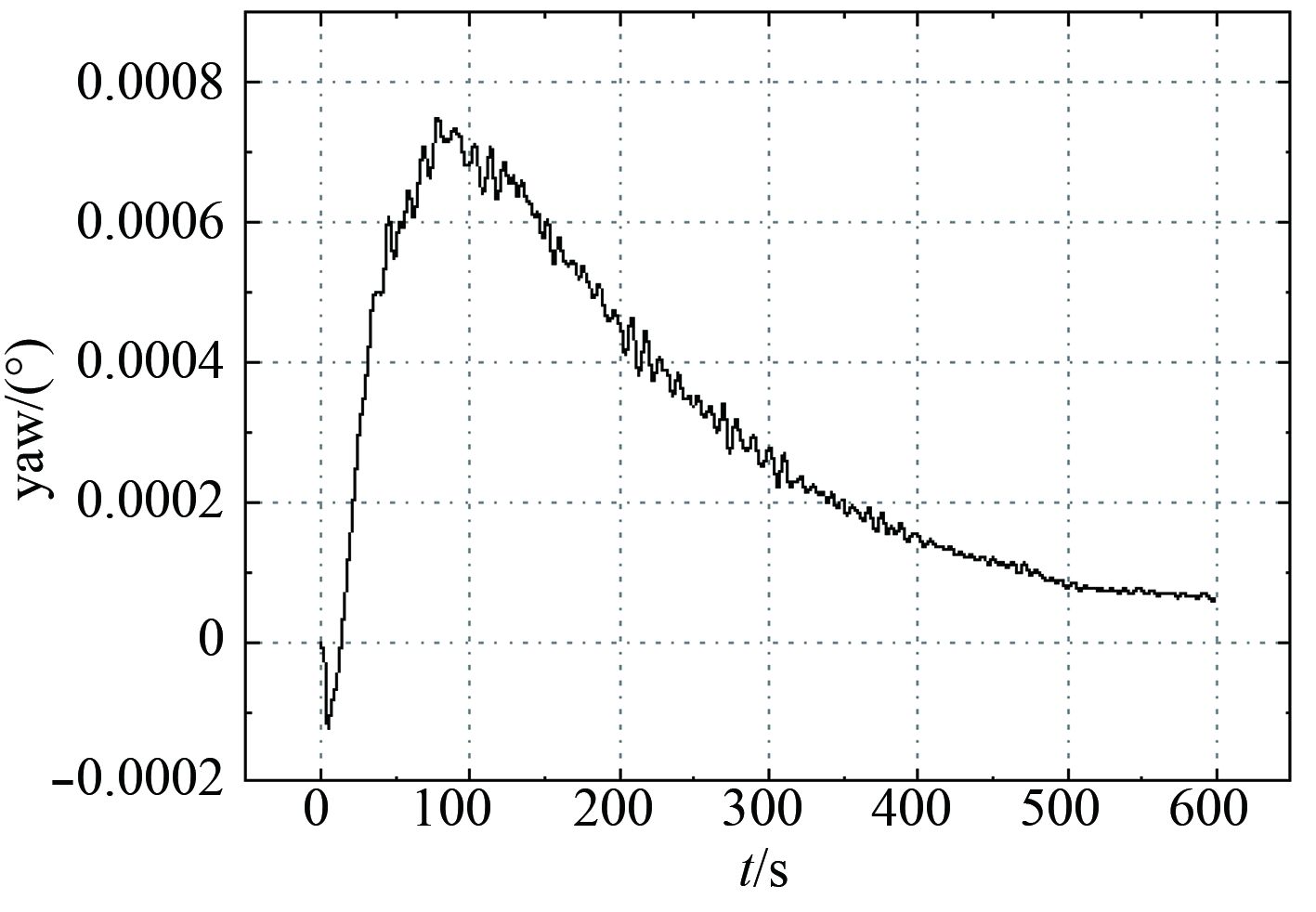
图 11 180°浪向角驳船首摇角 Fig. 11 Angle of yaw (180° wave angle) |
|
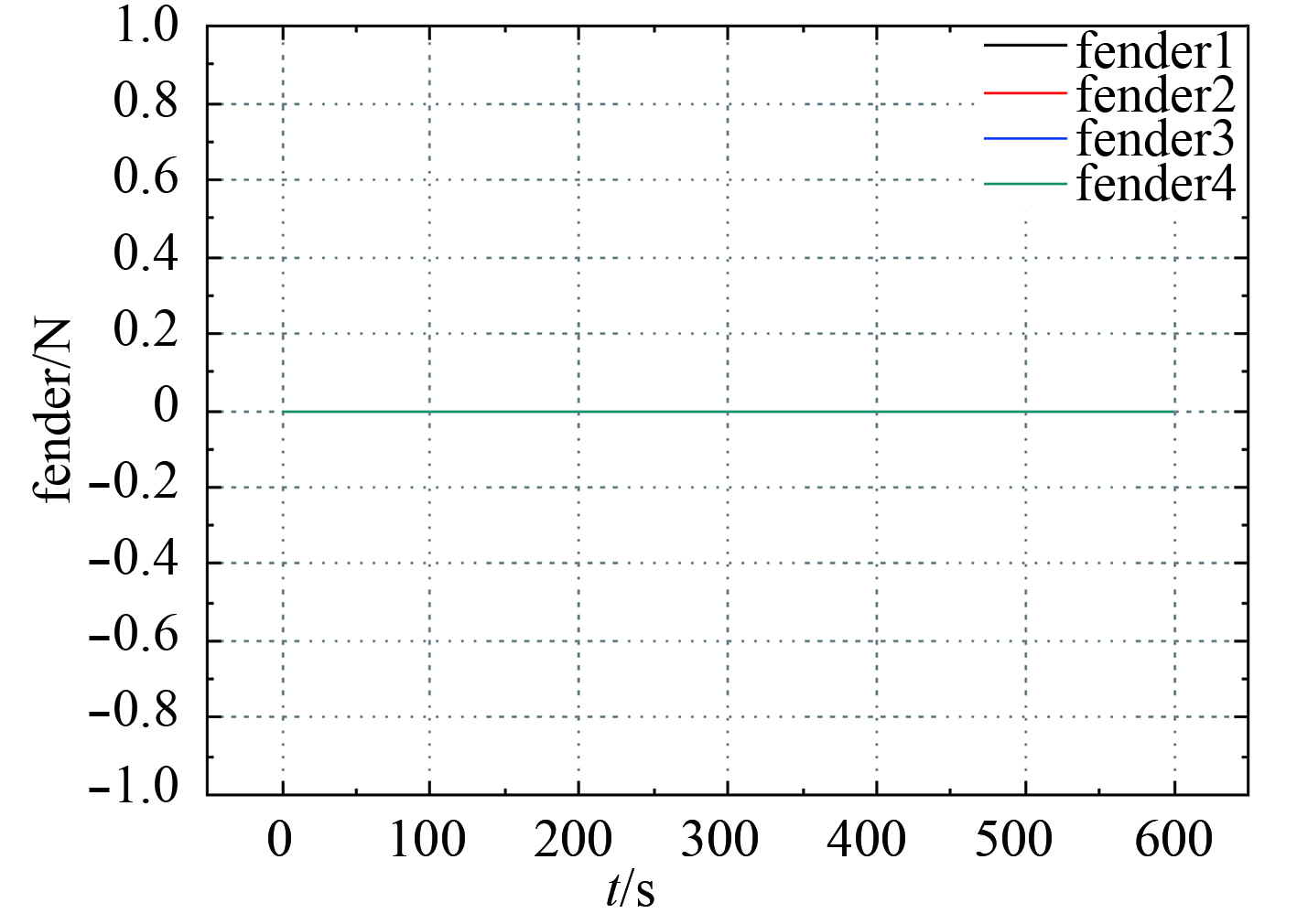
图 12 180°浪向角护舷靠垫力 Fig. 12 Fender forces (180° wave angle) |
180°浪向角工况下,环境力对驳船的横向影响极小,因此除了系统刚启动时的不稳定以外,其他时间段横向偏移几乎为0,护舷靠垫力也保持为0。
2.3.3 数值模拟结果分析数值模拟结果中,90°浪向角工况下,fender1和fender3上的最大护舷靠垫力都达到了理论最大值328.33 t,fender2和fender4上则没有护舷靠垫力出现,这一结果与90°工况下数值模拟的驳船轨迹结果相吻合;180°浪向角工况下,数值模拟结果显示各护舷靠垫上的靠垫力为0,这是由于180°工况下驳船受到x方向的扰动较小,故没有与护舷靠垫发生碰撞。
|
|
表 4 数值模拟护舷靠垫力统计 Tab.4 Simulation statistics of fender forces |
模型试验在上海交通大学海洋工程国家重点实验室的风浪流水池中进行,为保证可比性,模型试验对象与时域模拟对象为同一对象,缩尺比为λ=1∶36,实际水深为100.1 m,对应模型试验水池水深为2.78 m。
|
|
表 5 进船工况模型试验驳船模型主尺度 Tab.5 Main dimension of model during docking operation |
|
|
表 6 进船工况模型试验上部组块模型主要参数 Tab.6 Main dimension of upper block model during docking operation |
海洋环境的模拟主要包括对风、浪、流的模拟,模型试验环境载荷参数如表7所示。对不规则波的模拟采用ISSC谱,根据有义波高、周期及波谱进行模拟,海洋工程国家重点实验中中位于水池两边的造波机可以产生纵向和横向的不规则波。图13显示了模型试验中驳船在进船工况时的状态。
|
|
表 7 模型试验环境载荷参数 Tab.7 Environment condition parameter of model test |

|
图 13 模型试验中进船工况试验 Fig. 13 Docking operation model test |
试验采用自主开发的动力定位控制系统,程序采用六自由度光学运动测量仪获得驳船模型的实时运动信息,采用Kalman滤波估计海洋结构物的低频运动,并由模糊PID控制器计算所需的环境补偿力,总的推力和转矩进而分配到各个推进器上。
本试验共应用了5个不同的不规则波浪工况,试验过程中所有的测量数据都被记录在计算机中,以获得足够的数据进行统计分析。
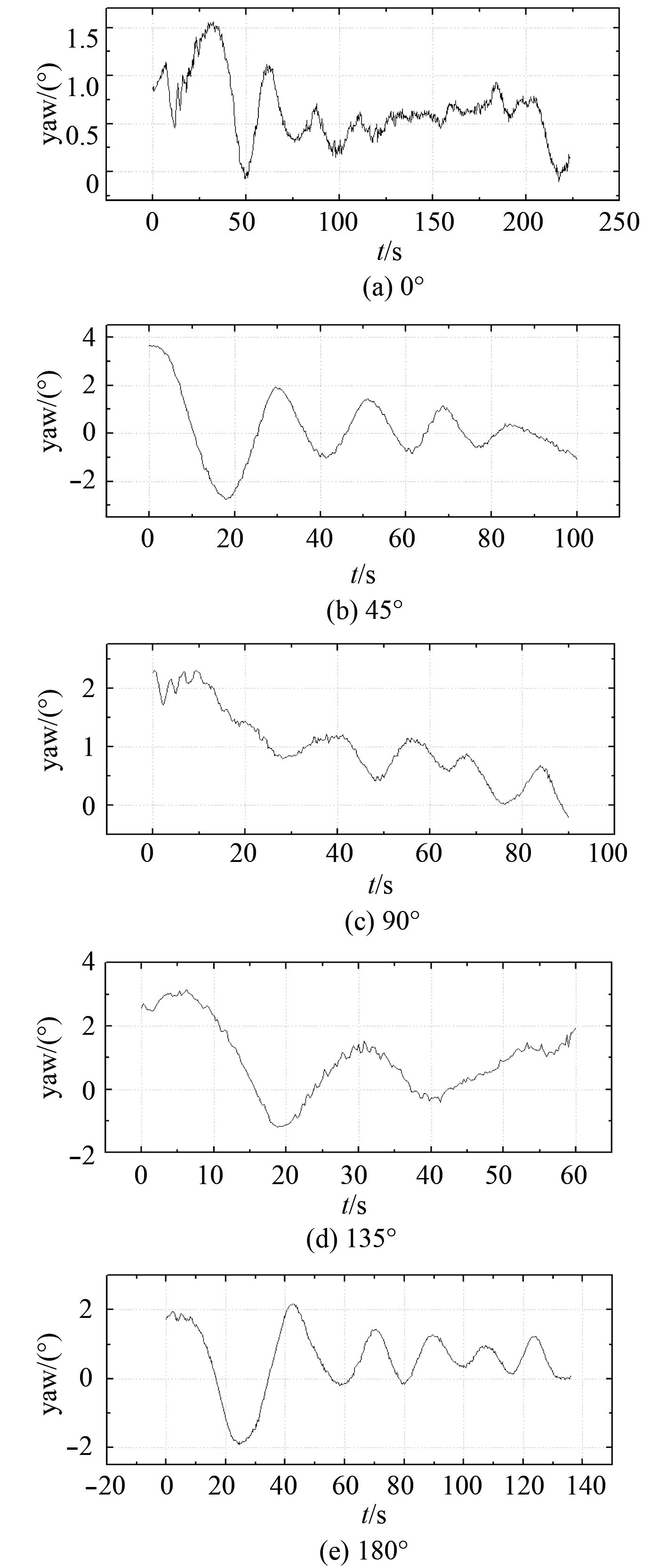
3.4 模型试验结果经处理后,5种浪向角下动力定位驳船运动轨迹如图14所示,定位目标点均为原点,驳船首向角如图15所示。同时,试验也采集了护舷靠垫力数据,统计结果如表8所示。

|
图 14 模型试验驳船运动轨迹 Fig. 14 Model test trail of movements |
|
图 15 模型试验驳船首摇角 Fig. 15 Model test angle of yaw |
|
|
表 8 模型试验护舷靠垫力最大值统计 Tab.8 Maximum fender forces of model test |
从靠垫压力来看,180°和0°时进船过程较顺利,对应的护舷靠垫力最大分别为158 t和185 t,在大多数时间里护舷靠垫压力值小于100 t。135°,90°,45°时,在大多数时间里护舷靠垫压力值大于 100 t,对应最大护舷靠垫压力值分别为205 t,214 t和212 t。180°,0°,90°进船难度较低,135°和45°进船较为困难。
4 结 语本文对某应用动力定位技术的浮托安装进船过程进行了数值模拟研究,在数值模拟的过程中考虑了护舷靠垫对进船过程中驳船的影响,得到了90°工况和180°工况下驳船的运动轨迹、首摇角时历曲线、护舷靠垫力时历曲线。此外,本文还讨论了该动力定位浮托安装进船过程的模型试验研究,通过对比结合得到以下结论:
动力定位浮托安装进船过程中,护舷靠垫对驳船有较明显的影响,特别是在90°浪向角工况下,护舷靠垫力也是在此工况下达到最大值,实际工程中需注意相应海洋环境下护舷靠垫设计的安全冗余。
从护舷靠垫力模拟结果上来看,数值模拟结果与模型试验结果存在一定的差异。在数值模拟结果中,护舷靠垫力在180°浪向角工况下保持为0,而在模型试验中,各个护舷靠垫都存在碰撞力,受撞击的情况较为明显;比较关系上,模型试验中90°工况下的平均最大护舷靠垫力为139.5 t,显著大于0°和180°工况下平均最大护舷靠垫力111.9 t和96.6 t,该结果与数值模拟结果相吻合。造成护舷靠垫力差异的原因可能有:1)模型试验中对海洋环境的模拟无法做到完全理想化,导致结果的差异;2)数值模拟只考虑了水平面上的二维问题,与实际情况存在差异,导致模拟结果与实际情况可能存在差异。从轨迹上来看,数值模拟中90°工况y方向最大偏移量为1.13 m,平均偏移量为0.65 m,而模型试验中,最大偏移量为3.10 m,平均偏移量为1.79 m,同样在180°工况下,数值模拟中的最大和平均偏移量分别为1.04×10–3 m和3.8×10–4 m,模型试验中最大和平均偏移量分别为3.66 m和0.32 m,二者的结果在数量级上吻合,但在数值上存在一定差异。除了前文所述2条原因之外,动力定位系统刚刚启动时系统尚未达到稳定状态也是导致误差的原因之一,会导致运动轨迹在定位初始阶段存在较大的偏移。
从驳船运动轨迹上来看,考虑护舷靠垫影响的数值模拟研究与模型试验研究结果具有一定的吻合,说明数值模拟研究对动力定位浮托安装进船过程具有一定的指导意义,在未来动力定位系统设计过程中,可使用数值模拟研究作为辅助手段。
| [1] | SØRENSEN A J. A survey of dynamic positioning control systems [J]. Annual Reviews in Control, 2011, 35. https://www.sciencedirect.com/science/article/pii/S1367578811000095 |
| [2] | 赵志高, 杨建民, 王磊, 等. 动力定位系统发展状况及研究方法[J]. 海洋工程, 2002, 20 (1): 91-97. |
| [3] | XIA J, HAYNE S, MACFARLANE G. Investigation into float-over installation of minimal platforms by hydrodynamic model testing [C]//Greece: Proceeding of OMAE2005 24th International Conference on Offshore Mechanics and Artic Engineering, 2005. |
| [4] | HU Zhi-huan, et al. Nonlinear dynamics and impact load in float-over installation [J]. Applied Ocean Research, 2017, 65. http://research-repository.uwa.edu.au/en/publications/nonlinear-dynamics-and-impact-load-in-floatover-installation(b15ce827-135b-4d25-bbe1-714ca2686e5d)/export.html |
| [5] | J G BALCHEN, N A JENSSEN and S SAELID. Dynamic positioning using Kalman filtering and optimal control theory [C]//In IFAC/IFIP Symposium on Automation in Offshore Oil Field Operation, 1976. |
| [6] | SØRENSEN A J, STRAND J P. Positioning of small-waterplane-area marine constructions with roll and pitch damping [J]. Control Engineering Practice, 2000, 8. https://www.sciencedirect.com/science/article/pii/S0967066199001550 |
| [7] | JORRIT-Jan SERRARIS. Time domain analysis for DP simulations [C]//Asme International Conference on Ocean, 2009: 595-605. |
| [8] | FALTINSEN O M. Sea loads on ships and offshore structures [M]. Cambridge: Cambridge university press, 1993. |
| [9] | MARIN. Marin dpsim user guide [M]. MARIN. |
| [10] | 许鑫. 浮托安装系统耦合动力响应研究[D]. 上海: 上海交通大学, 2014. |
 2018, Vol. 40
2018, Vol. 40
