2. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-sea Exploration, Shanghai 200240, China
随着船舶大型化的发展,大型散货船、油船、集装箱船普遍呈现方形系数大、平行中体长等船型特点,因而平面分段的需求量大。为了提高平面分段的建造效率,多数大型船厂组建了平面分段流水线,适用于各种规格的钢板及部件的装焊。
近年来,关于流水线调度问题的研究层出不穷,主要以流水车间调度问题和混合流水车间调度问题为研究对象,并应用诸如遗传算法、粒子群算法、蚁群算法、禁忌搜索法、模拟退火法等智能优化算法求解规模较大的、较复杂的调度问题[1 – 3]。在多数情况下,流水线调度问题的建模假设了加工时间和交货期为精确值。但由于机器因素、工人因素、环境因素等的影响,加工时间实难确定,一般只能得到加工时间的大概数值和可能变化的范围。另一方面,交货期也并非完全固定,而是可能具有一定的弹性,表现为一个与需求方满意度相关联的时间区间。因此,可以认为加工时间和交货期均模糊。多目标调度问题常见于实际生产,并受到学者重视。如Kahraman等[4]、Engine等[5]就分别应用人工免疫算法和分散搜索算法求解了多目标的、带模糊加工时间和模糊交货期的流水车间调度问题。从调度的特点来看,一般的平面分段流水线的调度可以看作是流水车间调度问题。目前,关于平面分段流水线调度问题的研究相对较少[6 – 7],且没有考虑生产过程中的模糊性或不确定性。本文主要研究在模糊的加工时间和交货期下,平面分段流水线的调度问题,建立平面分段流水线多目标模糊调度问题的数学模型,并设计一种改进的多目标粒子群算法对其进行求解。
1 问题描述平面分段是一类重要的船体分段,由钢板及部件在流水线上装焊而成。各船厂的平面分段流水线的工位设置不尽相同。本文以如图1所示的1条面向纵骨先安装法的平面分段流水线为例,研究其多目标模糊调度问题。该流水线配置了拼板、底板焊接、纵骨安装、纵骨焊接、纵桁及肋板装配、纵桁及肋板焊接、检查运出等7个工位。在建分段经由同步运输辊由一个工位输送至另一个工位。
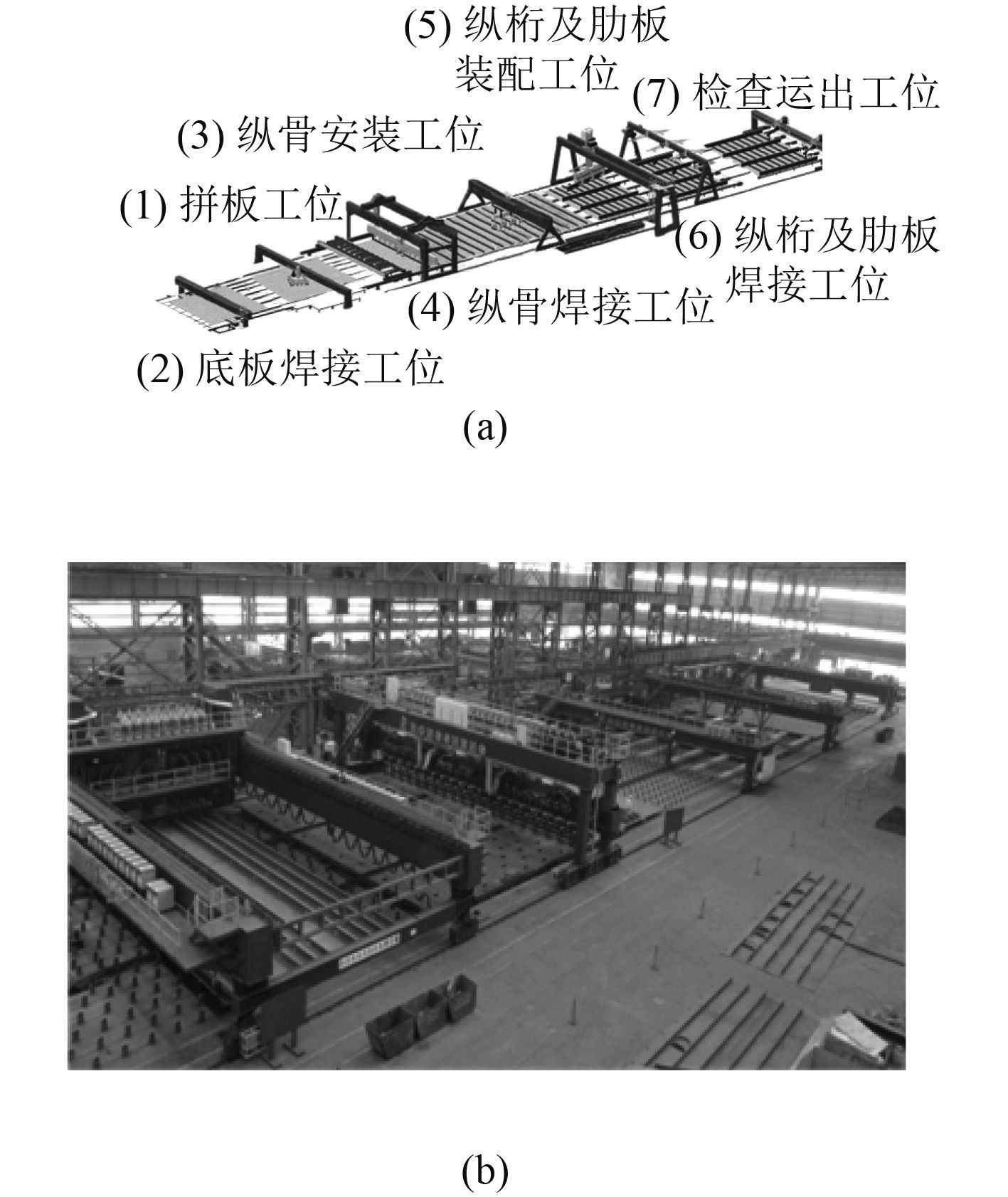
|
图 1 面向纵骨先安装法的平面分段流水线 Fig. 1 Assembly line for panel blocks |
平面分段流水线调度问题考虑如下:加工一批平面分段,任一分段的建造都须依次在各工位上完成相应的工序;每个工位一次只能对一个分段进行加工且每一个分段一次只能在一个工位上进行加工;各工位间没有缓冲工位,在建分段i需要在j-1工位上完成加工后才能进入j工位;在建分段i需要等其前一个在建分段在j工位上完成加工后才能进入j工位。另外,做出如下必要假设:所有分段可以在零时刻投入生产;加工过程中各平台持续可用;分段在各工位的加工时间和交货时间是模糊的,用模糊数表示;分段在各工位上加工前的准备时间包含于加工时间。
2 数学模型基于以上描述与假设,建立平面分段流水线多目标模糊调度问题的数学模型。
2.1 符号表示数学模型中的符号说明如下:
n为分段数量;m为工位数量;i为分段标号,
本文以三角模糊数描述模糊加工时间,表示为
平面分段作为总段的中间产品,过早完工将增加仓储成本,而拖期又会影响总段的装配。本文以梯形模糊数刻画模糊交货期,表示为
假设
| ${\tilde D_{{\pi _1},0}} = 0\text{,}$ | (1) |
| ${\tilde D_{{\pi _1},j}} = {\tilde D_{{\pi _1},j - 1}} + {\tilde p_{{\pi _1},j}},{\rm{ 1}} \leqslant j \leqslant m\text{。}$ | (2) |
| ${\tilde D_{{\pi _k},0}} = {\tilde D_{{\pi _{k - 1}},1}},{\rm{ }}2 \leqslant k \leqslant n\text{。}$ | (3) |
| $\begin{gathered} {{\tilde D}_{{\pi _k},j}} = \max \left( {{{\tilde D}_{{\pi _k},j - 1}} + {{\tilde p}_{{\pi _k},j}},{{\tilde D}_{{\pi _{k - 1}},j + 1}}} \right),{\rm{ }}2 \leqslant k \leqslant n,{\rm{ }} \\ {\rm{ 1}} \leqslant j \leqslant m - 1\text{。} \\ \end{gathered} $ | (4) |
| ${\tilde D_{{\pi _k},m}} = {\tilde D_{{\pi _k},m - 1}} + {\tilde p_{{\pi _k},m}},{\rm{ 2}} \leqslant k \leqslant n\text{。}$ | (5) |
| ${\tilde C_i} = {\tilde D_{{\pi _k},m}}\text{。}$ | (6) |
模糊完工时间与模糊加工时间具有相同的结构,也用三角模糊数描述,表示为

|
图 2 相关函数 Fig. 2 Correlation function |
完工时间总被希望切合于交货期。在模糊调度问题中,满意度极其重要,也是应用最广泛的指标之一[8]。它反映了模糊完工时间与模糊交货期的切合程度。满意度可通过式(7)计算,其表示如图2(c)所示。
| $A{I_i} = \frac{{area\left( {{{\tilde C}_i} \cap {{\tilde d}_i}} \right)}}{{area{{\tilde C}_i}}}\text{。}$ | (7) |
根据模糊流水线调度的特点及实际生产的一般要求,本文以最小化最大完工时间,最大化平均满意度为调度目标,如下:
| $\operatorname{Minimize} {\rm{ }}{f_1} = makespan = \mathop {\max }\limits_{i = 1,2,...,n} {\tilde C_i}\text{,}$ | (8) |
| $\operatorname{Maximize} {\rm{ }}{f_2} = \overline {AI} = \frac{1}{n}\sum\limits_{i = 1}^n {A{I_i}} \text{。}$ | (9) |
模糊流水线调度主要涉及模糊数的加法运算、取大运算、大小比较。对于三角模糊数
| $\tilde A + \tilde B{\rm{ = }}\left( {{a^1} + {b^1},{a^2} + {b^2},{a^3} + {b^3}} \right)\text{。}$ | (10) |
取大运算使用Lei近似准则[9]:
| $\text{若}\tilde A > \tilde B,\text{则}\max \left( {\tilde A,\tilde B} \right) = \tilde A \vee \tilde B \simeq \tilde A;\text{否则}\tilde A \vee \tilde B \simeq \tilde B\text{。}$ | (11) |
三角模糊数大小的比较采用以下3条准则[10]:
准则 1
准则 2
准则 3
粒子群(PSO)算法是一种规则简单、容易实现的进化算法。在PSO算法中,每一个粒子都具有速度和位置2个特征参数。其中,粒子的位置表征问题的解。PSO算法首先在可行解空间和速度空间随机初始化粒子群,继而通过不断地更新各粒子的速度和位置搜寻最优解。在D维搜索空间,粒子的速度和位置分别按式(12)和式(13)进行更新。
| $\begin{split}{{V}_q}\left( {k + 1} \right) = & \omega {{V}_q}\left( k \right) + {{r}_1}{c_1}\left[ {{X}_q^{pbest}\left( k \right) - {{X}_q}\left( k \right)} \right] + \\ &{{r}_2}{c_2}\left[ {{{X}^{gbest}}\left( k \right) - {{X}_q}\left( k \right)} \right]\text{,}\end{split}$ | (12) |
| ${{X}_q}\left( {k + 1} \right) = {{X}_q}\left( k \right) + {{V}_q}\left( {k + 1} \right)\text{。}$ | (13) |
其中,
需要指出,PSO算法在求解多目标问题上具有较大优势,主要表现在粒子群以内在的并行方式同时搜索多个非支配解,从而容易得到多个Pareto最优解。
4.2 按反Logistic曲线规律动态变化的惯性权重本文提出惯性权重随目标函数评价次数(Number of Function Evaluations,nFEs)按反Logistic曲线规律动态变化(inverse logistic inertia weight,ILIW),使
| $\omega {\rm{ = }}{\omega _{\rm min}}{\rm{ + }}\frac{{\left( {{\omega _{\rm max}}{\rm{ - }}{\omega _{\rm min}}} \right)}}{{1{\rm{ + }}\exp \left( {a \cdot \cos \left( {\displaystyle\frac{{nFE{s_{\rm max}}{\rm{ - }}nFEs}}{{nFE{s_{\rm max}}}} \cdot \pi } \right)} \right)}}\text{。}$ | (14) |
其中,
PSO算法中粒子的位置为连续值矢量,本文采用ROV(ranked-order-value)规则[11]将粒子的连续位置
设立具有特定规模的外部档案(external archive,EA)以保存算法在搜索过程中获得的非支配解,即所有的
| $fitnes{s_1}{\rm{ = }}{\left( {1{\rm{ - }}\exp \left( {{\rm{ - }}CD} \right)} \right)^{{\rm{ - }}\lambda }}\text{,}$ | (15) |
其中,CD为拥挤距离,
插入(Insert)、互换(Swap)和逆序(Inverse)是求解流水车间问题的3种常用邻域结构。为了系统地应用3种邻域结构,本文将其随机排列构造变邻域搜索(variable neighborhood search, VNS)算子,并直接作用于工件排序。具体而言,在某次调用VNS算子时,3种邻域结构随机按6种顺序中的1种(如Swap、Insert、Inverse的操作顺序)依次调整工件排序,直到目标函数值有所改进或达到基于变邻域搜索的最大目标函数评价次数(
在更新各粒子速度时,需要从EA中为其选取一个
| $fitnes{s_2}{\rm{ = }}{\left( {1{\rm{ - }}\exp \left( {{\rm{ - }}CD} \right)} \right)^\gamma }\text{,}$ | (16) |
其中,CD为拥挤距离,
本文调度实例求解的对象为某船厂拟建造的一批(20个)不同尺寸平面分段。其中,加工时间的最可能值(
在相同的算法条件和计算环境下,分别应用本文提出的改进多目标粒子群算法(MOPSO-ILIW-VNS),仅不采用非支配解动态维护策略的多目标粒子群算法(MOPSO-ILIW-VNS-2),仅引入按反Logistic曲线规律变化的动态惯性权重多目标粒子群算法(MOPSO-ILIW),仅嵌入VNS算子的多目标粒子群算法(MOPSO-VNS),以及带压缩因子[13]的多目标粒子群算法(MOPSO-CF)求解平面分段流水线多目标模糊调度问题。其中,MOPSO-VNS与MOPSO的惯性权重
引入C指标[14]、GD指标[15]和
本文应用5种算法分别独立地对实例进行100次求解,基于各算法的100次求解结果计算上述3个指标评价对5种算法进行评价。由于PF*未知,本文通过整合5种算法求解的所有OF构造一个参考Pareto前沿作为PF*。在计算GD指标和
以A1,A2,A3,A4和A5分别表示MOPSO-ILIW-VNS、MOPSO-ILIW-VNS-2、MOPSO-ILIW、MOPSO-VNS和MOPSO-CF。分别整合各算法在100次求解中得到的近似Pareto最优解集,形成对应的
|
|
表 1 C指标 Tab.1 C- metric |
5种算法各求得100个独立的OF,进而获得各算法的100个GD指标和100个
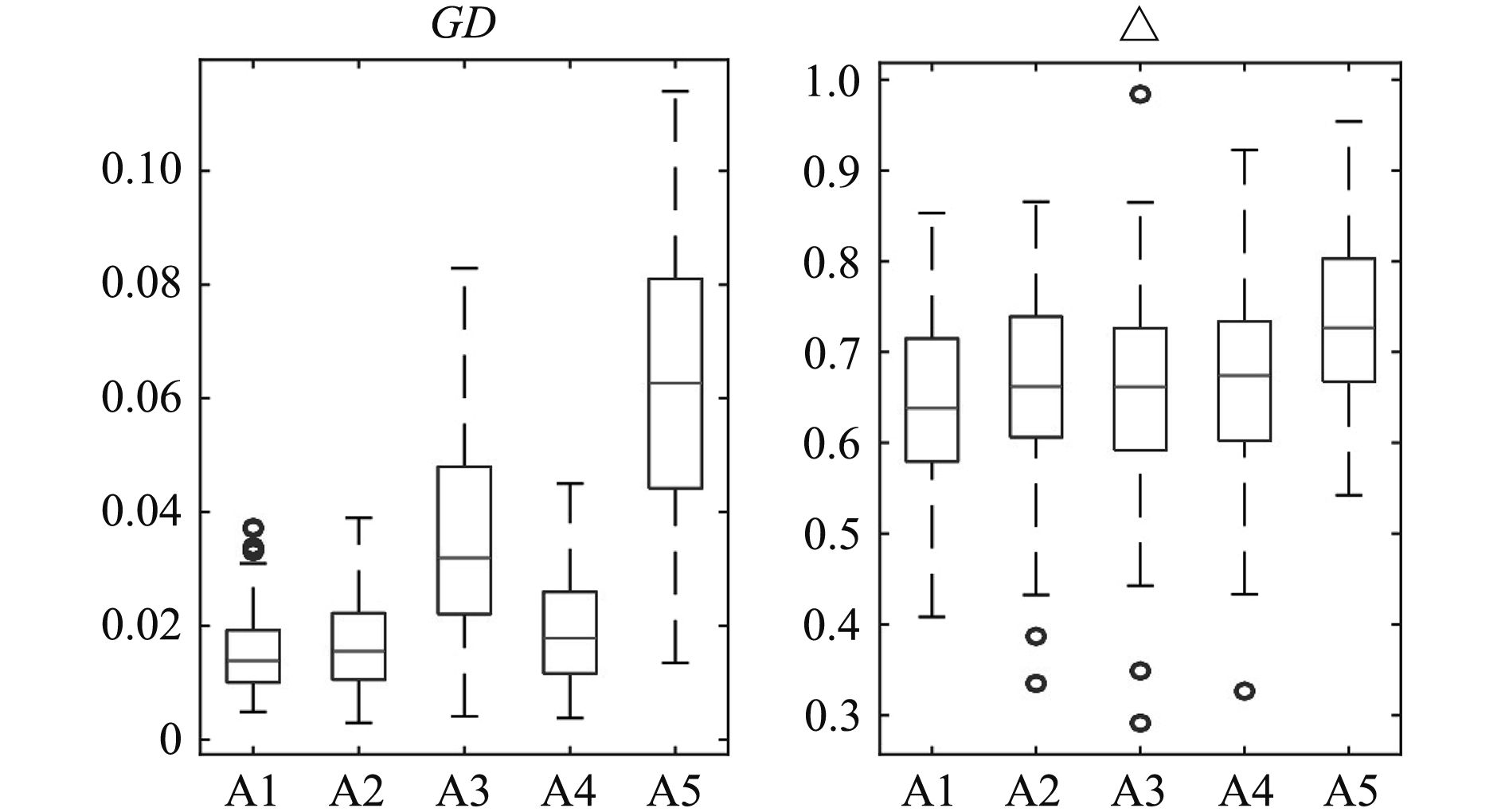
|
图 3 GD指标和Δ指标的箱线图 Fig. 3 Boxplots of the GD and Δ indicators |
|
|
表 2 GD指标和Δ指标的Wilcoxon秩和检验的结果 Tab.2 Results of the Wilcoxon rank-sum test for the GD and Δ indicators |
本文研究了模糊的加工时间和交货期下,平面分段流水线的调度问题。提出了一种引入按反Logistic曲线规律动态变化的惯性权重,并嵌入由3种邻域结构随机排列构造的变邻域搜索算子,同时采用基于拥挤距离的非支配解动态维护策略的改进多目标粒子群算法MOPSO-ILIW-VNS来求解平面分段流水线多目标模糊调度问题。结合实例数据,通过对多种算法进行比较,从解的覆盖度、收敛性和分布性等3方面证实了各项改进措施的有效性,以及MOPSO-ILIW-VNS算法的优越性。作者将继续开展并不断深入关于船舶建造的多目标模糊调度研究。后续研究将考虑其他更复杂的船舶建造生产线(如非完全混合的平面分段流水线[7])的多目标模糊调度问题。
| [1] | REZA HEJAZI S, SAGHAFIAN S. Flowshop-scheduling problems with makespan criterion: a review[J]. International Journal of Production Research, 2005, 43(14): 2895–2929. |
| [2] | RUIZ R, VÁZQUEZ-RODRÍGUEZ J A. The hybrid flow shop scheduling problem[J]. European Journal of Operational Research, 2010, 205(1): 1–18. |
| [3] | YENISEY M M, YAGMAHAN B. Multi-objective permutation flow shop scheduling problem: Literature review, classification and current trends[J]. Omega, 2014, 45: 119–135. |
| [4] | KAHRAMAN C, ENGIN O, YILMAZ M K. A new artificial immune system algorithm for multiobjective fuzzy flow shop[J]. International Journal of Computational Intelligence Systems, 2009, 2(3): 236–247. https://www.researchgate.net/profile/Mustafa_Yilmaz16/publication/232952163_A_New_Artificial_Immune_System_Algorithm_for_Multiobjective_Fuzzy_Flow_Shop/links/00b49521c423d8e777000000.pdf?origin=publication_list |
| [5] | ENGIN O, KAHRAMAN C, YILMAZ M K. A scatter search method for multiobjective fuzzy permutation flow shop scheduling problem: a real world application[M]. Computational Intelligence in Flow Shop and Job Shop Scheduling. Springer Berlin Heidelberg, 2009: 169–189. |
| [6] | HA T R, MOON C U, JOO C M, et al. A hybrid genetic algorithm for scheduling of the panel block assembly shop in shipbuilding[J]. Management Science, 2000, 17(1): 135–143. http://www.koreascience.or.kr/article/ArticleFullRecord.jsp?cn=GOGGCJ_2000_v17n1_135 |
| [7] | 张志英, 李殿勤. 船舶平面分段的非完全混合流水线调度[J]. 计算机集成制造系统, 2012, 18(11): 2435–2445. http://www.oalib.com/paper/4716220 |
| [8] | ABDULLAH S, ABDOLRAZZAGH-NEZHAD M. Fuzzy job-shop scheduling problems: A review[J]. Information Sciences, 2014, 278: 380–407. |
| [9] | LEI D. Fuzzy job shop scheduling problem with availability constraints[J]. Computers & Industrial Engineering, 2010, 58(4): 610–617. https://www.sciencedirect.com/science/article/pii/S0360835210000045 |
| [10] | SAKAWA M, KUBOTA R. Fuzzy programming for multiobjective job shop scheduling with fuzzy processing time and fuzzy duedate through genetic algorithms[J]. European Journal of operational research, 2000, 120(2): 393–407. |
| [11] | LIU B, WANG L, JIN Y H. An effective PSO-based memetic algorithm for flow shop scheduling[J]. Systems, Man, and Cybernetics, Part B: Cybernetics, IEEE Transactions on, 2007, 37(1): 18–27. |
| [12] | DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182–197. |
| [13] | CLERC M, KENNEDY J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J]. IEEE transactions on Evolutionary Computation, 2002, 6(1): 58–73. |
| [14] | ZITZLER E, THIELE L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach[J]. IEEE transactions on Evolutionary Computation, 1999, 3(4): 257–271. |
| [15] | VAN VELDHUIZEN D A, LAMONT G B. Multiobjective evolutionary algorithm research: A history and analysis[R]. Technical Report TR-98-03, Department of Electrical and Computer Engineering, Graduate School of Engineering, Air Force Institute of Technology, Wright-Patterson AFB, Ohio, 1998. |
 2018, Vol. 40
2018, Vol. 40
