2. 武汉第二船舶设计院,湖北 武汉 430064;
3. 中国舰船研究设计中心,湖北 武汉 430064
2. Wuhan Second Ship Design and Research Institute, Wuhan 430064, China;
3. China Ship Development and Design Center, Wuhan 430064, China
复合材料在船舶与海洋工程领域应用时,具有重量轻、力学性能优良、电磁声性能优良、耐腐蚀、容易维护等优点。因其优异特性,在船舶的各个领域中,应用越来越普遍。船体结构根据实际功能或者结构安装,对材料结构会有不同程度的开孔,因此在复合材料的设计中,不可避免的遇见开孔问题。Larry B.Lessarcd等[1]提出了一种损伤累积模型用于计算含孔层合板的应力、应变分析,同时也建立了复合材料层合板开孔的失效模型和破坏准则。Wu Hwai-chung等[2]研究了轴向各向同性开孔板、双向加载各向同性开孔板、受内压或轴向载荷的各向同性开孔圆柱壳。发现可将各向同性材料下开孔板的应力集中因子使用到正交各向异性材料下开孔板以及开孔圆柱壳。韩小平等[3]研究了有限宽层合板在开小孔情况下的应力集中问题。得到有限宽层合板在开小孔情况下的应力集中系数,还讨论分析了板宽/直径比、材料参数、层合板铺层等因素的影响。复合材料结构的失效模式主要包括基体撕裂、纤维断开、基体纤维剪切失效和层间分层,通常失效模式是2种或者多种模式同时出现的,且失效过程是渐进的。随着载荷的增加,不断积累的损伤会使结构刚度产生退化,直到整个结构破坏。因此渐进失效分析主要包含应力分析、材料退化准则分析以及失效准则分析[4]。韩小平等[5 – 7]对含孔复合材料的缝合补强进行了实验研究和有限元数值模拟研究,揭示了孔边应变―载荷在不同参数下的变化规律,对于缝合参数的设计给出了合理的范围。O′Neill[8]考虑加工方便研究了顺层非对称补强问题,结果比未补强结构的强度提高了5%~12%。寇长河等[9 – 10]通过试验对含圆孔的层合板进行了非对称补强研究。认为偏弯效应因非对称这种形式引起,因此非对称效果略差。姚辽军等[11 – 12]建立了复合材料层合板非线性三维渐进损伤模型,讨论了补片半径和补片铺层等对结果的影响。
本文首先归纳了复合材料层合板开孔特点以及常见的开孔补强形式。其次,在横向弯曲载荷下,针对插层对称补强、插层非对称补强2种补强形式,进行有限元数值模拟,分别讨论补片半径比和补片铺层这2个参数变化时,2种不同补强形式在x轴最大应力值(S11)和未补强模型进行对比,得到S11减小的比例;同时分析讨论补片半径比以及补片铺层变化时,2种不同补强形式下整体结构和不同厚度区S11的变化规律。最后讨论在不同补片铺层和补片半径比下,2种不同补强形式S11最大值的变化规律,得出S11最大值减小最多的补强形式。
1 补强形式对于复合材料层合板开孔补强的设计要求,主要包括[13]:1)开孔结构补强后的承载能力应该满足设计要求,应有一定的强度冗余;2)在工艺上,补强方案应该可行且容易实现,尽量减小补强重量,提高补强效率。对于层合板开孔主要有以下补强形式:开孔翻边补强、开孔缝纫补强、补片补强。
开孔翻边补强如图1所示,首先利用单向树脂在开孔附近铺放,然后对层合板开孔处进行下陷处理,形成补强部分,最后再经固化成形。对于这种形式已经做了很多实验和有限元研究[14 – 17],能取得一定的补强效果。此形式的补强因其自身的几何特性,过渡区的圆角区域是比较危险的位置,会产生应变和应力的极值以及分层现象。

|
图 1 开孔翻边补强形式 Fig. 1 Perforated flanging reinforcement form |
开孔缝纫补强图2所示,通过在开孔附近用缝线穿过层合板厚度方向来实现,主要目的是减少孔边的分层失效,增加层间强度。许多研究[18 – 20]对拉伸和压缩载荷下,未缝合和缝合后的结果进行分析对比,通过仿真和实验得到了缝合线的最佳模拟参数,认为存在一个最佳的缝合密度,不同相邻铺层的角度差对结果也会产生影响,但是开孔缝合补强后,在孔边局部区域会引起刚度增加,导致孔边应变、应力集中程度增大,即出现“局部强化”现象,这是设计中要考虑的一个特殊问题。
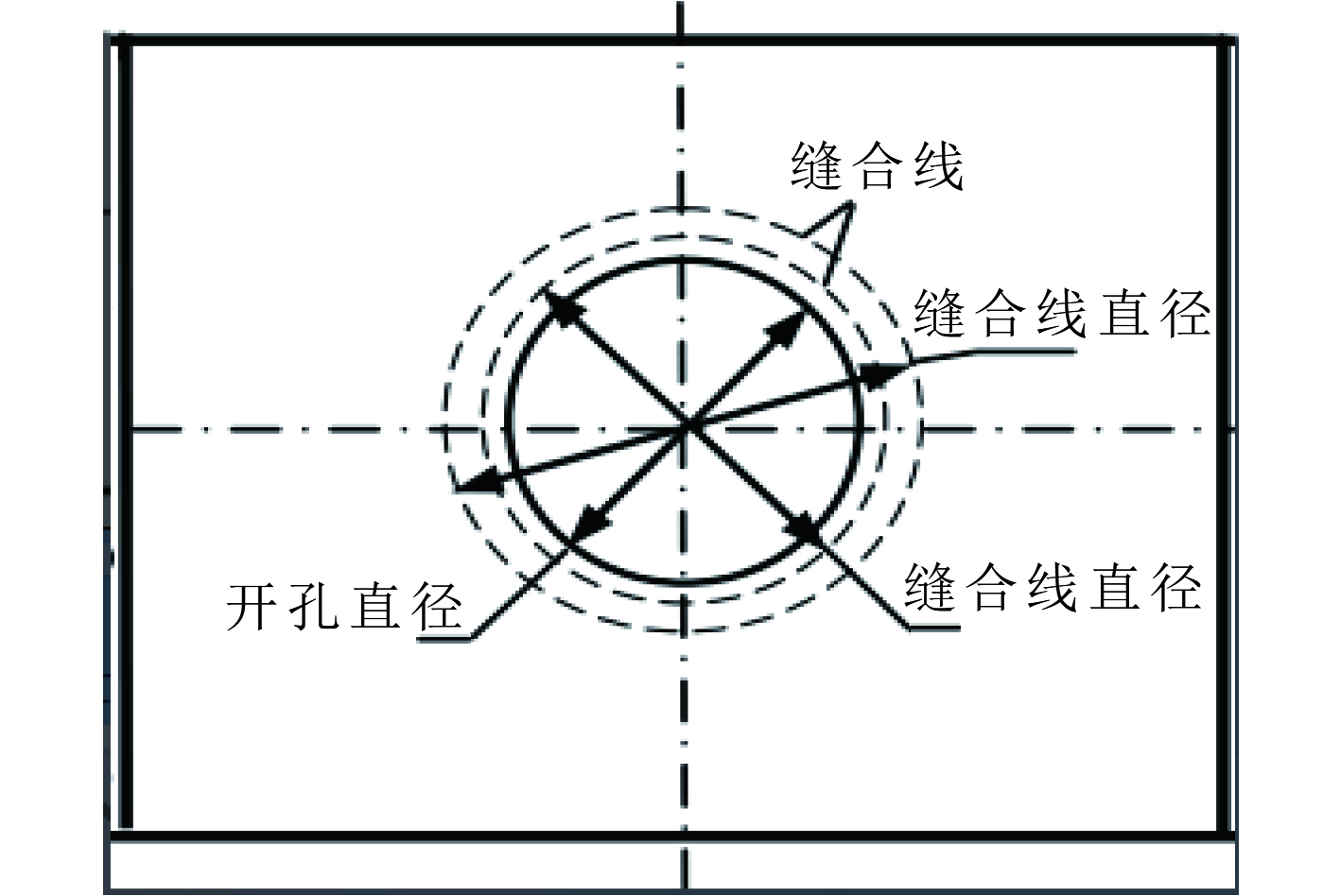
|
图 2 开孔缝纫补强形式示意图 Fig. 2 Perforated sewing reinforcement form |
补片补强通过不同的加工工艺,利用不同补片材料在开孔附近形成补强区,达到补强的目的[21]。在形式上,根据补片的位置安放,可以分为对称补强和非对称补强形式。补片补强主要包括:1)补片材料,2)加工工艺。一般来说补片材料主要包括金属和复合材料。加工工艺有共固化加工、二次固化加工、机械连接和胶接。螺栓连接的钛合金板补强如图3(a)所示。金属材料补片补强,一般采用机械连接,优势在于结构简单,工艺性好,成本较低,装拆方便。但是母板和补片需要单独加工。并且经过机械加工之后,复合材料层间敏感度增加,也会出现重量过重等问题。此外,螺栓的使用必须要钻孔,这会在打孔处出现应力集中等问题。复合材料补片和复合材料母板之间一般采用二次固化补强。即对预固化后的复合材料采用热固性胶膜进行二次胶接。母板和补片可以分别加工,连接效率高。胶黏剂也可以承受一定的应力。但是由于是二次固化,胶层位置会是最先发现失效的位置。复合材料板胶接的模型如图3(b)所示。

|
图 3 复合材料板开孔补强板 Fig. 3 Composite plate reinforced with holes |
本文研究的插层补强设计属于补片补强的一种。即预先将补片铺设在母板上,然后采用共固化工艺进行一次加工。微观剖面如图4所示。

|
图 4 插层补强模型 Fig. 4 Intercalation reinforcement model |
层合板几何示意图如图5所示。层合板的长250 mm,宽200 mm。板中心圆形开孔半径30 mm。层合板单层厚度0.2 mm,材料为T300/QY8911。基本力学性能参数如表1所示。层合板的母板铺层顺序为[45/–45/90/0/–45/45/0/–45/0/45]s,共20层,母板总厚度4 mm。
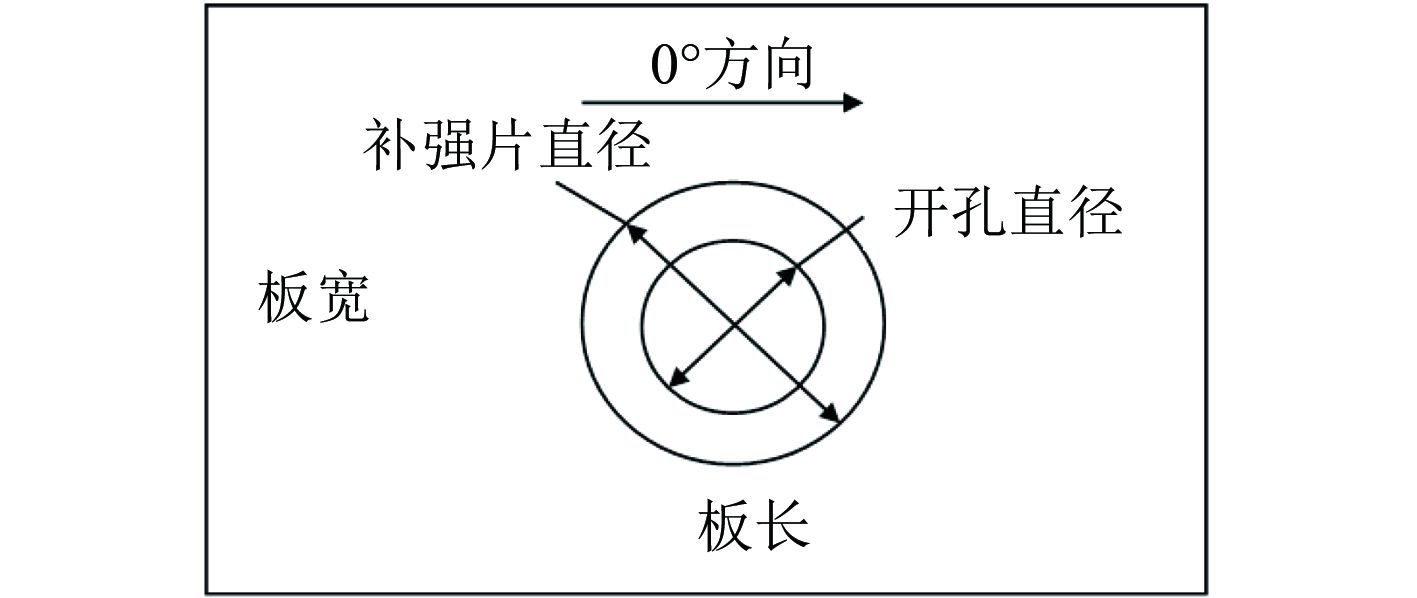
|
图 5 模型几何示意图 Fig. 5 Intercalation reinforcement model |
|
|
表 1 T300/QY8911材料基本力学性能参数 Tab.1 Properties of T300/QY8911 |
在Abaqus中进行有限元计算。采用实体单元建模,每层实体单元代表1层铺层,单元类型为C3D8。由于模型为对称模型,所以在实际建模中,采用1/4模型进行。
插层对称补强模型和插层非对称补强模型的有限元模型和单元划分如图6所示。
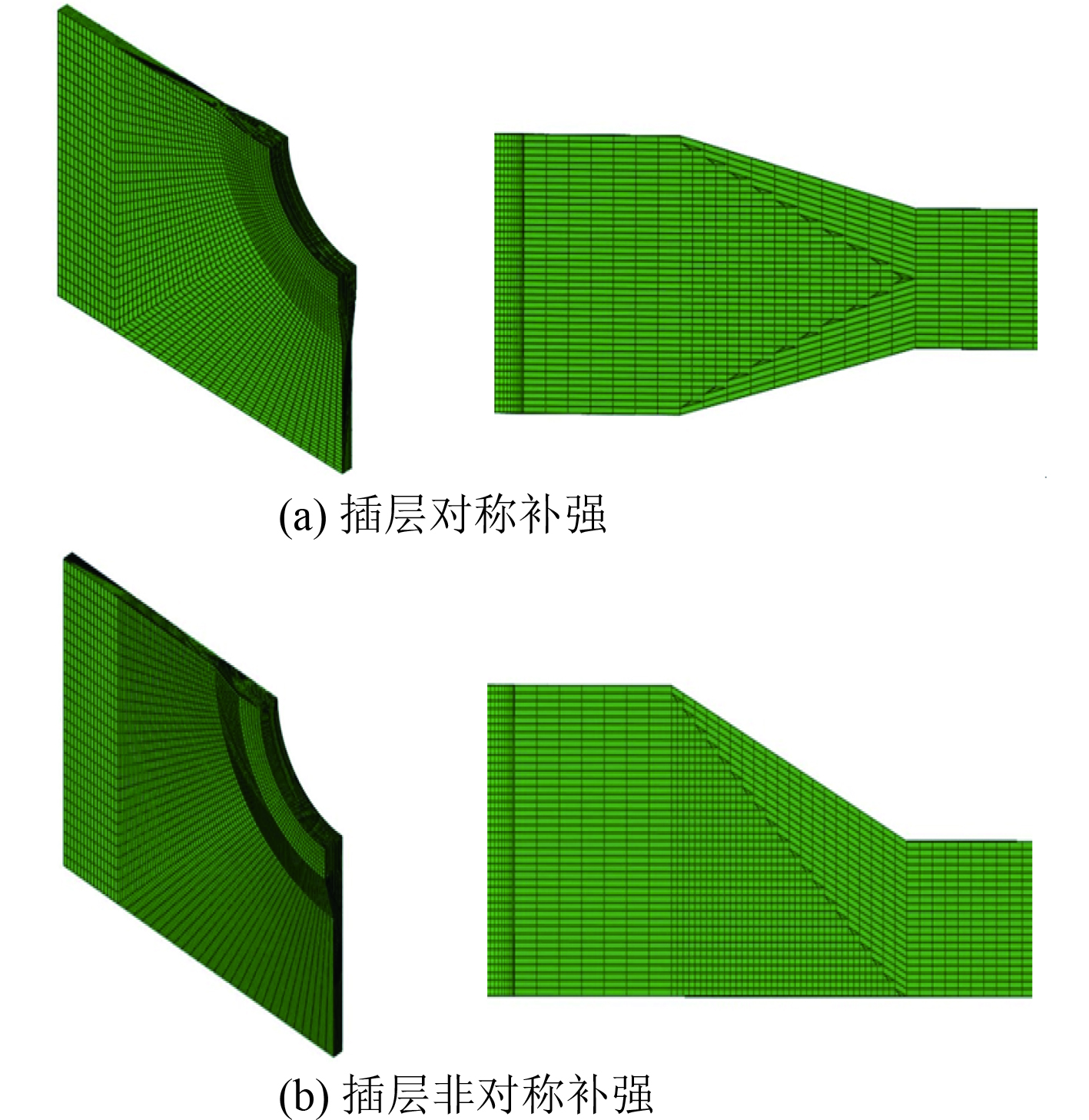
|
图 6 两种不同有限元模型 Fig. 6 Different finite element models |
由于递减设计让整体模型结构在厚度上产生了变化,需要关注不同厚度结构的受力情况。为了方便讨论补强结构受力,将补强后的结构分为如图7所示的母板区、过渡区和加厚区。

|
图 7 模型区域划分 Fig. 7 Model region division |
如图8所示,在实际建模时,选取一定的宽度,同时在这宽度两端的节点上同时施加大小相等、方向相反的节点力,形成纯弯矩。通过控制2个节点力的大小、距离和方向即可控制纯弯矩的大小和方向。在1/4模型中,在开孔的2个边采用对称边界条件。关于yz平面对称的边,其约束条件为U1=UR2=UR3=0;关于xz平面对称的边,其约束为U2=UR1=UR3=0。
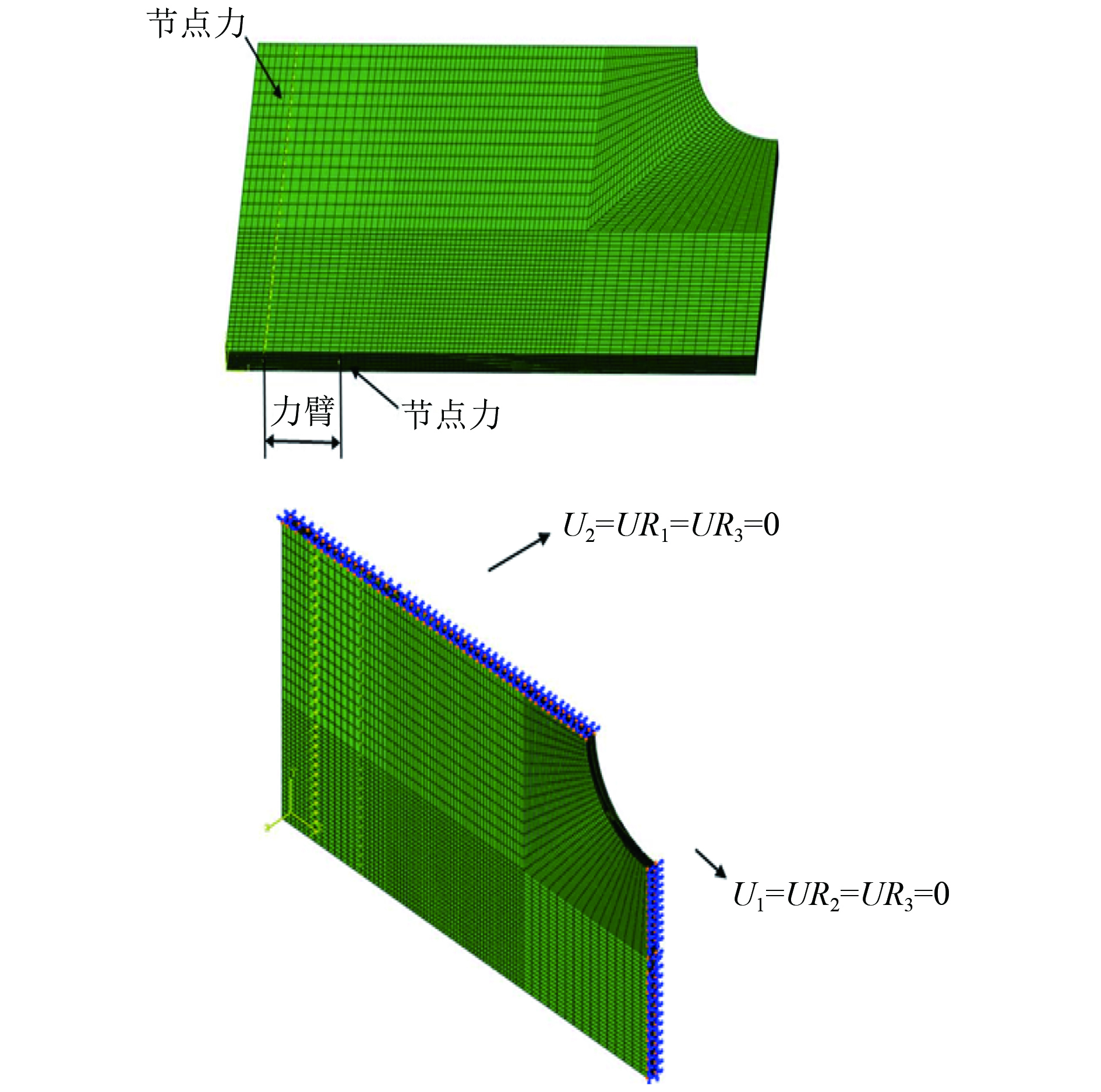
|
图 8 外载荷及边界条件 Fig. 8 Loads and boundary conditions |
为了研究补片铺层比例和顺序对补强效果的影响,本文选取38种不同补片铺层进行数字模拟计算。在这38个补片铺层方式中,主要分为单向铺层、斜交铺层、正交铺层和一般铺层。单层补片角度为0°,–45°,45°和90°。材料参数和母板相同,如表2所示。
|
|
表 2 补片铺层序号及铺层情况 Tab.2 Sequence number and layering of patch |
将补片半径和开孔半径的比值定义为补片半径比。当过渡区宽度从15 cm变化到40 cm,补片半径比为1.50~2.33,本文主要讨论表3所示的补片半径比。
|
|
表 3 补片半径比 Tab.3 Radius ratio of patch |
船体结构中的板为主要承受横向载荷的结构,尤其是弯矩载荷,因此本文主要讨论横向弯曲、不同补强形式下,层合板开孔补强问题。其中S11为模型在X轴应力值分量,是分析模型失效的重要参数,对设计有重要意义。因此本文主要讨论S11的变化规律。在不同弯矩值下,计算未补强模型S11最大值。
当弯矩为1 N·m时,S11云图如图9所示。随着弯矩的增加,S11最大值位置始终出现在模型自下而上和自上而下的第4层,也即由板外向板内的第1个0°铺层。其中负号和正号分别压应力和拉应力。其S11最大值随着横向弯曲载荷大小变化的规律如图所示。

|
图 9 未补强模型计算结果 Fig. 9 Loads and boundary conditions |
由图9可知,在不考虑失效的情况下,S11最大值随着横向弯曲载荷的增加而增加,且呈现线性变化,线性变化常量K的单位为距离的三次方,表示该模型在1个单位弯矩下的S11最大值。
3.2 插层对称补强设计计算结果 3.2.1 插层对称补强补片铺层对结果的影响通过计算可知,插层对称补强设计S11最大值随着横向弯曲载荷也且呈现线性变化,得出1个单位弯矩下的S11最大值。计算插层对称补强设计在不同补片铺层、不同补片半径比下S11最大值,并和未补强的S11最大值进行比较,计算S11最大值减少的百分比,

|
图 10 插层对称补强在不同补片铺层下S11最大值减少的百分比 Fig. 10 Percentage reduction of maximum value of S11 under different patch layers for intercalated symmetric reinforcement |
由图10(a)可知,当补片半径比为1.5时:1)在不同补片铺层比例和顺序下,S11最大值最多减少50.87%,为37号补片铺层;最小减少23.50%,为3号铺层。两者相差2.16倍。对于插层对称补强设计,在补片半径比为1.5时,不同补片铺层比例和顺序对S11影响较大。2)补片中0°层占比为60%左右时,S11减小幅度最大;但并不是0°层比例越多,S11越小,也和其他方向的补片铺层比例以及顺序有关。3)单向铺层补片、正交铺层补片和斜交铺层补片的S11下降幅度小于一般铺层补片。4)对比相同补片铺层比例,不同补片铺层顺序,S11最大值有的变化较大。
由图10(b)可知,当补片半径比为2.33时,在不同铺层比例和顺序下,S11最大值最多减少54.31%,为16号补强铺层;最小减少39.34%,为3号铺层。两者相差1.38倍。但是,和补片半径1.67,1.83和2.00的情况相比,对于一般铺层顺序,S11最大值下降幅度相差不大。
对于插层对称补强,所选的补片铺层顺序、比例以及补片半径,S11最大值最多能减少54.31%,最少能减少23.50%,这表明在横向弯矩载荷下,选择适合的补片铺层和补片半径,插层对称补强这种形式对复合材料开孔有较好的补强效果;S11的最大值和补片铺层比例、铺层顺序以及补片半径均有关系,并且相互影响;总体来说,单向铺层补片、正交铺层补片、斜交铺层补片S11最大值下降幅度小于一般铺层补片;随着补片半径的增加,一般铺层补片下S11的最大值均越来越接近。
3.2.2 补片半径比对结果的影响插层对称补强模型在不同补片铺层、不同半径比下,整体结构、加厚区、过渡区和母板区的S11最大值的计算结果(以17号和37号铺层的趋势为例)如图11所示,其中横坐标表示补片半径比,纵坐标表示单位弯矩下S11最大值。整体结构取模型拉应力和压应力的绝对值的最大值。

|
图 11 插层对称补强,不同补片铺层在不同半径比下,整体结构和各个区的S11最大值 Fig. 11 Symmetry reinforcement of intercalation, the maximum S11 value of the whole structure and each region under different radius ratio of different patch layers |
插层对称整体模型应力减小幅度变化如图12所示,其中横坐标表示补片半径比,37号铺层应力减小幅度对应主坐标轴,17号铺层应力减小幅度对应次坐标轴。这表明,随着补片半径的增加,S11减小幅度增加。产生这样的原因,可能是因为补片半径的增加,在插层对称补强这种形式下,使结构受力更加均匀,从而使得S11降低。
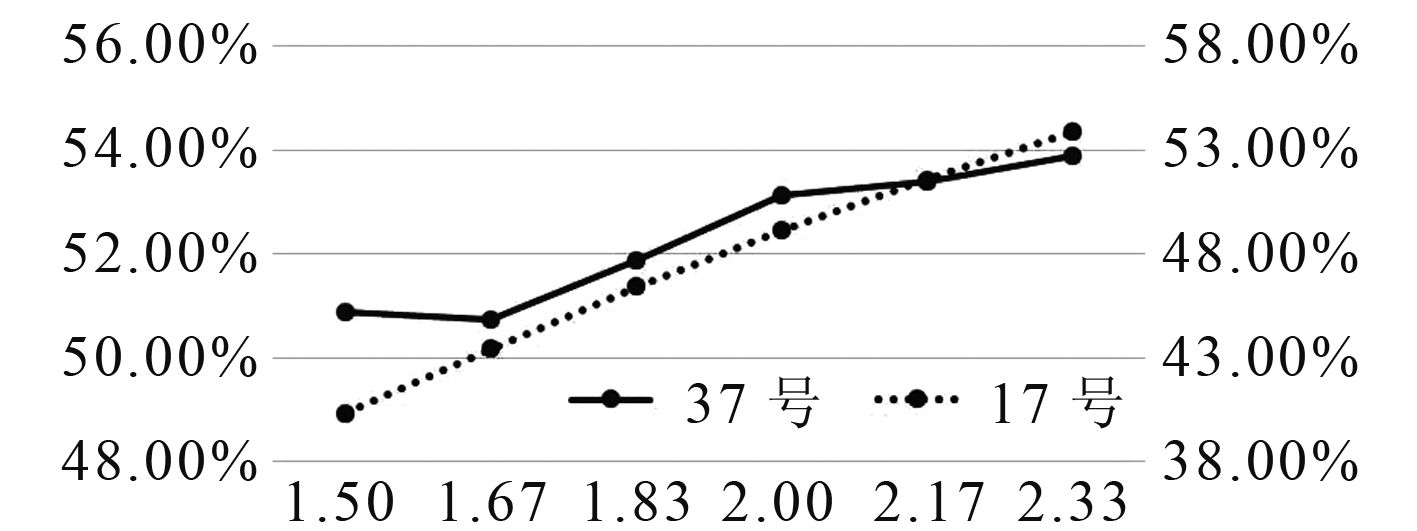
|
图 12 插层对称整体模型应力减小幅度变化图 Fig. 12 Amplitude of stress reduction in intercalated symmetric global model |
对于一般铺层,当0°层比例为60%及以上时,随着补片半径的增加,S11减小幅度相差在6%以内;当0°层比例为20%~50%时,随着补片半径的增加,S11减小幅度相差在8%~13%以内;对于单向铺层(0°,–45°除外)、正交铺层和斜交铺层,随着补片半径的增加,S11减小幅度相差在13%~16%以内。这表明,补强半径的变化对于单向铺层(0°,–45°除外)、正交铺层和斜交铺层补片的结果影响更大。
图13为19号铺层随着补片半径的增加,S11最大值位置有从加厚区逐渐向母板区变化的趋势。对比6和7,8和9,10和11,12和13号铺层结果可知,当补强片铺层比例相同,顺序相反,S11最大值大小相同,方向相反,且位置也对称。

|
图 13 整体模型S11最大值位置变化示意图 Fig. 13 Amplitude of stress reduction in intercalated symmetric global model |
对于加厚区,图14为1号铺层S11的变化趋势。其中横坐标表示补片半径比,加厚区应力对于主坐标轴。S11最大值出现在加厚区自上而下的第1个0°铺层(6号、8号、10号和12号铺层则出现在自下而上的第1个0°铺层)。对于母板区,图16中母板区应力对应次坐标轴。S11最大值出现在母板的自上而下的第1个0°铺层或者自下而上的第1个0°铺层。
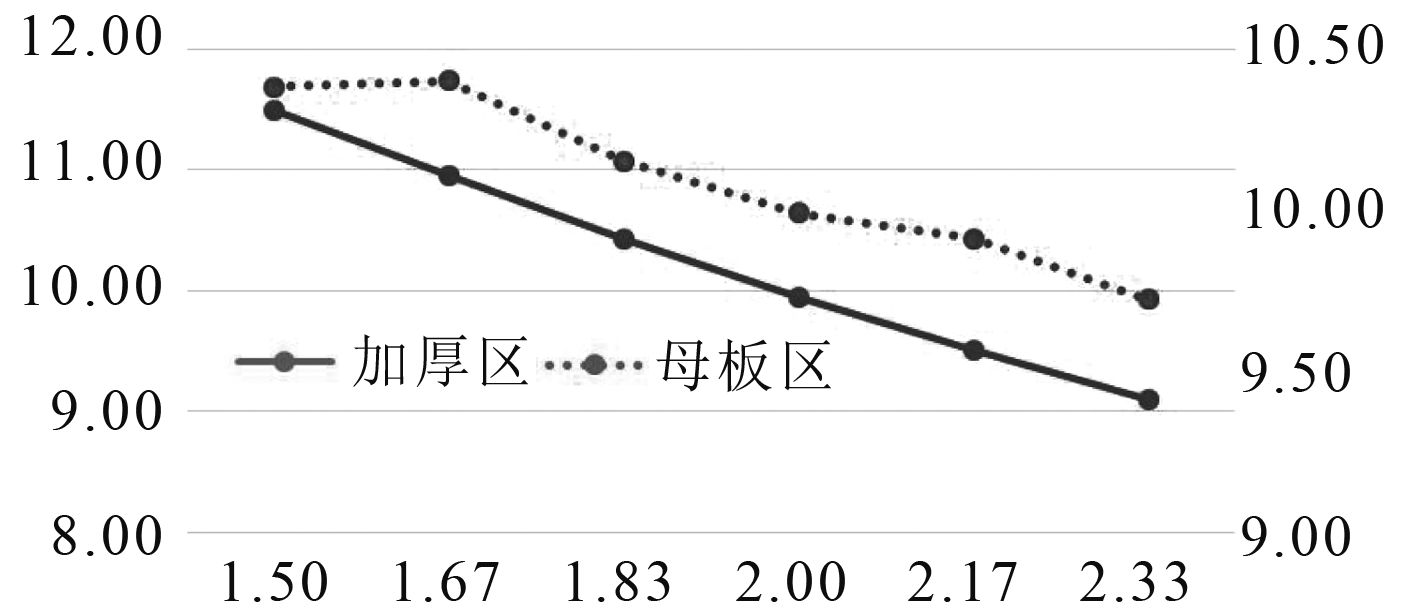
|
图 14 插层对称补强加厚区和母板区S11最大值变化图 Fig. 14 Maximum value of S11 in intercalated symmetric reinforcement and motherboard regions |
图15为过渡区2号和7号铺层S11的变化趋势,其中横坐标表示补片半径比,2号铺层应力对应主坐标轴,7号铺层应力对应次坐标轴。由图可看出,随着补片半径的增加,过渡区S11最大值会减小。非0°单向铺层和斜交铺层的S11最大值随着补片半径的增加而减小;全0°单向铺层、正交铺层和一般铺层的S11最大值随着补片半径增加而先增加后减小。
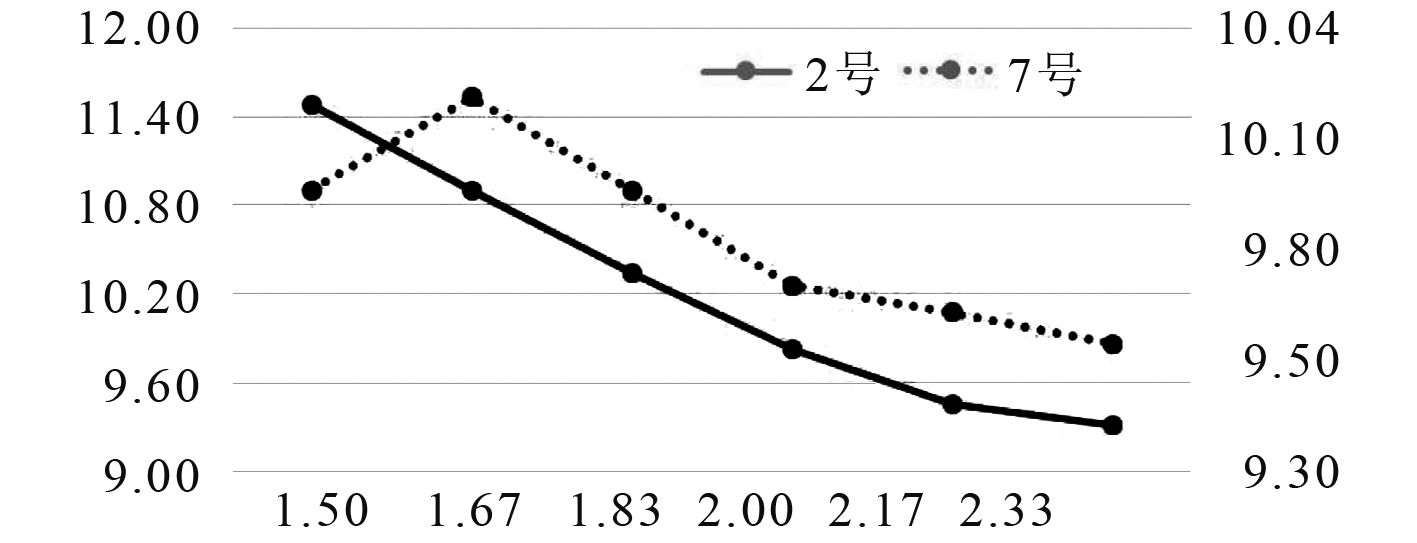
|
图 15 插层对称补强过渡区S11最大值变化图 Fig. 15 Maximum value of S11 in the symmetric reinforcement transition region of intercalation |
通过计算可知,插层非对称补强设计S11最大值随着横向弯曲载荷也呈现线性变化。
3.3.1 弯矩方向的影响由于插层非对称补强形式在几何结构上非对称,弯矩的施加也存在方向之分,因此需要讨论弯矩方向对非对称形式结果的影响。
通过计算,当弯矩大小相等,方向相反时,S11最大值大小相等,方向相反。之前受拉力的铺层,在弯矩方向变化时受压力,反之亦然。因此只需要讨论一个方向的弯矩计算即可。以1号铺层为例,如图16所示。

|
图 16 弯矩方向相反时,模型结果示意图 Fig. 16 Results in opposite direction of bending moment |
计算插层非对称补强设计在不同补片铺层、不同补片半径比下S11最大值,并和未补强的S11最大值进行比较,计算S11最大值减少了的百分比,计算方法为1减去补强应力和未补强应力之比,如图19所示。
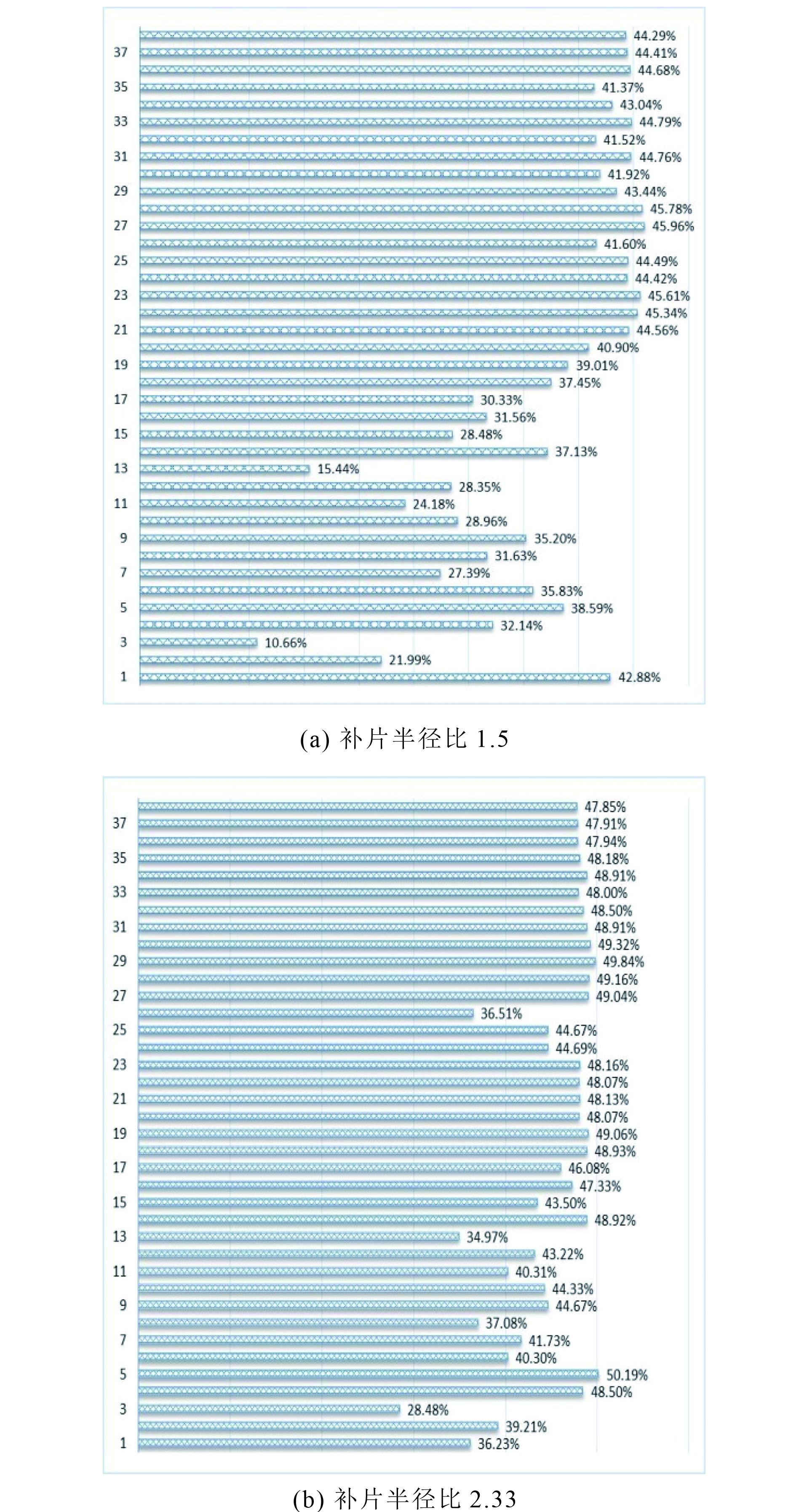
|
图 17 插层非对称补强在不同补片铺层下S11最大值减少的百分比 Fig. 17 Percentage reduction of maximum value of S11 under different patch layers for intercalated asymmetric reinforcement |
由图17(a)可知,当补片半径比为1.5时,1)在不同补片铺层比例和顺序下,S11最大值最多减少45.96%,为27号补片铺层;最小减少10.66%,为3号铺层。两者相差4.31倍。对于插层非对称补强设计,在补片半径比为1.5时,不同补片铺层比例和顺序对S11影响较大。2)补片中0°层占比为70%左右时,S11减小幅度最大;并不是0°层比例越多,S11越小,也和其他方向的补片铺层比例以及顺序有关。3)单向铺层补片(0°除外)、正交铺层补片和斜交铺层补片的S11下降幅度小于一般铺层补片。4)对比相同补片铺层比例,不同补片铺层顺序,S11最大值有的变化较大,如14,15,16和17号铺层,结果相差9%,;有的变化较小,如30,33,36,37和38号,这和具体补片铺层顺序有关。
由图17(b)可知,当补片半径比为2.33时,1)在不同铺层比例和顺序下,S11最大值最多减少50.19%,为5号补强铺层;最小减少28.48%,为3号铺层。对于插层非对称补强设计,在补片半径比为2.17时,对于一般铺层顺序,尤其是当0°层占比大于等于60%时,S11最大值下降幅度相差不大。2)整体来说,一般铺层补片,尤其是当0°层占比大于等于60%时,S11下降幅度大于单向铺层补片(0°单向铺层除外)、正交铺层补片和斜交铺层补片。
对于插层非对称补强,所选的补片铺层顺序、比例以及补片半径,S11最大值最多能减少50.19%,最少能减少10.66%,这表明在横向弯矩载荷下,选择适合的补片铺层和补片半径,插层非对称补强形式能取得较好的补强效果;S11最大值减小幅度取决于合适的铺层比例、铺层顺序以及补片半径,且这三者相互影响;总体来说,单向铺层补片、正交铺层补片、斜交铺层补片S11最大值下降幅度小于一般铺层补片;随着补片半径的增加,一般铺层补片下S11的最大值均越来越接近。
3.3.3 补片半径比对结果的影响计算插层非对称补强模型在不同补片铺层、不同半径比下,整体结构、加厚区、过渡区和母板区的S11最大值。图20为1号和2号铺层S11的变化趋势,其中横坐标表示补片半径比,纵坐标表示单位弯矩下S11最大值。其中负值表示压力,正值表示拉力,整体结构取模型拉力和压力的绝对值的最大值。

|
图 18 插层非对称补强,不同补片铺层在不同半径比下,整体结构和各个区的S11最大值 Fig. 18 Asymmetry reinforcement of intercalation, the maximum S11 value of the whole structure and each region under different radius ratio of different patch layers |
图18为1号和2号铺层S11的变化趋势,其中横坐标表示补片半径比,1号铺层应力减小幅度对应主坐标轴,2号铺层应力减小幅度对应次坐标轴。
对于一般铺层,当0°层比例为60%及以上时,随着补片半径的增加,S11减小幅度相差在7%以内,变化相比较小;当0°层比例为20%~50%时,随着补片半径的增加,S11减小幅度相差在10%~15%以内;对于单向铺层(0°,–45°除外)、正交铺层和斜交铺层,随着补片半径的增加,S11减小幅度相差在12%~19%以内,变化相比较大。这表明,补强半径的变化对于单向铺层(0°,–45°除外)、正交铺层和斜交铺层补片的结果影响更大。

|
图 19 插层非对称整体模型应力减小幅度示意图 Fig. 19 Amplitude of stress reduction in intercalated asymmetric global model |
同时,随着补片半径的增加,S11最大值位置有从加厚区逐渐向母板区和过渡区变化的趋势,图20为25号铺层S11值最大位置的变比情况。
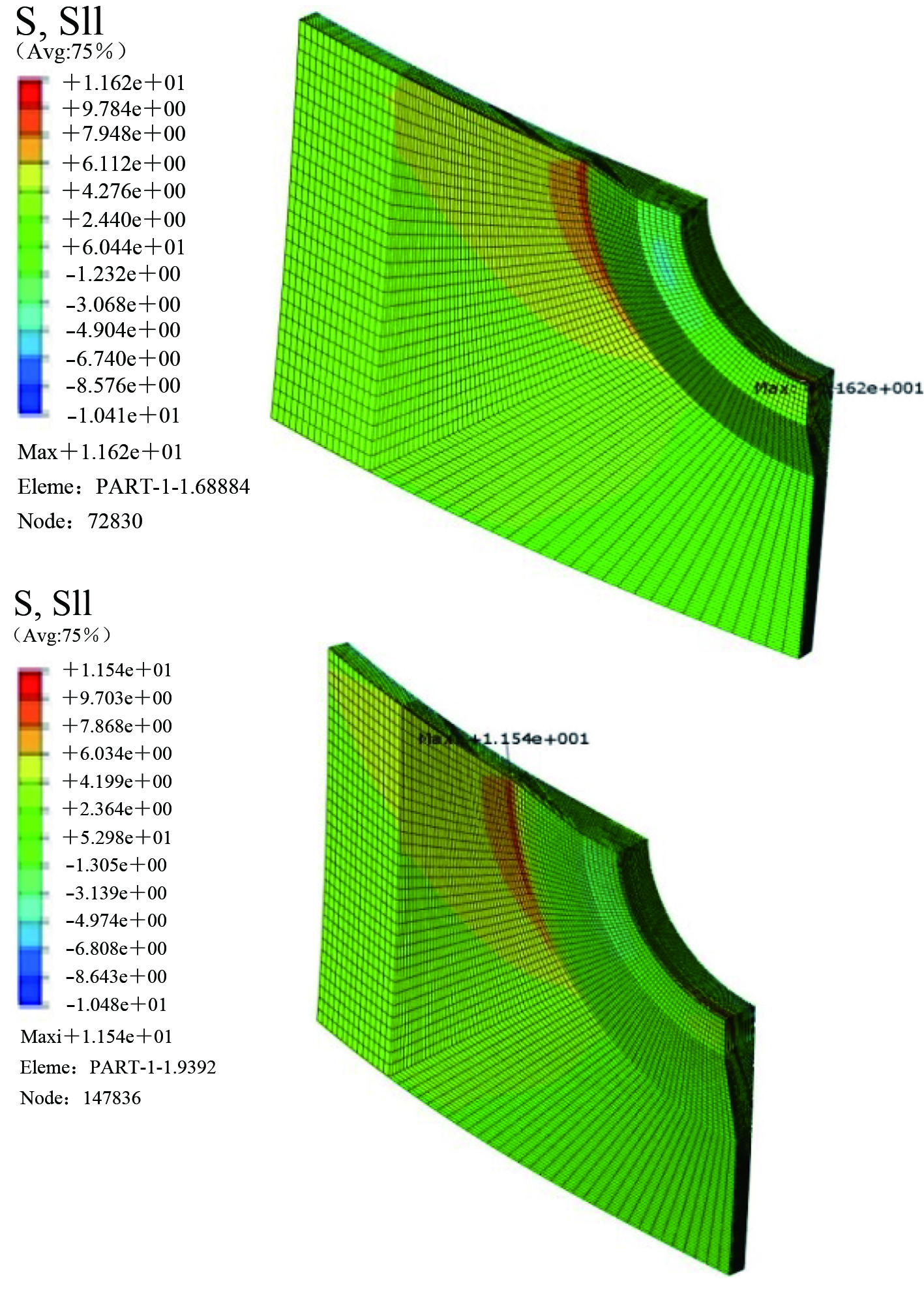
|
图 20 整体模型S11最大值位置变化示意图 Fig. 20 Location of maximum S11 of global model |
对于加厚区,由结果可知,对于不同补片铺层,加厚区S11最大值随着补片半径增加而减小。S11最大值出现在加厚区自上而下的第1个0°铺层。图21给出了1号铺层加厚区S11的计算结果,其中横坐标表示补片半径比,加厚区应力对应主坐标轴。
对于母板区由计算结果可知,对于不同补片铺层,母板区S11最大值随着补片半径增加而先增加后减小。S11最大值出现在母板自上而下的第1个0°铺层。
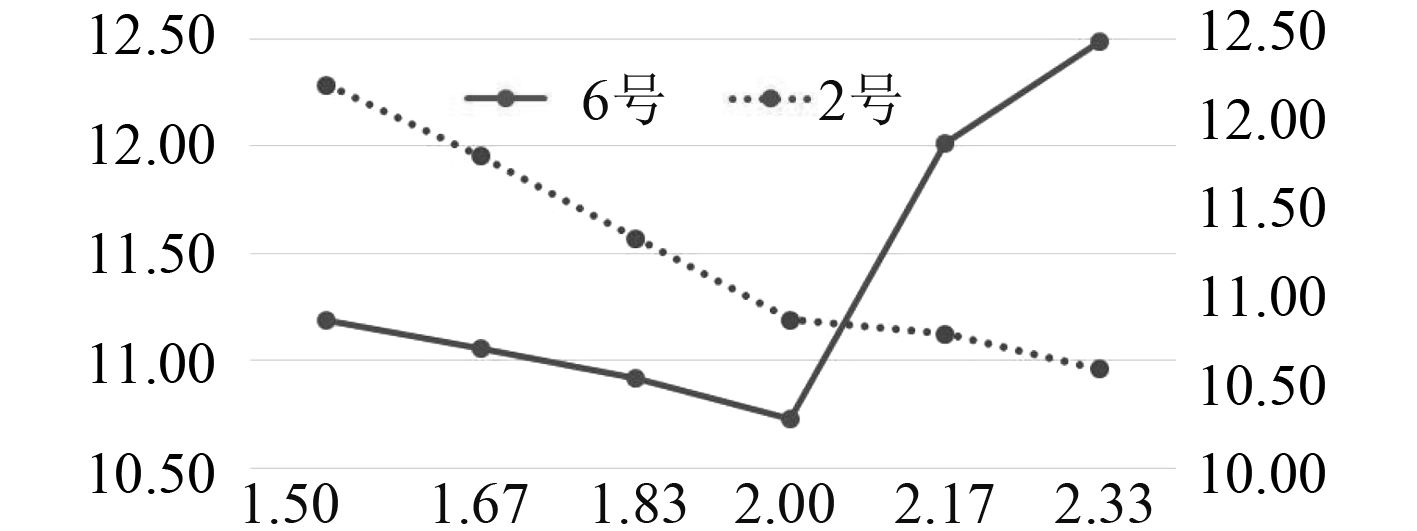
|
图 21 插层非对称补强加厚区和母板区S11最大值变化图 Fig. 21 Maximum value of S11 in intercalated asymmetric reinforcement and motherboard regions |
对于过渡区,图22给出了6号和2号铺层S11的变化趋势,其中横坐标表示补片半径比,6号铺层应力对应主坐标轴,2号铺层应力对应次坐标轴。
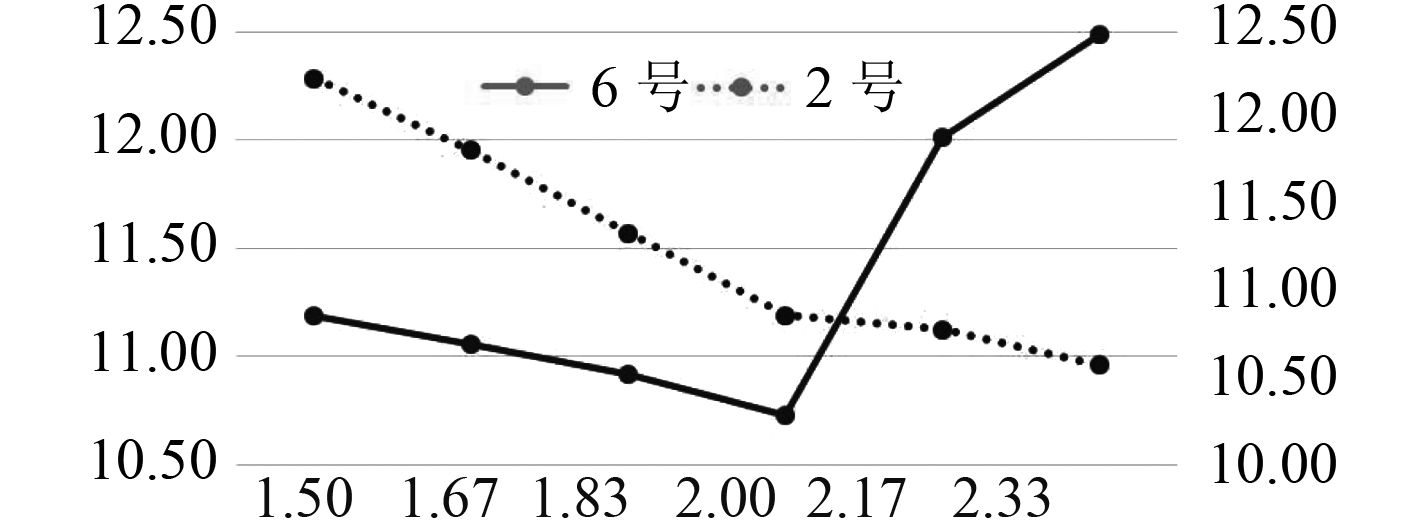
|
图 22 插层非对称补强过渡区S11最大值变化图 Fig. 22 Maximum value of S11 in the asymmetric reinforcement transition region of intercalation |
0°单向铺层、正交铺层以及一般铺层中,0°比例较高,且没有±45°的铺层;一般铺层中,0°铺层均在两端,随着补片半径的变化,S11最大值出现的位置由母板自上而下的第1个0°铺层变到整个过渡区自下而上的第1个0°铺层。其余铺层过渡区S11最大值的位置均在母板自上而下的第1个0°铺层。S11最大值位置的变化是引起S11大小规律发生变化的原因。
4 结 语根据以上计算结果与分析,可得出如下结论:
1)对于插层对称补强,所选的补片铺层以及补片半径,S11最大值最多能减少54.31%,最少能减少23.50%,这表明在横向弯矩载荷下,选择适合的补片铺层和补片半径,插层对称补强这种补强形式有较好的补强效果;但单向铺层补片、正交铺层补片、斜交铺层补片S11最大值下降幅度小于一般铺层补片;且随着补片半径的增加,一般铺层补片S11的最大值均越来越接近。
2)对于整体结构,插层对称补强随着补片半径的增加,S11最大值减小幅度总体呈增加趋势,且S11最大值位置有从加厚区逐渐向母板区变化;对于加厚区,S11最大值随着补片半径增加而减小;对于过渡区,非0°单向铺层和斜交铺层的S11最大值随着补片半径的增加而减小,全0°单向铺层、正交铺层和一般铺层的S11最大值随着补片半径增加而先增加后减小;对于母板区,S11最大值随着补片半径增加而先增加后减小。不同区域S11最大值出现在各自区域自上而下或者自下而上的第1个0°铺层。此外,补强半径的变化对于90°和45°的单向铺层、正交铺层和斜交铺层补片的结果影响更大。
3)对于插层非对称补强,所选的补片铺层以及补片半径,S11最大值最多能减少50.19%,最少能减少10.66%,这表明在横向弯矩载荷下,选择适合的补片铺层和补片半径,插层非对称补强能取得较好的补强效果。总体来说,单向铺层补片、正交铺层补片、斜交铺层补片S11最大值下降幅度小于一般铺层补片;随着补片半径的增加,一般铺层补片下S11的最大值均越来越接近。
4)对于整体结构,插层非对称补强0°单向铺层、正交铺层以及一般铺层中0°铺层在插层两端的铺层的S11减小幅度随着补片半径增加而先增加后减小,其余补片铺层的S11减小幅度随着补片半径增加而呈现增加趋势,且S11最大值位置有从加厚区逐渐向母板区和过渡区变化的趋势;对于加厚区,S11最大值随着补片半径增加而减小;对于过渡区,0°单向铺层、正交铺层以及一般铺层中0°比例较高且没有±45°的铺层的S11最大值随着补片半径的增加而先减小后增加;对于母板区S11最大值随着补片半径增加而先增加后减小。不同区域S11最大值出现在各自区域自上而下或者自下而上的第1个0°铺层。此外,补强半径的变化对于90°和45°的单向铺层、正交铺层和斜交铺层补片的结果影响更大。
| [1] | LESSARD L B, CHANG F K. Damage tolerance of laminated composites containing an open Hole and subjected to compressive loadings: Part II—experiment[J]. Journal of Composite Materials, 1991, 25(1): 44–64. |
| [2] | WU H C, MU B. On stress concentrations for isotropic/orthotropic plates and cylinders with a circular hole [J]. Composites Part B Engineering, 2003, 34(2): 127–134. |
| [3] | 韩小平, 郭章新, 朱西平, 等. 含孔复合材料层合板孔边的应力集中[J]. 复合材料学报, 2009, 26(1): 168–173. http://www.oalib.com/paper/4176741 |
| [4] | 张林. 复合材料层合板的逐渐失效分析[D]. 哈尔滨: 哈尔滨工业大学, 2009. |
| [5] | 韩小平, 曹效昂, 朱西平, 等. 孔口缝合补强对含孔层板应变集中影响的实验研究[J]. 复合材料学报, 2006, 23(4): 169–174. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=fhclxb200604029 |
| [6] | 韩小平, 曹效昂, 朱西平, 等. 复合材料开口缝合补强结构力学性能实验研究[J]. 工程力学, 2008, 25(1): 122–126. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hkclxb200801018 |
| [7] | 韩小平, 郭章新, 王彬, 等. 含孔层合板孔口缝合补强的数值模拟[J]. 复合材料学报, 2011, 28(3): 148–153. http://www.cqvip.com/QK/96080X/201103/38253703.html |
| [8] | O′NEILL G S. Asymmetric reinforcements of a quasi-isotropic graphite epoxy plate containing a circular hole [R]. AD-A119625MF, 1985. |
| [9] | 罗小东, 寇长河, 于卫东, 等. 复合材料层合结构开口的非对称补强研究[J]. 航空学报, 1994, 15(12): 1478–1481. |
| [10] | 寇长河, 汪彤, 郦正能, 等. 复合材料层合板开口补强研究[J]. 北京航空航天大学学报, 1997(04): 477–481. http://www.cqvip.com/QK/96080X/200505/20330349.html |
| [11] | 姚辽军, 赵美英, 李沛城. 基于CDM的复合材料层合板插层补强强度分析[J]. 西北工业大学学报, 2011, 29(5): 794–798. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xbgydxxb201105025 |
| [12] | 姚辽军, 赵美英, 万小朋. 基于CDM-CZM的复合材料补片补强参数分析[J]. 航空学报, 2012, 33(4): 666–671. |
| [13] | 杨乃宾, 章怡宁. 复合材料飞机结构设计[M]. 航空工业出版社, 2002. |
| [14] | 姜云鹏, 张庆茂, 王毅, 等. 复合材料层合板开口翻边补强试验和数值研究[J]. 复合材料学报, 2005, 22(5): 190–196. http://www.cqvip.com/QK/96080X/200505/20330349.html |
| [15] | 王毅, 姜云鹏, 岳珠峰. 压缩载荷作用下复合材料层合板结构开口翻边补强试验及数值模拟[J]. 机械强度, 2006, 28(6): 869–873. https://www.wenkuxiazai.com/doc/b84fb35dbe1e650e52ea996e.html |
| [16] | 王毅. 复合材料开口补强实验研究和设计分析[D]. 西安: 西北工业大学, 2006. |
| [17] | 王毅, 宋琳, 陈志远. 复合材料开口补强计算的有限元分析[J]. 河南化工, 2008, 25(7): 27–30. https://www.wenkuxiazai.com/doc/404e0e60ddccda38376baf68-2.html |
| [18] | 郭章新, 韩小平, 赵翔, 等. 孔口缝合补强对层间应力影响的数值模拟[J]. 机械强度, 2012(5): 730–736. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yylxxb200904037 |
| [19] | 沈创石, 韩小平, 郭章新, 等. 孔口缝合补强复合材料层合板渐进损伤分析[J]. 材料工程, 2014(1): 64–69. http://www.cnki.com.cn/Article/CJFDTotal-KXJS201209009.htm |
| [20] | 王彬, 韩小平, 郭章新, 等. 孔口缝合补强复合材料层合板的刚度退化及失效分析[J]. 科学技术与工程, 2012, 12(9): 2023–2028. http://www.cqvip.com/QK/84018X/201209/41351267.html |
| [21] | 张伟. 复合材料层合板开口补强技术研究[D]. 南京: 南京航空航天大学, 2012. |
 2018, Vol. 40
2018, Vol. 40
