2. 长江航道规划设计研究院,湖北 武汉 430011
2. Yangtze River Waterway Research Institute, Wuhan 430011, China
目前世界上很多大型船舶都采用液压无键联接的方式来固定桨榖与桨轴两者的相对位置。虽然此种安装方式应用十分广泛,但多数船厂在安装时仍然通过人工手动控制安装油压,螺旋桨无键安装配套设备的自动化程度不高,这不仅使得螺旋桨的安装质量无法得到保证,而且安装效率十分低下。
为解决螺旋桨安装精度和安装效率问题,在进行系统试验研究前,按照相似理论搭建试验模型,对实船的计算数据进行相似换算,在计算出试验模型的主要参数的基础上,对控制系统结构单元中的一些参数进行预估,确定了控制系统的设计原则[1]。与此同时,对系统进行验证分析,结果表明此系统的稳定性好,控制精度高,线性输出好,满足设计要求。通过实验验证了控制系统方案可以满足螺旋桨无键安装的要求。
1 控制系统建模螺旋桨无键安装液压伺服控制控制系统组成见图1,系统主要由放大器、电液伺服阀、泵组、液压缸、压力传感器以及位移传感器形成一个闭环控制系统。

|
图 1 控制系统组成 Fig. 1 Control system composition |

|
图 2 未校正的系统方框原理图 Fig. 2 Control system composition |
系统中油液流量满足连续性要求;忽略系统中各单向阀、溢流阀、安全阀、回油泵等的影响;忽略与液压缸活塞运行速度有关的粘性摩擦力的影响[2]。
1.1 数学模型 1.1.1 电液伺服阀电液伺服阀的动态特性与供油压力、输入信号幅值、油温、环境温度、负载条件等许多因素有关。一般情况下,电液伺服阀的传递函数通常用振荡环节来表示:
| ${G_{sv}} = \frac{{Q\left( {\rm{s}} \right)}}{{I\left( s \right)}} = \frac{{{K_{sv}}}}{{\frac{{{s^2}}}{{w_v^2}} + \frac{{2{\xi _v}}}{{{w_v}}}s + 1}}\text{。}$ |
式中:Ksv为电液伺服阀增益;wv为电液伺服阀固有频率;ξv为电液伺服阀阻尼比。经过前期计算得知,本系统需要匹配螺旋桨安装到预定位置的电液伺服阀固有频率比系统的固有频率要高出很多,亦可将电液伺服阀传递函数近似为比例环节:
| ${G_{sv}} = {K_{sv}}\text{。}$ |
经前期计算可知,将螺旋桨安装到预定位置,需要55 MPa的液压推力,变量机构的实质相当于一个阀控液压缸,在不受外力干扰的情况下,其传递函数为:
| ${W_a} = \frac{{Y\left( s \right)}}{{X\left( s \right)}} = \frac{{1/{A_a}}}{{s\left[ {\displaystyle\frac{{{s^2}}}{{w_s^2}} + \displaystyle\frac{{2{\xi _s}}}{{{w_s}}}s + 1} \right]}}\text{。}$ |
式中:Aa阀控变量机构活塞有效面积;ws为阀控变量机构固有频率;ξs为阀控变量机构阻尼比。计算后得知,变量机构的液压缸固有频率比较高,可将变量机构的传递函数简化成一个积分环节:
| ${W_a}\left( s \right) = \frac{{1/{A_a}}}{s}\text{,}$ |
轴向柱塞变量泵的排量为DP=aKp,变量泵的传递函数为Wp=npKp。式中np为变量泵的转速;Kp为变量泵排量梯度。
1.1.4 内环控制系统内环控制系统由比例放大器、电液伺服阀、变量机构、变量泵和压力传感器组成一个负反馈系统,在此系统中,设置压力传感器的增益为Kpf,令
| $\begin{split}& \frac{1}{{{K_{pf}}}} = {K_{svp}}\text{,}\\& \frac{1}{{{K_a}{K_{sv}}{n_p}{K_p}{K_{pf}}/{A_a}}} = {T_p}\text{。}\end{split}$ |
可得内环控制系统传递函数为:
| ${G_1}\left( s \right) = \frac{{{K_{svp}}}}{{{T_p}s + 1}}\text{。}$ |
由内环控制系统传递函数可以看出,其为惯性环节,其中Ksvp为内环控制系统的增益,Tp为时间常数。
1.1.5 液压缸液压缸是本系统中将液压能转换为机械能的执行元件,液压缸的传递函数为:
| ${W_g} = \frac{{Y\left( s \right)}}{{X\left( s \right)}} = \frac{{1/{A_g}}}{{s\left[ {\frac{{{s^2}}}{{w_h^2}} + \frac{{2{\xi _h}}}{{{w_h}}}s + 1} \right]}}\text{。}$ |
式中:Ag为液压缸活塞面积;wh为液压缸的固有频率,
在控制系统中,液压缸的固有频率和阻尼比对稳定性起到决定性的作用,由于液压缸的固有频率往往最低,而其他环节大部分可视为比例环节,所以开环系统的增益将受到液压缸固有频率的较大影响。
综合以上分析可得控制系统的传递函数方框原理如图2所示。

|
图 3 原系统Bode图 Fig. 3 Bode diagram of the original system |
系统的开环传递函数为:
| ${W_0}\left( s \right) = \frac{{{K_f}{K_x}{K_{svp}}/{A_g}}}{{s\left( {{T_p}s + 1} \right)\left[ {\frac{{{s^2}}}{{w_h^2}} + \frac{{2{\xi _h}}}{{{w_h}}}s + 1} \right]}}\text{,}$ |
系统的闭环传递函数为:
| $W\left( s \right) = \frac{{{K_x}{K_{svp}}/{A_g}}}{{s\left( {{T_p}s + 1} \right)\left[ {\frac{{{s^2}}}{{w_h^2}} + \frac{{2{\xi _h}}}{{{w_h}}}s + 1} \right] + {K_f}{K_x}{K_{svp}}/{A_g}}}\text{。}$ |
将螺旋桨推送到预定位置是螺旋桨液压伺服系统的主要任务。系统采用了高精度的位置传感器,可以使螺旋桨液压伺服系统达到控制性能好和控制精度高的目的,由于每个机构驱动负载大小不同,所以选用的伺服阀和液压缸也要求有较高的适应能力[3]。基于以上要求,经计算后,控制系统主要参数如表1所示。
|
|
表 1 系统参数 Tab.1 System parameters |
判断一个系统是否稳定,可以通过劳斯判据进行判断。在闭环传递函数中,其分母1+G(s)H(s)=0就是系统的特征方程。将特征方程写成s的多项式,即
| $\begin{array}{*{20}{c}}{{s^4}}\\{{s^3}}\\{{s^2}}\\{{s^1}}\\{{s^0}}\end{array}\;\;\left| {\;\;\begin{array}{*{20}{c}}{3.2777 \times {{10}^{ - 5}}} & {0.6059} & {17.6137}\\{3.6 \times {{10}^{ - 3}}} & 1 & 0\\{0.5968} & {17.6137} & {}\\{0.8938} & {} & {}\\{17.6137} & {} & {}\end{array}} \right.$ |
通过劳斯阵列可以看出:系统的特征方程的各项系数全部为正值,与此同时阵列的第1列全为正,说明该系统稳定。
2.2 频域分析在工程上,频域分析是广为采用的综合分析系统的方法。可以看出,螺旋桨液压伺服控制系统是一个4阶控制系统,较为复杂,如果系统中元件有增减,或元件参数有变化,将会对整个系统的频率特性产生影响,为了清楚表示出这些影响,系统将采用对数频率特性图(Bode图)进行稳定性分析[5]。在Matlab中,输入系统的传递函数,即可得出Bode图如图3所示。

|
图 4 校正后的系统方框原理图 Fig. 4 Schematic diagram of the system box after correction |
通过劳斯判据来判断系统的稳定性固然重要,但它不是唯一能刻画系统性能的准则,因为有的系统即使稳定,但其动态性能表现出很强的振荡。在系统Bode图中,可求出系统频率特性的性能指标,使系统有一定的稳定裕度。在开环系统Bode中,系统的幅值裕度为19.5 dB,相位裕度为15.7°,幅值穿越频率为16.7 rad/s,相角穿越频率为5.29 rad/s,由于幅值裕度和相位裕度均为正值,具有相对的稳定裕度,因此系统稳定。
在建立系统的传递函数时,忽略了其中的一些次要因素,由于系统的幅值裕度和相位裕度较小,系统运转之后会发现与实际运行的系统之间会有误差。为了获得满意的系统性能,应使幅值裕度大于20 dB,可以适当提高相位裕量,一般要大于45°为宜,使允许的最大偏差增大,即使开环增益和元件的时间常数在一定的范围内变化,也能保证系统的稳定性,这可以通过减小增益K达到。但是减小K值会造成系统的误差增大,不建议采用此种方法。因此,可以通过增加校正环节来改变系统的频率特性和性能指标。
2.3 误差分析作为一个电液位置伺服系统,本系统静态误差主要由下述因素引起:液压动力机构中的死区、电液伺服阀和放大器的零飘、位置传感器的零位误差。本I型系统在单位斜坡信号输入下,系统稳态误差为开环增益的倒数。
3 频域法滞后-超前校正螺旋桨液压伺服系统加载压力高,工况复杂,需要对校正后系统的动态和静态性能有更多更高的要求,滞后-超前校正适用于本系统的校正。施加滞后-超前校正环节,主要是利用其超前部分增大系统的相位裕度,以改善系统的动态性能;利用其滞后部分改善系统的静态性能[6]。
3.1 校正器设计要求系统的静态速度误差系数Kv=17.613 7s–1,由于系统的传递函数W0(s)为I型系统,所以其静态速度误差系数Kv就等于系统的开环增益K,校正后的系统相位裕度Pm>45°,增益裕度能够达到Gm≥20 dB。
滞后校正部分的传递函数为:
| ${G_{c1}}\left( s \right) = \frac{{1 + {T_1}s}}{{1 + \beta {T_1}s}}\text{,}$ |
工程上,一般选
超前校正部分的传递函数为:
| ${G_{c2}}\left( s \right) = \frac{{1 + \alpha {T_2}s}}{{1 + {T_2}s}}\text{。}$ |
式中:
| $\begin{array}{l}{G_{c1}}\left( s \right) = \displaystyle\frac{{1 + 0.5997s}}{{1 + 4.797s}}\text{,}\\[8pt]{G_{c2}}\left( s \right) = \displaystyle\frac{{1 + 1.715s}}{{1 + 0.015s}}\text{。}\end{array}$ |
将滞后超前校正传递函数串联到原系统中,可得到校正后的系统各项性能参数如图4所示。
|
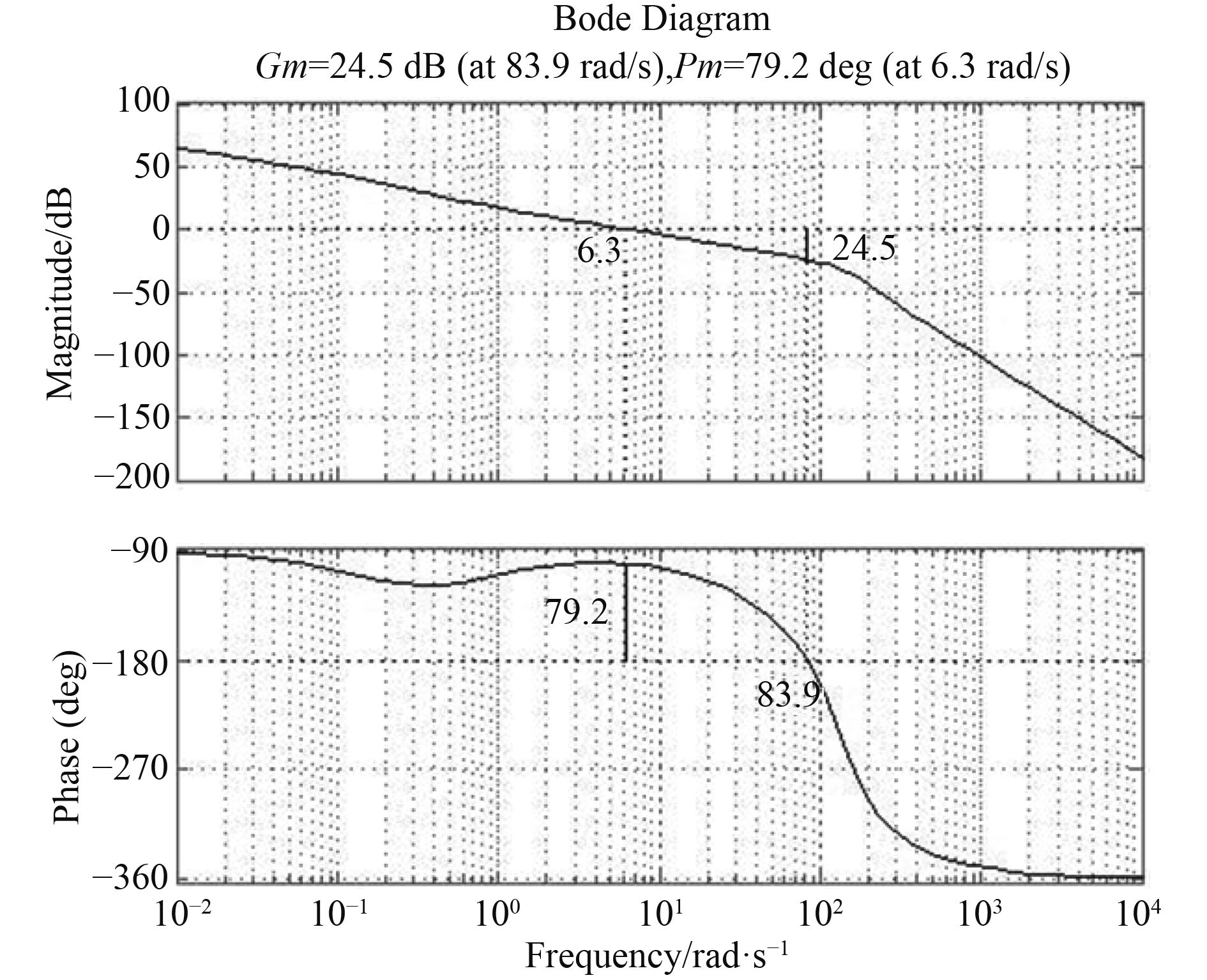
图 5 校正后系统开环Bode图 Fig. 5 Bode diagram of system open loop after correction |
|
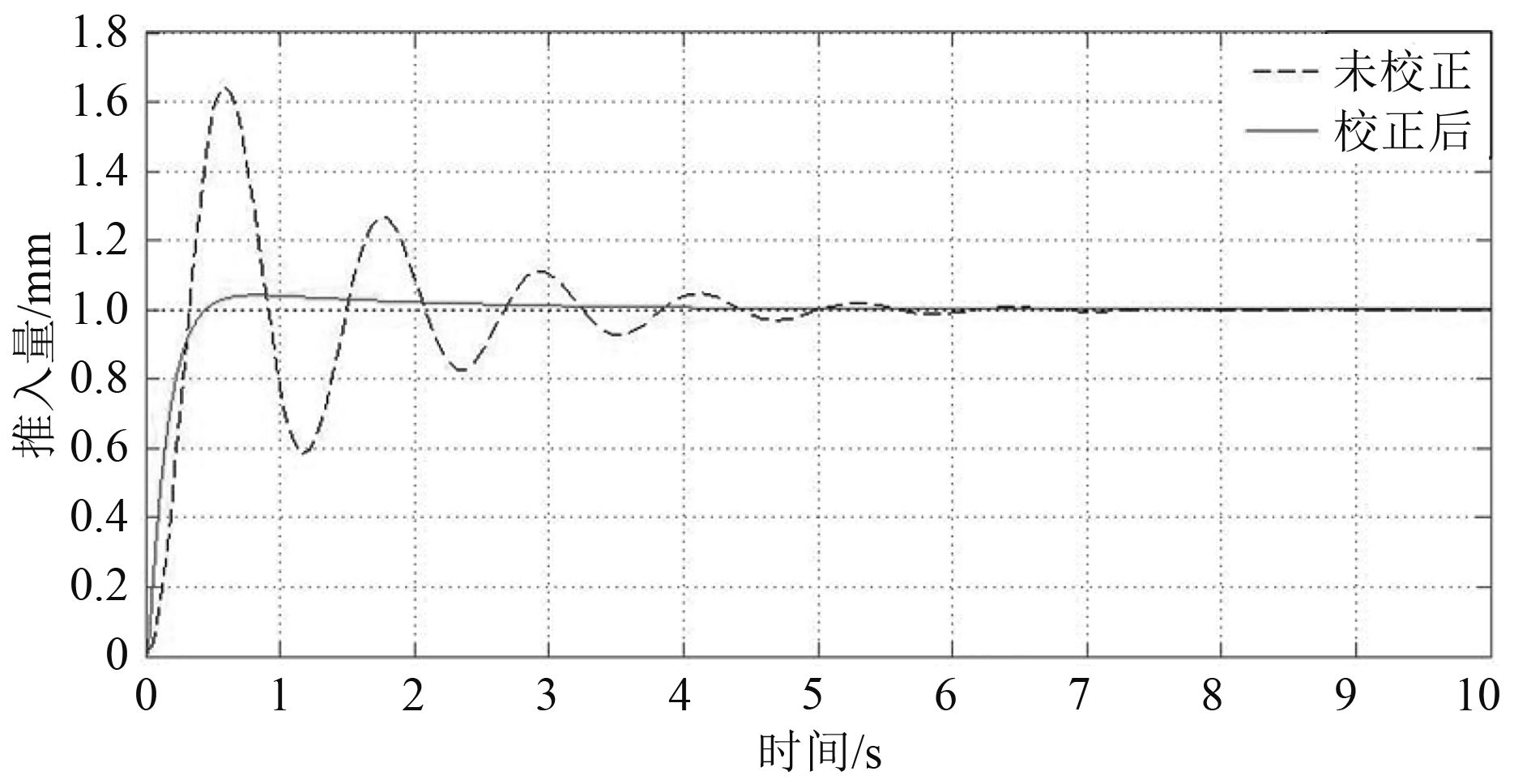
图 6 阶跃响应对比图 Fig. 6 Step response contrast diagram |
根据校正后的系统开环Bode图(见图5),可得出系统的幅值裕度为24.5 dB,相位裕度为79.2°,幅值穿越频率为83.9 rad/s,幅值穿越频率为6.3 rad/s,校正后的系统幅值裕度相比较校正前的系统提高了5 dB,系统的幅值裕度大于20 dB,相位裕度大于45°,达到了校正的要求,系统的稳态以及抗干扰性能进一步提高,达到了设计要求。
3.3 瞬态响应分析对校正后的控制系统进行时域分析,在Matlab/Simulink环境下建立螺旋桨无键液压伺服控制系统模型[7]。对线性系统而言,输入的变化并不会影响到动态响应的时间。因此,以单位阶跃响应作为模拟位移信号输入,仿真时长为10 s,得到如图6所示的响应曲线。
|
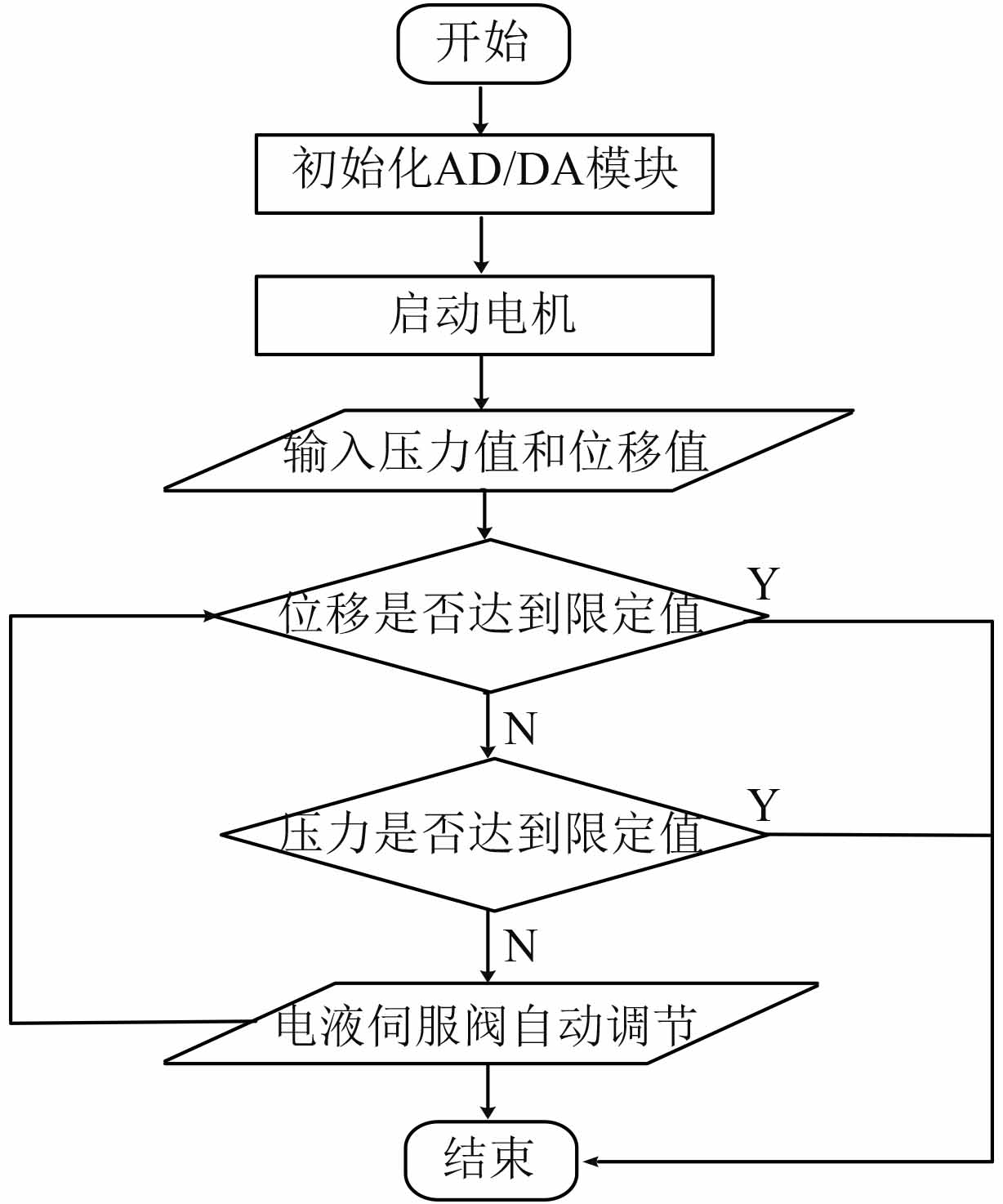
图 7 控制系统流程图 Fig. 7 Flow chart of control system |
从图中可以看出,系统的最大超调量由64.5%下降到4.21%,几乎达到没有超调,调整时间由原来的4.85 s下降到2.18 s,上升时间与原系统相同,几乎同为0.262 s,系统的瞬态响应情况大幅提升。
4 螺旋桨无键安装控制方案及其验证在无键螺旋桨液压安装前,根据文献[8]中相关公式对液压安装的油压和推入量进行理论计算,获得液压安装过程中的轴向油压和径向油压与推入量之间的关系曲线。如图7所示,首先系统开始运行,对AD/DA模块进行初始化,然后电机启动,在操作界面上输入设定轴向/径向压力值和推入量位移值,将计算获得的p-s曲线输入安装控制系统,实际安装时的油压随推入量的数值按照给定p-s曲线进行加载;然后系统会先判断推入量是否达到限定值,若达到则安装运行结束,若没有达到就会接着判断轴向/径向压力是否达到设定值,若没有达到则由电液伺服阀进行自动调节,若达到则安装运行结束[9-10]。与此同时,当发现位移传感器反馈值超出设定值时,为防止螺旋桨毂和螺旋桨轴等部件被破坏,需停止无键螺旋桨的液压安装,并分析故障原因。
|
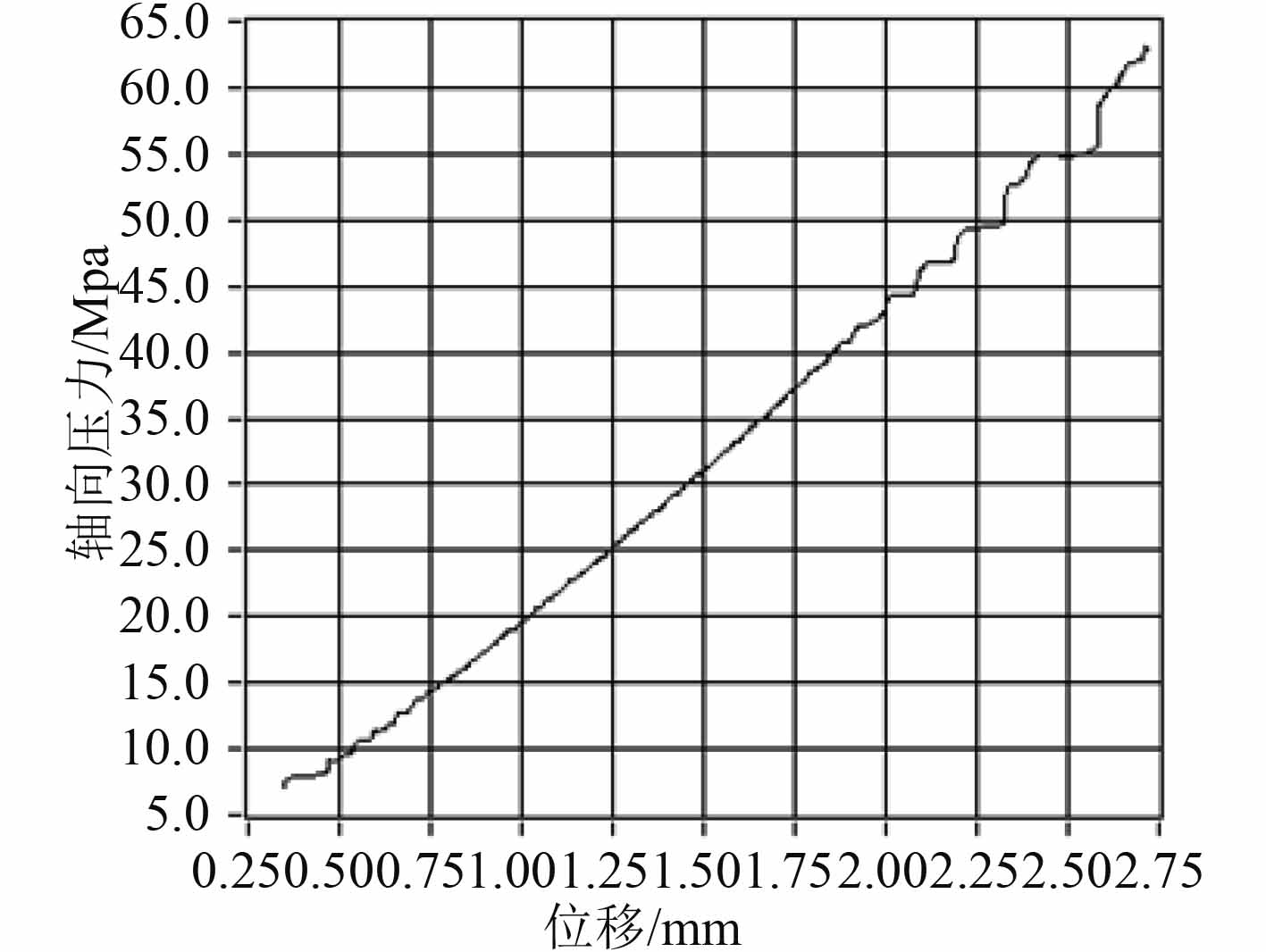
图 8 螺旋桨无键安装过程曲线图 Fig. 8 Curve diagram of keyless installation of propeller |
系统的控制目的是为了实现螺旋桨的无键安装自动化过程,并且保证其安装质量和安装效率[12]。在理论计算中得出当位移量为本实验台最佳推入量2.53 mm时,轴向压力为55 MPa,启动系统进行安装过程测试并记录其安装曲线,如图8所示。
由图可见,安装曲线呈线性分布向上,曲线平滑,基本符合完美安装,在轴向压力为55 MPa的情况下,精准的推入位移到了2.5 mm左右,与理论推入位移值2.53 mm的误差在正常范围,所以采用以上的控制系统和控制策略在本实验中可以达到安装要求。
5 结 语1)对螺旋桨无键安装液压伺服控制系统的主要环节建立了数学模型,并利用Matlab软件对其进行仿真分析,得到了系统对数频率特性各性能指标,由于相位裕量较小,同时,系统存在振荡和超调的情况,因此需要对系统进行校正。
2)采用滞后—超前校正方法对系统进行校正,校正后的系统频率特性指标为:幅值裕度为24.5 dB,相位裕度为79.2°,相角穿越频率为6.3 rad/s,幅值穿越频率为83.9 rad/s,达到了校正的目的和要求。
3)校正后与校正前相比,通过瞬态响应分析可得出,系统的最大超调量由64.5%下降到4.21%,几乎达到没有超调;调整时间由原来的4.85 s下降到2.18 s;上升时间几乎同为为0.262 s,系统的瞬态响应情况大幅提升,说明校正环节必要。
4)提出一种螺旋桨自动安装的方案,通过闭环控制的方式,在轴向压力为55 MPa的情况下,精准的推入位移到了2.5 mm,保证了安装精度。
| [1] | 但家梭. 无键螺旋桨液压安装过程测控系统的研发[D]. 武汉: 武汉理工大学, 2012. |
| [2] | 余武斌, 李德远, 黄亚农, 等. 潜艇舵机液压伺服控制系统数学模型分析[J]. 船舶工程, 2002(4): 38–42. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cbgc200204010 |
| [3] | 何兵. 基于Matlab/Simulink的液压位置伺服系统仿真[J]. 泸州职业技术学院学报, 2012(1): 25–28. http://www.cnki.com.cn/Article/CJFDTOTAL-LZZY201201007.htm |
| [4] | 机械设计手册(液压传动与控制)[M]. 北京: 机械工业出版社, 2007. |
| [5] | 赵广元. Matlab与控制系统仿真实践[M]. 北京: 北京航空航天大学出版社, 2009. |
| [6] | 张文, 陈建萍, 袁新娣, 等. 应用MATLAB实现自动控制系统的频域法校正[J]. 广东技术师范学院学报(自然科学), 2014(3): 12–14. http://www.cqvip.com/QK/97501A/201403/49156900.html |
| [7] | ROSS B. Protecting cirtical control system[J]. Network Security, 2012(3): 7–11. |
| [8] | 中国船级社. 钢质海船入级规范(第 3 分册)[S]. 北京: 人民交通出版社, 2012. |
| [9] | 胡旭晟, 范世东, 朱汉华. 无键螺旋桨液压安装方案分析[J]. 船舶工程, 2015(7): 30–33. http://www.cnki.com.cn/Article/CJFDTotal-CANB201507008.htm |
| [10] | 杨征瑞. 电液比例与伺服控制[M]. 北京: 冶金工业出版社, 2009. |
| [11] | KIAM H A, CHONG G, YUN Li. PID control system analysis, design and technology[J]. IEEE Transaction on Control system Technology, 2005. 13(4): 559–576. |
| [12] | 宋锦春, 陈建文. 液压伺服与比例控制[M]. 北京: 高等教育出版社, 2013. |
 2018, Vol. 40
2018, Vol. 40
