2. 中国人民解放军92067部队,广东 湛江 524000;
3. 海军工程大学 动力工程学院,湖北 武汉 430033
2. No.92067 Unit of PLA, Zhanjiang 524000, China;
3. College of Power Engineering, Naval University of Engineering, Wuhan 430033, China
螺旋桨推进轴系引起的船体尾部振动和噪声辐射,一直是人们重点关注和研究的问题。对于复杂连续结构的问题,目前研究的主要方法有有限元法、功率流有限元法和统计能量法等。在中低频段,采用功率流有限元法是分析复杂结构振动能量密度和强度的有效方法,该方法采用有限元法进行数值计算,从能量的角度来分析问题。因此,它不仅对各节点的能量进行分析,还能够弥补传统有限元法只适用于低频的缺陷。
关于功率流有限元的研究主要有:伍先俊等[1-2] 从功率流理论着手,结合Ansys和Isight软件,对组件功率流的计算方法和隔振系统进行研究,取得良好优化效果;贺云南等[3]将功率流有限元法和边界元结合,开发了以功率流有限元法( PFFEM)为基础的声辐射预测程序,对水下复杂结构—点力激励下潜艇的振动和声辐射特性进行预测,获得了良好效果;赵群等[4]基于振动的功率流理论和概率摄动法,提出了频域内振动传递路径的路径功率流传递度的新概念和方法,以此为基础研究功率流传递度对工程中不确定因素的敏感程度,从而指导系统结构参数的优化设计;陈炉云等[5]将功率流有限元法和声学边界元方程结合,将法向功率流定义为目标函数进行结构噪声问题研究,用遗传算法对一加肋板结构进行优化计算分析,计算结果验证了该方法的可行性和有效性。杨德庆等[6]给出基于有限元法的各种力学构件如隔振器、梁、板及其组合结构有限元功率流计算公式,研究了有限元功率流落差与振级落差这2种评价方法的优缺点。肖功煜等[7]基于功率流有限元法研究了板、壳结构的振动功率流特性,分析结构阻尼、阻尼器、加强筋等参数对结构功率流的影响。
从公开的文献资料来看,以功率流有限元法为基础对简单的梁、板、壳等结构进行优化研究较多,对复杂系统的结构优化研究较少。因此本文结合功率流有限元法和声学边界元法,对轴系-基座-壳体这一复杂系统进行研究,给出相应的减振降噪措施,利用入侵性野草算法(IWO)[8],以流经传递路径总功率流为目标函数,对相关设计参数进行优化,最后通过场点声压来分析比较该优化方法对系统声辐射优化的效果。
1 入侵性野草算法野草算法(Invasive Weed Optimization,IWO)是近年来提出的一种简单、有效的基于种群的优化算法,最早由Mehrabian和Lucus为解决数值优化问题而提出。该算法自提出以来,其较强的鲁棒性、自适应性和随机性使得其得到了广泛关注,并应用于解决实际多参数连续函数的优化问题中[9-10]。该算法启发于野草繁殖这一生物现象,其核心思想是每棵野草对环境具有不同的适应度,适应度高的野草会繁殖出更多的种子,从而具备该野草基因的种群存活率越高。因此该算法的目标找到更高适应度的野草。
该算法可分为4步:1)初始化;2)繁殖;3)空间分布;4)竞争性生存。设野草种群中野草的初始数量Pinit,最大种群规模为Pmax,最大迭代次数Imax、野草最大和最小可生成种子数Smax和Smin、非线性指数n,种子散布的初始步长σinit和最终值步长σfinal。野草种群中每根野草可根据自身适应度及种群中所有个体的最小适应度和最大适应度确定产生种子的数目。这样适应度高的可以产生较多的种子,适应度低产生较少的种子,采用这种机制可保证适应度高的野草能够最终生存下来。确定种子数量公式如下:
| ${S_c} = {\rm{floor}}\left[ {\frac{{abs\left( {{F_{\rm{cur}}} - {F_{\min }}} \right)}}{{{F_{\max }} - {F_{\min }}}}\left( {{S_{\max }} - {S_{\min }}} \right) + {S_{\min }}} \right], $ | (1) |
式中:Fcur,Fmax和Fmin分别为当前种群中当前野草适应度,最大适应度和最小适应度。
根据实际问题若每个野草个体变量维数D,某个父辈野草为
| ${X_{\rm{new}}} = {\left[ {{X_1} + {Z_1},{X_2} + {Z_2}, \cdots ,{X_D} + {Z_D}} \right]^{\rm T}},$ | (2) |
其中σcur计算公式如下:
| ${\rm{}}{\sigma _{\rm{cur}}} = {\left( {\frac{{{I_{\max}} - I}}{{{I_{\max}}}}} \right)^n}\left( {{\sigma _{\rm{ini}}} - {\sigma _{\rm{fin}}}} \right) + {\sigma _{\rm{fin}}}{\text{。}}$ | (3) |
式中:σini,σfin分别为标准方差初始值和最终设定值;Imax,I分别为最大迭代次数和当前迭代次数;n为非线性指数,可控制标准偏差衰减速度。根据式(3)可知,当迭代次数增加时σcur逐渐减小,这样适应度高的种群逐渐聚集,算法由全局搜索向局部搜索转移,从而优化野草种群的散布空间,最终目标值趋向收敛。
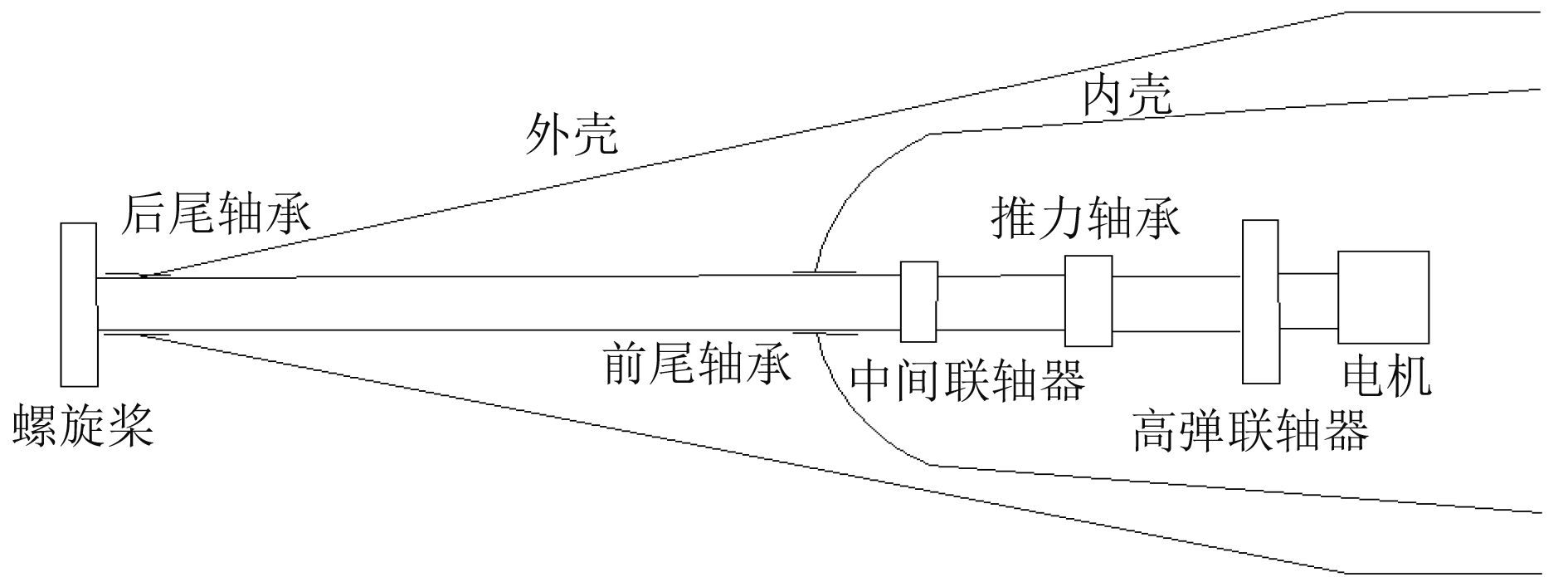
2 系统减振优化框架构建 2.1 系统模型建立以研究的推进轴系试验平台轴系为基础,建立轴系-基座-壳体系统模型。图1为系统尾部模型,壳体采用shell181单元,后尾轴承采用5个COMBI214单元支撑,前尾轴承采用4个COMBI214单元支撑,推力轴承支撑采用1个MTRI27单元(集成纵向推力块油膜刚度)和3个COMBI214单元支撑,电机支撑采用2个COMBI214单元支撑在电机壳体上。对于该系统其振动噪声主要来源激振力引起的轴系和尾部纵向耦合振动以及回旋耦合振动,因此本文提出的系统减振措施如下:在推力轴承和半联轴器间设1个纵向减振器;推力轴承右端加5个纵向吸振器;电机外壳到壳体之间采用4个隔振器支撑,电机外壳横向对称布置6个吸振器;前尾轴承处内壳外设4个吸振器上下左右均布,内壳内采用4个吸振器均布。纵向减振器采用MATRI27单元模拟,便于模拟轴系转动,所有吸振器和隔振器采用COMBI14单元,质量单元为MASS21。所优化的参数有纵向减振器质量X1、刚度X2和阻尼X3,推力轴承纵向吸振器质量X4、刚度X5和阻尼X6,电机外壳吸振器质量X7、刚度X8和阻尼X9,电机隔振器质量X10、刚度X11和阻尼X12,前尾轴承处内壳外吸振器质量X13、刚度X14和阻尼X15以及内壳内吸振器质量X16、刚度X17和阻尼X18。对于上述参数均给出上下限。因此,在采用IWO算法时,每个野草个体变量维数为D=18,则
|
图 1 系统尾部模型 Fig. 1 The system stern model |
本文研究的系统结构-声辐射优化往往是以尾部声场点的声压为目标函数,而场点声压一般是通过声边界元方程求解得来,若能求得结构边界表面上的声压分布即可对声场内任意场点的声压进行求解,在结构表面处,离散形式的声压[Pf]由下式计算:
| $\left[ { {P_f}} \right] = {\left[ { A} \right]^{ - 1}}\left[ { B} \right]\left\{ {{v_n}} \right\},$ | (4) |
式中,[A]和[B]为K×K阶复系数方阵边界元法影响系数矩阵,为激励频率的函数,与结构表面尺寸形状和插值函数有关,vn为结构表面节点法向速度。在结构边界表面处,由于声场的变化会引起流体对该结构处节点动压力[Fp],此时结构边界处节点力与流体动压力是等值方向的,因而流体动压力可表示为:
| $\left[ {{F_p}} \right] = \left[ { G} \right]\left[ { S} \right]\left[ {{P_f}} \right],$ | (5) |
式中,[G]为法矢量方向余弦转换阵,
| $\left[ { {F_p}} \right] = \left[ { G} \right]\left[ { S} \right]{\left[ { A} \right]^{ - 1}}\left[ { B} \right]\left\{ {{v_n}} \right\}$ | (6) |
对于轴系-基座-壳体系统,主要是研究系统在稳态激励作用下轴系传递到壳体上的功率流特性。因此稳态激励下,功率流计算式如下:
| $\begin{split}P\left( \omega \right) = & \frac{1}{2}Re\left( {F\left( \omega \right) \cdot {V^*}\left( \omega \right)} \right)=\\ & \frac{1}{2}\omega \cdot Im\left( {F\left( \omega \right) \cdot {U^*}\left( \omega \right)} \right){\text{。}}\end{split}$ | (7) |
则结构表面处第i个节点功率流法向分量可表达为:
| $\begin{split}{P_i}\left( \omega \right) = & \frac{1}{2}\omega \cdot Im\left( {\left[ { {F_p}} \right] \cdot \left\{ { {{{ u}^*}_n}} \right\}} \right) = \\& \frac{1}{2}\omega \cdot Im\left( {\left[ { G} \right]\left[ { S }\right]\left[ { {P_f}} \right] \cdot \left\{ {{{{ u}^*}_n}} \right\}} \right){\text{。}}\end{split}$ | (8) |
式中,
| ${P_a}\left( \omega \right) = \mathop \sum \limits_{n = 1}^s {P_i}\left( \omega \right),n = 1,2, \cdots ,s{\text{。}}$ | (9) |
对于本文所研究的系统,从轴系到壳体及结构表面其结构是确定的,因此[G][S]是一个常量,流入到结构表面的法向功率流主要是由螺旋桨激振力、电机激振力以及半联轴器和高弹不对中产生的激振力引起,传递的主要路径为后尾轴承、前尾轴承、推力轴承以及电机隔振器。假设轴系上功率流Ps传递到轴承基座时功率流传递为η1,轴承基座上功率流Pb传递到壳体表面时功率流传递率为η2,则有:
| ${P_a}\left( \omega \right) = {\eta _2} \cdot {P_b} = {\eta _1} \cdot {\eta _2} \cdot {P_s}{\text{。}}$ | (10) |
由式(10)可知,当轴承基座到壳体表面结构确定时,则传递率η2确定,则减少流经传递路径的功率流在很大程度上就能减小结构表面的功率流。因此对于该系统结构-声辐射优化的目标函数先从尾部场点声压转化到结构表面功率流,最终转换成减少流经传递路径的总功率流,即最终优化目标是流经传递路径的总功率流最小。这样处理具有许多优点:将声压(矢量)参数求解转化成功率流(标量)求解,对求解结果评估时可不用考虑场点位置等因素;大大减少计算量,因为该系统由于尾部结构表面划分成许多单元和节点,编号无序,这就增加了提取节点信息的难度,并且需要计算每个节点的功率流,计算量较大;避免了同时采用有限元和边界元之间转化时造成的误差等问题。
对于第R个传递路径有I个评价点,则流经该路径的总功率流评价公式为:
| $P_o^R = \sqrt {\mathop \sum \limits_i^I {{\left( {P_o^i} \right)}^2}} ,$ | (11) |
则适应度函数为:
| $f = \frac{1}{{\sqrt {\mathop \sum \nolimits_j^R P_o^j} }}\text{。}$ | (12) |
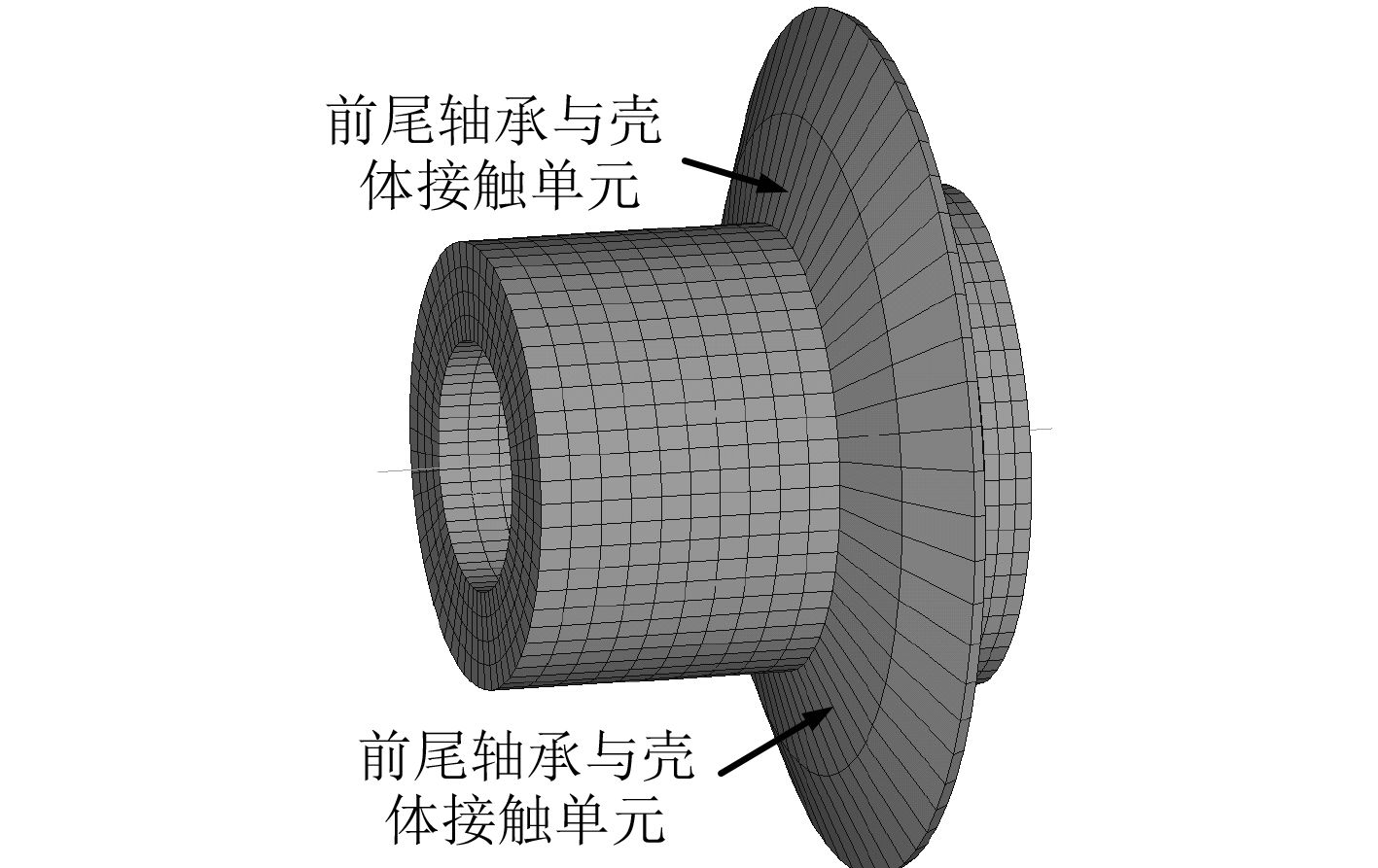
式中:R为传递路径数量R=4,对于后尾轴承和电机支撑轴承分别为I=5和I=4。对于前尾轴和推力轴承,考虑到两者上还需安装动力吸振器等因素,因此不能从轴承支撑处来评价,需从两者与壳体连接处的功率流来进行评价,对于前尾轴承,其连接处如图2和图3所示。对于这2处的功率流计算方法参考文献[6]。前尾轴承处共60个单元,评价节点共计I=224,推力轴承连接处为24个单元,评价节点共计I=75。由适应度函数可知,当流入传递路径的总功率流越小,则适应度越高,种群就会聚集下来,最终找到最合适的种子。
|
图 2 前尾轴承连接处 Fig. 2 Former stern bearing connected |

|
图 3 推力轴承连接处 Fig. 3 Thrust bearing bearing connected |
初始参数的设置对优化结果有一定的影响,特别是野草种群中野草数量的最大值Smax、非线性指数n,种子散布的标准差初始值σinit和标准差最终值σfinal。Smax并不是越大越好,太大反而影响IWO算法的效率,一般选取10~20之间的整数最佳,这里设定Smax=20;非线性指数n一般设置为3;标准偏差初始值应尽量大一些,以保证算法在迭代初期的搜索能力,一般设置为每个变量的解空间长度的1%~5%。标准偏差最终值影响算法的局部寻优能力,减小该数值可提高寻优的精度,但该值过小,会影响算法的收敛速度,且对精度提高不大,因此设置应当适中。表1给出了IWO算法参数的详细设置。
|
|
表 1 IWO算法的参数设置 Tab.1 Parameters of IWO algorithm |
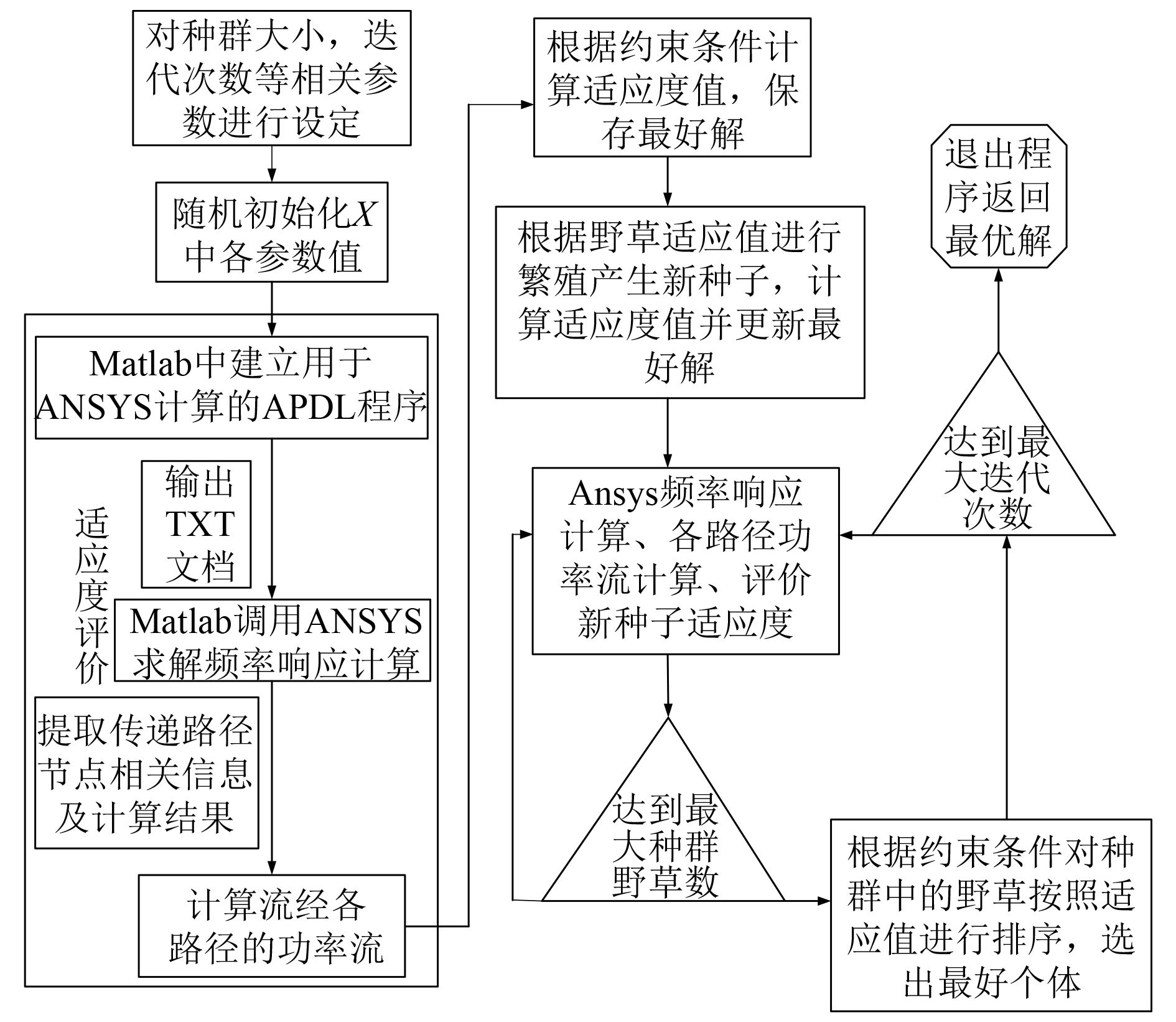
本文所用程序均在Matlab中进行,在适应度函数中需要调用Ansys进行频率响应计算,将传递路径上相关节点的力和位移信息导出,用于功率流计算。进行频率响应分析时,模型计算参数如下:螺旋桨、半联轴器、高弹联轴器及电机转子的极转动惯量分别为3 250 kg·m2,125 kg·m2,365 kg·m2和2 550 kg·m2;轴系密度、泊松比、弹性模量和切变模量分别为7 850 kg/m3,0.26、2.1E11 Pa和0.769E11 Pa;高弹联轴器扭转刚度kn=2.6E6 N·m/rad,径向刚度为7.8E6 N/m;壳体分双层壳体;轴系转速为70 r/min。相对应于该工况,分别计算支撑轴承的油膜动力特性系数和推力块上油膜动力特性系数[11],代入系统模型进行计算;计算所施加外载荷有螺旋桨激振力6个分量、电机驱动力矩、高弹和半联轴器不对中产生的激振力。由于轴系不对中和螺旋桨重力造成轴系呈弯曲状态,因而轴系在旋转时产生陀螺效应,为此本文先进行静态计算,再对轴系运转进行有预应力的频率响应分析,这样就可以将轴系变形时产生的弯曲应力和位移考虑到动态结果中,得到轴系在弯曲状态下的结果。优化过程见图4。
|
图 4 IWO算法优化过程 Fig. 4 Optimization procedure of IWO algorithm |
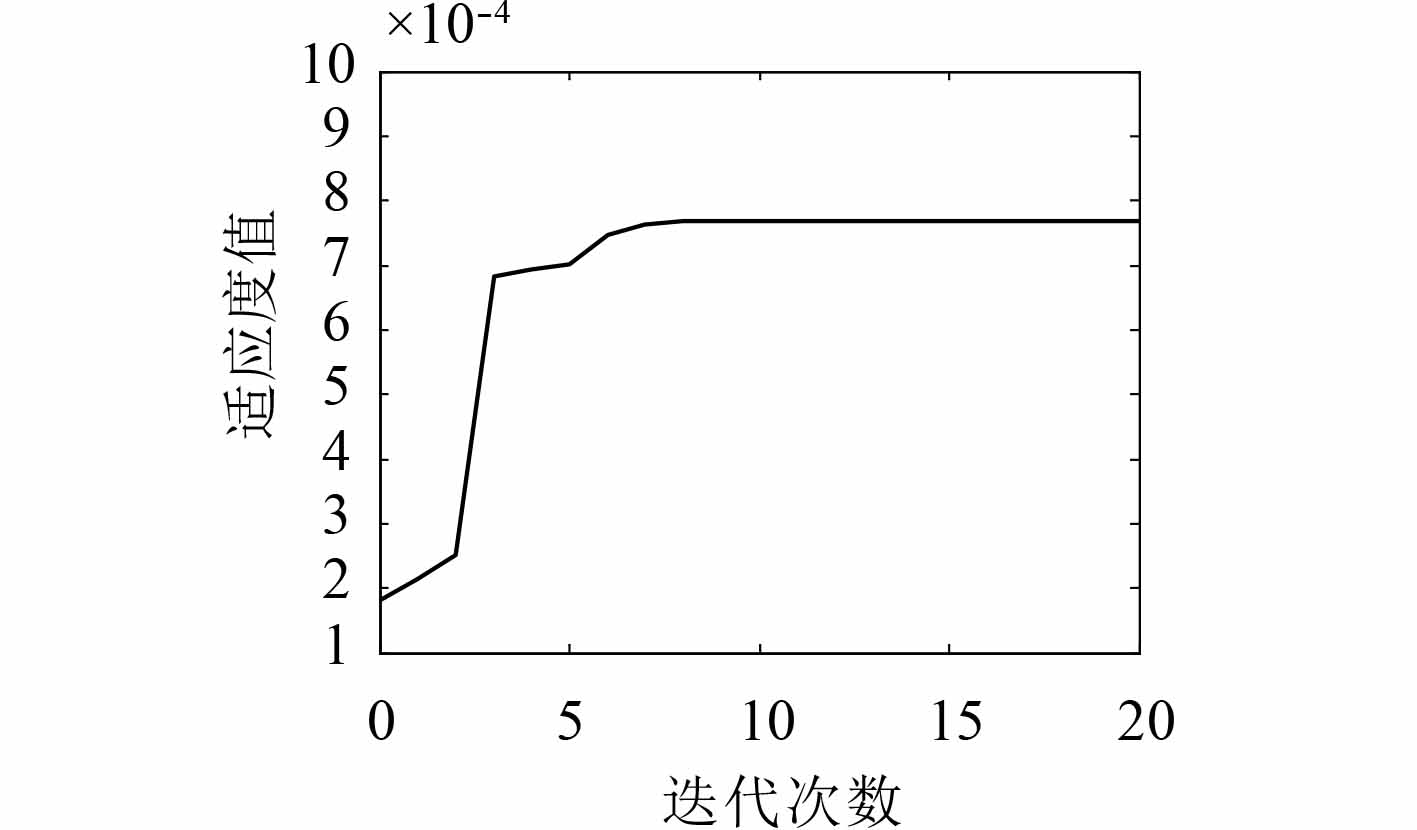
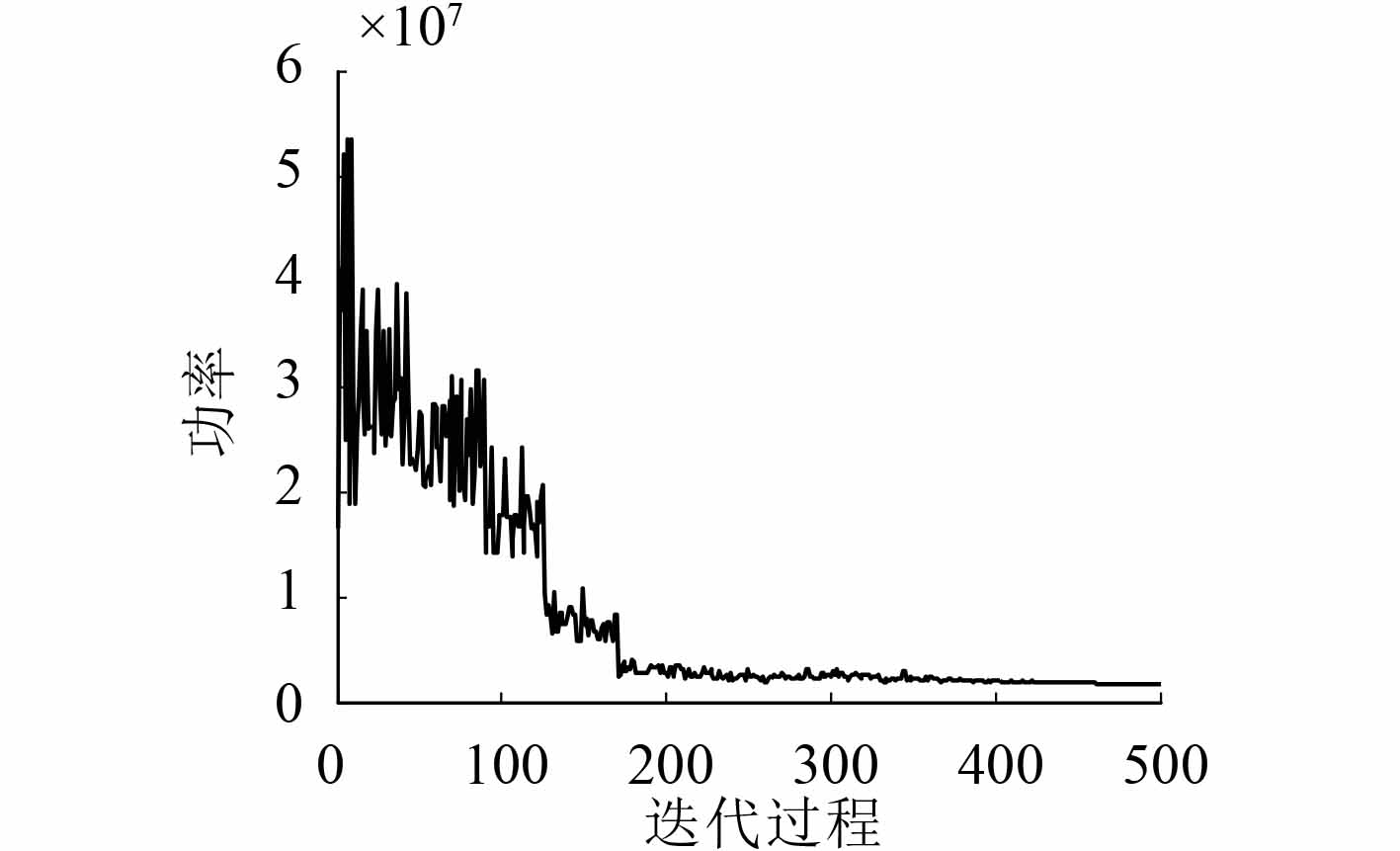
经迭代优化计算,得到相应结果。图5给出了适应度评价函数值随迭代次数的变化曲线。算法在约第172代基本达到收敛,且在进化初期具有较快的上升速度,能够避免陷入局部收敛,表明算法的收敛性能良好,可以寻求全局最优。图6为迭代过程与传递路径总功率流的变化曲线,反应了迭代过程中每个种子生成的总功率流。表2为最合适种子,即参数优化结果,共计18个参数。
|
图 5 适应度评价曲线 Fig. 5 Fitness value evaluation curve |
|
图 6 迭代过程 Fig. 6 Iterative process |
|
|
表 2 设计参数优化值 Tab.2 The value of design variable |
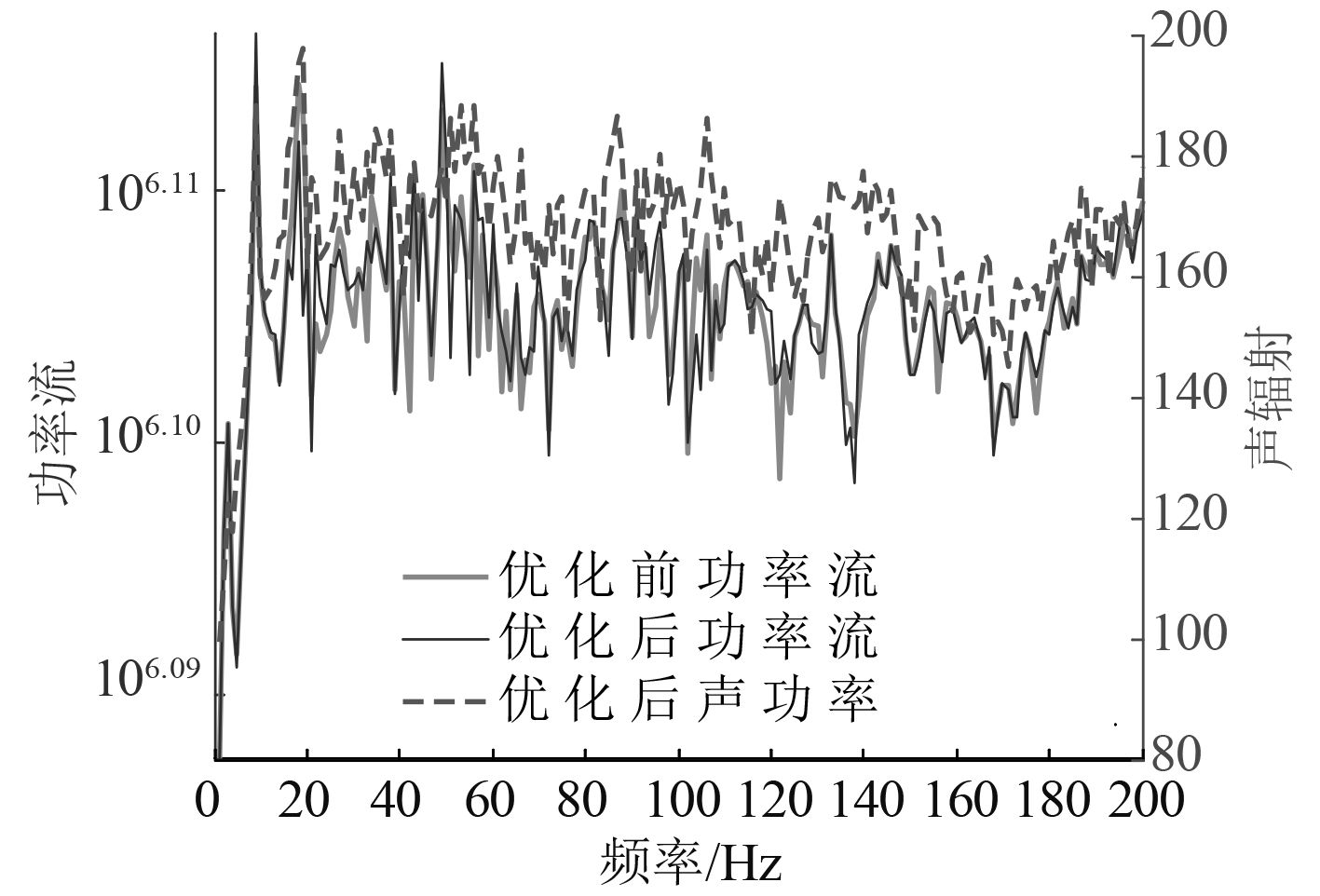
将优化后的参数代入到系统模型进行计算,得到相应结果。图7为流经传递路径的总功率流与壳体尾部某场点声压频率响应对比图。由图可知:优化后流经传递路径的总功率流与场点声压频率响应特性从整个频率段来看大体一致,但在中高频处某些点响应规律也不尽相同,这是由于流经传递路径的总功率流不仅仅是传递到壳体尾部,而是传递到整个壳体,且在这些中高频处,轴系与壳体的耦合振动往往是以整个壳体与轴系的共振响应为主,因此响应规律略有不同;而在中低频处,系统振动主要是尾部结构和轴系的耦合振动,场点也是选在尾部附近,因此两者响应规律基本一致。由此可见,通过流经传递路的总功率流来间接反映场点声压的响应规律可行。由图7还可知,优化后流经传递路径的总功率流有所减少,尤其是在频率19 Hz,27 Hz和34 Hz处,减少最为明显,但是,在频率为9 Hz,23 Hz和49 Hz处有所增大,对于中高频段其总功率流在优化后略有减小。
|
图 7 功率流和声辐射对比图 Fig. 7 Compare power flow and acoustic radiation |

|
图 10 19 Hz优化后场点声压云图 Fig. 10 19 Hz contours of filed point acoustic pressure after optimization |
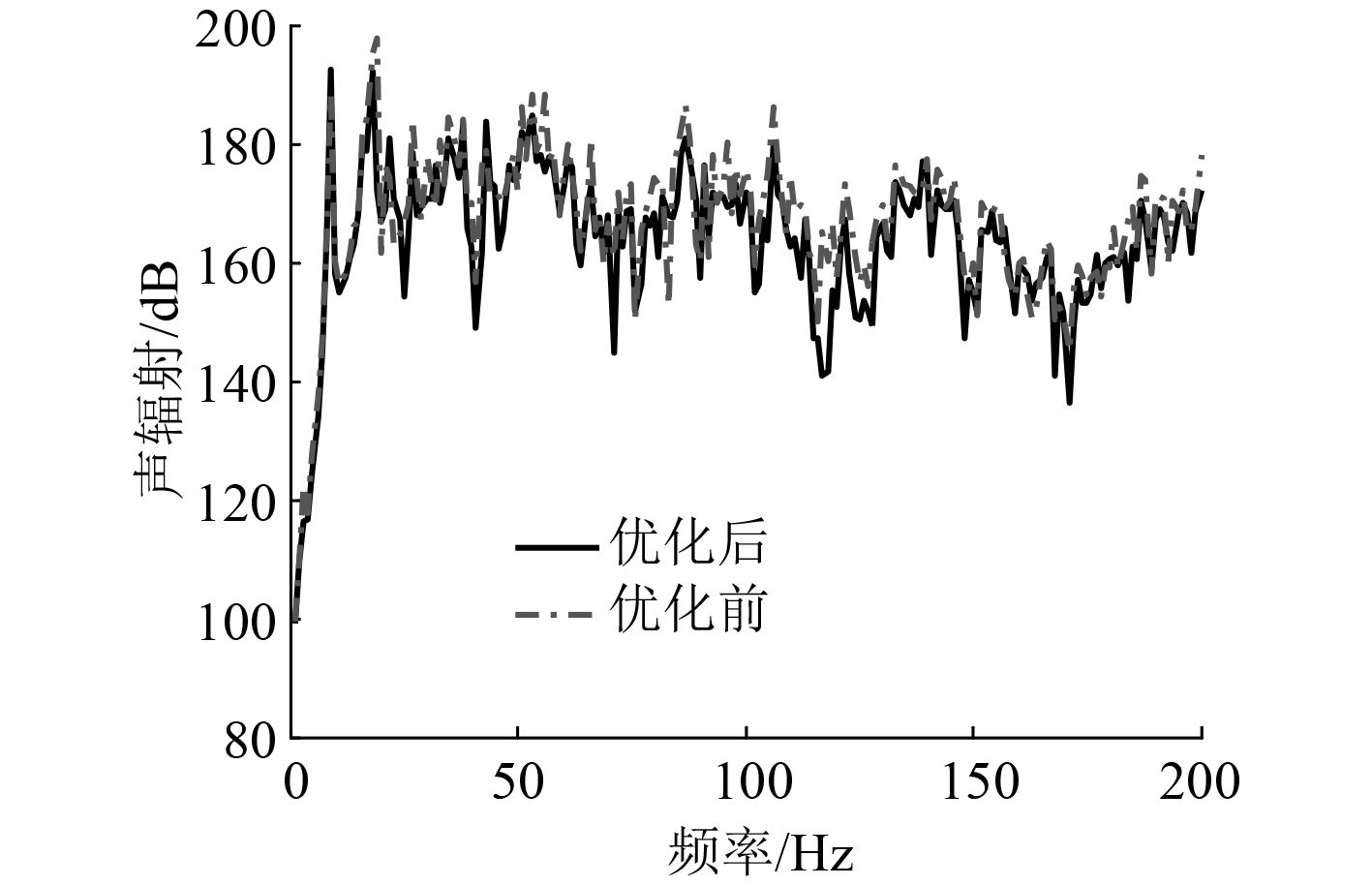
为验证图7中优化前后功率流的结果,采用声学边界元法,计算优化前后尾部某场点声压频率响应进行对比。由图8可知,在频率19 Hz,27 Hz和34 Hz处,场点声压减小最为明显,尤其是对主要声压做贡献的频率点19 Hz声压减小幅度最大。而在频率为9 Hz,23 Hz和49 Hz处场点声压有所增大,在23 Hz处增幅最大,对于中高频段其总功率流在优化后略有减小。对于这些声压增大的频率点,主要原因是系统尾部结构复杂,使得其共振频率点较多,频带较宽,而对于减振器、吸振器和隔振器本身减振频带较窄,加上本文对同一类吸振器和隔振器均采用相同频率吸振,这就造成整体减振频带不宽,会导致某些频率响应值不减反而增大。但是对于主要频率段还是能起到良好减振效果。通过计算对比分析,以流经传递路径的总功率流为目标函数,通过本文所采取的优化措施,能够有效地对轴系-基座-壳体这一复杂系统进行声辐射优化。若能采用多个不同参数的吸振器和隔振器进行优化,则能增加减振降噪的效果。
|
图 8 场点声压频率响应对比图 Fig. 8 Compare the frequency response of filed point acoustic pressure |
为更清楚了解本文采用的优化方法对系统减振降噪的效果,将频率为19 Hz时优化前场点声压云图9和优化后场点声压云图10。由图9可见,声压最高处分布在壳体尾部和壳体中部范围,峰值接近200 dB,在壳体中部水平方向上声辐射范围最大最广。由图10可见,经过优化后,壳体尾部和壳体中部声辐射明显减弱,峰值降到187 dB以内,尤其是壳体中部声辐射减弱最为明显。由此可见本文采用的优化计算方法有效可行。

|
图 9 19 Hz优化前场点声压云图 Fig. 9 19 Hz contours of filed point acoustic pressure before optimization |
本文以流经传递路径的总功率流为目标函数,采用IWO算法对纵向减振器、吸振器和隔振器的参数为设计变量,对轴系-基座-壳体系统进行声辐射优化,通过计算分析得到如下结论:
1)入侵性野草算是一种简单有效的优化方法,具有较好的适应性和随机性,能够很好的全局寻优。
2)减少流经传递路径的总功率流能够有效地减少壳体表面声辐射。
3)以流经传递路径的总功率流为目标函数能够大大减少计算量和简化问题,结合功率流有限元法和声学边界元法,从而为轴系-基座-壳体提供有效的优化和计算方法。
4)对于减振元件的参数设计应该多样化以增加减振频带,从而更有效地对轴系-基座-壳体减振降噪。
| [1] | 伍先俊, 程广利, 朱石坚. 最小振动功率流隔振系统ANSYS 优化设计[J]. 武汉理工大学学报(交通科学与工程版), 2005, 29 (2): 186–189. https://www.wenkuxiazai.com/doc/660da1a7a6c30c2259019ebd.html |
| [2] |
伍先俊, 朱石坚. 组件功率流计算法和iSIGHT 环境下隔振系统优化设计[J]. 船舶力学, 2006, 10 (2): 138–145.
WU Xian-jun, ZHU Shi-jian. Vibration power flow calculation based on component modal technique and isolation system optimization using iSIGHT[J]. Journal of Ship Mechanics, 2006, 10 (2): 138–145. http://doi.wanfangdata.com.cn/10.3969/j.issn.1007-7294.2006.02.018 |
| [3] |
贺云南, 何琳, 吕志强, 等. 功率流有限元法结果分析辐射噪声[J]. 船舶力学, 2006, 10 (5): 150–154.
HE Yun-nan, HE Lin, LV Zhi-qiang, et al. Radiation noise analysis using the results of power flow finite element method[J]. Journal of Ship Mechanics, 2006, 10(5): 150–154. http://www.cqvip.com/qk/91784A/200605/23293888.html |
| [4] |
赵群, 张义民, 赵晋芳. 振动传递路径的功率流传递度灵敏度分析[J]. 振动与冲击, 2009, 28(7): 183–186.
ZHAO Qun, ZHANG Yi-min, ZHAO Jin-fang. Sensitivity analysis of powerflow transfer probability for a vibration transfer path[J]. Journal of Vibration and Shock, 2009, 28(7): 183–186. |
| [5] | 陈炉云, 张裕芳. 基于功率流分析的结构声优化研究[J]. 振动与冲击, 2010, 29(10): 191–194. |
| [6] |
杨德庆, 罗放, 陈静. 有限元功率流落差计算方法研究[J]. 噪声振动与控制, 2009, 6: 127–131.
YANG De-qing, LUO fang, CHEN Jing. Power flow level difference finite element analysis[J]. Noise and Vibration Control, 2009, 6: 127–131. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zsyzdkz200906029 |
| [7] |
肖功煜, 刘微, 朱翔. 船舶板壳结构的振动功率流分析[J]. 船海工程, 2011, 40(6): 45–48.
XIAO Gong-yu, LIU Wei, ZHU Xiang. Structure vibration and energy flow characteristics of plates and shells of ships[J]. Ship & Ocean Engineering, 2011, 40(6): 45–48. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=whzc201106012 |
| [8] | FOUDAZI A, A R MALLAHZADEH, Pattern synthesis for multi-feed reflector antennas using invasive weed optimisation[J]. Microwaves, Antennas & Propagation, IET, 2012. 6(14): 1583–1589. |
| [9] | MEHRABIAN A R, LUCAS C. A novel numerical optimization algorithm inspired from weed colonization[J]. Ecological Informatics, 2006, 1(3): 355–366. https://www.sciencedirect.com/science/article/pii/S1574954106000665 |
| [10] | DASTRANJ A, H ABIRI, A MALLAHZADEH. Design of a broadband cosecant squared pattern reflector antenna using IWO algorithm[C]// Antennas and Propagation, IEEE Transactions on, 2013. 61(7): 3895–3900. |
| [11] | 石磊. 计入支承系统特性的船舶推进轴系动态校中研究[D]. 大连: 大连理工大学, 2010. |
 2018, Vol. 40
2018, Vol. 40
