畸形波(freak wave)是一种波高巨大、波峰异常尖瘦的不规则波[1 – 2],具有极强的非线性。Klinting等[3]认为,自然海况下,最大波高分别大于有效波高与前后相邻波高的2倍,而小于其波峰高度65%的波浪可称为畸形波。畸形波能量巨大,对海上平台及船舶构成很大的威胁,因而引起海洋工程界的特别重视。近些年来国外学者通过模型试验与基于势流理论的时域模拟方法对海洋结构物如半潜平台、FPSO遭遇畸形波过程进行研究,得到了平台在畸形波作用下运动响应的基本规律[4 – 6]。Rudman等[7]基于SPH方法,对畸形波砰击浪向角和预张力对张力腿平台运动的影响进行深入研究,并且对每一条张力腿的最大张力给出合理预测。Zhao等[8]基于自主研发的CIP模型开展了极端波浪条件下浮体两自由度响应的模拟研究,初步验证了CIP方法建立的波浪水槽对该类问题的适用性。
本文以Ansys Workbench为计算平台,重点研究浮体的中横剖面切片模型在畸形波作用下的载荷与运动响应问题,这样浮体结构的六自由度运动就可以简化为三自由度运动,即横摇、垂荡和横荡。载荷问题主要包括上浪水位和砰击压强,本文提出“单元贴片法”,便捷有效地解决了追踪浮式结构物表面“动点”的难题。
1 理论基础与控制方程 1.1 理论基础按照Longuet-Higgins[9]提出的经典海浪模型,固定点的波面表达式为:
| $\eta \left( {x,t} \right) = \sum\limits_{i = 1}^N {{A_i}} \cos \left( {{k_i}x - {\omega _i}t + {\theta _i}} \right)\text{。} $ | (1) |
式中:
| ${\theta _i} = - {k_i}{x_p} + {\omega _i}{t_p}{\text{。}}$ | (2) |
| ${A_i} = \sqrt {2{S_\eta }\left( {{{\hat \omega }_i}} \right)\Delta {\omega _i}}\text{。} $ | (3) |
式中:
| $\begin{split}\eta \left( {x,t} \right) = & \sum\limits_{i = 1}^N {\sqrt {2{S_\eta }\left( {{{\hat \omega }_i}} \right)\Delta {\omega _i}} } \cos \left( {{k_i}\left( {x - {x_p}} \right) - } \right. \\ &{\omega _i}(t - {t_p})){\text{。}}\end{split}$ | (4) |
连续性方程:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_i}}} = 0\;\;\;\;\left( {i = 1, \; 2} \right), $ | (5) |
N-S方程:
| $\begin{split}& \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right] - \\& \quad \frac{{\partial p}}{{\partial {x_i}}} + \rho {g_i}\;\;\;\;\left( {i = 1,\;2} \right){\text{。}} \end{split}$ | (6) |
式中:
自由液面的追踪采用VOF法,具体来说,采用流体体积函数法来标记自由液面,其表达式为:
| $\left\{ \begin{aligned}& \frac{{\partial {\alpha _q}}}{{\partial t}} + \frac{{\partial \left( {{u_i}{\alpha _q}} \right)}}{{\partial {x_i}}} = 0,\;\;\;\left( {i = 1,\;2} \right), \\& \sum\limits_{q = 1}^2 {{\alpha _q} = 1,\;\;\;\;\left( {q = 1,\;2} \right)}{\text{。}} \end{aligned} \right.$ | (7) |
式中:
本文在建立波物相互作用的二维数值模型时,将数值波浪水池与浮体共同定义一个“薄片”厚度(基于切片理论),使流场与浮体生成真实的交界面。由于波浪在宽度上与浮体一致,波物运动在任意纵剖面上的投影情况完全相同,因此可以看作是二维运动。这样,在宽度方向上,可以用一个紧贴运动浮体的面元(简称动面元)来代替该面元的中心点,如图1(a)所示,同时在流场中同一位置处挖出这样一个面元,如图1(b)所示,然后在耦合求解器中将二者以流固交界面的形式连接在一起,则通过追踪流场中的该动面元上的信息即可知道运动着浮体上的某个点上的信息。该动面元功能类似于物理试验中测量结构应变的“应变片”,故而本文将该面元称作“单元贴片”。

|
图 1 单元贴片法 Fig. 1 Patch element method |
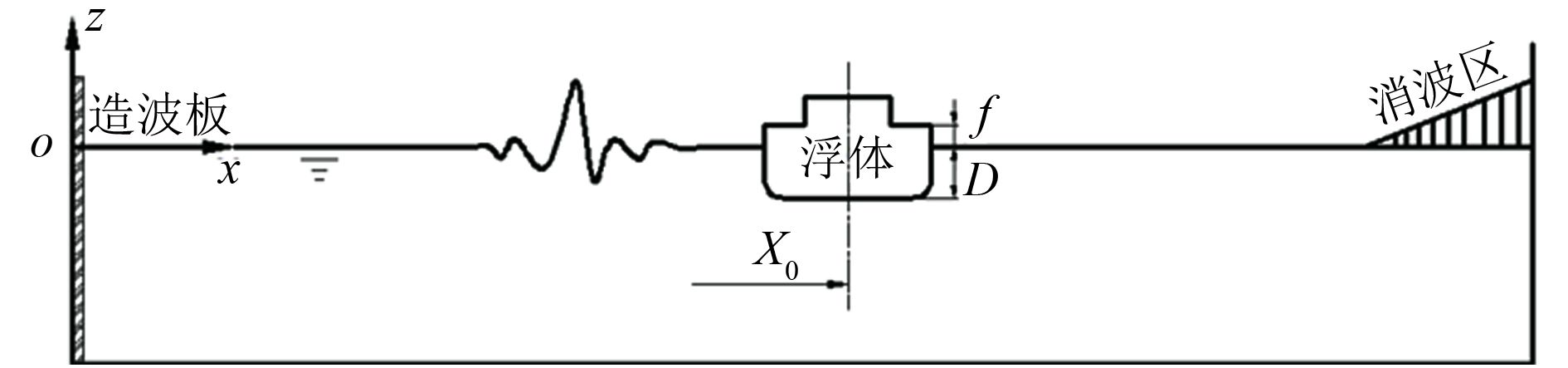
数值水池尺寸如下:长40 m,高3 m,水深2 m,尾部10 m为消波区域,如图2所示。结构物初始时刻处于正浮状态,与造波板的水平距离为
|
图 2 数值模型示意图 Fig. 2 Schematic diagram of the numerical model |
流场网格划分采用结构网格和非结构网格相结合的方法,浮体周围采用三角形非结构网格,通过动网格技术中的扩散光顺法来更新网格,以精确模拟浮体的运动。外围区域采用规则的四边形结构网格进行划分,如图2所示,流场网格数量为118 256。

|
图 3 浮体周围流场网格分布 Fig. 3 Mesh distribution of flow field around floating body |
水池顶部为pressure-inlet压力入口边界条件,底部及尾壁均为wall无滑移固壁条件,左端为piston运动边界,用以模拟平推式造波板的运动,其运动规律为:
| ${U_0}\left( t \right) = \frac{{{\omega _i}}}{{Tr\left( {{\omega _i}} \right)}}\eta \left( {0,t} \right){\text{。}} $ | (8) |
式中:
| $Tr\left( {{\omega _i}} \right) = \frac{{4{{\sin h }^2}\left( {{k_i}h} \right)}}{{\sin h \left( {2{k_i}h} \right) + 2{k_i}h}},$ | (9) |
将式(4)代入式(9)得到推板造畸形波的速度公式:
| $\!\!\!\!\!\!\!\!\! {U_0}\left( t \right) = \sum\limits_{i = 1}^N {\frac{{{{\bar \omega }_i}\sqrt {2{S_\eta }\left( {{{\hat \omega }_i}} \right)\Delta \omega } }}{{Tr\left( {{{\bar \omega }_i}} \right)}}} \cos \left( { - {{\bar k}_i}{x_p} - {{\bar \omega }_i}\left( {t - {t_p}} \right)} \right){\text{。}} $ | (10) |
在Fluent中采用非定常分离隐式求解器求解,压力方程选用加权体积力格式(Body Force Weighted),压力速度耦合方式采用PISO算法,体积分数法为几何重构(Geo-Reconstruct),压力参考值为一个标准大气压。流场采用 RNG k-e模式,动量方程中的瞬态项采用一阶迎风格式,时间步长为0.01 s。
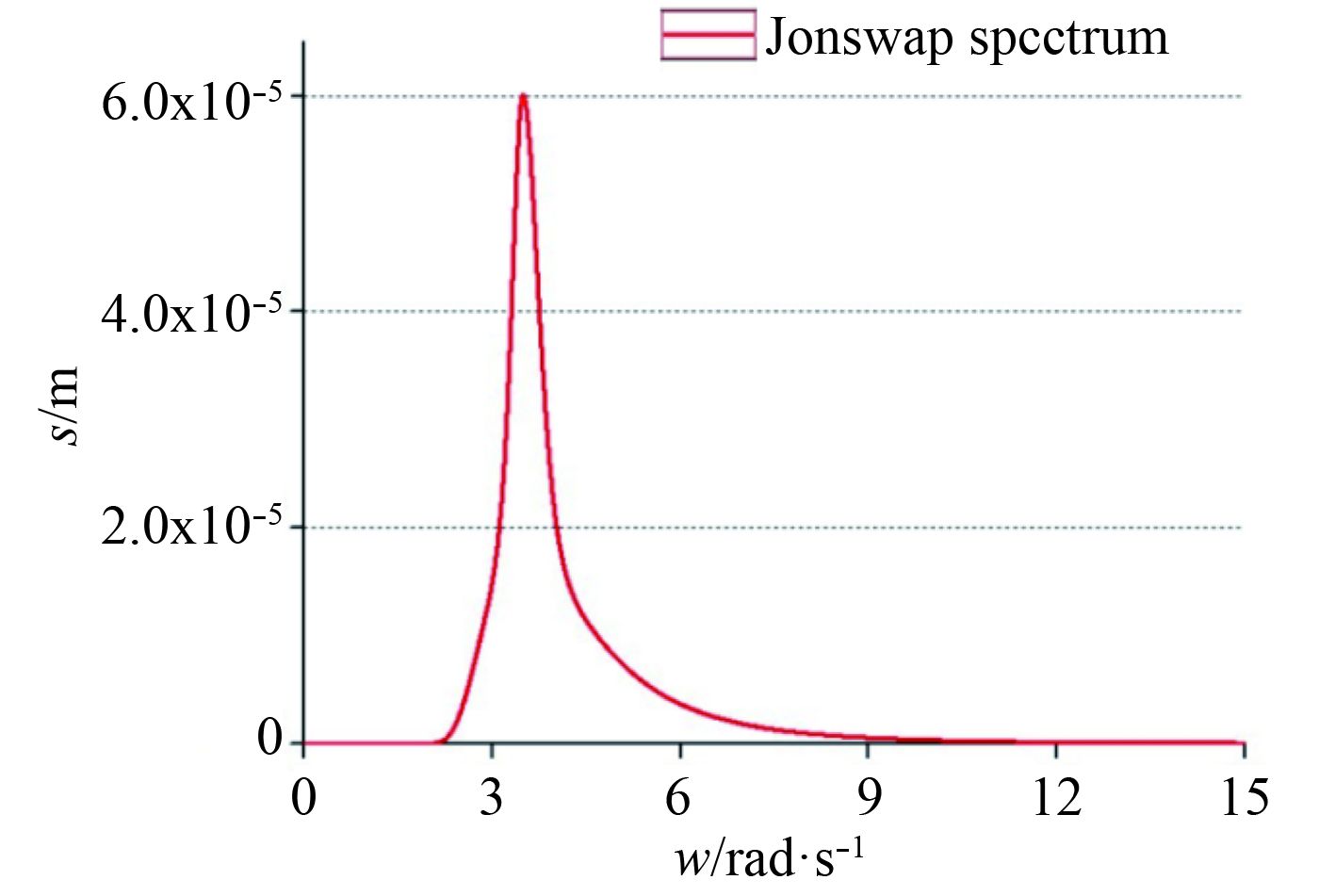
3.3 计算分析 3.3.1 畸形波的生成采用JONSWAP谱[10]描述随机海浪特性,谱峰周期
|
图 4 目标谱 Fig. 4 Shape of target wave spectrum |
设在目标谱的谱峰频率两侧分别略去能量峰值的0.1%和5%,由此可得频谱范围
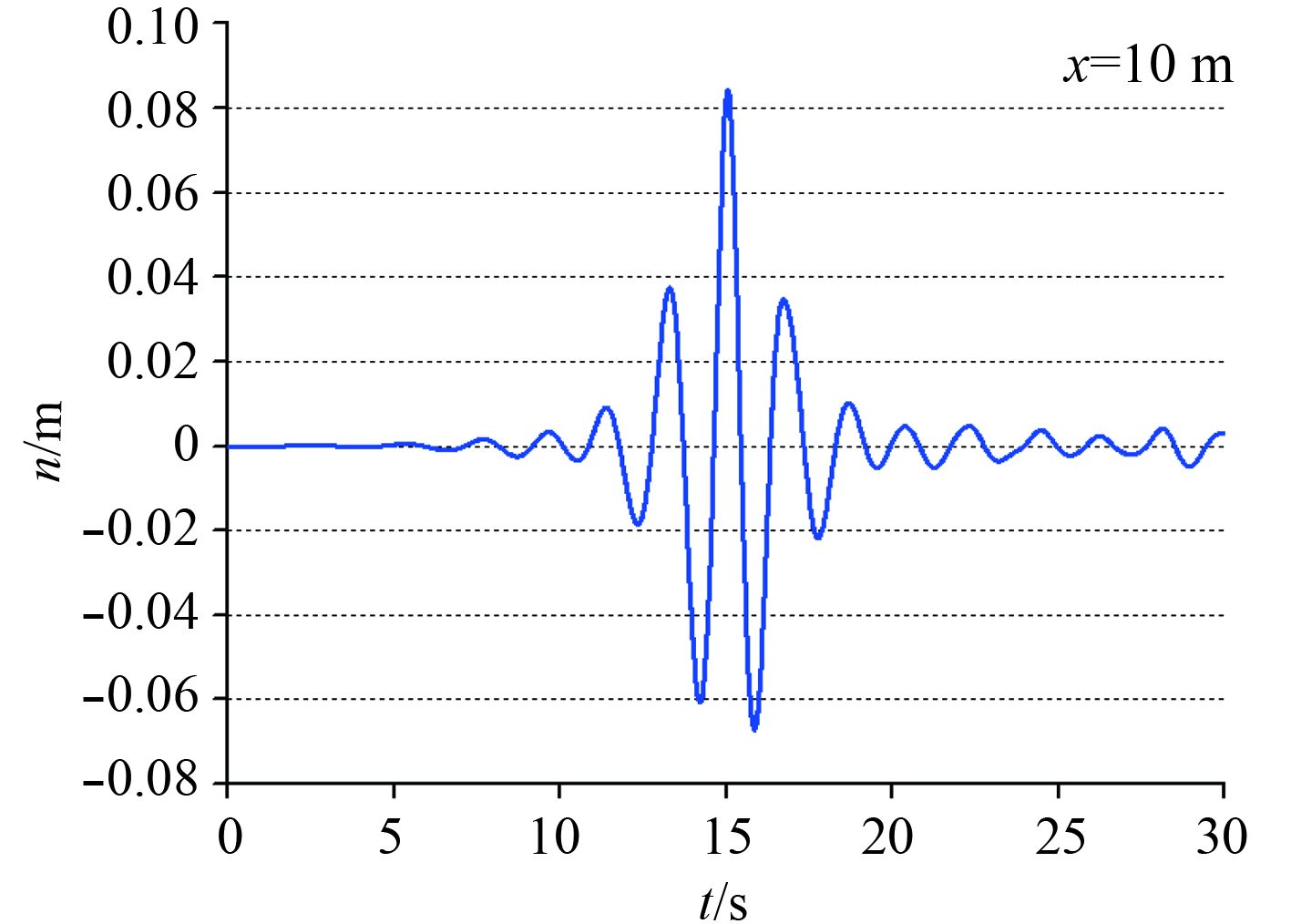
|
图 5 畸形波 Fig. 5 Freak wave |
从计算结果来看,聚焦幅值
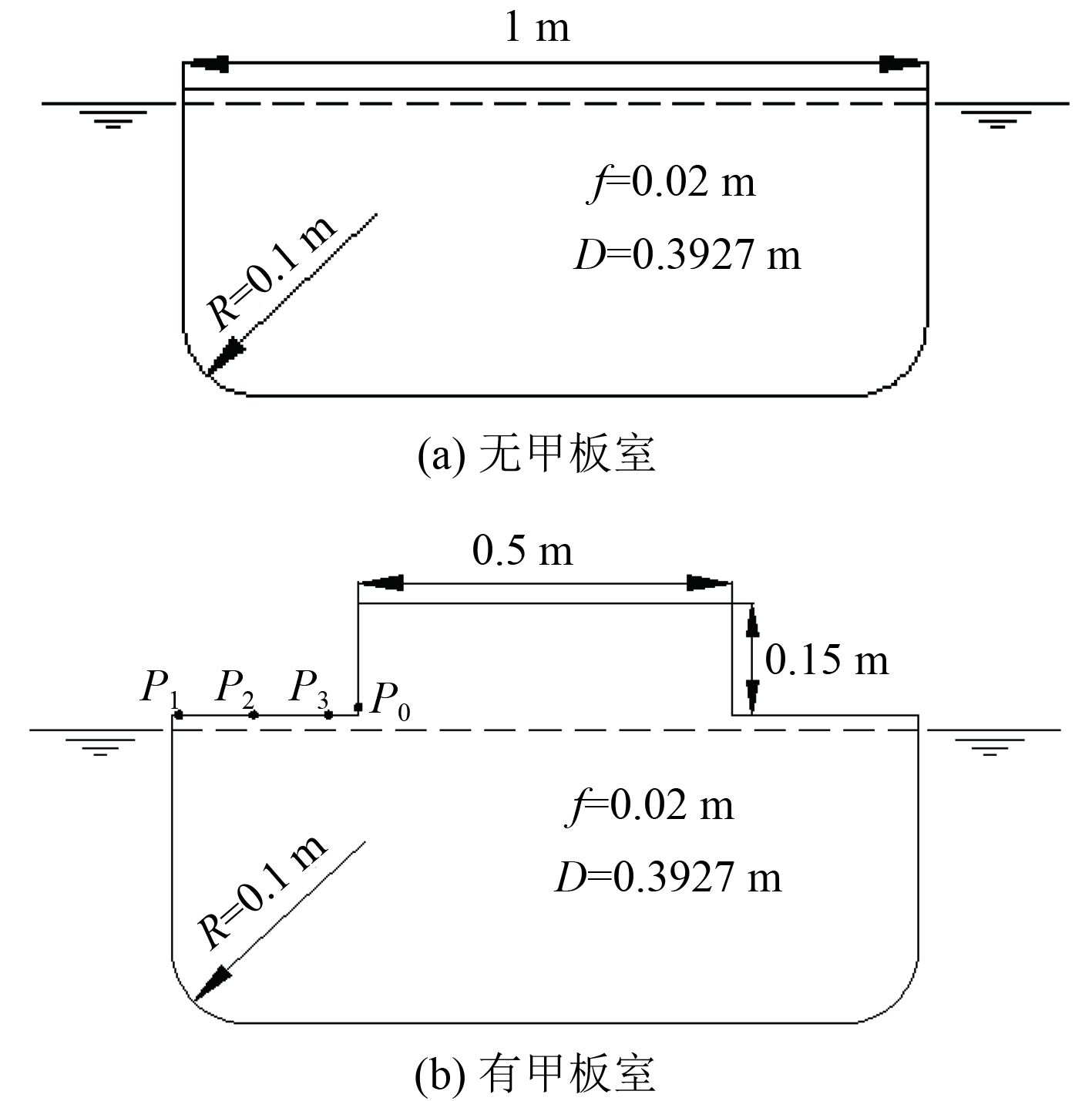
本节针对不同横截面浮体在畸形波中的运动响应进行计算分析,图6(a)为无甲板室浮体,6(b)为有甲板室浮体,浮体初始位置
|
图 6 不同横截面的浮体 Fig. 6 Floating bodies with different cross section |
图7给出了2种工况下浮体运动响应时历。由图可知,两者的垂荡运动变化在遭遇畸形波时刻及附近比较一致。甲板上浪水体冲击甲板室会造成浮体的横荡和横摇运动明显不同于无甲板室时的情况:有甲板室的浮体在遭遇畸形波之前甚至大幅度反向漂移,畸形波袭击过后,才逐渐向水池尾端漂移,并于t=25 s时达到与无甲板室浮体相同的横荡值;对于横摇运动,在遭遇畸形波之前,2种工况的横摇角变化几乎一致,之后约2 s内,无甲板室浮体的正向横摇角幅值大于有甲板室浮体的正向横摇角幅值,反向横摇角幅值则呈现相反的情况,约t=17 s后,有甲板室的横摇角幅值无论正反向均大于无甲板室的横摇角幅值,并且在受畸形波袭击后,较长时间处于剧烈的横摇运动中,不容易恢复正浮状态,既体现了很强的波物非线性作用的特征,又毫无规律可言。

|
图 7 不同横截面的浮体的运动响应时历 Fig. 7 Time history of the motion response of floating bodies with different cross section |
图8给出了不同时刻上述2种工况下畸形波与浮体相互作用时的流场形态、浮体运动姿态及浮体结构冯米斯应力云图。无甲板室浮体在遭遇畸形波袭击后,上浪水体会很快经甲板从另一侧流出,对浮体背浪一侧的流场造成扰动,从而进一步影响了浮体的运动状态;而有甲板室浮体在遭遇畸形波袭击后,由于甲板室壁的阻碍作用,上浪水体并未冲过甲板室,而是瞬间几乎全部被挡回,对浮体迎浪一侧的流场形成强烈干扰,甚至产生了气泡和漩涡,这对浮体结构大为不利。由于浮体结构刚性足够,因而可以承受畸形波浪的砰击而几乎不会产生变形。对于有甲板室的浮体而言,受到上浪水体的的猛烈砰击后,甲板室与甲板连接处会发生应力集中,极易造成结构破坏,在设计初期就应注意采取结构加强措施。

|
图 8 畸形波与不同横截面的浮体相互作用的云图 Fig. 8 Nephogram of interaction between freak wave and floating bodieswith different cross section |
为了探讨畸形波作用下抑制浮体漂移对甲板上浪的影响,对3.2.2节中浮体(图6(b))的横荡运动作了弹簧力抑制处理,使其在
|
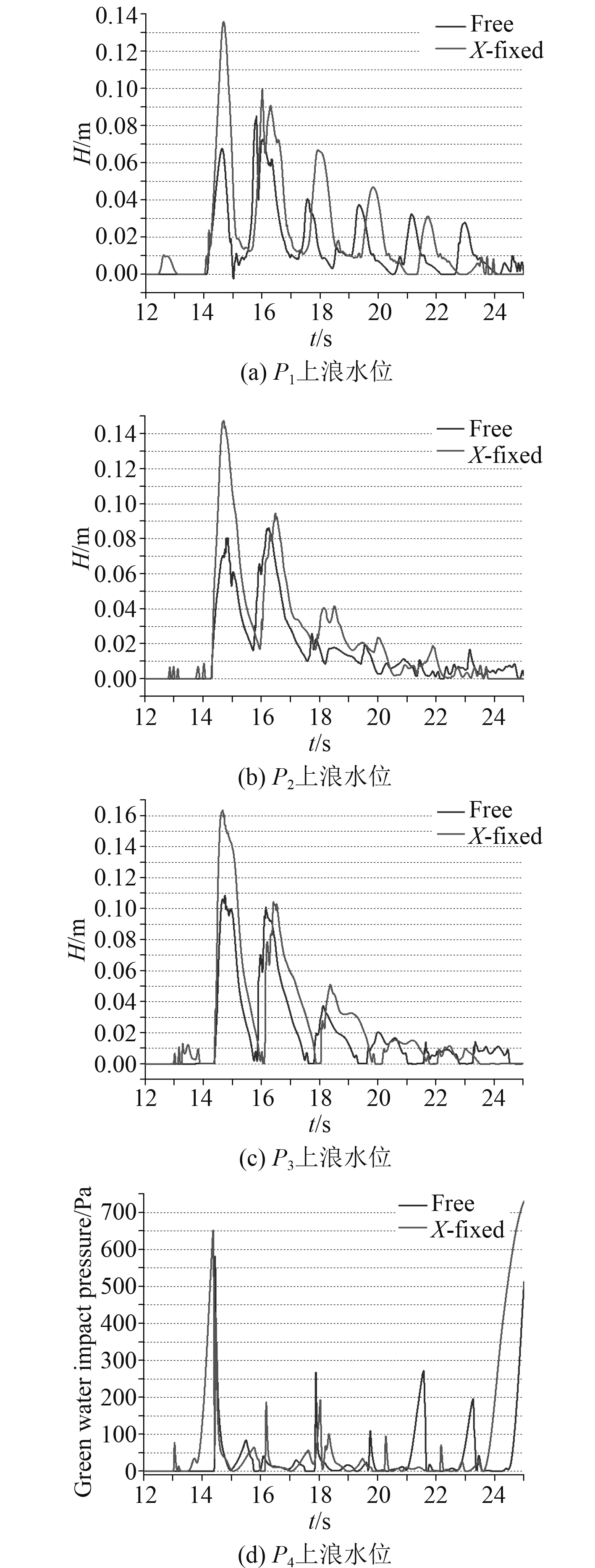
图 9 自由运动与抑制漂移两种情况下的监测点数值对比 Fig. 9 Comparison between free-floating and x-fixed on monitoring point data |
图9为浮体在自由浮动和限制漂移2种情况下的水动力监测点数值对比。从9(a)~9(c)中可以发现,在同一时刻,在遭遇畸形波的前后一段时间内,P1,P2,P3处的上浪水位依次递增,大约在第21 s后,P1,P2,P3处的上浪水位又依次递减,由此可以推断出甲板上浪的整个过程:伴随着畸形波浪到达,水体涌上甲板,当冲到甲板室壁时,水体顺着甲板室壁面迅速向上爬升,产生瞬时飞溅现象,接着水体翻卷回流。当畸形波列绕过浮体后,浮体摇荡仍在继续,且仍有少量水体涌上甲板,但其动能很大程度上减小,因此在受到甲板室阻挡时几乎没有发生飞溅现象,因而此时上浪水位变化也较为缓和。图9(d)中P0处监测到的上浪水体对甲板室壁的砰击压强时历证实了上述推断的合理性。
自由浮动情况下的甲板上浪水位整体上低于抑制漂移情况下甲板上浪水位,在14~19 s这段时间内显得尤为明显,对于P1和P2,仅在约23 s时,抑制漂移情况下的上浪水位被自由浮动情况反超,对于P3,这种水位反超现象提前约3 s。这主要是因为抑制浮体漂移后,浮体几乎无法顺浪前移,快速来袭的波浪遇到浮体壁面阻挡瞬时发生瞬时飞溅,后续的波浪在此瞬时堆积,一定程度上提升了涌上甲板的水体高度。而自由浮动情况下,由于浮体具有顺波浪方向的动能,这在一定程度上缓解了来袭波浪的冲击,因而涌上甲板的水体高度也相应地降低。2种工况下浮体的运动响应时历如图10所示。

|
图 10 自由运动与抑制漂移两种约束情况下的浮体运动响应时历 Fig. 10 Time history of the motion response of floating bodies under different constraint coditions, respectively as free-floating and x-fixed |
由图10可知,自由浮动和限制漂移2种约束情况下,浮体的垂荡在畸形波浪来袭之前几乎一致,在波浪聚焦开始的一段时间内出现偏差,且自由浮动情况下的垂荡值大于抑制漂移情况下的垂荡值,约第20 s过后2种情况下的垂荡值又持平。抑制漂移后,浮体的横摇运动比自由浮动时的情况更加剧烈,畸形波来袭前后,浮体从右倾约6°的极值短时间内摇摆到左倾约12°的极值,摆幅可达约18°,而对于自由浮动的浮体,相同时间范围内的摆幅约为13°。
3.3.4 浮体在水池中的放置地点对甲板上浪的影响为了探究浮体在水池中的放置地点对甲板上浪的影响,本节将3.2.2节中浮体(图6(b))分别放置于距水池左端10 m、9.5 m和10 m处,且均抑制掉其横荡运动,使其在
|
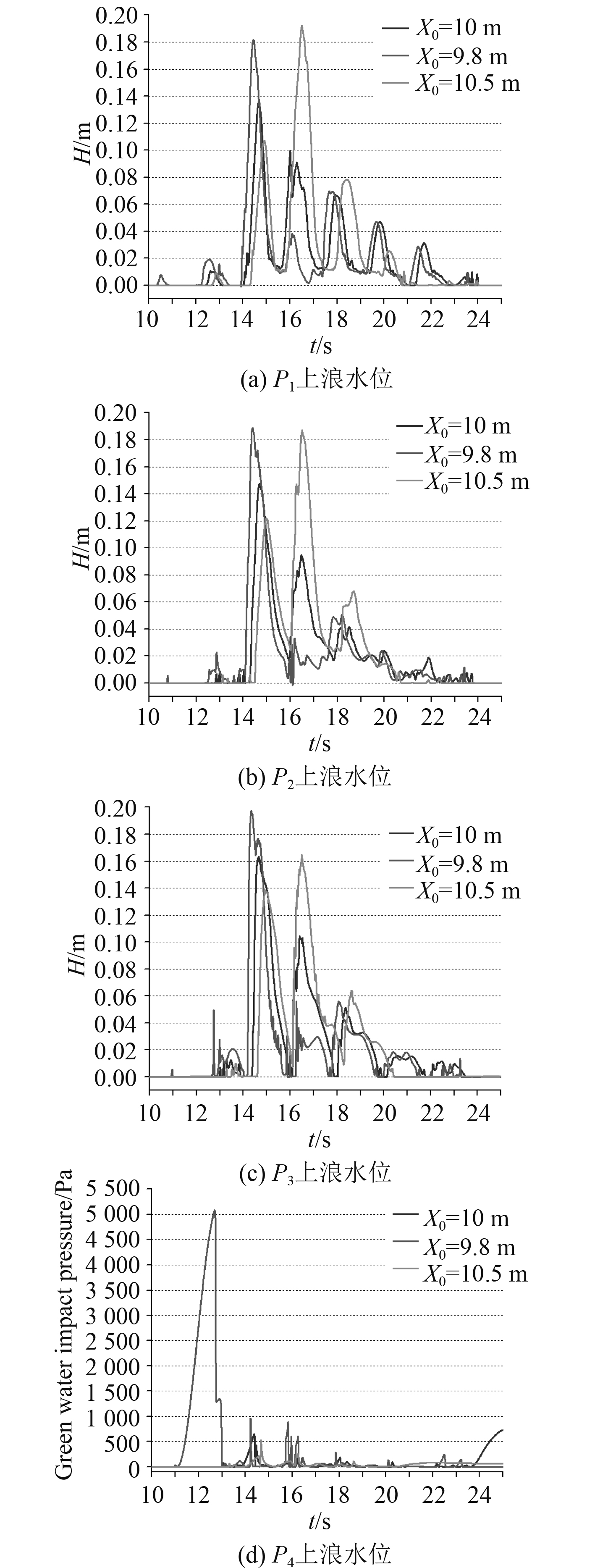
图 11 浮体不同放置位置情况下的监测点数值对比 Fig. 11 Comparison among different positions of floating body on monitoring point data |
图11给出了浮体上的水动力监测点数据时历。比较同一放置地点、不同水位监测点的数据可知,在设计波能聚焦时刻附近,离甲板边缘相对较远的水位监测点的上浪水位也相对较高,这主要是因为波浪涌上甲板后在甲板上短时间堆积,遇到甲板室壁瞬间翻卷回流,一部分水体越过甲板室壁继续向前流动,甲板室前的上浪水体则通常呈现前低后高的近似梯形或三角形分布[11];比较不同放置地点、同一水位监测点的数据可知,在波能聚焦时刻附近,距造波板相对较近的同一水位监测点的上浪水位相对较高。同时观察P0砰击压强时历可发现,浮体位于
|
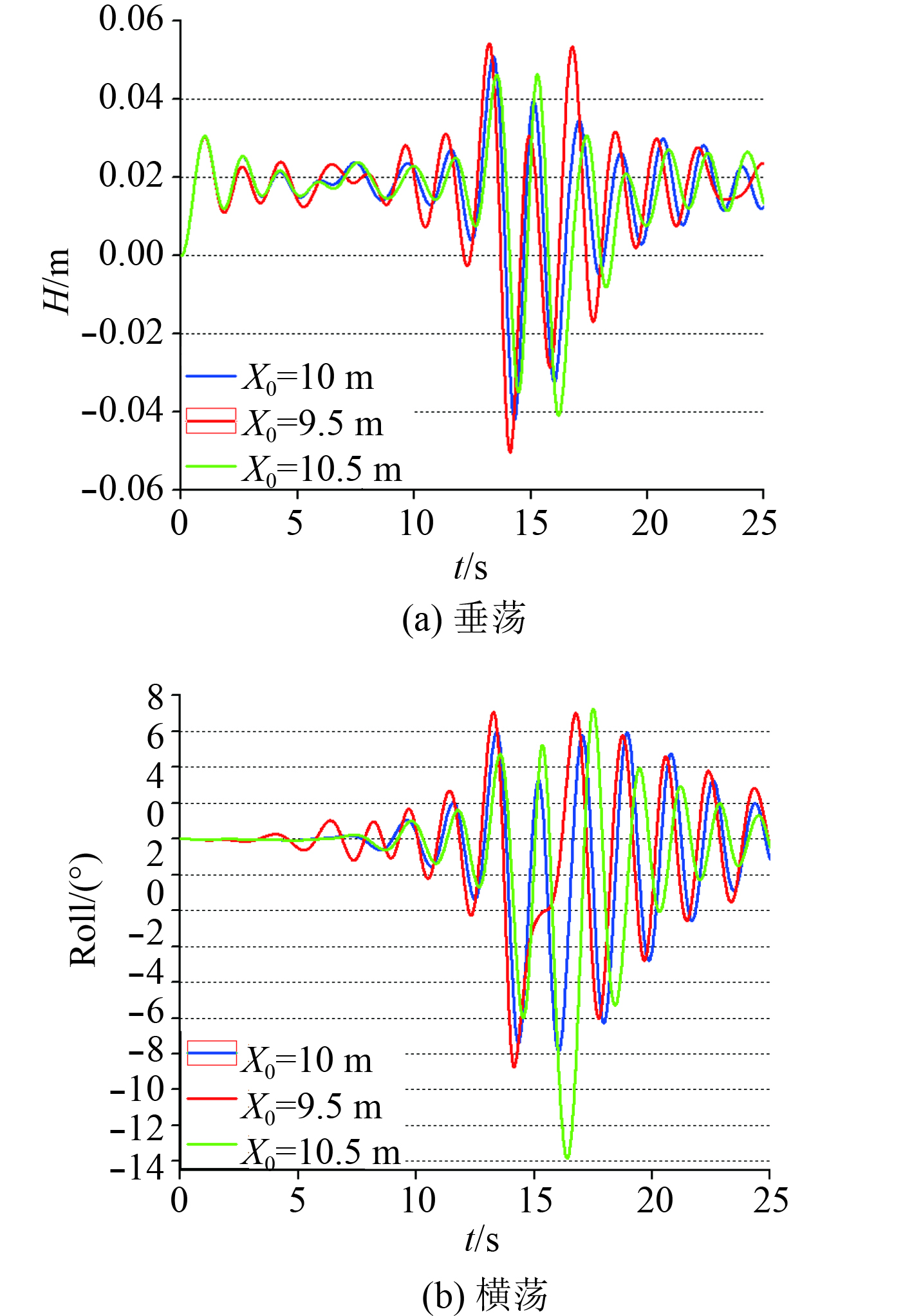
图 12 不同放置地点情况下的浮体运动响应时历 Fig. 12 Time history of the motion response of floating bodies located at different positions |
由图12可知,浮体在
1)基于线性波叠加原理,采用能量聚焦方法生成了畸形波。
2)基于流固耦合理论与切片原理,对不同横截面浮体在畸形波中的运动响应进行计算分析,结果表明,相较于无甲板室浮体而言,有甲板室浮体在提高浮体重心高度的同时,会显著改变上浪水体的运动形态,对浮体所处的流场,特别是迎浪一侧造成强烈干扰,进而使得浮体运动更加非线性化。
3)提出“单元贴片”研究方法,分别对自由浮动及抑制漂移2种情况下浮体与畸形波相互作用的载荷与响应问题进行了对比研究,发现甲板上浪水体对迎浪侧的流场形成强烈的扰动,并不同程度地伴随着气泡和漩涡的产生,而背浪一侧则显得相对平静一些,而上浪水体的剧烈砰击使得上层建筑与甲板连接处的结构冯米斯应力值瞬间增加,容易使此处材料发生屈服失效甚至破坏,故应注意采取适当的结构加强措施。同时,抑制浮体漂移后,相应的上浪水位高度、上浪水体砰击压强及浮体的横摇运动也增加,但垂荡运动在波浪聚焦处开始减小。基于上述方法,对浮体在水池中不同位置时的甲板上浪情况进行数值模拟,结果表明,浮体处于同一位置时,在设计波能聚焦时刻附近,离甲板边缘相对较远的水位监测点的上浪水位相对较高;浮体处于不同位置时,在波能聚焦时刻附近,距造波板相对较近的同一水位监测点的上浪水位相对较高。
| [1] |
杨冠声, 董艳秋, 陈学闯. 畸形波(freak wave)[J]. 海洋工程, 2002, (4): 105–108.
YANG Guan-sheng, DONG Yan-qiu, CHEN Xue-chuang. Freak wave[J]. The Ocean Engineering, 2002, (4): 105–108. https://www.atlantis-press.com/php/download_paper.php?id=25863501 |
| [2] | KIMURA A, OHTA T. Probability of the freak wave appearance in a 3-dimensional sea condition[C]// Proceedings of the Coastal Engineering Conference, 1994, 23–28. |
| [3] | KLINTING P, SAND S. Analysis of prototype freak waves. Conf. on nearshore hydrodynamics[C]// ASCE. 1987: 618–632. |
| [4] | GUNTHER F C, CHRISTIAN E S, KATJA S. Freak wave impact on semisubmersible time-domain analysisof motions and forces [C]// Proceeding of The Thirteenth (2003) International Offshore and Polar Engineerin Conference. 2003, 449–456. |
| [5] | GUNTHER F C, MARCO K. Influence of the bow shape on loads in high and steep waves [C]// Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering. 2010: OMAE 2010–2014. |
| [6] | GUNTHER F C, SURESH R, MARCO K. Time domain comparison with experiments for ship motions and structure loads on a container ship in abnormal waves [C]// Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering. 2011: OMAE 2011–50316. |
| [7] | RUDMAN M, CLCARY P W. Rogue wave impact on a tension leg platform: the effect of wave incidence angle and mooring line tension[J]. Ocean Engineering, 2013(61): 123–138. https://www.sciencedirect.com/science/article/pii/S0029801813000218 |
| [8] | ZHAO Xi-zeng, HU Chang-hong. Numerical and experimental study on a 2-D floating body under extreme wavc conditions[J]. Applied Ocean Research, 2012, 35: 1–13. |
| [9] | LONGUET-HIGGINS M S, COKELET E D. The deformation of steep surface waves on water. I. A numerical method of computation[J]. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 1976, 350(1660): 1–26. |
| [10] | 赵艳. 强非线性波与海洋浮式结构物的相互作用[D]. 镇江: 江苏科技大学, 2014. |
| [11] |
刘利琴, 王宾, 沈文君. 甲板上浪船舶的横摇运动[J]. 振动. 测试与诊断, 2012(S1): 14–19, 146.
LIU Li-qin, WANG Bin, SHEN Wen-jun. The rolling motion of the ship of green water[J]. Journal of Vibration, Measurement & Diagnosis, 2012(S1): 14–19, 146. http://www.cqvip.com/QK/97495X/2012S1/1003445404.html |
 2018, Vol. 40
2018, Vol. 40
