水下潜器是一种在海洋、河流与湖泊等水下环境中进行探测作业的装置,潜器系统通常由潜器主体以及作为其轨迹与姿态控制装置的导管螺旋桨组成,潜器主体体内可根据不同的水下探测作业要求搭载不同类型的水下化学或物理参数监测传感器。水面操作人员可以通过脐带缆等对导管螺旋桨发出控制指令来实施对其轨迹与姿态操纵[1 – 4]。水下潜器在水下运动时,由于导管螺旋桨的旋转以及水下潜器的运动,使水下潜器所在水域的流场发生变化。水下潜器在水中作业的过程中,由于海域环境的复杂性,使其运动状态发生非线性的改变。准确地模拟出水下潜器在复杂运动状态下的水动力特性,有利于提高对导管螺旋桨水动力特性的认识,尤其是在研究复杂运动对导管螺旋桨水动力特性的影响,为设计出运动控制性能优良的水下潜器系统提供参考。
现阶段利用计算流体力学对水下潜器系统中螺旋桨在水下环境中水动力特性的研究中,往往采用相对性原理,即水下潜器系统保持位置不变,对来流环境进行设置使其满足螺旋桨前进时的进速[5-8],这种相对性原理使得水域流场发生较大改变,并不能客观地体现出由水下潜器系统运动所产生的水动力特性。文献[9]中采用了动网格与滑移网格混合技术,研究了水下潜器系统在运动过程中水动力特性和导管螺旋桨的推力特性变化。但是,作者对水下潜器系统和导管螺旋桨的研究仅局限在直线运动的过程中,未对回转等其他复杂型运动下其水动力特性进行研究。文献[10]中利用滑移网格技术模拟导管螺旋桨的旋转运动,在研究回转状态下导管螺旋桨的水动力特性时,采用导管螺旋桨与来流形成不同的夹角进而间接模拟其回转运动过程,这种方法同样利用了相对运动的原理,因此,并不能动态地模拟出导管螺旋桨回转运动过程时的水动力特性。
本文对水下潜器回转运动的整个过程进行动态模拟,对两侧导管螺旋桨在回转运动状态时的推力特性进行分析对比,研究了两侧导管螺旋桨产生不同推力的原因。利用多相流空化模型模拟处于空泡影响下的水下潜器系统及导管螺旋桨回转运动时的推力特性。首先对水下潜器系统进行三维模型的构建,采用动网格动态层方法和滑移网格技术模拟导管螺旋桨的旋转回转运动,其中对导管螺旋桨所在计算域的运动方式定义采用加载UDF文件,程序中运用了DEFINE_ZONE_MOTION宏。同时利用计算流体力学方法对计算域内求解N-S方程,进而计算得到水下潜器系统及导管螺旋桨回转运动过程的推力特性。
1 数学模型及计算方法 1.1 控制方程、湍流模型假定流体是不可压的,则导管螺旋桨在水下运动过程中的连续方程和动量方程分别为:
| $\frac{{\partial {u_i}}}{{\partial {x_i}}} = 0\text{,}$ | (1) |
| $\rho \frac{{\partial \left( {{u_i}{u_j}} \right)}}{{\partial {x_j}}} \!=\! -\! \frac{{\partial P}}{{\partial {x_j}}} \!+\! \rho {g_i} \!+\! \rho \frac{\partial }{{\partial {x_j}}} \! \left[ {u\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} \!+\! \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \rho \overline {u_i'u_j'} } \right]\text{。}$ | (2) |
式中:ui,uj均为速度分量时均值(i,j=1,2,3);P为压力时均值;ρ为流体密度;u为流体粘性系数;gi为重力加速度分量;
在基于均质多相在传输方程的模型中,使用以下的一系列控制方程来描述空化流场:
| $\frac{{\partial {\rho _m}}}{{\partial t}} + \frac{{\partial \left( {{\rho _m}{u_j}} \right)}}{{\partial {x_j}}} = 0\text{,}$ | (3) |
| $\begin{split}\frac{{\partial {\rho _m}{u_i}}}{{\partial t}} + & \frac{{\partial \left( {{\rho _m}{u_i}{u_j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \\& \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\mu _t}} \right)\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}} - \frac{2}{3}\frac{{\partial {u_i}}}{{\partial {x_j}}}{\delta _{ij}}} \right)} \right]\text{,}\end{split}$ | (4) |
| $\frac{{\partial \left( {{\alpha _v}{\rho _v}} \right)}}{{\partial t}} + \frac{{\partial \left( {{\alpha _v}{\rho _v}{u_j}} \right)}}{{\partial {x_j}}} = R\text{。}$ | (5) |
式中:t为时间,s;i和j为坐标方向;ui为速度分量;ρm,ρv,ρl分别为不同相的密度,kg/m3;δij为克罗内克数;αv为汽相体积分数;μ,μt为黏度,kg/(m·s);R为各个相之间的质量传输率,kg/(m3·s)。
| ${\rho _m} = {\rho _v}{\alpha _v} + {\rho _l}\left( {1 - {\alpha _v}} \right)\text{,}$ | (6) |
| $\mu = {\mu _v}{\alpha _v} + {\mu _l}\left( {1 - {\alpha _v}} \right)\text{,}$ | (7) |
式中:μl,μv分别为液相和蒸汽相动力黏度。
| $R = {R_e} - {R_c}\text{,}$ | (8) |
式中:Re,Rc分别为蒸汽生成率和蒸汽凝结率。
本文采用RNG k-ε湍流模型,由于在该模型中平均流动中的旋转、旋流等情形给予了考虑,因此该模型能够较好处理那些应变率较高和高弯曲度的流动情形。其方程如下:
| $\frac{{\partial \rho k}}{{\partial t}} \!\!+\!\! \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_j}k} \right) \!=\! - \frac{2}{3}\rho k\frac{{\partial {u_k}}}{{\partial {x_k}}} \!\!+\!\! \frac{\partial }{{\partial {x_j}}} \! \left( {\frac{{{\mu _{eff}}}}{{{\sigma _k}}}\frac{{\partial k}}{{\partial {x_j}}}} \right) \!\!+\!\! {G_k} \!-\! \rho \varepsilon \text{,}$ | (9) |
| $\begin{split}& \frac{{\partial \rho \varepsilon }}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {\rho {U_j}\varepsilon } \right) = \\ & -\! \left[ {\left( {\frac{2}{3}{C_{\varepsilon 1}} \!-\! {C_{\varepsilon 3}} \!+\! \frac{2}{3}{C_\mu }{C_\eta } \cdot \frac{{k\partial {u_k}}}{{\varepsilon \partial {x_k}}}} \right)\rho \varepsilon \frac{{\partial {u_k}}}{{\partial {x_k}}} \!+\! \frac{\partial }{{\partial {x_j}}}\left( {\frac{{{\mu _{eff}}}}{{{\sigma _\varepsilon }}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right)} \right] \!+\! \\& {\rho \displaystyle\frac{\varepsilon }{k}\left[ {\left( {{C_{\varepsilon 1}} - {C_\eta }} \right){G_k} - {C_{\varepsilon 2}}\rho \varepsilon } \right]}\text{。}\end{split}$ | (10) |
式中:
本文水下潜器系统采用立式的对称翼型壳体结构,同时在对称翼型壳体上有2个鱼雷状浮体,推进装置采用直径为75 mm的Ka 4-70/19A标准导管螺旋桨。具体尺寸参照表1,导管螺旋桨的具体尺寸参照表2。在对水下潜器建立模型的过程中,忽略对计算结果影响较小以及本身尺寸较小的几何构件,水下潜器主体与导管螺旋桨的几何模型如图1所示。
|
|
表 1 水下潜器主体几何尺度 Tab.1 Geometric dimensions of underwater vehicle |
|
|
表 2 导管螺旋桨几何尺度 Tab.2 Geometric dimensions of ducted propeller |

|
图 1 水下潜器主体及导管螺旋桨模型 Fig. 1 Model of underwater vehicle and ducted propeller |
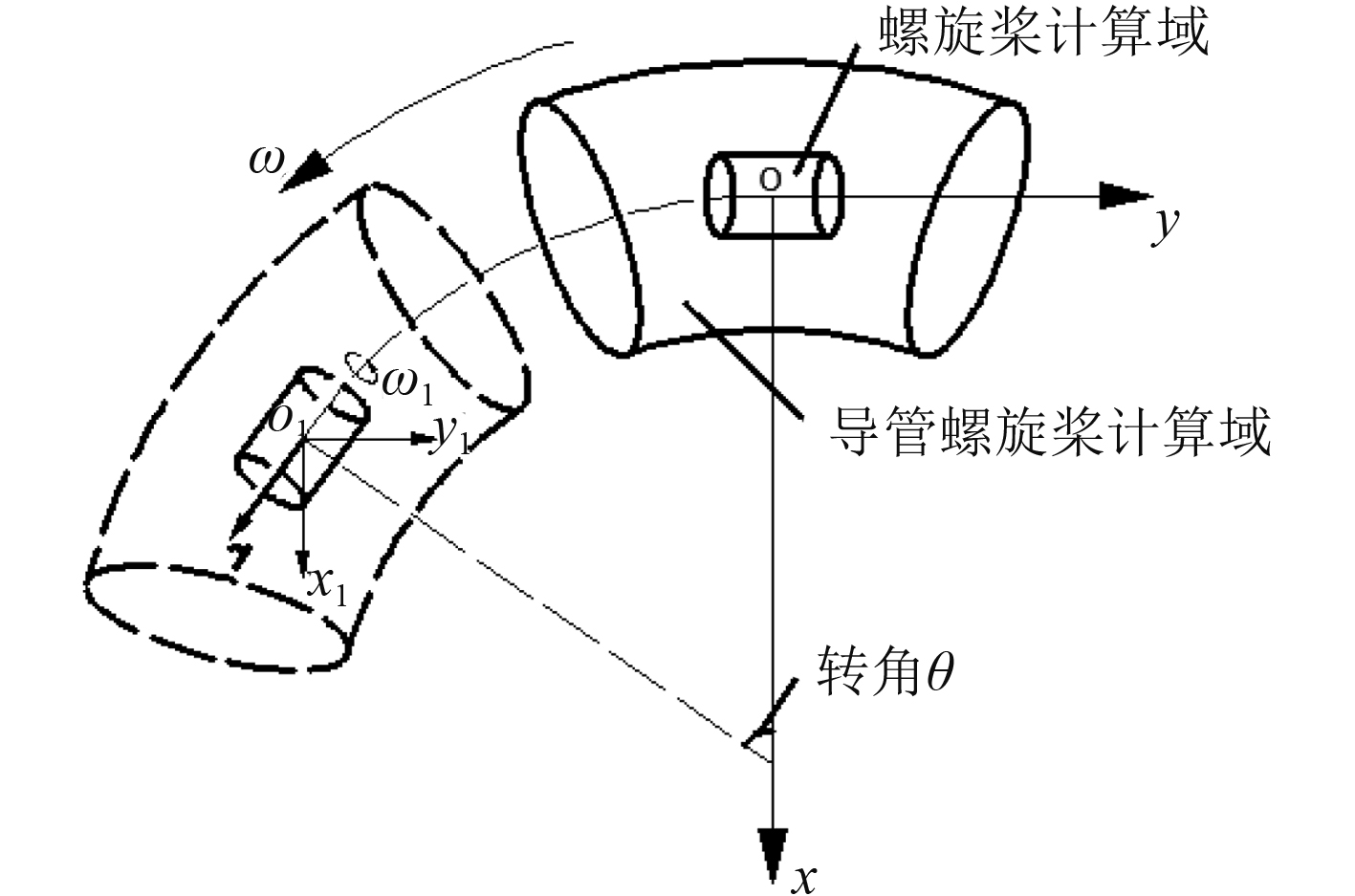
由于水下潜器回转运动时,主体与导管螺旋桨需绕一固定参考轴进行回转运动,而导管螺旋桨在随主体一起进行回转运动时,自身也需绕轴进行转动。因此对于包括导管螺旋桨的计算域而言,其旋转轴随时间而变化,这就需要对螺旋桨的运动过程进行模型分析,图2为单独导管螺旋桨进行回转运动时的示意图。
|
图 2 单独导管螺旋桨进行回转运动示意图 Fig. 2 Diagram of single ducted propeller with rotary motion |
根据图2所示,导管螺旋桨在绕一固定轴进行角速度为ω旋转的同时也绕自身一轴线进行角速度为ω1的旋转运动。
根据旋转角速度以及螺旋桨中心所在的初始位置可以计算出t秒后导管螺旋桨中心的位置坐标,取xoy平面为基准面,运动时间t后其中心位置坐标可以表示为:
| $\left\{ \begin{array}{l}x = a \cdot \sin \left[ {0.5\omega \cdot \left( {t + \Delta t} \right)} \right] \cdot \sin\left[ {0.5\omega \cdot \left( {t + \Delta t} \right)} \right]\text{,}\\y = a \cdot \sin\left[ {0.5\omega \cdot \left( {t + \Delta t} \right)\left] { \cdot \cos} \right[0.5\omega \cdot \left( {t + \Delta t} \right)} \right]\text{。}\end{array} \right.$ | (11) |
图2中,
| $\left\{ \begin{array}{l}{x_1} = \sin\left[ {\omega \cdot \left( {t + \Delta t} \right)} \right]\text{,}\\{y_1} = - \cos\left[ {\omega \cdot \left( {t + \Delta t} \right)} \right]\text{。}\end{array} \right.$ | (12) |
式(11)中,a为导管螺旋桨中心的初始位置到固定旋转轴轴心处距离的2倍,ω为绕固定轴旋转的角速度。
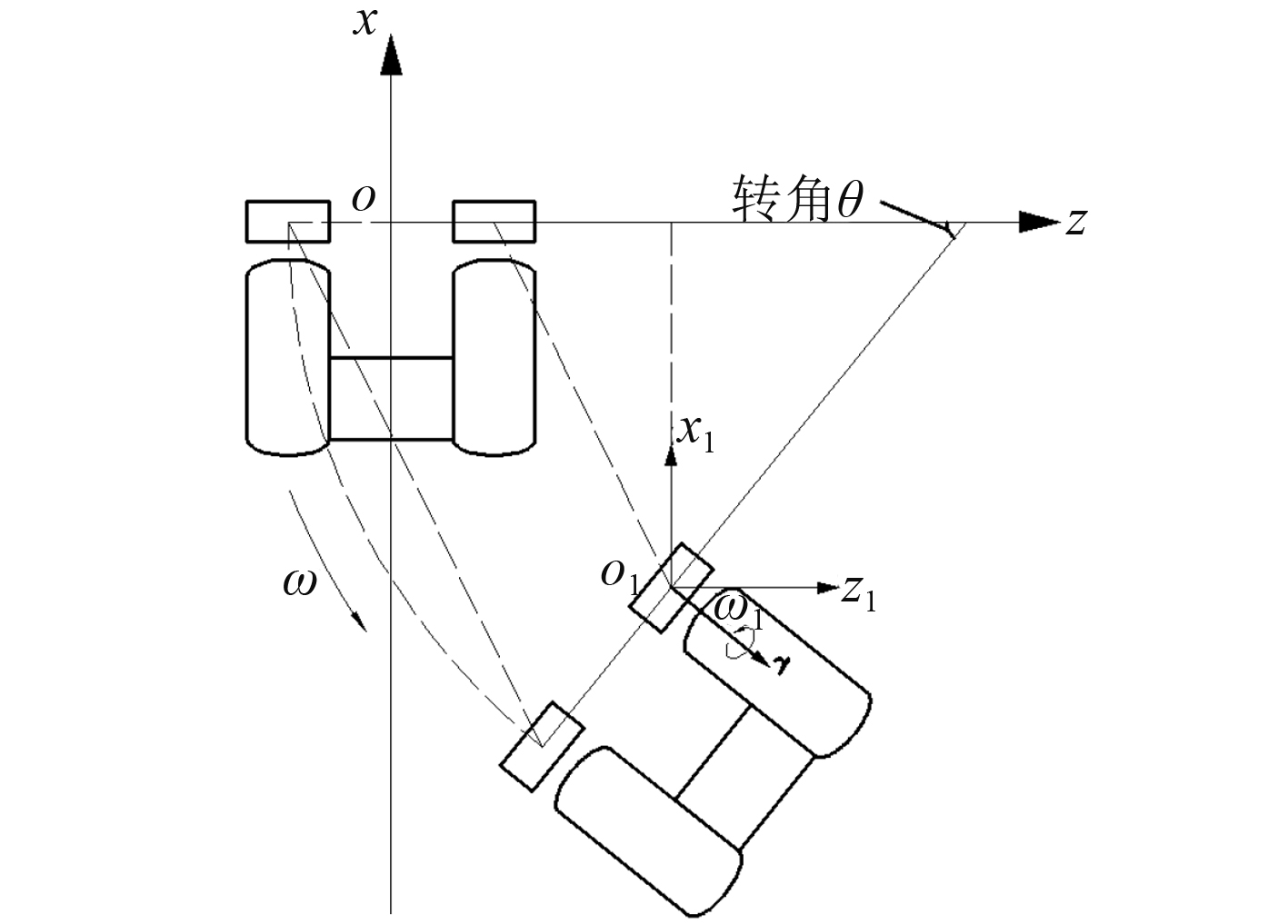
1.4 水下潜器的运动方式水下潜器主体与2个导管螺旋桨进行回转运动时,由于中心位置的选取不同,导管螺旋桨的参考轴也会不同,本文将中心位置选取在与2个导管螺旋桨中心连线的中点处,目的在于方便计算导管螺旋桨中心位置的坐标,以及旋转轴矢量的坐标形式。水下潜器主体与导管螺旋桨一起进行回转运动的示意图如图3所示。
|
图 3 水下潜器进行回转运动示意图 Fig. 3 Diagram of underwater vehicle with rotary motion |
根据图3所示,水下潜器主体在绕一固定轴进行角速度为ω的旋转运动,而2个导管螺旋桨除了随水下潜器主体一起运动外,同时也绕自身的一轴线进行角速度为ω1的旋转运动。
根据旋转角速度以及导管螺旋桨中心所在的初始位置可以计算出t秒后导管螺旋桨中心的位置坐标,取xoz平面为基准面,运动时间t后左导管螺旋桨的中心位置坐标可以表示为:
| $ \left\{\!\!\!\! \begin{array}{l}x = - a \cdot \sin \left[ {0.5\omega \cdot \left( {t + \Delta t} \right)} \right] \cdot \sin\left[ {0.5\omega \cdot \left( {t + \Delta t} \right)} \right]\text{,}\\z = {z_0} + a \cdot \sin\left[ {0.5\omega \cdot \left( {t + \Delta t} \right)\left] { \cdot \cos} \right[0.5\omega \cdot \left( {t + \Delta t} \right)} \right]\text{。}\!\!\!\!\!\!\!\!\! \end{array} \right.$ | (13) |
图3中,
| $\left\{ \begin{array}{l}{x_1} = - \cos\left[ {\omega \cdot \left( {t + \Delta t} \right)} \right]\text{,}\\{z_1} = \sin\left[ {\omega \cdot \left( {t + \Delta t} \right)} \right]\text{。}\end{array} \right.$ | (14) |
式(13)中,a为左导管螺旋桨中心的初始位置到固定旋转轴轴心处距离的2倍,ω为绕固定轴旋转的角速度,z0′为左导管螺旋桨中心的初始位置坐标,Δt为时间步长。
同理,运动时间t后右导管螺旋桨的中心位置坐标可以表示为:
| $\!\left\{ \!\!\!\!\! \begin{array}{l}x' \!\!=\!\! \! -\! b \cdot \sin \left[ {0.5\omega \cdot \left( {t + \Delta t} \right)} \right] \cdot \sin\left[ {0.5\omega \cdot \left( {t \!+\! \Delta t} \right)} \right]\text{,}\\z' \!\!=\!\! {z_0}' \!\!+\! b \cdot \sin\left[ {0.5\omega \cdot \left( {t \!+\! \Delta t} \right)\left] { \cdot \cos} \right[0.5\omega \cdot \left( {t \!+\! \Delta t} \right)} \right]\text{。}\end{array} \right.$ | (15) |
旋转轴矢量用坐标形式表示为:
| $\left\{ \begin{array}{l}{x_1}' = - cos\left[ {\omega \cdot \left( {t + \Delta t} \right)} \right]\text{,}\\{z_1}' = sin\left[ {\omega \cdot \left( {t + \Delta t} \right)} \right]\text{。}\end{array} \right.$ | (16) |
其中,b为右导管螺旋桨中心的初始位置到固定旋转轴轴心处距离的2倍,ω为绕固定轴旋转的角速度,z0′为右导管螺旋桨中心的初始位置坐标,Δt为时间步长。
为了准确模拟水下潜器的回转运动过程,采用加载UDF文件对水下潜器的运动方式进行定义。程序中运用到DEFINE_ZONE_MOTION宏。
1.5 空化模型水和水蒸汽之间的转换通过空化模型来描述。根据对单一介质密度定义的方式不同,计算空化的模型分为基于输运方程的模型和基于状态方程的模型。本文空化模型采用Zwart-Gerber-Belamri模型。
| ${R_e} = {F_{vap}}\frac{{3{\alpha _{ruc}}\left( {1 - {\alpha _v}} \right){\rho _v}}}{{{R_B}}}\sqrt {\frac{2}{3}\frac{{{P_v} - {P}}}{{{\rho _l}}}}, \,\,\,\;\;{\text{当}}P < {P_v}\text{;}$ | (17) |
| ${R_c} = {F_{cond}}\frac{{3{\alpha _v}{\rho _v}}}{{{R_B}}}\sqrt {\frac{2}{3}\frac{{P - {P_v}}}{{{\rho _l}}}}, \,\,\,\;\;{\text{当}}P > {P_v}\text{。}$ | (18) |
式中:αruc为成核位置体积分数,取5×10–4;RB为空泡半径,m,取1.0×10–5;P、Pv分别为流场压力和汽化压力,Pa;Fvap,Fcond为2个经验校正系数。
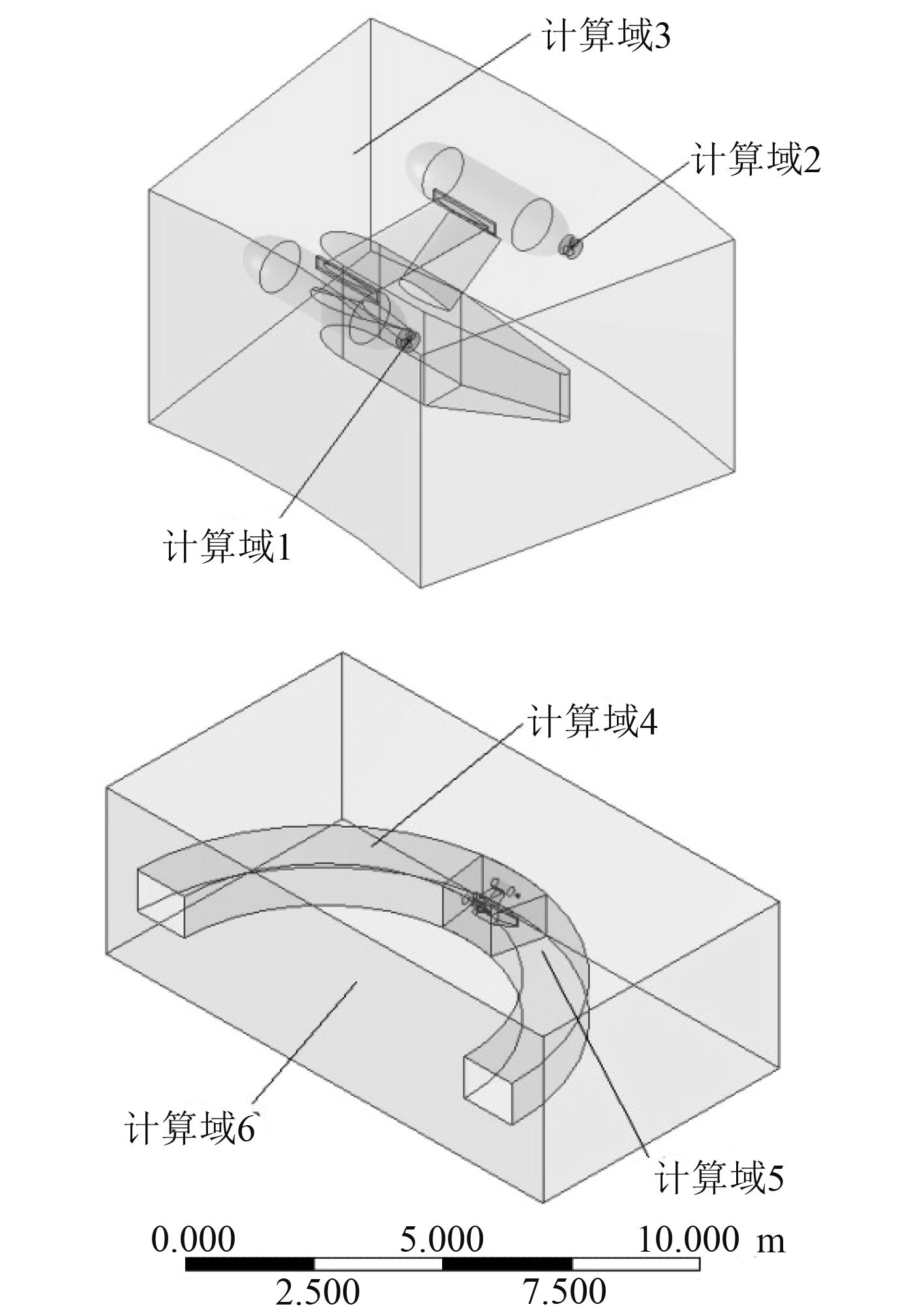
1.6 计算域网格的划分根据水下潜器的运动方式,本次模拟的计算域被划分成了六部分,分别为2个包括螺旋桨的计算域1和计算域2,1个包括水下潜器主体的计算域3,2个圆弧型计算域4和计算域5,最外围的一个方形计算域6。各个计算域对网格划分的要求也不同,例如,2个螺旋桨计算域和水下潜器主体所在的计算域以及最外层的计算域采用非结构网格的划分方式,而2个圆弧型的计算域则采用结构网格的划分方式。在各个计算域的交界面处,采用interface方式进行连接。计算域的划分如图4所示。在整个计算域中,导管螺旋桨表面及水下潜器主体设置为无滑移的壁面条件,入口设置为速度是0.5 m/s无空泡的来流,出口设置为无空泡溢出的压力出口,具体边界条件设置如表3所示。
2 数值模拟与结果分析模拟水下潜器在回转半径为4.5 m时的回转运动过程,水下潜器做回转运动时的角速度为0.314 rad/s,导管螺旋桨的转速为1 500 r/min,图5为初始时刻及完成回转运动后计算域网格在xoz平面的变化情况。
|
图 4 计算域的划分图 Fig. 4 Partition diagram for the domain |
|
|
表 3 边界条件的设置 Tab.3 Setting of boundary conditions |

|
图 5 计算域网格在xoz平面的变化图 Fig. 5 The grid variation diagram of domain in xoz plane |
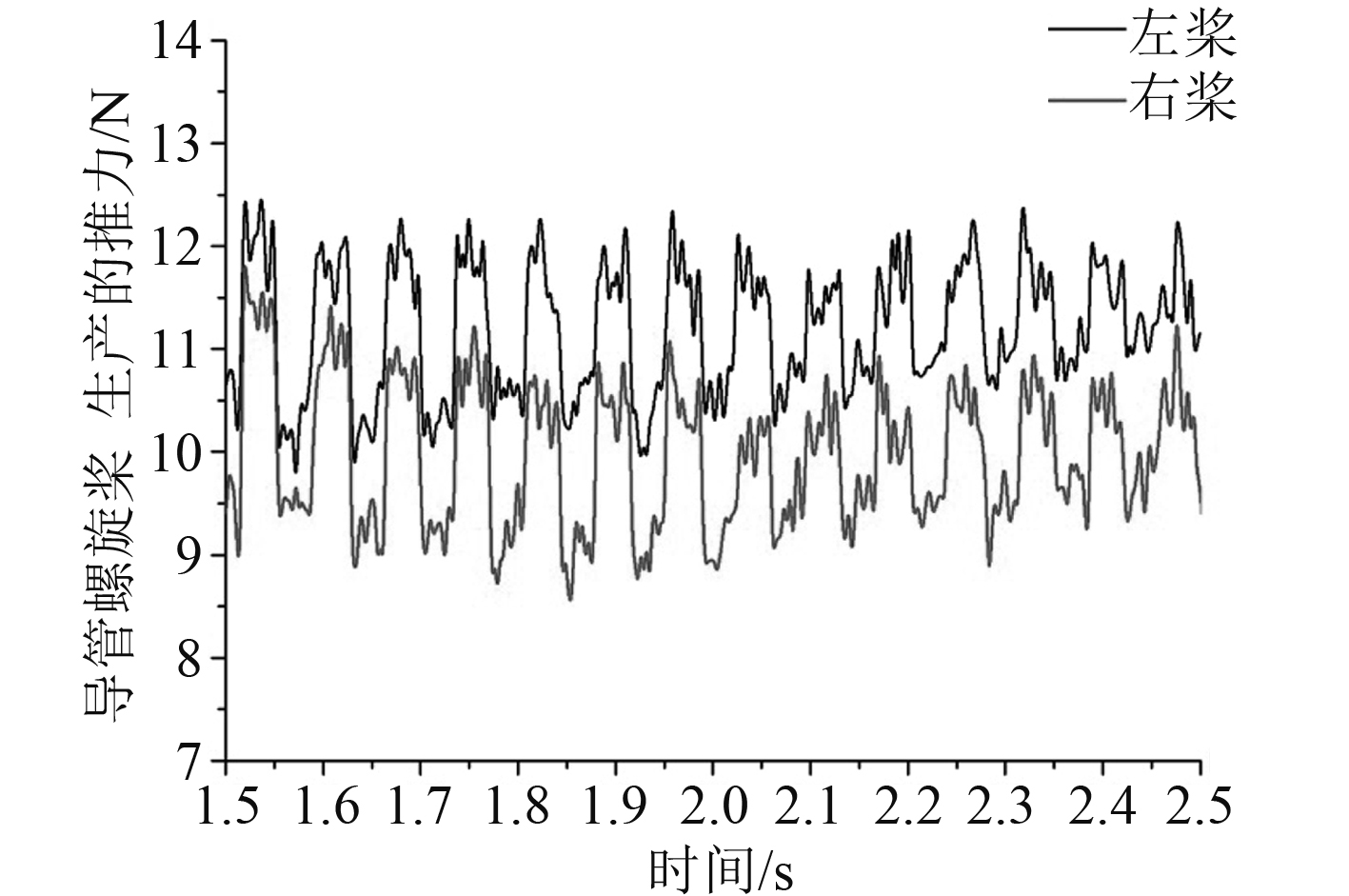
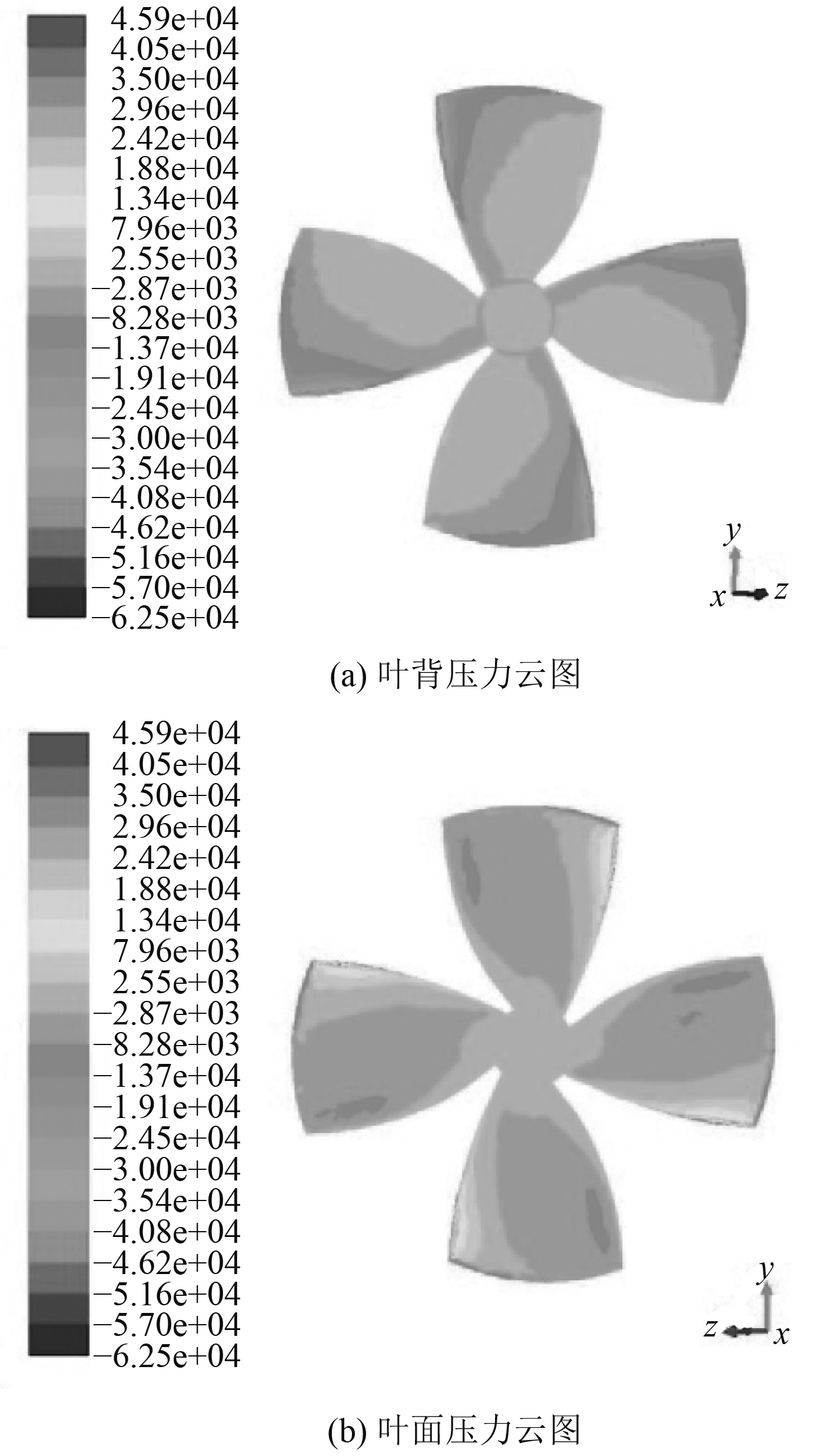
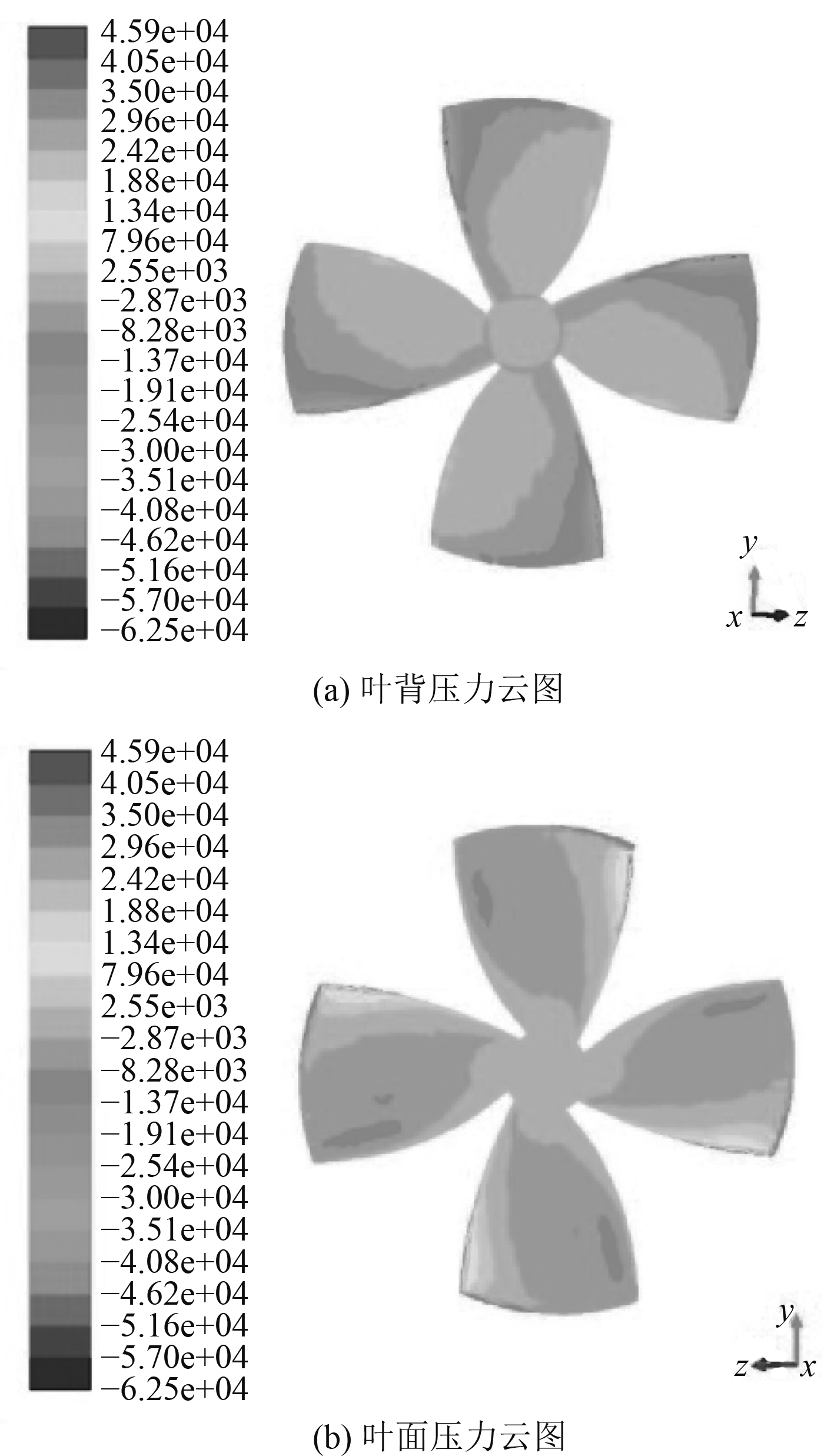
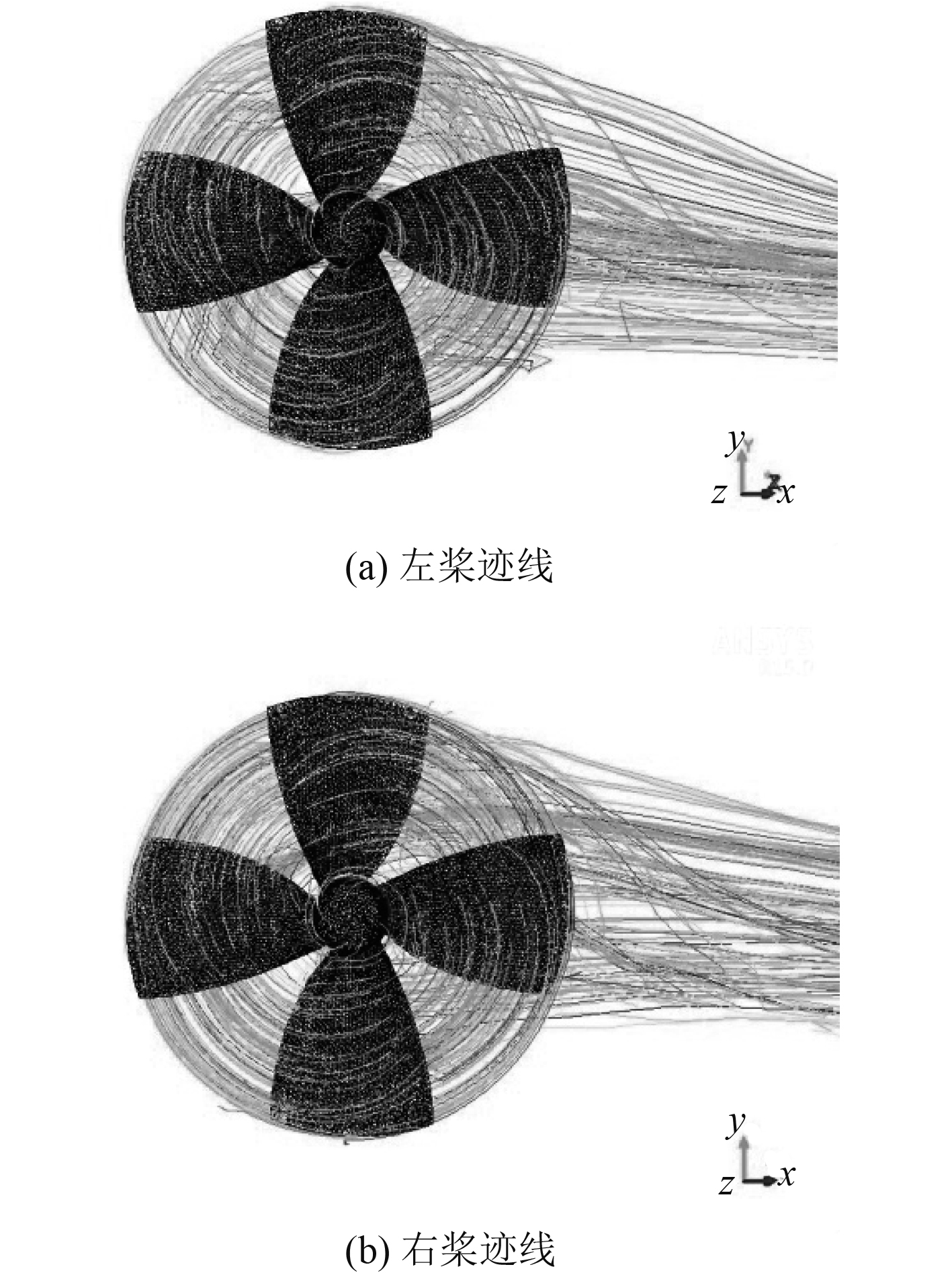
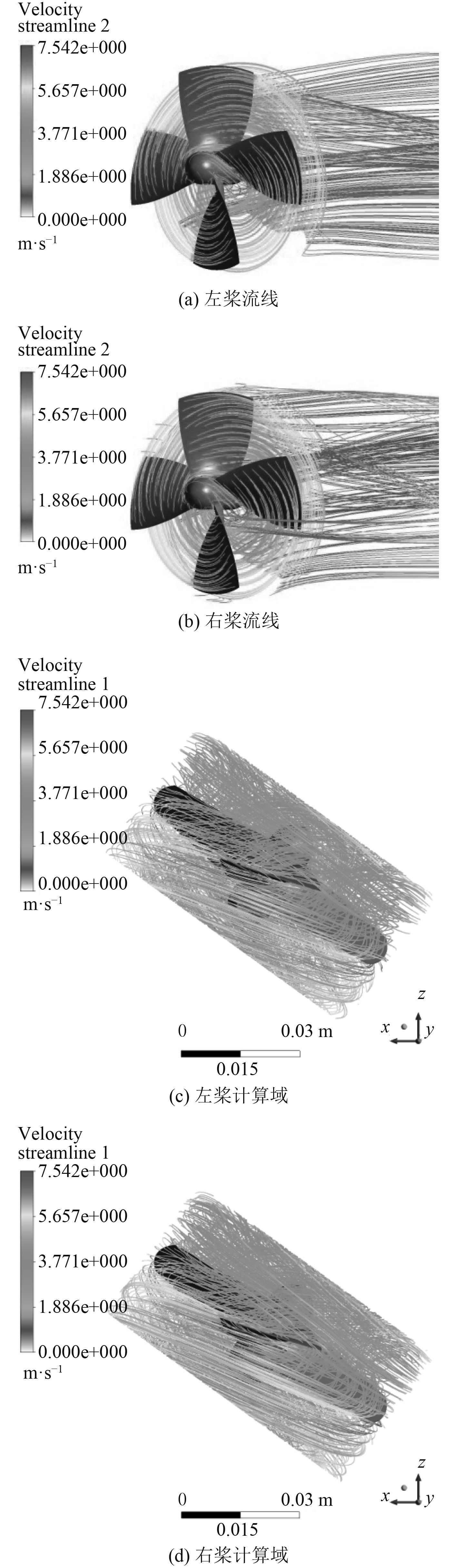
从图5中计算域网格在xoz平面的变化情况来看,水下潜器完成了回转运动过程,导管螺旋桨实现了变轴旋转运动,从局部网格图中可以看出,在每个计算域interface的交界面处,网格保持较高的连续性,证实了该运动过程的准确性。通过螺旋桨计算域的变化情况可以看出,在水下潜器进行回转运动时,2个导管螺旋桨产生的推力为xz方向的合成推力。图6为左右2个导管螺旋桨在x和z方向上产生的合成推力在达到稳定时随时间的变化曲线。图7和图8分别给出了左右导管螺旋桨桨叶叶背与叶面的压力云图,云图标尺为压力,Pa。图9给出的是水下潜器周围流场的迹线变化图。图10给出了左右导管螺旋桨周围流场的迹线图。图11给出了左右导管螺旋桨周围流场的流线变化图,云图标尺为流体速度,m/s。
|
图 6 两导管螺旋桨的合成推力随时间变化曲线 Fig. 6 The thrust curves of two ducted propeller with time changed |
|
图 7 左导管螺旋桨压力云图 Fig. 7 The pressure contour of left ducted propeller |
|
图 8 右导管螺旋桨压力云图 Fig. 8 The pressure contour of right ducted propeller |

|
图 9 水下潜器周围流场迹线变化图 Fig. 9 The path line around the flow field of underwater vehicle |
|
图 10 螺旋桨周围流场迹线图 Fig. 10 The path line around the flow field of propeller |
|
图 11 螺旋桨周围流场流线图 Fig. 11 The streamline around the flow field of propeller |
从图6结果可知,水下潜器的2个导管螺旋桨的推力最终随时间进程的增加逐渐趋于稳定,从最终达到稳定变化的导管螺旋桨推力曲线来看,左侧导管螺旋桨产生的推力值大于右侧导管螺旋桨产生的推力,从上述模拟条件中可以看出,在水下潜器进行单向性的回转运动时,来流从水下潜器右侧流向左侧,由理论及实验可知,导管螺旋桨在同转速的前提下,进速越大,其产生的推力值会越小。从图9可以看出,由于来流条件的影响,基于相对运动的原理,使得两侧导管螺旋桨及水下潜器在x方向的进速增大,而左侧导管螺旋桨由于受到右侧主体的阻挡使其受到的来流速度小于右侧导管螺旋桨受到的来流速度,即左侧导管螺旋桨的相对进速小于右侧导管螺旋桨的相对进速,因此,左侧导管螺旋桨产生的合成推力大于右侧导管螺旋桨产生的合成推力。通过对图11中导管螺旋桨流场变化的分析可以得出,螺旋桨的高速旋转改变了周围流场流体的流速,观察云图中的结果可以得知,螺旋桨桨叶叶梢周围流体流速较高,高于其他相对半径处的流体流速,当沿着相对半径向桨毂靠近时,流场中流体的流速随之降低。
3 结 语本文通过利用动网格和滑移网格技术对水下潜器系统及导管螺旋桨的回转运动过程进行了动态模拟,数值计算出在回转运动过程中导管螺旋桨所产生的推力情况,文中提出的回转运动数学模型经数值模拟计算证实是正确的,可以确保水下潜器回转运动的完成。利用动网格技术可以消除相对运动的影响,更能真实地反映使水下潜器在水下的运动过程。同时通过对回转运动数学模型的计算为日后研究更为复杂的运动方式提供了参考。
通过对数值模拟的结果分析可知:1)水下潜器完成了回转运动过程,通过对比运动前后计算域网格的变化情况,可以验证本文回转运动数学模型的准确性。2)通过数值模拟计算得到的结果可以得知导管螺旋桨所产生的推力最终趋于周期稳定变化,在水下潜器进行单向性的回转运动时,由于受到右侧来流的影响,使左侧导管螺旋桨的相对进速小于右侧导管螺旋桨的相对进速,两侧导管螺旋桨进速的不同导致了左侧导管螺旋桨产生的推力大于右侧导管螺旋桨产生的推力。3)螺旋桨的高速旋转改变了周围流场流体的流速,观察螺旋桨流场流线云图中的结果可以得知,螺旋桨桨叶叶梢周围流体流速较高,高于其他相对半径处的流体流速,当沿着相对半径向桨毂靠近时,流场中流体的流速随之降低。
| [1] | AVILA J P J, ADAMOWSKI J C. Experimental evaluation of the hydrodynamic coefficients of a ROV through Morison’s Equation [J]. Ocean Engineering, 2011, 38: 2162–2170. |
| [2] | JAULIN L. Robust set-membership state estimation; application to underwater robotics [J]. Automatica, 2009, 45: 202–206. |
| [3] | LI J H, JUN B H, LEE P M, et al. A hierarchical real-time control architecture for a semi-autonomous underwater vehicle [J]. Ocean Engineering, 2005, 32: 1631–1641. |
| [4] | 陈健, 吴家鸣, 徐灜, 等. 立式翼型主体拖曳式水下潜器的设计及操纵性能[J]. 海洋技术学报, 2015, 34(4): 1–6. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hyjs201504001 |
| [5] |
吴家鸣, 崔寅, 邓威, 等. 控制动作下的带缆遥控水下机器人水动力特性分析[J]. 华南理工大学学报: 自然科学版, 2012, 40(4): 150–157.
WU Jia-ming, CUI Yin, DENG Wei, et al. Hydrodynamic characteristics of tethered underwater robot under control manipulations [J]. Journal of South China University of Technology: Natural Science Edition, 2012, 40(4): 150–157. http://www.cqvip.com/QK/94312X/201204/42204580.html |
| [6] |
吴家鸣, 郁苗, 朱琳琳. 带缆遥控水下机器人水动力数学模型及其回转运动分析[J]. 船舶力学, 2011, 15(8): 827–843.
WU Jia-ming, YU Miao, ZHU Lin-lin. A hydrodynamic model for a tethered underwater robot and dynamic analysis of the robot in turning motion [J]. Journal of Ship Mechanics, 2011, 15(8): 827–843. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cblx201108001 |
| [7] |
赖华威, 刘月琴, 吴家鸣. 基于CFD方法的螺旋桨性能计算与分析[J]. 船海工程, 2009, 38(4): 131–135.
LAI Hua-wei, LIU Yue-qin, WU Jia-ming. Calculation and Analysis of Propeller Performance by CFD [J]. Ship and Ocean Engineering, 2009, 38(4): 131–135. http://www.doc88.com/p-9873795635469.html |
| [8] |
吴家鸣, 叶志坚, 金晓东, 等. 水下潜器导管螺旋桨在转艏摆动中的推力特性分析[J]. 华南理工大学学报: 自然科学版, 2015, 43(12): 141–148.
WU Jia-ming, YE Zhi-jian, JIN Xiao-dong, et al. Analysis of thrust characteristics of ducted propellers in underwater vehicle with yawing motion [J]. Journal of South China University of Technology: Natural Science Edition, 2015, 43(12): 141–148. http://www.cnki.com.cn/Article/CJFDTotal-HNLG201512021.htm |
| [9] | 林育胜, 吴家鸣, 李林华. 超小型水下机器人通过狭窄隧道的水动力性能[J]. 广州航海学院学报, 2016, 24(4): 1–4. http://d.old.wanfangdata.com.cn/Periodical/gzhhgdzkxxxb201604001 |
| [10] |
吴家鸣, 邓威, 赖华威. 回转状态下导管螺旋桨水动力特性的数值模拟[J]. 华南理工大学学报: 自然科学版, 2010, 38(7): 90–96.
WU Jia-ming, DENG Wei, LAI Hua-wei. Numerical simulation of hydrodynamic characteristics of ducted propeller in turning motion [J]. Natural Science Edition, 2010, 38(7): 90–96. https://www.wenkuxiazai.com/doc/65a52150f01dc281e53af07b.html |
 2018, Vol. 40
2018, Vol. 40
