调节阀作为船舶海水系统中最常规的设备,其主要作用是调节海水系统的压力、流量等参数。流量调节阀在工作时流道内存在湍流、漩涡、分离、空化等复杂的流动现象[1-5],水力能量大量转化为摩擦耗能、热能、声能等。随着船舶系统对调节阀低噪声性能的要求越来越高,传统的单流道调节阀已无法适应高压差的运行工况,必须对传统流道进行优化降低调节阀流噪声。本文针对上述问题,运用CFD的手段对原调节阀的内流道流场进行分析,从改变调节阀能量损耗分布的角度提出流道优化方案,并对优化流道进行了验证性数值分析,可为高压差流量调节阀流噪声控制提供参考。
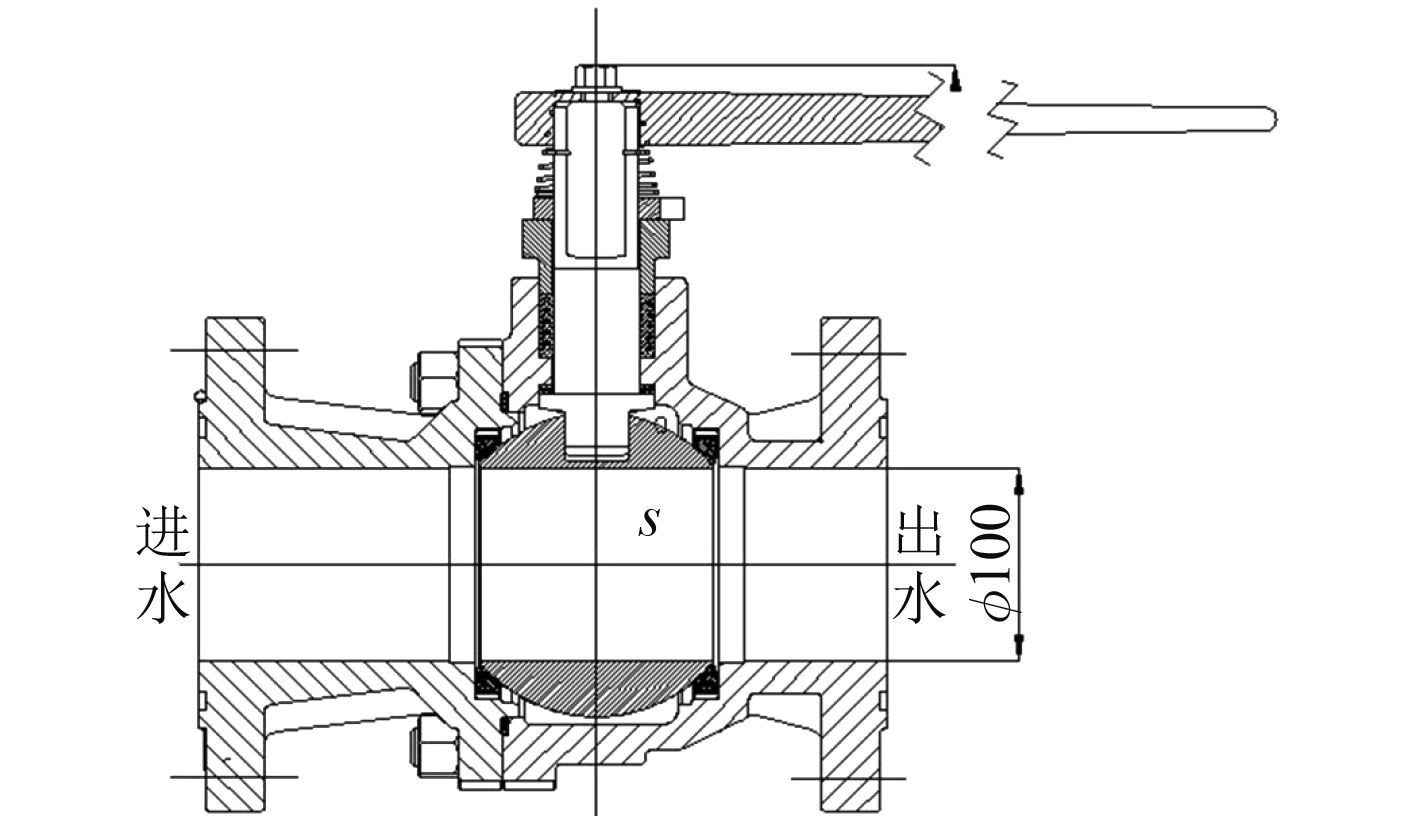
1 流道几何模型和数值方法介绍 1.1 几何模型图1是流量调节阀的结构图,传统球阀采用大通径单流道,通过手动、电动或者液动控制球体通道轴线与管道轴线之间的角度达到调节阀门开度的目的,进而调节阀门流量。阀门进出口通道与球体通道共同构成阀门的流道。调节阀进出口管道及阀芯的通径均为100 mm。
|
图 1 流量调节阀结构简图 Fig. 1 Structure diagram of regulating valve |
流量调节阀内流道如图2所示,本文采用全阀模型作流场计算,完全按阀门图纸生成数值计算域,利用三维设计软件CATIA建立几何模型,画出流量调节阀的内部流场。为保证流体进口稳定、出口充分发展和符合实验情况,对阀门流道进行了修正,即阀前和阀后分别加长1 000 mm,同时只保留管道和阀芯结构,对阀门其他结构做简化处理。

|
图 2 原阀内流道模型 Fig. 2 Original valve flow-path model |
流量调节阀水力性能与流噪声特性相关,本文采用流体动力学计算方法计算调节阀内流道流场和优化后的调节阀流道流场,下面简单介绍所采用计算方法。
对流道内流体流动状态进行求解计算时,首先利用基于
在笛卡尔坐标系下,不可压缩的粘性流动采用张量的形式表示的时均化连续性方程和RANS方程可以写为:
| $\frac{{\partial p}}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\rho {u_i} = 0\text{,}$ | (1) |
| $\begin{split}\frac{{\partial \rho {u_i}}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\rho {u_i}{u_j} = - \frac{{\partial \rho }}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} -\\\rho \overline {u_i'u_j'} + {S_i},\;\; {{ i, j = 1,2}}\text{。}\end{split}$ | (2) |
式中:
基于
| $\frac{{\partial \rho k}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\rho {u_j}k = \frac{\partial }{{\partial {x_j}}}\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}\frac{{\partial k}}{{\partial {x_j}}} + {P_k} - {\beta '}\rho k\omega \text{,}$ | (3) |
| $\frac{{\partial \rho \omega }}{{\partial t}} \!+\! \frac{\partial }{{\partial {x_j}}}\rho {u_j}\omega = \frac{\partial }{{\partial {x_j}}}\mu \!+\! \frac{{{\mu _t}}}{{{\sigma _k}}}\frac{{\partial \omega }}{{\partial {x_j}}} \!+\! {D_\omega } \!+\! \alpha \frac{\omega }{k}{P_k}\! -\! \beta \rho {\omega ^2}\text{。} \! \! \! \!$ | (4) |
式中:
LES模型认为湍流是由大小不同尺度的涡组成,流场瞬时变量由滤波函数可分为大涡运动和小涡运动,大尺度涡可由瞬态N-S方程直接模拟,不直接模拟小尺度涡,其对大尺度涡的影响采用亚格子模型模拟。经过滤波函数处理的大涡模拟控制方程为:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\rho \overline {{u_i}} = 0\text{,}$ | (5) |
| $\frac{{\partial \rho \overline {{u_i}} }}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\rho {u_i}{u_j} = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial xj}}\mu \frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}} - \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}}\text{。}$ | (6) |
式中:
在数值格式方面,速度和压力的耦合采用PISO方法,对流项使用二阶迎风格式来离散,控制方程中的扩散项使用二阶精度的中心差分格式离散,湍流各项均采用二阶迎风差分格式,时间项采用有界二阶精度的中心差分格式。
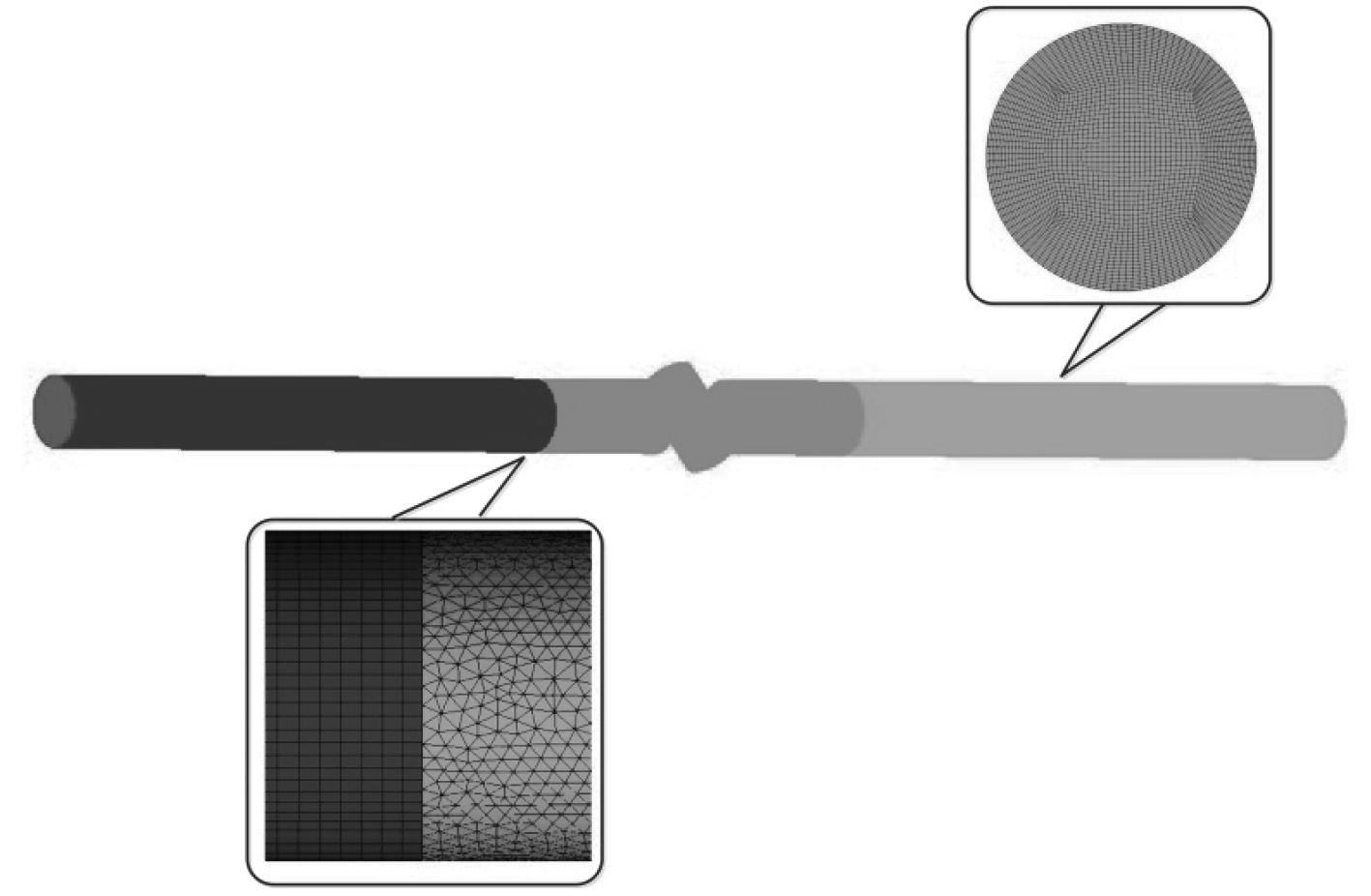
2 原流道流场计算结果 2.1 结构离散及边界条件利用CATIA建模之后,将调节阀内流道三维实体导入ICEM进行流场计算的前处理工作。计算域内网格分布是流体流动控制方程数值离散的基础,网格质量将对计算的敛散性和计算结果的精度产生直接影响。阀芯附近流道拓扑结构复杂,阀门两端延长管道拓扑结构相对简单,为兼顾计算效率和计算精度,采用混合网格的划分方案,即流量调节阀附近采用非结构化的四面体网格且网格适度细化,两端延长管道采用结构化的六面体网格,管道及阀内壁面附近采用加密的边界层网格,3种网格总数约为236万,如图3所示。经过多次调整保证
|
图 3 内流道网格模型 Fig. 3 Flow-path mesh model |
根据船舶海水系统流量调节阀典型的高压差运行工况特点,流量调节阀进口压力高达1.8MPa。水舱与大气相通,背压为一个标准大气压。故进口边界设为压力进口1.8MPa,出口边界设为压力出口0。海水介质属于粘性流体,在管壁以及阀芯内壁出,速度的边界条件满足无滑移条件,即固壁上的速度。
2.2 流场计算结果分析流量调节阀内流道计算采用计算流体力学通用软件Fluent,计算的工况点流量选择120 t/h,根据数值试验确定阀门开度为38°。首先利用RANS模型对计算域进行定场计算,计算稳定后采用LES模型进行非定场计算。LES大涡模拟在模拟湍流、漩涡脱落及压力脉动等方面具有较大优势,先进行定场计算的目的是加快非定场计算收敛的速度。
图4是原调节阀内流道压力分布云图,从图上可以看出,最低压力区出现在阀后区域,并且低压区面积较大,最低压力为–4.036×105Pa,此压力低于常温下的饱和蒸汽压力,因此阀后海水发生空化,诱发空化噪声。在调节阀前后高压差的作用下,海水介质经过阀门时,流通面积收缩导致海水流速迅速提高。由伯努利方程[6]可知,海水流速迅速增大伴随着海水压力的迅速降低,直到低于饱和蒸汽压力发生空化。海水介质流速过大、压力过低的原因是阀门阻力较小,在高压差的工况下,阀门开度较小就能满足工况的流量要求。图5为原阀内流道速度分布云图,在流通面积达到最小时,海水流速达到最大,分别位于阀芯进口处和阀芯出口处,最大值为47.93 m/s。
图6是原调节阀内流道湍动能分布云图,湍动能与流体介质的速率变化有关,能直接反映速率变化的快慢,湍动能高的部位说明流体速率变化的梯度比较大,速率变化梯度大容易形成强大的剪切层,强剪切层在大雷诺数流动中会失稳卷成漩涡,从而形成涡流噪声[7-8]。因此阀门设计时,应尽量使流道内流体介质流速均匀、平稳,这也是阀门降噪关注的重点。从湍动能云图可以看出,调节阀内流道最高湍动能为182.8 m2/s2,流速急剧变化的区域主要集中阀芯出口以及阀后区域。
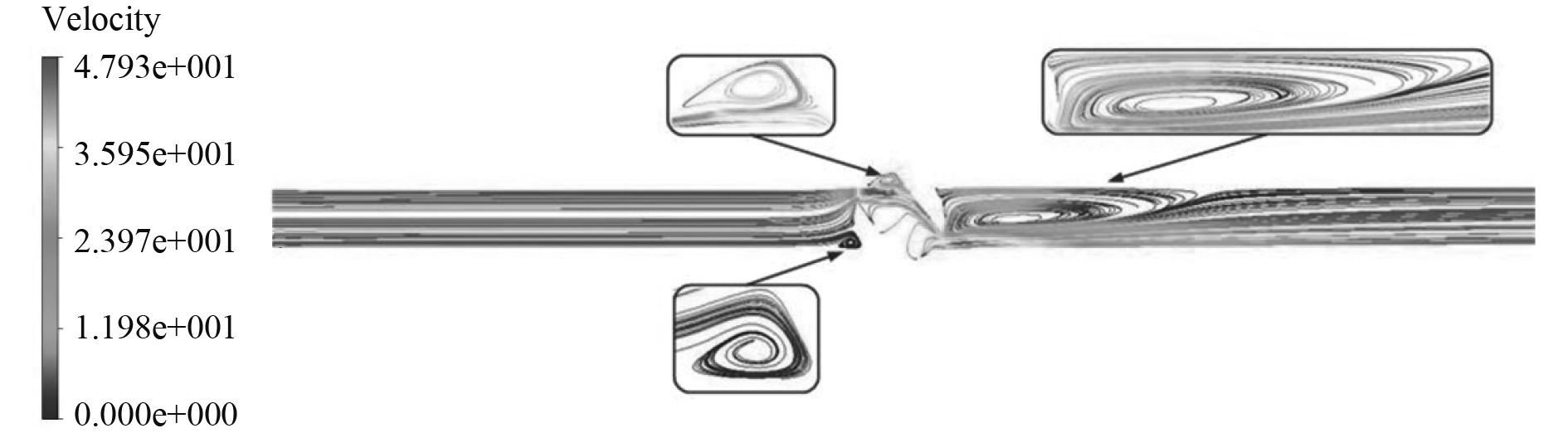
图7是原调节阀内流线图,从图中可以看出阀芯进口下缘、阀芯上缘以及阀芯出口下缘均出现局部漩涡结构,漩涡的出现对流场的稳定性造成影响,消除漩涡是阀门降噪的优化方向之一。

|
图 4 原阀内流道压力分布云图 Fig. 4 Pressure distribution nephogram of original valve flow-path |

|
图 5 原阀内流道速度分布云图 Fig. 5 Velocity distribution nephogram of original valve flow-path |

|
图 6 原阀内流道湍动能云图 Fig. 6 Turbulent kinetic energy distribution nephogram of original valve flow-path |
|
图 7 原阀内流道流线 Fig. 7 Streamline of original valve flow-path |
调节阀的节流过程可归结为在节流件的局部流阻上损耗能量,流体介质在阀门上的节流损失主要转化为摩擦耗能、热能、声能等。当阀门阻力系数一定时,相同工况下原阀门和优化后的阀门产生的水力功耗相同,因此流量调节阀的低噪声优化应着力于调整损耗能量的分配上,即尽量抑制水力能量向声能转化,减小声能在水利功耗中的整体占比。
一般而言,流量调节阀的水力设计方法主要有3种:结构法、射流法和粘滞阀[9]。
1)结构法是通过构造调节阀通流部分的结构使工作液体流向受到结构改变而损耗能量,常见的构造结构类型有突然扩张、转弯、阻碍等,本文中的流量调节阀原流道结构即为此类。
2)射流法是利用主流面积与节流面积之间的差异引起速度聚变从而达到损耗能量的目的。工作液体进入节流口和流出节流口时都伴随着射流压降损失。
3)粘滞法是使调节阀内的工作液体与调节阀通流部分的内壁面产生粘性摩擦进而损耗水力能量。为满足节流件的阻力系数,一般会选择增大调节阀流道内的通流面积。粘滞法的设计思路可提高摩擦耗能、热能在水力损耗中的占比,抑制损耗能量向声能和振能转化。
根据上节调节阀内流道流场分析可知,原流量调节阀流噪声突出的主要原因为:大流量工况下,阀门开度较小,流体流速较高形成射流,且开度较小时阀芯与主流间夹角太小,导致流体突然转向,增加流场的不稳定性,速率梯度较大,诱发阀芯前后漩涡的形成,射流和漩涡均导致能量损耗向声能集中。
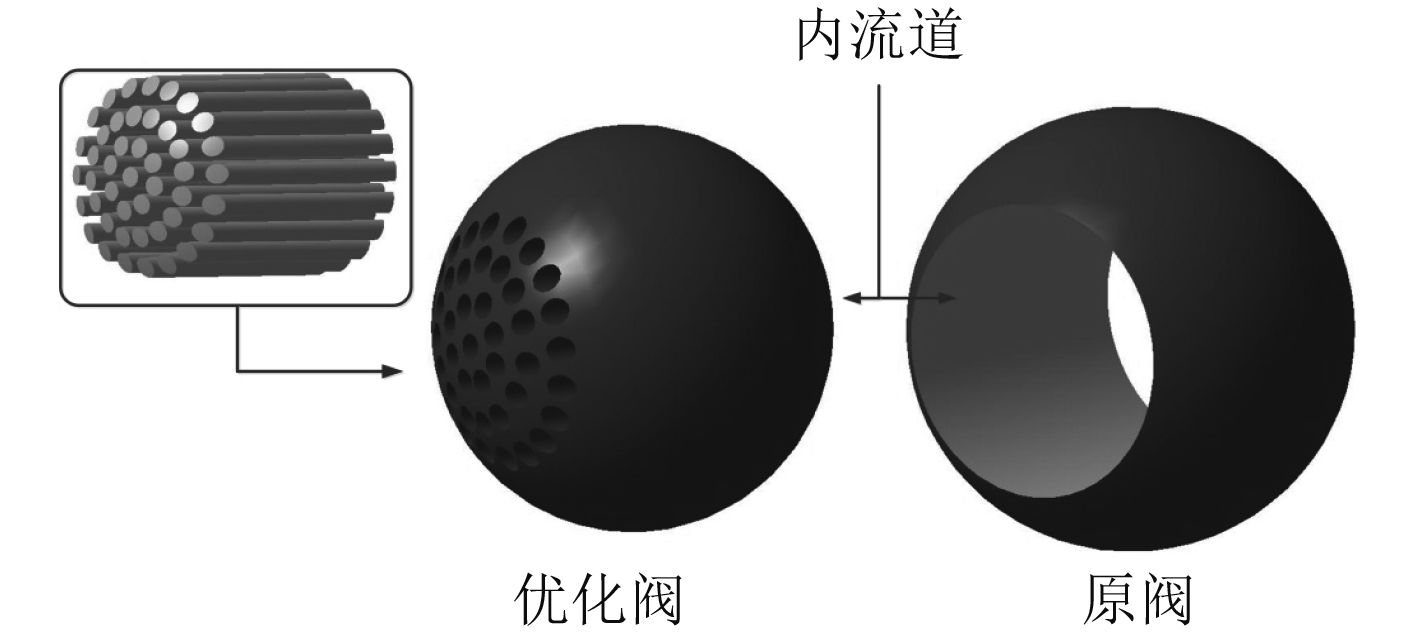
本文基于粘滞法,提出对原阀内流道进行分割的优化设计方案,将阀芯大通径单流道改进为小通径多流道,增大工作液体与通流内壁面的摩擦面积,提高摩擦耗能在水力能量损耗中的占比,相应减小声能占比,因此流噪声可得到抑制。优化后的阀芯通流面积减小,所以相同阻力系数下,优化后的阀门开度也会相应增大,阀芯与主流夹角变小,可避免流体突然大角度转向引起流动不稳定。优化结构模型如图8所示。
|
图 8 原阀和优化阀球体模型 Fig. 8 Original valve and optimized valve sphere model |
在相同工况下对优化后的流道流场进行数值计算,流量调节阀的开度由数值试验确定,保证计算模型与原阀内流道计算模型具有相同的阻力系数。
优化流道压力分布如图9所示,从图中可以看出优化流道中最低压力为–0.21 MPa,相对于原阀的最低压力–0.40 MPa有所提高,阀后低压区面积大幅减小,海水的空化现象得到有效抑制。由图10可知,优化流道的最大流速由47.93 m/s降到43.22 m/s,流道内整体的流速下降说明优化流道摩擦面积增大,阀门内流体介质受到的阻力增大,水力耗能中摩擦耗能占比增加,声能占比减小,并且流速降低的同时湍流强度会随之降低,相应湍流噪声强度降低。
优化流道的湍动能分布如图11所示,从图中可以看出最高湍动能为156 m2/s2,相对于优化前的阀门最高湍动能182.8 m2/s2明显下降,说明阀门优化流场参数分布更均匀,流速的变化更加平稳,湍动能的降低意味着流噪声得到很好的抑制。
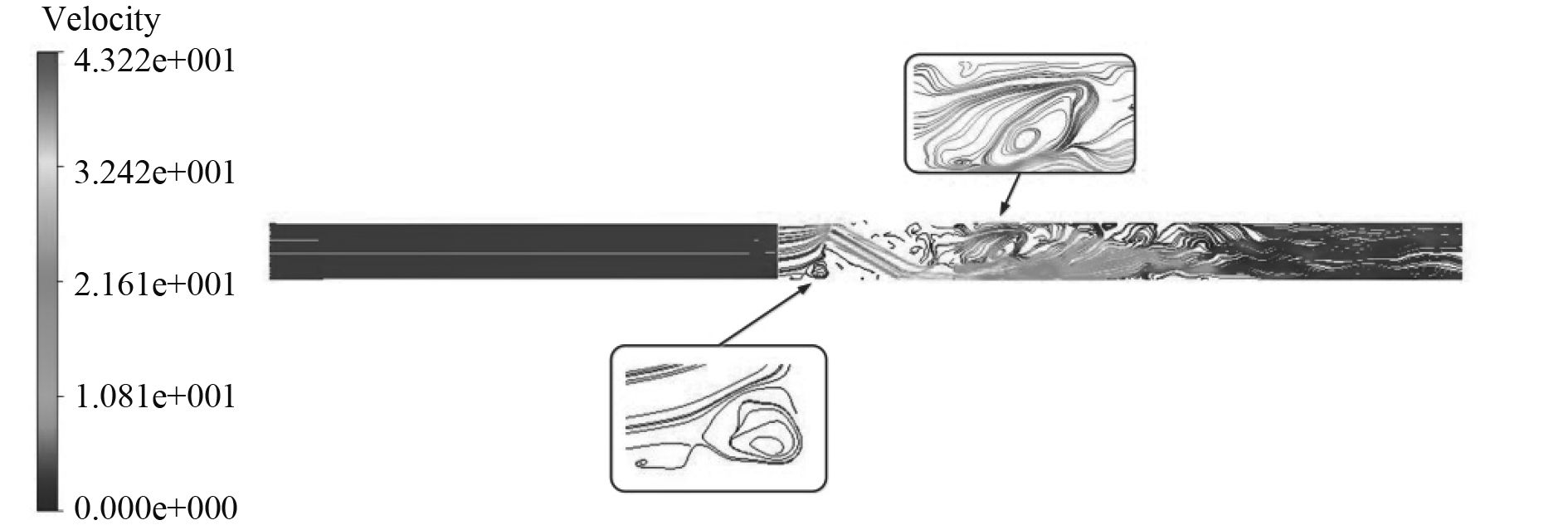
优化流道的流线如图12所示,从图中可以看出流道优化后阀芯进口下缘和阀芯后部的漩涡范围和强度均有所减小,阀芯内部的漩涡由于流道被分割得到完全地消除,因此优化流道后调节阀的涡流噪声得到抑制,低噪声优化效果明显。

|
图 9 优化流道压力分布云图 Fig. 9 Pressure distribution nephogram of optimized valve flow-path |

|
图 10 优化流道速度分布云图 Fig. 10 Velocity distribution nephogram of optimized valve flow-path |

|
图 11 优化流道湍动能云图 Fig. 11 Turbulent kinetic energy distribution nephogram of optimized valve flow-path |
|
图 12 优化流道流线图 Fig. 12 Streamline of optimized valve flow-path |
本文采用计算流体力学方法对流量调节阀的内流道流场进行分析,基于流场分析结果,提出了分割流道的低噪声优化设计方案,并对优化后的流道流场进行仿真计算,得出以下结论:
1)高压差工况下,由于阀门的节流作用,阀芯出口处流体压力迅速降低,低于饱和蒸汽压力,阀后局部发生空化,引起空化噪声;阀门流道结构突变引起流体流速变化不均匀,剪切层失稳在阀芯前后及内部卷成漩涡,形成涡流噪声。
2)通过对调节阀内流道进行分割优化设计,以小通径、多流道代替大通径、单流道,使阀门内流道摩擦面积增大,摩擦耗能在水利损耗中占比增加,减小了水力能量向声能的转化;优化后的流道最大流速降低,最低压力提高,湍动能下降,流道内流体流动更平稳,阀门流噪声得到有效抑制,优化方案为流量调节阀的低噪声优化设计提供了参考方向。
| [1] |
颜凌云, 武鹏飞, 包宗贤, 等. 纯水溢流阀的噪声控制研究[J].液压与气动, 2012(3): 23-25.
YAN Ling-yun, WU Peng-fei, BAO Zong-xian, et al. Noise control of water hydraulic relief valve[J].Chinese Hydraulics and Pneumatics, 2012(3):23-25. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU201108003002.htm |
| [2] |
刘进, 阎兆立, 程晓斌, 等. 基于空化辐射噪声的检测方法实验研究[J].应用声学, 2014, 33(1): 60-65.
LIU Jin, YAN Zhao-li, CHENG Xiao-bin, et al. Experimental research on pump cavitation detection dased on acoustic radiation[J].Journal of Applied Acoustics, 2014, 33(1):60-65. |
| [3] |
刘翠伟, 李玉星, 王武昌, 等. 输气管道气体流经阀门气动噪声产生机理分析[J].振动与冲击, 2014, 33(2): 152-157.
LIU Cui-wei, LI Yu-xing, WANG Wu-chang, et al. Analysis on the mechanism of aero-acoustics noise generated by gas flow through valves of natural gas pipelines[J].Journal of Vibration and Shock, 2014, 33(1):60-65. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_zdycj201402029 |
| [4] |
李树勋, 丁强伟, 徐晓刚, 等. 超(超)临界多级套筒调节阀空化抑制模拟研究[J].华中科技大学学报(自然科学版), 2015, 43(3): 37-41.
LI Shu-xun, DING Qiang-wei, XU Xiao-gang, et al. Numerical study on cavitation suppression in ultra-supercritical multistage sleeve control valve[J].Journal of Science and Technology (Nature Science Edition), 2015, 43(3):37-41. http://d.wanfangdata.com.cn/Periodical_hzlgdxxb201503008.aspx |
| [5] | BINOD K S, HIMADRI C, PRADIPTA B M, et al. Dynamic simulation of a pressure regulation and shut-off valve[J].Computer and Fluid, 2014, 101(20): 233-240. |
| [6] |
吴克启, 舒朝晖.高等流体力学[M]. 北京: 中国电力出版社, 2009.
WU Ke-qi, SHU Chao-hui. Advanced Fluid Mechanics[M]. Beijing: China Electric Power Press, 2009. |
| [7] |
许玮健, 靳国永, 王雪仁, 等. 阀门管路系统声传播特性仿真分析[J].声学技术, 2015, 34(4): 153-156.
XU Wei-jian, JIN Guo-yong, WANG Xue-ren, et al. Simulation analysis of acoustics propagation of piping system with valve[J].Technical Acoustics, 2015, 34(4):153-156. |
| [8] |
刘少刚, 刘海丰, 舒海生, 等. 通海阀内流道优化降低流噪声[J].哈尔滨工程大学学报, 2013, 34(4): 511-516.
LIU Shao-gang, LIU Hai-feng, SHU Hai-sheng, et al. Flow noise reduction of outboard valves based on internal flow path optimization[J].Journal of Harbin Engineering University, 2013, 34(4):511-516. http://www.cqvip.com/QK/92273A/201304/45974643.html |
| [9] |
何涛, 王秋波, 王锁泉, 等. 低噪声迷宫式控制阀设计原理及数值分析[J].船舶力学, 2017, 21(2): 127-137.
HE Tao, WANG Qiu-bo, WANG Suo-quan, et al. Low noise design principle and numerical analysis on labyrinth control valves[J].Journal of Ship Mechanics, 2017, 21(2):127-137. |
 2018, Vol. 40
2018, Vol. 40
