波形膜盘联轴器是在膜片和膜盘联轴器基础上进行研发的一种新型挠性联轴器,其核心元件为高强度高韧性不锈钢膜盘组(见图1)。联轴器的传递扭矩及补偿各种不对中功能均是通过波形膜盘的弹性变形实现的,故波形膜盘的受力分析是波形膜盘联轴器的设计关键[1 – 2]。而膜盘型线过渡圆角的设计直接关系到整个膜盘薄弱点的分布,因此有必要对波形膜盘型线过渡圆角进行设计优化,以改善膜盘的受力分布,增大联轴器的安全系数。
|
图 1 波形膜盘组 Fig. 1 Waveform diaphragm unit |

|
图 2 波形膜盘型线图 Fig. 2 Waveform diaphragm molded lines |
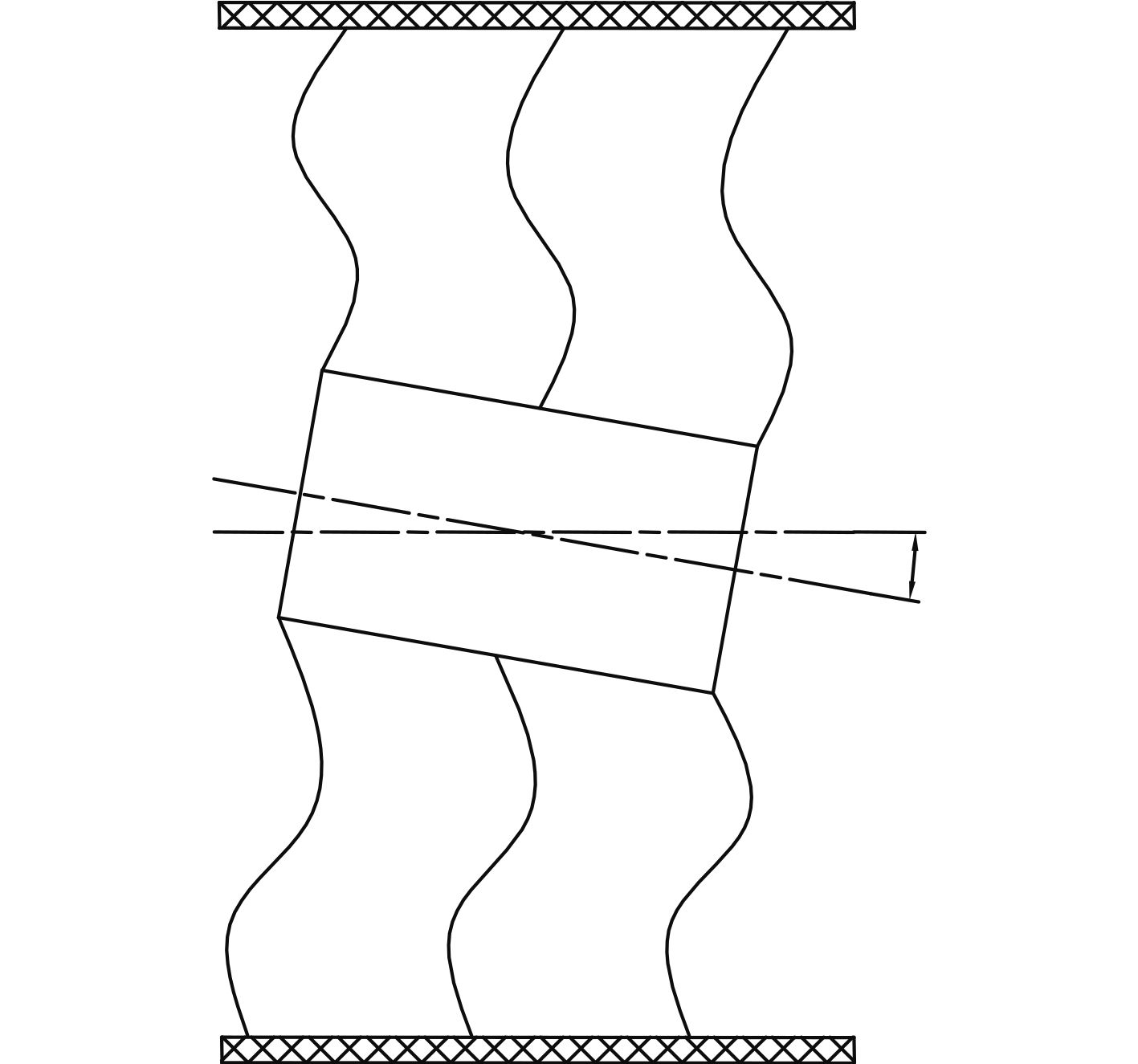
波形膜盘的型线部分为一个周期的正弦曲线(见图2),而两端的轮缘与轮毂为等厚直线,由于型线部分相对于轮毂及轮缘较薄,更容易变形,因此型线部分的设计是整个膜盘设计的关键。将多片波形膜盘叠合在一起形成波形膜盘组件,通过膜盘型线部分的三维变形来传递扭矩以及补偿机组在运行过程中出现的各种不对中现象[3 – 4]。
以西气东输项目燃压机组中所用的波形膜盘联轴器为例。波形膜盘组件由12件波形膜盘叠合而成,膜盘轮毂与轮缘均为1.2 mm厚,而型线部分为一个完整周期的正弦曲线,具体参数为X=–4sin(0.108 331×(Y–104)),其中Y∈(104,157.5),即膜盘型线内半径为104 mm,型线外半径为157.5 mm,厚度为0.4 mm。膜盘联轴器的额定功率为25 000 kW,转速5 200 r/min,轴向补偿2.5 mm,角向补偿0.25°。
2 波形膜盘过渡圆角初步设计及分析根据普通膜盘的设计经验,型线过渡处一般采用相切的圆弧进行平滑过渡,以达到减小应力集中的作用。因此首先将波形膜盘的过渡圆角设计为与型线末端相切的圆弧,如图3所示。
|
图 3 过渡圆角初步设计 Fig. 3 Preliminary design of transition fillet |
在Ansys软件内,应用APDL(Ansys参数化设计语言)进行参数化建模[5 – 6],采用PLANE25单元对膜盘进行四边形单元网格划分[7 – 8]。获得波形膜盘有限元模型如图4所示。

|
图 4 波形膜盘有限元模型 Fig. 4 FE model for waveform diaphragm |
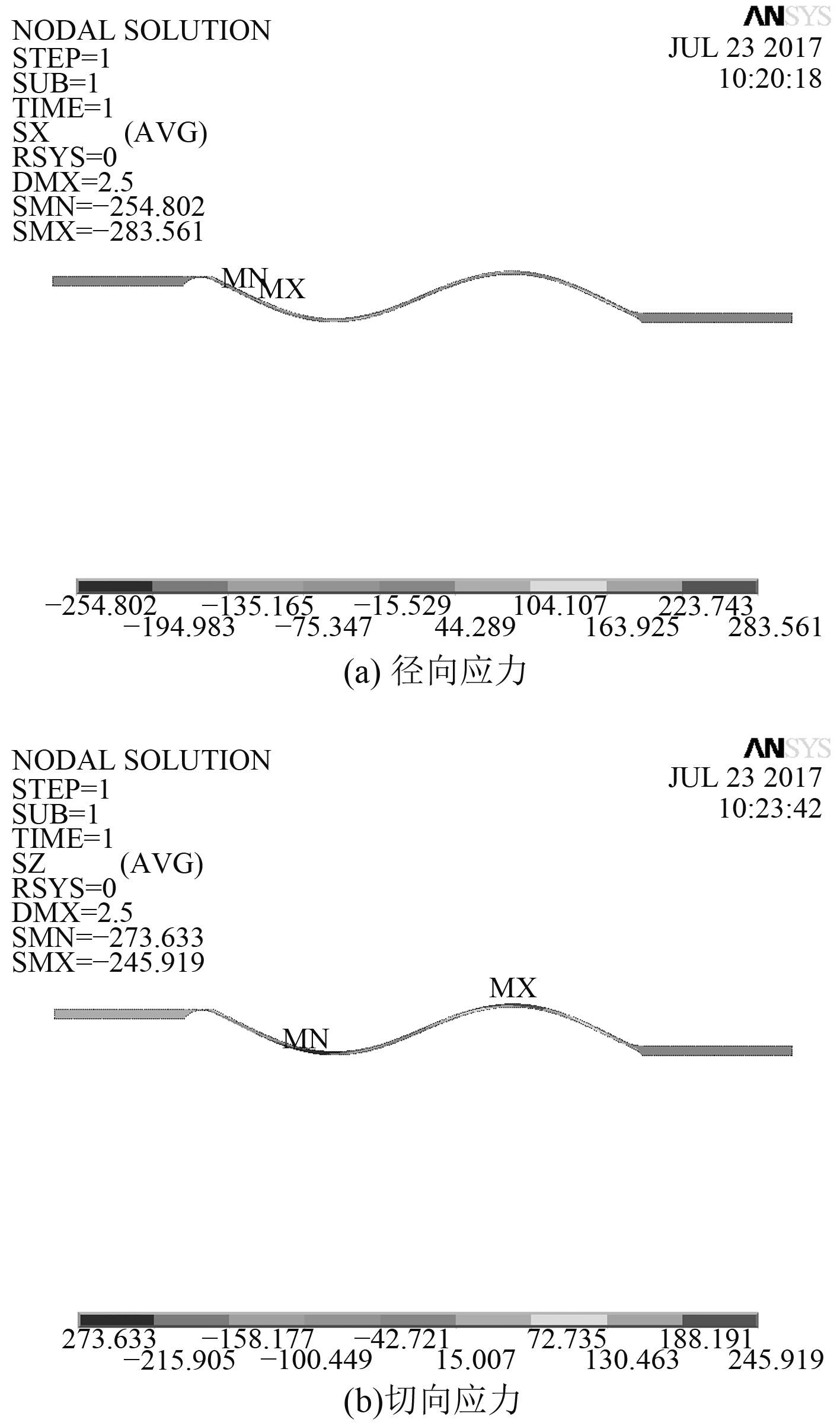
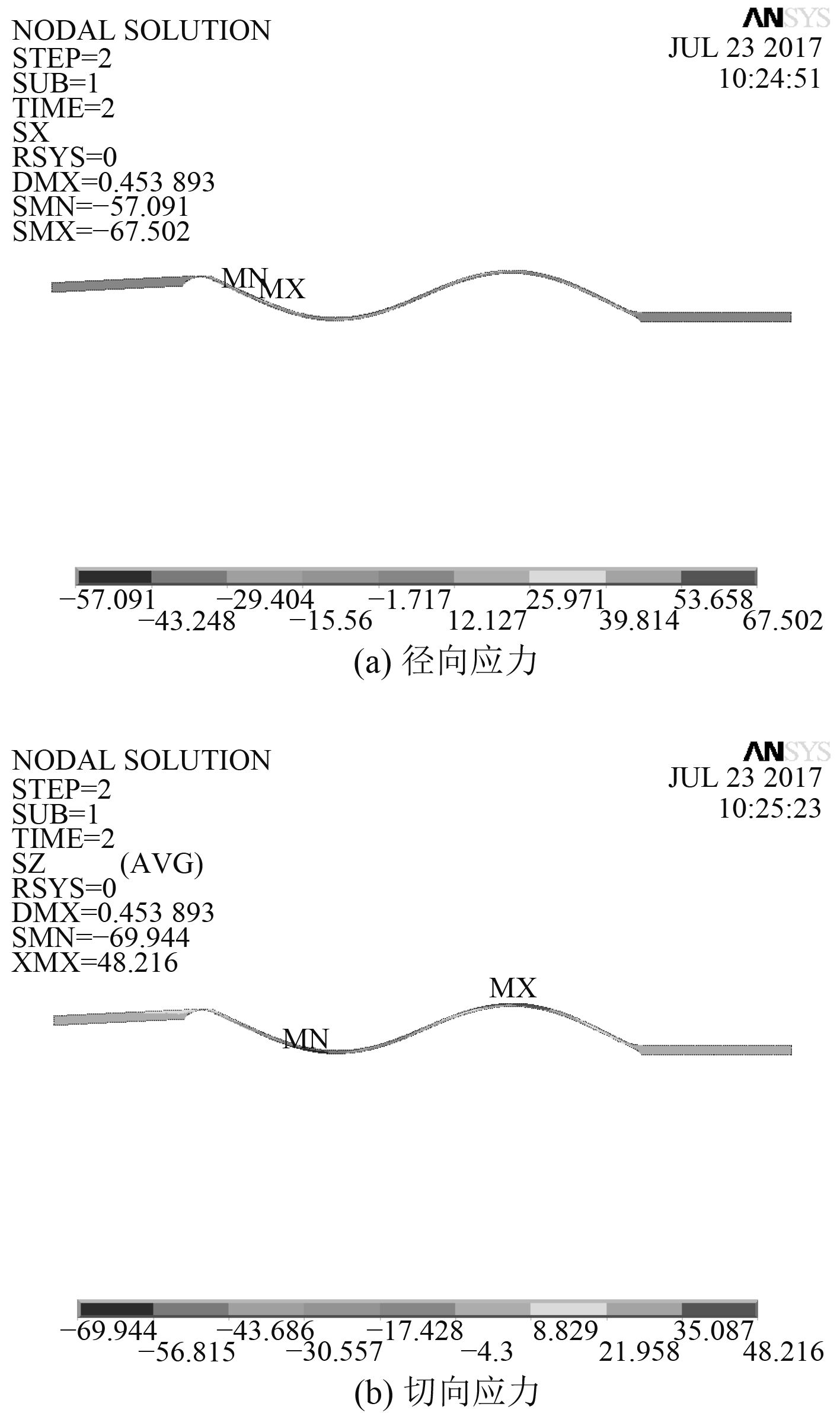
分别对波形膜盘有限元模型施加轴向载荷、角向载荷、离心力载荷和扭矩载荷,波形膜盘在不同载荷下的切向力、径向力及剪应力分布如图5~图8所示
|
图 5 轴向载荷下的应力分布 Fig. 5 Stress distribution at axial load |
|
图 6 角向载荷下的应力分布 Fig. 6 Stress distribution at angular load |
|
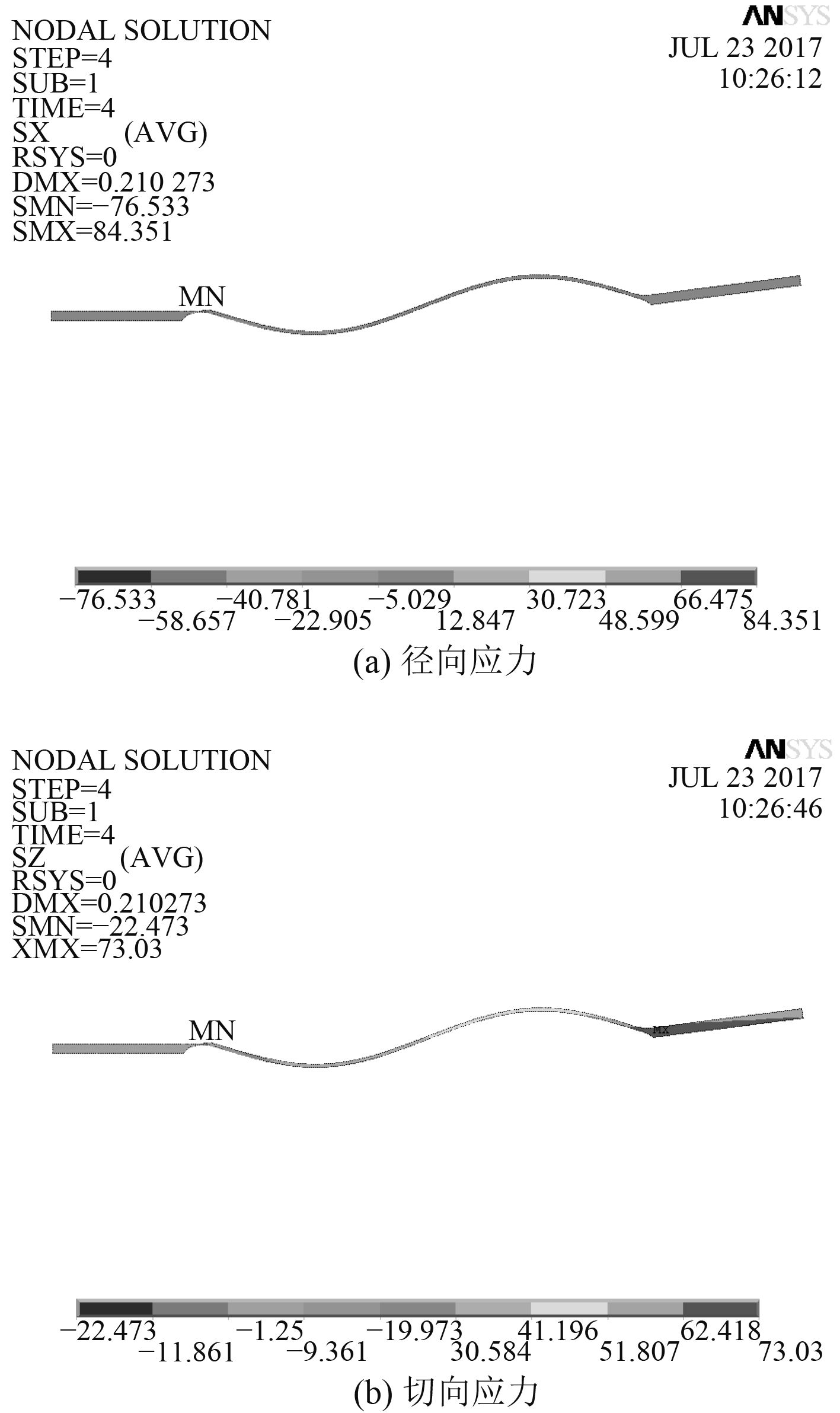
图 7 离心力载荷下的应力分布 Fig. 7 Stress distribution at centrifugal load |
|
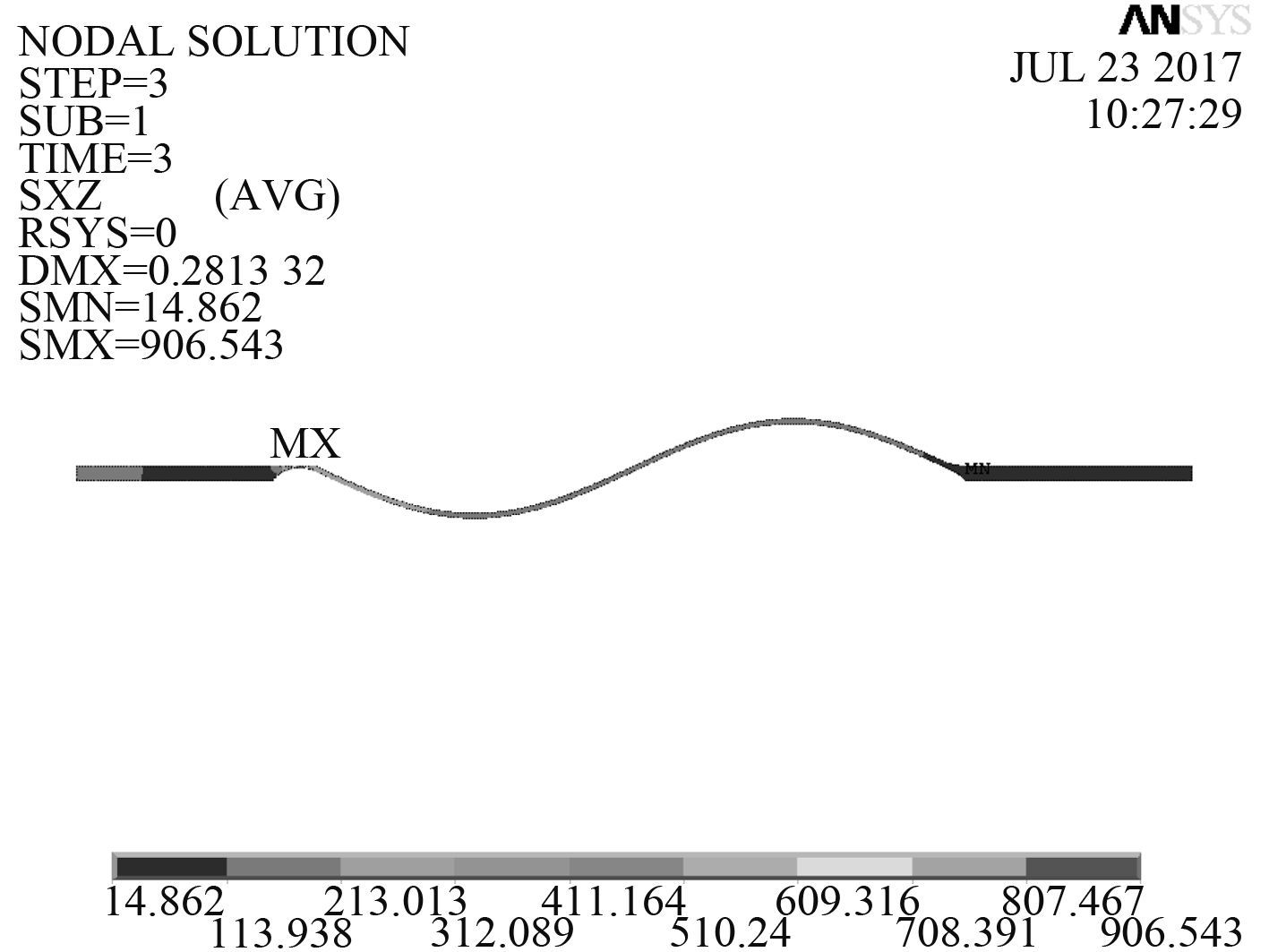
图 8 扭矩载荷下的剪应力分布 Fig. 8 Stress distribution at torque load |
经分析可知,波形膜盘在轴向载荷和角向载荷下的应力最大值均在型线内部,而在离心力载荷作用下的切向应力及径向应力虽然在型线的边缘处,但其应力值较小,不做特别关注。只有在扭矩载荷作用下的剪应力的最大值分布在型线内侧且应力值较大,故波形膜盘型线过渡圆角的优化设计主要是对波形膜盘型线与轮毂处的过渡圆角进行优化设计[9]。
3 波形膜盘过渡圆角优化设计不同过渡圆角时,在扭矩载荷作用下的最大剪应力如表1所示。
|
|
表 1 不同过渡圆角下的最大剪应力 Tab.1 Maximum shear stress at different transition fillet |
由图8及表1可知,在扭矩载荷作用下,波形膜盘的最大剪应力位于型线与轮毂的过渡圆角处,且圆角越小最大剪应力越小,越有利于波形膜盘的扭矩传递,但过渡圆角不能为0,否则也会造成较大的应力集中。
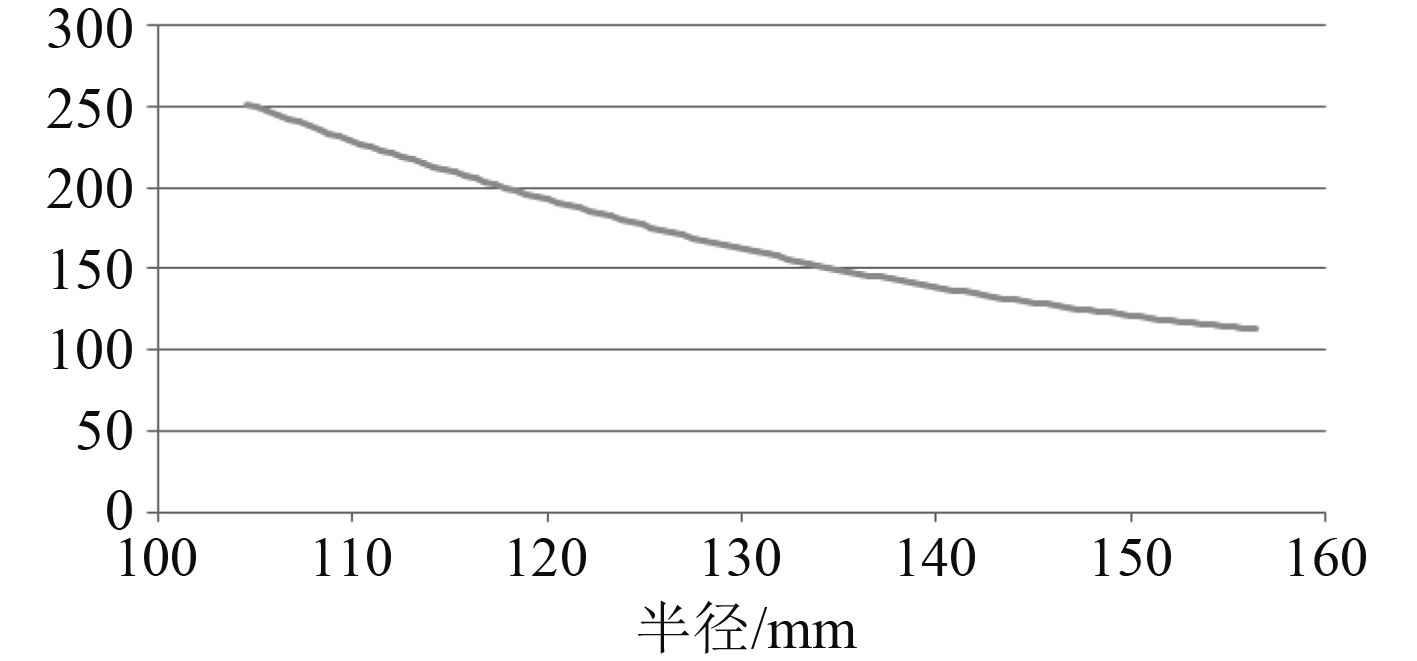
但是经研究发现,即使在过渡圆角为0.5时,膜盘的最大剪应力仍然位于过渡圆角处,以圆角半径为0.5 mm为例,此时型线部分剪应力分布如图9所示,最大剪应力为250.79 MPa,其远小于整个膜盘上的最大应力,即远小于过渡圆角处的最大应力,这与膜盘的设计准则并不相符。证明根据普通膜盘设计经验得到的相切过渡圆弧设计并不适合波形膜盘型线过渡圆弧的设计。
|
图 9 型线上剪应力分布 Fig. 9 Shear stress distribution on molded lines |
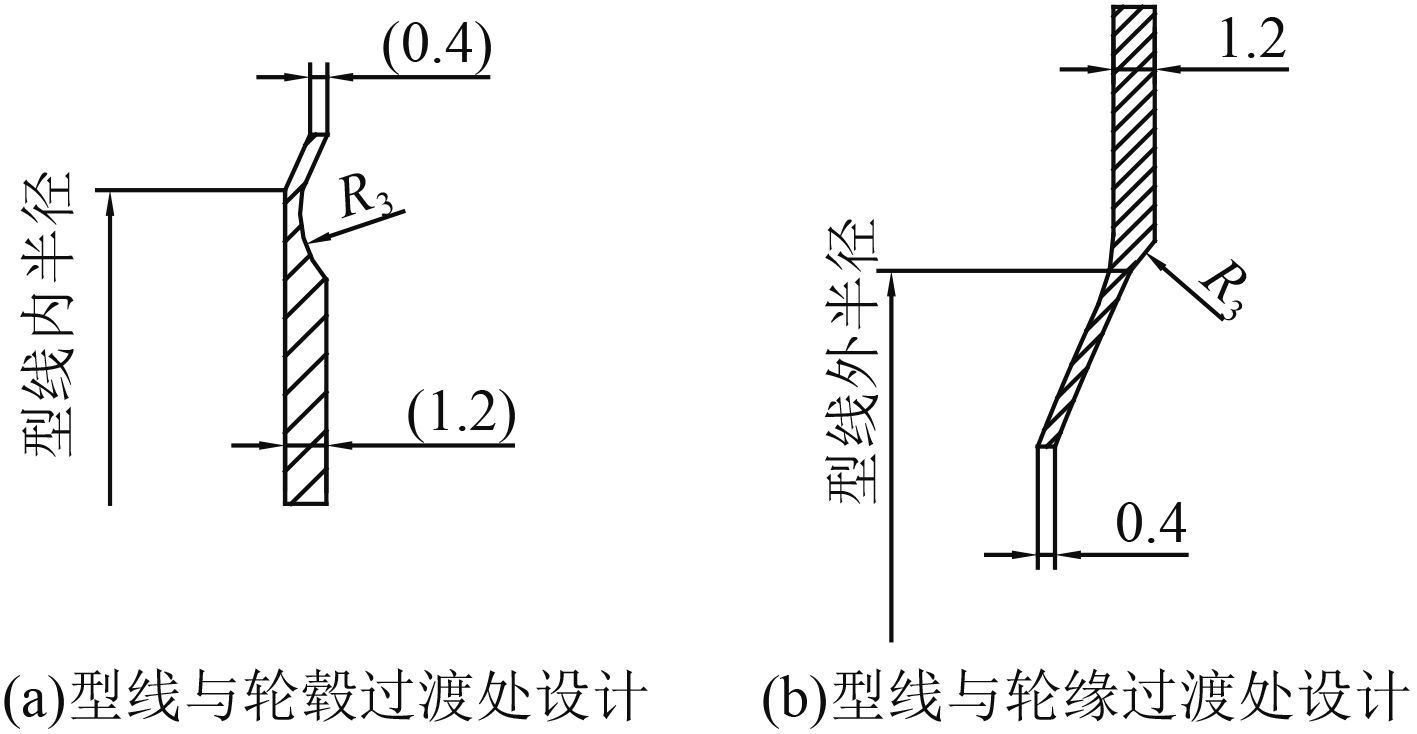
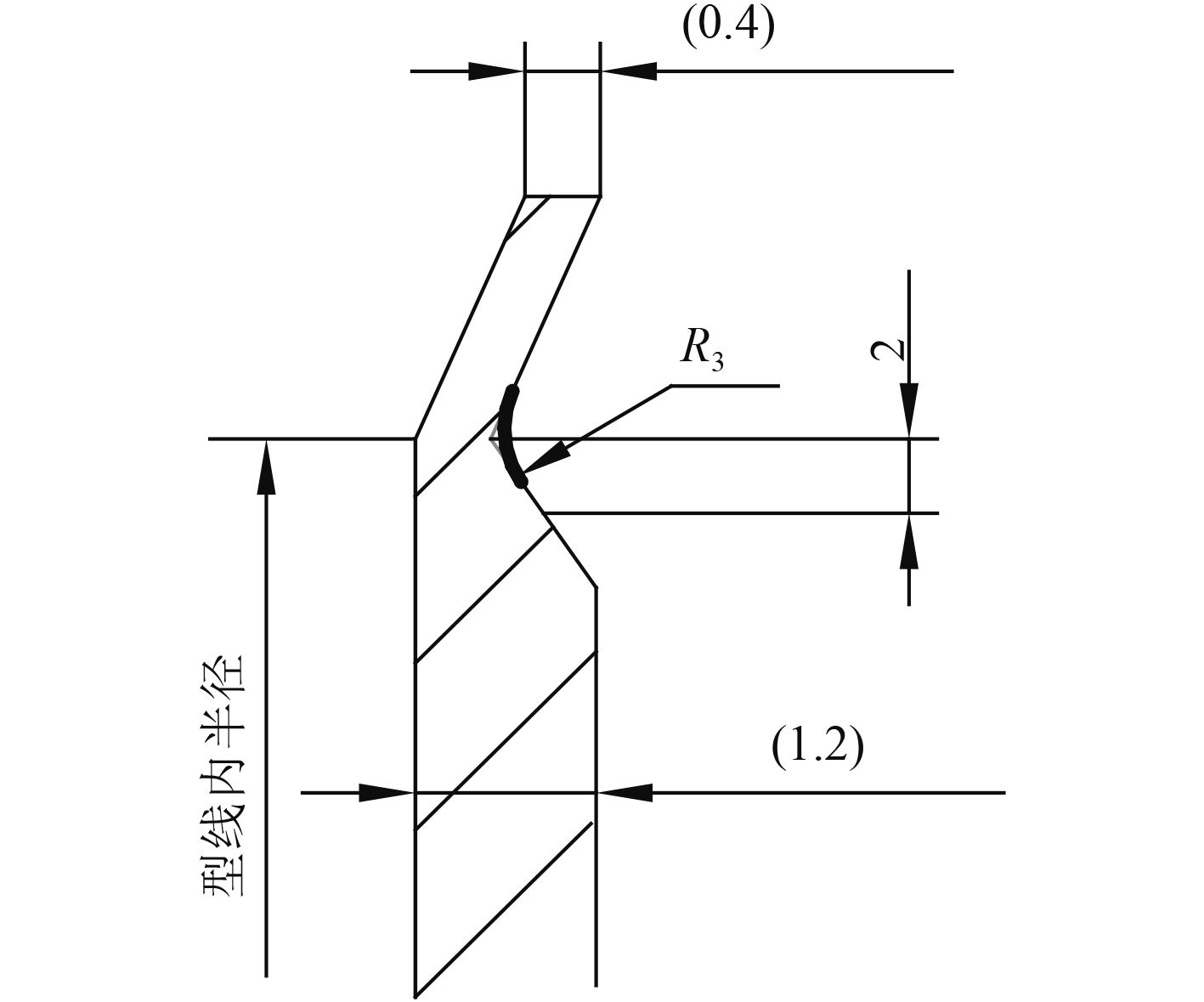
因此,将型线过渡处做如图10所示的改进设计。即在型线末端与轮毂处首先采用一定距离的斜线过渡,然后在斜线与型线的交汇处倒圆角。不同圆角半径下的最大剪应力如表2所示。
|
图 10 新型过渡圆角方案 Fig. 10 New transition fillet programme |
|
|
表 2 不同过渡圆角下的最大剪应力 Tab.2 Maximum shear stress at different Transition fillet |
对比表1和表2可知,新型过渡圆角可以更好地降低波形膜盘在扭矩载荷作用下的应力集中,从而增大联轴器的安全系数,保证联轴器的安全运行。
而表2各数据对比发现,除圆角半径为0时造成较大的应力集中外,随着圆角半径的增加,最大剪应力减小不大,但会增加型线部分膜盘的厚度,从而降低膜盘的变形能力,故在设计波形膜盘过渡圆角时建议根据实际情况采用1 mm或者2 mm为宜。
4 结 语本文通过建立波形膜盘的有限元模型,在传统膜盘联轴器设计经验的基础上提出了新型的适合波形膜盘的型线过渡圆角设计方案。通过不同方案的仿真对比,得出如下结论:
1)在型线末端与轮毂处首先采用一定距离的斜线过渡,然后在斜线与型线的交汇处倒圆角,可大大降低型线与轮毂过渡处的应力集中现象;
2)在理论分析上,过渡圆角越大越好,但随着圆角增大,其对最大剪应力的减小影响很小,故建议在设计波形膜盘过渡圆角时根据实际情况采用1 mm或者2 mm为宜。
| [1] | 高鹏. 膜片联轴器优化设计方法研究[J]. 机械工程师, 2015(10): 56–58. |
| [2] | 李波, 卢波, 刘翠平. n型结构膜盘联轴器型面设计与有限元分析[J]. 机电工程, 2016, 33(8): 955–959. |
| [3] | 岳彭, 赵宇, 刘欣欣. 不同型面膜盘特性分析[J]. 舰船科学技术, 2013(12): 83–87. |
| [4] | 方建敏. 双曲线型面膜盘联轴器疲劳寿命分析[C]//第六届中国航空学会青年科技论坛, 2014:443–446. |
| [5] | 邱兆国, 张凤鹏, 白景辉. 弹性膜盘联轴器盘面曲线的设计与有限元分析[J]. 机械设计与制造, 2010(7): 32–33. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jxsjyzz201007013 |
| [6] | 廖晖, 何玉林, 杜静. 联轴器的膜片强度疲劳有限元分析[J]. 机械与电子, 2008, Vol. 05, P227–231. |
| [7] | ANSYS. Inc. Ansys modeling and meshing guide[M]. ANSYS. Inc, 2004. |
| [8] | 刘霜, 王心丰. 基于ANSYS的挠性叠片联轴器的轴向不对中分析[J]. 机械 研究与应用, 2003, 16(3): 42–43. http://www.cqvip.com/QK/96761X/200303/8385147.html |
| [9] | 艾平贵, 朱如鹏. 基于ANSYS的膜盘联轴器膜盘的应力与模态分析[J]. 机械工程师, 2008(1): 124–125. http://www.cnki.com.cn/Article/CJFDTOTAL-JXGU200801063.htm |
 2018, Vol. 40
2018, Vol. 40
