0 引　言

低频回声隐身技术是当前水下战领域的一项关键技术，受到各个国家的重视。回声隐身技术可分为有源隐身技术和无源隐身技术。无源隐身技术主要包括外形设计法、吸声材料法^[1]，有源隐身技术主要途径包括有源对消^{[2 – 3]}和智能材料^{[4 – 5]}。有源对消隐身技术是在目标上装备有对消设备，根据入射声场和被保护目标的散射函数产生适合对消的声波，采用相干手段使目标散射场和人为引入的辐射场在敌方声呐探测方向相干对消，在声呐接收处与目标真实回波相抵消，从而减弱声呐接收到的真实回波，达到隐身效果。曲长文等^{[2 – 3]}研究了自由场中的对消波幅相条件及误差分析，从理论上指出舰船的散射特性需要考虑海洋背景对雷达波散射的影响。曹志华^[4]提出了在自由场中实现特定方向上雷达隐身所需的有源加载信号产生方法。然而，相关工作都是针对自由场或单界面上目标的雷达隐身进行有源对消分析，没有对浅海波导中目标回声有源对消隐身效果进行研究。

在浅海环境中，信道传输和目标散射之间存在强烈的耦合作用^[6]，导致接收位置的声波是直达波和来自波导表面和底部的多途反射的叠加，并非唯一的入射角和散射角。当此时有源对消隐身技术仅仅利用敌方声呐探测方向的目标散射函数来产生对消声场时，可能会导致隐身效果较差。本文的主要目的是对浅海环境中利用敌方声呐探测方向的散射函数构建对消声场的可行性进行分析。本文首先简单介绍了浅海中目标的散射声场、对消声场模型，然后，通过研究圆盘目标在不同浅海环境中的隐身效果，对有源对消的可行性进行分析。

1 浅海中目标散射及对消声场分析

考虑深H的浅海波导中目标对点声源的散射问题，假设波导中是不依赖距离的分层介质，目标位于等声速层中，声源和接收位于目标的远场。点声源和目标都不靠近波导的上下界面，它们在水下的深度分别为D₀和D。

以目标中心O为原点，z轴正轴垂直向下，建立圆柱坐标系O（ρ，φ，z）。浅海波导中点源的矢径为 $\overrightarrow {{{{r}}_0}} = \left( {{\rho _0},{\varphi _0},{z_0}} \right)$ ，场点的矢径 ${\vec{ r}} = \left( {\rho ,\varphi ,z} \right)$ 。其散射声场为^[7]

$\begin{split}& {p_s}({{r}}\left| {{{{r}}_0})} \right. = A\mathop \sum \limits_{m = 1}^M \mathop \sum \limits_{n = 1}^M \frac{{{{\left( {4\pi } \right)}^2}}}{k} \times [{A_m}\left( {{r}} \right){A_n}\left( {{{{r}}_0}} \right)\times\\ & S\left( {\pi - {\alpha _m},\beta ;\pi - {\alpha _n},{\beta _i}} \right) - {B_m}\left( {{r}} \right){A_n}\left( {{{{r}}_0}} \right)\times\\ & S\left( {{\alpha _m},\beta ;\pi - {\alpha _n},{\beta _i}} \right){\rm{}}- {A_m}\left( {{r}} \right){B_n}\left( {{{{r}}_0}} \right)\times\\& S\left( {\pi - {\alpha _m},\beta ;{\alpha _n},{\beta _i}} \right) + {B_m}\left( {{r}} \right){B_n}\left( {{{{r}}_0}} \right)S\left( {{\alpha _m},\beta ;{\alpha _n},{\beta _i}} \right)\text{。}\end{split}$

(1)

式中：

$\begin{array}{l}{A_m}\left( {{r}} \right) = \displaystyle\frac{i}{{d\left( 0 \right)}}\frac{1}{{\sqrt {8\pi {\xi _m}\rho } }}{u_m}\left( z \right)N_m^{\left( 1 \right)}{e^{i\left( {{\xi _m}\rho + {\gamma _m}D - \frac{\pi }{4}} \right)}}\text{，}\\{B_m}\left( {{r}} \right) = \displaystyle\frac{i}{{d\left( 0 \right)}}\frac{1}{{\sqrt {8\pi {\xi _m}\rho } }}{u_m}\left( z \right)N_m^{\left( 2 \right)}{e^{i\left( {{\xi _m}\rho - {\gamma _m}D - \frac{\pi }{4}} \right)}}\text{，}\\{A_n}\left( {{{{r}}_0}} \right) = \displaystyle\frac{i}{{d\left( {{z_0}} \right)}}\frac{1}{{\sqrt {8\pi {\xi _n}{\rho _0}} }}{u_n}\left( {{z_0}} \right)N_n^{\left( 1 \right)}{e^{i\left( {{\xi _n}{\rho _0} + {\gamma _n}D - \frac{\pi }{4}} \right)}}\text{，}\\{B_n}\left( {{{{r}}_0}} \right) = \displaystyle\frac{i}{{d\left( {{z_0}} \right)}}\frac{1}{{\sqrt {8\pi {\xi _n}{\rho _0}} }}{u_n}\left( {{z_0}} \right)N_n^{\left( 2 \right)}{e^{i\left( {{\xi _n}{\rho _0} - {\gamma _n}D - \frac{\pi }{4}} \right)}}\text{，}\end{array}$

分别为入射和散射的下行、上行平面波分量的幅度。A为声源幅度；d（z）为深度z处的密度；u_n（z）为简正波深度函数； $S\left( {\alpha ,\beta ;{\alpha _i},{\beta _i}} \right)$ 为目标平面波散射函数；其中 $({\alpha _i},{\beta _i})$ 为入射声源方位，（α，β）为场点空间方位；M为简正波的数目。第n阶模态的水平和垂直波数分量分别为 ${\xi _n} = k\sin {\alpha _n}$ ， ${\gamma _n} = k\cos {\alpha _n}$ 。k为波数。简正波的深度函数可写为上行、下行的平面波分量表达形式：

${u_n}\left( z \right) = N_n^{\left( 1 \right)}{e^{i{\gamma _n}\left( {z + D} \right)}} + N_n^{\left( 2 \right)}{e^{ - i{\gamma _n}\left( {z + D} \right)}}\text{。}$

(2)

其中： $N_n^{\left( 1 \right)}$ 和 $N_n^{\left( 2 \right)}$ 为第n阶简正波上行、下行的平面波分量的幅度。

式（1）可应用于浅海波导中刚性、绝对软、阻抗边界等目标的散射声场计算。由于浅海波导中目标的存在，每一个入射的简正波都转化为能够存在的所有M阶简正波。M阶简正波会产生4M²的散射分量，浅海波导中目标散射和声传播是耦合的，但每一入射、散射平面波对的传播和目标散射是解耦的。

在波导条件下，目标声中心处接收到的入射声场为^[8]：

${p_i}\left( {0\left| {{{{r}}_0}} \right.} \right) = \frac{i}{{d\left( {{z_0}} \right)}}\sqrt {\frac{{2\pi }}{{{\xi _n}{\rho _0}}}} \mathop \sum \limits_{n = 1}^M {u_n}\left( 0 \right){u_n}\left( {{z_0}} \right){e^{i\left( {{\xi _n}{\rho _0} - \frac{\pi }{4}} \right)}}\text{，}$

(3)

利用式（2）和式（3），可将入射声场写为

${p_i}\left( {0\left| {{{{r}}_0}} \right.} \right) = 4\pi A\mathop \sum \limits_{n = 1}^M [{A_n}\left( {{{{r}}_0}} \right) - {B_n}\left( {{{{r}}_0}} \right)]\text{。}$

(4)

当仅仅利用敌方声呐探测方向的散射函数来实现有源对消技术时，需接收到入射信号的同时，即在目标声中心处发射 $ - {p_i}\left( {0\left| {{r_0}} \right.} \right)*S\left( {\alpha ,\beta ,{\alpha _i},{\beta _i}} \right)/k$ 的对消信号，则空间任意一点r处接收到的对消声场为：

$\begin{split}& {P_d}\left( {{{r}}{\rm{|}}{{{r}}_0}} \right) = - A{\left( {4\pi } \right)^2}\left( {\mathop \sum \limits_{n = 1}^M [{A_n}\left( {{{{r}}_0}} \right) - {B_n}\left( {{{{r}}_0}} \right)]} \right)\times\\ & \left( {\mathop \sum \limits_{m = 1}^M [{A_m}\left( {{r}} \right) - {B_m}\left( {{r}} \right)]} \right)\frac{{S\left( {\alpha ,\beta ,{\alpha _i},{\beta _i}} \right)}}{k}\text{，}\end{split}$

(5)

隐身效果可表示为：

$T = 20\lg \left| {\frac{{\Delta p\left( {{{r}}{\rm{|}}{{{r}}_0}} \right)}}{{{p_S}\left( {{{r}}{\rm{|}}{{{r}}_0}} \right)}}} \right|\text{，}$

(6)

式中： $\Delta p = {p_S} + {p_d}$ ，为对消余场^[9]。其决定于目标散射声场与对消声场的幅度差 $\Delta B = 20\lg \left| {\frac{{{p_S}}}{{{p_d}}}} \right|$ 和相位差∆φ。隐身效果可进一步表示为

$T = 10\lg \left| {1 + {{10}^{\left( {\frac{{ - \Delta B}}{{10}}} \right)}} + 2 \times {{10}^{\left( {\frac{{ - \Delta B}}{{20}}} \right)}}\cos\left( {\Delta \varphi } \right)} \right|\text{。}$

(7)

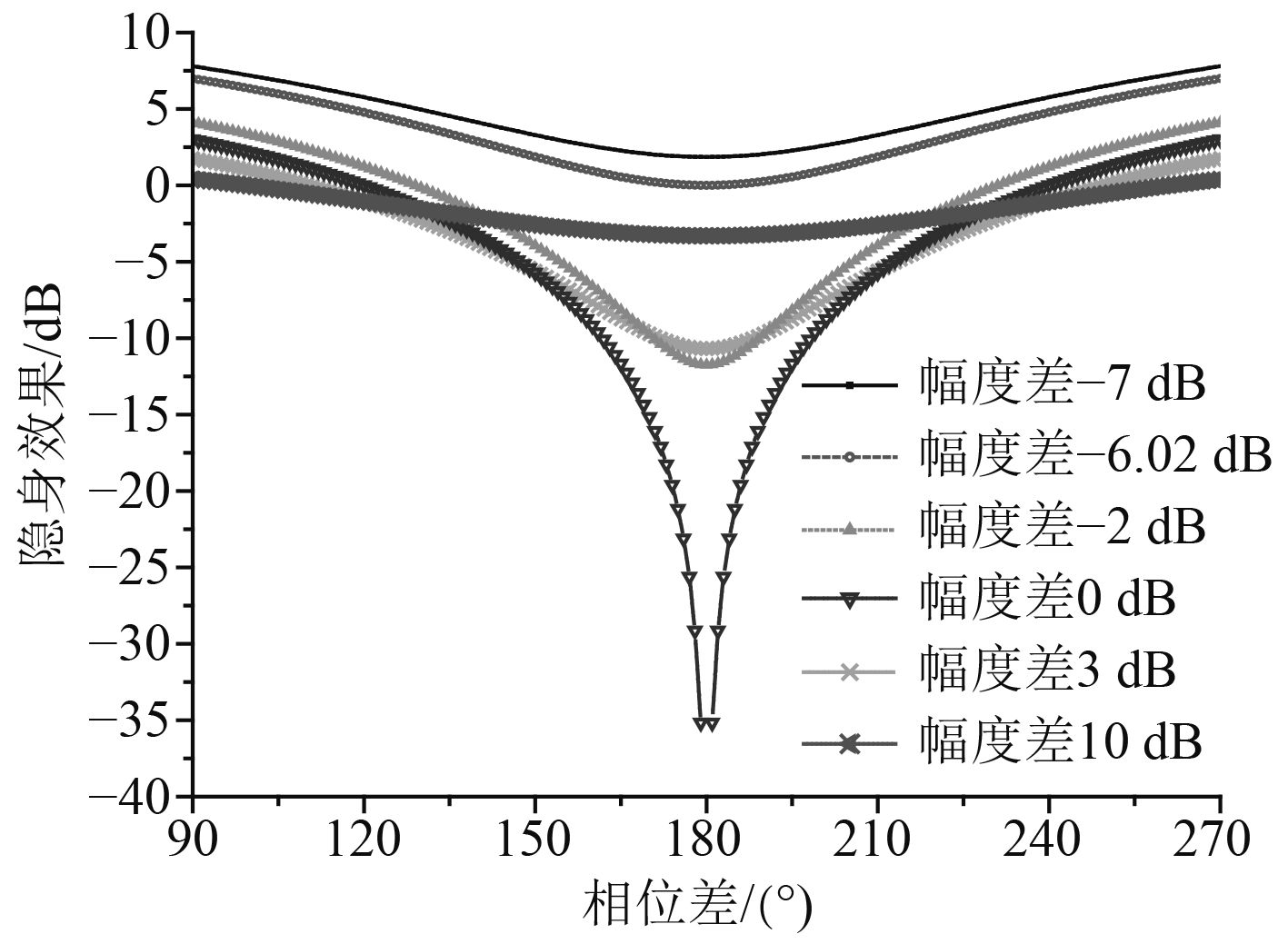
目标散射与对消声场之间的幅度差和相位差对隐身效果的影响如图1所示，从图中可以看出，当幅度差小于–6.02 dB时，即使相位差满足（2n+1）π的最佳对消条件，但由于幅度差太小仍会使T>0，对隐身起反作用。随着幅度差逐渐增加，为使隐身效果保持低于0 dB，对相位差要求越来越低，但这是以降低最大隐身能力为代价的。如幅度差达到10 dB时，相位差允许在最佳对消条件的基础上起伏80°，但由于幅度差太大，最佳隐身效果才–3.3 dB。

从式（5）可以看出，波导中接收到的对消声场显著不同于波导中的目标散射声场。波导中的目标散射声场随入射、散射简正波模态的方向变化。在对消声场模型中，由于假定传播和散射是解耦的，对消声场只依赖于声源和接收相对目标的方位，与入射、散射简正波模态的方向无关。但当目标的收发分置散射函数在给定波导模态的水平掠入射角范围内约是常数时，式（1）与式（5）误差较小，隐身效果可能较好。

波导模态的水平掠入射角范围可表示为

$\pm \Delta {\rm{\varPsi }} = \pm \left( {\frac{\pi }{2} - {\alpha _{{}_N}}} \right)\text{。}$

(8)

式中： ${\alpha _{{}_N}} = {\tan ^{ - 1}}\left( {\displaystyle\frac{{{\xi _{{}_N}}}}{{{\gamma _{{}_N}}}}} \right)$ 。这里，N定义为在给定接收深度上，与波导中所有模态和得到的散射声压小于1 dB时的最少模态数。因此，N和ΔΨ是随距离变化的，一般是随距离减小，直到模态剥离。

2 浅海中有源对消可行性分析

下面对浅海环境中利用敌方声呐探测方向的目标散射函数构建对消声场的可行性进行分析。假设浅海水深60 m，均匀水层密度1 000 kg/m³，声速1 500 m/s. 海底为粘土或细沙构成的无限大半空间。粘土密度1 420 kg/m³，声速1 520 m/s，衰减0.075 dB/（km·Hz）。细沙密度1 900 kg/m³，声速1 700 m/s，衰减0.2 dB/（km·Hz）。声源与接收合置，与目标都位于水下30 m深度上，声源级0 dB（1 m处参考声压1 μPa）。目标采用圆盘。圆盘有不均匀的散射函数^[6]，后向–3 dB主瓣波束宽度为λ/L（λ为波长，L为圆盘直径）。

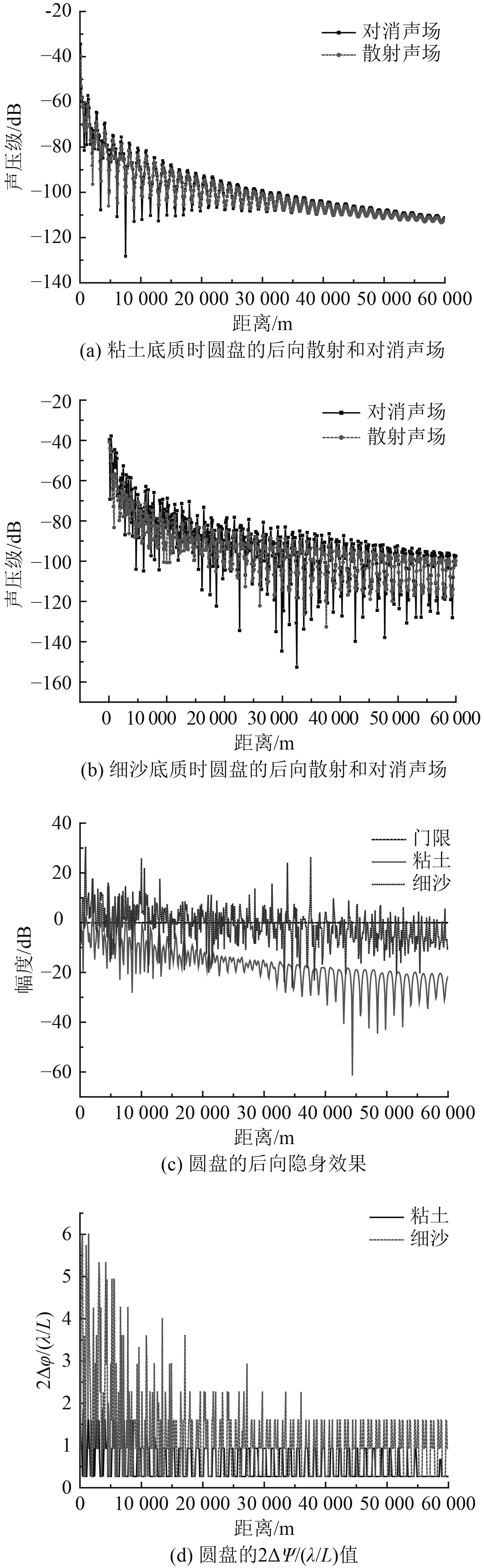
2.1 底部介质对有源对消可行性的作用

当半径10 m的刚性圆盘竖直放置在不同底质的Pekeris波导中，500 Hz声呐信号垂直于圆盘平面入射时，后向接收到的目标散射声场和对消声场、隐身效果分析如图2所示。从图中可以看出，散射声场、对消声场和2ΔΨ/（λ/L）都随距离起伏，且整体趋势都是随距离增加起伏逐渐减小。在粘土底质pekeris波导中，在距离10 km后，2ΔΨ/（λ/L）值小于1，后向隐身效果都在门限值以下，特别随距离进一步增大到20 km后，有10 dB以上的隐身效果；而在细沙底质pekeris波导中，即使距离60 km，2ΔΨ/（λ/L）值仍大于1，出现对隐身起反作用的情况。但随着距离增大，2ΔΨ/（λ/L）逐渐减小，可看出散射与对消声场幅度差也逐渐减小，隐身效果也向好的趋势发展。

对于同样的声呐频率、目标尺寸，粘土底质比细沙底质更有利于有源对消的使用。这是因为在距离大于几个波导深度后，ΔΨ限制在底部介质的临界掠入射角范围内，粘土和细沙的临界掠入射角分别为9.3°、28°，因此粘土比细沙有更小的简正波阶数、ΔΨ和2ΔΨ/（λ/L），导致粘土底质中散射声场与对消声场的幅度差和相位差小。随着距离的增加，对隐身起反作用的情况会消失。这是由于随着距离变远，起作用的简正波阶数变小，2ΔΨ/（λ/L）值会小于1。

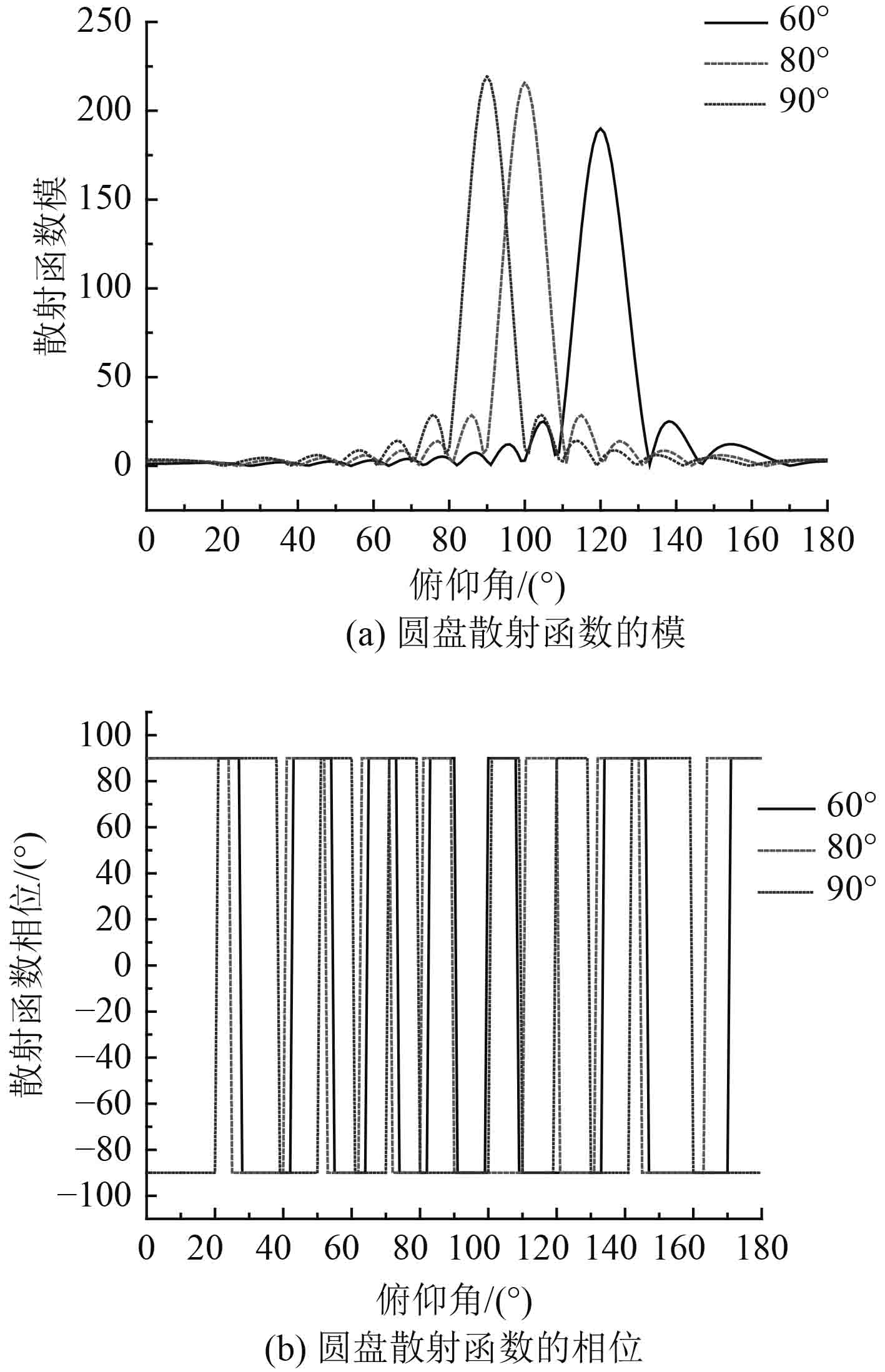
半径10 m的竖放刚性圆盘，500 Hz单频信号从β_i=0垂直圆盘平面方位以不同俯仰角α_i=60°，80°，90°入射时，散射函数S（α，β=0；α_i，β_i=0）如图3所示。从图中可以看出，正横入射时的主瓣总是最窄瓣，–3 dB主瓣宽度为λ/L，为8.6°。散射函数主瓣中的相位是常数。

2.2 目标尺寸和频率对有源对消可行性的作用

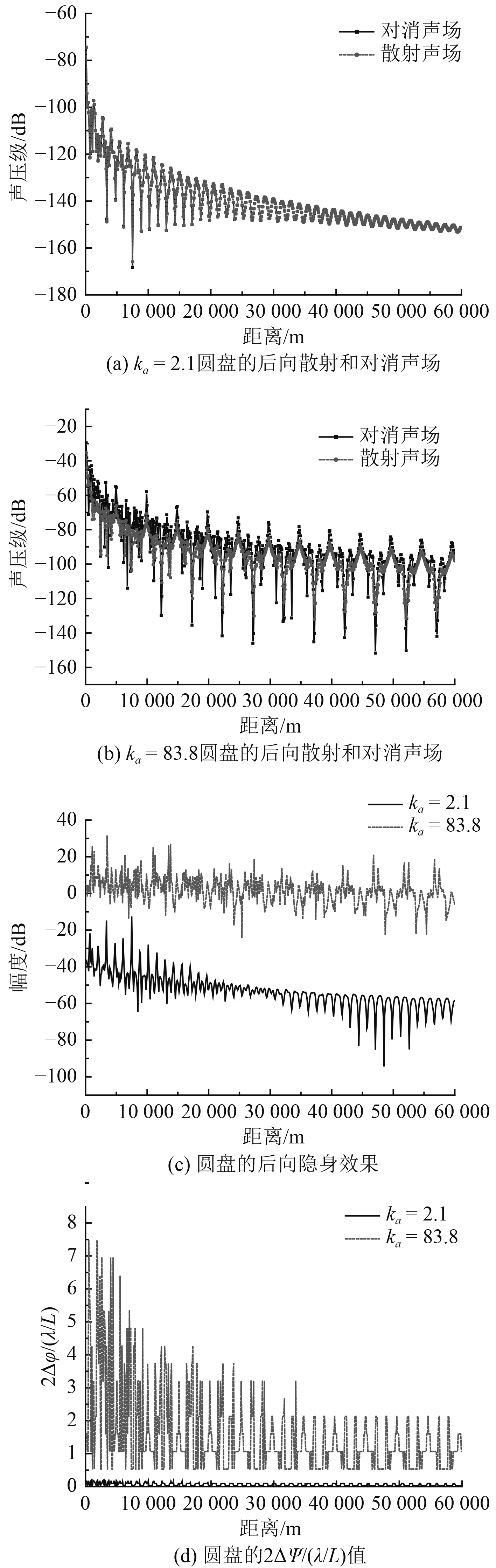
当半径1 m，10 m的刚性圆盘竖直放置在粘土底质Pekeris波导中，相应的500 Hz、2 000 Hz声呐信号垂直于圆盘平面入射时，后向接收到的目标散射声场和对消声场、隐身效果分析如图4所示。从图中可以看出，在k_a为83.8的大值时，2ΔΨ/（λ/L）值大于1，出现很多对隐身效果起反作用的情况；在k_a为2.1的小值时，2ΔΨ/（λ/L）值远小于1，后向隐身效果很好。再结合图2（c），显然对给定目标，降低频率后，隐身效果会变得更好。

3 结　语

　　本文以圆盘为目标，对浅海环境中利用敌方声呐探测方向的自由场散射函数构建对消声场的可行性进行分析，得到以下结论：1）当目标的复杂散射函数在主要波导模态的水平掠射角±ΔΨ范围内约是常数时，隐身效果基本有效。2）当环境参数不变时，随着距离的增加，有源对消隐身效果变得更好，对隐身起反作用的情况会消失。3）对于给定的目标，当降低频率后，有源对消隐身效果会变得更好。本文所用的计算模型很理想，认为声呐信号是单频长脉冲、水面和水底都是绝对平整的、目标位于水平分层介质的等声速层内、混响干扰比实际接收到的目标回声信号小的多，可以忽略。要想对浅海中目标的有源对消回声隐身进行精确的研究，还需进一步建立不平整海底及海面随机起伏波导中、目标处于不均匀声速层、脉冲信号形式下接收到的混响信号和目标回波信号模型。