近年来,水下机器人技术快速发展,特别是水下无人航行器(Unmanned Underwater Vehicle,UUV)体积小、运用灵活,往往能够抵近港口、岛屿等目标区域进行作业[1]。像UUV这类小型水下平台已经成为了水文数据测算、情报侦察、目标打击的重要载体。因此,在重要港口、岛屿建立近场水下预警系统,用于侦察水下小目标也就越来越紧迫。水下航行器的辐射噪声是其最为重要的目标特性,可以作为探测的重点信号。但随着新材料和减振降噪技术的应用,水下航行器的辐射噪声级越来越低,以至于声传感器阵列在远处无法发现目标。基于这种情况,需要声传感器能在相对近的区域对小目标进行准确定位,进而毁伤。
在声传感器阵列的近场区域,近场波束形成通过搜索包含方位和距离参数信息的权值,获得搜索空间的谱图,谱图最大峰值对应的坐标是声源目标的位置。矢量水听器可以同时测量声压和振速信息,相比与标量声压水听器拥有更大的数据处理空间[2 – 4]。本文结合矢量水听器,研究任意平面阵型的矢量水听器阵列的近场波束形成算法[5],为近场区域声源定位问题提供一种新的思路,更适用于工程中的实际应用。
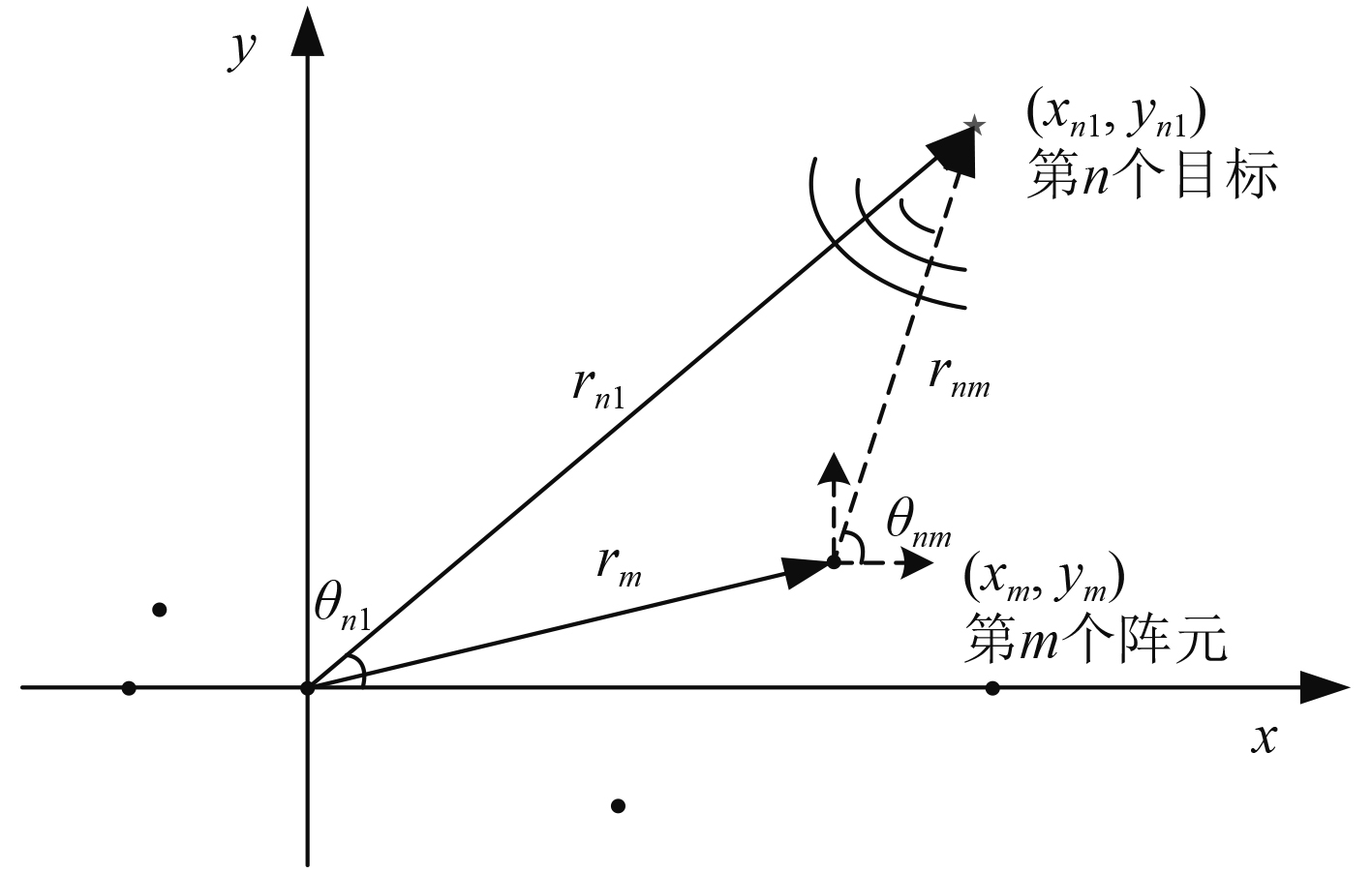
1 矢量阵近场测量模型本文考虑在平面空间中,由M个任意排列的矢量水听器组成的传感器阵列,接受N个窄带信源目标的辐射噪声信号。为方便表述,设第1个矢量水听作为坐标原点建立坐标系,阵元和目标的空间位置如图1所示。
|
图 1 近场目标与阵列的位置示意图 Fig. 1 Positions of near-field targets and array |
图中,平面阵中第m个矢量水听器的坐标为
一般当阵元距离阵列的距离
可以计算出第
| ${r_{nm}} = {\left[ {{{\left( {{r_{n1}}\cos {\theta _{n1}} - {x_m}} \right)}^2} + {{\left( {{r_{n1}}\sin {\theta _{n1}} - {y_m}} \right)}^2}} \right]^{1/2}}\text{,}$ | (1) |
所以,第m个矢量水听器接收的声压信号
| $\begin{split}& {p_m}(t) = \sum\limits_{n = 1}^N {\frac{{{r_{n1}}}}{{{r_{nm}}}}{s_n}\left( t \right)} {e^{(j{k_n}({r_{n1}} - {r_{nm}})}}) + {n_{mp}}(t)\text{,}\\& t = 1,2,...,{N_t}\text{。}\end{split}$ | (2) |
式中:
近场情况下,矢量水听器接收的声压和振速信号不再完全相关,关系比较复杂。根据Euler方程,单个二维矢量水听器的振速和声压信号关系可用下式表示:
| $\left[ {\begin{array}{*{20}{c}}{{v_{mx}}}\\{{v_{my}}}\end{array}} \right] = \frac{{{p_m}}}{{{Z_{nm}}}}\left[ \begin{array}{l}\cos {\theta _{nm}}\\\sin {\theta _{nm}}\end{array} \right]{\rm{ + }}\left[ {\begin{array}{*{20}{c}}{{n_{mx}}}\\{{n_{my}}}\end{array}} \right]\text{。}$ | (3) |
式中:
| $\left\{ {\begin{aligned} & {\cos {\theta _{nm}} = \displaystyle\frac{{{r_{n1}}\cos {\theta _{n1}} - {x_m}}}{{{r_{nm}}}}} \text{,}\\ &{\sin {\theta _{nm}} = \displaystyle\frac{{{r_{n1}}\sin {\theta _{n1}} - {y_m}}}{{{r_{nm}}}}} \text{,}\\ &{{Z_{nm}}{\rm{ = }}\displaystyle\frac{1}{{1 - j\frac{{{\lambda _n}}}{{2\pi {r_{nm}}}}}}} \text{。}\end{aligned}} \right.$ | (4) |
综上,平面二维矢量阵接收的
| $\begin{split}{{X}}(t) =& \left[ {\begin{array}{*{20}{c}}{{p}}\\{{{{v}}_{{x}}}}\\{{{{v}}_{{y}}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{{{A}}_{{p}}}}\\{{{{A}}_{{p}}} \odot {{{u}}_{{x}}}}\\{{{{A}}_{{p}}} \odot {{{u}}_y}}\end{array}} \right]{{s}}(t) + \left[ {\begin{array}{*{20}{c}}{{{{n}}_p}(t)}\\{{{{n}}_{vx}}(t)}\\{{{{n}}_{vy}}(t)}\end{array}} \right]=\\& {{C}}({{\theta}}, {{r}}){{s}}(t) + {{n}}(t)\text{。}\end{split}$ | (5) |
式中:
可见,本文是在式(6)的矢量阵近场测量模型下研究利用近场波束形成算法对声源目标参数
近场波束形成实质上是对矢量水听器阵列接收的信号进行加权求和,通过搜索包含空间点方位与距离信息的权值,得到在整个搜索空间的空间谱。空间谱的峰值坐标可以作为目标信号的方位和距离的估计值。根据矢量阵近场测量模型,可以得到近场波束形成器的输出为:
| $Y(t) = {{{W}}^H}(\theta ,r){{X}}(t)\text{,}$ | (6) |
式中:
| $P(\theta ,r) = E\left\{ {{{\left| {Y(t)} \right|}^2}} \right\} = {{W}}{(\theta ,r)^H}{{RW}}(\theta ,r)\text{,}$ | (7) |
式中:
设平面空间中任意搜索点的坐标为
| $\begin{split}& {{W}}({\theta _s},{r_s}) = [{{{a}}^{\rm T}}({\theta _s},{r_s}),{{{a}}^{\rm T}}({\theta _s},{r_s}) \odot {{{u}}_{sx}},\\& {{{a}}^{\rm T}}({\theta _s},{r_s}) \odot {{{u}}_{sy}}{]^{\rm T}}{\rm{ = }}{{c}}({\theta _s},{r_s})\text{。}\end{split}$ | (8) |
式中:
因此,近场矢量阵CBF的输出空间谱函数为
| ${P_{CBF}}({\theta _s},{r_s}) = {{c}}{({\theta _s},{r_s})^H}{{Rc}}({\theta _s},{r_s})\text{。}$ | (9) |
为了让目标入射的信号无失真的输出,并且使矢量水听器阵列的总的输出功率最小,这样可以保证最大化抑制非目标信号[6 – 7]。因此,Capon提出了MVDR波束形成器,其加权矢量的设计问题可以表述为:
| $\begin{split}& \min \left\{ {{{W}}{{(\theta ,r)}^H}{{RW}}(\theta ,r)} \right\}\\& {\rm{s}}{\rm{.t}}{\rm{. }}{{W}}(\theta ,r){{c}}({\theta _s},{r_s}) = 1\text{。}\end{split}$ | (10) |
在功率最小的约束下,解得最优权向量为:
| ${{{W}}_{opt}}({\theta _s},{r_s}) = \frac{{{{{R}}^{ - 1}}{{c}}({\theta _s},{r_s})}}{{{{{c}}^H}({\theta _s},{r_s}){{{R}}^{ - 1}}{{c}}({\theta _s},{r_s})}}\text{。}$ | (11) |
对应的近场矢量MVDR波束形成器输出空间谱函数为:
| $\begin{split}& {P_{MVDR}}({\theta _s},{r_s}) = {{{W}}^H}_{opt}{{{R}}^{ - 1}}{{{W}}_{opt}}=\\& 1/({{c}}{({\theta _s},{r_s})^H}{{{R}}^{ - 1}}{{c}}({\theta _s},{r_s}))\text{。}\end{split}$ | (12) |
由式(9)和式(12)可见,通过对阵列近场区域逐点扫描,计算出不同位置点上的加权矢量,即可求得空间谱,谱峰位置即目标点。
3 仿真及实测数据分析本节主要通过数值仿真和实测数据分析本文所研究的基于任意平面阵形的矢量水听器阵列对声源目标的定位能力。
3.1 仿真分析1)对双声源目标的定位能力分析
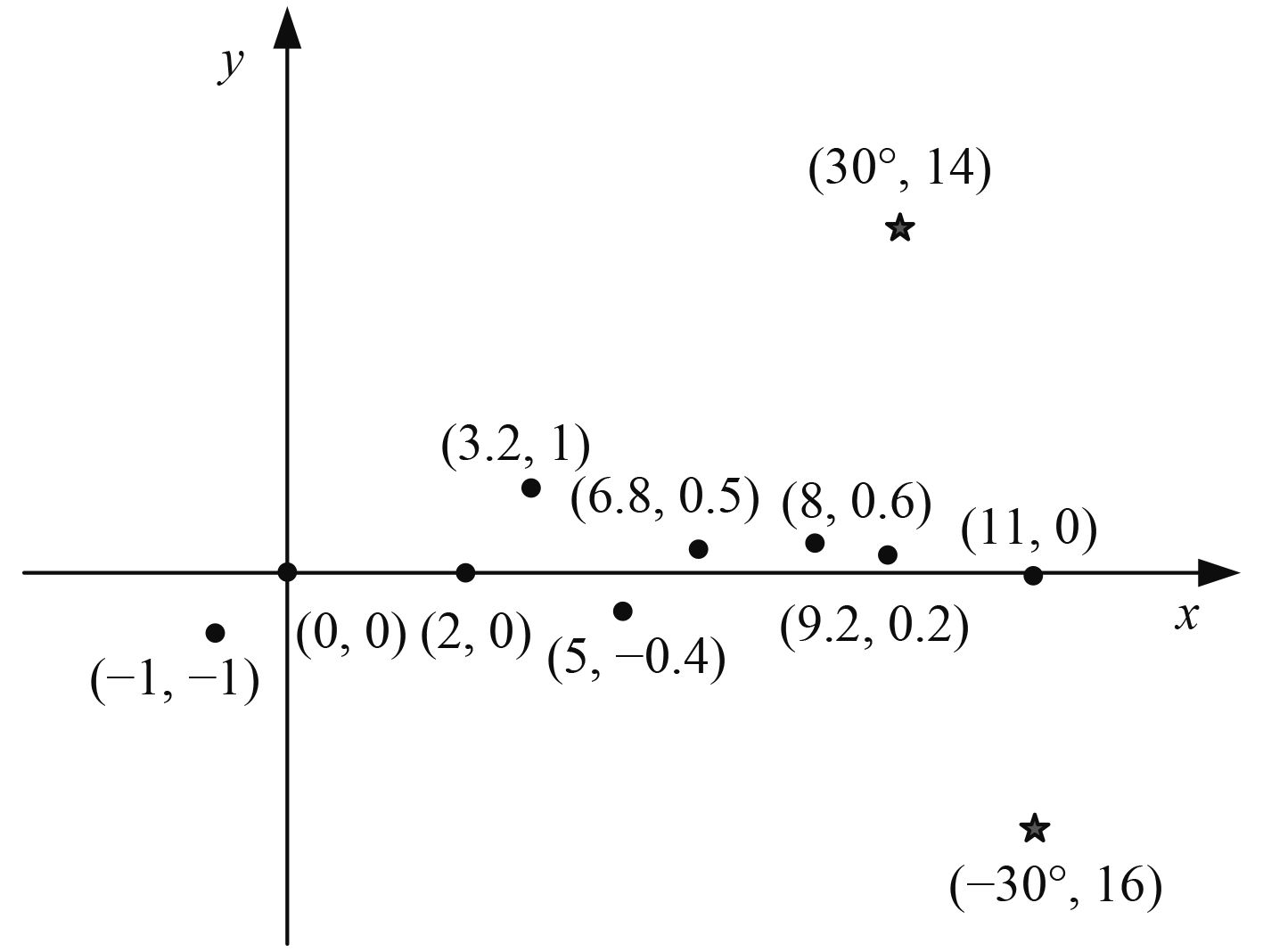
假设在平面中存在2个相互独立的单频声源目标,按球面波的模型传播到已知坐标的9个任意排列的矢量水听器阵列上。声源的频率为1 480 Hz,声速为1 480 m/s,坐标分别为(–30°,14 m),(30°,16 m)。以第1个水听器的声压信号为基准,加入信噪比为5dB的噪声。矢量水听器阵列坐标分别为(0,0),(–1,–1),(2,0),(3.2,1),(5,–0.4),(6.8,0.6),(8,0.6),(9.2,0.2),(11,0),空间位置分布如图2所示。
|
图 2 双声源目标的空间分布图 Fig. 2 Positions of double targets and array |
分别利用近场矢量CBF和近场矢量MVDR波束形成完成平面空间谱估计,得到归一化空间谱三维分布如图3和图4所示。

|
图 3 双声源近场矢量CBF定位 Fig. 3 Double targets located by near-field vector CBF |
|
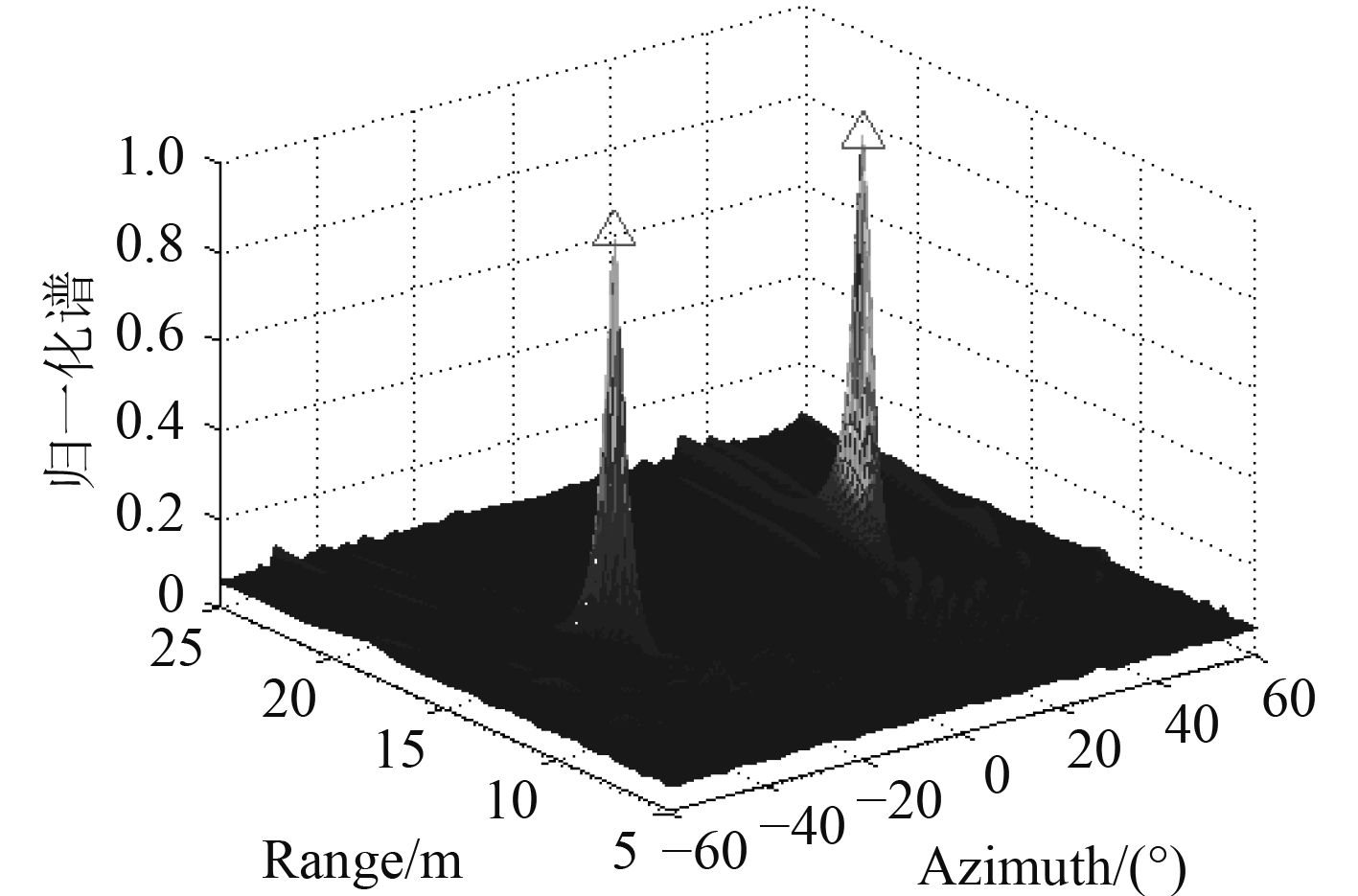
图 4 双声源近场矢量MVDR定位 Fig. 4 Double targets located by near-field vector MVDR |
图中,三角处为目标的真实位置,从图3和图4的仿真结果可以看出,任意平面阵形的矢量水听器阵列利用近场CBF和近场MVDR算法可以对双声源进行定位。近场矢量MVDR相比较于常规波束形成而言,其波束的主瓣更窄、旁瓣更低,具有更高的分辨率,可以对目标进行更准确定位。
2)矢量波束形成性能分析
通过100次Monte Carlo仿真求出每次最大峰值的坐标,并与真实值作比较,计算估值均方根误差(Root Mean Square Error,RMSE)。方位角的RMSE计算定义为:
| $RMSE(\theta ) = \sqrt {\frac{{\sum\limits_{m = 1}^M {{{({{\hat \theta }_m} - \theta )}^2}} }}{M}}\text{。} $ | (13) |
式中:
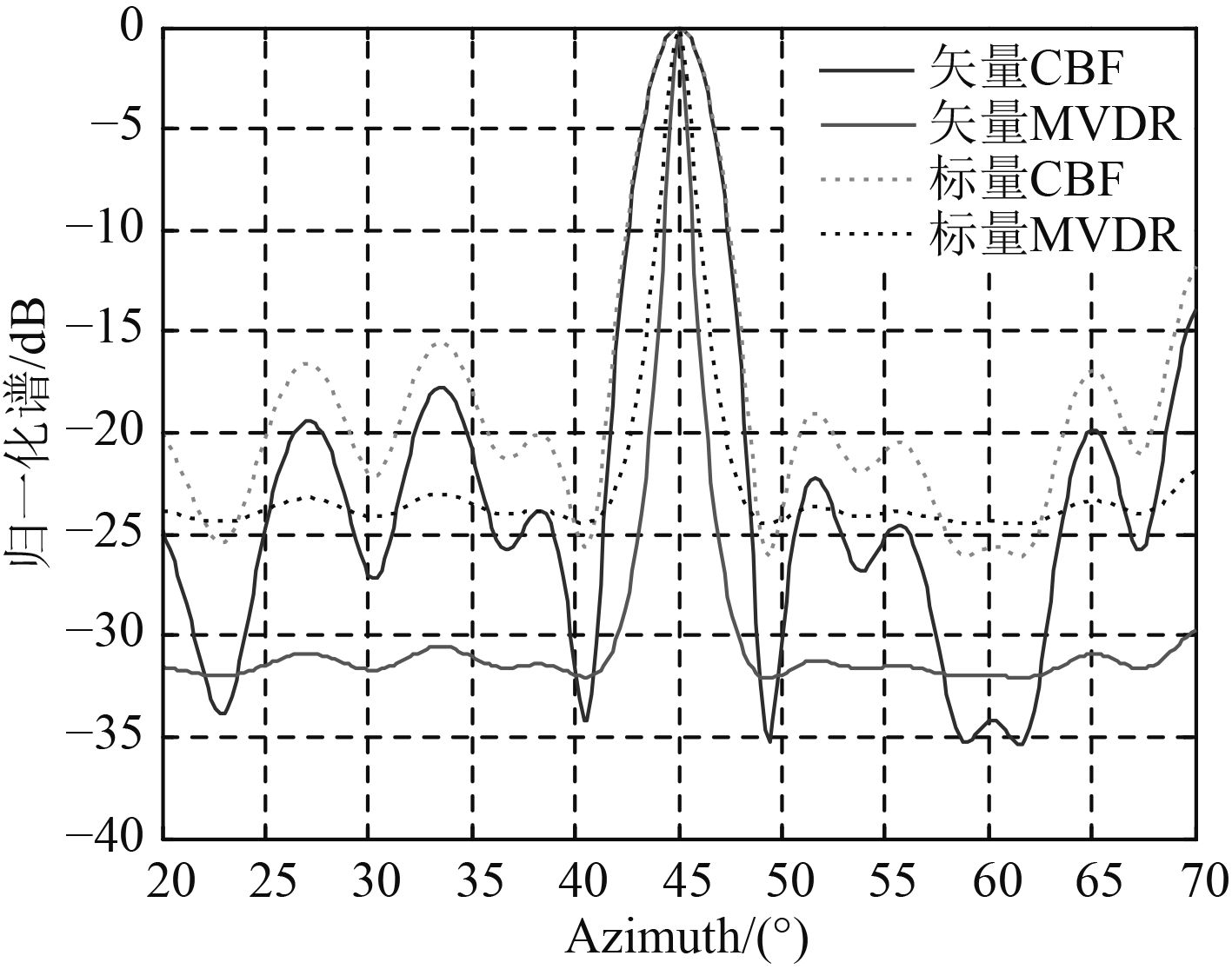
考虑一个近场声源目标,其坐标为(45°,20 m),信噪比范围为–20 dB到10 dB,其他参数与仿真1中一致。分别利用矢量阵CBF、矢量阵MVDR、标量阵CBF、标量阵MVDR四种算法对目标进行定位,其方位角和距离参数估计值的RMSE随信噪比的变化见图5和图6所示。为了更好的对比4种算法的性能,当信噪比SNR=0 dB时,通过100次Monte Carlo仿真求出平均空间谱图,其沿方位角和距离参数的剖面图如图7和图8所示。

|
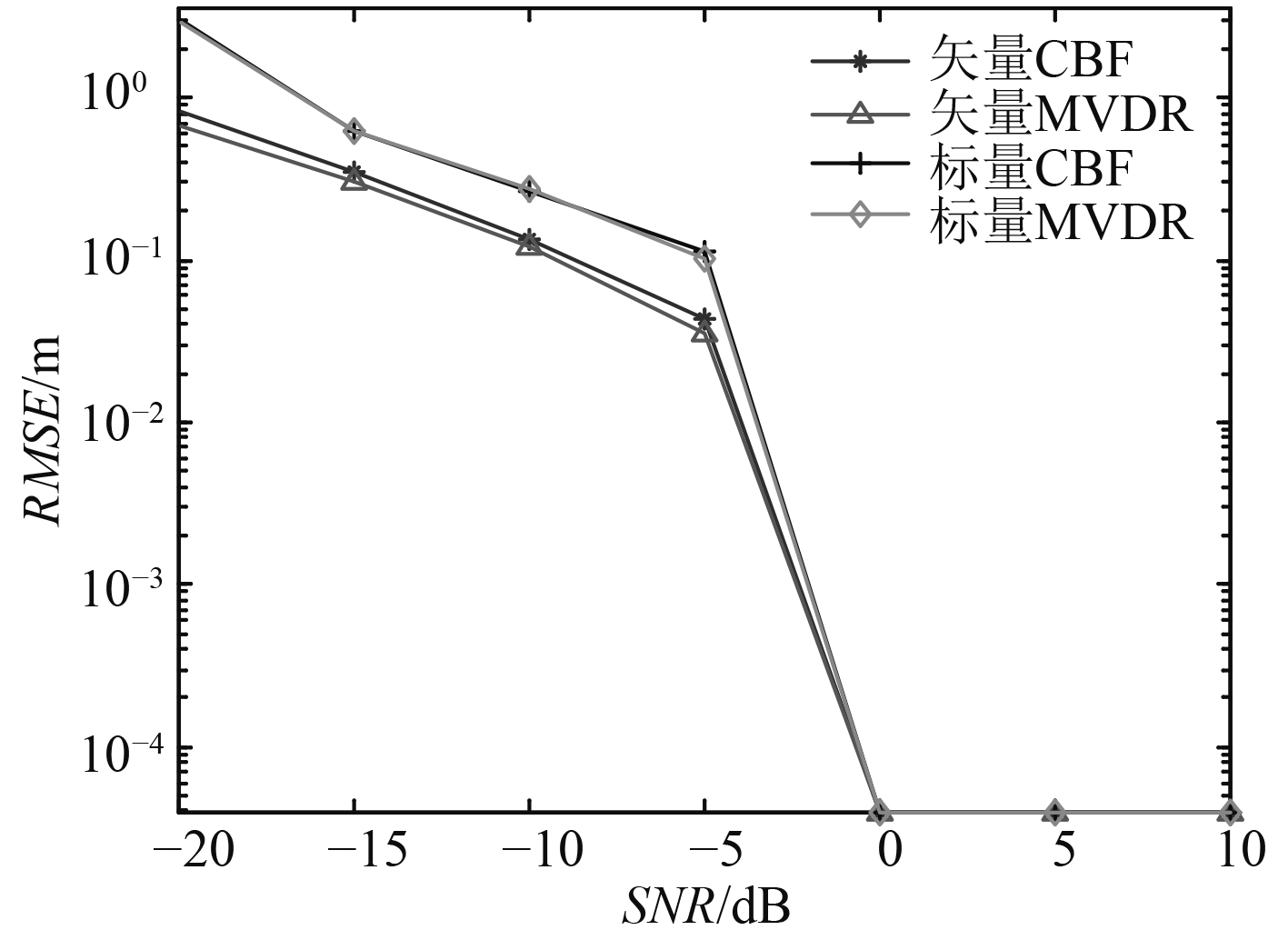
图 5 方位角估值的RMSE随信噪比变化 Fig. 5 Azimuth estimator’s RMSE vs SNR |
|
图 6 距离估值的RMSE随信噪比变化 Fig. 6 Range estimator′s RMSE vs SNR |
|
图 7 SNR=0 dB方位谱图 Fig. 7 Azimuth spectrum when SNR=0dB |
|
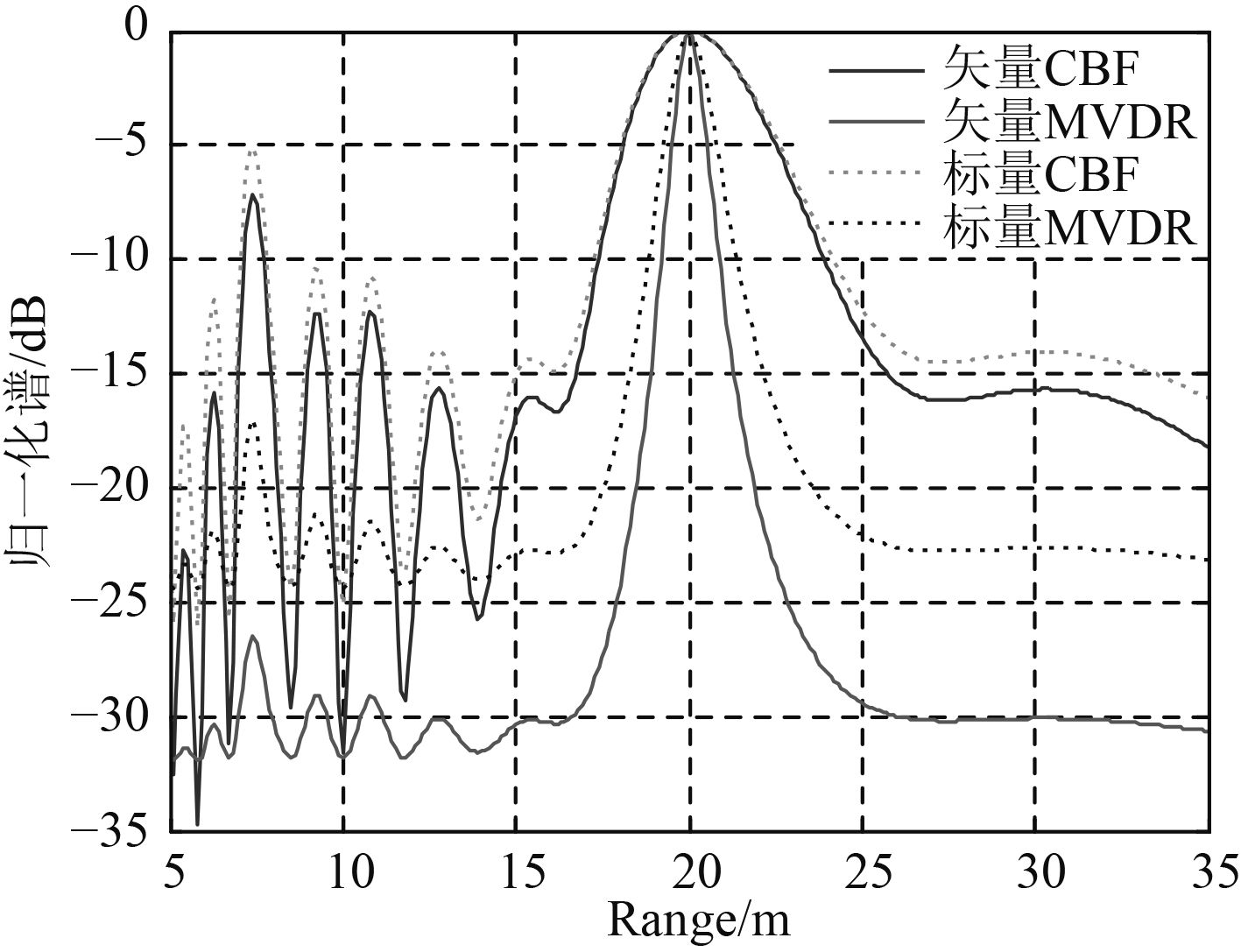
图 8 SNR=0 dB距离谱图 Fig. 8 Range spectrum when SNR=0dB |
从图5和图6可知,在水听器数目和布放位置相同的条件下,4种定位算法估值的RMSE都随信噪比的增大而不断减小。信噪比大于0 dB以后,RMSE基本几乎为0,不再变化,也说明这4种算法都能2两种波束形成算法得到的方位角和距离估计值的RMSE明显小于标量阵波束形成算法,算法的稳定性更好。而且,MVDR算法相比于常规波束形成估计得到的方位角和距离参数的RMSE略小,精度较高。从图7和图8中的方位谱、距离谱可以看出,虽然在SNR=0 dB时,估计值的RMSE几乎为0,4种方法都能完成对目标定位。但基于矢量阵MVDR的空间谱主瓣较窄,旁瓣低,且旁瓣波动最小,而标量CBF算法的定位性能最差,因此基于矢量阵MVDR更适用于近场声源目标的定位。
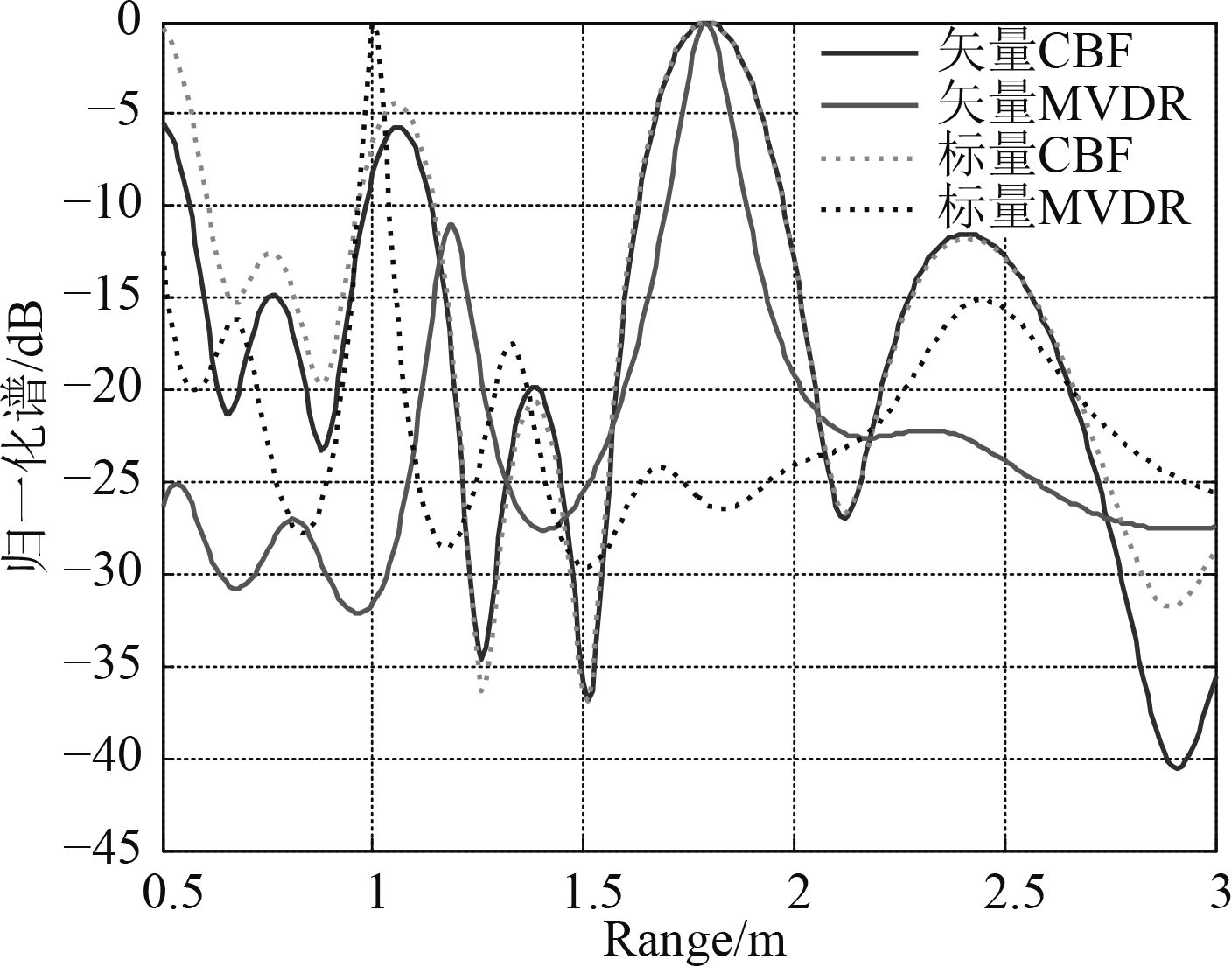
3.2 试验数据分析为了验证矢量水听器阵对实际水中目标定位能力,利用湖中试验测得的数据进行分析。阵列是由4个二维矢量水听器组成的均匀线阵,阵元间距为0.75 m。声源为发射换能器,到第1个矢量水听器的距离为1.8 m左右,夹角约为34°。声源发射频率为3 150 Hz的单频信号(通过对接收信号进行频谱分析得到的中心频率),利用本文中的4种算法对数据进行处理,得到的空间谱剖面图如图9和图10所示。

|
图 9 实测数据方位谱图 Fig. 9 Azimuth spectrum of measured data |
|
图 10 实测数据距离谱图 Fig. 10 Range spectrum of measured data |
从图中可见基于矢量阵近场波数形的谱峰坐标与预置参数基本一致,且矢量阵MVDR算法主瓣分辨率更高,旁瓣波动最小。标量阵近场波数形成算法相对较差,其中标量MVDR算法已经失效,与仿真结果基本一致。
4 结 语为提高重点港口、岛屿的水下近场预警防御能力,本文提出利用任意平面阵形的矢量水听器阵列,结合常规波束形成和MVDR算法对水下近场声源目标进行定位。测量模型和算法通过仿真和实测数据进行验证,首先仿真分析了矢量阵常规波束形成和矢量阵MVDR算法对双声源目标定位能力,仿真结果可以看出矢量阵MVDR有更高的定位精度。另外对比分析了矢量阵和标量阵波束形成对方位角和距离参数估值的RMSE随信噪随信噪比的变化,发现都随SNR的增大而RMSE不断减小,且信噪比大于0 dB后,估值误差几乎为0。且矢量阵波束形成算法性能优于标量阵波束形成算法,矢量阵MVDR算法分辨率最高,相比其他几种算法更适用于水下近场预警防御。
| [1] | 陈强. 水下无人航行器[M]. 北京: 国防工业出版社, 2014. |
| [2] | NEHORAI A, PALDI E. Acoustic vector-sensor array processing[J]. IEEE Transactions on Signal Processing, 1994, 42(9): 2481–2491. |
| [3] | 时洁. 基于矢量阵的水下噪声源近场高分辨率定位识别方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2009. |
| [4] | 余桐奎. 矢量声压组合基阵MVDR近场聚焦波束形成[J]. 舰船科学技术, 2012, 34(6): 60–63. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jckxjs201206014 |
| [5] | 熊鑫, 章新华, 卢海杰, 等. 基于任意阵的最小方差无失真响应聚焦波束形成的被动定位方法[J]. 应用声学, 2010, 29(6): 73–76. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yysx201006011 |
| [6] | CAPON J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE, 2005, 57(8): 1408–1418. |
| [7] | 王川, 梅继丹, 孙磊, 等. 近场MVDR聚焦波束扫描声图定位方法研究[J]. 海洋技术学报, 2010, 29(2): 56–59. http://edu.wanfangdata.com.cn/Periodical/Detail/hyjs201002014 |
 2018, Vol. 40
2018, Vol. 40
