声呐设备通常采用换能器阵列和波束形成方法处理水声信号[1]。传统的波束形成方法是延时求和,这种方法可以简单有效的处理窄带水声信号,但是随着频率的升高,延时求和方法形成的波束变窄并且产生旁瓣[2],这会使得水声信号产生严重的失真。为了不失真的处理宽带水声信号,就要求在工作频带范围内形成恒定束宽的波束,并且尽可能减小旁瓣。
因此提出了很多基于信号处理理论的恒定束宽波束形成方法[3 – 6]和旁瓣抑制方法[7 – 9],这些方法通常将宽带划分为多个窄带,在每个窄带中对水声信号进行处理,这使得阵列必须采用随频率变化的复杂阵元权重,并且频带越宽计算越复杂。由美国海军研究实验室提出的恒定束宽换能器(CBT)阵列[10 – 12],经过了多年的发展[13 – 15],可以采用不随频率变化的简单Legendre函数阵元权重,实现宽频带范围内恒定束宽的波束,并且具有较小的旁瓣[16]。
和其他恒定束宽阵列一样,CBT阵列有一定的工作频率限制。CBT理论表明,对于Legendre函数加权的球冠或者圆弧形换能器,只存在工作频率下限,即高于此频率时即具有恒定束宽的波束特性[11]。然而CBT阵列是由离散的换能器组成,阵元间距会导致旁瓣[16]。为了使旁瓣小于某一特定值,通常将认为CBT阵列的工作频率上限与常规的直线形阵列一样,须满足阵列理论的要求,即阵元间距须小于波长的一半[17 – 18]。然而研究表明,圆弧形CBT阵列的工作频率上限比阵列理论要求的高[15, 19],所以根据阵列理论设计的CBT阵列没有充分利用其工作频带,浪费了频带资源。因此本文系统计算分析CBT阵列的工作频率上限。
1 阵列工作频率上限理论分析 1.1 直线形阵列直线形阵列的结构如图1(a)所示,其中坐标原点O取为阵列中心,阵列方向取为x轴方向。不难得到在远场空间任意点P处的声压
| $p\left( \theta \right) = \frac{{{\rm{e}}^{ - {j}{kr}}}}{r}\int_{ - L/2}^{L/2} {A\left( l \right){{\rm{e}}^{{j}kl\sin \theta }}{\rm{d}}l}\text{。} $ | (1) |
式中:l为阵列上任意一点Q的x坐标;L为阵列的长度;
| $p\left( \theta \right) = \frac{{{{\rm{e}}^{ - {{j}}k\left[ {r + \left( {N + 1} \right)d/2} \right]}}}}{r}\sum\limits_{n = 1}^N {A\left( n \right){{\rm{e}}^{{{j}}knd\sin \theta }}}\text{。} $ | (2) |
式中:
注意到式(2)中求和号外的项与θ无关,即与波束的形状无关,因此波束形状完全由式(2)中的求和部分决定。另外注意到
| $F\left\{ {A\left( n \right)} \right\} = \sum\limits_{n = 1}^N {A\left( n \right){{\rm{e}}^{{{j}}n\varOmega }}}\text{。} $ | (3) |
式中:Ω为数字角频率。对比式(2)和式(3)不难发现,远场声压
圆弧形阵列的结构如图1(b)所示,其中坐标原点O取为圆弧的圆心,阵列位于x-O-z平面,取z方向为圆心到阵列中点的方向。根据几何关系,不难得到在远场空间任意点P处的声压
| $p\left( \theta \right) = \frac{{{{\rm{e}}^{ - {{j}}kr}}}}{r}\int_{ - \pi }^\pi {A\left( \psi \right){{\rm{e}}^{{{j}}k{r_0}G\left( {\varphi ,\theta ,\psi } \right)}}{r_0}{\rm{d}}\psi }\text{。} $ | (4) |
式中:
同样考虑圆弧形阵列由N个等距排列的点源组成,考虑到通常对阵列所在平面的声压分布更为感兴趣,即
| $p\left( \theta \right) = \frac{{{{\rm{e}}^{ - {{j}}k\left( {r + a\cos \theta } \right)}}}}{r}\sum\limits_{n = 1}^N {A\left( n \right){{\rm{e}}^{{{j}}k{r_0}\cos \left( {n\Delta \psi - \theta - \frac{{N + 1}}{2}\Delta \psi } \right)}}}\text{。} $ | (5) |
式中:Δψ为相邻2个点源的圆心角之差。由式(5)可见,n与θ耦合,无法进行与直线形阵列类似的DTFT分析,阵列的声压分布较为复杂且不具有周期性,因此须采用数值方法分析圆弧形阵列的工作频率上限。类似的,对于二维球面阵和柱面阵,也可以通过类似分析得到相同的结论。
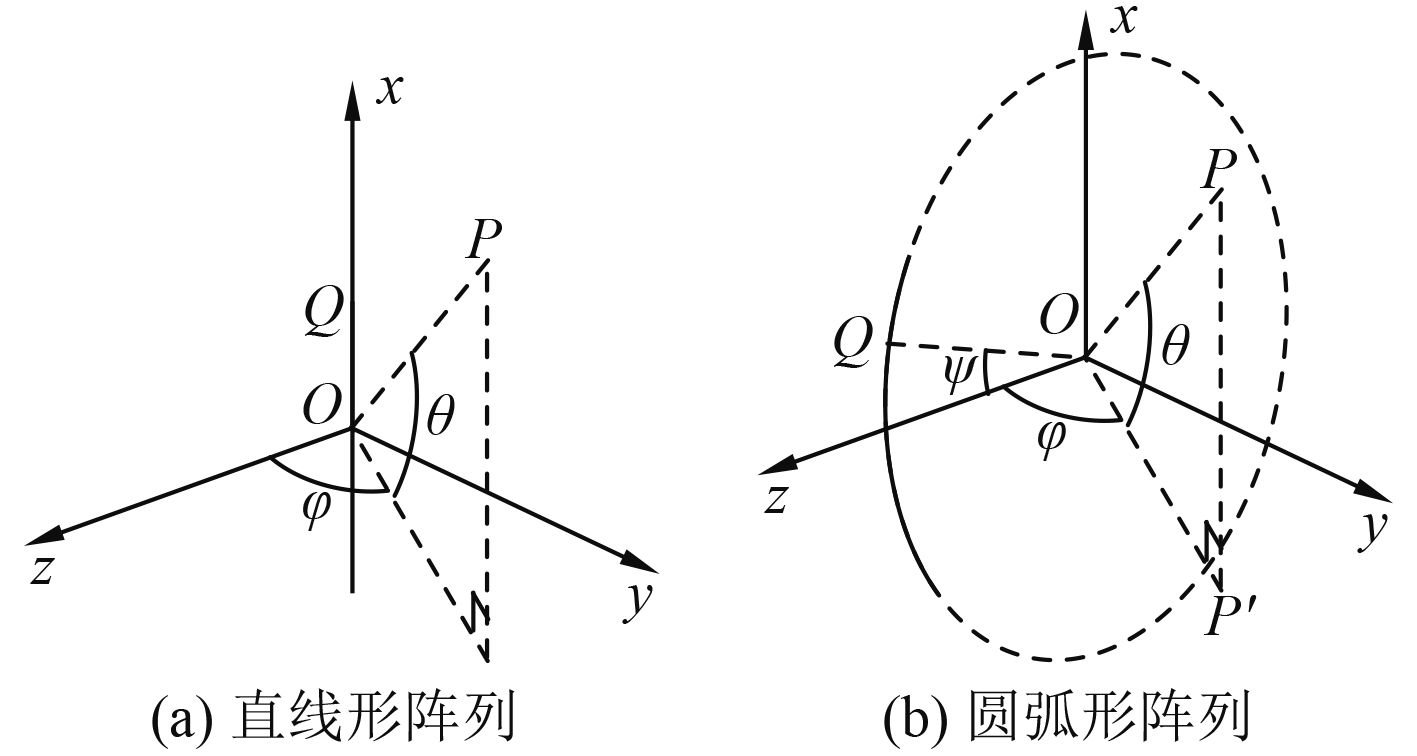
|
图 1 直线形和圆弧形阵列示意图 Fig. 1 Geometries of a straight-line array and a circular array |
圆弧形CBT阵列如图2(a)所示,其中表示阵元的黑色圆点越大表示其阵元权重越大。圆弧形CBT阵列的阵元权重满足
| $A\left( \psi \right) = \left\{ {\begin{array}{*{20}{c}}{{{{P}}_\nu }\left( {\cos \psi } \right),\;\;\;\;\;\;\psi \leqslant {\theta _0}}\text{,}\\{0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\psi > {\theta _0}}\text{。}\end{array}} \right.$ | (6) |
其中,
| $p\left( \theta \right) \approx \left\{ {\begin{array}{*{20}{c}}{\rho c{r_0}{{{P}}_\nu }\left( {\cos \theta } \right)\frac{{{{\rm{e}}^{{{j}}k\left( {r - {r_0}} \right)}}}}{r},\;\;\;\;\;\;\theta \leqslant {\theta _0}}\text{,}\\{0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\theta > {\theta _0}}\text{。}\end{array}} \right.$ | (7) |
由式(7)可见,远场声压的角度θ和波数k解耦,波束形状不随频率的变化而变化,因而具有恒定束宽的波束特性。另外注意到式(6)中,当
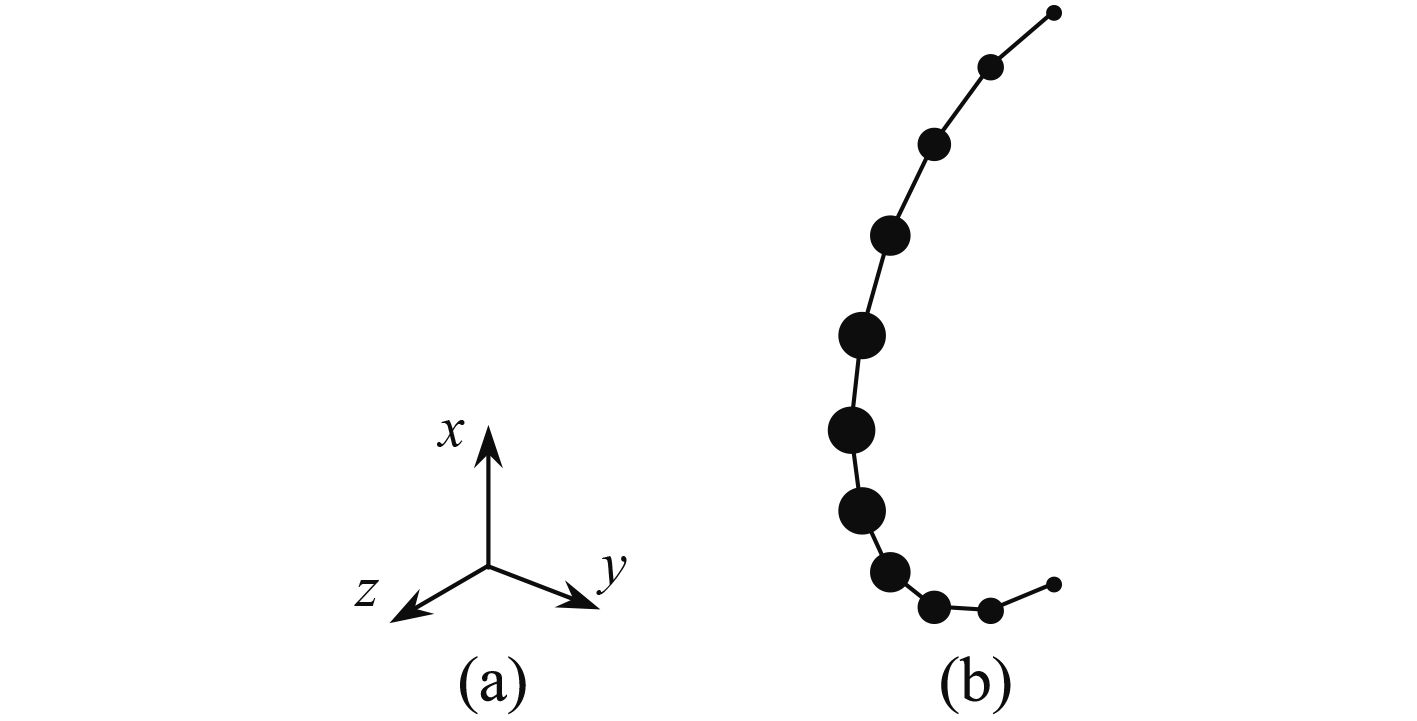
|
图 2 圆弧形CBT阵列示意图 Fig. 2 Geometries of the circular CBT arrays |
实际情况下CBT阵列由离散的换能器组成,离散阵列会导致旁瓣和主瓣的纹波。如图3所示不同情况下圆弧形CBT阵列的波束,这里假定阵元为点源,图中黑色粗线为由式(7)计算得到波束的理论值,灰色细线为不同频率下的离散圆弧形CBT阵列的波束,相邻频率对应的波长相差
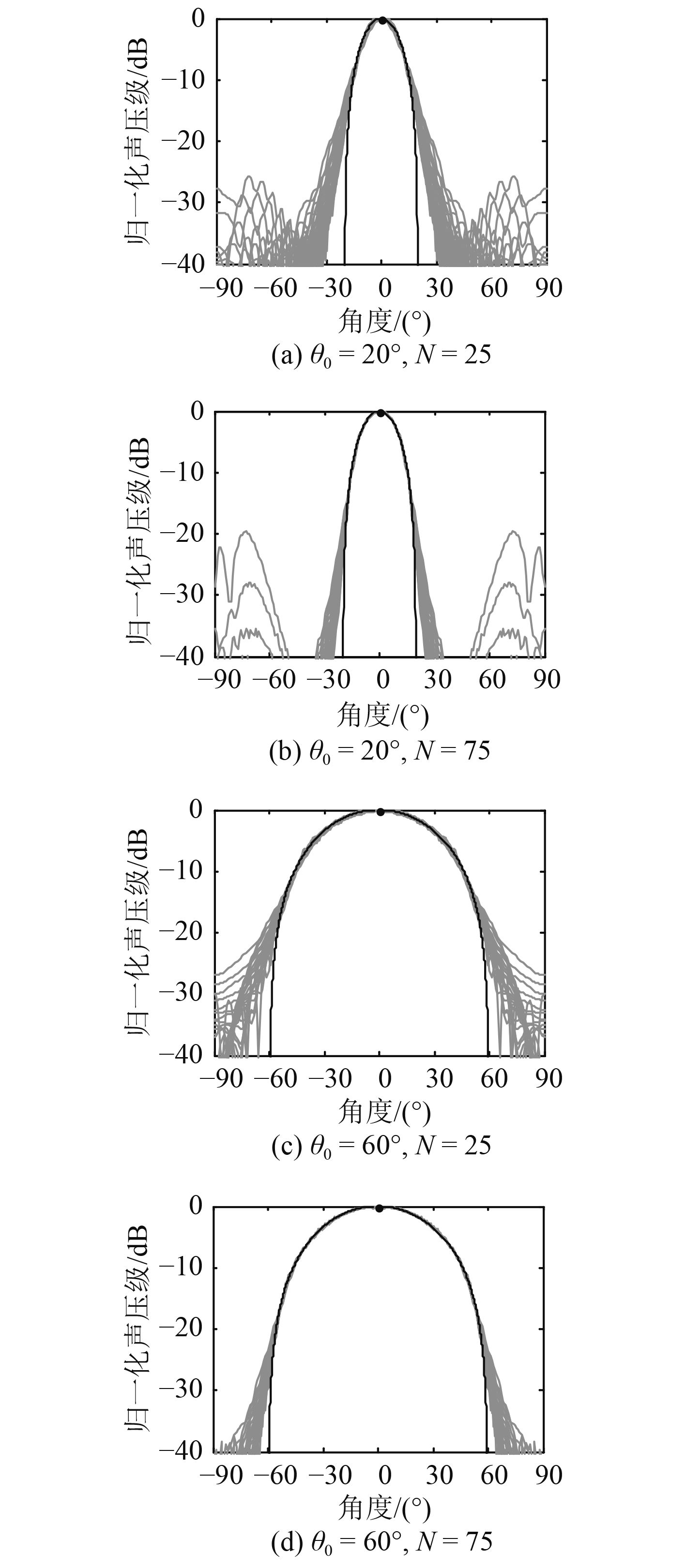
|
图 3 不同情况下圆弧形CBT阵列的波束 Fig. 3 Beam pattern of the circular CBT array in various cases |
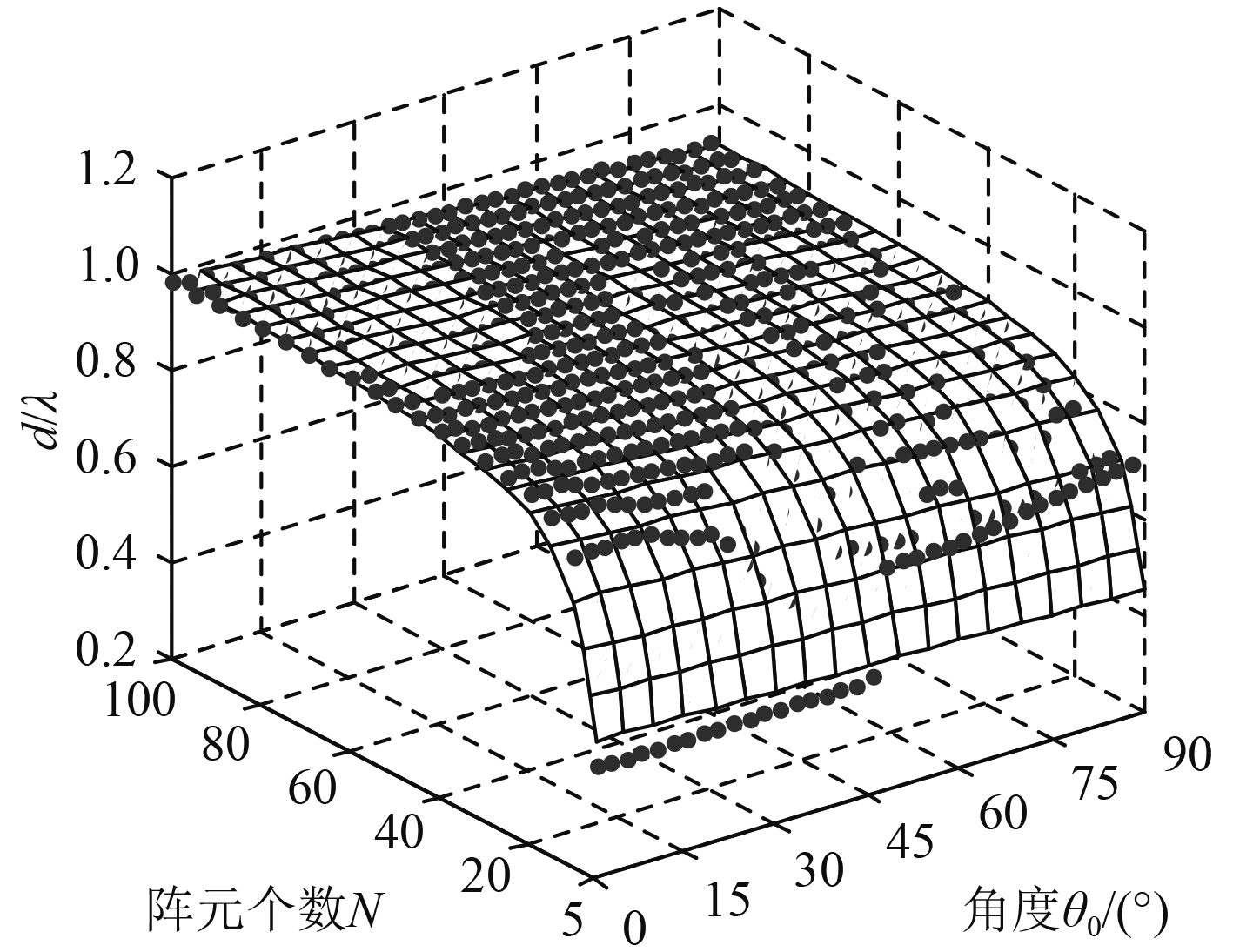
|
图 4 圆弧形CBT阵列的工作频率上限 Fig. 4 Upper limit of the operating frequency of the circular CBT array |
可以设定SIDE和RIPP的最大值,这样可以采用数值计算方法得到圆弧形CBT的工作频率上限对应的
| $\frac{d}{\lambda } = a\left( {1 + \frac{b}{N}} \right) \cdot \left( {1 + c{\theta _0}} \right)\text{,}$ | (8) |
其中:a,b,c为拟合系数;
| $\frac{d}{\lambda } = \left( {1 - \frac{{2.7}}{N}} \right) \cdot \left( {1 - \frac{{{\theta _0}}}{{1000}}} \right)\text{。}$ | (9) |
考虑到通常情况下,声呐的N不会太小,统计
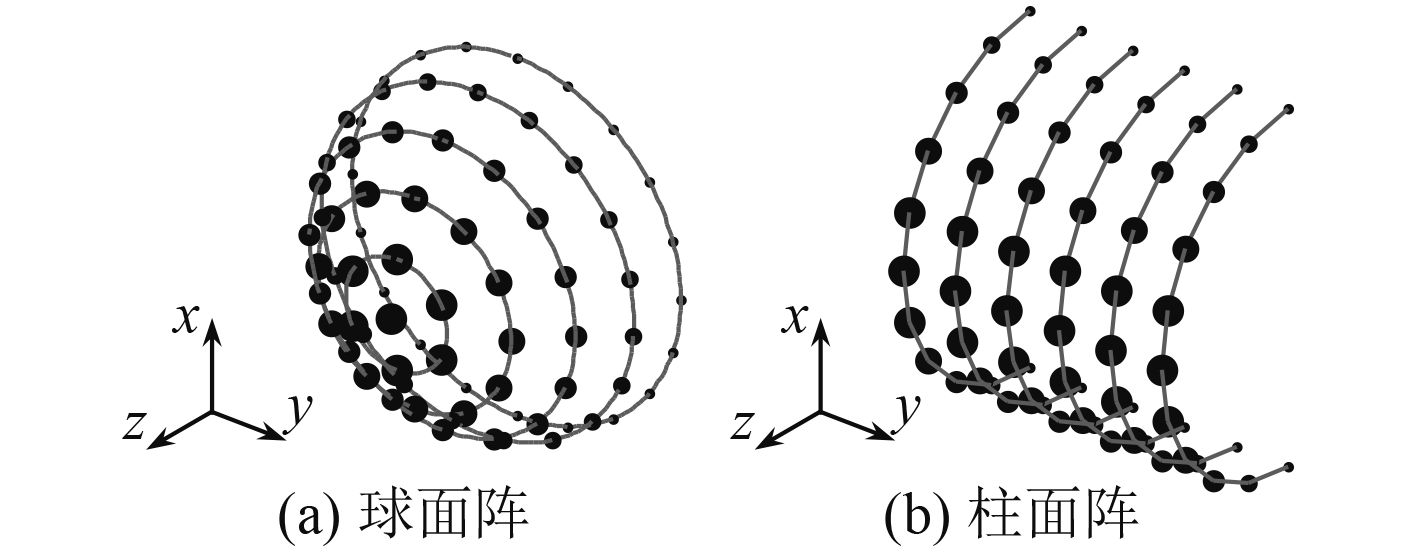
二维CBT阵列包括球面CBT阵列和柱面CBT阵列。对于球面CBT阵列,其阵元满足的曲面方程为
| $A\left( {x,y,z} \right) = \left\{ {\begin{array}{*{20}{c}}{{{{P}}_\nu }\left( {\frac{z}{{{r_0}}}} \right),\;\;\;\;\;\theta \leqslant {\theta _0}}\text{,}\\{0,\;\;\;\;\;\;\;\;\;\;\;\;\;\theta > {\theta _0}}\text{。}\end{array}} \right.$ | (10) |
其中
|
图 5 二维CBT阵列示意图 Fig. 5 Geometries of the two-dimensional CBT arrays |

|
图 6 圆弧形CBT阵列的工作频率上限 Fig. 6 Upper limit of the operating frequency of the circular CBT array |
同样考虑SIDE≤–20 dB,RIPP≤3 dB,这样计算得到
| $\frac{d}{\lambda } = \left( {1 - \frac{{2.3}}{N}} \right) \cdot \left( {1 - \frac{{{\theta _0}}}{{400}}} \right)\text{。}$ | (11) |
而对于柱面CBT阵列,式(8)简化为式(9)。同样对
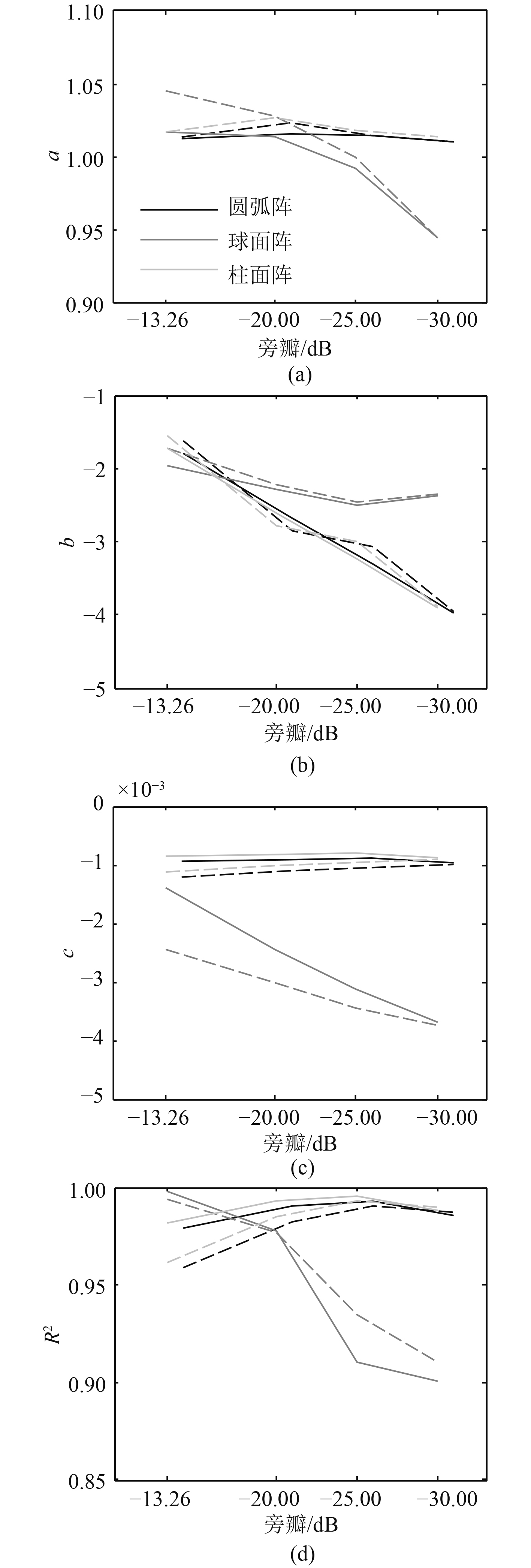
可以考虑旁瓣SIDE和主瓣纹波RIPP对频率上限的影响。如图7所示,为不同的SIDE和RIPP要求情况下各个阵列的工作频率上限对应的
|
图 7 不同情况下的拟合参数 Fig. 7 Fitting parameters in various cases |
同样可以对

|
图 8 使90%情况下都满足要求的工作频率上限 Fig. 8 Upper limit of the operating frequency at which 90% of the cases meet the requirements |
首先,理论分析了CBT阵列的工作频率上限。对于延时直线形CBT阵列,可以得到工作频率上限的理论解,即需满足阵列理论的要求,阵元的间距需小于最大工作频率对应的波长的1/2。而对于圆弧形CBT阵列,无法得到理论解,需采用数值方法求解。
其次,采用数值方法分析了主瓣纹波不大于3 dB、旁瓣不大于–20 dB时的圆弧形CBT阵列的工作频率上限,并采用最小二乘法对结果进行拟合,给出了具体的拟合公式。结果表明圆弧形CBT阵列的工作频率上限要大于阵列理论规定的工作频率上限,大部分情况下工作频率上限可以拓展至少0.76个倍频程。此外还进一步分析了球面CBT阵列和柱面CBT阵列,其中球面CBT阵列的工作频率上限略小,但大部分情况下仍比阵列理论规定的工作频率上限大0.57个倍频程;而柱面CBT阵列的结果和圆弧形CBT阵列的结果几乎一致。
最后,分析了主瓣纹波和旁瓣的不同要求对工作频率上限的影响。结果表明,主瓣纹波的影响较小,而旁瓣的影响较大。
| [1] |
闵瑞红, 肖杰雄. 世界潜艇综合声呐系统发展现状及趋势 [J]. 舰船科学技术, 2013, 35(2): 134–141.
MIN Rui-hong, XIAO Jie-xiong. The state and development of submarine integrated sonar systems around the world [J], Ship Science and Technology 2013, 35(2): 134–141. http://www.cqvip.com/QK/94984X/201302/45045632.html |
| [2] |
鄢社锋, 马远良. 基于二阶锥规划的任意传感器阵列时域恒定束宽波束形成 [J]. 声学学报, 2005, 30(4): 309–316.
YAN She-feng, MA Yuan-liang. Broadband constant beamwidth beamforming for arbitrary sensor arrays in time domain via second-order cone paogramming [J]. Acta Acustica, 2005, 30(4): 309–316. http://www.cnki.com.cn/Article/CJFDTOTAL-XIBA200504006.htm |
| [3] |
甘甜, 王英民. 一种稳健的恒定束宽波束形成方法 [J]. 声学学报, 2012, 37(1): 18–24.
GAN Tian, WANG Ying-min. A robust broadband beamforming method of constant beam width [J]. Acta Acustica, 2012, 37(1): 18–24. http://doi.wanfangdata.com.cn/10.3969/j.issn.1001-2400.2007.01.033 |
| [4] |
付彦, 刘劲军. 一种基于Notch滤波器的恒定束宽波束形成技术 [J]. 声学技术, 2013, 32(1): 50–53.
FU Yan, LIU Jin-jun. Constant beamwidth beamforming based On adaptive filter. [J]. Technical Acoustics, 2013, 32(1): 50–53. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sxjs201301012 |
| [5] |
黄聪, 李迪. 基于相干干扰抑制的时域恒定束宽波束形成 [J]. 哈尔滨工程大学学报, 2017, 38(1): 25–30.
HUANG Cong, LI Di. Constant beamwidth beamforming in time domain based on coherent interference suppression [J]. Journal of Harbin Engineering University, 2017, 38(1): 25–30. |
| [6] |
鄢社锋, 马晓川. 宽带波束形成器的设计与实现 [J]. 声学学报, 2008, 33(4): 316–326.
YAN She-feng, MA Xiao-chuan. Designs and implementations of broadband beamformers [J]. Acta Acustica, 2008, 33(4): 316–326. http://www.cqvip.com/QK/90012X/200804/27723338.html |
| [7] |
鄢社锋, 侯朝焕, 马晓川, 等. 基于凸优化的时域宽带旁瓣控制自适应波束形成 [J]. 声学学报, 2007, 32(1): 5–9.
YAN She-feng, HOU Chao-huan, Ma Xiao-chuan, et al. Convex optimization based FIR beamforming with sidelobe control [J]. Acta Acustica, 2007, 32(1): 5–8. http://www.cqvip.com/qk/90012X/20071/23617611.html |
| [8] |
幸高翔, 蔡志明. 旁瓣约束方向不变恒定束宽波束自适应综合 [J]. 声学技术, 2009, 28(2): 172–175.
XING Gao-xiang, CAI Zhi-ming. Synthesis of adaptive steering-invariant constant-beamwidth pattern with sidelobe constraints [J]. Technical Acoustics, 2009, 28(2): 172–175. http://www.cqvip.com/QK/95855X/200902/30229577.html |
| [9] |
夏欢, 张兴敢, 柏业超. 一种改进的共形阵方向图综合方法 [J]. 数据采集与处理, 2016, 31(4): 761–766.
XIA Huan, ZHANG Xing-gan, BAI Ye-chao. Improved method for conformal array pattern synthesis [J]. Journal of Data Acquisition and Processing, 2016, 31(4): 761–766. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sjcjycl201604014 |
| [10] | JARZYNSKI J, TROTT W J. Array shading for a broadband constant directivity transducer [J]. J. Acoust. Soc. Am., 1978, 64(5): 1266–1269. |
| [11] | ROGERS P H, BUREN A L. New approach to a constant beamwidth transducer [J]. J. Acoust. Soc. Am., 1978, 64(1): 38–43. |
| [12] | BUREN A L, LUKER L D, JEVNAGER M D, et al. Experimental constant beamwidth transducer [J]. J. Acoust. Soc. Am., 1983, 73(6): 2200–2209. |
| [13] | FENG X, SHEN Y, KEELE D B, et al. Directivity-customizable loudspeaker arrays using constant-beamwidth transducer (CBT) overlapped shading [C]//Audio Engineering Society Convention, Audio Eng. Soc., New York, 2015. |
| [14] |
朱舸, 沈勇, 夏洁, 等. 恒定束宽扬声器线阵列优化研究 [J]. 应用声学, 2017, 36(2): 95–104.
ZHU Ge, SHEN Yong, XIA Jie, et al. Optimization of constant beam-width transducer line array [J]. Journal of Applied Acoustics, 2017, 36(2): 95–104. |
| [15] | KEELE D B. The application of broadband constant beamwidth transducer (CBT) theory to loudspeaker arrays [C]//Audio Engineering Society Convention 109, Audio Eng. Soc., Los Angeles, 2000. |
| [16] | KEELE D B. Full-sphere sound field of constant-beamwidth transducer (CBT) loudspeaker line arrays [J]. J. Audio Eng. Soc., 2003, 51(7/8): 611–624. |
| [17] | ANDERSON B E, HUGHES W J, HAMBRIC S A. Grating lobe reduction in transducer arrays through structural filtering of supercritical plates [J]. J. Acoust. Soc. Am., 2009, 126(2): 612–619. |
| [18] | WOOH SC, SHI Y. Optimum beam steering of linear phased arrays [J]. Wave Motion, 1999, 29(3): 245–265. |
| [19] | KEELE D B. A performance ranking of seven different types of loudspeaker line arrays [C]//Audio Engineering Society Convention 129, Audio Eng. Soc., San Francisco, 2010. |
| [20] |
杜功焕, 朱哲民, 龚秀芬. 声学基础(第2版) [M]. 南京: 南京大学出版社, 2001.
DU Gong-huan, ZHU Zhe-min, GONG Xiu-fen. Fundamentals of acoustics (2nd edition) [M]. Nanjing: Nanjing University Press, 2001. |
| [21] | KEELE D B. Implementation of straight-line and flat-panel constant beamwidth transducer (CBT) loudspeaker arrays using signal delays [C]//Audio Engineering Society Convention 113, Audio Eng. Soc., Los Angeles, 2002. |
| [22] | URBAN M, HEIL C, BAUMAN P. Wavefront sculpture technology [J]. J. Audio Eng. Soc., 2003, 51(10): 912–932. |
 2018, Vol. 40
2018, Vol. 40
