在船舶推进领域中,因永磁同步电机具有体积小、结构简单、惯量小、功率因数高等优点而被广泛应用。其各环路的控制方式通常采用结构简单、鲁棒性强的传统PID控制技术。而在实际工作条件下,永磁同步电机往往被要求工作在高速度、负载扰动大的工况中,运用传统的PID控制策略对其进行控制,很难达到理想的控制效果。文献[1]的结论指出,基于分数阶微积分理论的PID控制器其动态和静态性能优于整数阶PID控制器,当被控对象为分数阶模型时,优势更为明显。文献[2]将分数阶PI控制器应用到永磁同步电机的调速控制系统中,有效提高了系统的抗干扰能力。随着分数阶微积分理论的不断完善,分数阶PIαDβ控制策略得到了控制领域的很大关注。文献[3]结合预瞄跟随理论设计了分数阶PIαDβ控制器,并应用于智能车的控制系统中,在系统模型参数发生变化时,能够很好的保证系统的稳定性。文献[4]采用Ziegler- Nicholes经验公式结合向量法来设计分数阶控制器并引入到液压伺服系统中,使系统获得了良好的稳态精度。
分数阶PIαDβ控制器是传统PID控制器向分数阶领域的推广,它比传统PID多了2个参数,积分项阶次α和微分项阶次β,因此具有更为灵活的调节范围。然而随着参数增多,分数阶PIαDβ控制器的参数整定变得较为困难。文献[5]将模糊自适应的思想应用到分数阶PIαDβ控制器的设计中,给出了参数的自适应规律。文献[6]采用反向传播神经网络对分数阶控制器的参数进行实时调整,利用该方法设计的控制器要比传统PID控制器的控制精度有所提高。本文设计了一种基于径向基神经网络的分数阶PIαDβ控制器。由于径向基神经网络收敛快速,结构简单,自适应能力强,便于实现对复杂的非线性系统进行控制。将它应用于分数阶PIαDβ控制器参数的在线整定,可以很好地解决控制器参数选取的难题,从而有利于分数阶控制器的实际应用。同时对船用永磁同步电机建立基于RBF神经网络分数阶PIαDβ的控制系统,有助于提高电机控制的综合性能。
1 分数阶PIαDβ控制器 1.1 分数阶微积分的定义分数阶微积分理论有特定的计算逻辑和描述方法,与整数阶微积分理论不相同。分数阶微积分算子一般被描述为
| $_aD_t^\alpha = \left\{ \begin{array}{l}{{\rm d}^\alpha }/{\rm d}{t^\alpha },\;\;\;\;\;\;\;\;R(\alpha ) > 0\text{,}\\1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;R(\alpha ) = 0\text{,}\\\int_a^t {{{({\rm d}\tau )}^{ - \alpha }},\;\;\;R(\alpha ) < 0}\text{。} \end{array} \right.$ |
式中:a和t为微积分算子的上下限;α为算子的任意阶次;R(α)为α的实部[7]。
在分数阶微积分理论的长期探索中,形成了3种分数阶微积分定义,分别为Grünwald-Letnikov定义、Riemann-Liouville定义和Caputo定义[8]。这里仅介绍Riemann-Liouville定义。Riemann-Liouville分数阶微分的定义为:
| $_aD_t^\alpha f(t) = \frac{1}{{\Gamma (n - \alpha )}}{\left( {\frac{{\rm d}}{{{\rm d}t}}} \right)^n}\int_a^t {\frac{{f(\tau )}}{{{{(t - \tau )}^{\alpha + 1 - n}}}}} {\rm d}\tau \text{,}$ | (1) |
Riemann-Liouville分数阶积分的定义为:
| $\begin{array}{l}_aI_t^\gamma f(t) = \displaystyle\frac{1}{{\Gamma ( - \gamma )}}\int_a^t {\frac{{f(\tau )}}{{{{\left( {t - \tau } \right)}^{\gamma + 1}}}}{\rm d}\tau } \text{,}\\[12pt]\Gamma (z) = \displaystyle\int_0^\infty {{e^{ - t}}} {t^{z - 1}}{\rm d}t\text{。}\end{array}$ | (2) |
式中,n为整数,微积分算子的阶次α在(n–1,n)区间内取值,γ∈R–,Γ(z)为伽马函数。
1.2 分数阶PIαDβ控制器及其离散传统PID控制器的数学模型为:
| $u(t) = {K_p}e(t) + {K_i}\int_0^t {e(\tau )} {\rm d}(\tau ) + {K_d}\frac{{{\rm d}e(t)}}{{{\rm d}t}}\text{,}$ | (3) |
式中:e(t)为系统的误差。
分数阶PIαDβ控制器是整数阶PID控制器的扩展,将式(3)推广到分数阶领域可得分数阶PIαDβ控制器的表达式为:
| $u(t) = {K_p}e(t) + {K_{i0}}I_t^{ - \alpha }e(t) + {K_{d0}}D_t^\beta e(t)\text{。}$ | (4) |
根据文献[6]中的方法对分数阶PIαDβ控制器进行离散,由于分数阶微积分算子α和β的取值范围一般在区间[0,1]之间,则综合考虑式(1),式(2)和式(4)可得类似于增量式PID控制器离散形式的分数阶PIαDβ控制器的离散表达式为:
| $u(k) = u(k - 1) + {K_p}a + {K_i}\frac{b}{{\Gamma (\alpha )}} + {K_d}\frac{c}{{\Gamma (1 - \beta )}}\text{,}$ | (5) |
| $a = e(k) - e(k - 1)\text{,}$ | (6) |
| $b = \sum\limits_{i = 1}^k {\frac{{e(i)}}{{{{(k + 1 - i)}^{1 - \alpha }}}} - \sum\limits_{i = 1}^{k - 1} {\frac{{e(i)}}{{{{(k - i)}^{1 - \alpha }}}}} } \text{,}$ | (7) |
| $c = \sum\limits_{i = 1}^k {\frac{{e(i)}}{{{{(k + 1 - i)}^\beta }}} - 2\sum\limits_{i = 1}^{k - 1} {\frac{{e(i)}}{{{{(k - i)}^\beta }}} + \sum\limits_{i = 1}^{k - 2} {\frac{{e(i)}}{{{{(k - 1 - i)}^\beta }}}} } } \text{。}$ | (8) |
式中:k为运算次数且是大于或等于3的整数;e(1)=e(2)近似为0。
2 RBF神经网络分数阶PIαDβ控制器 2.1 RBF神经网络的结构RBF神经网络一般为包含输入层、隐层和输出层的3层网络结构,隐层输入到输出的映射是非线性的,而输出层的输入与输出为线性关系[9]。网络的结构如图1所示。

|
图 1 径向基神经网络的结构 Fig. 1 Structure of radial basis function neural network |
在网络结构中
| ${h_i} = \exp \left( { - \frac{1}{{2{\sigma _i}^2}}{{\left\| {X - {C_i}} \right\|}^2}} \right)\text{。}$ |
| $ym = {\omega _1}{h_1} + {\omega _2}{h_2} + \cdot \cdot \cdot {\omega _m}{h_m}\text{。}$ | (9) |
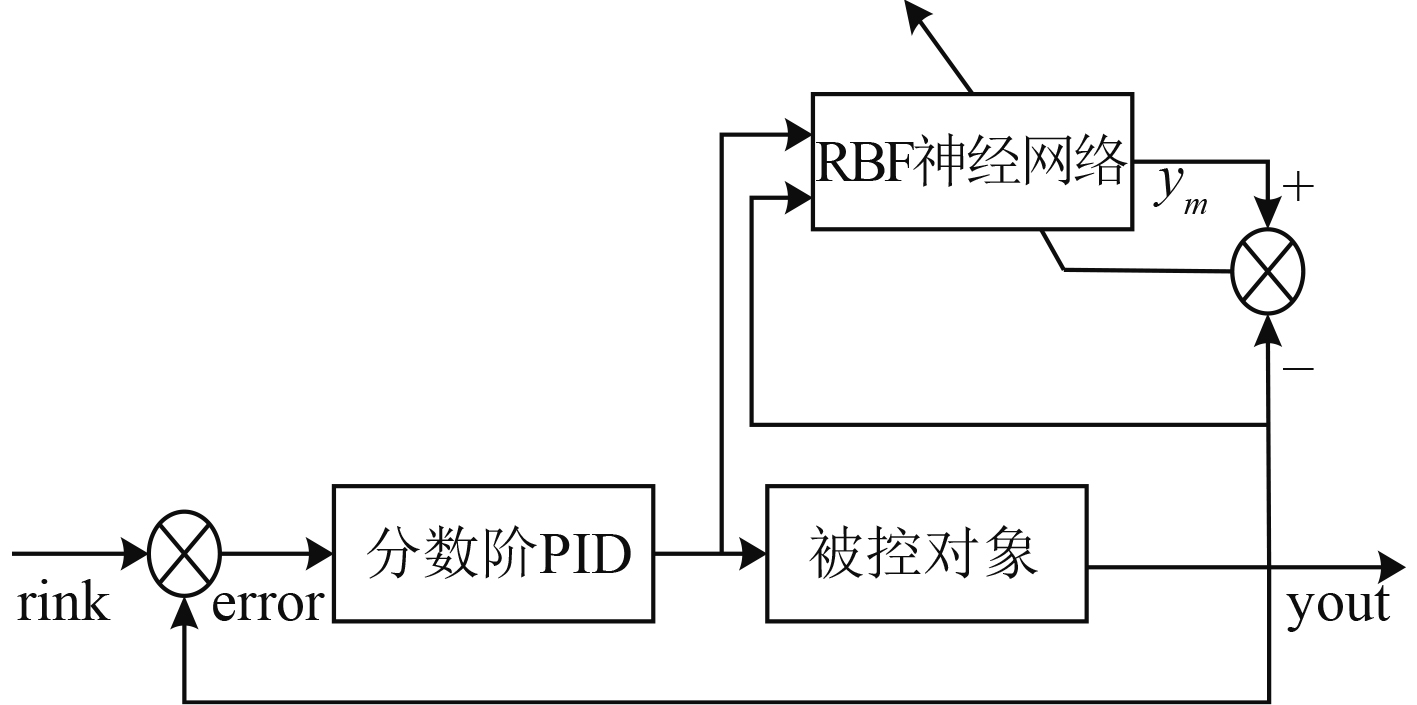
本文将RBF神经网络作为辨识器对分数阶PIαDβ控制器的参数进行实时调节,控制结构如图2所示。设计的RBF神经网络包括3个输入节点、6个隐层节点和1个线性输出节点。神经网络的输入分别为被控对象的输入、被控对象的输出和上一时刻的被控对象输出。
|
图 2 RBF神经网络整定控制器参数的结构 Fig. 2 Structure of RBF neural network tuning controller parameters |
设在k时刻被控对象的输入为u(k),输出为yout(k),辨识网络的输出为ym(k),则辨识系统的指标可表示为:
| $J = \frac{1}{2}{(yout(k) - ym(k))^2}\text{。}$ |
在辨识器整定分数阶PIαDβ控制器参数的过程中,网络的隐层节点中心值cij、基宽参数σi和输出权值ωi被实时调节,调节的方式则根据梯度下降法来实现。具体的调节公式如下:
| $\begin{array}{l}{\omega _i}(k) = {\omega _i}(k - 1) + \eta (yout(k) - ym(k)){h_i}+\\\;\;\;\;\;\;\;\;\;\;\; a\left( {{\omega _i}(k - 1) - {\omega _i}(k - 2)} \right)\text{,}\\{\sigma _i}(k) = {\sigma _i}(k - 1) + \eta \Delta {\sigma _i} + a\left( {{\sigma _i}(k - 1) - {\sigma _i}(k - 2)} \right)\text{,}\\{c_{ij}}(k) = {c_{ij}}(k - 1) + \eta \Delta {c_{ij}} + a\left( {{c_{ij}}(k - 1) - {c_{ij}}(k - 2)} \right)\text{。}\end{array}$ |
式中:η为学习速率;a为动量因子。
| $\begin{array}{l}\Delta {\sigma _i} = (yout(k) - ym(k)){\omega _i}{h_i}\frac{{{{\left\| {X - {C_i}} \right\|}^2}}}{{{\sigma _i}^3}}\text{,}\\\Delta {c_{ij}} = (yout(k) - ym(k)){\omega _i}\frac{{{x_i} - {c_{ij}}}}{{{\sigma _i}^2}}\text{。}\end{array}$ |
在分数阶PIαDβ控制器参数整定的过程中,首先根据积分阶次α和微分阶次β对控制系统的影响以人工的方式进行调节并选取适当的值。其次由辨识器对Kp,Ki,Kd三个参数进行整定。
参数整定的指标取:
| $\begin{array}{l}E(t) = \displaystyle\frac{1}{2}error{(k)^2}\text{,}\\error(k) = rin(k) - yout(k)\text{。}\end{array}$ | (10) |
式中:rin(k)为k时刻系统的给定输入。
Kp,Ki,Kd三个参数通过采用梯度下降法进行调节,结合式(5)、式(6)、式(7)、式(8)和式(10)可得各参数变化量的表达式为:
| $\begin{align}\Delta {K_p} =& - {\eta _p}\frac{{\partial E}}{{\partial {K_p}}} = - {\eta _p}\frac{{\partial E}}{{\partial yout}}\frac{{\partial yout}}{{\partial u}}\frac{{\partial u}}{{\partial {K_p}}}=\\& {\eta _p}error(t)\frac{{\partial yout}}{{\partial u}}a\text{,}\\\Delta {K_i} =& - {\eta _i}\frac{{\partial E}}{{\partial {K_i}}} = - {\eta _i}\frac{{\partial E}}{{\partial yout}}\frac{{\partial yout}}{{\partial u}}\frac{{\partial u}}{{\partial {K_i}}}=\\& {\eta _i}error(t)\frac{{\partial yout}}{{\partial u}}\frac{b}{{\Gamma (\alpha )}}\text{,}\\\Delta {K_d} = & - {\eta _d}\frac{{\partial E}}{{\partial {K_d}}} = - {\eta _d}\frac{{\partial E}}{{\partial yout}}\frac{{\partial yout}}{{\partial u}}\frac{{\partial u}}{{\partial {K_d}}}=\\&{\eta _d}error(t)\frac{{\partial yout}}{{\partial u}}\frac{c}{{\Gamma (1 - \beta )}}\text{。}\end{align}$ |
式中:ηp,ηi,ηd为Kp,Ki,Kd三个参数对应的学习速率;∂yout/∂u为被控对象的Jacobian信息[9],可以通过神经网络的辨识获得,由式(9)得其表达式为:
| $\frac{{\partial yout}}{{\partial u}} \approx \sum\limits_{i = 1}^6 {{w_i}{h_i}} \frac{{{c_{i1}} - u(k)}}{{\sigma _i^2}}\text{。}$ |
永磁同步电机在三相静止坐标系下的电压平衡方程式[10]为:
| $\begin{split}&\left[ {\begin{array}{*{20}{l}}{{U_A}}\\{{U_B}}\\{{U_C}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{R_A} + P{L_A}}&{P{M_{AB}}}&{P{M_{AC}}}\\{P{M_{BA}}}&{{R_B} + P{L_B}}&{P{M_{BC}}}\\{P{M_{CA}}}&{P{M_{CB}}}&{{R_C} + P{L_C}}\end{array}} \right]\\&\left[ {\begin{array}{*{20}{l}}{{i_A}}\\{{i_B}}\\{{i_C}}\end{array}} \right] - {\omega _r}{\varphi _r}\left[ {\begin{array}{*{20}{l}}{\sin \theta }\\{\sin \left(\theta - \frac{2}{3}\pi \right)}\\[2pt]{\sin \left(\theta + \frac{2}{3}\pi \right)}\end{array}} \right]\text{。}\end{split}$ | (11) |
式中:UA,UB,UC为三项绕组的电压;RA,RB,RC为三项定子绕组的电阻;LA,LB,LC为三相绕组的电感;P为微分算子;ψr为转子永磁体磁链;θ为ψr与A项绕组间的夹角;ωr为转子角频率;Mxy=Myx为绕组间的互感。
由式(11)经坐标转换得到dq0坐标系下的电压方程为:
| $\left[ \begin{array}{l}{U_d}\\{U_q}\end{array} \right] = \left[ {\begin{array}{*{20}{c}}{{R_s} + p{L_d}} & {{\rm{ - }}{{\rm{L}}_q}{\omega _r}}\\{{L_d}{\omega _r}} & {{{\rm{R}}_s} + p{L_q}}\end{array}} \right]\left[ \begin{array}{l}{I_d}\\{I_q}\end{array} \right] + {\omega _r}{\psi _r}\left[ \begin{array}{l}0\\1\end{array} \right]\text{。}$ |
式中:Ud,Uq均为电机的直交轴电压;Rs均为电枢绕组的电阻;Ld,Lq均为直交轴电感;Id,Iq均为直交轴电流。
在dq0坐标系下的电磁转矩方程为:
| ${T_e} = \frac{3}{2}{n_p}\left( {{\psi _r}{I_q} + ({L_d} - {L_q}){I_d}{I_q}} \right)\text{,}$ |
式中np为电机磁极对数。
电机的机械动力学方程为:
| ${T_e} - {T_L} - B{\omega _m} = J\frac{{{\rm d}{\omega _m}}}{{{\rm d}t}}\text{。}$ |
式中:TL为电机负载转矩;B为电机阻尼系数;J为电机转动惯量;ωm为电机机械角速度。
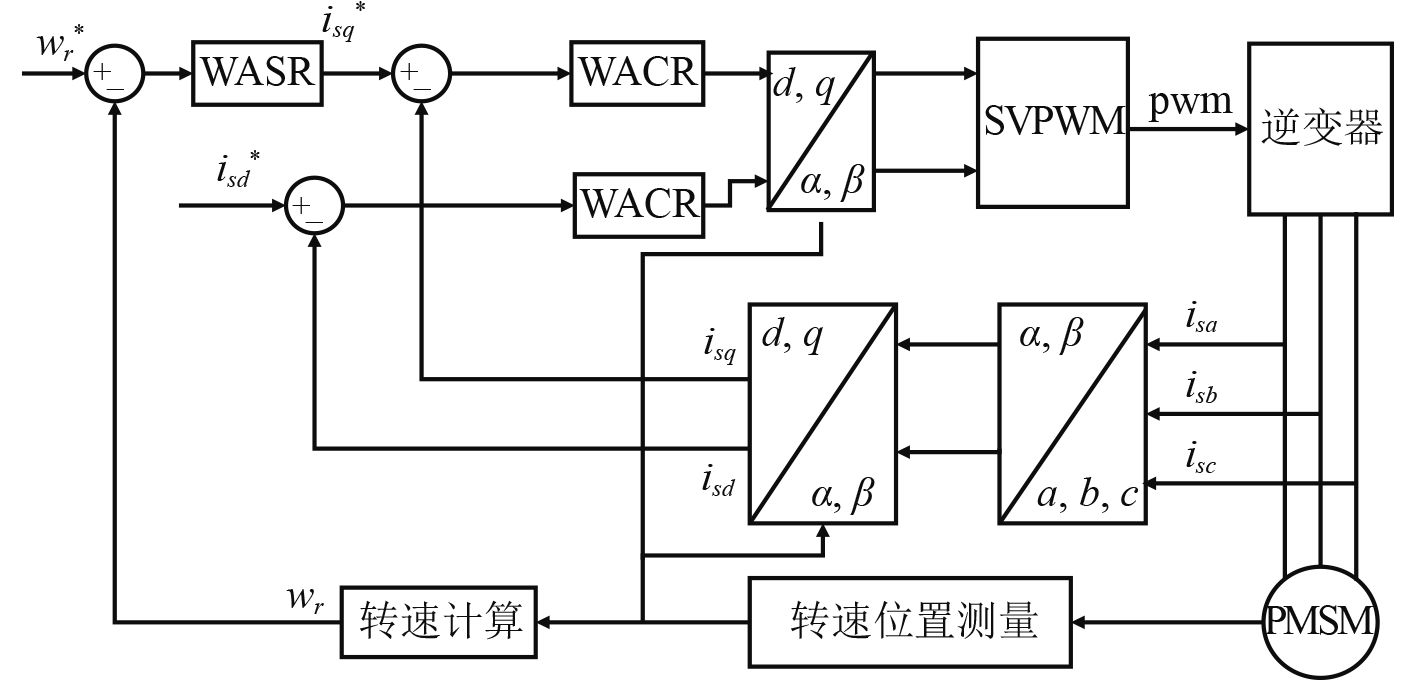
4 系统仿真船用永磁同步电机的调速系统一般采用双闭环级联的控制结构,如图3所示[11]。系统的内环为电流环,外环为速度环。电流环的调节器WACR使用传统的PI控制器,速度环的调节器采用设计的RBF神经网络分数阶PIαDβ控制器。
|
图 3 船用永磁同步电机控制结构 Fig. 3 Control structure of marine permanent magnet synchronous motor |
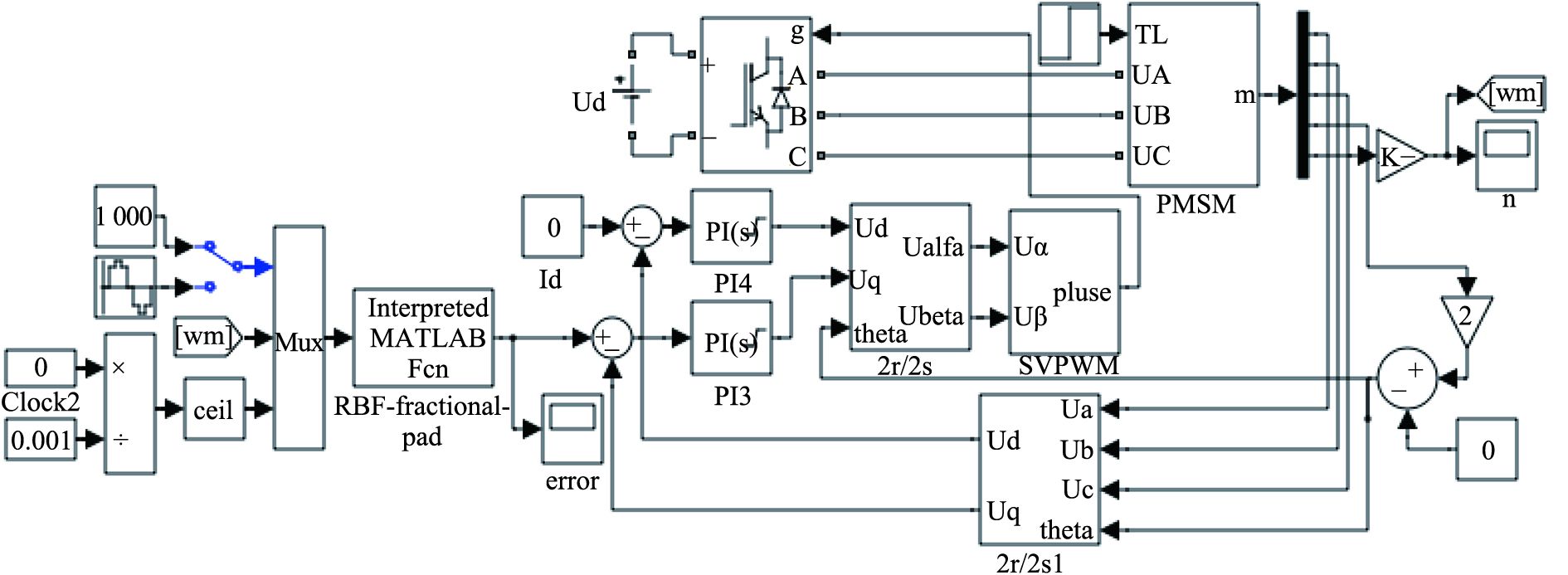
在Matlab/simulink下搭建船用永磁同步电机矢量控制的仿真模型如图4所示,模型中电机参数设置如下:极对数为2,定子电阻为0.875 Ω,直交轴电感为8.37 mH,转动惯量为0.083 2 kg·m2,转子永磁体磁链为0.175 Wb。经过反复仿真调试,当电流环交轴PI控制器的比例系数取5,积分系数取2.8,电流环直轴PI控制器的比例系数取6,积分系数取2.8时,可使电流环回路响应速度较快且无超调。当RBF神经网络分数阶PIαDβ控制器中的参数学习速率取0.3,动量因子取0.05,Kp,Ki,Kd的初值取3,0.5,0.1,对应的学习速率取0.2,0.2,0.02,微分项阶次β取0.96,积分项阶次α取0.89,隐层中心值cij的初值取100,隐层节点的基宽σi的初值取150,输出权值ωi的初值取80时调速效果较好。
|
图 4 船用永磁同步电机速度控制仿真模型 Fig. 4 Simulation model of speed control for marine permanent magnet synchronous motor |
为了验证RBF神经网络分数阶PIαDβ控制器的性能,这里将传统PID控制器、分数阶PIαDβ控制器和设计的控制器分别应用于电机的调速系统中并进行对比仿真实验。在模拟实际运行环境的情况下,得到的仿真结果如下:
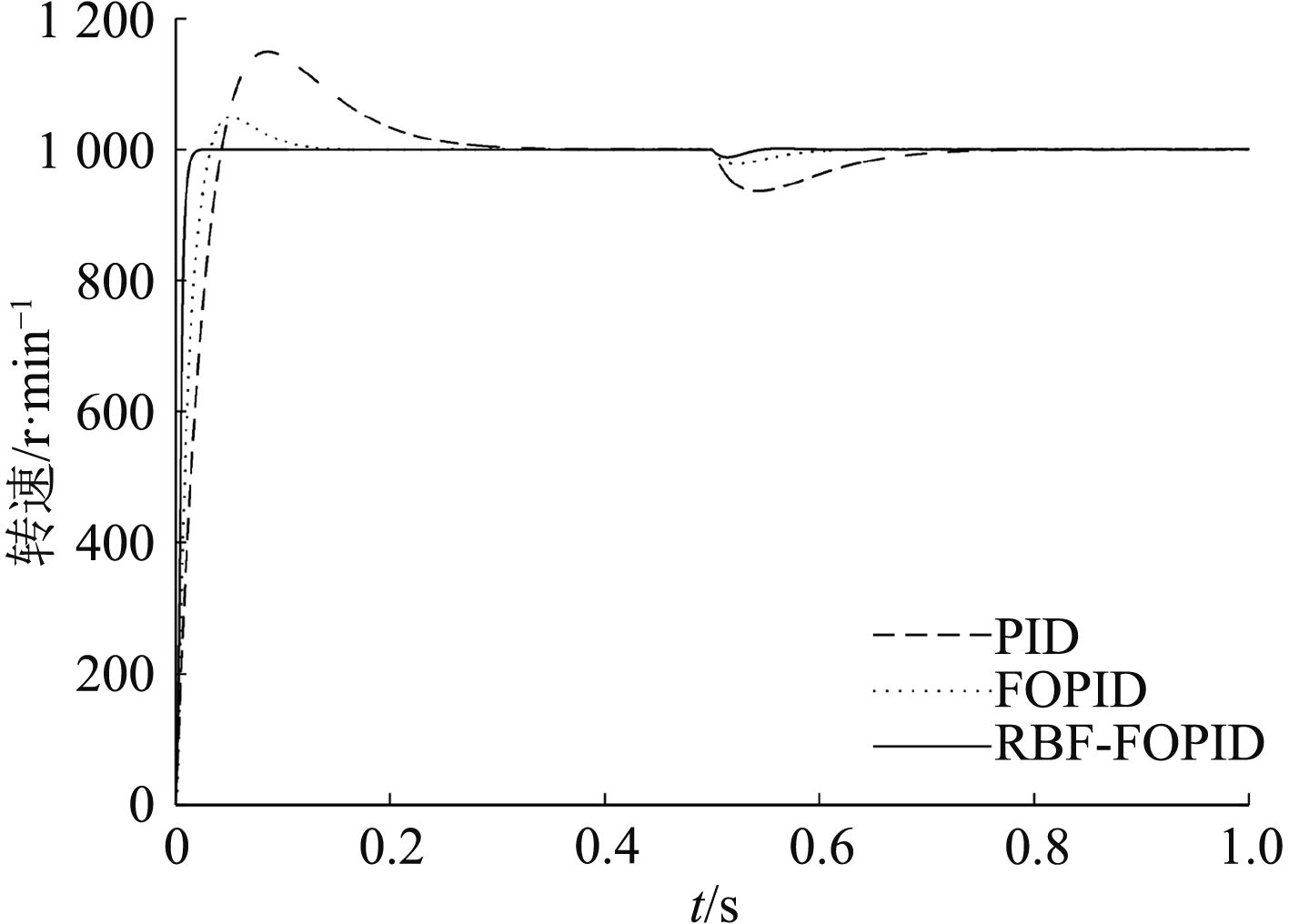
1)电机空载启动,给定转速为1 000 r/min,在t=0.5 s时刻突加负载力矩TL=30 N·m,得到的转速变化曲线和转速误差变化曲线如图5和图6所示。
|
图 5 电机转速的变化曲线 Fig. 5 The curves of motor speed |
|
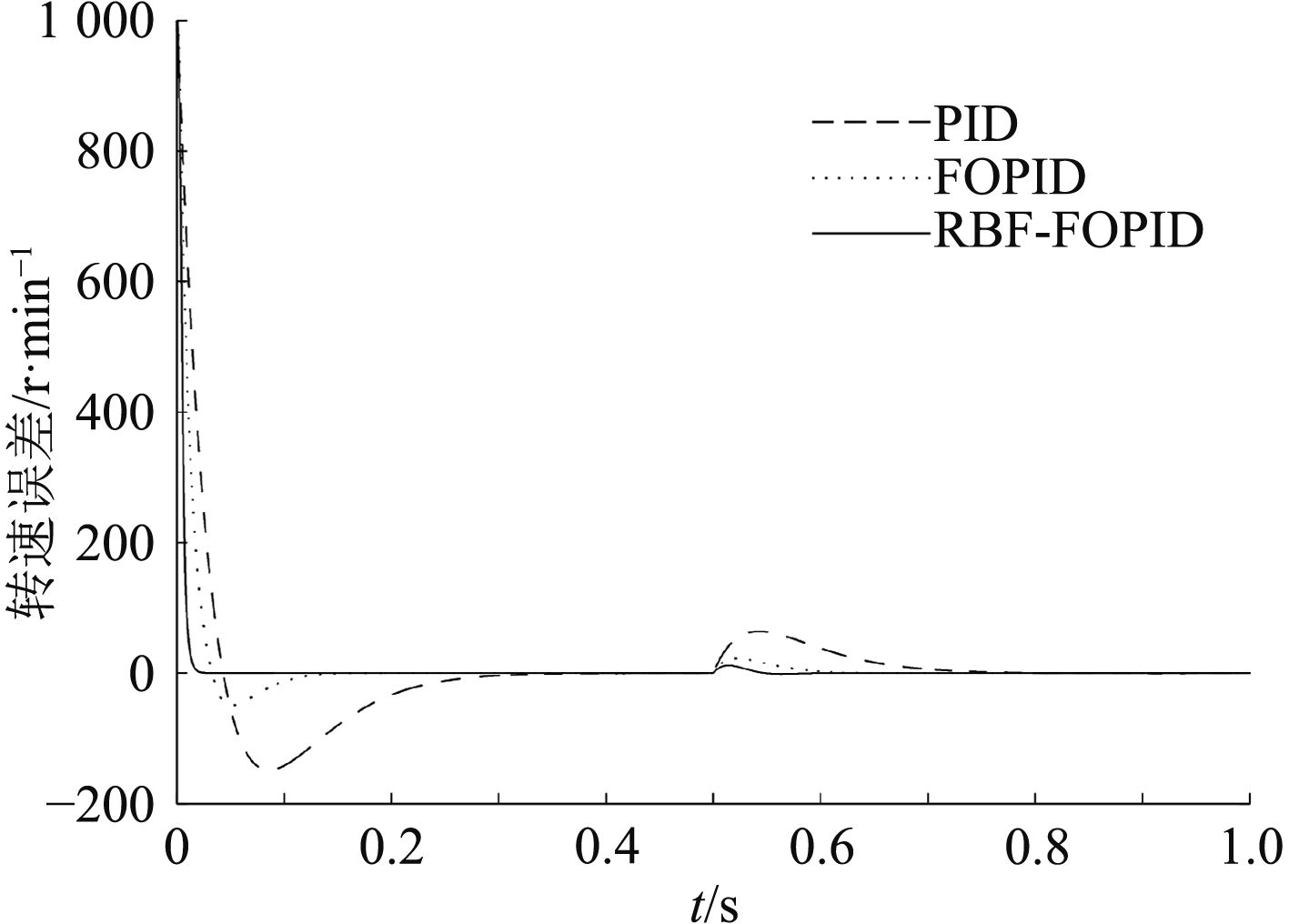
图 6 电机转速误差的变化曲线 Fig. 6 The curves of motor speed error |
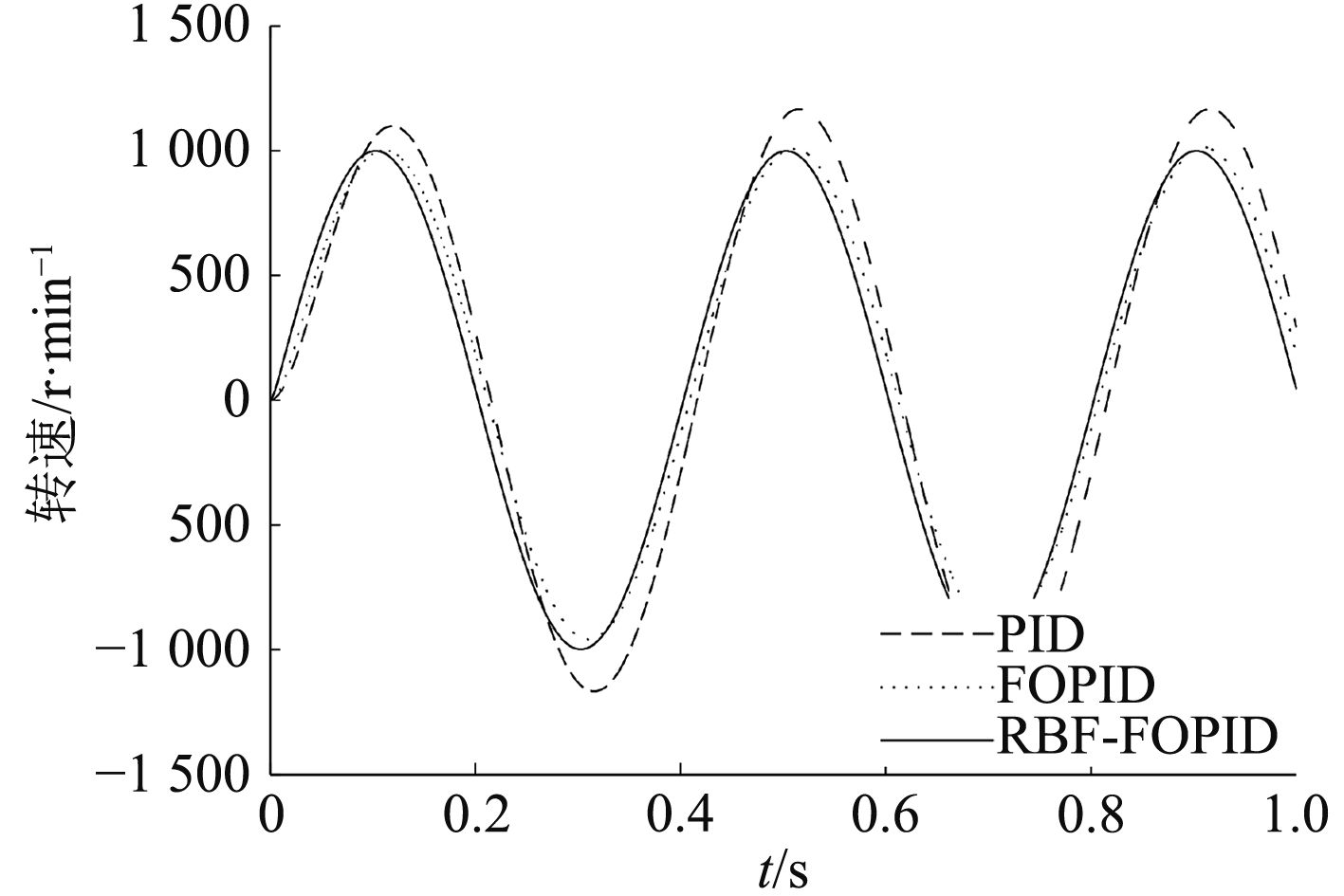
2)在给系统施加30 N·m负载力矩的情况下,给定速度为正弦波,周期为0.5 s,峰值为1 000 r/min。在系统运行1 s后得到的转速变化曲线和跟随误差变化曲线如图7和图8所示。
|
图 7 跟踪正弦波时电机转速的变化曲线 Fig. 7 The curves of the motor speed tracking sine wave |
|
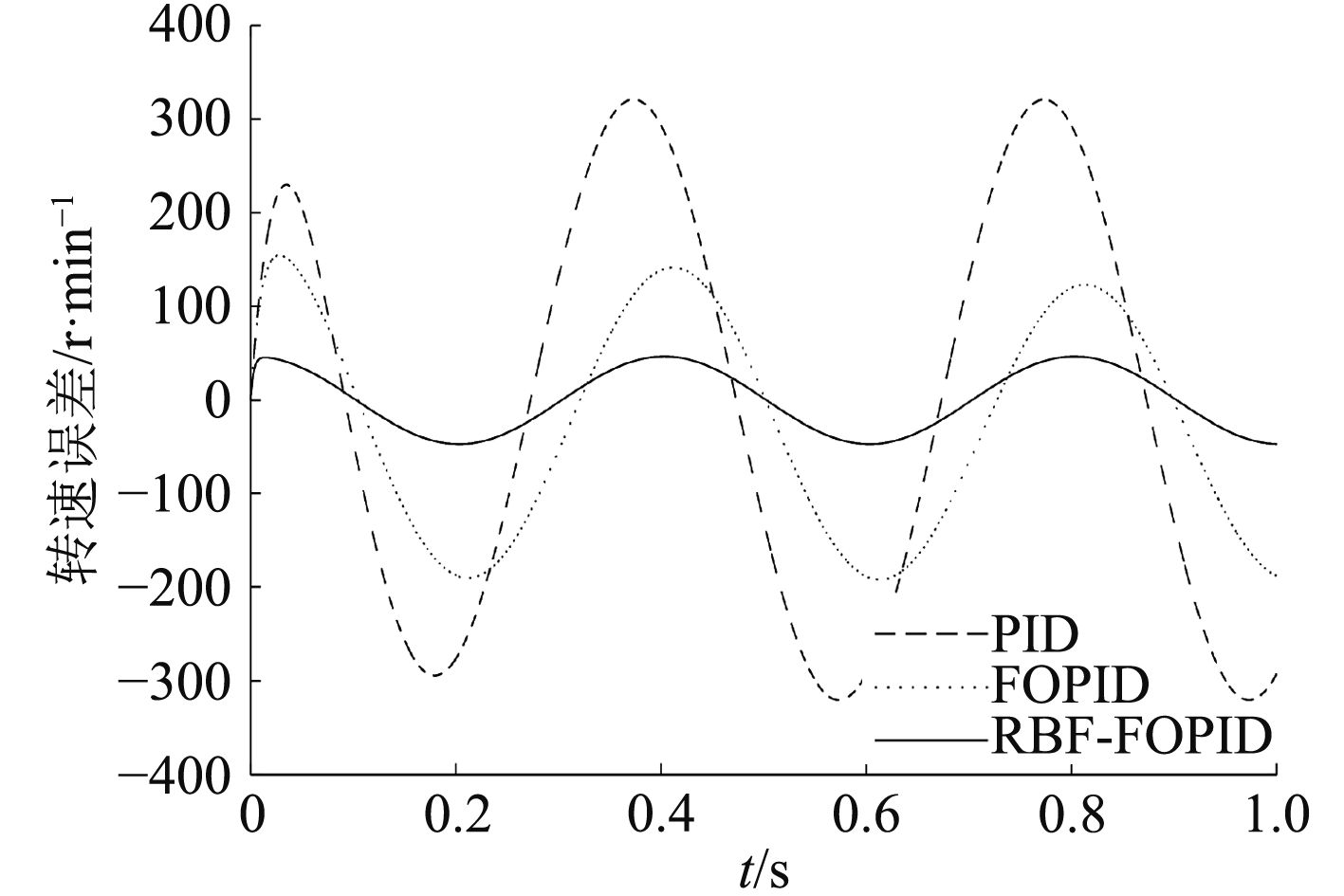
图 8 跟踪正弦波时电机转速误差的变化曲线 Fig. 8 The error curves of the motor speed tracking sine wave |
由图5和图6的波形可以看出,采用传统PID的速度调节器,在空载启动时超调量达到了16.7%,负载发生变化后,需0.3 s的调节时间方可使转速恢复到设定值。分数阶PID控制器的超调量较小为4.3%,调节时间较短为0.1 s。而RBF神经网络分数阶PIαDβ控制器的超调量几乎为0,调节时间仅为 0.08 s。在给定转速为正弦波的条件下,由图7和图8可以得出传统PID控制器的转速跟踪误差在–300~300 r/min之间,分数阶PID控制器的跟踪误差范围较小,在–150~150 r/min之间,RBF神经网络分数阶PIαDβ控制器的跟踪误差仅在–50~50 r/min之间变化。通过以上的数据对比可以说明RBF神经网络分数阶PIαDβ控制器在限制超调量,稳定跟踪方面性能较为优越。
5 结 语本文将RBF神经网络、分数阶微积分理论和PID控制理论相结合,设计了一种用于解决船用永磁同步电机工作在高速度、大负载扰动下难以实现良好性能的速度调节器。通过与分数阶PIαDβ控制器和传统PID控制器的对比仿真实验表明,RBF神经网络分数阶PIαDβ控制器响应速度快、鲁棒性强,能够提高船用永磁同步电机调速系统的控制精度,增强系统对时变速度的跟踪性能。
| [1] |
薛定宇, 赵春娜. 分数阶系统的分数阶PID控制器设计[J]. 控制理论与应用, 2007, 24(5): 771–776.
XUE Ding-yu, ZHAO Chun-na. Fractional order PID controller design for fractional order system[J]. Control Theory and Applications, 2007, 24(5): 771–776. https://www.wenkuxiazai.com/doc/cf237a02b52acfc789ebc9e2-2.html |
| [2] | 薛薇, 李永丽, 路鸦立. 永磁同步电机分数阶智能积分调速控制[J]. 电机与控制学报, 2015, 19(5): 67–73. http://www.cqvip.com/QK/90977A/201505/664891947.html |
| [3] | 吴振宇, 赵亮, 冯林. 基于分数阶PID控制器的智能车控制[J]. 控制工程, 2011, 18(3): 401–404. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jczdh201103020 |
| [4] | BAI Duan-yuan, WANG Chun-yang. Parameter calibration and simulation of fractional PID controller for hydraulic servo system[C]//In Proc. of the 28st the Chinese conference Decision and Control conference (CCDC), Yinchuan, China in May 28–30, 2016: 1704–1708. |
| [5] | 梁涛年, 陈建军, 王媛, 等. 分数阶系统模糊自适应分数阶PIλDμ控制器[J]. 北京工业大学学报, 2013, 39(7): 1040–1045. http://www.eope.net/gxjmgc/CN/abstract/abstract16224.shtml |
| [6] |
毛书军, 盛贤军. 一种神经网络分数阶PID控制器的实现[J]. 计算机应用, 2014, 34(s2): 166–168.
MAO Shu-jun, SHENG Xian-jun. Implementation of an neural network fractional order PID controller[J]. Journal of Computer Applications, 2014, 34(S2): 166–168. http://d.wanfangdata.com.cn/Periodical_jsjyy2014z2046.aspx |
| [7] | 王春阳. 分数阶控制系统设计[M]. 北京: 国防工业出版社, 2014: 4–21. |
| [8] |
李姗姗, 赵春娜, 关永, 等. 分数阶微积分定义的一致性在HOL4中的验证[J]. 计算机科学, 2016, 43(3): 23–26.
LI Shan-shan, ZHAO Chun-na, GUAN Yong, et al. Formalization of consistency of fractional calculus in HOL4[J]. Computer Science, 2016, 43(3): 23–26. |
| [9] | 周品. MATLAB神经网络设计与应用[M]. 北京: 清华大学出版社, 2013: 232–238. |
| [10] | 阮毅, 陈伯时. 电力拖动自动控制系统: 运动控制系统[M]. 北京: 机械工业出版社, 2009: 243–246. |
| [11] | 王瑞萍. 基于分数阶控制器的永磁同步电动机速度控制研究[D]. 广州: 华南理工大学, 2012. |
 2018, Vol. 40
2018, Vol. 40
