SCR系统的作用是将废气中的NOx通过与NH3反应,从而实现将有害的NOx还原为无毒害作用的N2[1],在众多的脱硝技术中,SCR技术能够有效降低烟气中NOx的含量[2]。在该反应过程中,催化剂的活性是反应能够高效进行的重要保障。烟气中的飞灰对催化剂的性能有很大的影响,Hans Sobolewski等[3]通过研究表明,烟气中的灰尘对催化剂的冲蚀与堵塞,会在一定程度上引起催化剂活性的物理惰性,Karina Rigby等[4]研究表明,烟气中的灰尘对催化剂孔道的堵塞也会引起催化剂活性的物理惰性。文小于等[5]研究表明,废气中含有的大量碱金属会对催化剂参数很强的化学毒害作用,导致催化剂活性降低。
排烟中的积灰松散,其形成原因是燃烧产生的灰粒随排烟漂浮至催化剂表面,细小的灰粒在层流状态下聚集于SCR反应器的上游部位,凝聚并最终掉落到催化剂表面,形成搭桥、堵塞。松散型积灰主要受重力、范德华力、表面张力作用,不受化学力作用[6]。资料显示这种积灰的粘结强度在50~250 Pa之间,较容易清除[7]。为降低积灰对柴油机以及SCR系统影响,需要采用吹灰装置及时地将积灰清除。压缩空气在船舶上易得,一般都能达到较好地吹扫效果。
喷孔的孔径大小、压缩空气压力的大小这些参数都会对喷孔的性能产生较大的影响,孔径太大会浪费掉大量的压缩空气,孔径太小又达不到吹扫效果,因此,本文对基于压缩空气式的SCR吹灰装置进行有限元分析,利用计算流体动力学的软件来分析喷孔直径、喷射压力、气耗比、吹扫强度之间的关系。
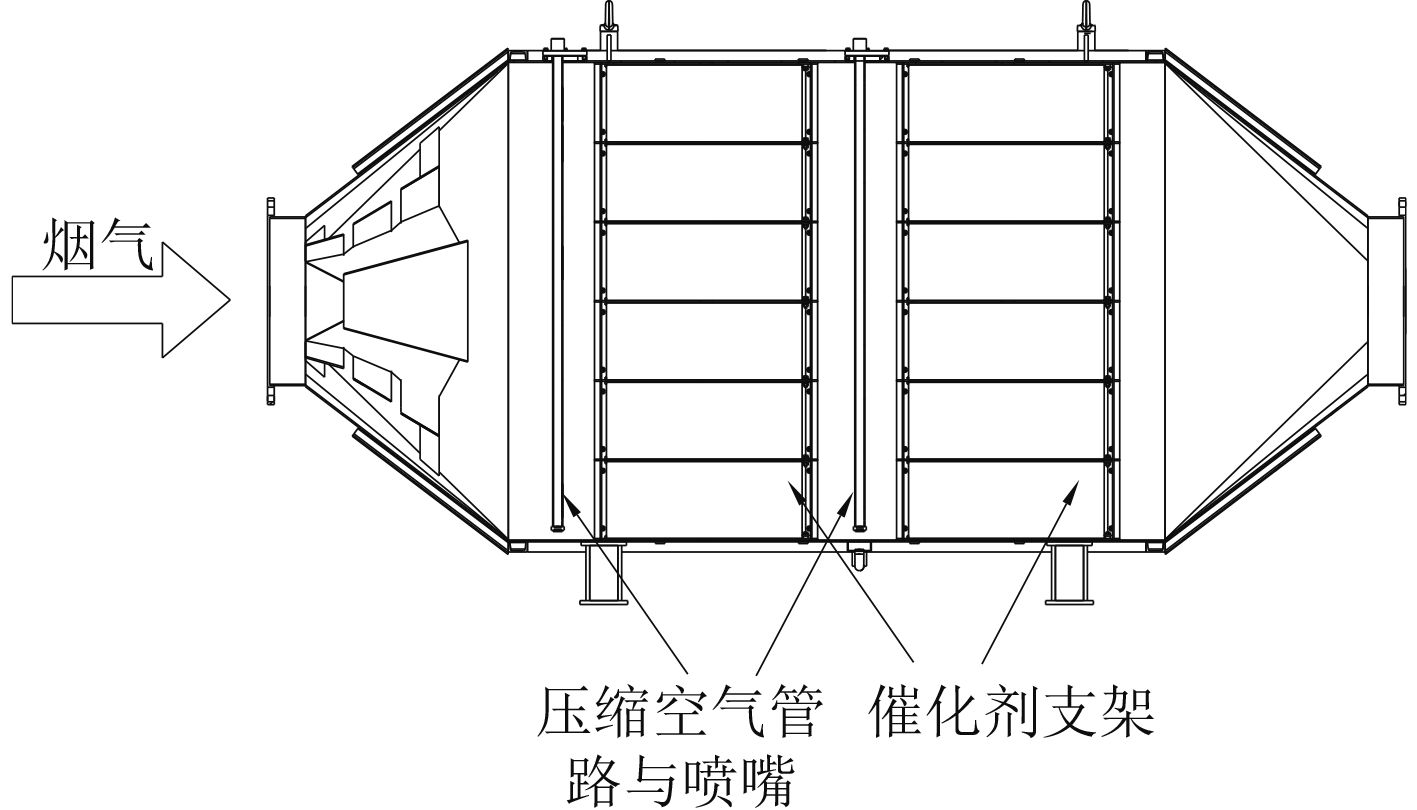
1 吹灰装置布置吹灰装置中的吹灰管路布置与催化剂前,与烟气的入口呈现就近原则,其布置方案如图1所示,某型低速柴油机的SCR吹灰器管路布置如图2所示。
|
图 1 催化剂与吹灰管路布置示意图 Fig. 1 Schematic diagram of catalyst and soot blowing pipeline |

|
图 2 SCR反应器吹灰器管路 Fig. 2 SCR reactor soot blower pipe |
压缩空气进入吹灰器的管路,高压空气从管路上的小孔喷出,从而实现对于沉积在催化剂表面的机会进行清除。
2 喷孔有限元模型本文选择压缩空气式的吹扫方式。在吹扫管路中上面有很多吹扫小孔,为获得最佳的吹扫方案,首先要获得单个喷孔在不同孔径、不同工况下的吹扫特性,综合耗气量、吹扫范围、管路布置方案等因素以确定管路喷孔数量和喷孔布置位置,从而确定最优的压缩空气管路与喷孔的布置方案。
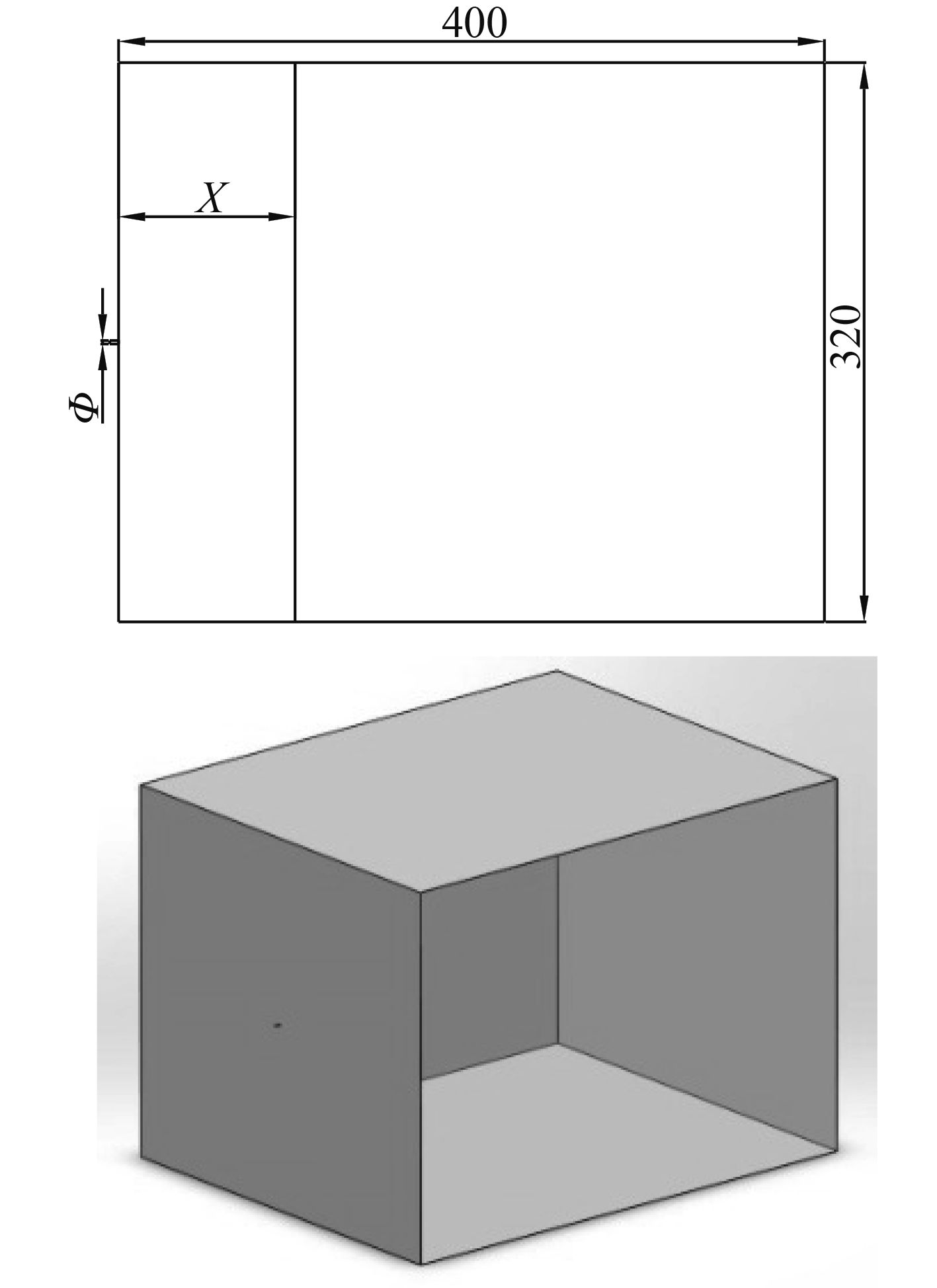
2.1 喷孔几何模型从喷孔的可加工性等角度出发,分别选择喷孔直径为1 mm,1.5 mm,2 mm,2.5 mm 等4种方案进行研究。压缩空气管路选择船用不锈钢管。从催化剂的规格以及计算经验的角度出发,选择喷孔计算域的尺寸为320 mm×320 mm×400 mm,X表示截面与喷孔末端的距离。喷孔计算域的二维模型和三维模型如图3所示。
|
图 3 喷孔计算域模型 Fig. 3 Calculation model of noozle |
结构网格在拓扑结构上相当于矩形域内的均匀网格,节点定义在每一层的网格线上,且每一层上节点数都相等,这样使复杂外形的贴体网格生成比较困难。非结构网格没有规则的拓扑结构[8 – 9],也没有层的概念,网格节点的分布随意,因此具有灵活性。
由于本模型相对较为简单,能够较好地对模型进行六面体网格划分[10 – 12],所以采用网格质量相对较高、计算时间较短、收敛性较好的六面体网格进行划分。网格划分结果如图4所示。

|
图 4 网格模型 Fig. 4 Mesh model |
本模型采用六面体网格划分网格质量在0.65~1,网格质量较高,能够满足计算精度的需求。网格划分节点数约为23万个,单元数约为25万个。
2.3 数值计算方法与边界条件本文的流场计算分析是基于纳维-斯托克斯方程(N-S)进行求解[13],利用商用的Fluent软件作为计算平台,对该模型就行流场分析计算。N-S方程在直角坐标系中可以写成:
| $\begin{split}& \rho \frac{{{\rm d}u}}{{{\rm d}t}} = - \frac{{\partial p}}{{\partial x}} + \rho X + \mu \Delta u\text{,}\\& \rho \frac{{{\rm d}v}}{{{\rm d}t}} = - \frac{{\partial p}}{{\partial y}} + \rho Y + \mu \Delta v\text{,}\\& \rho \frac{{{\rm d}w}}{{{\rm d}t}} = - \frac{{\partial p}}{{\partial z}} + \rho Z + \mu \Delta w\text{。}\end{split}$ |
式中:u,v为沿着x,y方向上的速度分量;t为时间;p为压力;ρ为密度;ν为运动粘性系数。在不同条件下,N-S方程的数学性质也不一样。
在CFD中湍流控制一般选择k-ε两方程计算模型,标准k-ε湍流模型,是针对湍流发展非常充分的湍流流动来建立的,是一种针对高Re数的湍流计算模型,标准k-ε模型中,对于Reynolds应力的各个分量,假定粘度系数μt相同。而在弯曲流线的情况下,湍流各向异性,μt应该是各向异性的张量,因此标准k-ε模型对于强旋流、弯曲壁面流动或弯曲流线流动时,会产生一定失真。
Realizable k-ε模型已被有效地用于各种不同类型的流动模拟,包括旋转均匀剪切流、包含有射流和混合流的自由流动、管道内流动、边界层流动,以及带有分离的流动等。
本文采用的湍流模型为Realizable k-ε两方程湍流模型[14 – 15],因为气体流动较为复杂,湍流模型能较为真实地描述流动中主要的物理过程,有较好的通用性和精度,且不需要太大的计算量,是目前应用最广、在科学研究及工程实际中得到广泛检验和成功应用的模型。在此模型中k方程及ε方程如下:
| $\begin{split}& \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\& \quad{G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k}\text{,}\\& \frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \frac{\partial }{{{x_j}}}\left( {\rho \varepsilon {u_j}} \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \\& \rho {C_1}{S_E} - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }} + {C_{1E}}\frac{\varepsilon }{k}{C_{3\varepsilon }}{G_b} + {S_\varepsilon }\text{。}\end{split}$ |
因为在流体流动过程中遵循质量守恒与动量守恒,质量守恒方程又称连续性方程:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = {S_m}\text{,}$ |
在惯性坐标系中i方向上的动量守恒方程为:
| $\frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} + \rho {g_i} + {F_i}\text{。}$ |
采用速度与压力耦合的Coupled方法进行求解,压力、密度、动量等均采用求解精度较高的二阶迎风格式进行离散。喷孔进口设置压力入口,压力取值分别为5~20 bar,选择计算域出口为压力出口,设置为标准大气压。
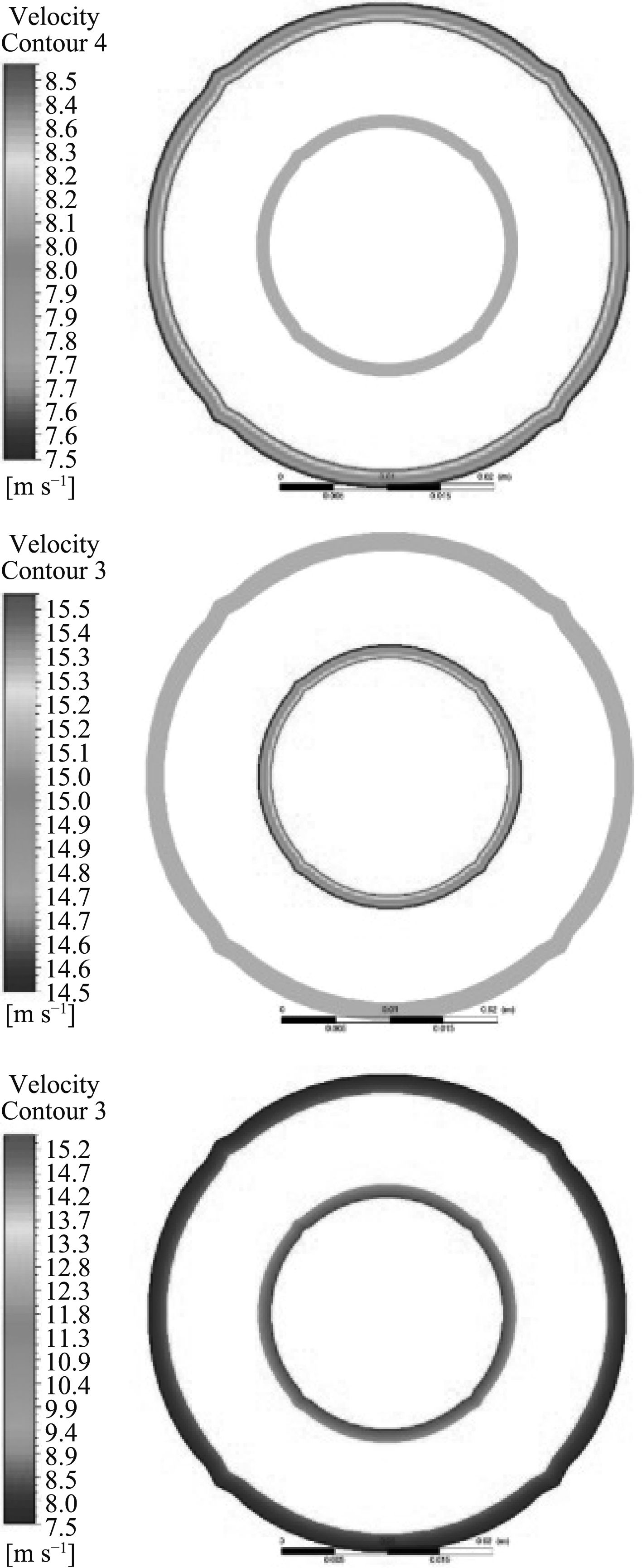
3 有限元分析 3.1 吹扫强度与气流速度关系根据动量定理Ft=mv,可以推导为F=v×(m/t),m/t为压缩空气流经截面的质量流量,kg/s,通过Fluent软件可以计算出在某一截面上的平均作用力,也可以剪切出在某一速度区间内的在截面上所形成的面积。根据P=F/S,可求得此截面上压强。以下计算的是喷孔直径为1 mm,喷射压力为5 bar,距喷孔为200 mm,不同速度范围的剪切面速度,如图5所示。
|
图 5 剪切面速度云图 Fig. 5 Diagram of shear plane velocity |
在X=200 mm截面上以速度范围7.5~8.5 m/s和14.5~15.5 m/s区域形成2个圆环。通过计算,可以得到在此剪切截面的面积以及在此截面上的平均作用力如表1所示。
|
|
表 1 不同速度范围内剪切面面积、作用力、压强 Tab.1 Shear surface area,force,pressure of different velocity scale |
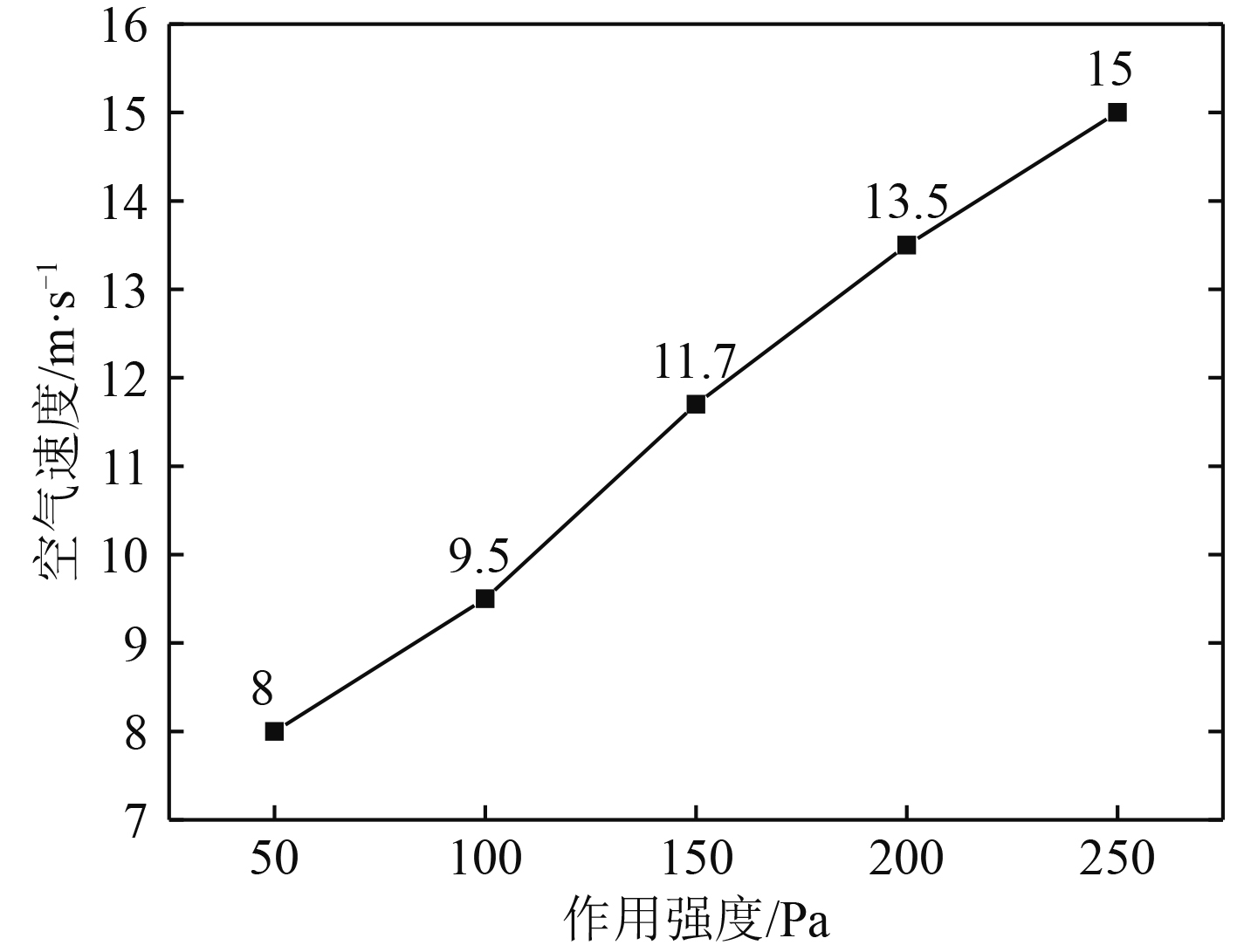
根据此原则,确定了作用强度分别为50 Pa,100 Pa,150 Pa,200 Pa,250 Pa所对应的空气速度,如图6所示。
|
图 6 空气速度与作用强度关系图 Fig. 6 Relationship between air velocity and action intensity |
通过作用强度f与空气速度v之间的关系曲线可得作用强度在50~250 Pa之间时,空气速度与作用强度之间呈线性关系,拟合方程为:
| $v = 0.036f + 6.14\text{,}$ |
式中:v为空气速度,m/s;f为作用强度,Pa。
3.2 吹扫范围与孔径、压力关系吹扫范围L是指空气速度大于15 m/s的区域面积等效圆的直径称为吹扫范围,要想获得较大的吹扫范围就需要有较多的空气消耗,但是空气消耗量过大对气源以及整体空气的供应提出不小的挑战。吹扫范围、耗气量由压缩空气喷孔直径和喷射压力共同决定。模拟采用喷孔直径分别为1 mm,1.5 mm,2 mm,2.5 mm,压缩空气管路壁厚为5 mm,在压力为5 bar,10 bar,15 bar,20 bar,25 bar,30 bar在X=200 mm截面的吹扫范围。模拟结果如图7所示。
|
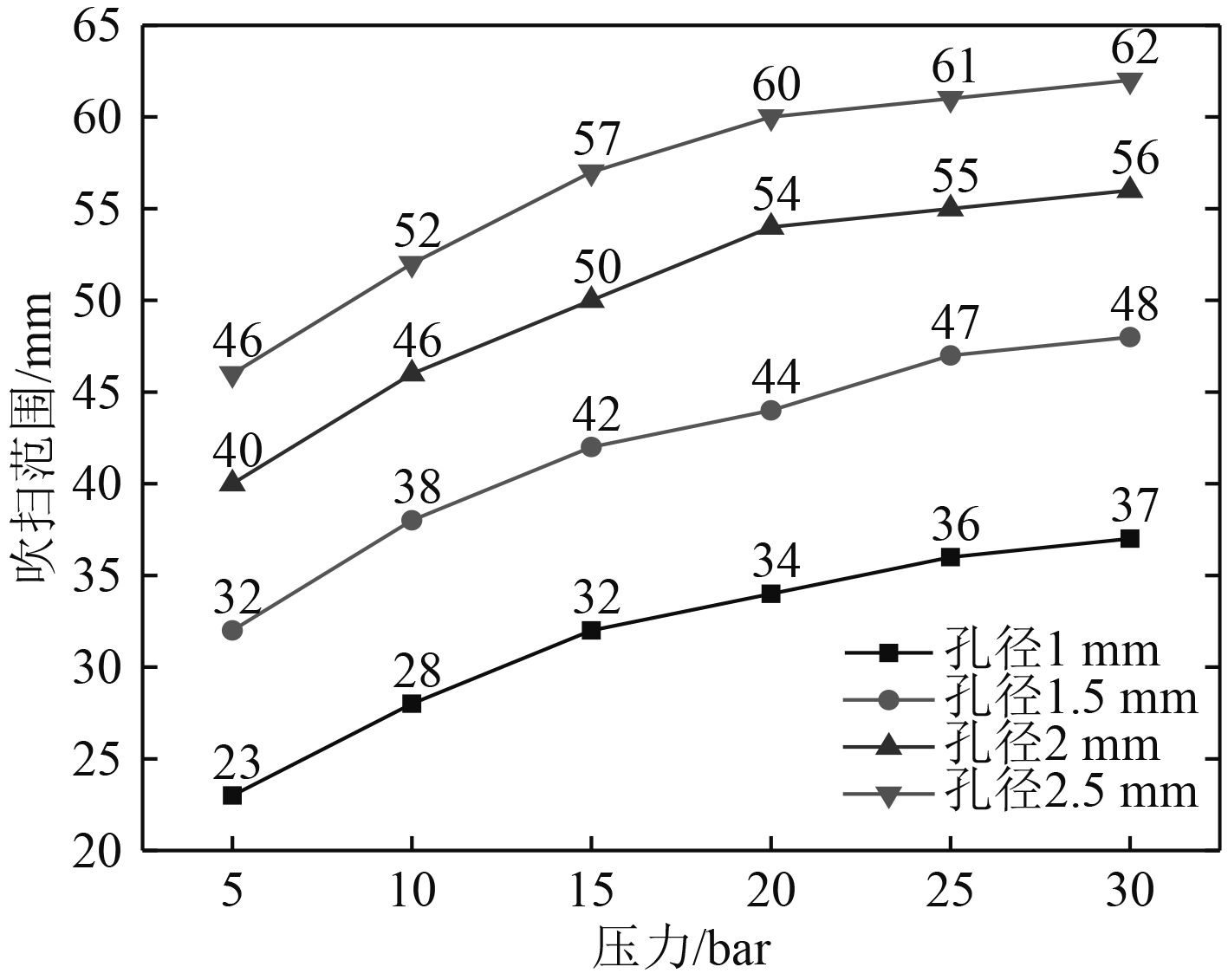
图 7 不同孔径下吹扫范围随压力变化图 Fig. 7 Variation of the sweep range with pressure under different pore sizes |
由以上模拟结果可知:
1)在喷孔直径1 mm,1.5 mm,2 mm,2.5 mm,压力5 bar,10 bar,15 bar,20 bar,25 bar,30 bar的条件下,吹扫范围在23~62 mm之间。
2)喷孔直径相同时,随着压力的增加,吹扫范围逐渐增加,但增加的趋势逐渐平缓,例如:孔径1 mm随着压力从5 bar增加至30 bar,吹扫范围增量ΔL逐渐由5 mm减小至1 mm。
3)吹扫压力相同时,随着喷孔孔径的增大,吹扫范围逐渐增加,增加的趋势逐渐平缓,例如:压力为10 bar时,孔径由1 mm逐渐增加至2.5 mm时,吹扫范围的增量ΔL逐渐由10 mm减小至6 mm。
3.3 耗气量Q与孔径、压力关系通过计算获得耗气量随着孔径与压力的变化关系,喷孔直径分别为1 mm,1.5 mm,2 mm,2.5 mm,压缩空气管路壁厚为5 mm,在压力为5 bar,10 bar,15 bar,20 bar,25 bar,30 bar下耗气量曲线,如图8所示。
|
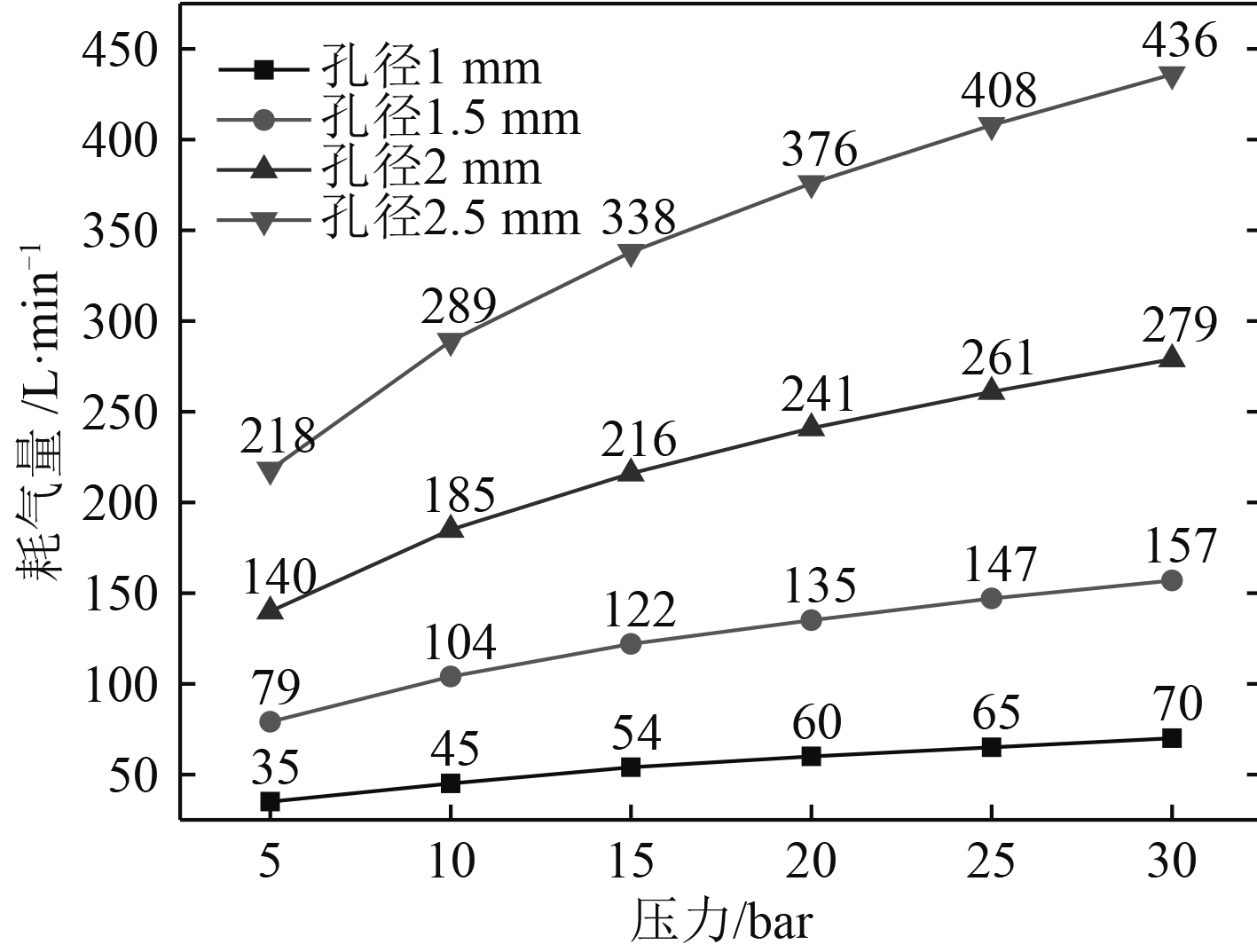
图 8 不同孔径下耗气量随压力变化图 Fig. 8 Variation of gas consumption with pressure under different pore sizes |
通过以上模拟结果可知:
1)在喷孔直径1 mm,1.5 mm,2 mm,2.5 mm压力5 bar,10 bar,15 bar,20 bar,25 bar,30 bar的条件下,耗气量在35~436 L/min之间。
2)喷孔直径相同时,随着压力的增加耗气量逐渐增加,但增加的趋势逐渐平缓,例如孔径1 mm,在5~30 bar之间,耗气量增量的增加量ΔQ由10 L/min逐渐减小至5 L/min,耗气量的变化趋势与吹扫范围相符。
3)吹扫压力相同时,随着喷孔孔径的增大,耗气量逐渐增加,趋势逐渐上扬,例如:压力为10 bar时,孔径由1 mm逐渐增加至2.5 mm时,耗气量增量的增量ΔQ逐渐由59 L/min增加至104 L/min。由此可见喷孔直径对耗气量的影响远大于压力对耗气量的影响。
3.4 气耗比α与喷孔直径、喷射压力之间关系耗气量与喷孔孔径、喷气压力之间关系,在喷孔直径、吹扫压力、吹扫范围和耗气量之间寻求平衡,定义气耗比。定义气耗比α是吹扫范围L与耗气量Q之比的100倍,如下式所示:
| $\alpha {\rm{ = 100}} \times \frac{L}{Q}\text{。}$ |
由上式可知:耗气量一定时,气耗比与吹扫范围成正比;吹扫范围一定时,气耗比与耗气量成反比。气耗比越大则在消耗相同体积的压缩空气所覆盖的面积越大,压缩空气的利用率也就越大,说明经济性较好。模拟计算结果如图9所示。
|
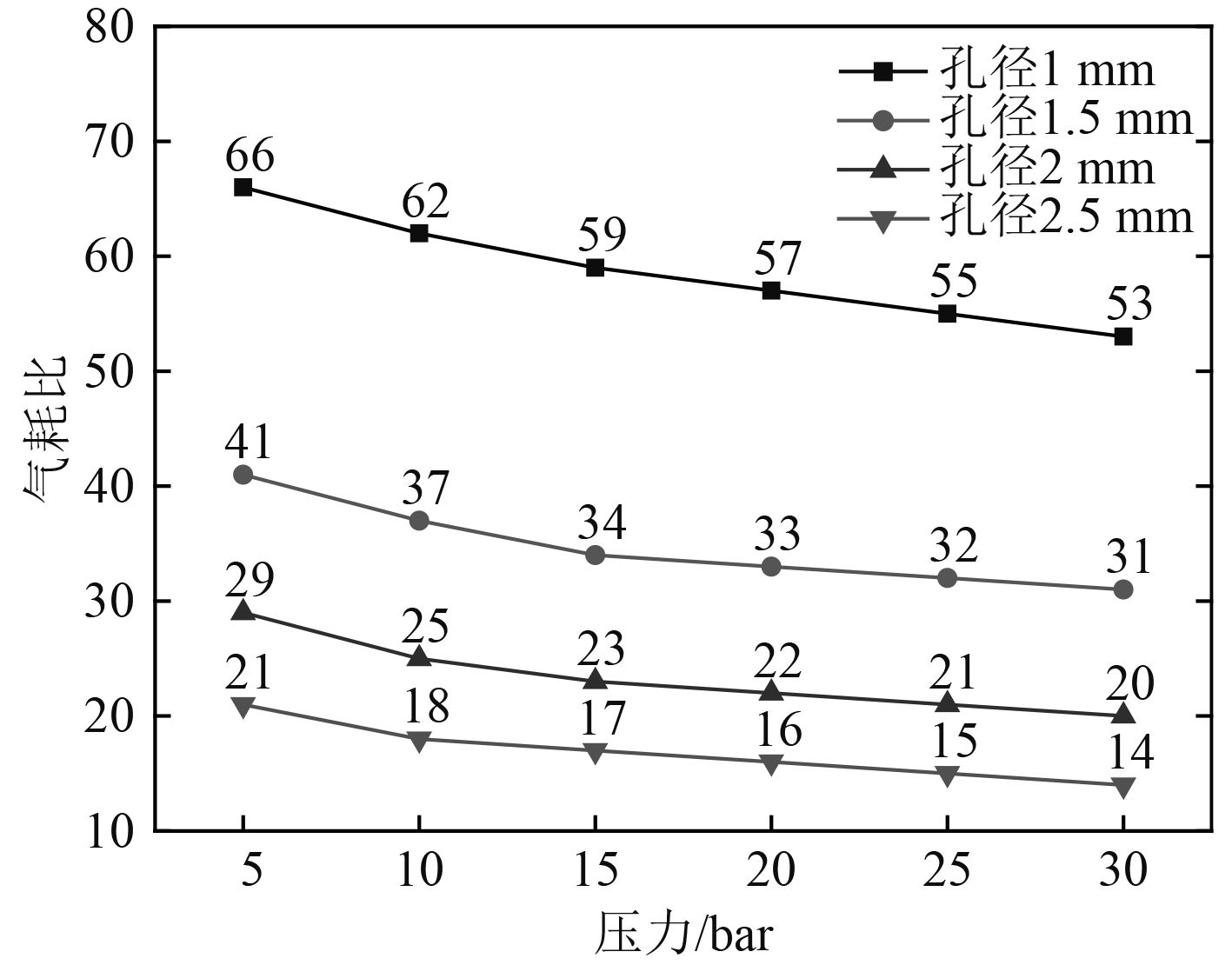
图 9 不同孔径下气耗比随压力变化图 Fig. 9 Variation of gas consumption ratio with pressure under different pore sizes |
由以上模拟结果可知:
1)在喷孔直径1 mm,1.5 mm,2 mm,2.5 mm,压力5 bar,10 bar,15 bar,20 bar,25 bar,30 bar的条件下,耗气比在14~66之间。
2)喷孔直径相同时,随着压力的增加,气耗比逐渐减小。就本模型而言,随着压力的增大,吹扫的经济性逐渐变差。
3)吹扫压力相同时,随着喷孔孔径的增大,气耗比逐渐减小,趋势逐渐上扬。例如,压力为10 bar时,孔径由1 mm逐渐增加至2.5 mm时,耗气比减小量Δα逐渐由25减小至8。由此可见,本模型中喷孔直径越大,压缩空气吹扫的经济性也就越差。
4 结 语本文基于Fluent软件对SCR吹灰装置的性能进行分析,比较了喷孔孔径、喷射压力、吹扫范围、吹扫强度、气耗比、耗气量之间的关系,得到如下结论:
1)在一定的作用强度范围之内,空气速度与作用强度呈现出线性关系,空气速度随作用强度的增大而增大,通过模拟计算准确地确定了作用强度与空气速度的关系。
2)在压缩空气的压力一定时,喷孔孔径越小,吹扫范围越小,耗气量越小,气耗比越大。要达到较大范围的吹扫效果,应该将喷孔的喷射压力控制在20 bar以下,在20 bar上提高喷射压力吹扫强度有所加强,但是效果不是很明显。
3)当压缩空气压力控制在20 bar时,孔径在1 mm到2 mm之间随着孔径的增大,吹扫范围平均每毫米增加20 mm,耗气量平均每毫米增加181 L/min。但是当孔径在2~2.5 mm之间时,随着孔径的增大,吹扫范围平均每毫米增加12 mm,耗气量平均每毫米增加270 L/min.。因此,从喷孔的性能角度出发,喷孔的大小应该控制在2 mm。从经济性的角度出发,孔径越小气耗比越高,尤其是当孔径小于1.5 mm时,其经济的性能提高十分显著。
| [1] | 董尧清. 中重型车用柴油机欧Ⅳ排放首选SCR路线[J]. 汽车电子发动机控制, 2004(10): 7–8. https://www.wenkuxiazai.com/doc/b37d459bec3a87c24028c48b.html |
| [2] | 吕宏俊, 吴迅海. 选择性催化还原脱硝技术应用的若干关键问题[C]//中国环境保护优秀论文精选. 2006: 305–310. |
| [3] | HANS S, MICHEAL H. Large particle ash (LPA) screen retrofits at coal fired units in Indiana and Ohio[C]//Proceeding of Environmental Controls Conference, U.S. Department of Energy. 2006. |
| [4] | KARINA R, ROBERT J, RONALD N. SCR catalyst design issues and operating experience: coals with high arsenic concentrations and coals from the Power Generation Conference. Florida, 2000. |
| [5] | 文小于, 陶莉, 周艳明. 飞灰对SCR脱硝系统的影响[J]. 湖南电力, 2014, 34(6): 51–54. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hndl201406015 |
| [6] | 岑可法. 锅炉和热交换器的积灰、结渣、磨损和腐蚀的防止原理和计算[M]. 北京: 科学出版社, 1994. |
| [7] | 胡琛. 声波除灰技术的研究[D]. 北京: 东北电力大学, 2000. |
| [8] | SHEPHERD J F, JOHNSON C R. Hexahedral mesh generation constrains[J]. Engineering with Computers, 2008, 24(3): 195–213. |
| [9] | 带星, 崔汉国, 李正民, 等. 基于子域重构的扫掠体六面体网格划分方法[J]. 浙江大学学报(工学版), 2014, 48(10): 1788–1794. http://www.cqvip.com/QK/90076A/201410/663161348.html |
| [10] | 李海峰, 吴冀川, 刘建波, 等. 有限元网格剖分与网格质量判定指标[J]. 中国机械工程, 2012, 23(3): 368–377. http://doi.wanfangdata.com.cn/10.3969/j.issn.1004-132X.2012.03.026 |
| [11] | BLACKER T. Automated conformal hexahedral meshing constraints, challenges and opportunities[J]. Engineering with Computers, 2001, 17(3): 201–210 |
| [12] | KAWAMURA Y, ISLAM M S, SUMI Y. A strategy of automatic hexahedral mesh generation by using an improved whisker-weaving method with a surface mesh modification procedure[J]. Engineering with Computers, 2008, 24(3): 215–229. |
| [13] | 黄伟峰, 高志, 黎安伟, 等. 基于Reynolds方程和基于N-S方程的干气密封性能分析对比[J]. 清华大学学报(自然科学版), 2010, 50(11): 1820–1824. http://www.cqvip.com/qk/93884X/201011 |
| [14] | LI C, JI S M, TAN D P. Softness abrasive flow method oriented to tiny scale mould structural surface[J]. International Journal of Advanced Manufacturing Technology, 2012, 61(9–12): 975–987 |
| [15] | 李琛, 马玉山, 高强, 等. 基于Realizable k-ε模型的控制阀流场特性研究[J]. 宁夏大学学报(自然科学版), 2014, 35(4): 328–331. https://link.springer.com/article/10.1631/jzus.A1400154 |
 2018, Vol. 40
2018, Vol. 40
