未来的船舶动力推进系统将由机械化向电气化转变,同时,模块化、电气化、集成化也是未来船舶动力发展方向,船舶综合电力系统更是国内外争相研究的主要目标,螺旋桨的机械轴带推进将改为电气连接,以三相异步电机带动螺旋桨进行推进,控制电机的转速来实现对船速的控制。但是三相异步电机是一个高阶、非线性、强耦合的多变量系统[1 – 3],多输入多输出,电机参数易受环境影响,具有不稳定性,同时根据船舶运行条件需要对电机转速进行频繁转化,这对电机性能、控制精度及稳定性提出了很高要求,如何实现三相异步电机控制的智能化、精确化也成为各国的研究热点。为此,建立1套准确实用的船用三相异步电机的控制仿真模型对实际的船舶电机运行具有一定的指导意义。
基于上述原因及研究现状,本文建立了船用三相异步电机实用数学模型,运用Matlab/Simulink软件对所设计的基于矢量控制策略的船用三相异步电机进行模块化、结构化建模仿真[4],建立转速外化、电流内化双闭环的控制系统,并验证了其准确性;同时对比分析转速分段PI控制与传统PI控制在空载启动、连续突加突减负载时对电机动态调速性能的优化影响,结合数据验证了转速分段PI的优越性及有效性。
1 船用三相异步电机数学模型在对三相异步电机性能计算和分析时,做如下合理假设[1 – 5]:
1)忽略空间谐波,设三相绕组对称,在空间互差
2)忽略磁路饱和,各绕组的自感和互感都恒定;
3)忽略铁心损耗;
4)不考虑频率变化和温度变化对绕组电阻的影响。
参考文献[1,5]可建立三相异步电机在同步旋转d-q轴坐标系下的数学模型。
磁链方程:
| $\left[ {\begin{array}{*{20}{l}}{{\psi _{{{sd}}}}}\\{{\psi _{{{sq}}}}}\\{{\psi _{{{rd}}}}}\\{{\psi _{{{rq}}}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{l}}{{L_{{s}}}}&0&{{L_{{m}}}}&0\\0&{{L_{{s}}}}&0&{{L_{{m}}}}\\{{L_{{m}}}}&0&{{L_{{r}}}}&0\\0&{{L_{{m}}}}&0&{{L_{{r}}}}\end{array}} \right]\left[ {\begin{array}{*{20}{l}}{{i_{{{sd}}}}}\\{{i_{{{sq}}}}}\\{{i_{{{rd}}}}}\\{{i_{{{rq}}}}}\end{array}} \right]\text{,}$ | (1) |
电压方程:
| $\begin{split}\left[ {\begin{array}{*{20}{l}} {{u_{{{sd}}}}}\\{{u_{{{sq}}}}}\\{{u_{{{rd}}}}}\\{{u_{{{rq}}}}}\end{array}} \right] \!= &\!\! \left[ {\begin{array}{*{20}{l}}{{R_{{s}}} + {L_{{s}}}p}\!\!&\!\!{ - {\omega _1}{L_{{s}}}}\!\!&\!\!{{L_{{m}}}p}\!\!&\!\!{ - {\omega _1}{L_{{m}}}}\\{{\omega _1}{L_{{s}}}}\!\!&\!\!{{R_{{s}}} + {L_{{s}}}p}\!\!&\!\!{{\omega _1}{L_{{m}}}}\!\!&\!\!{{L_{{m}}}p}\\{{L_{{m}}}p}\!\!&\!\!{ - {\omega _{{s}}}{L_{{m}}}}\!\!&\!\!{{R_{{r}}} + {L_{{r}}}p}\!\!&\!\!{ - {\omega _{{s}}}{L_{{r}}}}\\{{\omega _{{s}}}{L_{{m}}}}\!\!&\!\!{{L_{{m}}}p}\!\!&\!\!{{\omega _{{s}}}{L_{{r}}}}\!\!&\!\!{{R_{{r}}} + {L_{{r}}}p}\end{array}} \right] \left[ {\begin{array}{*{20}{l}}{{i_{{{sd}}}}}\\{{i_{{{sq}}}}}\\{{i_{{{rd}}}}}\\{{i_{{{rq}}}}}\end{array}} \right]\text{,}\end{split}$ | (2) |
电磁转矩方程:
| ${T_{{e}}} = {n_p}{L_{{m}}}\left( {{i_{{{sq}}}}{i_{{{rd}}}} - {i_{{{sd}}}}{i_{{{rq}}}}} \right)\text{,}$ | (3) |
运动方程:
| $p\omega = \frac{{{n_p}}}{J}({T_e} - T{}_L)\text{。}$ | (4) |
式中:
由上式可知,坐标变换,有效减少了输入量输出量,使得数学模型更加简单直观,有助于分析研究,但从方程中各个状态量之间仍存在交叉耦合,则需对电机进行按转子磁场定向矢量控制[2],通过坐标变换对定子电流的频率、相角及幅值进行同时控制以实现对定子电流励磁分量、转矩分量的独立控制。将d轴与转子主磁通方向重合,按转子主磁通定向后,转子等效电流
| ${T_e} = {n_p}{L_m}({i_{sq}}{i_{rd}} - {i_{sd}}{i_{rq}}) = {n_p}{L_m}{i_{sq}}{i_r} = {n_p}\frac{{{L_m}}}{{{L_r}}}{\psi _r}{i_{sq}}\text{,}$ | (5) |
考虑三相异步电机为鼠笼型,则有
| $\begin{split}\left[ {\begin{array}{*{20}{l}}{{u_{sd}}}\\{{u_{sq}}}\\0\\0\end{array}} \right] \!= &\!\! \left[ {\begin{array}{*{20}{l}}{{R_s} + {L_s}p}\!\!&\!\!{ - {\omega _1}{L_s}}\!\!&\!\!{{L_m}p}\!\!&\!\!{ - {\omega _1}{L_m}}\\{{\omega _1}{L_s}}\!\!&\!\!{{R_s} + {L_s}p}\!\!&\!\!{{\omega _1}{L_m}}\!\!&\!\!{{L_m}p}\\{{L_m}p}\!\!&\!\!0\!\!&\!\!{{R_r} + {L_r}p}\!\!&\!\!0\\{{\omega _s}{L_m}}\!\!&\!\!0\!\!&\!\!{{\omega _s}{L_r}}\!\!&\!\!{{R_r} + {L_r}p}\end{array}} \right]\left[ {\begin{array}{*{20}{l}}{{i_{sd}}}\\{{i_{sq}}}\\{{i_{rd}}}\\{{i_{rq}}}\end{array}} \right]\text{,}\end{split}$ | (6) |
展开式(6)得:
| ${i_{sd}} = \frac{{{T_r}p + 1}}{{{L_m}}}{\psi _r}\text{,}$ | (7) |
| ${\omega _1} - \omega = {\omega _s} = \frac{{{L_m}}}{{{T_r}{\psi _r}}}{i_{sq}}\text{。}$ | (8) |
式中:
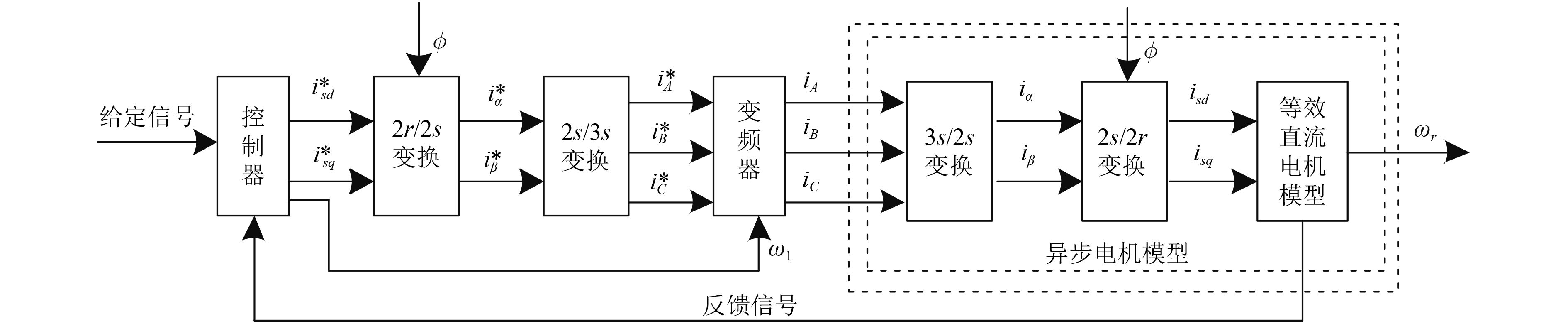
按照转子磁场定向矢量控制策略得到如图1所示的三相异步电机矢量控制结构图。将定子侧输入电流
| ${T_e} = {n_p}\frac{{{L_m}}}{{{L_r}}}{\psi _r}{i_{sq}}\text{,}$ | (9) |
| ${\psi _r} = \frac{{{L_m}}}{{{T_r}p + 1}}{i_{sd}}\text{,}$ | (10) |
| $\phi = \int_0^t {({n_p}{\omega _r} + \frac{{L{}_m{i_{sd}}}}{{{T_r}{\psi _r}}})} {\rm d}t\text{。}$ | (11) |
|
图 1 三相异步电机矢量控制结构框图 Fig. 1 Block diagram of vector control for three phase asynchronous motor |
为实现电机转速快速响应及提高抗扰能力,采用转速外环、转矩内环的双闭环的控制系统。传统单参数PI调节很难同时满足快速性及稳定性,为提高快速性则必然会产生超调,为实现稳态无误差系统则响应缓慢,因此为解决这个矛盾冲突,采用转速分段PI控制,其原理为根据调节器输入实际值与设定值的偏差的大小选择不同的PI参数以获得最优控制,达到调节时间短、无超调的稳定控制目的。根据控制原理,电机负载急剧变化会导致转速剧烈波动,为满足系统要求需把转速环校正成
| $T_e^* = {K_p}(\omega _{ref}^* - {\omega _r}) + {K_i}\int {(\omega _{ref}^* - {\omega _r})} {\rm d}t\text{。}$ | (12) |
其闭环控制的等效图可简化为如图2所示。其中
| ${W_s} = \frac{{{k_p}(\tau s + 1)}}{{J\tau {s^2}(T{}_{sum}s + 1)}}\text{,}$ | (13) |
式中:
| ${K_p} = \frac{{J(h + 1)}}{{2h{T_{sum}}}}\text{。}$ | (14) |

|
图 2 电机转速PI闭环控制框图 Fig. 2 Block diagram of motor speed PI closed loop control |
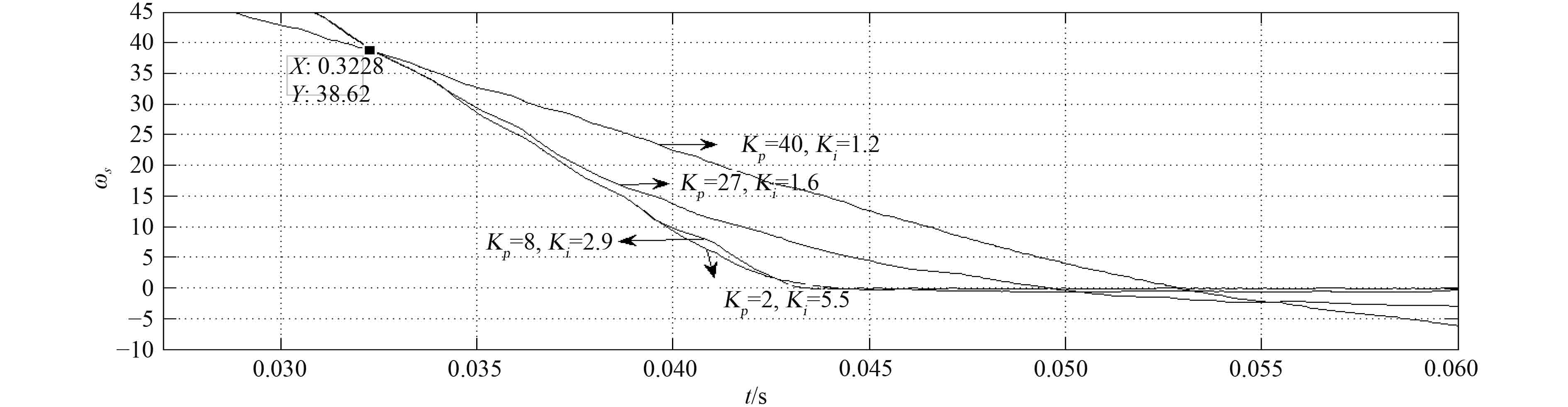
上述的参数设计都是在忽略高次项、忽略滞后作用、采用合并小惯性环节等条件下取的近似值[7 – 8],利用频域分析法得到的参数只是近似值,需要进行不断调试,最终获得满足系统要求的设计值。转速差随PI参数变化如图3所示,当下限值
|
图 3
转速差值
|
|
|
表 1 转速分段区设定 Tab.1 Setting of speed segmented region |
|
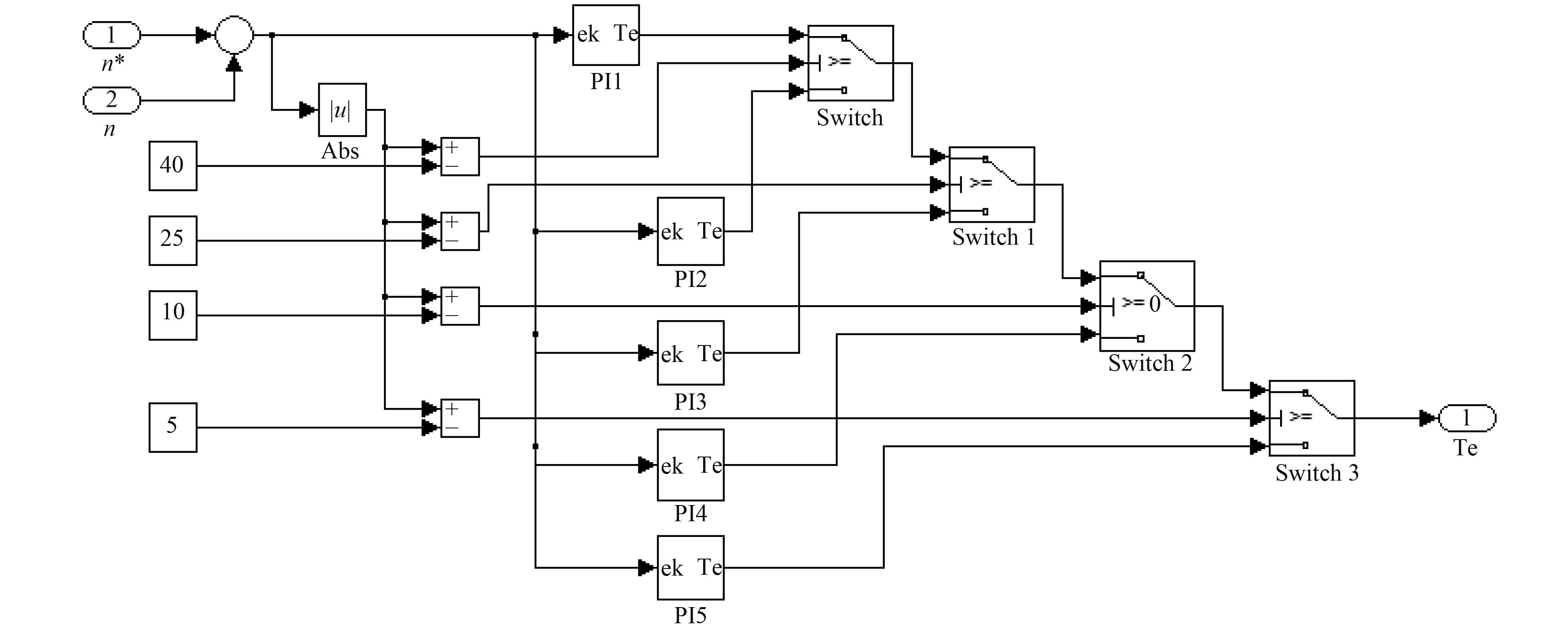
图 4 转速分段PI调节器模块 Fig. 4 Regulator module of speed segment PI |
转矩观测模型如图5所示,输入电机定子三相电流

|
图 5 矢量控制模块 Fig. 5 Module of Vector control |
Park变换模块实现静止坐标系定子三相参考相电流
| $\left[ {\begin{array}{*{20}{l}} {{i_d}}\\ {{i_q}}\\ {{i_0}} \end{array}} \right] = {\rm{ }}\frac{2}{3}\left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\cos \left( {\theta - 120{\rm{^\circ }}} \right)}&{\cos \left( {\theta + 120{\rm{^\circ }}} \right)}\\ { - \sin \theta }&{ - \sin \left( {\theta - 120{\rm{^\circ }}} \right)}&{ - \sin \left( {\theta + 120{\rm{^\circ }}} \right)}\\ {1/2}&{1/2}&{1/2} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_a}}\\ {{i_b}}\\ {{i_c}} \end{array}} \right]$ | (15) |
根据式(13)建立Park模块3s/2r数学模型,搭建模块如图6所示。模块输入为d-q旋转坐标系位置信号

|
图 6 3s/2r模块 Fig. 6 Module of 3s/2r |
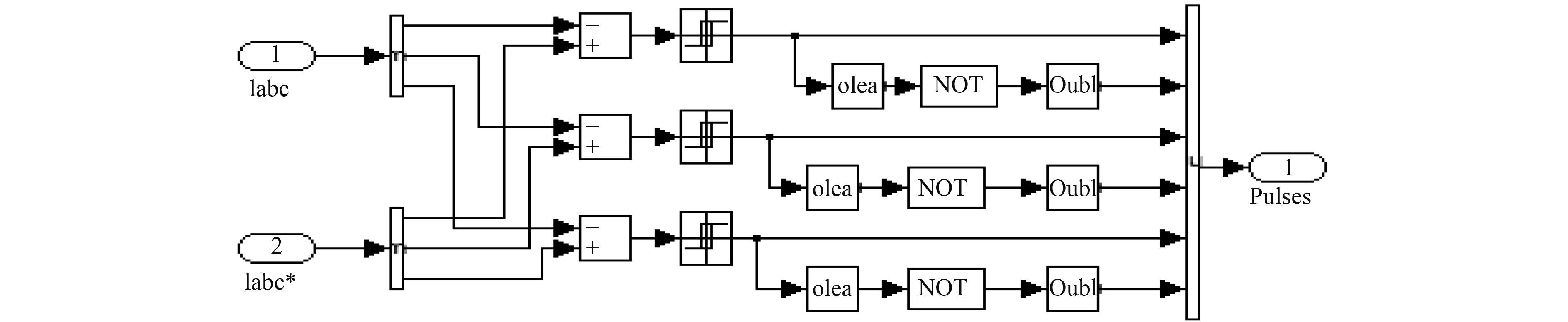
电流滞环PWM调节器利用给定的三相电流信号
|
图 7 PWM电流滞环模型 Fig. 7 Model of PWM current hysteresis loop |
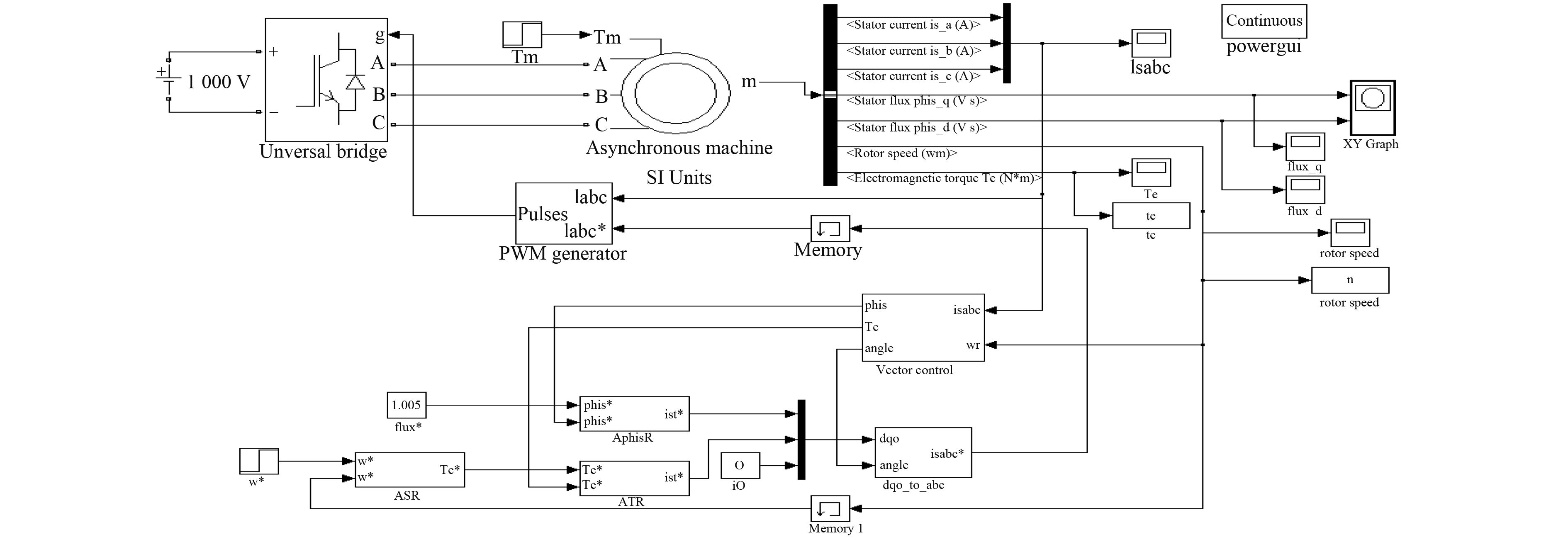
把各个模块顺序依次连接,建立三相异步电机矢量控制系统Matlab仿真如图8所示。异步电机额定参数:PN=4 kW,UN=400 V,f=50 Hz,Rs=1.405 Ω,Rr=1.395 Ω,Lls=Llr=0.005 839 H,Lm=0.172 2 H,p=2,nN=1 430 r/min,根据异步电机额定电压空载运行下,可测得转子磁通为1.005 Wb,故令给定转子磁链
|
图 8 三相异步电机矢量控制系统仿真模型 Fig. 8 Vector control simulation model of three phase asynchronous motor |
给定转速

|
图 9 突加60 N·m负载时转速曲线 Fig. 9 Speed-time curve of 60 N·m sudden load |
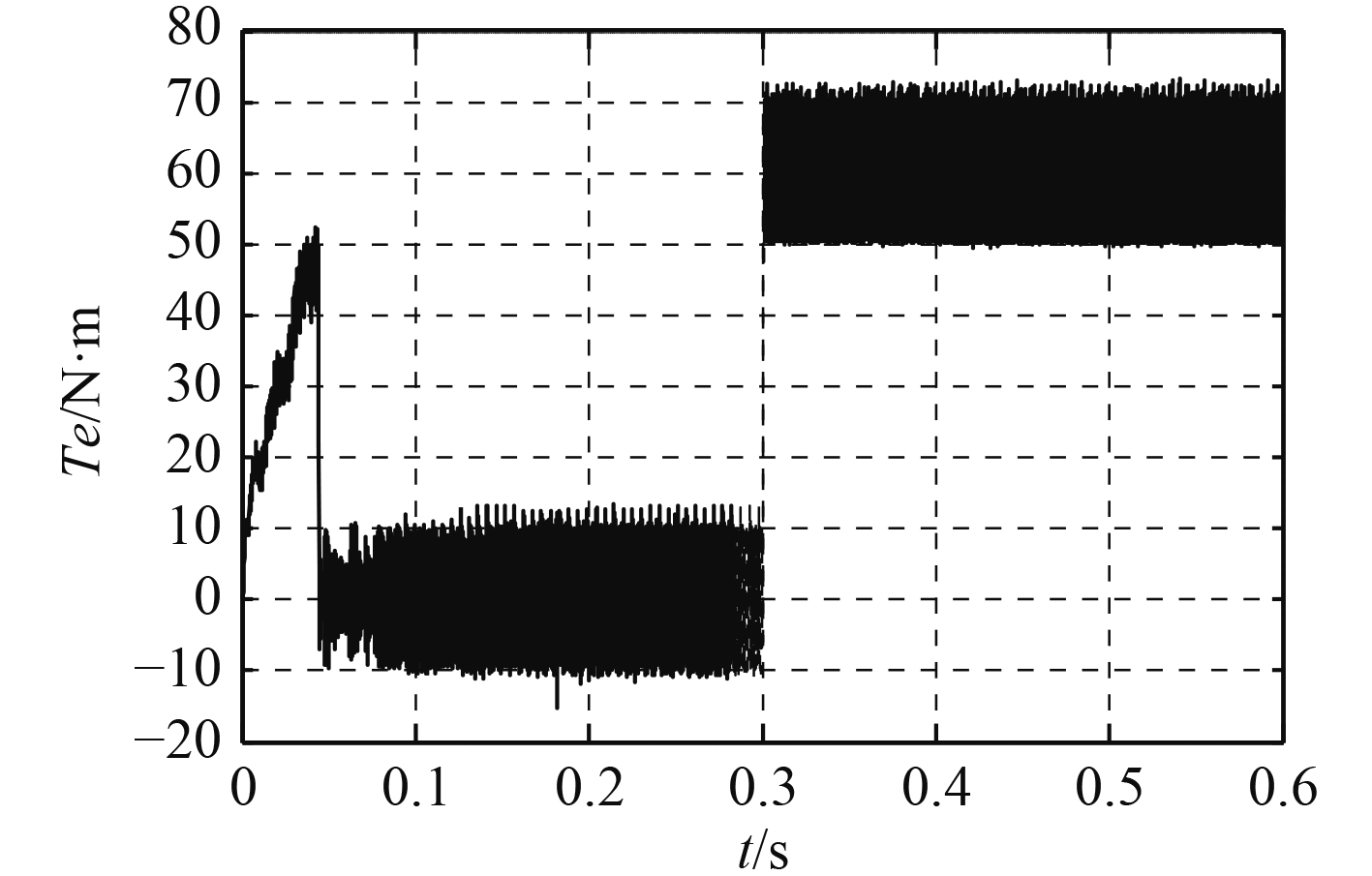
2种PI控制响应速度基本一致,传统PI转速稳定在102 rad/s,突加负载后转速突降至92.7 rad/s,而转速分段PI控制转速稳定在100.5 rad/s,突加负载后下降至97.4 rad/s;从曲线可以看出转速分段PI控制电机转速能够快速地跟随给定值,稳态误差极小,理论上可达到无静差调速,同时抗扰能力强。由于转矩环限幅作用,转矩波形如图10所示,瞬间启动值不大且最终稳定在负载值60 N·m,转矩有小幅值脉动是由于三相定子电流畸变、电流滞环带宽幅值导致。
|
图 10 突加60 N·m 电机转矩曲线 Fig. 10 Torque-time curve of 60 N·m sudden load |
空载启动,给定初始转速50 rad/s,0.3 s突加至100 rad/s,0.5s再突减至70 rad/s,转速仿真对比如图11所示。在初期,2种PI控制在快速性上基本一致,当快进入设定值时,转速分段PI控制比传统单PI控制响应更快,更早达到设定值;当稳定时,传统PI控制的稳态转速分别为51.5 rad/s,101.5 rad/s,70.5 rad/s,转速分段PI控制分别为50.2 rad/s,100.3 rad/s,70 rad/s,对比可知所设计的分转速段PI控制在快速性及稳态无静差调速性能上比传统单PI控制优越。

|
图 11 电机转速变化曲线 Fig. 11 Speed-time curve of motor |
本文对船用三相异步电机在旋转坐标系下的数学模型进行分析,采用转子磁链定向控制策略建立三相异步电动机转速外环、转矩内环的仿真模型,在传统转速环单PI控制的基础上提出转速环分段式PI调节较为有效的控制方法;仿真结果表明所设计的电机转速环分段PI调节器能够实现优化控制三相异步电机的动态性能,与传统转速环单个PI控制相比,在空载启动突加负载及连续突加突减转速情况下,转速环分段PI控制可使船舶电机满足抗干扰能力强、稳定运行无静差、快速响应。
| [1] | 阮毅, 陈伯时. 电力拖动自动控制系统[M]. 北京: 机械工业出版社, 2010. |
| [2] | 周元钧. 交流调速控制系统[M]. 北京: 机械工业出版社, 2013. |
| [3] |
贾瑞, 康锦萍. 基于Matlab/Simulink的异步电机矢量控制系统仿真[J]. 华北电力技术, 2011(9): 18–25.
JIA Rui, KANG Jin-ping. Simulation of asynchronous motor vector control system based on Matlab/Simulink[J]. North China Electric Power, 2011(9): 18–25. http://doi.wanfangdata.com.cn/10.3969/j.issn.1003-9171.2011.09.004 |
| [4] |
纪志成, 薛花, 沈艳霞. 基于Matlab交流异步电机矢量控制系统的仿真建模[J]. 系统仿真学报, 2004, 16(3): 384–388.
JI Zhi-cheng, XUE Hua, SHEN Yan-xia. Modeling and simulation of AC asynchronism motor vector control system based on Matlab[J]. Journal of System Simulation, 2004, 16(3): 384–388. https://www.wenkuxiazai.com/doc/f9c1c8f67c1cfad6195fa72f.html |
| [5] |
谢雅, 黄中华, 左金玉. 三相交流异步电机矢量控制系统仿真建模[J]. 湖南工程学院学报, 2013, 23(1): 1–4.
XIE Ya, HUANG Zhong-hua, ZUO Jin-yu. Simulation modeling of AC three-phase asynchronous motor vector control system[J]. Journal of Hunan Institute of Engineering, 2013, 23(1): 1–4. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hngcxyxb-zr201301001 |
| [6] | 胡寿松. 自动控制原理[M]. 北京: 科学出版社, 2013. |
| [7] |
李文静, 熊光熠. 基于MATLAB的异步电动机矢量控制变频调速系统的仿真[J]. 电力学报, 2006, 21(2): 146–153.
LI Wen-Jing, XIONG Guang-yi. Simulation of vector control and variable-frequency regulating speed system of asynchronous machine based on Matlab[J]. Journal of Electric Power, 2006, 21(2): 146–153. https://www.wenkuxiazai.com/doc/9faa35e0b8f67c1cfad6b84c.html |
| [8] |
程启明, 李月娥, 程伊曼, 等. 基于Matlab/Simulink交流电机矢量控制系统建模与仿真[J]. 华东电力, 2010, 38(5): 0740–0744.
CHENG Qi-ming, LI Yue-e, CHENG Yi-ma, et al. Modeling and simulation of vector control system of alternating current motor based on Matlab/Simulink[J]. East China Electric Power, 2010, 38(5): 0740–0744. http://d.wanfangdata.com.cn/Periodical_hddl201005053.aspx |
 2018, Vol. 40
2018, Vol. 40
