2. 青岛远洋船员职业学院 机电系,山东 青岛 266071
2. Qingdao Ocean Shipping Mariners College, Qingdao 266071, China
船舶电力系统的发电设备主要为柴油发电机组,它是船舶电力系统的核心。与陆地电力系统相比,船舶电力系统在容量、负载功率、输电方式等方面均存在很大差异。船舶电网输电距离短、容量小、输电电压低,倘若启动消防泵、首侧推等大功率负载,会对电网造成较大冲击。为了保证柴油发电机组在突然投入或切除大功率负载时的运行稳定性,必须详细研究柴油发电机组正常带载启动和突加、突卸负载时转速、电压电流、功角和功率等物理量的变化情况,分析其受扰动的影响程度,为改善柴油机转速控制、发电机励磁控制等提供理论依据。这就需要建立精确的船舶柴油发电机组的数学模型并进行仿真研究。电力系统是强非线性系统,所以必须建立船舶柴油发电机组的非线性模型。目前,很多文献对船舶发电机组都采用简化模型,这样虽然方便了电力系统的稳态分析,但在突加突减负载时,势必会引起误差,采用降阶简化模型的动态仿真已经不能反映电力系统的实际运行状况[1]。本文建立了船舶柴油发电机组的七阶数学模型,能够保证暂态仿真精度。
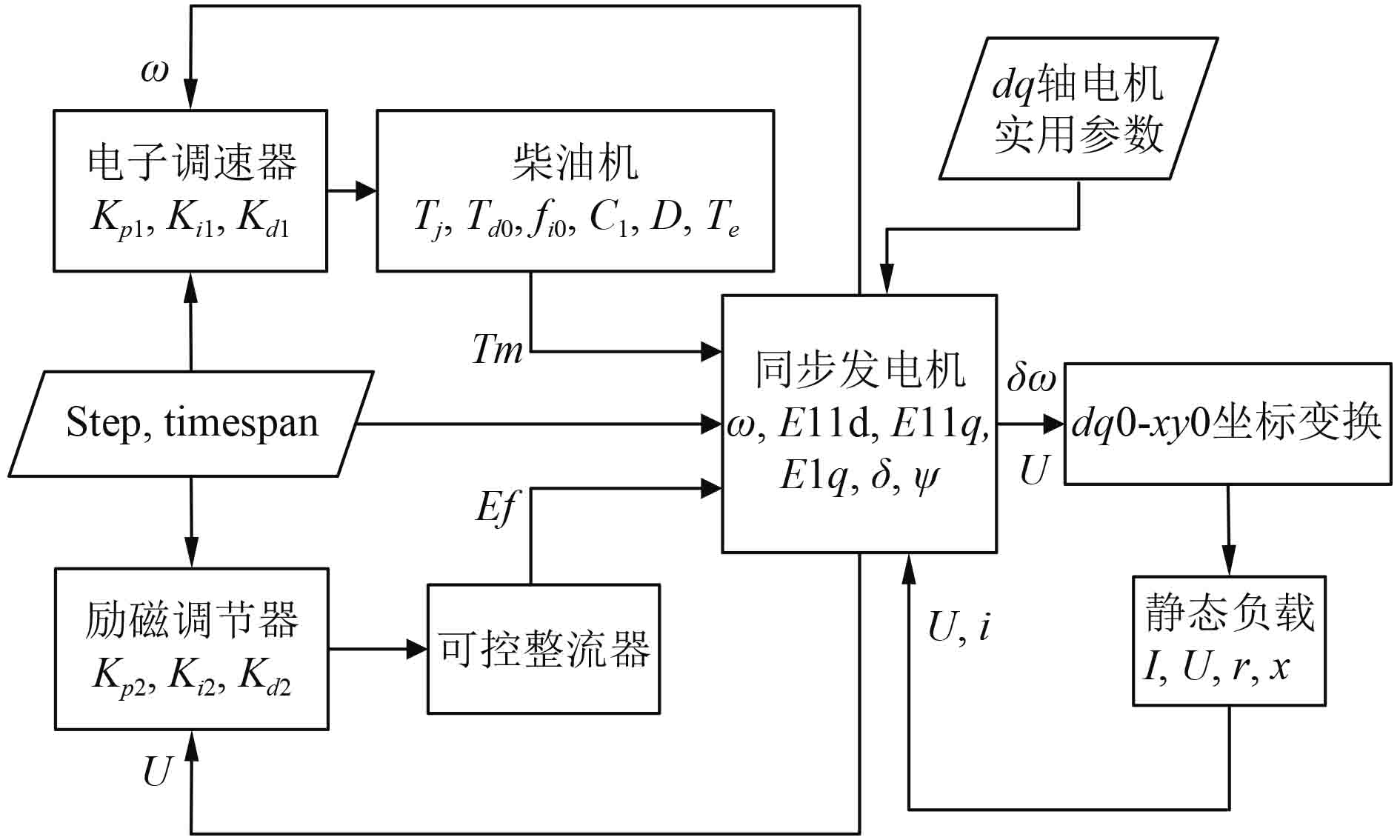
1 船舶柴油发电机组系统船舶柴油发电机组主要由同步发电机、四冲程柴油机及其调速系统和发电机励磁系统组成[2],系统框图如图1所示。柴油机供给发电机原动力,其调速系统通过检测实际转速和设定转速的差,调节柴油机的供油量,构成转速的闭环控制,在一定负载变化范围内保证发电机的转速稳定,从而保证输出电压和频率稳定。发电机的励磁系统通过检测发电机端电压和负载电流调节励磁电流大小,构成电压的闭环控制。
船舶柴油发电机组的数学模型包括同步发电机的数学模型、柴油机及调速器的数学模型、发电机励磁系统的数学模型。数学模型可以用微分方程组的形式描述,也可以用传递函数或状态方程的形式描述,后两者更适用于线性系统建模。故本文以微分方程组的形式来描述船舶柴油发电机组的数学模型。
|
图 1 船舶柴油发电机组系统框图 Fig. 1 System diagram of marine diesel generator |
同步发电机是船舶柴油发电机组的核心,集旋转与静止、电磁变化与机械运动于一体,实现电能与机械能变换,其动态性能十分复杂,而其动态性能又直接影响柴油发电机组的性能[3]。故应对同步发电机作深入分析,考虑其定子绕组的暂态过程、阻尼绕组以及励磁绕组的暂态过程和转子的动态过程,建立同步发电机的7阶非线性数学模型[4]。将发电机铭牌的有名值参数归算到自身容量基准值下的标幺值,通过选取各绕组标幺值的基值,确保标幺值互感可逆(第一约束)及保留传统的标幺电机参数(第二约束),同步发电机dq0坐标下经过派克变换的标幺值方程如下:
1)电压方程
| $\left\{ \begin{array}{l}{u_d} = \displaystyle\frac{{\rm d}}{{{\rm d}{t_{}}}}{\varPsi _d} - {\omega _{}}{\varPsi _q} - {r_a}{i_d}\text{,}\\{u_q} = \displaystyle\frac{{\rm d}}{{{\rm d}{t_{}}}}{\varPsi _q} + {\omega _{}}{\varPsi _d} - {r_a}{i_q}\text{,}\\{u_0} = \displaystyle\frac{{\rm d}}{{{\rm d}{t_{}}}}{\varPsi _0} - {r_a}{i_0}\text{。}\end{array} \right.$ | (1) |
| $\left\{ \begin{array}{l}{u_f} = \displaystyle\frac{{\rm d}}{{{\rm d}t}}{\varPsi _f} + {r_f}{i_f}\text{,}\\{u_D} = \displaystyle\frac{{\rm d}}{{{\rm d}{t_{}}}}{\varPsi _D} + {r_D}{i_D} \equiv 0\text{,}\\{u_Q} = \displaystyle\frac{{\rm d}}{{{\rm d}{t_{}}}}{\varPsi _Q} + {r_Q}{i_Q} \equiv {\rm{0}}\text{。}\end{array} \right.$ | (2) |
2)磁链方程
| $\begin{split}& \left[ {\begin{array}{*{20}{c}}{{\varPsi _{{\rm{ }}dq0}}}\\{{\varPsi _{fDQ}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{\varPsi _d}}\\{{\varPsi _q}}\\{{\varPsi _0}}\\{{\varPsi _f}}\\{{\varPsi _D}}\\{{\varPsi _Q}}\end{array}} \right] = \\& \left[ {\begin{array}{*{20}{c}}{{X_d}}&0&0&{{X_{ad}}}&{{X_{ad}}}&0\\0&{{X_q}}&0&0&0&{{X_{aq}}}\\0&0&{{X_0}}&0&0&0\\{{X_{ad}}}&0&0&{{X_f}}&{{M_R}}&0\\{{X_{ad}}}&0&0&{{M_R}}&{{X_D}}&0\\0&{{X_{aq}}}&0&0&0&{{X_Q}}\end{array}} \right]\left[ {\begin{array}{*{20}{r}}{ - {i_d}}\\{ - {i_q}}\\{ - {i_0}}\\{{i_f}}\\{{i_D}}\\{{i_D}}\end{array}} \right]\text{。}\end{split}$ | (3) |
为了将变量if,uf,Ψf折合到定子侧的实用物理量,以便在定子侧进行分析及度量,故引入以下5个定子侧等效实用变量:
1)定子励磁电势
| ${{{E}}_{{f}}}{{ = }}{{{X}}_{{{ad}}}}\frac{{{{{u}}_{{f}}}}}{{{{{r}}_{{f}}}}}\text{,}$ | (4) |
2)电机q轴空载电动势
| ${E_q} = {X_{ad}}{i_f}\text{,}$ | (5) |
3)电机q轴瞬变电动势
| ${E_q}' = \frac{{{X_{ad}}}}{{{X_f}}}{\varPsi _f}\text{,}$ | (6) |
4)电机q轴超瞬变电动势
| ${E_q}'' = \frac{{{X_{ad}}}}{{{X_f}{X_D} - {X_{ad}}^2}}({X_{D1}}{\varPsi _f} + {X_{f1}}{\varPsi _D})\text{,}$ | (7) |
5)电机d轴超瞬变电动势
| ${E_d}'' = - {X_{ad}}{var\varPsi _Q}/{X_Q}\text{。}$ | (8) |
将以上变量表达式代入同步发电机dq0坐标下的标幺值方程组中,经过变形得到下列微分方程。
1)定子电压方程
| $\begin{aligned}& {u_d} = \frac{{{\rm d}{\varPsi _d}}}{{{\rm d}t}} - \omega {\varPsi _q} - {r_a}{i_d}\text{,}\\& {u_q} = \frac{{{\rm d}{\varPsi _q}}}{{{\rm d}t}} + \omega {\varPsi _d} - {r_a}{i_q}\text{。}\end{aligned}$ | (9) |
其中,磁链表达式为:
| $\begin{aligned}& {\varPsi _d} = {{E''}_q} - {{X''}_d}{i_d}\text{,}\\& {\varPsi _q} = - {{E''}_d} - {{X''}_q}{i_q}\text{。}\end{aligned}$ | (10) |
2)转子电压方程
f绕组 :
| ${{{T'}}_{{{d0}}}}\frac{{{{\rm d}}{{{{E'}}}_{{q}}}}}{{{{{\rm d}t}}}}{{ = }}{{{E}}_{{f}}}{{ - }}\frac{{{{{X}}_{{d}}}{{ - }}{{{{X''}}}_{{d}}}}}{{{{{{X'}}}_{{d}}}{{ - }}{{{{X''}}}_{{d}}}}}{{{E'}}_{{q}}}{{ + }}\frac{{{{{X}}_{{d}}}{{ - }}{{{{X'}}}_{{d}}}}}{{{{{{X'}}}_{{d}}}{{ - }}{{{{X''}}}_{{d}}}}}{{{E''}}_{{q}}}\text{,}$ | (11) |
D绕组:
| ${T''_{d0}}\frac{{{\rm d}{{E''}_q}}}{{{\rm d}t}} = - {E''_q} + {E'_q} - \left( {{{X'}_d} - {{X''}_d}} \right){i_d}\text{,}$ | (12) |
Q绕组:
| ${T''_{q0}}\frac{{{\rm d}{{E''}_d}}}{{{\rm d}t}} = - {E''_d} + \left( {{X_q} - {{X''}_q}} \right){i_q}\text{。}$ | (13) |
3)转子运动方程
| $\left\{ \begin{array}{l}{T_J}\displaystyle\frac{{{\rm d}\omega }}{{{\rm d}t}} = {T_m} - {T_e} - D\left( {\omega - 1} \right)\text{,}\\\displaystyle\frac{{{\rm d}\delta }}{{{\rm d}t}} = \omega - 1\text{。}\end{array} \right.$ | (14) |
4)电磁转矩表达式
| ${T_e} = {E''_q}{i_q} + {E''_d}{i_d} - \left( {{{X''}_d} - {{X''}_q}} \right){i_q}{i_d}\text{。}$ | (15) |
以上构成了同步发电机7阶数学模型的非线性微分方程组。
2.2 柴油机及其调速系统数学模型柴油机组在负荷发生变化时,其稳定运行将会遭到破坏,造成柴油机组的加速或减速。根据力学原理,柴油机在非平衡状态下的运动方程为:
| $J\frac{{{\rm d}\Delta \omega }}{{{\rm d}t}} = \Delta {T_d} - \Delta {T_r}\text{。}$ | (16) |
其中:
| ${\left( {\frac{{\partial {T_d}}}{{\partial {f_i}}}} \right)_0} = \frac{{{T_{d0}}}}{{{f_{i0}}}}\text{,}$ | (17) |
于是柴油机在非平衡状态下的运动方程为:
| $J\frac{{{\rm d}\Delta \omega }}{{{\rm d}t}} + {C_1}\Delta \omega = \frac{{{T_{d0}}}}{{{f_{i0}}}}\Delta {f_i} - \Delta {T_r}\text{,}$ | (18) |
因此柴油机调速器的数学模型为:
| $\Delta {f_i} = {k_p} \cdot \Delta \omega + {k_i} \cdot \int_0^h {\Delta \omega } {\rm d}t + {k_d} \cdot \frac{{{\rm d}\Delta \omega }}{{{\rm d}t}}\text{。}$ | (19) |
励磁系统向发电机提供励磁电流,起着调节电压、保持发电机端电压恒定的作用。船舶同步发电机励磁控制系统按照励磁电流的获得方式可分为3类:直流励磁机他励方式、静止自励方式、交流励磁机他励方式。静止励磁方式的自励静止励磁装置目前使用较为普遍[5],本文采用这种励磁装置。自励静止励磁系统由同步发电机、PID励磁调节器、可控整流器和互感器组成,根据励磁系统的原理,可以求得其数学模型为:
| ${E_f} = {k_p} \cdot \Delta U + {k_i} \cdot \int_0^h {\Delta U} {\rm d}t + {k_d} \cdot \frac{{{\rm d}\Delta U}}{{{\rm d}t}}\text{。}$ | (20) |
对船舶柴油发电机组一系列物理量在大扰动下的变化进行仿真和分析,就必须求解其数学模型对应的微分方程组和代数方程组。微分方程组的求解方法主要有隐式梯形积分法、改进欧拉法和龙格–库塔法[6]。在现今电力系统暂态稳定性分析中,微分方程数值求解多用隐式梯形积分法,用该方法进行船舶柴油发电机组暂态和稳态分析时,对电力系统方程式:
| $\frac{{\rm d}y}{{{\rm d}t}} = f(y,z,t)\text{,}$ | (21) |
先根据梯形法则将其化为tn~tn+1时步的差分代数方程组:
| ${y_{n + 1}} = {y_n} + \frac{h}{2}\left[ {f({y_n},{z_n},{t_n}) + f({y_{n + 1}},{z_{n + 1}},{t_{n + 1}})} \right]\text{,}$ | (22) |
| ${{g(}}{{{y}}_{{{n + 1}}}}{\rm{,}}{{{z}}_{{{n + 1}}}}{\rm{,}}{{{t}}_{{\rm{n + 1}}}}{\rm{) = 0}}\text{。}$ | (23) |
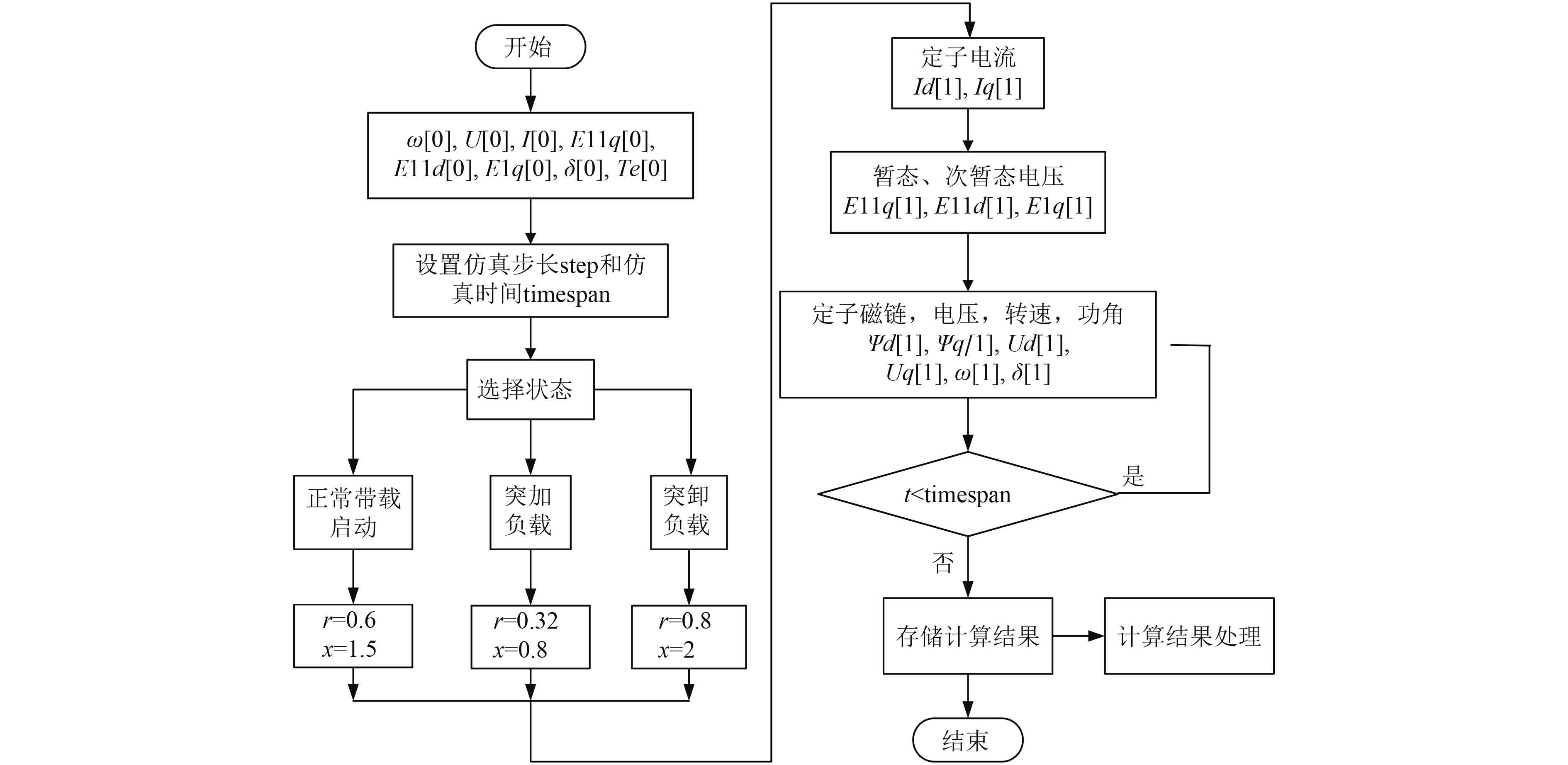
再和代数方程(23)联立求解。其实质为求解一组非线性代数方程组。故本文选择该数值算法作为求解船舶柴油发电机组7阶非线性数学模型的算法。根据上述隐式梯形积分法原理,只要设定发电机组的转速、电压、电流、功率等参数初始值和仿真步长、仿真时间以及在不同扰动下的负载,即可利用C#实现模型求解,求解流程如图2所示,只要时间t未达到设置好的仿真时间times pan,物理量w,U,I,Te等就会通过各自的表达式计算出当下步长的数值解,循环结束之后,分别得到各自的一组数组解。
|
图 2 C#求解流程图 Fig. 2 Solution flow chart of C# |
根据上文所建立的船舶柴油发电机组的非线性数学模型和C#求解模型的程序流程图,分析大扰动下船舶柴油发电机组在突加、突卸负载时转速和电压的变化情况,从而确定船舶柴油发电机组在受到扰动后的稳定性,为改善发电机转速调节和励磁控制等环节的精度提供理论依据。
4.1 船舶柴油发电机组仿真参数取值表1列出了算法程序中用到的所有参数取值,发电机实用参数的取值参考了康明斯UCM系列型号有阻尼凸极机同步电机主要参数典型值,柴油机模型中的参数是参考6250GZC型船用柴油机参数确定的[7]。其主要参数为:额定功率Ph=600 HP,缸数i=6,机组的飞轮转矩GD2=1 004 kg·m2,柴油机惯性时间常数TJ=2.1 s。
|
|
表 1 算法程序参数取值 Tab.1 Parameter value of algorithm |
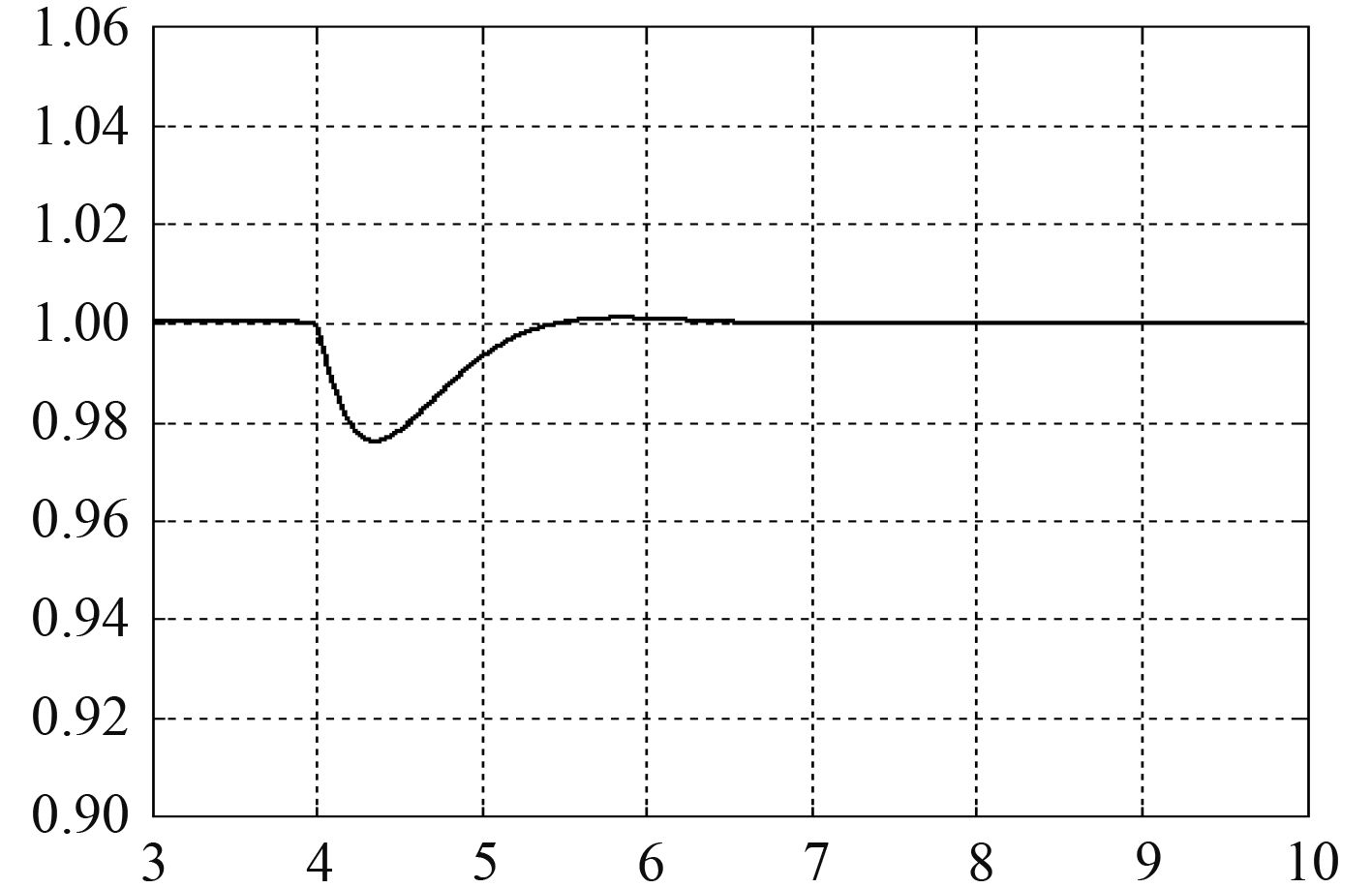
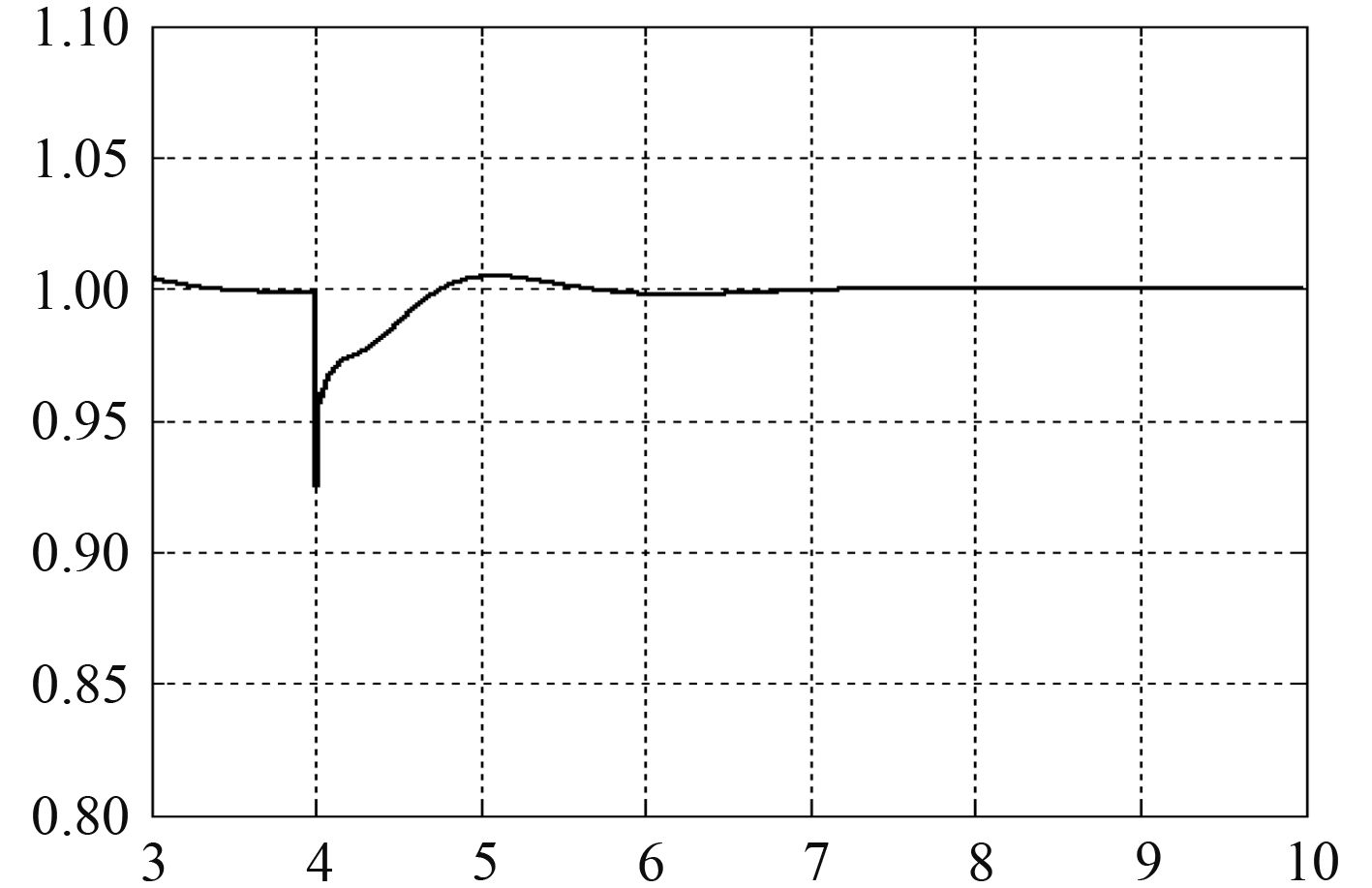
突加负载时,柴油发电机组的负载电流突增,会引起发电机转速的暂时下降和电网电压的暂时下降。这时,选取负载的阻抗值为r=0.32,x=0.8,z=0.86,即突加46.8%负载,在t=4 s时给予扰动,响应曲线如图3和图4所示。
|
图 3 突加负载时转速变化曲线 Fig. 3 Speed change curve under sudden load |
|
图 4 突加负载时电压变化曲线 Fig. 4 Voltage change curve under sudden load |
突卸负载时,柴油发电机组的负载电流突降,会引起发电机转速的暂时上升和电网电压的暂时上升。这时,选取负载的阻抗值为r=0.8,x=2,z=2.15,即突卸33%负载,在t=4 s时给予扰动,响应曲线如图5和图6所示。
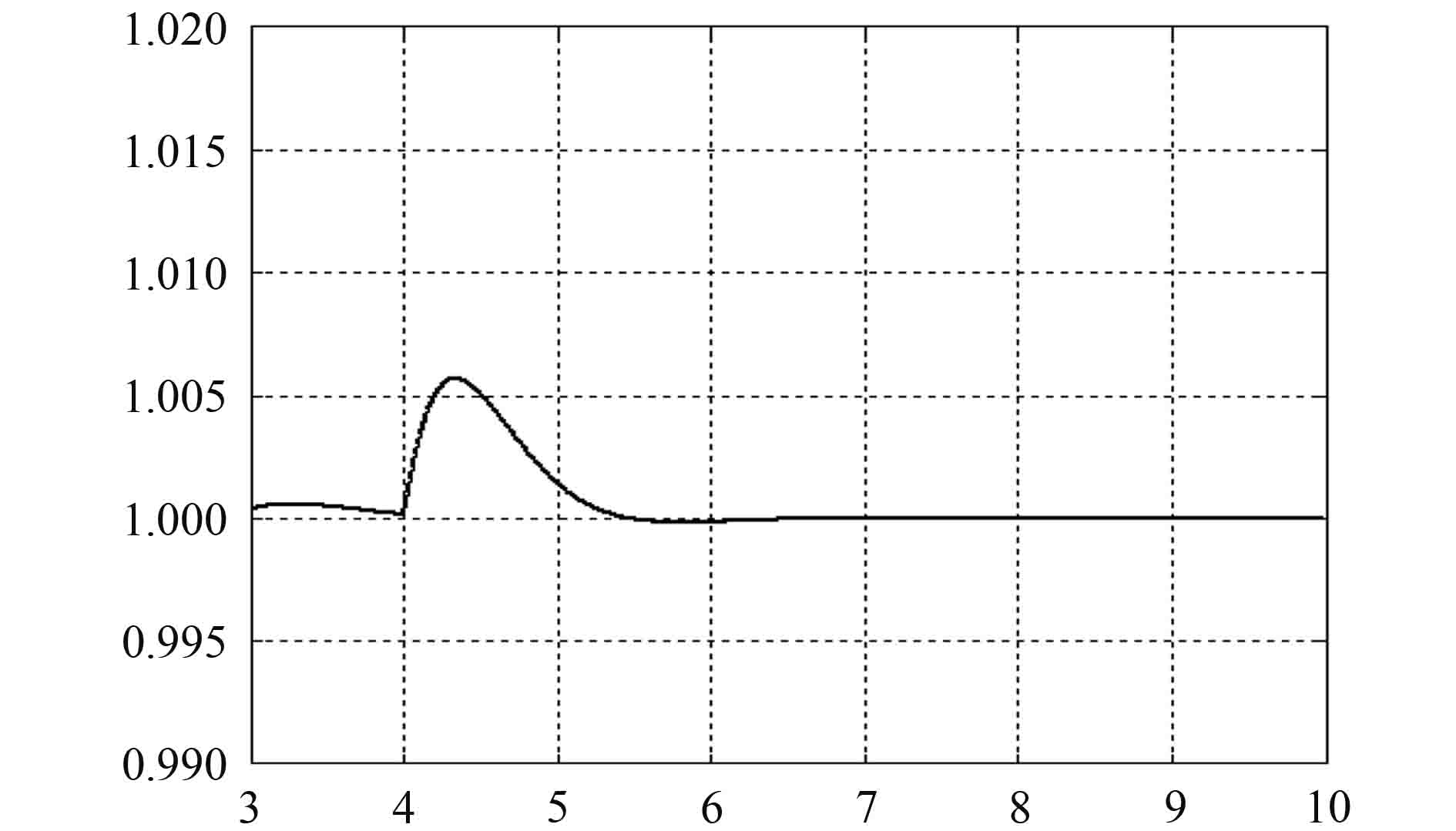
|
图 5 突卸负载时转速变化曲线 Fig. 5 Speed change curve of sudden unloading |
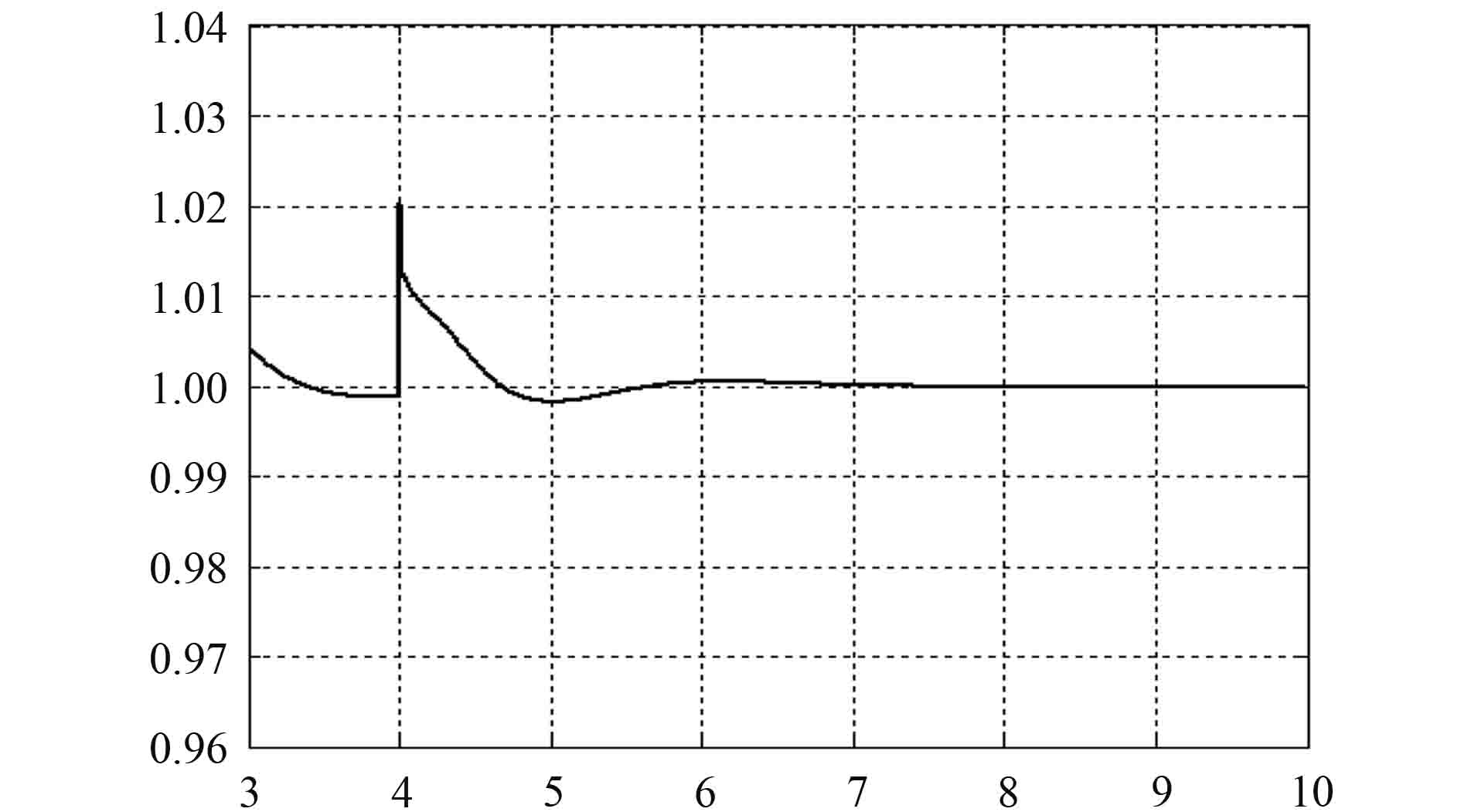
|
图 6 突卸负载时电压变化曲线 Fig. 6 Voltage change curve of sudden unloading |
在突加负载时,发电机组的动态调速率为2.4%,稳定时间为1.4 s;动态电压变化率为7.7%,稳定时间为1.28 s。在突卸负载时,发电机组的动态调速率为0.7%,稳定时间为1.5 s;动态电压调整率为2.1%,稳定时间为1.2 s。根据《钢质海船入级与建造规范》中的规定,当转速为额定转速时,突加负载时的瞬态电压值不低于额定电压的85%,突卸负载时,瞬态电压值不超过额定电压的120%,电压恢复到稳定值3%以内所需的时间应不超过1.5 s,可见仿真结果的指标完全符合要求[8]。
5 结 语船舶柴油发电机组不同于陆地发电机组,具有特殊性。本文通过分析船舶柴油发电机组的系统组成原理,建立了同步发电机的7阶非线性数学模型、柴油机调速系统的数学模型、励磁系统的数学模型。采用隐式梯形积分法在C#下求解了船舶柴油发电机组的非线性微分方程组。最后,选取了特定型号的柴油发电机组并根据非线性方程组的求解结果,进行了仿真验证。结果表明本文所建立的船舶柴油发电机组的非线性数学模型完全符合标准。
| [1] | 李东辉, 张均东, 何治斌. 教学实习船电力系统建模与仿真[J]. 上海交通大学学报, 2008, 48(2): 190–193. http://www.docin.com/p-21744540.html |
| [2] | 谭磊. 船舶综合电力系统暂态仿真研究及可视化实现[D]. 哈尔滨: 哈尔滨工程大学, 2013. |
| [3] | 王超, 王刚. 非线性特性在船舶电力系统中的研究及仿真[J]. 舰船科学技术, 2015, 37(1): 161–164. |
| [4] | 谢心怡, 刘彦呈. 基于时域仿真法的大扰动下船舶电站暂态稳定分析[J]. 大连海事大学学报, 2011, (04): 59–63. http://www.cqvip.com/QK/92863X/201305/47364315.html |
| [5] | ZHU J, SI G, DIAO L, et al. Modeling and nonlinear dynamic analysis of fractional permanent magnet synchronous generators[J]. 2016 IEEE Control Conference. 2016: 10487–10491. http://journals.sagepub.com/doi/full/10.1177/1077546314545099 |
| [6] | MILANO F. On current and power injection models for angle and voltage stability analysis of power systems[J]. IEEE Transactions on Power Systems, 2016, 31(3): 2503–2504. |
| [7] | 戴远航, 陈磊, 张玮灵, 等. 基于多支持向量机综合的电力系统暂态稳定评估[J]. 中国电机工程学报, 2016, (5): 1173–1180. http://www.doc88.com/p-9945632396809.html |
| [8] | 中国船级社. 钢质海船入级与建造规范[M]. 北京: 人民交通出版社, 2012. |
 2018, Vol. 40
2018, Vol. 40
