浮式结构物在深水资源开发领域正起到越来越重要的作用。由于钢制悬链线系泊缆的力学特性稳定,长期交变荷载作用下不必担心塑性老化问题,因此是目前浮式结构所采用的主要定位形式之一[1]。然而此类型系泊系统的不足之处在于:当水深增加以后,由于水中缆绳重量大,导致系泊载荷占用浮体大量储备浮力;缆绳与铅垂线夹角随水深增加而减小,造成定位效率逐渐降低;缆绳全部重量由上端锚机承受,造成系泊设备选型困难[2 – 4]。为此近年来工程界出现了一些采用设置水下浮筒的单点与多点系泊系统以解决上述难点问题[5],如图1所示。
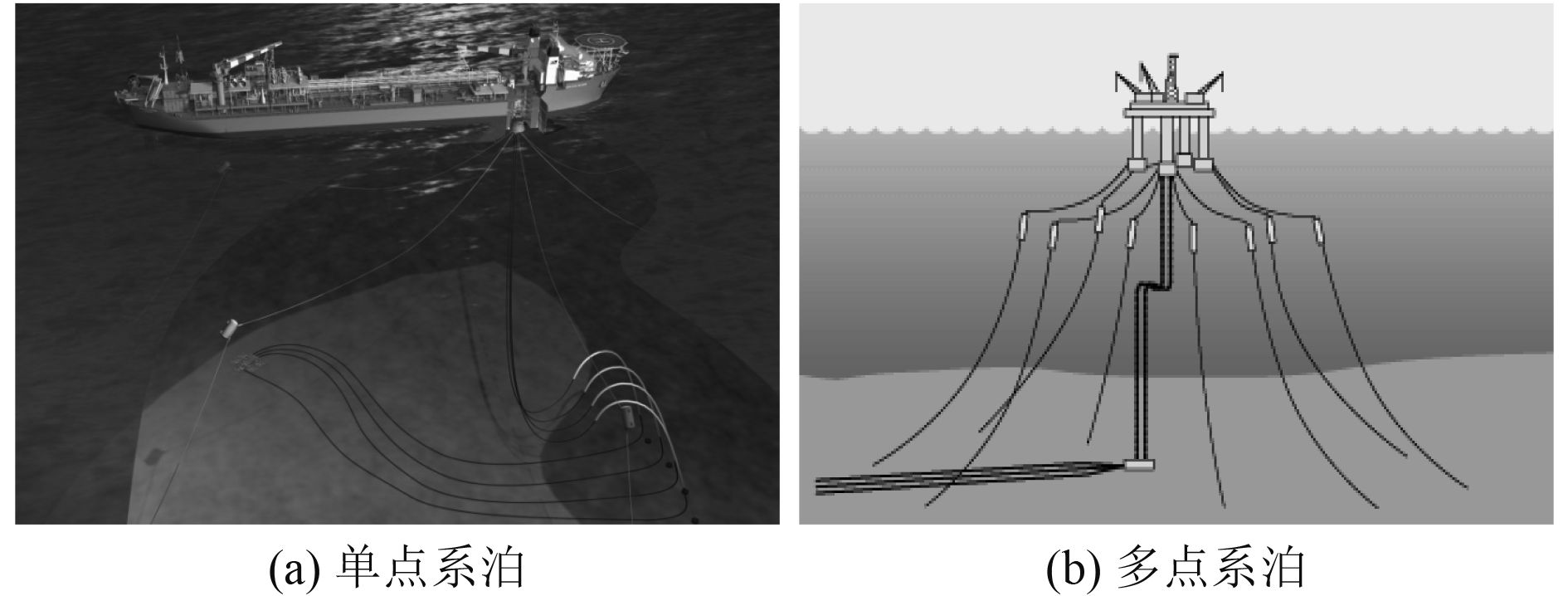
|
图 1 配备水下浮筒的深水浮式平台系泊系统 Fig. 1 Mooring system of floating platform with submergible buoy in deepwater |
当配备水下浮筒以后,缆绳的大部分重量将由水下浮筒承受,从而节约大量系泊载荷,并降低了系统对于锚机承载能力的要求;同时由于有效控制了导缆孔处缆绳角度,系泊回复性能得以保障;增大了缆绳与其他水下设施的垂向间距,安全性有所提高,确实达到了性能优化的目的。但会引出一些新的问题,系泊浮筒更容易受到流体载荷的作用,此外浮筒的动力响应也将增加缆绳的设计载荷;增加了连接硬件的使用,系泊安装费用明显上升;水中缆绳呈多段悬链线型,传统的悬链线方程将不再适用,设计分析难度提高[6]。因此在设计阶段如何根据现有的缆绳规格与设计要求,确定出合适的浮筒位置与净浮力大小,从而在有限的设备资源条件下,尽量提高系统的回复性能并降低系泊载荷,是设计者面临的难点问题,为此本文以一座试验半潜式平台的系泊系统为例,研究浮筒位置、净浮力大小以及海流流速等对于缆绳静力特性的影响,以期得出一些规律性的认识,为今后的深水系泊设计工作提供借鉴与参考。
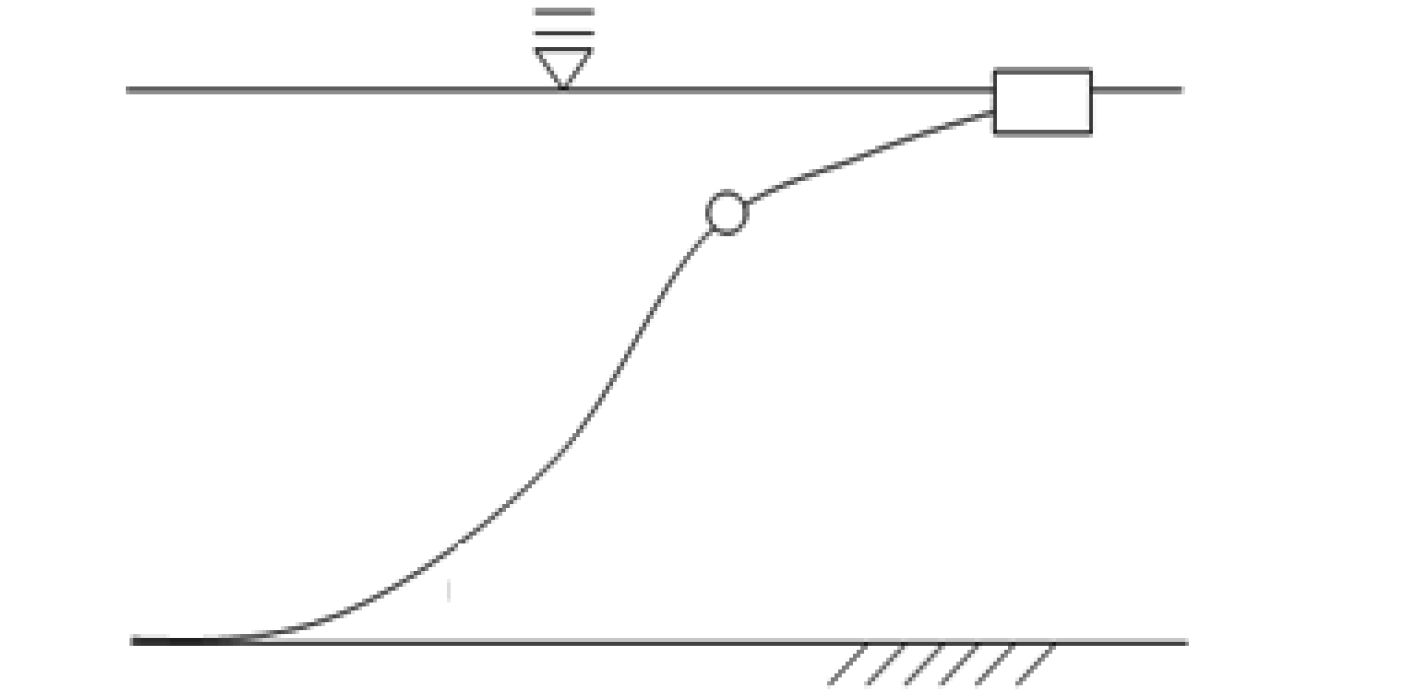
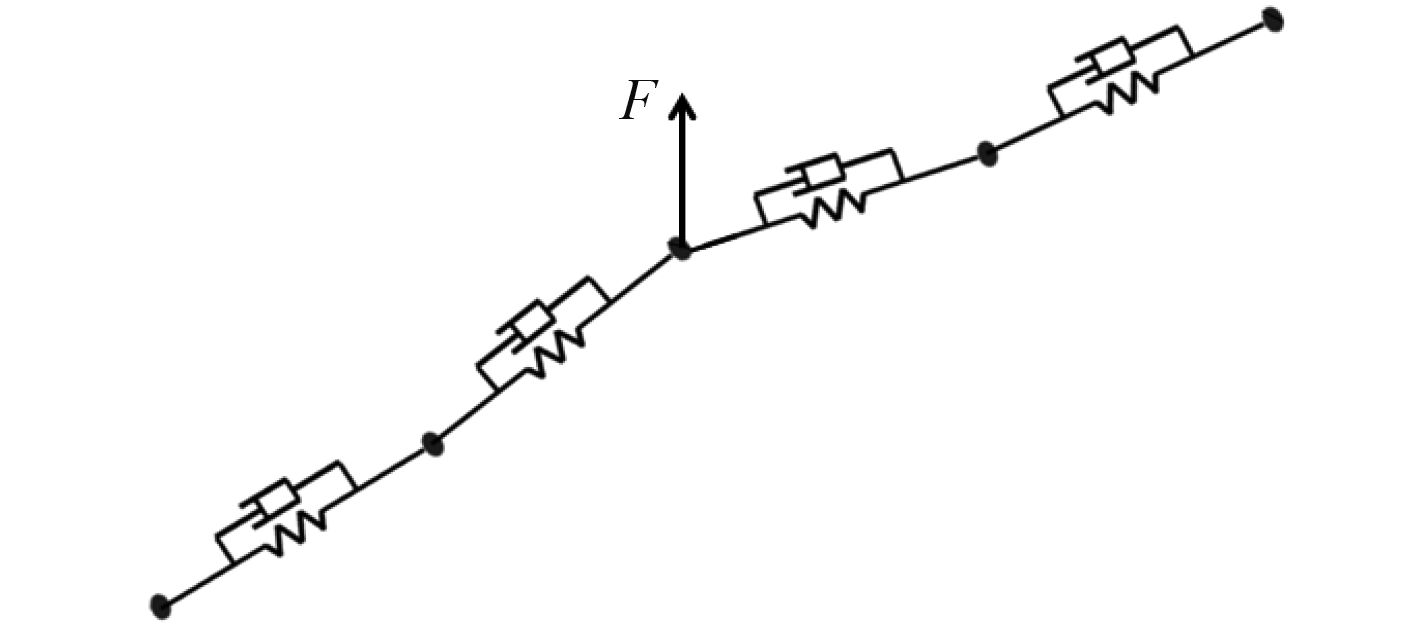
1 缆绳力学模型的建立依据集中质量法建立缆绳力学模型。将整体缆绳离散成为许多质点,之间用无质量的轴向弹簧与阻尼器相连接,浮筒对于缆绳的作用则模拟成为作用于某质点上的集中力,缆绳的整体示意图和局部分段的力学模型如图2与图3所示。
|
图 2 缆绳水中构型 Fig. 2 Configuration of mooring line |
|
图 3 缆绳局部力学模型 Fig. 3 Partial mechanical model of mooring line |
某一质点
| $\left\{ {{F_k}} \right\} = \left\{ {F_{GBT}^k} \right\} + \left\{ {F_T^k} \right\} + \left\{ {F_D^k} \right\} + \left\{ {F_I^k} \right\}\text{。}$ | (1) |
其中:
| $F_T^k = \left( {F_{TH}^k + F_{TD}^k} \right)\overrightarrow {{t_k}} - \left( {F_{TH}^{k - 1} + F_{TD}^{k - 1}} \right)\overrightarrow {{t_{k - 1}}}\text{。} $ | (2) |
其中:
| $F_{TD}^k = - {\mu _k}\left( {\overrightarrow {{v^k}} - \overrightarrow {{v^{k - 1}}} } \right)\overrightarrow {{t_k}}\text{。} $ | (3) |
其中:
根据Morison方程,分段
| $\begin{split}\vec F_d^{{l_k}} =& - \frac{1}{2}{\rho _f}A_T^kC_{dt}^k\left| {\overrightarrow {v_r^k} \cdot \overrightarrow {{t_k}} } \right|\left( {\overrightarrow {v_r^k} \cdot \overrightarrow {{t_k}} } \right)\overrightarrow {{t_k}} - \\&\frac{1}{2}{\rho _f}A_N^kC_{dn}^k\left| {\overrightarrow {v_r^k} \cdot \overrightarrow {{h_k}} } \right|\left( {\overrightarrow {v_r^k} \cdot \overrightarrow {{h_k}} } \right)\overrightarrow {{h_k}} \text{。}\end{split}$ | (4) |
其中:
| $\overrightarrow {v_r^k} = \overrightarrow {{v^{sk}}} - \overrightarrow {v_f^{sk}} \text{。}$ | (5) |
其中:
在流体附加惯性力方面,仅考虑法向,缆绳分段上作用的流体附加惯性力可表示为:
| $\overrightarrow F _I^{{l_k}} = - \frac{1}{4}{\rho _f}\pi {D^2}C_M^k\left( {\overrightarrow {\dot v_f^{sk}} \cdot \overrightarrow {{h_k}} } \right)\overrightarrow {{h_k}} \text{。}$ | (6) |
其中:
将其等效到质点上得到缆绳质点上的等效流体粘性阻尼力可表示为:
| $\overrightarrow F _d^k = \frac{1}{2}\left( {\overrightarrow F _d^{{l_k}} + \overrightarrow F _d^{{l_{k - 1}}} + \overrightarrow F _I^{{l_k}} + \overrightarrow F _I^{{l_{k - 1}}}} \right)\text{。}$ | (7) |
以1座试验半潜式平台的系泊缆绳作为算例进行研究。该平台作业水深为1 500 m,容许出现的最大水平偏移约为100 m(约7%的作业水深),缆绳采用锚链-钢缆-锚链三段组合式设计,如表1所示。顶部预张力520 t,此时系泊水平辐射半径为2 900 m。
|
|
表 1 单根缆绳结构组成 Tab.1 The composition of mooring line |
采用集中质量法对缆绳进行划分离散,各部分缆绳的节点编号与分段数如表2所示。
|
|
表 2 缆绳分段与节点编号范围 Tab.2 Mooring line component and corresponding envelope of nodes numbering |
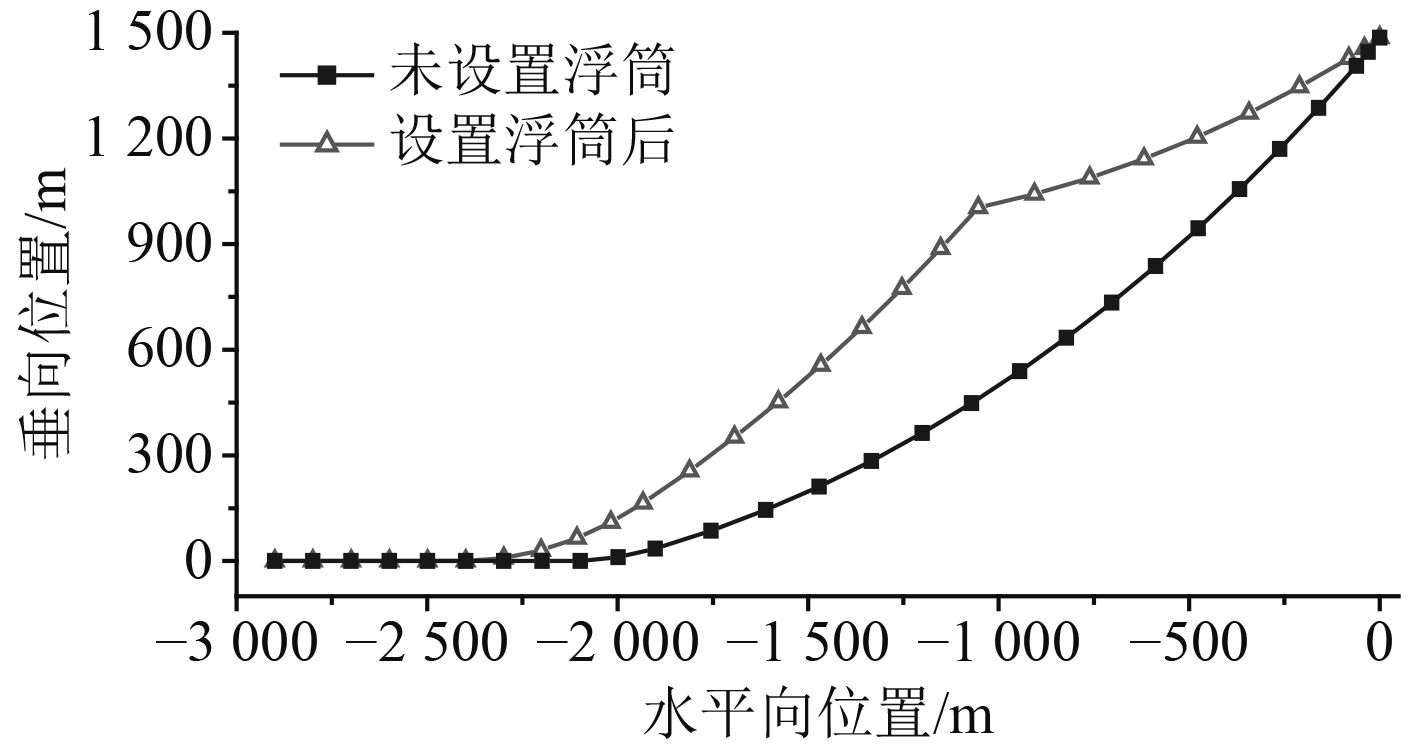
现采用水下浮筒对单根缆绳进行优化。在19号节点处设置净浮力为300 t的水下浮筒,保持其他参数不变,缆绳水中构型的对比如图4所示,预张力与系泊载荷,水平回复刚度曲线以及不同位置的缆绳张力随浮体水平偏移量的对比情况如图5~图7所示。
|
图 4 缆绳水中构型对比 Fig. 4 Comparison of mooring line configuration |
|
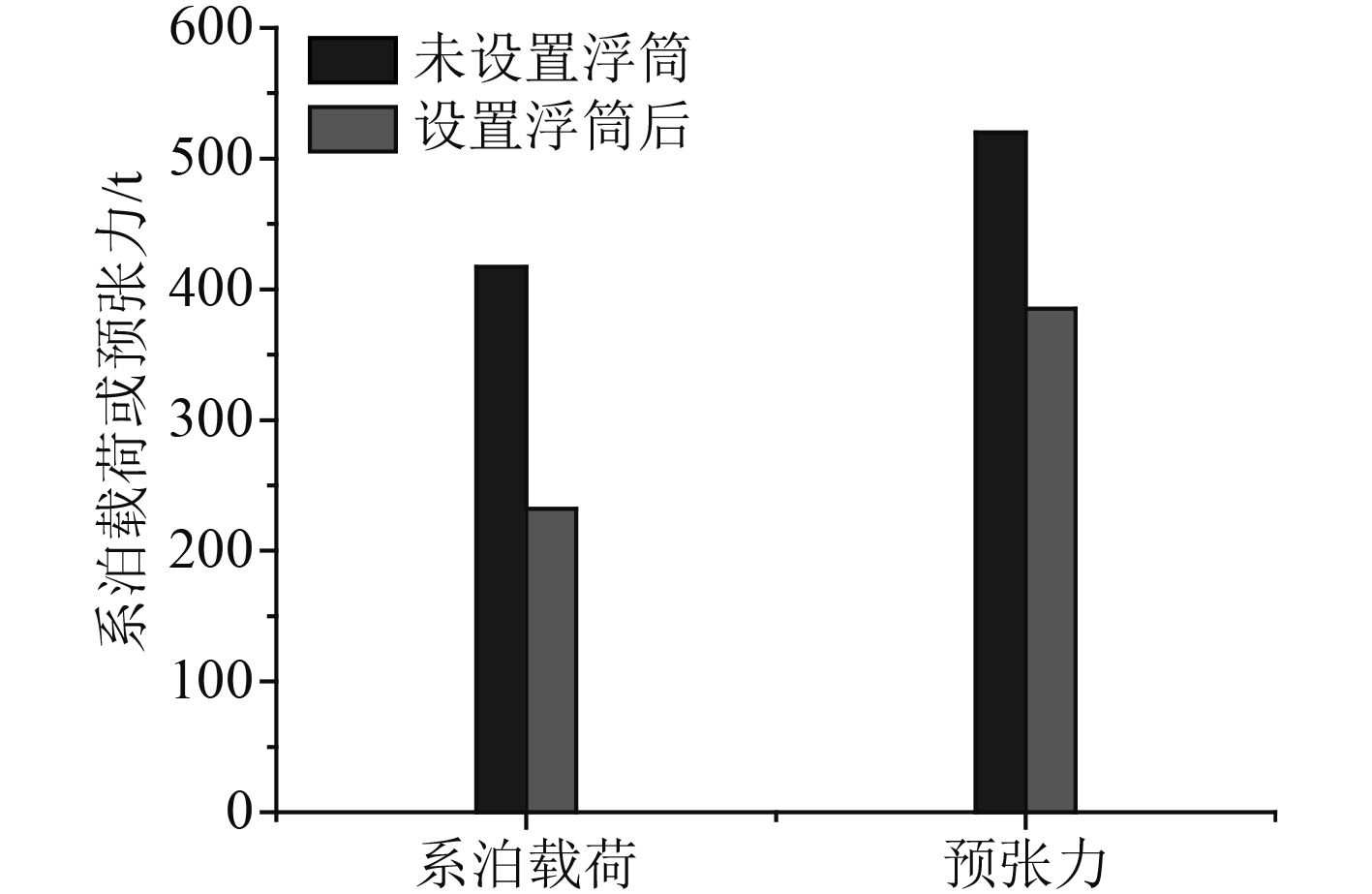
图 5 系泊载荷与预张力对比 Fig. 5 Comparison of mooring load and pretension |
|
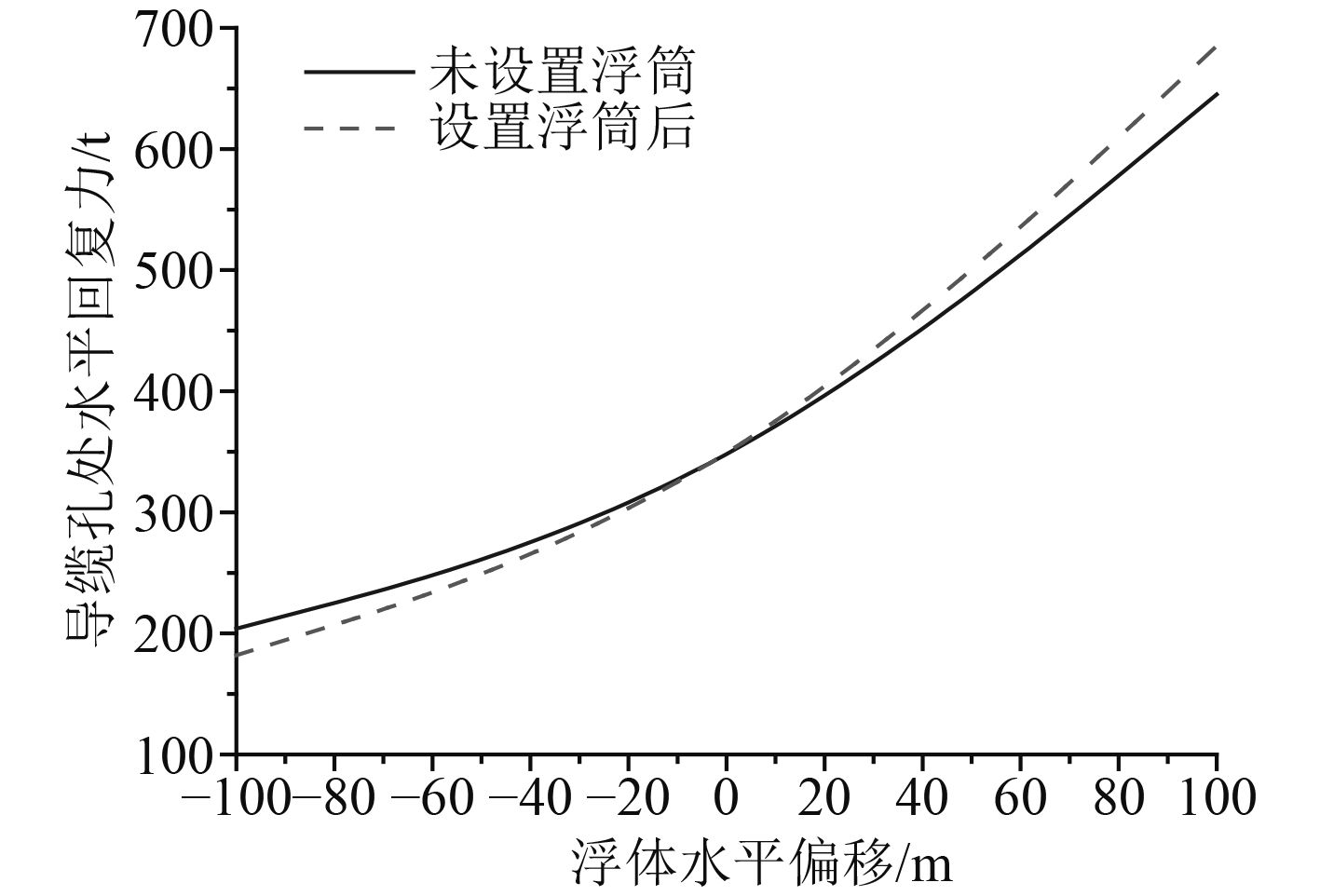
图 6 缆绳水平刚度对比 Fig. 6 Comparison of horizontal restoring stiffness |
|
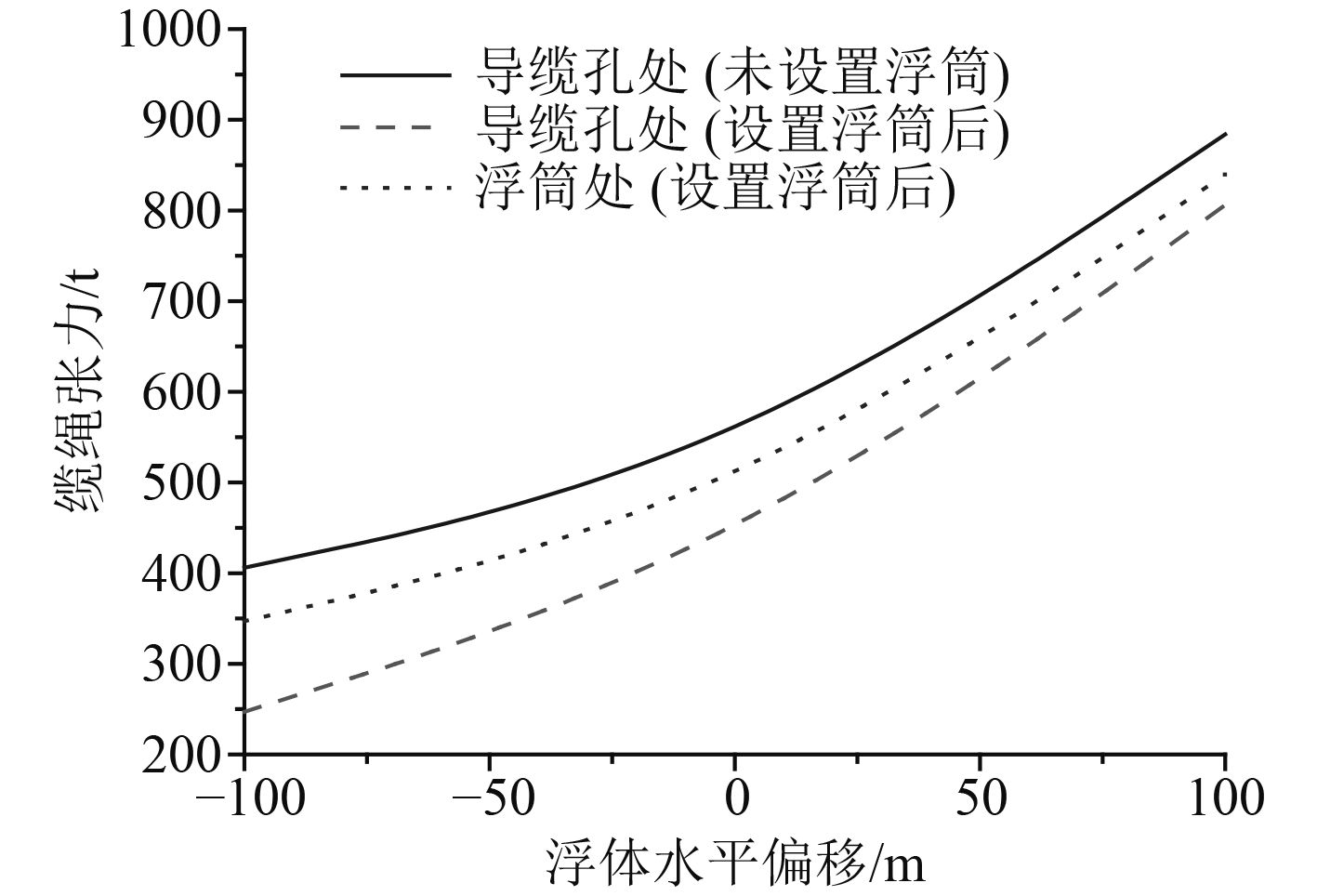
图 7 不同位置处缆绳张力对比 Fig. 7 Comparison of tension at different location |
通过图5~图7发现,设置水下浮筒以后,单根缆绳的水平回复刚度有所提高,系泊载荷只有原先的50%左右,而预张力与加载浮筒前相比,下降了25%左右,确实达到了性能优化的目的。在缆绳张力方面,缆绳不同位置的最大系泊张力均小于加载浮筒前。值得注意的是,设置系泊浮筒导致最大张力位置的改变,即浮筒下端缆绳的系泊张力将大于导缆孔处,成为缆绳规格选取的决定因素。
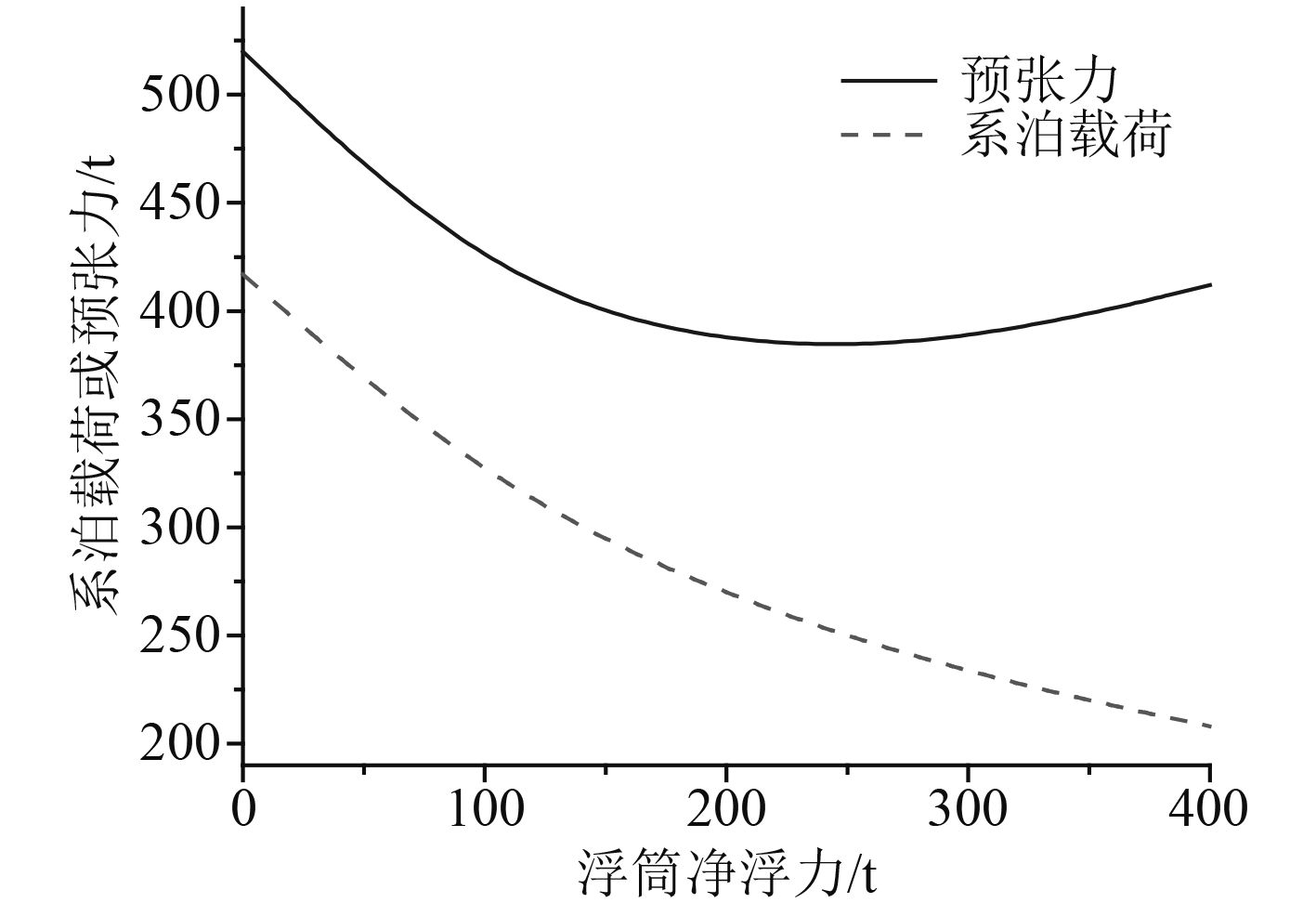
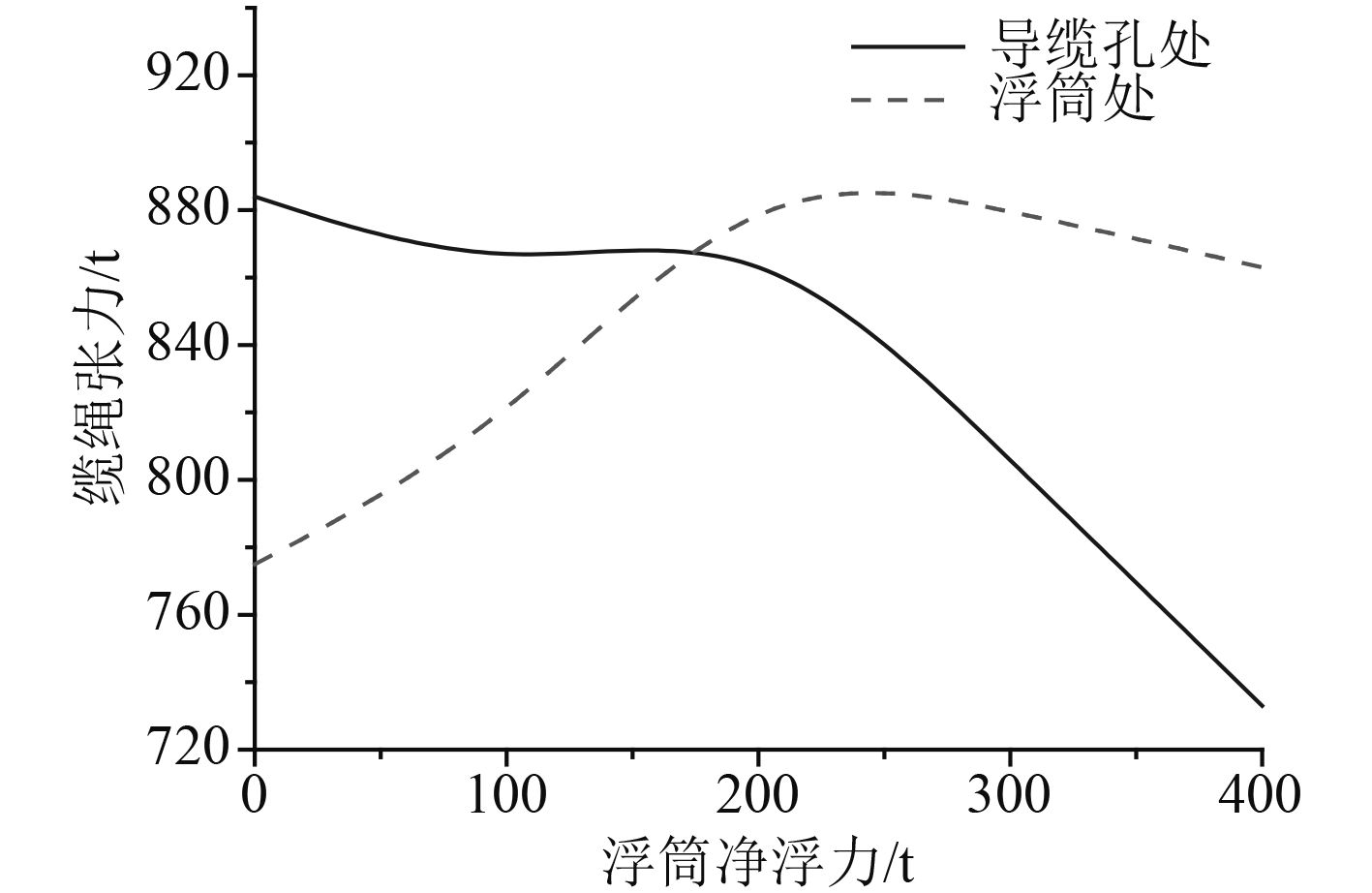
2.1 浮筒净浮力的影响现研究浮筒净浮力的影响。保持缆绳规格、锚固点与浮筒位置不变,使浮筒净浮力由0~400 t变化,图8为预张力与系泊载荷的变化曲线,图9为平台出现极限水平偏移(100 m)时缆绳的系泊张力。
通过图8和图9发现,当浮筒净浮力逐渐增加时,系泊载荷将持续降低,但导缆孔处所需设置的预张力则出现了先减小后增大的现象,并在浮筒净浮力为200 t时取得最小值;而在缆绳张力方面,导缆孔处系泊张力随浮筒净浮力的增加而减小,浮筒处系泊张力则先减小后增大,通过单根缆绳的水平回复刚度曲线发现,当浮筒净浮力为200 t时,单根缆绳的水平恢复性能最强。上述计算表明:在给定缆绳规格与浮筒位置前提下,浮筒的净浮力大小存在最优值,此时缆绳的预张力最小,水平恢复能力却最强,此外导缆孔处与浮筒节点处的最大缆绳张力也最为均衡,实现资源的合理配置,优化效果最好。
|
图 8 预张力与系泊载荷的变化曲线 Fig. 8 Curves of mooring load and pretension |
|
图 9 缆绳系泊张力的变化曲线 Fig. 9 Curves of tension at different location |
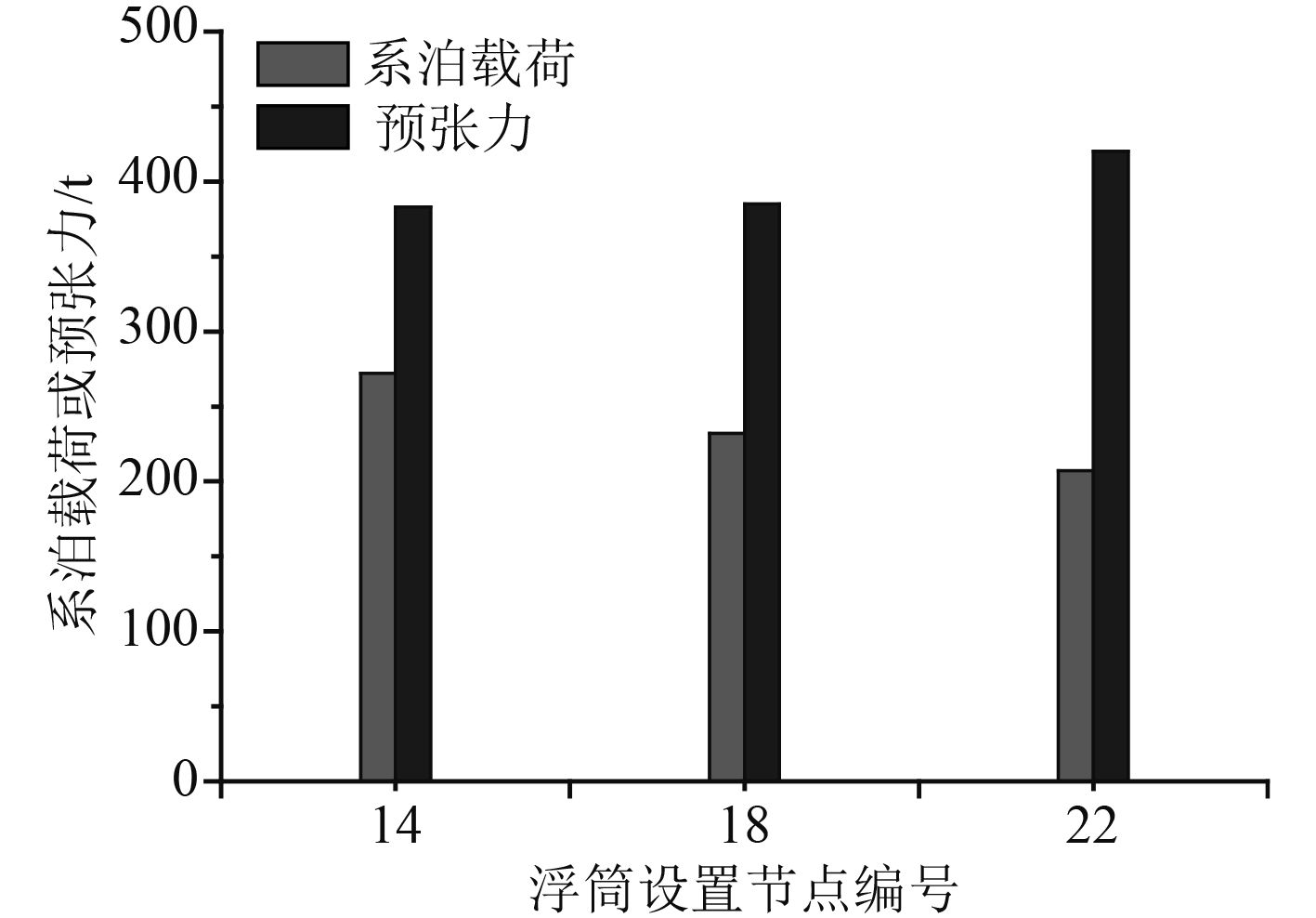
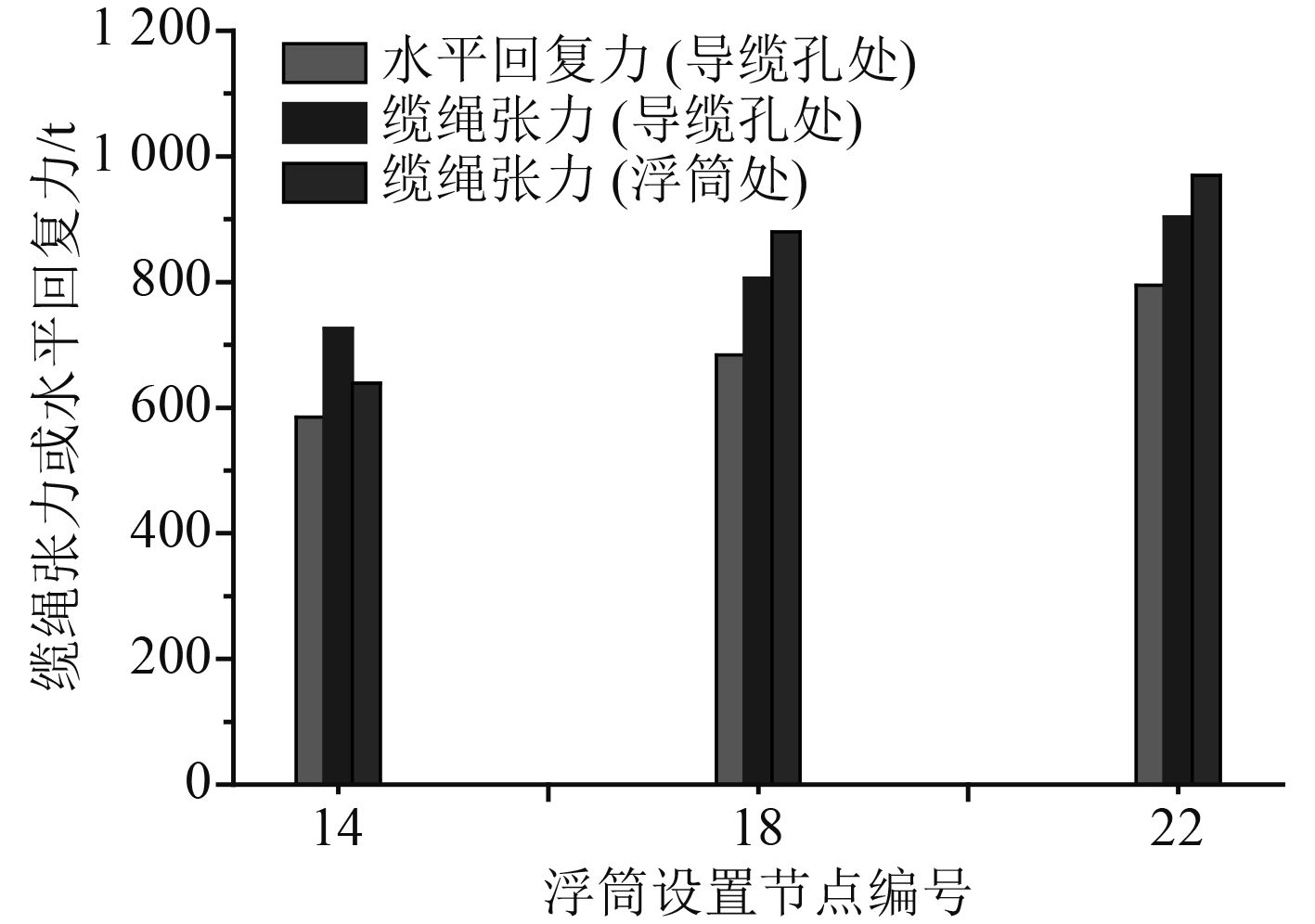
现研究浮筒位置的影响。选取浮筒净浮力为200 t,保持缆绳规格与锚固点位置不变,使浮筒逐渐由缆绳中部向导缆孔方向移动,图10为预张力与系泊载荷随浮筒位置的变化情况,图11为假设平台出现极限水平偏移(100 m)后缆绳张力与回复力的变化情况。
|
图 10 预张力与系泊载荷的变化曲线 Fig. 10 Curves of mooring load and pretension |
|
图 11 缆绳张力的变化曲线 Fig. 11 Curves of tension at different location |
由图10和图11发现:当浮筒位置逐渐向导缆孔方向移动时,系泊载荷逐渐降低,而预张力却逐渐增大;在系泊张力方面,浮筒位置越靠近导缆孔处,当平台出现极限水平偏移时,导缆空处缆绳的水平回复力越大,而浮筒处系泊张力上涨最快,可能成为缆绳规格选取的制约因素。上述计算表明:若想尽量提高系泊水平刚度,应使浮筒位置尽量靠近导缆孔处,但此时浮筒处的系泊张力会快速上涨,因此对该位置的缆绳规格应予以加强。
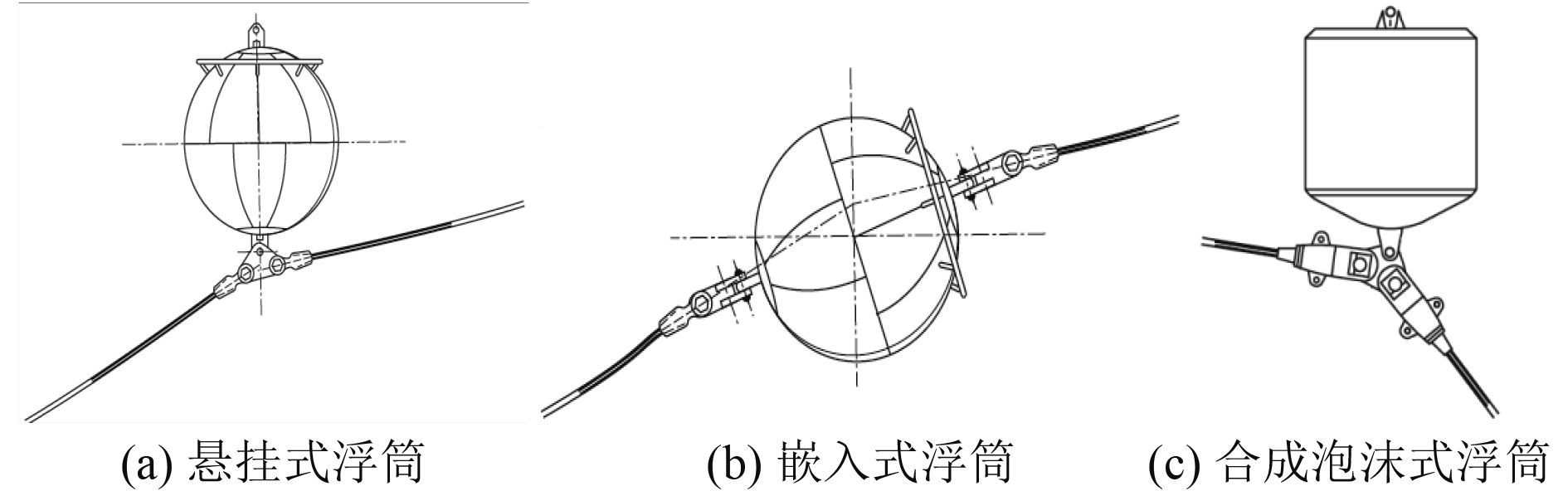
2.3 浮筒海流力的影响现研究海流流速的影响。为此必须首先确定浮筒的外形尺寸,目前最常见的水下浮筒有3种类型如图12所示。
|
图 12 常见的水下浮筒形式[5] Fig. 12 Normal submersible buoy configurations |
为简化计算本文中假设浮筒为圆柱式合成泡沫型。若浮筒净浮力为200 t,合成泡沫的密度为0.1 g/cm3,则浮筒的大致尺寸规格为:直径6 m,高为8 m,属于大尺度构件,可根据文献[5]中提供的计算半潜式平台船体构件海流力的计算公式进行估算:
| ${F_{cs}} = {\text{515}}{\text{.62 }}\left( {{C_d}{A_c}} \right)V_c^2\;\text{,} \quad {\rm N}\text{。}$ | (8) |
其中:
|
|
表 3 浮筒水平向海流力计算结果 Tab.3 Result of horizontal current force act on the buoy |
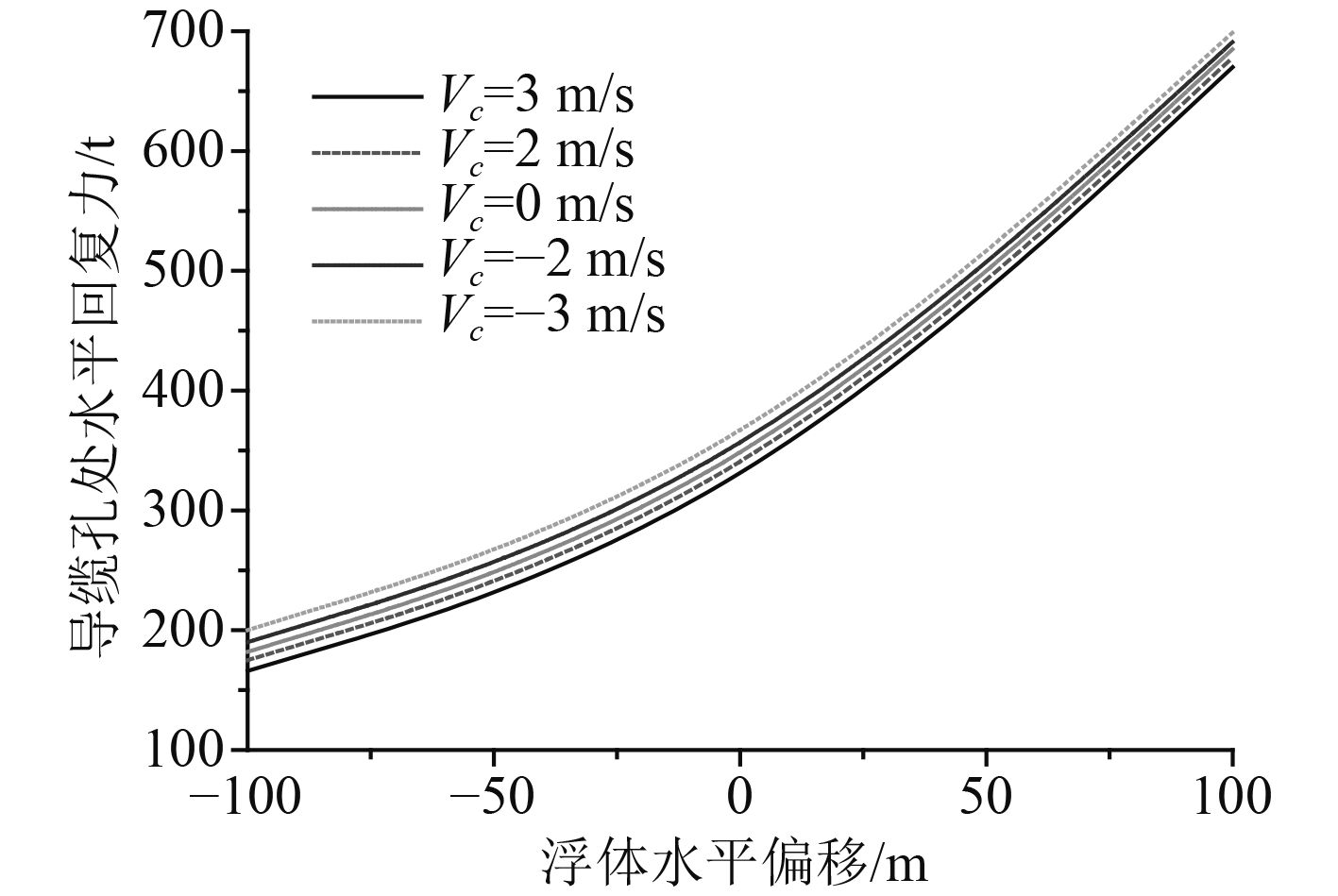
通过表3可知,在常规海流流速作用下,浮筒受到的水平向海流力远小于垂向的净浮力,因此水中浮筒可基本保持正浮状态。现将海流力作为水平向集中力加载到缆绳节点上,而作用于系泊缆绳上的海流力则采用Morison公式进行计算,图13为不同海流流速下缆绳水平回复刚度曲线的变化情况,图14为平台出现极限水平偏移时缆绳张力的变化情况。
|
图 13 缆绳水平刚度变化曲线 Fig. 13 Curve of horizontal restoring stiffness |
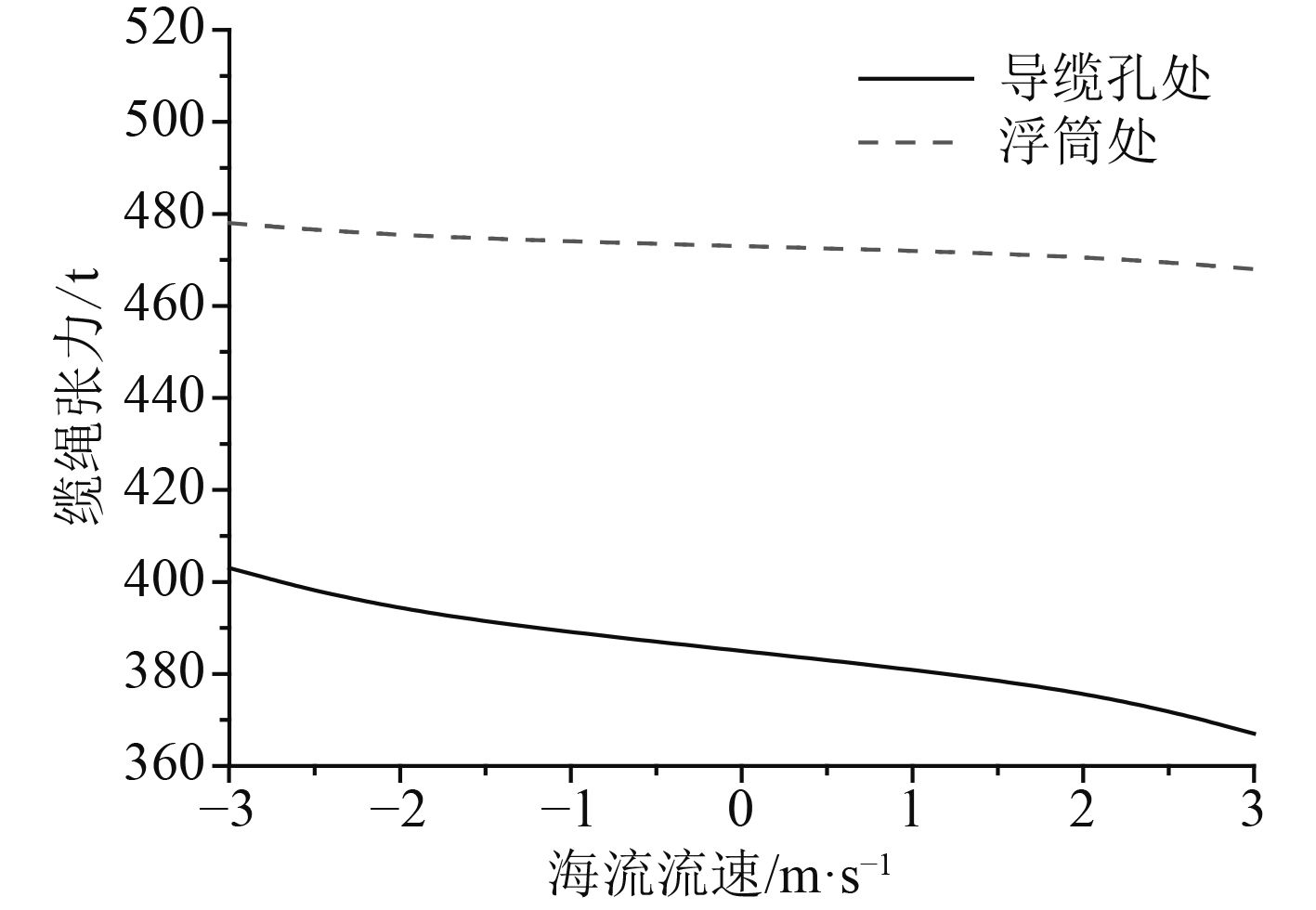
|
图 14 不同位置缆绳张力的变化 Fig. 14 Curve of tensions at different location |
由图13与图14发现,当海流流速逐渐提高时,缆绳的水平回复刚度有所降低,导缆孔处缆绳张力的变化范围大于浮筒处,张力的变化量与浮筒本身所受到的水平向海流力相接近。
3 结 语本文依据集中质量法建立深水系泊缆绳柔性力学模型,研究了浮筒位置、净浮力大小以及海流流速等对于缆绳静力特性的影响,得到如下结论:
1)设置水下浮筒可有效降低系泊载荷与预张力,提高缆绳水平回复刚度,从而起到改善系泊性能的目的,但可能导致最大张力位置的改变,即当平台出现较大水平偏移后,浮筒下端处缆绳的系泊张力上涨很快,有可能超过导缆孔成为整根缆绳强度校核的制约因素。
2)水平恢复刚度方面,在给定缆绳规格与浮筒位置的前提下,浮筒的净浮力将存在最优值,此时缆绳所需施加的预张力最低,但水平恢复性能却最强,此外缆绳不同位置处的系泊张力也最为均衡;浮筒位置也会对缆绳的静力特性产生明显影响,若想提高系泊刚度,应使浮筒位置靠近导缆孔处,若想控制系泊张力,则应使浮筒尽量位于缆绳的中部位置。
3)常规海流流速下浮筒受到的水平向海流力远小于净浮力,因此若采用悬挂式水下浮筒,则水中浮筒基本可保持正浮状态,海流流速对于缆绳静力特性的影响程度也较小。
| [1] | 李志海, 徐兴平, 黄慧丽. 海洋平台系泊系统发展[J]. 石油矿场机械, 2010, 39(5): 75–78. |
| [2] | 由纪昆. 新型深水系泊技术[J]. 中国水运, 2008, 8(2): 34–35. http://doi.wanfangdata.com.cn/10.3969/j.issn.1006-7973-C.2008.02.016 |
| [3] | 王言英, 肖越. 深水锚泊的新概念与新技术[J]. 船舶工程, 2004, 26(2): 1–3. |
| [4] | HASLUM H A, TUE J. Red hawk polyester mooring system design and verification[C]//Offshore Technology Conference Proceedings. Houston: Offshore Technology Conference, 2005. |
| [5] | American petroleum institute. Design and analysis of station keeping systems for floating structures[S]. API Recommended Practiced 2SK, 2005. |
| [6] | 陆中杰, 周国平. 深水锚系泊作业技术应用初探[J]. 船舶设计通讯, 2011(Z1): 67–72. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cbsjtx2011z1013 |
| [7] | 黄勇. 系泊浮筒的设计与动力分析[J]. 中国水运, 2009, 9(1): 5–7. |
 2018, Vol. 40
2018, Vol. 40
