2. 船舶振动噪声重点实验室,湖北 武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China
橡胶材料具有高弹性,减振效果好,被广泛应用于各类船舶装置中,起到衰减和吸收装置振动噪声的作用。橡胶减振器是船舶降噪减振系统中的关键部件,其性能的好坏对船舶舱室内部生活环境、机械装置的使用寿命有重要的影响。静刚度为评价橡胶减振器性能的重要指标,其对减振器传递率有着重要的影响,过高的静刚度会使得减振器的传递率变得很高,而过低的静刚度又使减振器承载性能太差。目前广泛以静刚度为橡胶减振器设计的参考指标。通常设计人员先大体上确定减振器结构后进行模具设计,制作出减振器的样品,然后对样品的静刚度进行检测,如减振器未达到要求,再对模具和橡胶胶料硬度进行调节。通过周而复始的试验,最终到达减振器设计要求[1]。
运用试验反复验证的方法纵然能实现减振器的优化生产,但此过程需要耗费大量的人力物力,成本较高。因此,近年来广泛应用有限元仿真法进行减振器的设计生产[2-3],很大程度节约了成本。
本文选取某型船用减振器为研究对象,通过理论推导得到静刚度计算模型,利用Pro/E三维绘图软件建立橡胶减振器几何模型,再结合有限元仿真软件Abaqus对橡胶减振器的静刚度计算结果进行验证,并利用静刚度计算模型进行结构尺寸的设计,很大程度上缩短了减振器设计周期。
1 静刚度模型橡胶减振器在各类船舶装置上使用广泛,具有性能稳定、减振效果优良等特点,此外,橡胶减振器的尺寸范围大,在狭窄的舱内空间内使用仍然不受限制[4]。静刚度作为确保减振系统具有良好力学性能的关键参数,应保持在一个相对恒定的水平。由于金属和橡胶的粘结强度高于橡胶强度本身,因此,橡胶减振器的静刚度主要由橡胶元件的性能决定。
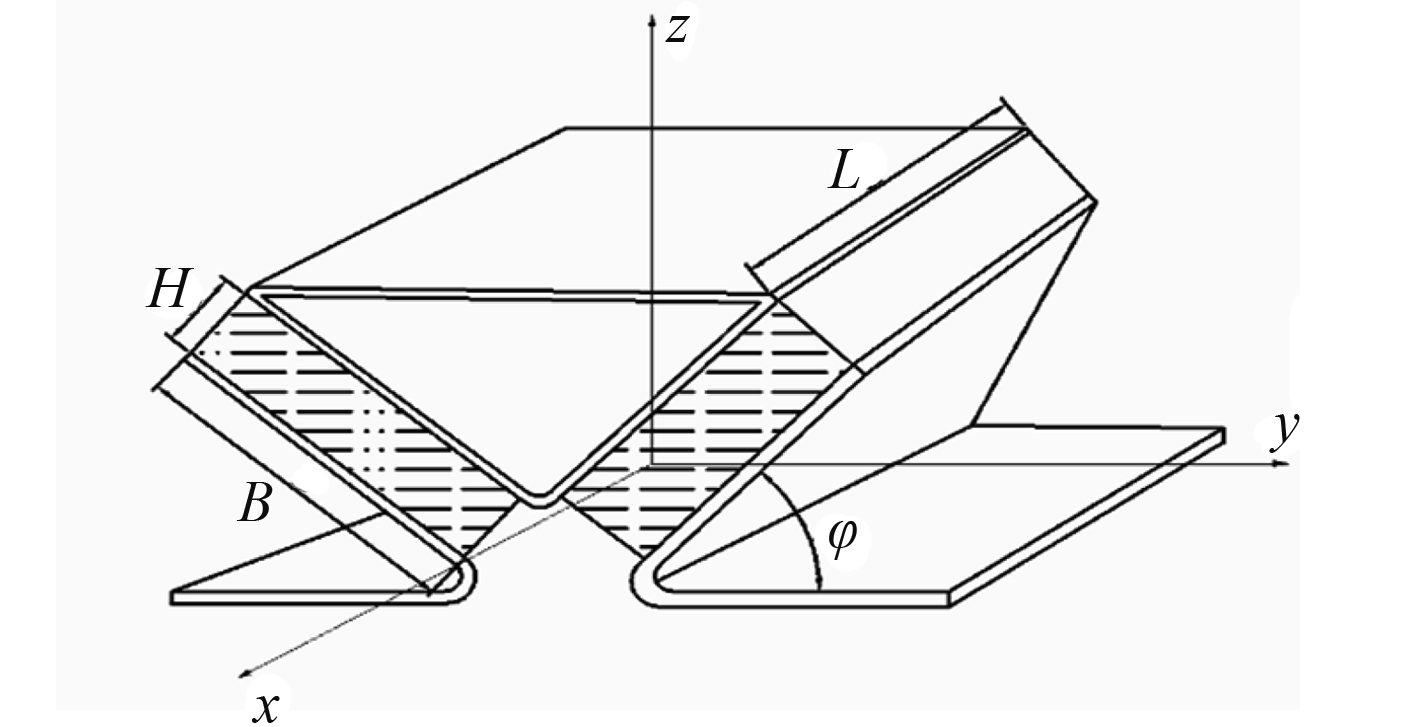
图1为某型橡胶减振器的结构简图,虚线填充部分表示橡胶材料,承担着整个减振器的减振功能,无填充部分为金属件,起着限位和支撑作用。
|
图 1 橡胶减振器结构示意图 Fig. 1 The structure of rubber absorber |
如图1所示,橡胶受到切向应力和正向应力,产生正应变和切应变,在正应力下,橡胶材料刚度为[5-6]:
| $K = \frac{A}{H}{m_z}E\text{。}$ |
式中:E为橡胶材料的弹性模量;mz为正向形状系数;A为受压面积;H为橡胶材料原始厚度。在切应力下,橡胶材料的剪切刚度为:
| ${K_T} = \frac{S}{L}{m_x}G\text{。}$ |
式中:G为剪切模量;mx为切向形状系数;S为受剪面积;L为原始高度。
对橡胶元件进行分析,得到垂直于橡胶—金属接触面的正向刚度为
| ${K_\alpha } = \frac{{{A_L}{m_z}}}{H}E\text{,}$ |
式中:
| ${K_\beta } = \frac{{{A_L}{m_x}}}{H}G\text{,}$ |
式中:
| ${K_z} = 2{K_\alpha }\left( {\cos {\phi ^2} + \frac{1}{k}\sin {\phi ^2}} \right)\text{,}$ |
其中,
|
|
表 1 橡胶减振器初始尺寸 Tab.1 The initial size of rubber absorber |
橡胶减振器的弹性体为丁腈橡胶,其具有耐油性好、阻尼大、耐热性高等优点,广泛作为一般动力装置的减振材料。丁腈橡胶的应力应变曲线程典型的非线性,其本构模型较为复杂,不能简单地像描述线性材料那样描述橡胶材料。关于橡胶材料本构模型橡胶已有大量研究[7-8],在小变形情况下,可采用多项式本构模型来模拟超弹属性,其应变能可表示为:
| $W\left( {{I_1},{I_2}} \right) = \sum\limits_{i,j = 0}^n {{C_{ij}}} {\left( {{I_1} - 3} \right)^i}{\left( {{I_2} - 3} \right)^j} + \sum\limits_{i = 1}^n {\frac{1}{{{D_i}}}{{\left( {J - 1} \right)}^{2i}}} \text{。}\!\!\!$ |
式中:W(I1,I2)为应变能函数;Cij为Rivlin系数;I1和I2 分别为第一和第二Green应变不变量;J为橡胶变形前后体积比;Di决定橡胶材料是否可压缩。如果采用两参数的Mooney-Rivlin本构模型,则式(6)变为
| $W = {C_{10}}\left( {{I_1} - 3} \right) + {C_{01}}\left( {{I_2} - 3} \right) + \frac{1}{{{D_1}}}{\left( {J - 1} \right)^2}\text{,}$ |
弹性常数为:
| $\begin{aligned}& G = 2({C_{01}} + {C_{10}}),\;K = \frac{2}{{{D_1}}}\text{,}\\& E = \frac{{9KG}}{{3K + G}},\;\nu = \frac{{3K - 2G}}{{6K + 2G}}\text{。}\end{aligned}$ |
式中:G为橡胶剪切模量;E为橡胶弹性模量;ν为泊松比,当丁腈橡胶看作不可压缩材料时,J=1;
本文采用Mooney-Rivlin本构模型来描述橡胶材料,采用线性本构来描述金属件,材料参数如表2所示。
|
|
表 2 材料本构模型及参数 Tab.2 The parameter of material constitutive model |
由于橡胶减振器在生产过程中,橡胶材料与金属件表面经过特殊的硫化处理,其接触面粘接强度甚至比橡胶材料本身强度更高,因此,橡胶与金属件接触面可定义为三向固定的边界条件,得到如图2所示的有限元分析模型,橡胶部分单元用杂交型单元C3D8H模拟,金属部分用减缩型C3D8R单元模拟。

|
图 2 橡胶减振器有限元模型 Fig. 2 The finite elements model of rubber absorber |

|
图 3 变载下橡胶减振器垂向位移 Fig. 3 The vertical displacement under variable load |
|
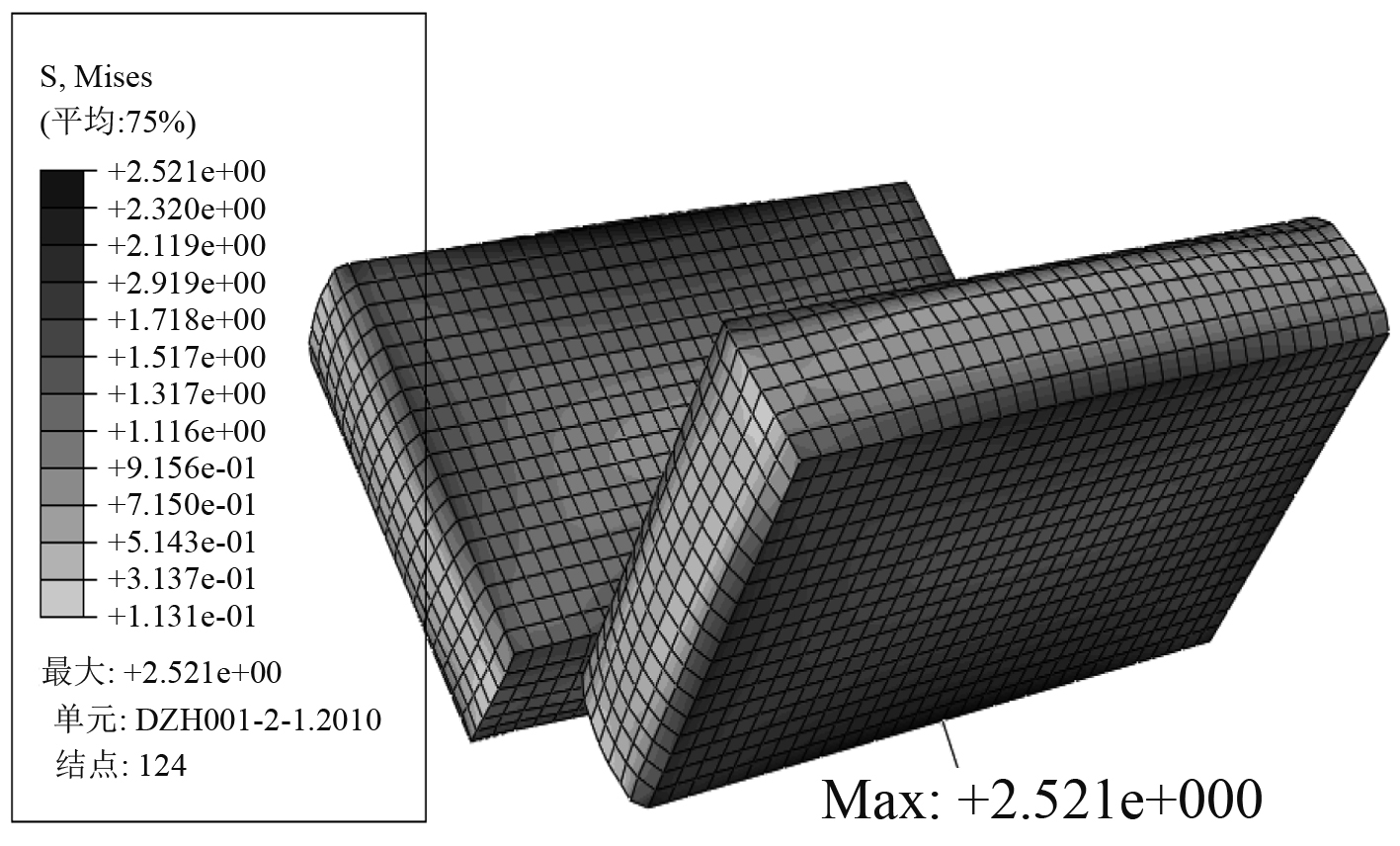
图 4 11 kN下橡胶元件平均应力云图 Fig. 4 The von Mises of rubber under 11 kN |
在橡胶减振器上表面建立耦合的约束,使整个上表面受到合力与耦合点相同,在耦合约束点施加向下的载荷,对橡胶减振器进行静力分析,得到不同载荷下橡胶减振器的载荷—位移关系(见图3),从图中可以看出,位移和载荷约成线性关系,说明橡胶在小变形下可以看成线弹性材料。图4表示橡胶元件在11 kN下的等效应力,从图中可以看出,橡胶元件在与金属接触面上受到的应力最大,因此橡胶与金属面的粘结力决定着整个橡胶减振器的刚度上限。
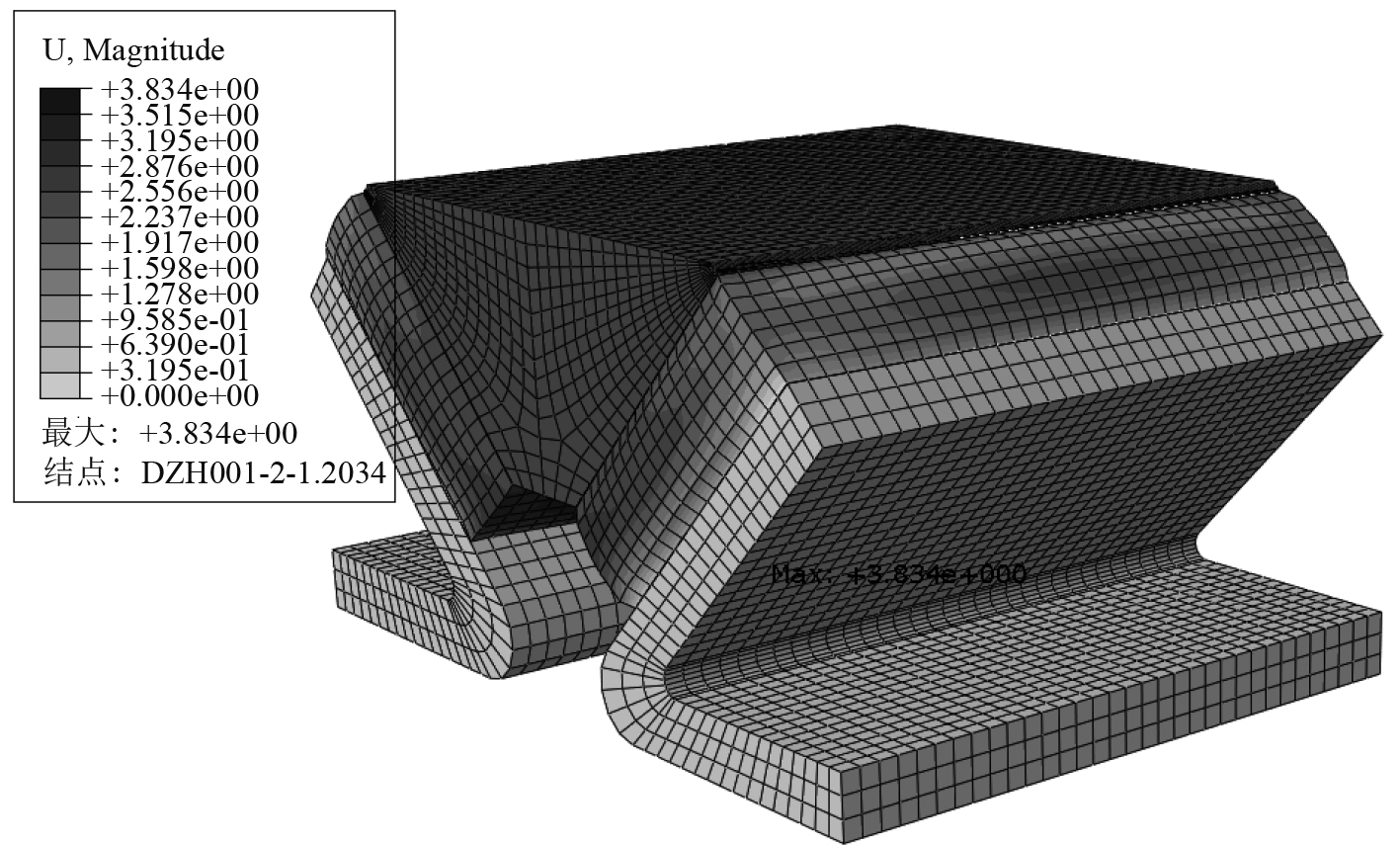
2.3 静刚度仿真计算在橡胶减振器上表面耦合约束点施加2 kN和10 kN的载荷,计算得到图5和图6橡胶减振器的位移云图,从图中可以看出,橡胶减振器的最大变形发生在橡胶件下端面,上表面垂向位移为0.56 mm和2.556 mm,可计算得到静刚度为3 636.4 N/mm和3 912.4 N/mm。理论计算结果为3 726.8 N/mm。静刚度理论结果和仿真结果误差范围均在5%以内,橡胶减振器的仿真结果与理论结果吻合较好,可以判断所建立的静刚度理论计算模型基本无误。

|
图 5 2 kN下橡胶减振器的垂向位移 Fig. 5 The vertical displacement under 2 kN |
|
图 6 10 kN下橡胶减振器的垂向位移 Fig. 6 The vertical displacement under 10 kN |
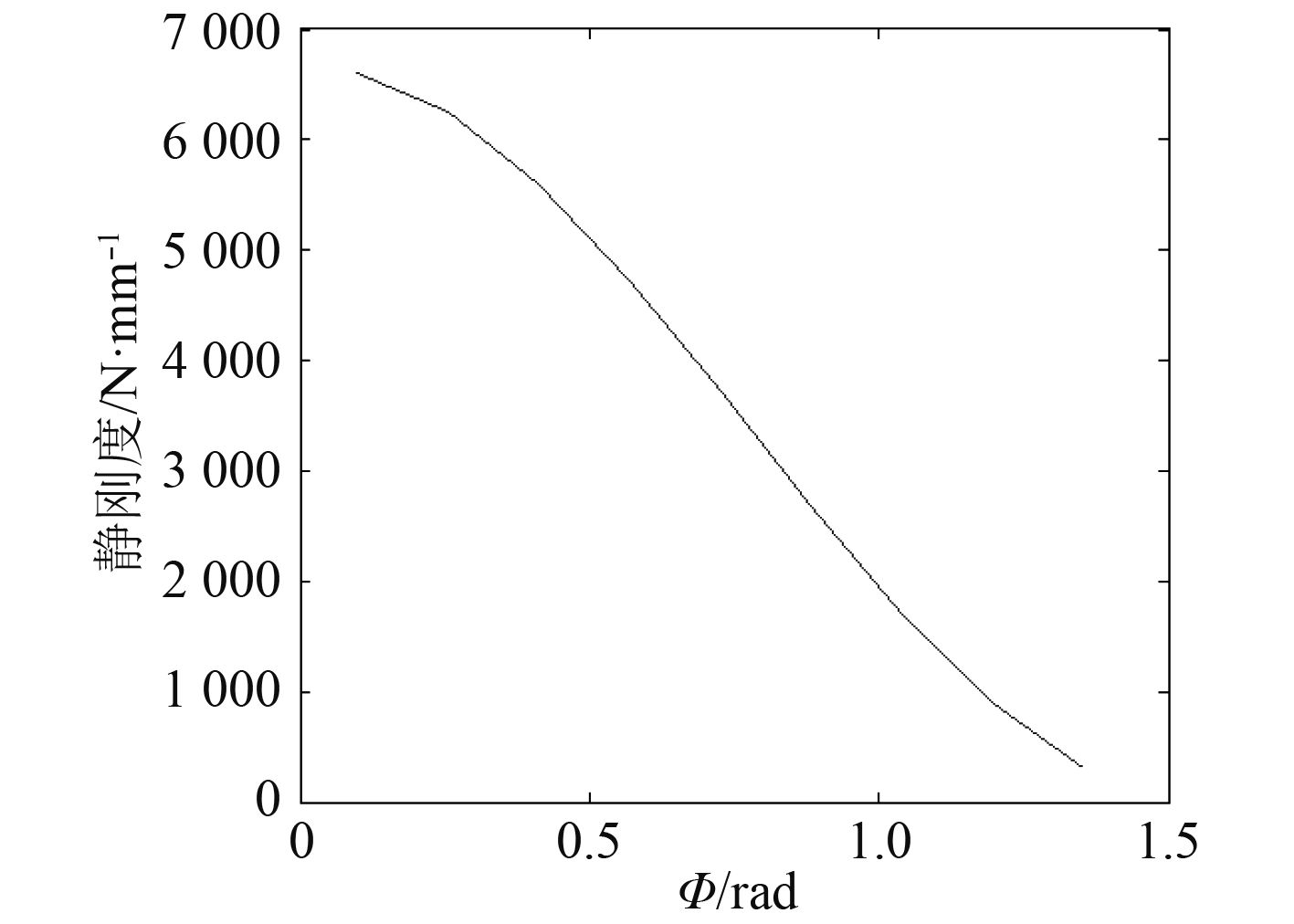
当橡胶减振器几何尺寸H,B,L恒定时,调整橡胶元件与水平基座的角度Φ,可得到如图减振器的静刚度变化曲线,从图7可以看出,当角度Φ增大时,减振器的垂向静刚度逐渐减小。当橡胶减振器的几何尺寸B,L,Φ恒定时,调整橡胶元件的厚度H,得到静刚度与橡胶元件厚度H的关系(见图8)。
|
图 7 静刚度随橡胶元件角度Φ变化 Fig. 7 The value of static stiffness with variable Φ |
|
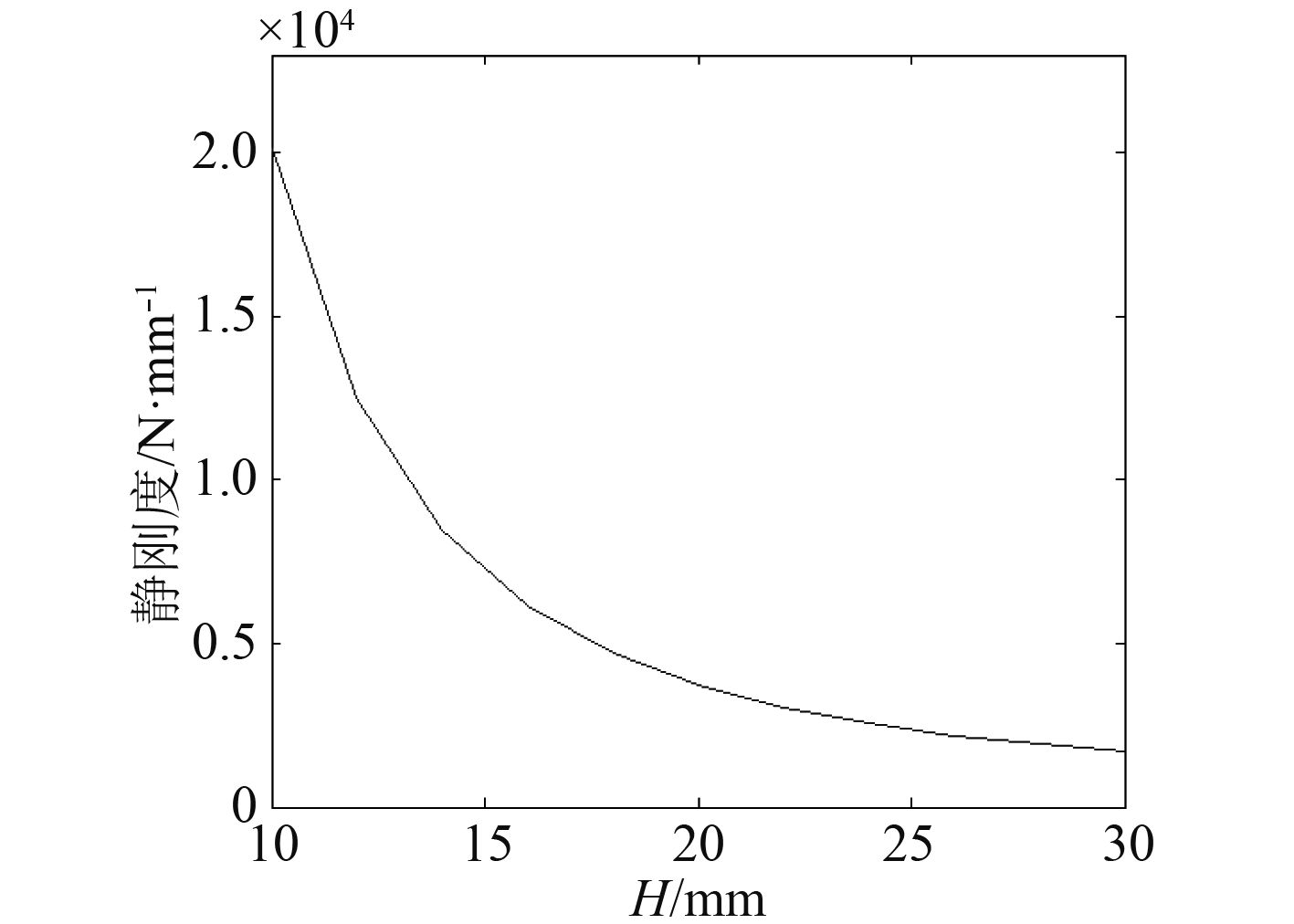
图 8 刚度随橡胶块厚度H变化 Fig. 8 The value of static stiffness with variable H |
当橡胶元件厚度增大时,橡胶减振器刚度急剧下降,继续增加橡胶元件厚度,减振器刚度下降趋势渐缓,静刚度约恒定在2 000 N/mm。此外,橡胶元件为减振器减振部件,增加橡胶元件厚度能显著提高减振效率,但由于船舱内空间狭窄,橡胶减振器高度受限,本文在设计橡胶减振器外形结构尺寸时,需要满足3点:1)减振器静刚度必须达到使用要求;2)限位金属基座高度不能太低,否则失去限位功能;3)橡胶垂向高度不能超过金属限位基座高度的1/2,否则当减振器失效破坏时,垂向摆动过大,使机器损坏,但也不能低于限位器高度的1/4,否则减振性能将大大降低。根据上述3点要求,建立橡胶减振器设计约束条件,对橡胶减振器进行设计。
|
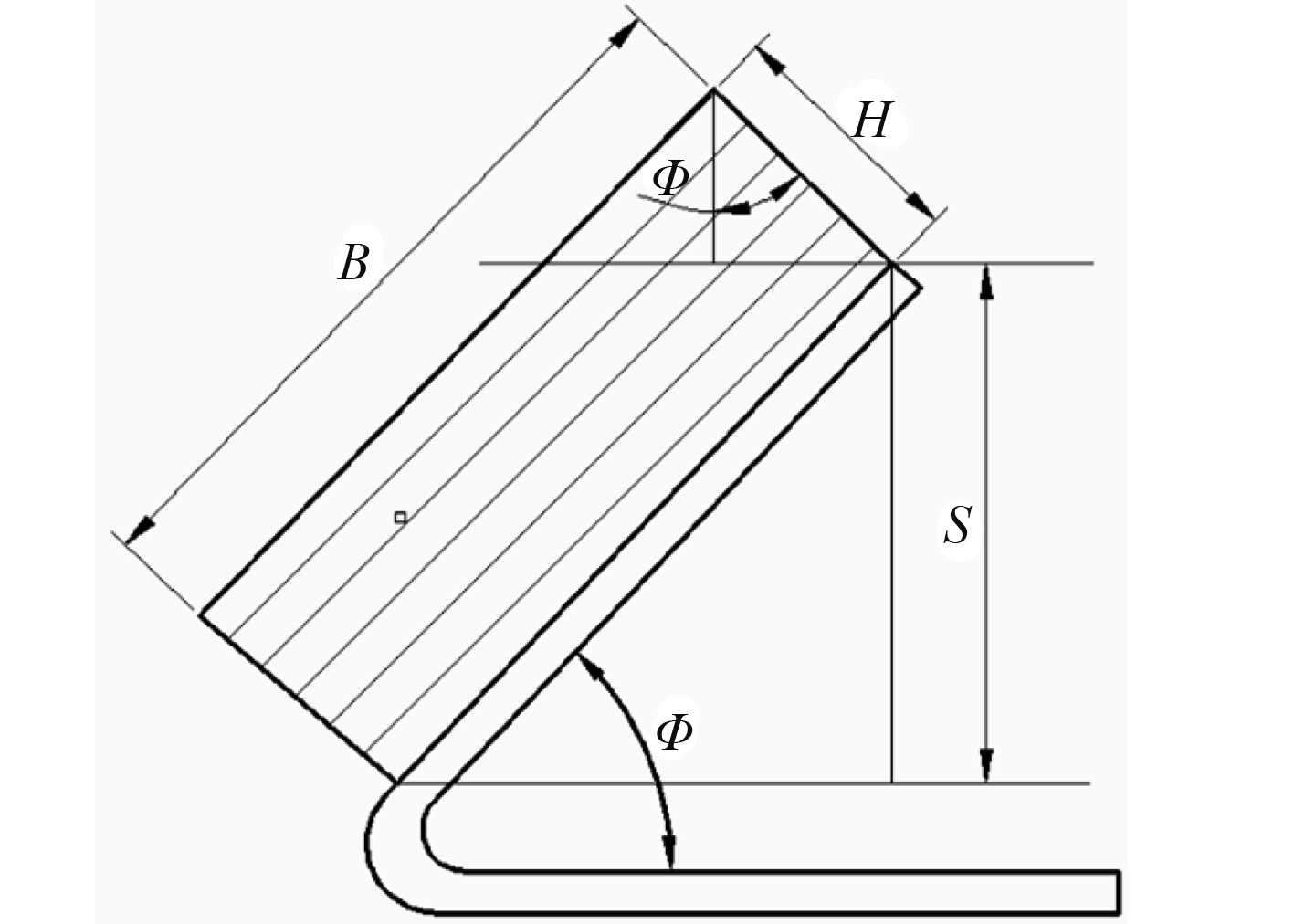
图 9 橡胶减振器垂向轮廓图 Fig. 9 The vertical sketch of rubber absorber |
图9为橡胶减振器横截面轮廓,根据橡胶减振器设计要求及几何尺寸关系,建立橡胶如下减振器的约束方程
| $ \begin{aligned}& {\frac{s}{{4H}} \leqslant \cos \phi \leqslant \frac{s}{{2H}}}\text{,}\end{aligned}$ |
| $\begin{aligned}{K_z} = 2{K_\alpha }\left( {\cos {\phi ^2} + \frac{1}{k}\sin {\phi ^2}} \right) = 4000\text{。}\end{aligned}$ |
式中:s为限位器高度,且

|
图 10 约束条件下H与Φ关系 Fig. 10 The relation curve of H and Φ under constraint condition |
如图10所示,图中三维网格曲面为静刚度变化趋势曲面,两深色曲线为约束条件,在两曲线之间与三维曲面相交部分所形成的有限长度曲线为满足假定刚度和限位器高度的橡胶减振器尺寸,从图10中可以看出,可将将此曲线简化为线性线段,得到满足约束条件下的橡胶元件厚度H与Φ的关系:
| $H = - 32.7\phi + 45.6\;\text{,}\;{\text{其中}}\phi \in \left( {\frac{\pi }{5},\frac{{2\pi }}{7}} \right)\text{。}$ |
通过计算式(11),可得到在满足假定静刚度和限位器高度条件下,不同Φ对应的橡胶元件厚度H。从而为橡胶减振器设计提供参考。
4 结 语本文以某船用橡胶减振器为研究对象,通过理论分析得到减振器的静刚度计算公式,利用有限元软件建立橡胶减振器仿真分析模型,计算初始结构尺寸下橡胶减振器的静刚度,得到理论计算结果与仿真计算结果误差范围在5%以内,证明建立的橡胶减振器静刚度理论模型满足要求。根据理论模型,对橡胶减振器进行结构尺寸设计,得到在额定静刚度和限位器高度下,橡胶减振器中橡胶元件厚度和与水平角度关系,可为此类型橡胶减振器的设计生产提供参考。
| [1] |
第海龙. 某型重卡橡胶减振器优化设计[D]. 长沙: 湖南大学, 2011.
DI Hai-long. The optimization of rubber spring of heavy-duty truck[D]. Changsha: Hunan University, 2011. |
| [2] | IAVORNIC C, PRAISACH Z I, VASILE O, et al. Study of stress and deformation in elastomeric isolation systems using the Finite Element Method[C]//International Conference on Siqnal Processing, Computational Geometry & Artificial Vision, 2011: 239–244. |
| [3] | WENBIN S, ZHENGHUA L. Finite element analysis of static elastic characterization of the rubber isolators in automotive dynamic system[J]. Sae Transaction, 2003(112): 185–193. |
| [4] |
李中郢, 卢正人. 金属橡胶减振器组合刚度特性研究[J]. 哈尔滨工业大学学报, 2005(10): 23–25.
LI Zhong-ying, LU Zheng-ren. Research on combined stiffness characteristic of metal rubber damper[J]. Journal of Harbin Institute of Technology, 2005(10): 23–25. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hebgydxxb200510007 |
| [5] | 严济宽. 机械振动隔离技术[M]. 上海: 上海科学技术文献出版社, 1985. |
| [6] | 程昌钧, 朱媛媛. 弹性力学[M]. 上海: 上海大学出版社, 2005. |
| [7] | 孙延奎. 橡胶减振器的设计与优化[D]. 青岛: 青岛科技大学, 2016. |
| [8] |
余天超, 刘夫云, 孙永厚. 基于ABAQUS的橡胶减振器参数化优化设计[J]. 计算机仿真, 2013, 30(10): 119–202.
YU Tian-chao, LIU Fu-yun, SUN Yong-hou. Rubber shock absorber based on ABAQUS parametric optimization design [J]. Computer Simulation , 2013, 30(10): 119–202. http://www.cnki.com.cn/Article/CJFDTotal-JSJZ201310050.htm |
 2018, Vol. 40
2018, Vol. 40
