对快速性要求较高的船舶常通过增加推进器的数量来保证高航速,多轴推进装置应运而生。但中低航速有时采用部分轴工作制,主机或传动系统出故障时多轴推进装置也被迫采用部分轴工作制。
部分轴工作时,不工作螺旋桨则成为拖桨。拖桨有自由拖桨和锁轴2种状态。一般情况下自由拖桨阻力要小于锁轴拖桨阻力[1],且自由拖桨也常用。本文以双轴推进装置为例,研究自由拖桨阻力的影响因素及其对船舶快速性的影响,为主机遥控系统联控曲线的设计和使用管理人员应急工况下推进装置的科学使用提供理论依据。
众所周知,不工作桨的螺距不同时,其拖桨阻力和拖桨力矩也不相同。但不工作桨的螺距置于什么位置时拖桨阻力最小业内持有2种观点,一种是认为应将不工作桨螺距设置在0推力螺距,另一种认为应将不工作桨螺距设置在最大螺距,如机械止档位置。事实上在自由拖桨和锁轴拖桨2种情况下“不工作调距桨螺距处在什么位置以使不工作桨的拖桨阻力最小”所得的结论不同。本文利用建模仿真手段对某CODOG推进系统单桨工况的自由拖桨阻力特性进行仿真计算和原理分析。
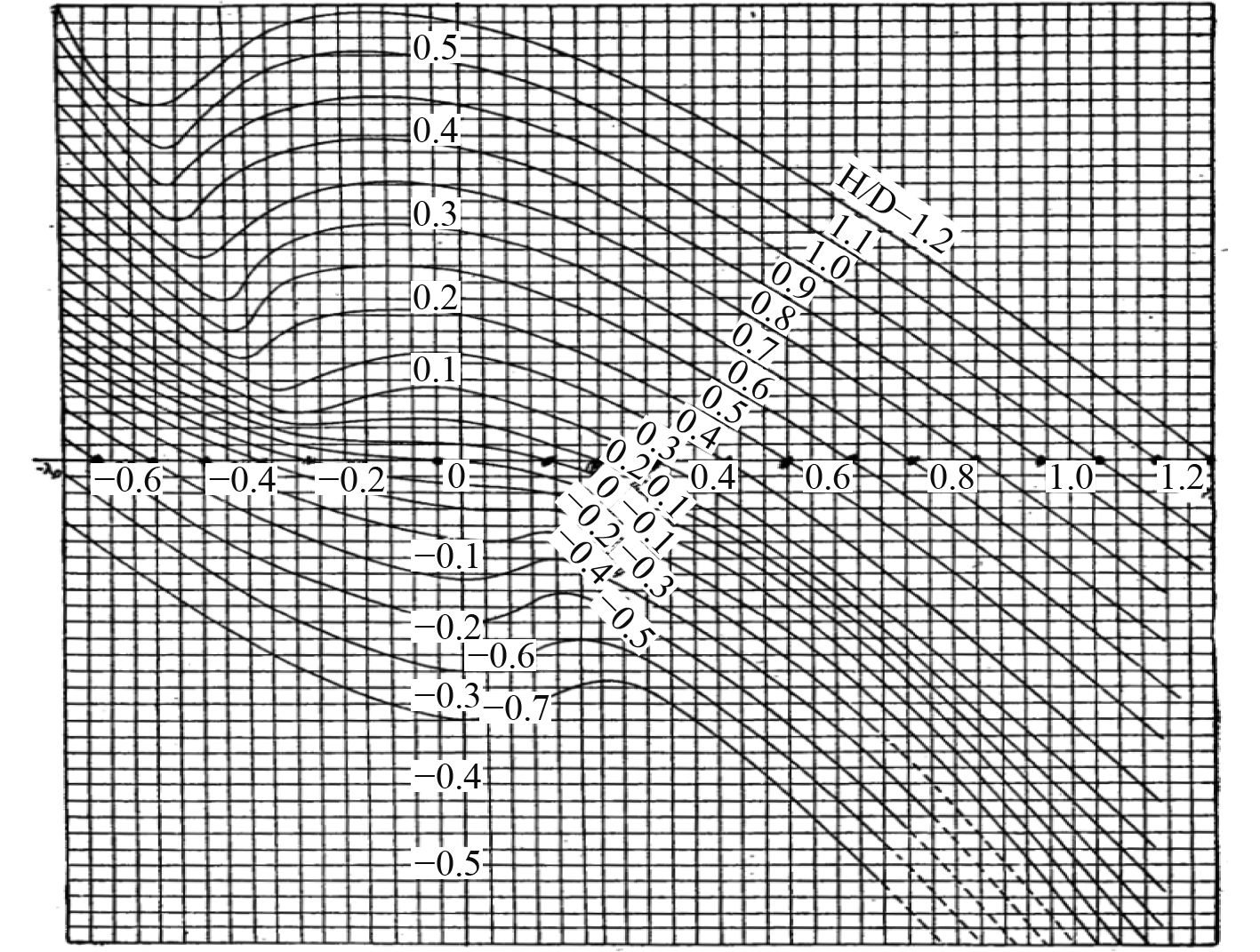
1 调距桨水动力性能数值计算一般情况下调距桨只做若干螺距的敞水试验,而且进速系数J的范围较小。某调距桨敞水试验结果如图1所示。而完整的调距桨敞水特性曲线如图2所示。可见这种敞水试验的结果仅代表了调距桨主要螺距下的水动力性能,用于稳态工况的快速型计算,它并不能反映调距桨完整的敞水特性,不适用于动态过程的机动性、操纵性等计算。

|
图 1 某调距桨桨敞水特性试验曲线 Fig. 1 Open water performance of CPP from test |
|
图 2 完整的调距桨敞水特性曲线 Fig. 2 Whole open water performance of CPP |
为了得到调距桨完整的敞水特性曲线,本文对某5叶大侧斜调距桨在均匀来流下的三维粘性流场采用求解RANS方程(雷诺时均方程)的方法进行了CFD数值计算。采用SST湍流模型,并利用有限体积法对RANS偏微分方程进行离散,进而对其进行数值求解。定常不可压粘性流畅数值求解的控制方程为[2]:
| $\frac{{\partial {u_i}}}{{\partial {x_i}}} = 0\text{,}$ | (1) |
| $\begin{split}& \frac{\partial }{{\partial t}}(\rho {u_i}) + \frac{\partial }{{\partial {x_j}}}(\rho {u_j}{u_i}) = - \frac{{\partial p}}{{\partial {x_i}}} + \\& \frac{\partial }{{\partial {x_j}}}[(\mu + {\mu _t})(\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}})] + {f_i}\text{。}\end{split}$ | (2) |
式中:f为质量力;μ为流体动力粘性系数;μt为湍流动力粘性系数;ρ为流体密度;p为压力;ui(i=x,y,z)分别表示x,y,z三个方向上的雷诺平均速度分量。
利用CFD方法对调距桨敞水特性进行数值计算分为3个步骤:1)对调距桨的三维几何结构进行建模;2)对流场计算域进行离散,包括调距桨桨叶、桨毂壁面与计算流场域之间的区域;3)对每个三维网格节点进行数值求解。
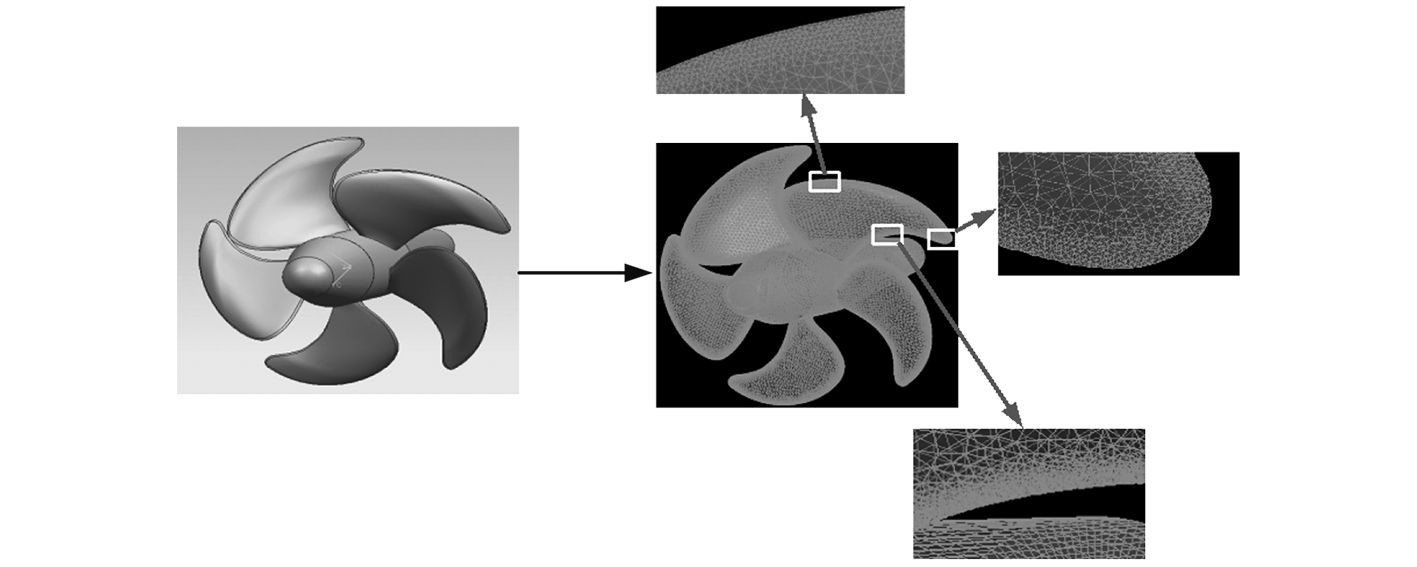
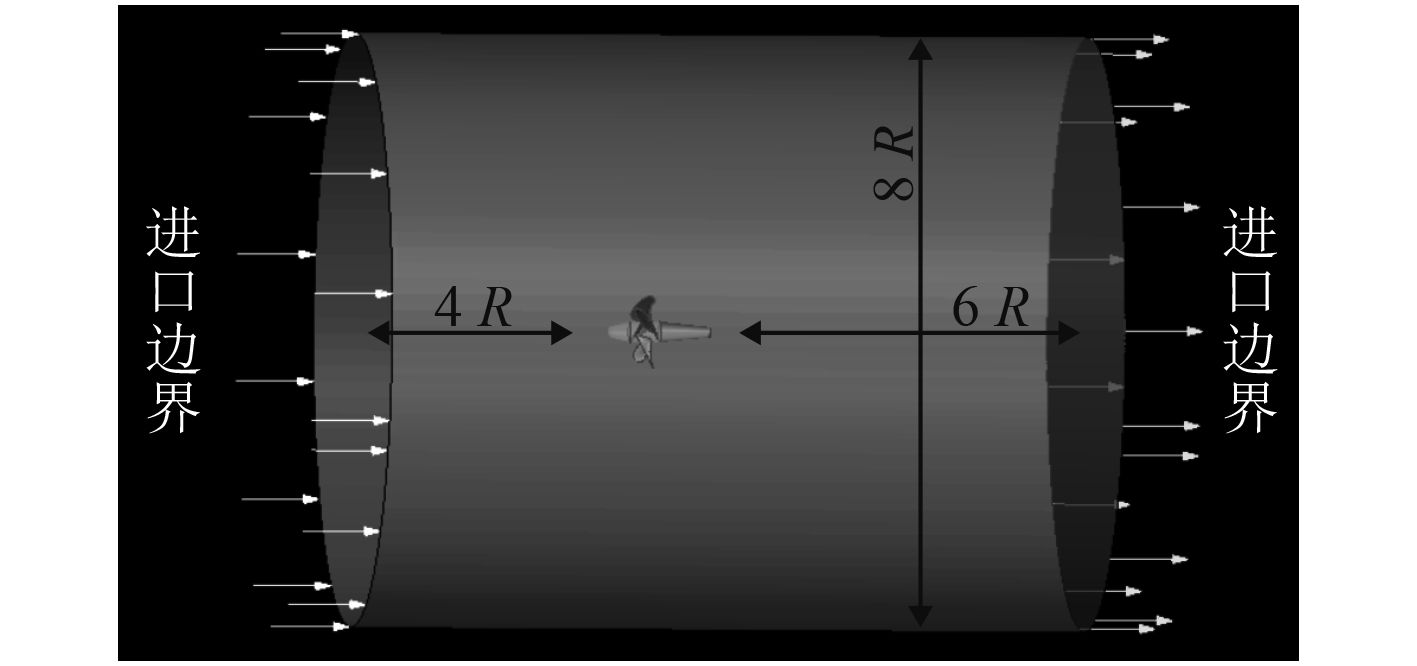
该调距桨在设计螺距下的几何建模与计算网格划分如图3所示。在桨叶的导边、随边以及叶稍等流动剧烈的位置计算网格相对比较小,这能够更好地适应其几何形状以准确描述流动。考虑到调距桨几何结构为回转体,故将流场计算区域取为与桨同轴线的圆柱体,圆柱体高度为桨直径的10倍,圆柱体直径为桨直径的8倍,调距桨置于距离进口4倍直径处,如图4所示。根据参考文献[2],该圆柱体流场区域对于调距桨数值计算来说已经充足。
|
图 3 调距桨几何建模与计算网格划分 Fig. 3 Geometrical model and calculating grid of CPP |
|
图 4 计算区域与调距桨的相对位置 Fig. 4 Relative position of CPP and calculating region |
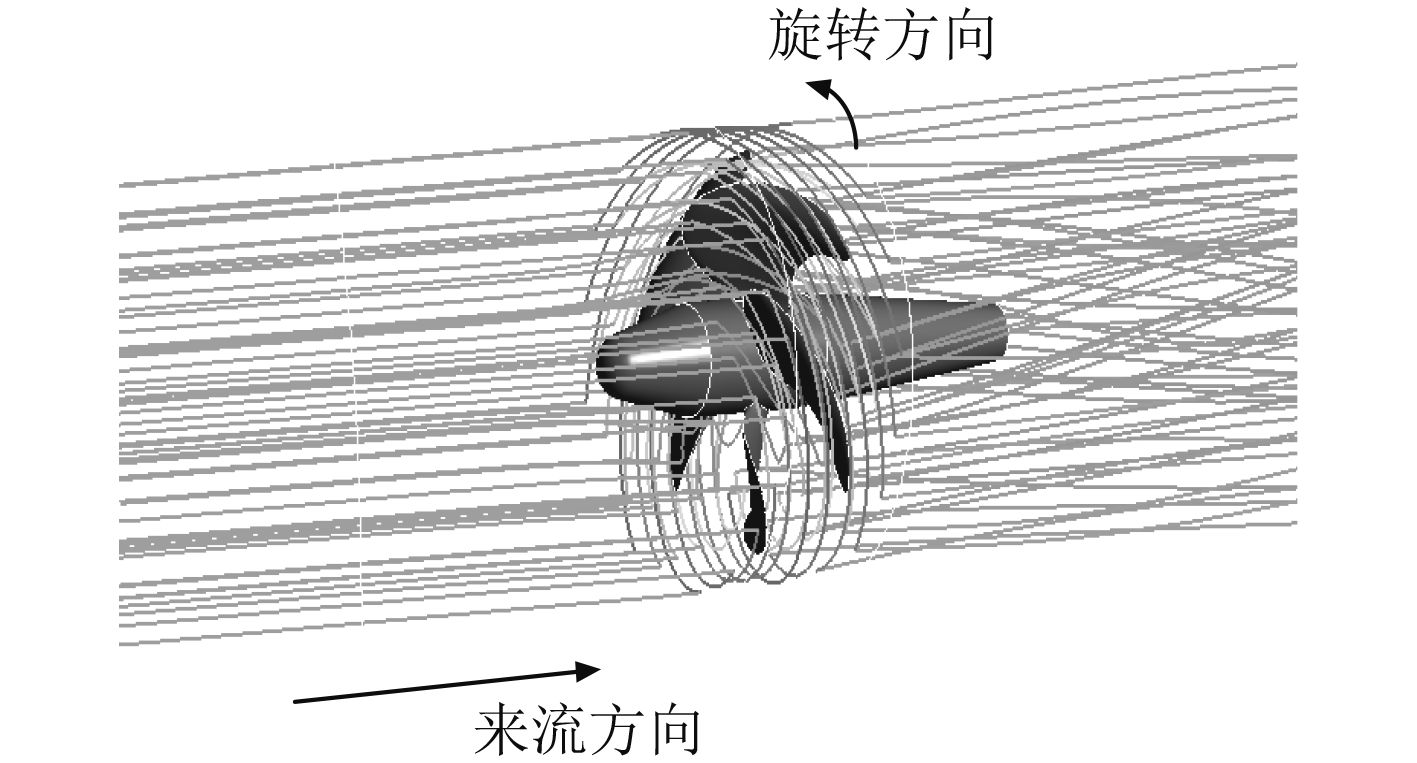
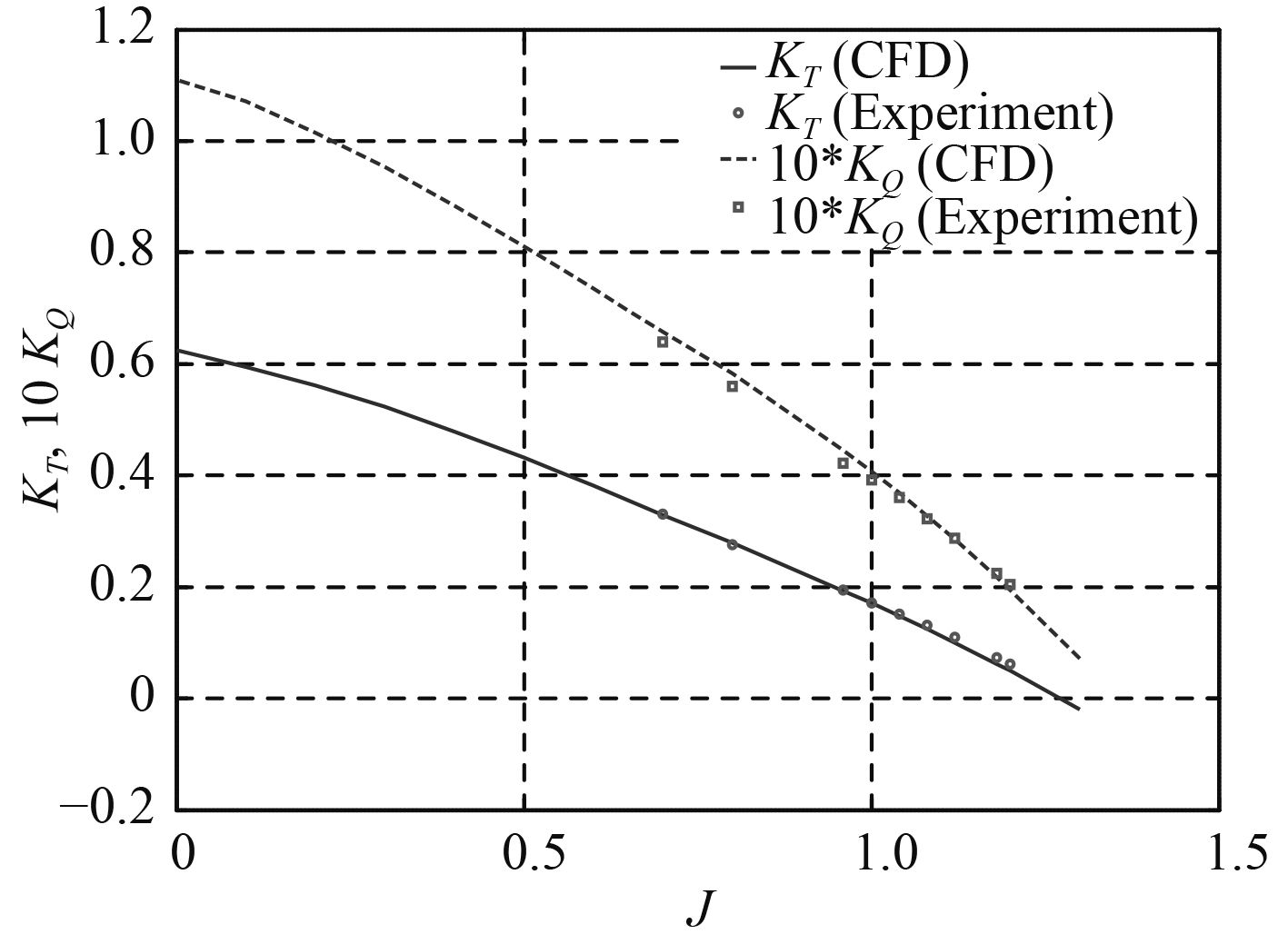
对该调距桨设计螺距下水动力性能数值计算得调距桨流场域内的流线分布如图5所示,不同进速系数J下推力系数KT和力矩系数KQ计算结果与设计螺距敞水特性试验结果的比较见图6,可见CFD计算结果与敞水特性试验结果吻合良好。
|
图 5 调距桨前后流场流线分布 Fig. 5 Streamline distribution of CPP |
|
图 6 调距桨敞水特性CFD计算结果校验 Fig. 6 CFD result verification of CPP performance |
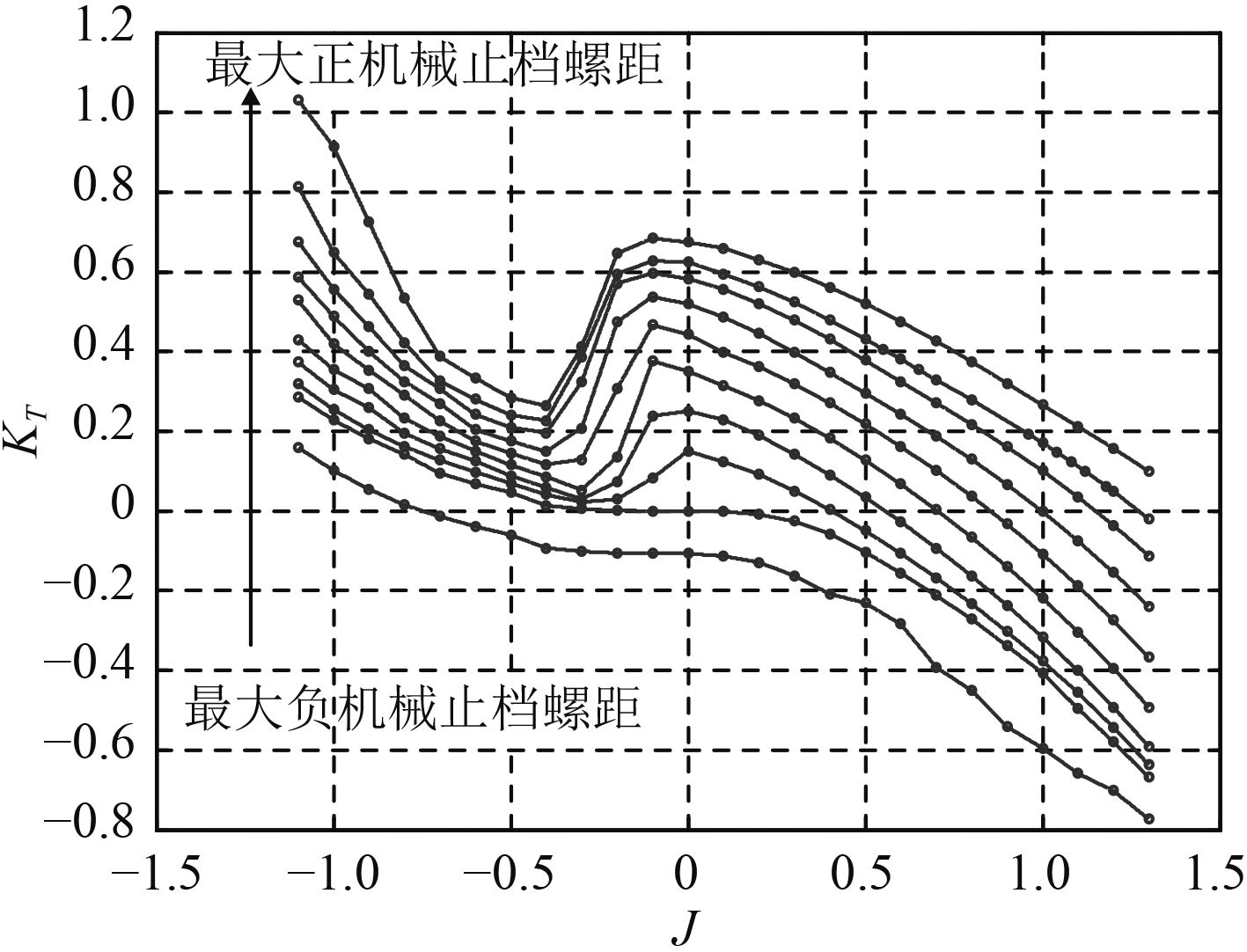
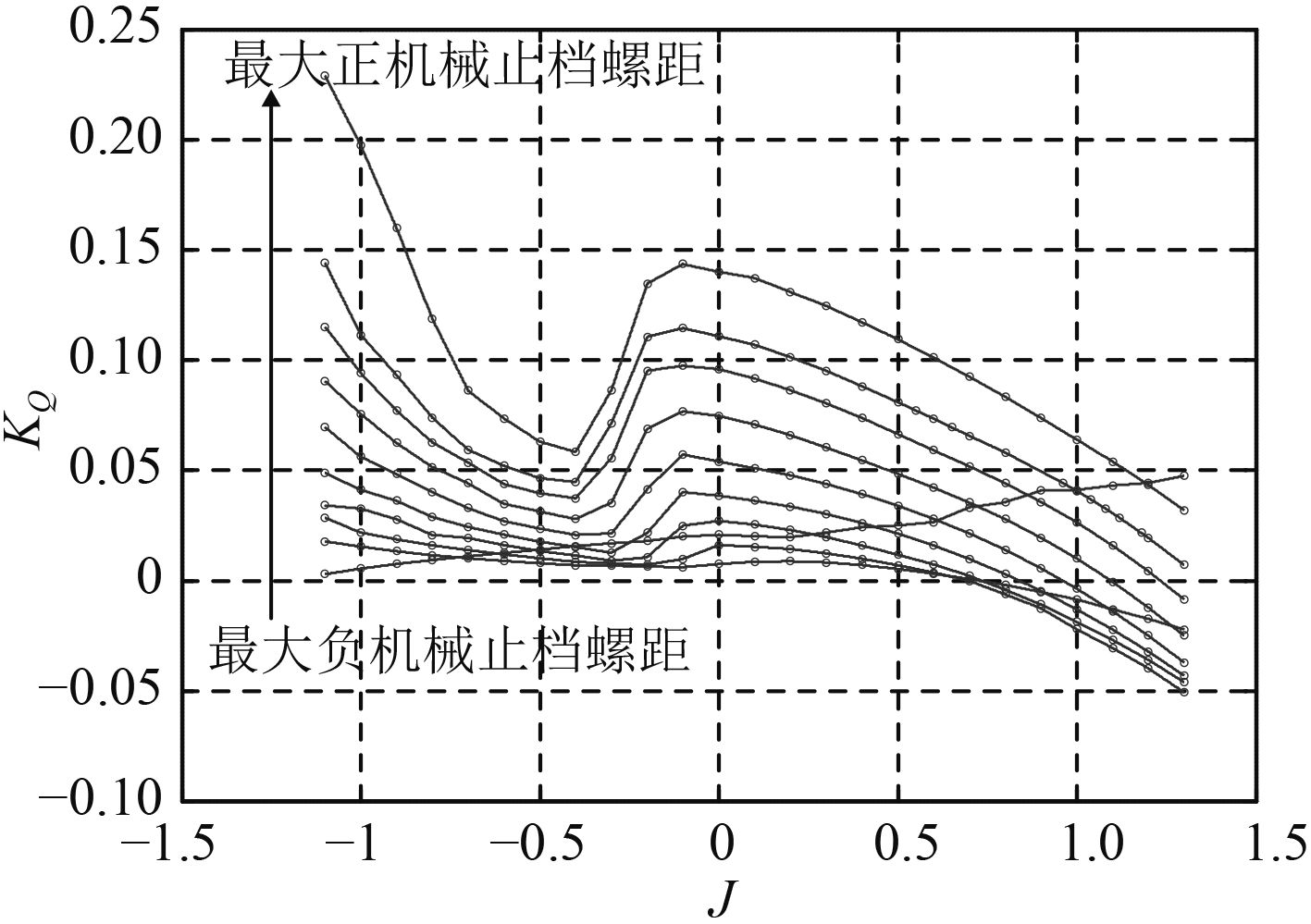
对该调距桨各螺距下的敞水特性进行CFD计算,得到敞水特性图谱如图7和图8所示。螺距由该调距桨最大正机械止档螺距变化至零螺距,各螺距之间的间隔取为0.2。图中还包括最大负机械止档螺距。进速系数J由–1.1变化至1.3,步长取为0.1。对于设计螺距的计算,由于需要与试验数据进行比对,故J按照试验值取得。
|
图 7 调距桨推力系数CFD计算结果 Fig. 7 CFD result of KT |
|
图 8 调距桨力矩系数CFD计算结果 Fig. 8 CFD result of KQ |
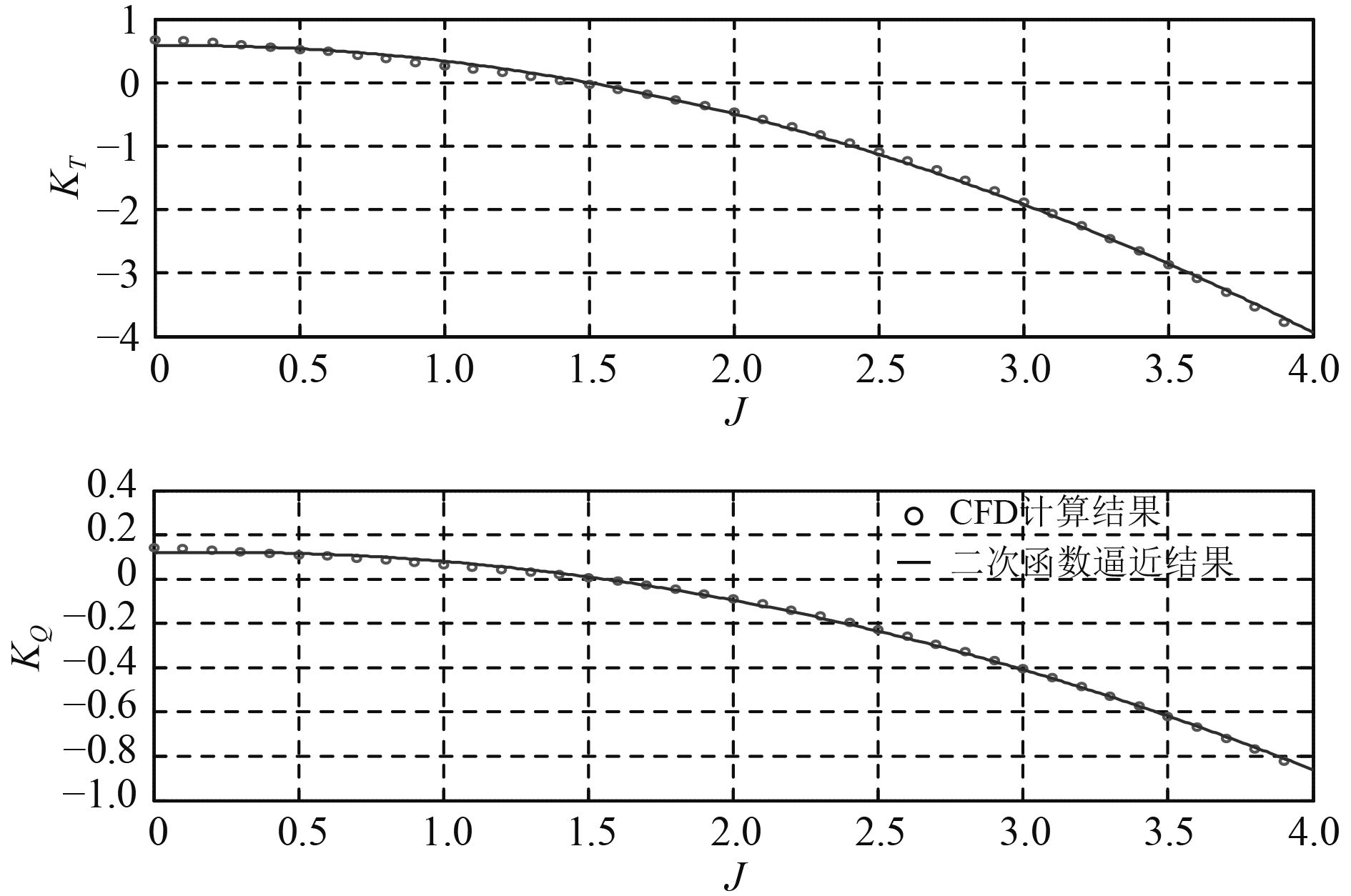
由CFD计算结果及图2所示的完整敞水特性图谱可见,当进速系数较大时,推力系数KT和力矩系数KQ均与进速系数J近似呈二次函数的关系。因此可根据计算得到的各螺距下的KT和KQ值来确定上述二次函数的系数,进而由外延的方法确定大进速系数下的水动力特性。为了验证这一关系,以该桨最大正车机械止档螺距为例,对该螺距进行大进速系数下的CFD计算,并利用二次函数对J≥0部分的数据进行逼近,CFD计算与二次函数逼近结果的比较见图9。
|
图 9 大进速系数时的CFD计算结果与二次曲线拟合结果比较 Fig. 9 Compare between CFD and conic fit result under big advance ratio |
由图9可见,二次函数能够很好地描述大进速系数时推力系数KT和力矩系数KQ随进速系数J的变化关系。本文以在各螺距下计算得到的KT和KQ值为基础,利用二次函拟合来外延得到大进速系数下的水动力特性。
根据CFD计算以及二次函数拟合得到的调距桨敞水性能,利用BP神经网络插值的方法,将各螺距下KT和KQ随J的变化关系由“线工况”扩展到整个“面工况”[3]。这就建立了调距桨推力系数KT和力矩系数KQ与螺距比H/D和进速系数J的映射关系。
2 CODOG推进系统仿真模型在Simulink环境下建立了CODOG推进系统仿真模型,如图10所示,由于本文研究的四机双桨推进系统是由2套完全相同的CODOG结构组成,因此仅给出其中1套CODOG结构的仿真模块。该模型包括调速器、柴油机、燃气轮机、液力偶合器、减速齿轮箱、轴系、船体(阻力)等部件的仿真子模型。船体阻力以及船桨影响系数(如推力减额、伴流系数、调距桨旋转效率)根据相关的试验数据结合采用插值的方法得到。将各部件的仿真模型依据各动力参数和运动参数的耦合关系可集成为整个推进系统的仿真模型(见图10)。

|
图 10 CODOG推进系统仿真模型 Fig. 10 Simulation model of CODOG propulsion system |
单桨工况下,由工作桨产生推力来克服船体阻力以及拖桨阻力。因此在稳定状态下,推力和阻力之间满足关系:
| ${T_p} - R - {T_R} = 0\text{。}$ | (3) |
式中:Tp为工作桨推力;R为船体阻力;TR为拖桨阻力。单桨工况稳定时,拖桨转速为定值,因此不工作桨所在的轴系满足力矩平衡方程,即
| ${Q_R} - {Q_f} = 0\text{。}$ | (4) |
式中:QR为拖桨的水动力矩;Qf为拖桨轴系的摩擦力矩。根据式(3)和式(4)中各变量的计算方法,得到以下方程组:
| $\left\{ \begin{array}{l}{K_T}\rho {n^2}{D^4} - R(V_s) - {K_{TR}}\rho {n_R}^2{D^4} = 0\text{,}\\{K_{QR}}\rho {n_R}^2{D^5} - {Q_f}({n_R}) = 0\text{。}\end{array} \right.$ | (5) |
式中:KT为工作桨推力系数;KTR为不工作桨推力系数;KQR为不工作桨的水动力力矩系数;VS为航速;R为船体阻力与航速的对应关系;Qf为轴系摩擦力矩与转速的对应关系;n为工作桨转速;nR为拖桨转速;ρ为海水密度;D为调距桨直径。因此,当工作桨转速n、螺距H/D和不工作桨螺距H/DR确定后,式(5)中的变量为VS和nR,显然方程组(5)封闭,但该方程组是隐式的,若式(5)中的隐函数通过拟合方法化为显式则会影响方程的精度,因此采用四阶龙格-库塔法迭代求解式(5)得到VS和nR的值,进而得到TR及QR。
从整个推进系统“船-机-桨”匹配的角度来看,式(5)在求解过程中还必须满足主机在正常工作范围这个条件,即主机的输出功率在其最大持续功率(MCR)限制线以下。本文通过调整工作桨螺距H/D来控制主机输出功率,这可以使主机在单桨工况下仍能工作在额定工况,即工作在额定转速,并按照军用标准规定相对于MCR有一定的功率储备,本文取额定工况下主机功率储备为10%。
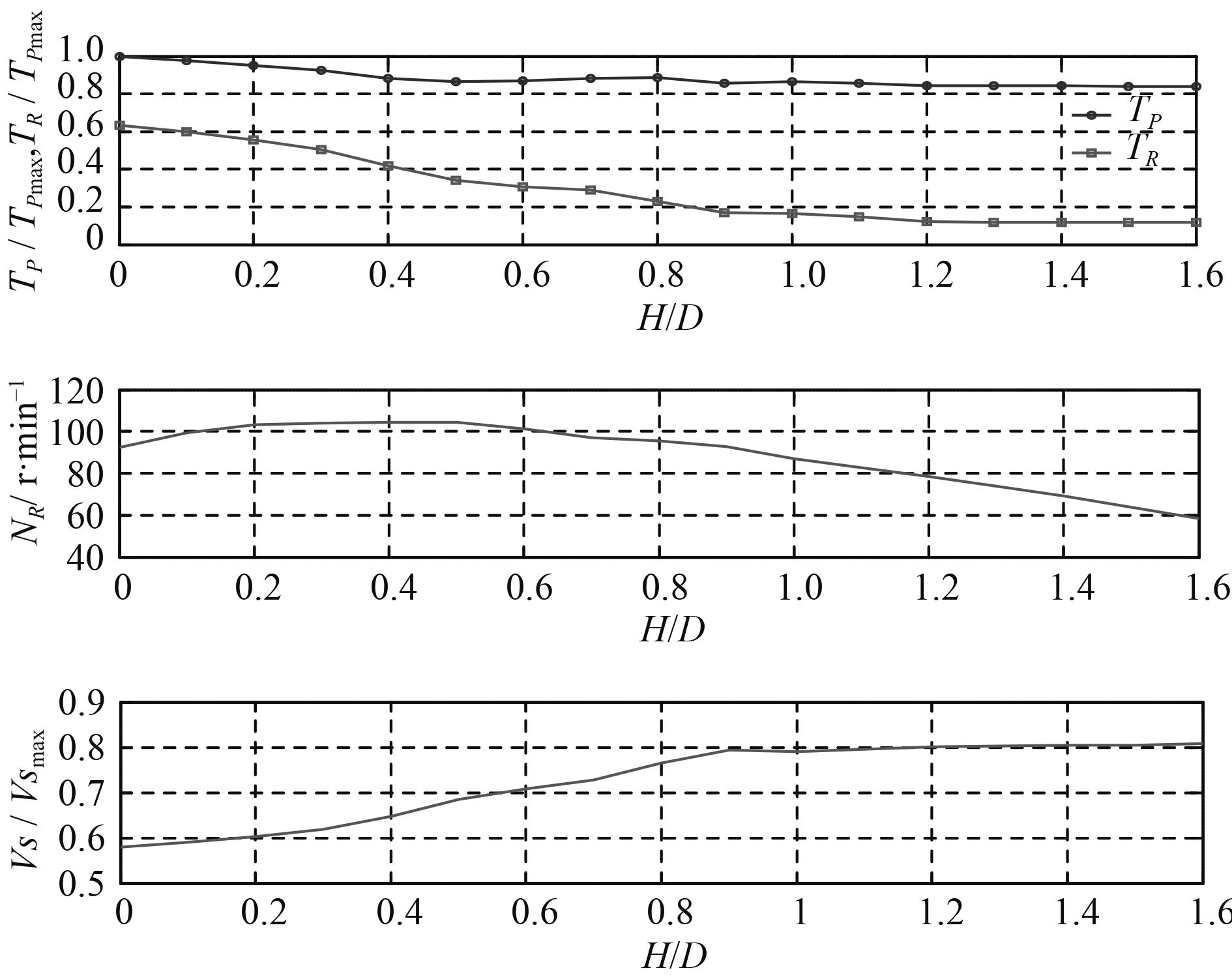
3.1 主机工作在额定工况时的单桨工况仿真为了比较单桨工况下,不工作桨螺距(H/DR)对推进性能的影响,本文对工作桨螺距H/D从最大正螺距到零螺距之间的17个螺距进行仿真计算。以柴油机单桨工况为例,计算时调整H/D保证柴油机工作在额定工况,仿真结果如图11所示,VSmax为柴油机双桨工况巡航额定航速。
|
图 11 柴油机单桨工况稳态特性仿真结果 Fig. 11 Steady-state characteristics simulation result of single diesel working condition |
仿真结果表明,在工作柴油机发出额定功率的前提下,随着H/DR的增大,TR减小,VS升高。因此将H/DR置于最大正螺距位置时可使单桨工况有最佳的快速性。对于单燃气轮机工况来说,与柴油机工况的区别仅仅是主机输出功率提高,而主机功率仅仅是式(5)的限制条件,不会改变H/DR对推进性能的影响规律,故燃气轮机单桨工况与柴油机单桨工况有相同的结论。因此对于CODOG推进系统单桨工况来说,将自由拖转的不工作桨螺距H/DR设定为最大螺距时,舰船的快速性最好。
对于TR来说,其大小随着H/DR的增大呈单调减小的趋势,而nR随H/DR呈现非单调变化的趋势,因为nR由VS和H/DR二者决定,而VS又受到H/DR的影响,因此呈现出nR随H/DR变化的非单调现象。
3.2 拖桨工况影响因素分析为了分析航速VS和拖转桨螺距H/DR对拖桨工况的影响,本文分析2类单桨工况,将VS和H/DR对拖桨工况的影响剥离开来进行计算。具体做法如下:
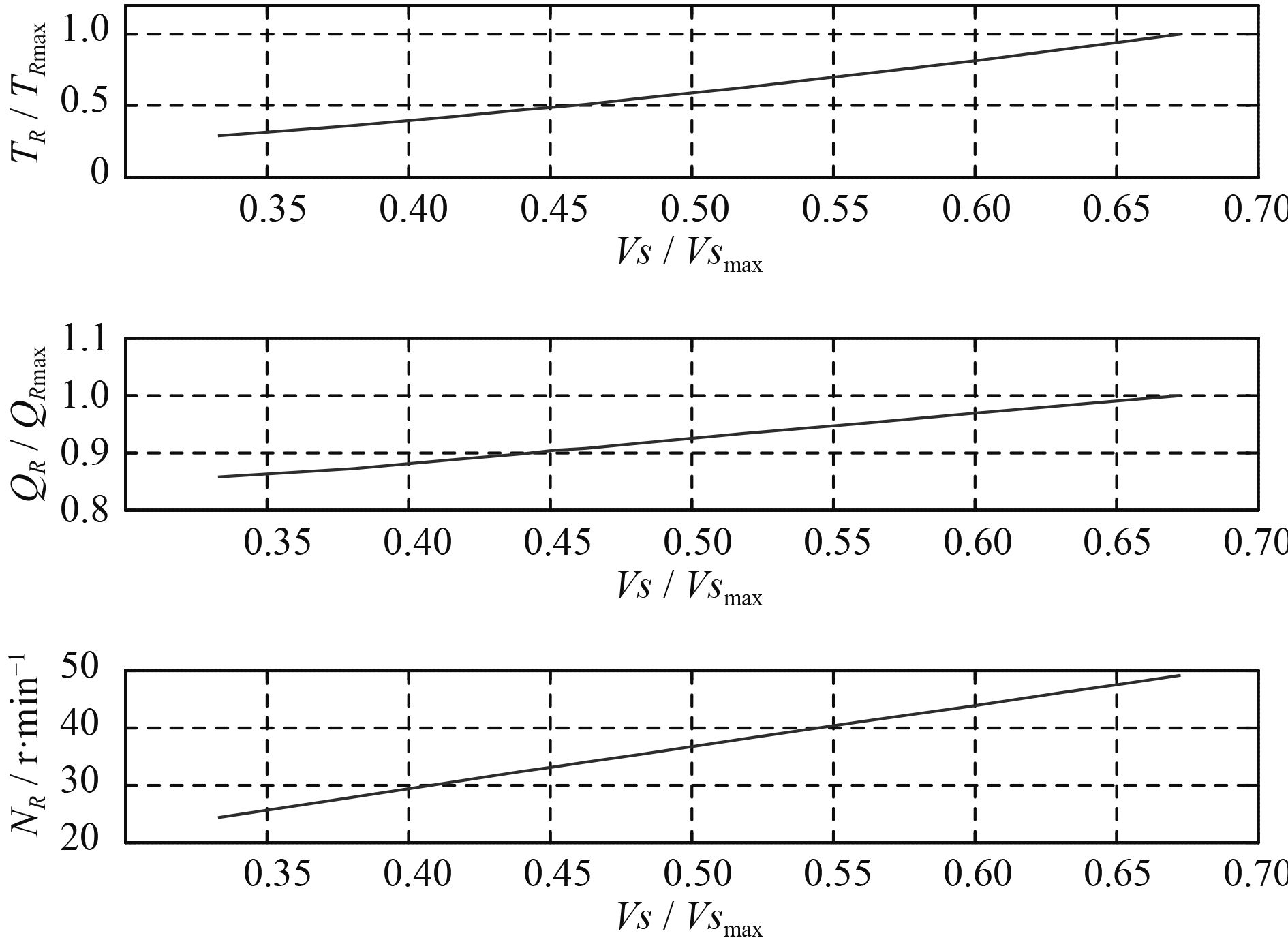
工况1 将H/DR设定为最大螺距,取H/D为使主机工作在额定工况,通过改变主机转速n来改变VS,分析TR、QR以及nR随n即VS的变化关系。仿真结果如图12所示。随着n即VS的增大,TR、QR和nR单调递增。
|
图 12 拖桨阻力、力矩与转速随航速的变化关系 Fig. 12 Relationship between propeller’s dragged resistance, torque, rev and ship speed |
工况2 取H/D为当拖转桨螺距为最大螺距且主机工作在额定工况所对应的螺距值,通过改变主机转速n使航速VS保持定值,分析TR、QR以及nR随H/DR的变化关系。计算时选择合适的航速VS以保证主机转速和H/DR变化时主机不超负荷(取VS=0.56×VSmax)。
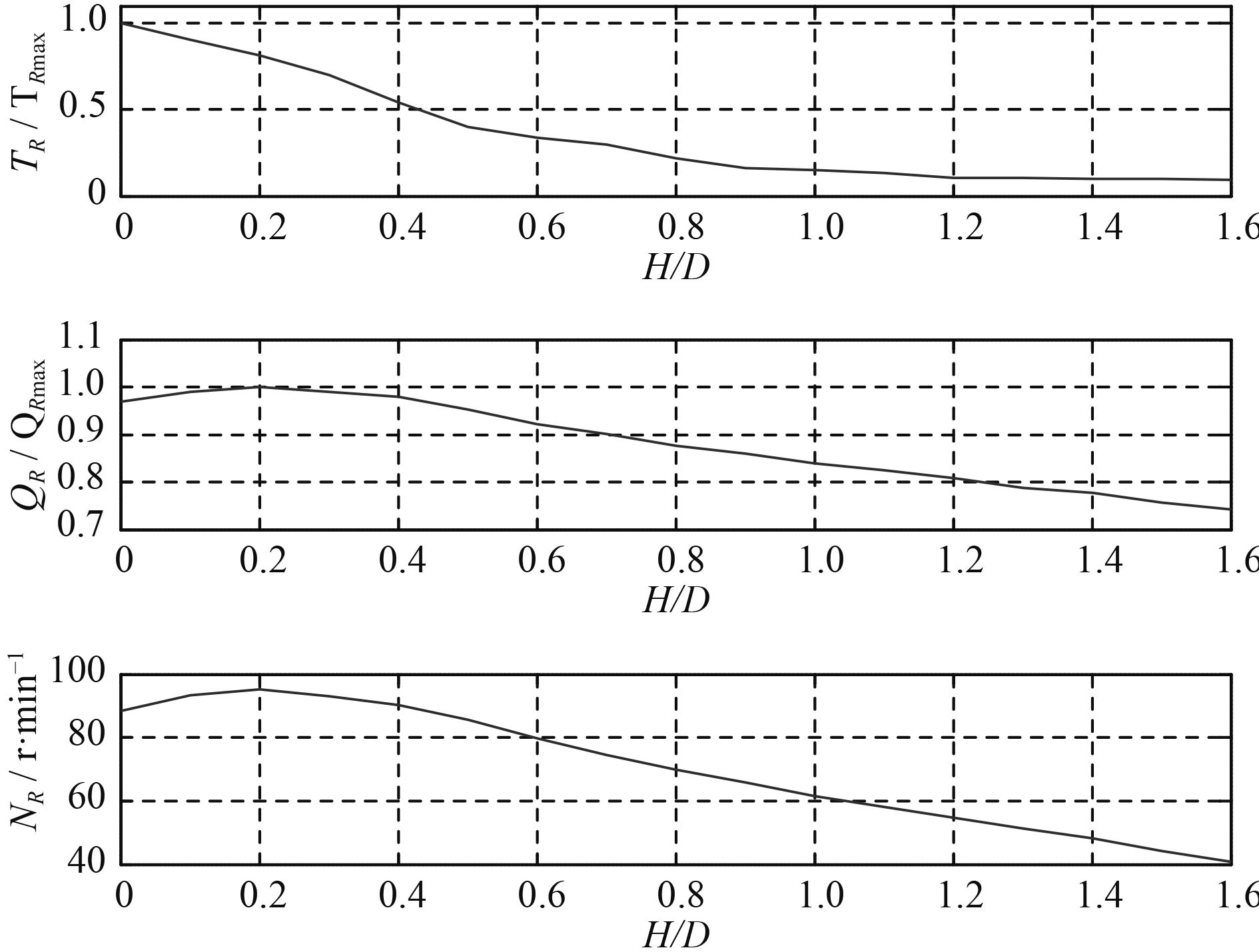
|
图 13 拖桨阻力、力矩与转速随拖桨螺距的变化关系 Fig. 13 Relationship between propeller’s dragged resistance, torque, rev and pitch |
仿真结果如图13所示,VS不变时,TR随H/DR的增大单调减小,而nR和QR随H/DR的增大呈先增大再减小的变化趋势,而且nR和QR随H/DR的变化趋势一致。这是由于式(5)中的Qf(nR)是nR的线性函数,而当轴系力矩平衡时QR=Qf,因此QR也是nR的线性函数,因此nR和QR有相同的变化趋势。
可见航速VS和转桨螺距H/DR对拖桨工况的影响呈现明显的规律性。由于单桨工况下,TR,QR,nR直接或间接由方程组(5)确定,因此,对于工况1仿真得到的TR、QR、nR随VS的变化规律,当H/DR变化时,拖桨工况的相关参数仍会有相同的规律;同理,对于工况2仿真得到的TR,QR和nR随H/DR的变化规律,当VS变化时,拖桨工况的相关参数也有相同的规律。因此,当VS和H/DR确定后,TR,QR和nR也随之确定。
4 结 语本文通过CFD方法对某调距桨敞水特性进行数值计算,并通过设计螺距下的敞水试验数据验证了其准确性。利用二次函数对该桨大进速系数时的敞水特性进行拟合和外延,扩大了该桨敞水特性的范围。在Simulink环境下建立了该推进系统“船-桨-机”仿真模型,对该型推进系统单桨工况的稳态特性进行仿真计算,并分析其影响因素,然后进一步对单桨工况的动态过程进行了仿真计算和结果分析。有结论如下:
1)单桨工况下,当不工作桨自由拖转时,将其螺距设定为最大值时有最小的拖桨阻力和拖桨力矩,船舶的快速性最好。
2)影响不工作桨水动力特性的因素有航速和不工作桨螺距2个。航速越高,拖桨阻力、拖桨力矩以及拖桨转速越大;不工作桨螺距越大,拖桨阻力越小,拖桨力矩与拖桨转速先略微增加而后减小至最小值。
| [1] | 王永生. 全柴联合动力装置稳、动态特性和工作制研究[D]. 武汉: 华中科技大学, 2005. |
| [2] | 杨琼方, 王永生, 张志宏, 等. 大侧斜螺旋桨敞水性能的RANSEs模拟[J]. 湖南科技大学学报, 2008, 23(4): 66–70. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xtkyxyxb200804016 |
| [3] | 王永生, 丁江明. 液力偶合器通用外特性的数学建模[J]. 机械工程学报, 2005, 41(4): 225–228. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jxgcxb200504045 |
| [4] | 单铁兵. 四桨两舵船舶螺旋桨不同工况下水动力性能及船体操纵性研究[D]. 哈尔滨: 哈尔滨工程大学, 2008. |
| [5] | WANG Yong-sheng, DENNIS N A, ZHANG Yu-sheng. A practical approach of developing mathematical model for all speed governors[J]. Journal of Shanghai Jiaotong University, 2005, 2: 175–181. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=shjtdxxb-e200502016 |
| [6] | 林缨. 联合动力装置控制策略及其仿真研究[D]. 上海: 上海交通大学, 2004. |
| [7] | 张维竞. 舰船动力装置系统仿真[M]. 上海: 上海交通大学出版社, 2007. |
 2018, Vol. 40
2018, Vol. 40
