随着航运事业的发展和军用需求的增加,船舶的主机功率不断提高、吨位越来越大,从而使得船舶振动激振力加大、抵抗振动的结构动刚度变小,导致产生较大的船体振动,使船体的振动问题日益突出[1]。目前,对于结构的振动响应优化问题研究的不够充分,其原因是振动响应优化问题在优化求解方面有着庞大的计算量。基于模态贡献量的动态响应优化是一种相对便捷的优化设计方法。通过找出结构的振动优势模态,根据优势模态的振型,设计出能够抑制这些振型振动的方案,有针对性地增加相应优势模态的阻尼比,从而达到更有效的减振效果[2 – 4]。
经过几十年发展,模态贡献量可以通过多种模态识别方法得到[5]。自20世纪70年代出现的最小二乘复指数法[6],能够获取与模态贡献量相对应的左特征向量[7]。HarvardVold[8]在1982年率先提出了多参考点复指数法,建立了脉冲响应、特征值及模态贡献量之间的复指数矩阵关系方程。在国内外的研究现状里,对模态贡献量的研究分析也变得越来越多。Leuridan J和Van H der Auweraer[9]论述了使用正交多项式法,估算结构的振型与模态贡献量。宋文等[2]明确给出了模态贡献量的计算公式,并计算了一种支撑结构各阶的模态贡献,通过优势模态进行了振动响应的优化设计。
本文基于Abaqus/Standard模态贡献量插件,提出2种优势模态的选取方法,并分别根据以上2种方法选取了结构振动响应的优势模态,其对结构振动抑制效果进行对比,并通过算例论证了2种优势模态在结构整体振动响应影响程度,为后续的结构振动优化打下良好的基础。
1 基于Abaqus/Standard的优势模态选取方法研究 1.1 模态贡献量在Abaqus/Standard中的应用在Abaqus/Standard有限元软件中有1套比较成熟的模态贡献量计算插件MCF(Modal Contribution Factors),模态贡献量(MCF)插件是一个分析噪声、振动和声振粗糙度(NVH)的应用程序,可以输出模态频响分析,也可以分析每一个模态对结构振动或声学响应的贡献度。
当在Abaqus/Standard里分析一个模态频响,其响应是通过振型和相应的模态振幅的线性叠加计算而来。对于一个典型的结构噪声或结构分析,模态的数量可以数以百计。使用者需要仔细检查这些个体模式模态,然后找到或排列优势模式(对总响应做出主要贡献的模态)。每个模态对总结构或声学响应的贡献率可称为模态贡献系数。典型的Abaqus/Standard模态频响分析,对每一个基本态都进行固有频率分析,然后进行多重稳态动力学分析步(多重载荷下)。插件读取数据库输出的以下变量生成分析:
1)场输出的每一个固有频率分析步里必须包括节点位移。此外,如果进行的是声固耦合分析,场输出的每个固有频率分析步必须包括节点孔隙或声压。
2)每个固有频率分析步后,必须至少有一个模态叠加的稳态动力学分析步(不可以使用直接法或子空间法)。
3)在每个模态叠加稳态动力学分析步里,历史输出里必须包括广义位移和广义位移的相位角。
1.2 优势模态的选取方法研究运用模态坐标法,其基向量为系统的模态振型,模态振型是结构做无阻尼振动时其变形能的固有平衡状态,此状态下各阶模态之间互不耦合,振动响应可以表示为各阶模态贡献之和[2],即
| $P(\bar x;\varOmega ) = \sum\limits_{\alpha = 1}^N {{p_\alpha }(\bar x;\varOmega )} = \sum\limits_{\alpha = 1}^N {{\phi _\alpha }(\bar x){q_\alpha }(\varOmega )} \text{,}$ | (1) |
式中:
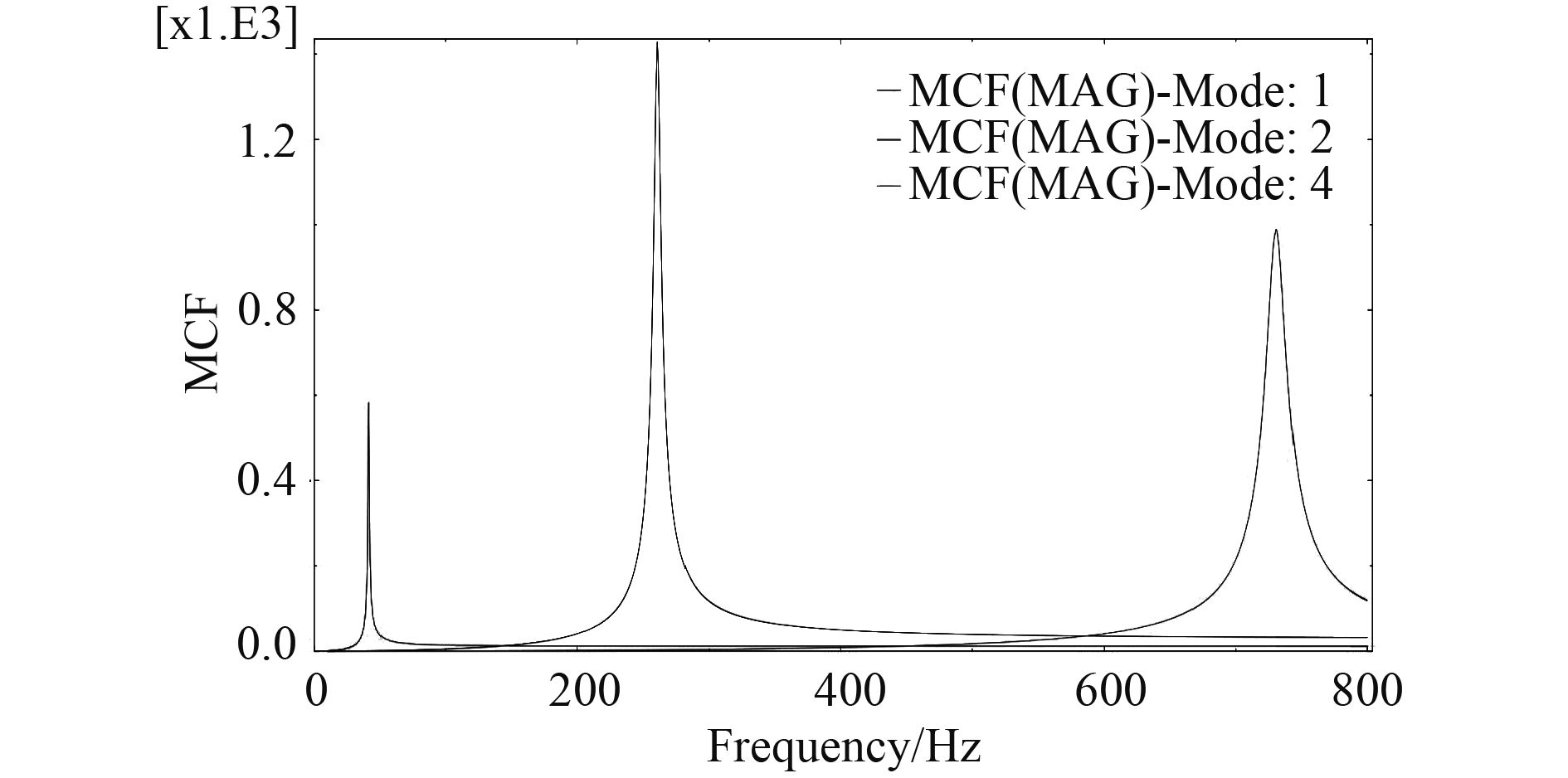
现以已求得的某结构单个响应点的模态贡献量频域响应图(见图1)为例,由图可知,在此响应点的各阶模态固有频率点上,均有明显的模态贡献量峰值,而每一阶响应频段范围大小并不相同,因此,可以考虑分别用以下2种方式对各阶的模态贡献量进行评价:
|
图 1 模态贡献量频域曲线 Fig. 1 Frequency of domain curves of MCF |
1)峰值法
选取所有响应节点m在各阶模态α固有频率点A上的模态贡献量峰值,并做线性平均,得到各阶模态贡献量
| $\begin{aligned}{p_\alpha }({x_A};\varOmega ) =& \sum\limits_{m = 1}^M {{p_{\alpha m}}({x_A};\varOmega )} = \sum\limits_{m = 1}^M {{\phi _{\alpha m}}({x_A}){q_\alpha }(\varOmega )} \text{,}\\& MC{F_\alpha }_{({x_A})} = \frac{{{p_\alpha }({x_A};\varOmega )}}{{\sum\limits_{\alpha = 1}^N {{p_\alpha }({x_A};\varOmega )} }}\text{。}\end{aligned}$ | (2) |
2)全频段法
把每个模态的响应范围考虑进去,将各阶模态α上所有节点m在全频段的模态贡献量做线性平均得到各阶模态贡献量
| $\begin{aligned}{p_\alpha }(\bar x;\varOmega ) =& \sum\limits_{m = 1}^M {{p_{\alpha m}}(\bar x;\varOmega )} = \sum\limits_{m = 1}^M {{\phi _{\alpha m}}(\bar x){q_\alpha }(\varOmega )} \text{,}\\&MC{F_\alpha }_{(\bar x)} = \frac{{{p_\alpha }(\bar x;\varOmega )}}{{\sum\limits_{\alpha = 1}^N {{p_\alpha }(\bar x;\varOmega )} }}\text{。}\end{aligned}$ | (3) |
下面以1个算例分析研究2种模态贡献量评价方法所选取的优势模态,哪一种对结构整体的振动响应影响较大。
2.1 算例模型建立尺寸为200 mm(长)×20 mm(宽)×2 mm(高)的悬臂梁,材料为钢,采用壳单元建模,单元划分为S4R四节点单元,如图2所示,模型右侧单边固支,频响输出点为除固支边外的板中间的8个节点,激励点位于中线靠左侧,如图2所示。

|
图 2 算例模型 Fig. 2 Model of case |
计算前800 Hz内所有模态的固有频率,稳态动力学计算选择模态叠加法,计算10~800 Hz频段内的动态响应,模态阻尼全部选取1%。
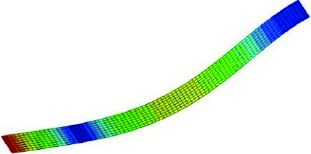
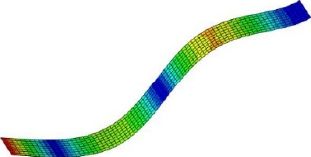
2.2 基于模态贡献量的优化设计及结果分析 2.2.1 模型的前800 Hz频段内固有频率及振型模型前800 Hz频段内共有5个振型,如表1所示。
|
|
表 1 仿真模型1至5阶振型 Tab.1 1st to 5th vibration mode of simulation |
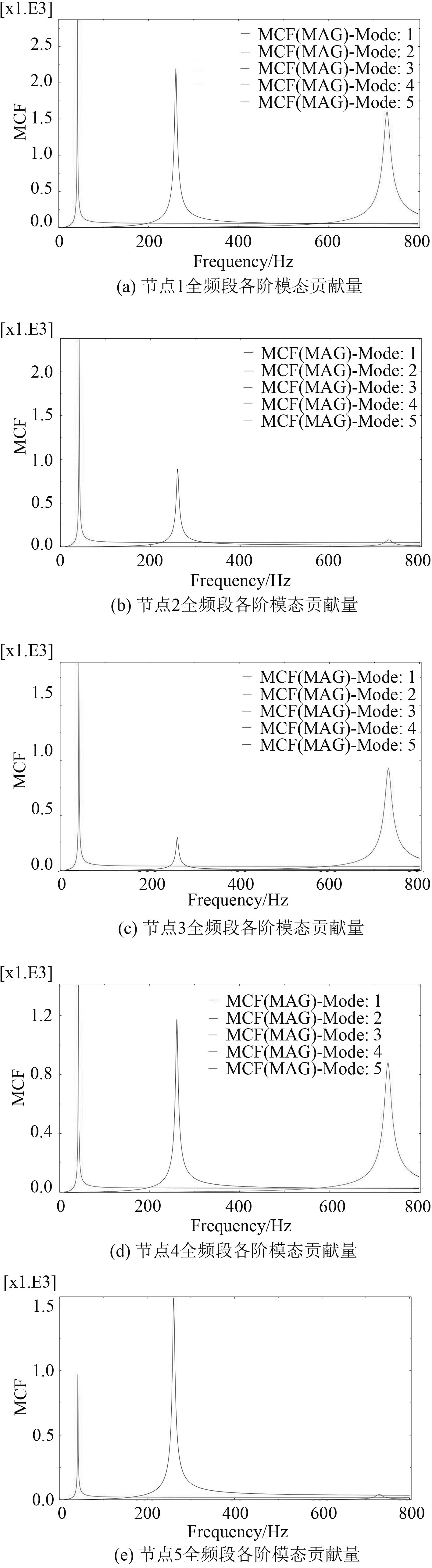
计算的各输出节点的模态贡献量曲线结果如图3所示。接下来分别用2种方法对结构的模态贡献量进行评价。
|
1)峰值法
从输出文件中找出各模态所有节点的模态贡献量峰值,得到表2。
|
|
表 2 各模态所有节点的模态贡献量峰值 Tab.2 Peak value of MCF of output node |
分析8个输出节点的
①由于第3阶是X-Y水平面的弯曲振型,第5振型是沿模型Y轴中线的扭转振型,模型Y轴中线的模态幅值为0,全部为此模态振动的驻点,而激励点也在模型的Y轴中线,根据式(2),激励在这2阶的模态力为0,无法激起此振型,因此,第3阶、第5阶的模态贡献量为0;
②在1阶模态中,各个节点的振型位移随着节点编号的增加而减小,而其模态贡献量的峰值同样随之减小。同样,2阶、4阶的各个节点模态贡献量峰值的变化趋势与节点所在的模态振幅变化趋势相同。
2)全频段法
把每个模态所有节点的模态贡献量幅值在全频段内进行线性平均,结果如表3所示。由表3可知,4阶模态为此激励下前800 Hz的优势模态。
|
|
表 3 全频段内各模态所有节点的模态贡献量 Tab.3 MCF of output node in full-band |
由表3可看出:
虽然1阶模态的
每个响应节点在全频段内的模态贡献量变化趋势与节点在模态振幅上的变化趋势相同,说明由表2所得出的结论②不仅适用于
为了验证哪一种方式得出的优势模态对整体振动响应影响最大,分别将1阶、4阶的模态阻尼比由1%调整到2%,且为了论证增加优势模态的阻尼比对结构振动优化的高效性,分别做另外3组将其模态的阻尼比由1%调整到2%的对比试验,结果见表4。
|
|
表 4 改变模态阻尼比后的总加速度级 Tab.4 Acceleration level after changing modal damping ratio |
由表4可以得出结论:在同等条件下改变模态阻尼比,增加由
得出分别增加1阶、2阶、4阶模态阻尼后节点1的模态贡献量曲线图,如图4所示。
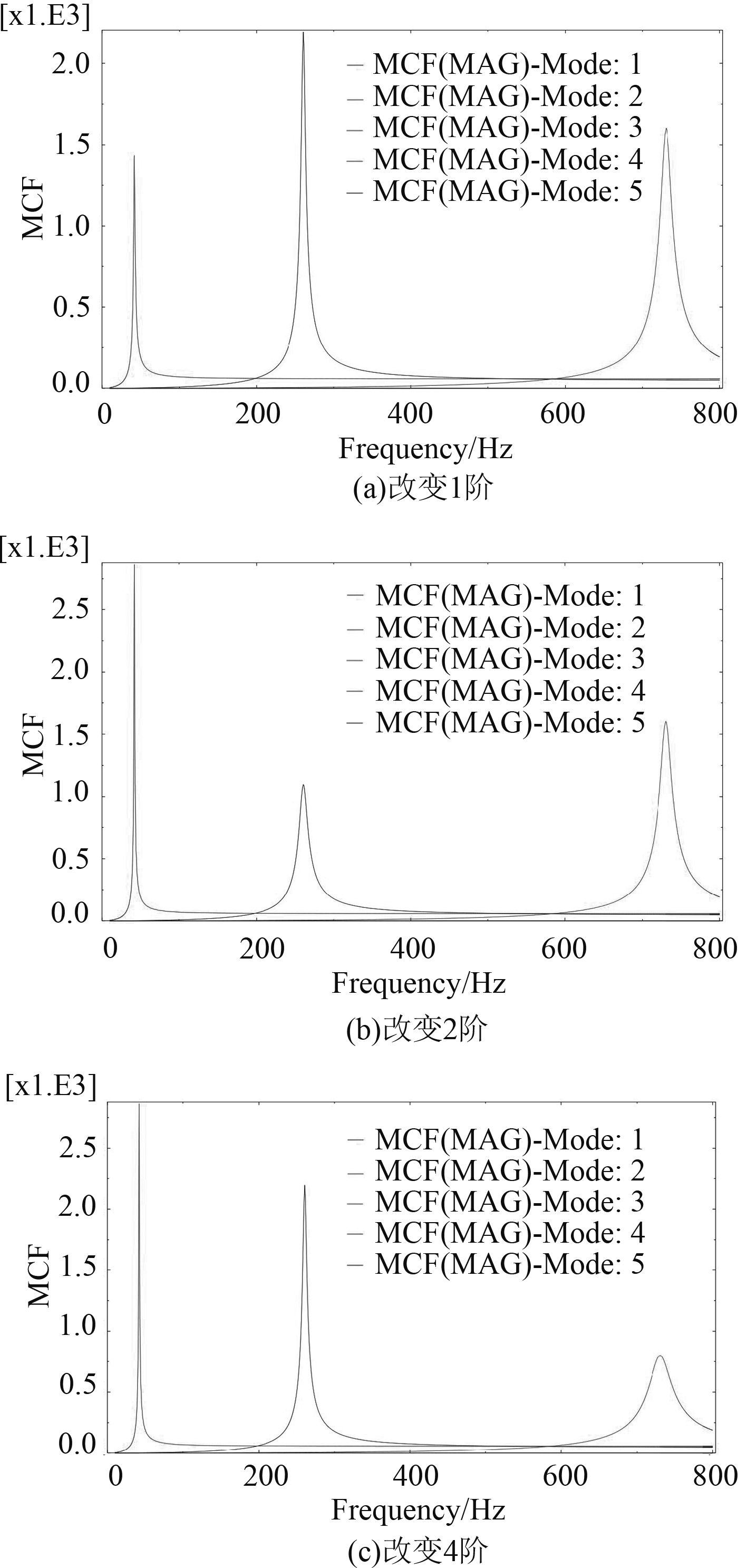
|
图 4 改变各阶模态阻尼比后节点1各阶模态贡献量 Fig. 4 First 5 vibration modes’ MCF of 1st output node after changing modal damping ratio |
由图4可以看出,增加各阶的模态阻尼比只会降低相应阶数的模态贡献量峰值,对其响应范围影响不大。因此,不可否认的是,利用
4阶模态为Z向2个周期的弯曲振动,因此可以考虑在结构合理的位置增加抑制Z向弯曲振动的阻尼材料,同时1阶和2阶分别是Z向1个周期的弯曲振动和Z向1.5个周期的弯曲振动,Z向弯曲振动的阻尼材料同样可以抑制1阶模态和2阶模态。
3 结 语本文基于Abaqus/Standard中模态贡献量插件的应用,提出了2种优势模态的选取方法,并通过算例论证了2种优势模态对振动响应的影响,可以得出以下结论:
1)增加由
2)增加由
3)如果某一阶的模态贡献量所占比重为0,则改变其模态阻尼比不会对振动响应有影响;
4)不管是峰值法或是全频段法,各个节点模态贡献量的变化趋势与节点所在的模态振幅变化趋势相同。
| [1] | 陈志坚. 舰艇振动学[M]. 北京: 国防工业出版社, 2010: 1–5. |
| [2] |
宋文, 梁跃, 高爱军, 等. 基于模态贡献量法支撑结构振动控制方法[J]. 鱼雷技术, 2015(6): 439–443.
SONG Wen, LIANG Yue, GAO Ai-jun, et al. Vibration control of engine support structure based on modal contribution method[J]. Torpedo Technology, 2015(6): 439–443. |
| [3] | DU Hua-jun, YU Bai-sheng. Vibration suppression of a conical honeycomb satellite adapter subjected to constrained layer damping[J]. Chinese Journal of Applied Mechanics, 2003, 20(3): 5–9. |
| [4] | DU Hua-jun, HUANG Wen-hu, ZOU Zhen-zhu. Passive vibration control of aerospace supporter [J]. Chinese Journal of Applied Mechanics, 2002, 19(3): 10–13. https://www.researchgate.net/publication/296400684_Passive_vibration_control_of_aerospace_supporter |
| [5] | 梁静. 车体模态贡献分析及其对振动影响研究[D]. 成都: 西南交通大学, 2011. |
| [6] | 傅志方, 华宏星. 模态分析理论与应用[M]. 上海: 上海交通大学出版社, 2000: 73–107. |
| [7] | 沃德·海伦, 等. 模态分析理论与实验[M]. 北京: 北京理工大学出版社, 2001: 2–25. |
| [8] | 曹树谦, 张文德, 萧龙翔. 振动结构模态分析理论、实验与应用[M]. 天津: 天津大学出版社, 2002: 181–236. |
| [9] | AUWERAER V H, LEURIDAN J. Identification of structural parameters from dynamic response data[M], 1978: 165–174. |
 2018, Vol. 40
2018, Vol. 40