2. 高性能船舶与深海开发协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, China
舰船螺旋桨相关问题的研究一直以来都是最具挑战性的问题之一。在过去很长一段时间内,螺旋桨的性能、激振力、噪声等问题只能通过实验方法[1 – 2]来研究。随着相关理论知识的完善,研究者开始使用升力线、升力面、面元法等势流方法[3]来研究螺旋桨的相关问题。近年来,随着计算机性能的提升以及CFD计算的快速发展,越来越多的研究者使用RANS方法[4 – 5]对螺旋桨相关问题进行数值研究。
尽管CFD技术在不断进步,但是网格问题仍然是影响CFD计算准确性的最重要的因素之一。一般来说,CFD计算网格分为结构网格和非结构网格两大类。文献[6]通过对敞水螺旋桨进行数值模拟比较了结构网格和非结构网格(四面体网格)的优缺点。实际上,对于复杂结构来说,获得结构网格所需的努力比获得非结构网格要大得多。尽管目前很多商业软件,比如Gambit,ICEAM-CFD,TrueGrid等,提供了强大的结构网格划分工具,但是半自动化的网格划分方法仍然需要大量的时间才能获得高质量的结构网格。在文献[7]中,使用了70个左右的块结构来离散螺旋桨的旋转区域。众所周知,使用多块结构能得到较高质量的结构网格,但是增加块结构的数量并调整每一个块结构的位置非常耗时。对于舰船螺旋桨来说,复杂扭曲的结构正是限制网格质量提升的主要原因。
目前常用的3种非结构网格有四面体网格(Tetrahedral mesh)、修剪网格(Trimmed cell)以及多面体网格(Polyhedral mesh)。针对复杂结构的流场,非结构网格生成方法具有较高的鲁棒性以及效率来获得高质量的网格。以上所述也正是非结构网格[8 – 11]得到广泛应用的原因。然而,考虑到3种不同非结构网格的形状特性,选择不同的网格类型对研究不同问题的数值结果可能有不同程度的影响。文献[12]在对船舶龙骨的水动力性能的研究中比较使用了四面体网格和修剪网格。而对于系统全面地比较这3种非结构网格的文章则非常少。众所周知,对于在数值研究领域的工作者,在开始新问题的研究之前,工作重点之一就是要分析问题,然后决定选择哪一种网格类型。看似简单的工作其实影响着CFD计算的各个方面。因此,本研究最单纯的目的就是为数值模拟领域的工作人员在对复杂流场的模拟时根据不同问题选择网格类型提供一个参考。
本文在螺旋桨的数值模拟中,对3种主流的非结构网格进行了大量的比较,从网格生成效率、网格计算效率到计算的准确性等。其中,计算的准确性又从2个方面进行比较,宏观量(螺旋桨推力和扭矩)和微观量(涡结构、尾流压力场和局部流场)。为了更清楚地说明问题,每组比较都在3套不同粗细的网格上进行,并分析了网格数量变化对数值结果的影响。网格划分和数值模拟工作都在双精度的STAR-CCM+平台上进行。
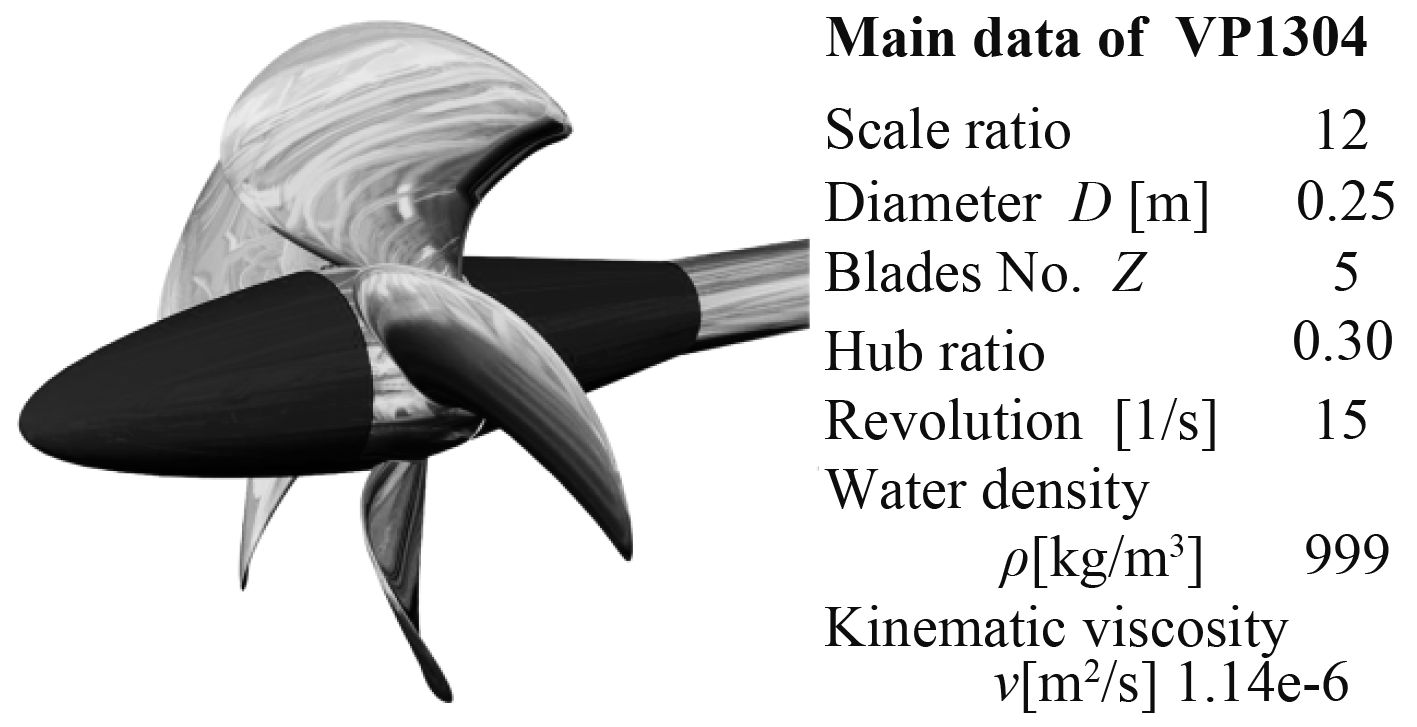
1 数值方法 1.1 研究对象根据第27届ITTC推进委员会的建议,本文选择常规桨VP1304(亦称PPTC桨)进行研究。该桨由SVA在Potsdam Model Basin设计。为了避免桨叶与桨轴之间的间隙(可调螺距桨)对数值结果产生负面影响,本文对该间隙进行了填补处理。对于该桨,有大量的实验数据可用来对数值结果进行验证。图1为该桨的几何模型和主尺度要素。图2为数值模拟的计算域,其中D为螺旋桨的直径。左侧为速度入口,右侧为压力出口。除旋转域外,还有网格过渡区、尾流捕捉区等。过渡区和尾流区的设计主要是用来捕捉螺旋桨的泄涡。图3为过螺旋桨几何中心某一剖面上的网格(修剪网格)。可以看出,对桨叶附近、旋转域、过渡区、尾流区的网格进行不同程度加密。注意,过渡区包含着整个旋转域,使用统一单元尺寸设置可以在交界面上生成共形网格,以减少数据交换带来的误差。速度入口的速度值根据下式计算V=JND,其中J为进速系数,N为转速。根据实验条件,螺旋桨转速为15 rps;螺旋桨进速系数为0.6,0.8,1.0,1.2,1.4。
|
图 1 螺旋桨形状和主尺度要素 Fig. 1 Propeller geometry and main particulars |

|
图 2 螺旋桨数值模拟计算域 Fig. 2 Computational domain for propeller simulation |

|
图 3 过螺旋桨几何中心剖面的网格示意图 Fig. 3 Computational mesh on a plane through the geometric center of the propeller |
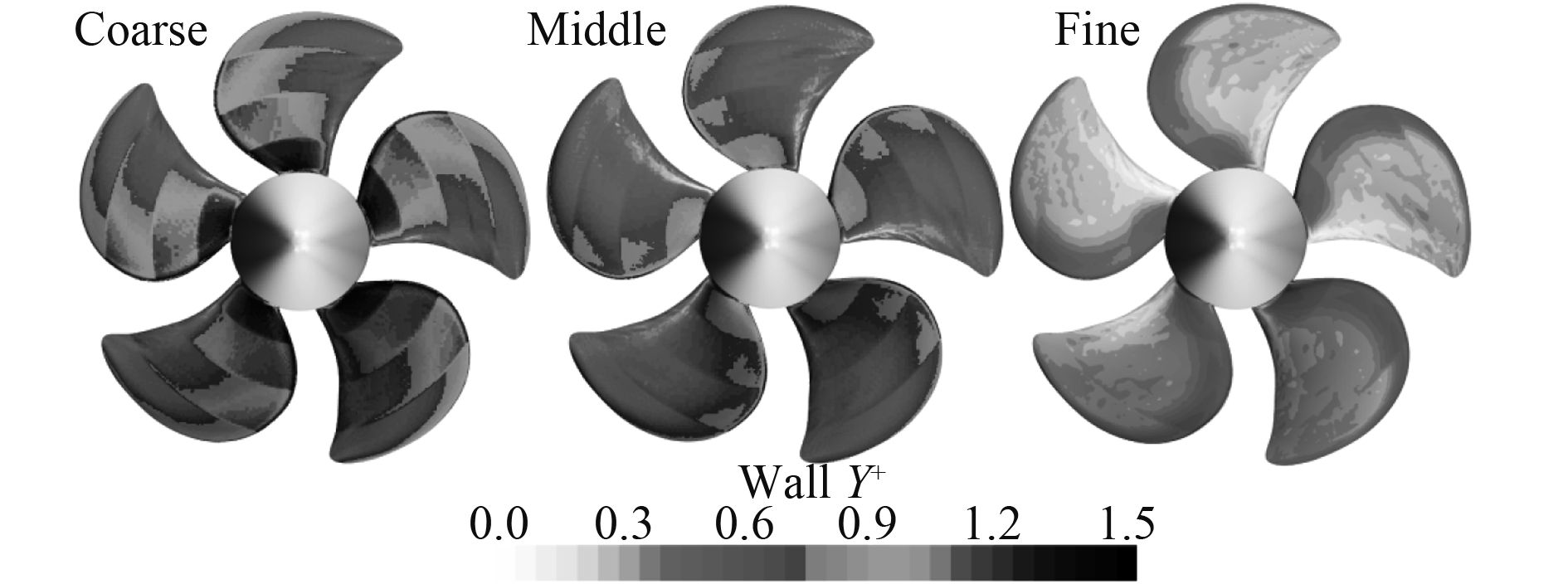
本文所有的比较在3套不同粗细的网格上进行。为了比较的公平,计算域同一粗细水平的3种网格的数量基本一致,见表1。相同网格数量Case的计算占用计算机资源(RAM和ROM)也一致。图4为3种不同粗细网格时桨叶壁面的Y+值分布图(J=1.4)。可以看出,使用最粗的网格时,Y+值也在1附近。使用最精细的网格时,所有Y+值都在0.6以下。
|
|
表 1 三种不同网格分辨率Case的网格数量统计(单位:百万) Tab.1 Mesh number statistics of three cases with different mesh resolutions |
|
图 4 不同粗细网格的桨叶表面Wall Y+云图分布 Fig. 4 Wall Y+ distribution on the blade surface in three cases |
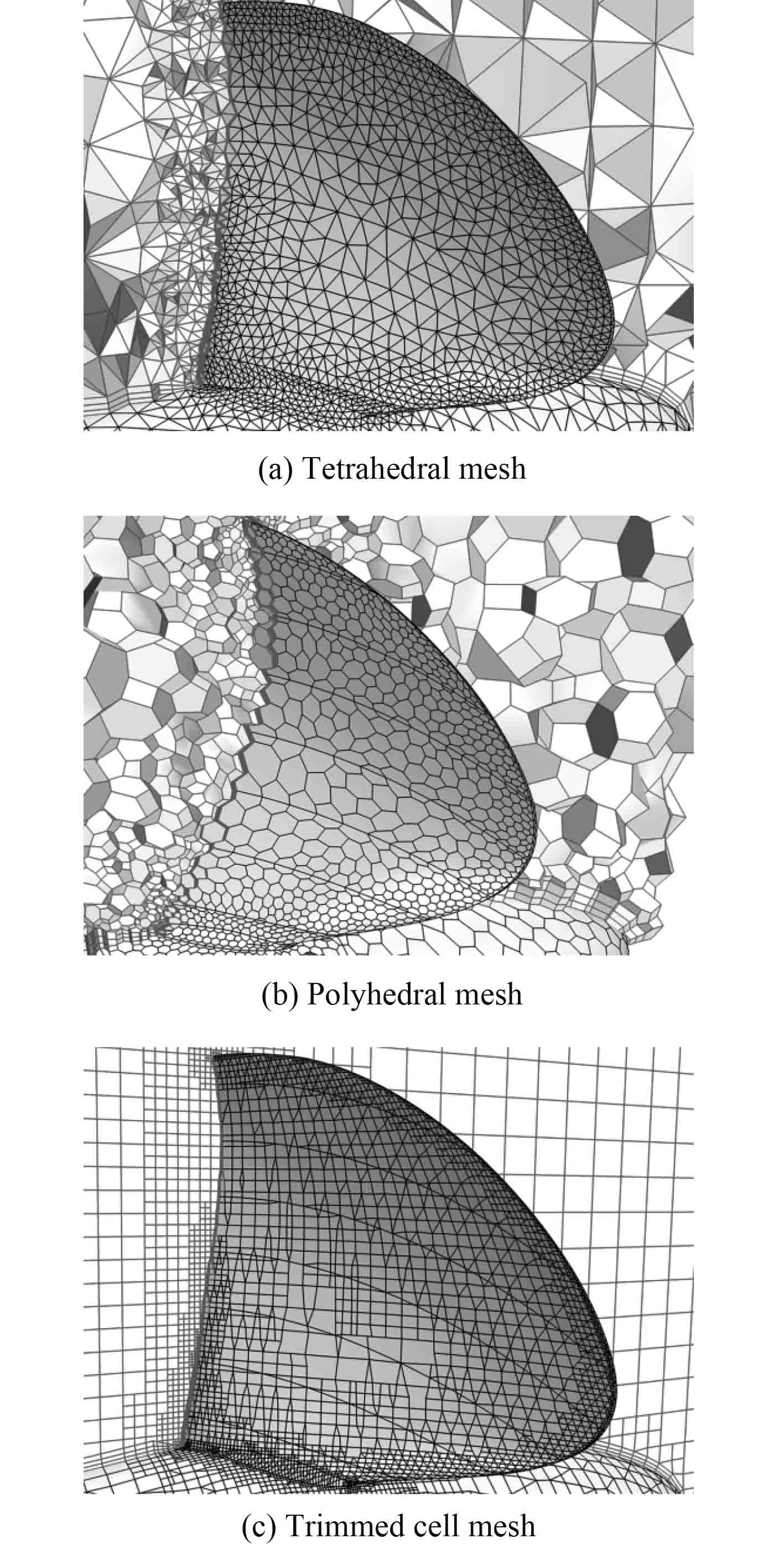
图5所示为使用3种不同的非结构网格方法获得的桨叶表面和局部的网格图(同一网格数量水平)。桨叶表面分布着15层边界层网格。直观上看:修剪网格和结构六面体网格非常类似,单元排列方向基本一致;四面体网格则在桨叶附近的数量极多,而较远区域的网格尺寸则较大;多面体网格的特征明显,由于每个单元具有多个面,因此在桨叶附近的网格质量较好,近场到远场的单元大小过渡也较缓和。
|
图 5 桨叶表面与局部的计算网格分布 Fig. 5 Computational mesh on the blade surface and near the propeller |
表2为螺旋桨敞水性能的数值结果(3种不同网格,3组不同网格数量,共9个Case)。表3为网格数量变化对敞水性能影响的研究结果(使用中等数量网格和最精细网格计算)。可以看出,当网格数量变化时,KT和10KQ的相对变化值都在2%以内。表4为数值结果的预报相对误差百分数(使用最精细网格),参考值为螺旋桨敞水性能的实验值[1]。在较小的进速系数时,使用3种网格的预报结果和实验值很接近。而在较大的进速系数时,比如J=1.4,三者的预报误差高达20%左右。产生这么大相对误差的主要原因是在大进速系数下,KT和10KQ的绝对值极小,使得预报更加困难。
|
|
表 2 螺旋桨敞水性能的数值结果 Tab.2 Numerical results of propeller open water performance |
|
|
表 3 网格数量变化对数值结果的影响 Tab.3 Influence of mesh number variation on numerical results |
|
|
表 4 螺旋桨敞水性能数值结果的验证 Tab.4 Validation of numerical results of propeller open water performance |
表5为使用3种不同网格类型对计算域进行离散所需的时间以及完成计算所需的时间的统计(最精细网格)。为了公平比较,所有的Case在同一台PC上运行,CPU为Intel I7-4450,频率为3.6 GHz。网格划分和数值计算都采用6核心并行运算。从表中可以看出:生成四面体网格所需的时间最少:而生成多面体网格所需的时间几乎是四面体的5倍;生成修剪网格的时间很接近生成四面体网格的时间。由于本文所使用的网格数量在500万左右,因此比较3种网格的生成效率似乎意义不大。但如果网格数量达到千万级别,那么网格生成效率就值得引起关注。
网格计算效率一直是人们关心的重点。表5记录的时间为完成5个工况所需的时间,螺旋桨敞水性能的计算采用动参考系模型计算。每个工况迭代500步。表5为迭代2 500步所需的时间。使用四面体网格完成计算只需不到8 h的时间,而使用多面体网格所需的时间几乎需要16 h。使用修剪网格所需的时间则需要10 h。
|
|
表 5 网格生成效率和网格计算效率的比较 Tab.5 Comparison of mesh generation efficiency and mesh calculation efficiency |
从表3可以看出,使用多面体网格时,网格数量变化对KT和KQ的影响最小。比较而言,四面体网格数量变化对结果的影响最大。
从表4可以看出,不管是在较小的进速系数还是在较大的进速系数时,使用四面体网格计算的结果都要比其他2种网格稍好一些。
总体来说,对于螺旋桨宏观力来说,使用3种网格预报的结果相差不是很大。
3.3 漩涡结构在使用动参考系模型(定常方法)获得螺旋桨的敞水性能后,使用滑移网格进行非定常模拟比较3种非结构网格对漩涡结构的预报情况。图6为使用Q准则获得的漩涡等值面图(Q=200s–2)。首先,使用四面体网格预报的漩涡结构远没有其他2种网格的效果好,这主要取决于网格的形状。多面体和修剪网格的特性使得在较粗略的网格小预报的涡结构也非常的光滑。其次,网格数量的增加,对涡结构的模拟效果的提升非常明显。但是比较而言,修剪网格的预报结果最好,多面体网格其次,四面体网格最差。最后,从图中可以看出,螺旋桨脱落的涡有叶梢涡(A)、随边涡(B)和叶根涡(C)3种。从图中看,使用四面体网格预报的叶根和随边的涡结构并没有持续到远场。改善四面体网格这种缺陷需要进一步提高网格分辨率。而对于四面体网格来说,单元尺寸缩小一倍,网格数量会成倍的增加。
图6对尾流中的湍流速度脉动量的均方根值(q)进行比较。众所周知,当流体绕过旋转的叶片会发生严重的脉动。然后,流体流向远方,q值减少。在数值模拟中,由于耗散作用的存在,这种脉动值可能会过早的结束。如图所示,在近场,使用3种网格预报的q值基本一致,但是在远场,修剪网格预报的q值最大,多面体网格预报值其次。比较说明,修剪网格预报的结果最好,耗散最少。主要原因在1.2节有提到,修剪网格与结构六面体网格类似。网格排流和流场一致,使得数值耗散作用较小。

|
图 6 螺旋桨桨叶泄涡的数值模拟结果比较 Fig. 6 Comparison of numerical results of vortices shedding from the propeller blades |
图7所示为距螺旋桨桨盘面X/R=0.528的一平面(下游)上的静压云图的比较(J=1.4)。总得来说,3种网格预报的压力云图类似。5个高压区由5个桨叶对流体的阻碍作用而形成;5个低压区由5个桨叶叶尖脱落的梢涡引起。比较来说,三者明显的区别是:使用四面体网格预报的压力云图的等值线很不规则(改善云图的方法只能通过进一步加密网格来达到),使用修剪网格预报的结果则非常光顺。定量地比较,使用修剪网格预报的高压区的值比其他2种网格预报的值要大一些。产生这一现象的原因是因为修剪网格排列可以与流体方向基本一致,使的计算耗散量小的多。从而能保证尾流区的压力场能得到很好的预报。而四面网格和多面体网格由于自身的几何特性使得数值耗散较修剪网格要大一些。

|
图 7 距螺旋桨0.528R的平面(下游)的静压云图的比较 Fig. 7 Comparison of static pressure on a plane 0.528R from the propeller (downstream) |
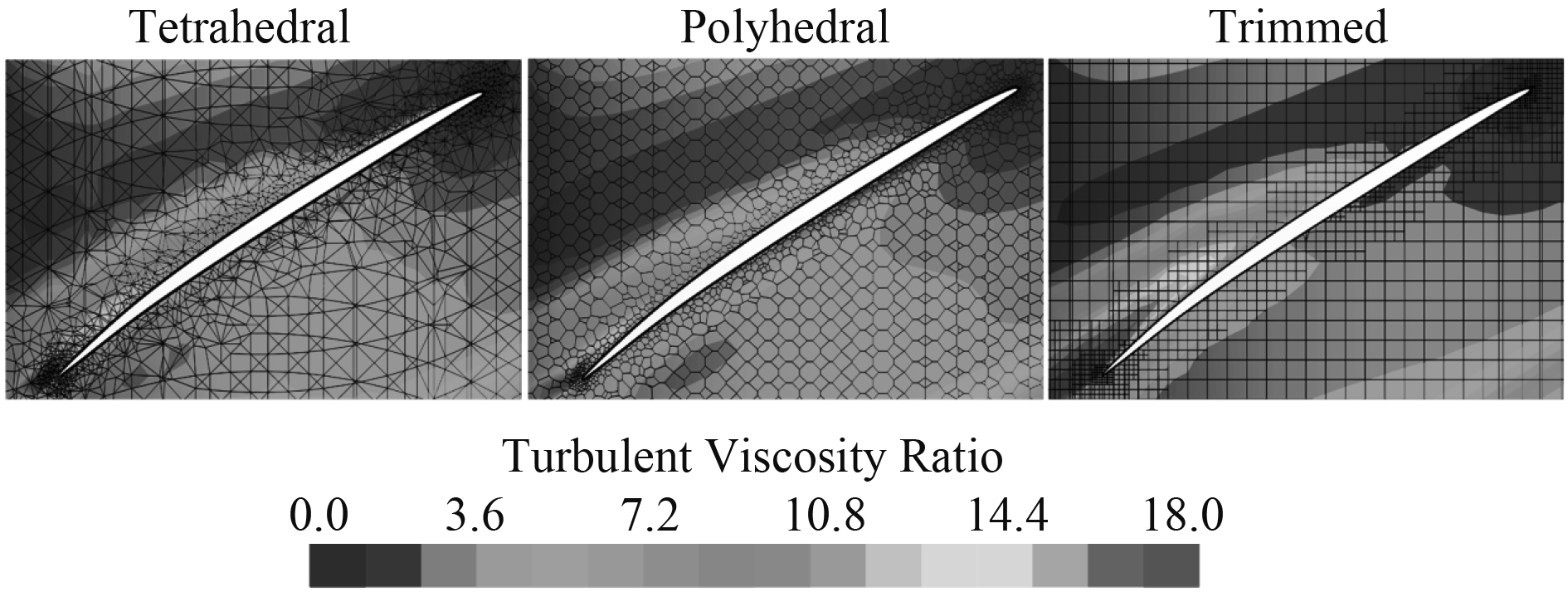
图8所示为桨叶0.75R剖面的湍流粘性比云图的比较。总体来说,3种网格预报的云图非常类似。当流体从右侧流至桨叶导边的时,雷诺数较小,湍流强度较小,因此湍流粘性比是个极小值(靠近0)。而当流体流至桨叶随边时,随着雷诺数的增大,以及流体绕过桨叶发生分离等,使得湍流强度迅速增大。从图中可以看出,湍流粘性比达到18。从图中可以看出,在边界层内(非常靠近桨叶地方),3种网格预报的结果一致。在距桨叶随边稍远一点的地方,使用修剪网格预报的湍流粘性比的值是三者中最大的。
|
图 8 桨叶局部(0.75R剖面)流场的比较 Fig. 8 Comparison of local flow over 0.75R blade section |
本文通过对敞水螺旋桨的数值模拟,分别从网格生成效率、网格计算效率,数值预报准确性等3个方法比较了3种主流的非结构网格在螺旋桨相关问题数值模拟中的优缺点。数值预报的准确性又从宏观(螺旋桨敞水性能)和微观(桨叶泄涡、尾流压力场和局部流场)2个方面进行。所有的物理量都在3套不同粗细的网格上进行比较,并探讨了3种网格数量变化对数值结果的影响。主要结论如下:
从宏观量(螺旋桨敞水性能)来说,3种网格预报的结果相差不大。比较而言,四面体网格的结果稍好,但是四面体网格数量变化对结果的影响较大。这说明,使用四面体网格需要较大量级的计算网格,如果使用其他类型的网格,较小数量的网格就能预报较好的结果。
从效率上来看,四面体网格无论是网格生成效率还是计算效率,都是三者中最高的。值得注意的是,多面体网格的生成时间和计算时间分别四面体网格的5倍和2倍。修剪网格的生成效率和计算效率略低于四面体网格,但比多面体网格要好的多。本文对效率的研究结果只是针对几百万网格级别,这可能使得对效率的研究不那么重要。如果网格数量达到千万级别,那么计算效率对科研的重要性就凸显出来了。
从微观量来看,无论是泄涡结构、压力场以及局部流场等,使用修剪网格的计算结果都是三者中最好,多面体网格其次,四面体网格最差。为了提高四面体网格对微观量的预报准确性,只有通过提高网格分辨率来实现。但是由于四面体网格的几何特性,缩小1倍的单元尺寸,网格数量会成倍的增长。
本文研究的结果可以为数值领域的工作人员在面对复杂的数值模拟选择网格时提供参考,如果只关心研究物体的宏观受力,并且对计算时间要求严格时,则可以选择四面体网格。如果对流场的细节关心,同时又对时间有要求,则可以选择修剪网格。如果不关心计算时间,而研究的物体非常复杂(网格的质量很难保证)时,则可以选择多面体网格。
| [1] | BARKMANN U. Potsdam propeller test case (PPTC) - open water tests with the model propeller VP1304 report 3752[C]// Schiffbau-Versuchsanstalt Potsdam, 2011, 4. |
| [2] | KUMAI T, TAMAKI I, KISHI J, et al. On a method of measurement of propeller bearing force exciting hull vibrations[J]. Journal of the Society of Naval Architects of Japan, 1970, 128: 85–90. |
| [3] | HOSHINO T. Hydrodynamic analysis of propellers in unsteady flow using a surface panel method [J]. Journal of the Society of Naval Architects of Japan, 1993, 174: 71–87. http://www.doc88.com/p-6991566283384.html |
| [4] | JI B, LUO X, PENG X, et al. Numerical analysis of cavitation evolution and excited pressure fluctuation around a propeller in non-uniform wake[J]. International Journal of Multiphase Flow, 2012, 43: 13–21. |
| [5] | RHEE S H, JOSHI S. CFD validation for a marine propeller using an unstructured mesh based RANS method [C]// The 4th Joint Fluids Summer Engineering Conference, American Society of Mechanical Engineers, 2003: 1157-1163. |
| [6] | MORGUT M, NOBILE E. Influence of grid type and turbulence model on the numerical prediction of the flow around marine propellers working in uniform inflow [J]. Ocean Engineering, 2012, 42(3): 26–34. https://www.sciencedirect.com/science/article/pii/S0029801812000273 |
| [7] | DI MASCIO A, MUSCARI R, DUBBIOSO G. On the wake dynamics of a propeller operating in drift [J]. Journal of Fluid Mechanics, 2014, 754: 263–307. |
| [8] | NAKISA M, MALIK A M A, AHMED Y M, et al. Propeller effect on 3D flow at the stern hull of a LNG carrier using finite volume method[J]. Applied Mechanics & Materials, 2014, 554: 566–570. https://www.scientific.net/AMM.554.566 |
| [9] | SHENG H, ZHU X Y, GUO C Y, et al. CFD simulation of propeller and rudder performance when using additional thrust fins [J]. Journal of Marine Science and Application, 2007, 6(4):27–31. |
| [10] | GUO C, DOU P, JING T, et al. Simulation of hydrodynamic performance of drag and double reverse propeller podded propulsors [J]. Journal of Marine Science and Application, 2016, 15(1):16–27. https://link.springer.com/content/pdf/10.1007/s11804-016-1337-y.pdf |
| [11] | MOUSAVI B, RAHROVI A, KHERADMAND S. Numerical simulation of tonal and broadband hydrodynamic noises of non-cavitating underwater propeller [J]. Polish Maritime Research, 2014, 21(3): 46–53. |
| [12] | MYLONS D, TURKMEN S, KHORASANCHI M. Numerical study of asymmetric keel hydrodynamic performance through advanced CFD [C]// The Third International Conference on Innovation in High Performance Sailing Yachts, 2013. |
 2018, Vol. 40
2018, Vol. 40
