2. 海军工程大学 舰船工程系,湖北 武汉 430033
2. Department of Naval Architecture Engineering, Naval University of Engineering, Wuhan 430033, China
钢板结构在长期使用过程中,会不可避免的与所在环境介质发生相互作用而变质或损伤,导致钢板结构机械力学性能的下降。例如,在工程实际中,钢板结构被广泛应用于舰船、潜艇、海洋平台、油气管道等海洋工程中,处于该类海洋环境中的钢板结构多数存在较为严重的腐蚀损伤问题。其中,坑点腐蚀是一种常见而又极具危害的腐蚀损伤形式[1]。坑点腐蚀是一种局部腐蚀损伤形式,由金属表面物理、化学的不均匀性引起,一般集中在很小的区域,往往沿着重力方向发展。近年来,国内外研究人员对工程结构中钢板结构的坑点腐蚀问题的重视程度逐渐提高,并进行了相关的研究工作。
TSCF[2]根据点蚀损伤钢板的弯曲试验,理论推导了一个包含弯曲刚度、质量、边界条件和尺寸等参数的点蚀损伤钢板等效厚度计算公式。Daidora[3]提出了一种用于估计结构腐蚀后剩余厚度的数学方法。Flaks[4],Paik[5 – 6]等开展了点蚀损伤板构件及老龄船舶极限强度的研究。Dunbar[7],Nakai[8 – 10]等开展了点蚀损伤对船舶典型构件局部强度的影响研究。Huang[11]采用非线性有限元软件(FEM)研究了点蚀损伤板的极限强度。徐强[12]建立了点蚀损伤壳板的力学模型,以超参数壳元为基础推导了坑点腐蚀壳体单元,并以坑点腐蚀壳体单元为基础开展了算例分析。徐强[13]分别采用PCSE、基于MPC的Shell-Solid集成以及Solid三种有限元方法对含点蚀损伤的深海耐压球壳的强度和稳定性进行了对比计算。Rahbar-Ranji[14 – 16]运用FEM研究了含有不规则表面的腐蚀损伤板的极限强度、塑性断裂强度和抗弯强度。
研究人员对点蚀损伤钢板在静态载荷作用下的剩余强度评估问题进行了大量研究,但对点蚀损伤钢板在动态载荷作用下的动态响应研究较少。本文利用有限元软件Ansys/LS-DYNA,分析了点蚀损伤对固支钢板在空中爆炸冲击波载荷作用下动态响应的影响。
1 数值计算模型采用非线性动力有限元分析软件Ansys/LS-DYNA,对含点蚀损伤钢板在空中爆炸载荷作用下的动态响应进行数值模拟研究。数值模型中,采用Lagrange网格建模,钢板采用8节点的Solid164三维实体单元模拟。靶板四边固支约束,建立全尺寸模型。
数值计算模型建立在Cartesian直角坐标系中,钢板承受爆炸载荷的迎爆面位于XOY平面,钢板厚度方向朝炸药一侧定义为Cartesian坐标系Z轴正方向。
本文数值计算中,研究对象为6 mm厚的船用钢板,其平面尺寸为0.5×0.5 m2,钢板结构承受的载荷为50 kg TNT当量炸药在距结构中心3 m处爆炸产生的空爆冲击波载荷,比例爆距为0.814,其中,炸药中心位于Cartesian直角坐标系的Z轴。
钢板受到的空爆冲击波载荷通过关键字*LOAD_BLAST_ENHANCED施加[17],钢板受载面承受的空爆冲击波载荷通过式(1)计算[18]:
| $P(\tau ) = {P_{{r}}} \cdot {\cos ^2}\theta + {P_{{i}}} \cdot (1 + {\cos ^2}\theta - 2\cos \theta )\text{,}$ | (1) |
式中:θ为冲击波入射角;Pr为反射压力;Pi为入射压力。
钢板采用双线性弹塑性本构模型Plastic_Kinematic,其应变率效应由Cowper-Symonds模型描述:
| ${\sigma _{{d}}} = \left( {{\sigma _0} + \beta \frac{{E{E_{\tan }}}}{{E - {E_{\tan }}}}{\varepsilon _{{p}}}} \right)\left[ {1 + {{\left( {\frac{{\dot \varepsilon }}{C}} \right)}^{1/n}}} \right]\text{,}$ | (2) |
式中:σd为动态屈服强度;σ0为静态屈服强度;E为弹性模量;Etan为切线模量;εp为有效塑性应变;
|
|
表 1 钢板的材料参数 Tab.1 Material parameters of plate |
吴有生[20]基于能量法,在考虑钢质平板结构塑性大变形时的应变关系及中面膜力影响的基础上,推导了一个计算空中爆炸载荷作用下平板结构塑性变形的公式,见文献[20]式(23),该式具有较好的预测准确性,该式计算平板中心最终状态下的挠度值的表达式为:
| $\begin{split}& \frac{{3\sqrt 3 {\pi ^2}\left( {{a^2} + {b^2}} \right) + 256ab}}{{32\sqrt 3 ab}}h{\sigma _s}{\omega _0}^2 + \\& \quad \quad \frac{{\sqrt 3 \pi \left( {{a^2} \!\!+\!\! {b^2}} \right) \!\!+\!\! 8ab}}{{2\sqrt 3 ab}}{h^2}{\sigma _s}{\omega _0} \!\!=\!\! 8\frac{{ab{A_i}^2}}{{\rho h}}{Q^{4/3}}{r^{ - 2}}\text{。}\end{split}$ | (3) |
式中:a和b分别为平板长、宽的一半;h为平板厚度;σs为平板材料的屈服极限;ω0为平板中心最终状态下的挠度值;Q为炸药的TNT当量;r为爆距。
为了研究数值计算模型单元划分对计算结果的影响,改变完好板的网格单元尺度,对完好板在空爆载荷作用下的变形情况进行数值模拟,并运用式(3)与数值计算结果进行对比,以验证数值计算方法的准确性。
首先,探讨板平面方向网格单元尺度对完好板在空爆载荷作用下的变形的影响,选取板厚度方向单元尺寸为1 mm,板平面方向单元尺寸为2 mm×2 mm,2.5 mm×2.5 mm,4 mm×4 mm,5 mm×5 mm和10 mm×10 mm,如表1所示。不同单元尺寸下板中心挠度值时程曲线如图1(a)所示。由图可知,当板平面单元尺寸不大于5 mm×5 mm时,板中心挠度值时程曲线保持非常好的一致性,但当板平面单元尺寸大于5 mm×5 mm时,板中心挠度值时程曲线的差异开始增大。因此,选定板平面单元尺寸为5 mm×5 mm。
其次,探讨板厚度方向网格单元尺度对完好板在空爆载荷作用下的变形的影响,板平面方向单元尺寸为5 mm×5 mm,厚度方向单元尺寸分别为1 mm,1.5 mm,2 mm和3 mm,如表2所示。不同单元尺寸下板中心挠度值时程曲线如图1(b)所示。由图可知,当板厚方向单元尺寸不大于1.5 mm时,板中心挠度值时程曲线保持较好的一致性,但当板厚方向单元尺寸大于1.5 mm时,板中心挠度值时程曲线的差异开始增大。因此,选定板厚方向单元尺寸不大于1.5 mm。
另外,如表2所示,列出了板中心最大挠度值的数值计算结果与式(3)计算结果,其中,取板弹性振动阶段多个挠度值的极大值和极小值的平均值为板中心最大挠度值。对比可知,板单元尺寸为5×5×1 mm3和5×5×1.5 mm3时数值计算结果与式(3)计算结果吻合较好。最终确定的完好板与含点蚀损伤板的单元划分示意如图2所示。
|
|
表 2 单元尺寸对数值计算结果的影响 Tab.2 Mesh sensitivity analysis showing the predicted maximum deflection (mm) of an uncorroded plate (0.5 m×0.5 m) |

|
图 1 不同单元尺寸条件下完好钢板最大挠度值数值计算结果 Fig. 1 Mesh sensitivity analysis showing the predicted maximum deflection (mm) of an uncorroded plate (0.5 m×0.5 m) |

|
图 2 数值计算模型单元划分示意图 Fig. 2 Finite element models of uncorroded and corroded plate |
根据实际船体结构中点蚀损伤的分布情况,船体结构板表面的点蚀损伤的分布非常飞散[11]。文献[8]指出,散货船舱肋骨结构表面的点蚀坑形状为圆锥形,油轮船底板结构表面的点蚀坑形状呈球形。散货船舱肋骨和油轮船底板结构表面的点蚀坑的直径/深度比值范围分别大致稳定在10:1到8:1和4:1到6:1。而点蚀坑的最大直径范围通常在25~80 mm。本文研究中,取点蚀坑的形状为圆锥形,其直径为40 mm[8]。
图3为典型的点蚀损伤模式示意图,为了研究点蚀损伤发生位置对固支钢板结构在空爆冲击波载荷作用下动态响应的影响,考虑了不同的点蚀损伤模式,即单面-迎爆面点蚀损伤,单面-背爆面点蚀损伤及双面点蚀损伤;例如,在图3(b)中,1-1-4表示在点蚀位置,钢板迎爆面点蚀坑最大深度为1 mm,完好层最小厚度为1 mm,背爆面点蚀坑最大深度为4 mm。

|
图 3 典型点蚀坑的尺寸示意 Fig. 3 Geometry of representative corrosion pit |
为了研究点蚀损伤分布密度对固支钢板结构在空爆冲击波载荷作用下动态响应的影响,考虑了不同的点蚀损伤分布密度。如图4所示,列出了不同点蚀损伤分布密度下的点蚀坑分布示意。
定义DOP(Degree of pit)为钢板表面点蚀面积占钢板表面积的比值,即点蚀分布密度,用以表征钢板的腐蚀强度,表达式为
| $DOP = \left\{ \begin{array}{l}\frac{1}{{ab}}\sum\limits_{i = 1}^n {{S_{pi}}} \times 100\% ,\;\;\;\;\;\;\left( {{\text{单面腐蚀工况}}} \right)\text{;}\\\frac{1}{{4ab}}\sum\limits_{i = 1}^n {{S_{pi}}} \times 100\%, \;\;\;\;\left( {{\text{双面腐蚀工况}}} \right)\text{。}\end{array} \right.$ |
式中:a和b分别为钢板的长度和宽度;n为点蚀坑数量;

|
图 4 点蚀坑分布示意图(0.5×0.5 m2) Fig. 4 FE models of the corroded plates with regular distributed corrosion pits (0.5×0.5 m2) |
考虑了不同的点蚀损伤深度,即1 mm,3 mm和5 mm,计算并比较不同点蚀损伤深度下固支钢板结构在空爆冲击波载荷作用下的最大挠度值(保持点蚀损伤模式和点蚀损伤分布密度一致)。计算结果如图5所示。
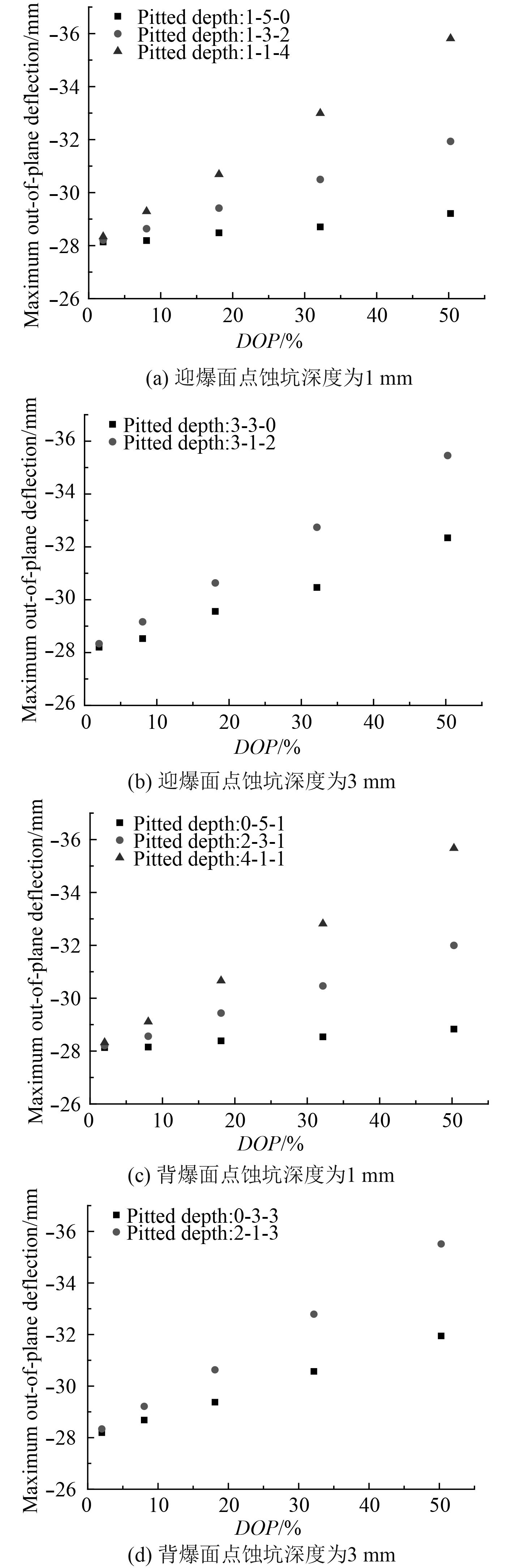
|
图 5 点蚀深度对点蚀损伤板最大挠度值的影响数值计算结果 Fig. 5 Variation of the maximum out-of-plane deflection,as a function of DOP in plates with different corrosion depth |
从图5(a)~图5(d)中可以明显看出,保持DOP不变的条件下,随着点蚀深度的增加,板最大挠度值随之增大,且随着DOP的增大,该趋势愈加明显;另外,在特定损伤模式下,随着DOP的增大,板最大挠度值随之增大,且随着点蚀总深度的增加,板最大挠度值增大的效果越来越显著。
2.4.2 点蚀损伤分布密度的影响考虑了不同的点蚀损伤分布密度,即DOP分别为2.01%,8.04%,18.10,32.17%和50.27%,计算并比较不同点蚀损伤分布密度条件下固支钢板结构在空爆冲击波载荷作用下的最大挠度值(保持点蚀损伤深度和点蚀损伤模式一致),其中,考虑了单面损伤和双面损伤2种不同的损伤模式。计算结果如图6所示。
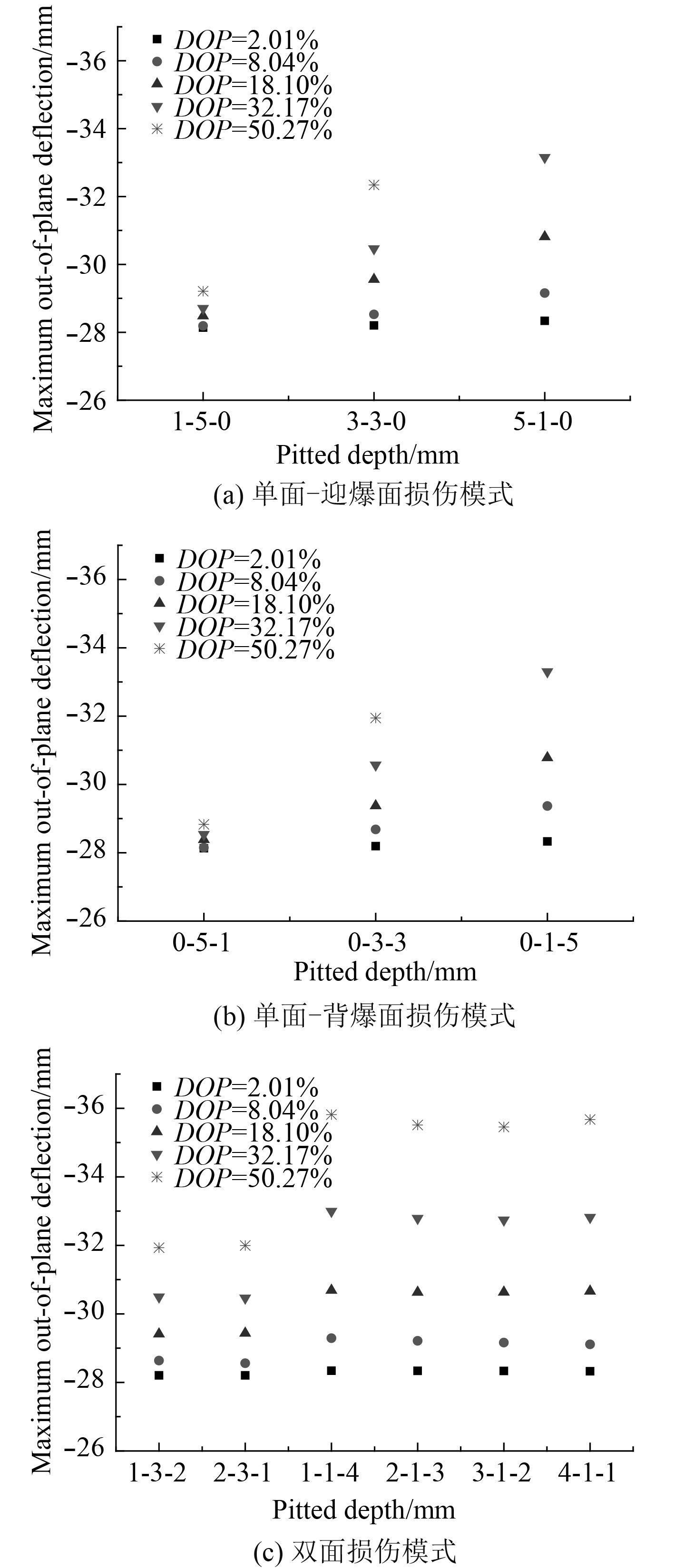
|
图 6 点蚀坑分布密度对点蚀损伤板最大挠度值的影响数值计算结果 Fig. 6 Variation of the maximum out-of-plane deflection,as a function of corrosion patterns with different DOP in plates |
从图6(a)~图6(c)中可以明显看出,无论是单面损伤还是双面损伤,在特定损伤模式下,随着DOP的增大,板最大挠度值呈增大的趋势,且随着点蚀总深度的增大,该趋势愈加明显。
2.4.3 点蚀损伤分布位置的影响考虑了不同的点蚀损伤分布位置,即迎爆面单面点蚀损伤、背爆面单面点蚀损伤及双面点蚀损伤,计算并比较在不同的点蚀损伤分布模式条件下固支钢板结构在空爆冲击波载荷作用下的最大挠度值(保持点蚀损伤深度和点蚀损伤分布密度一致)。
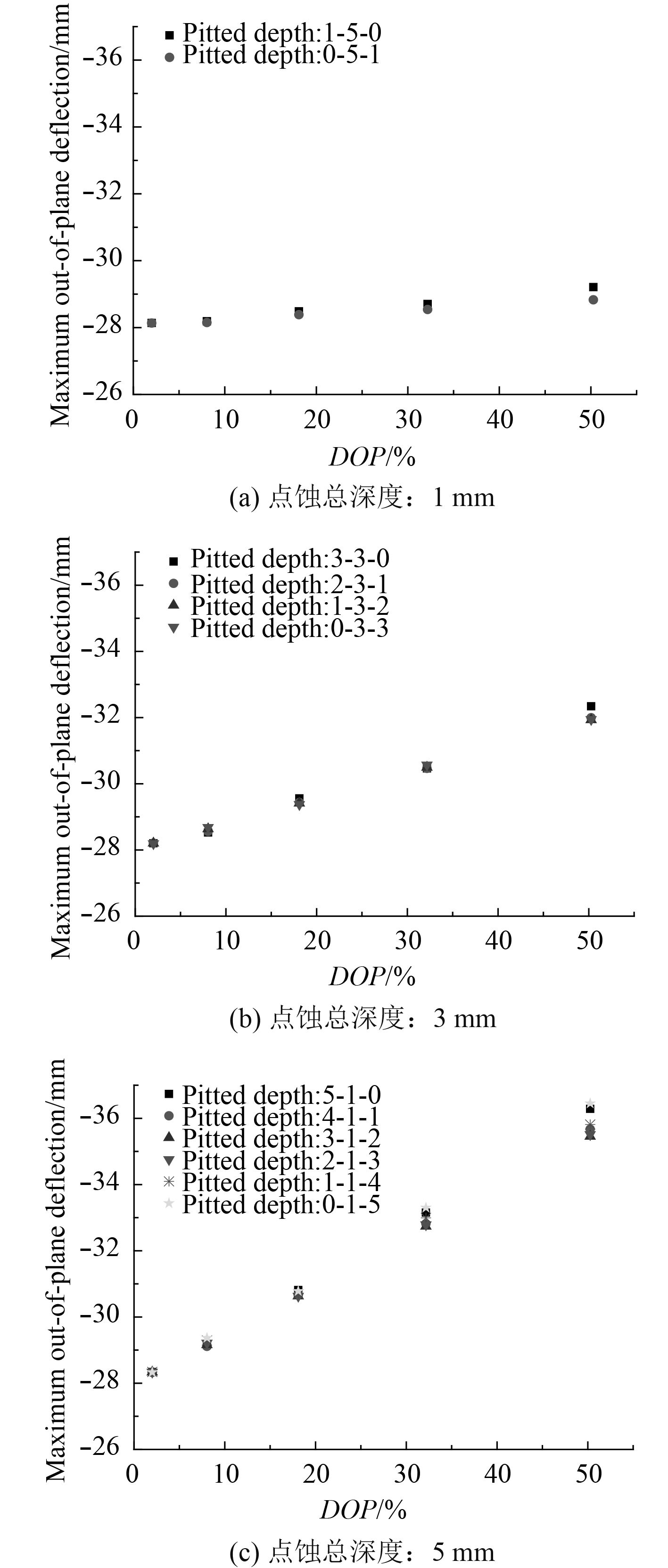
|
图 7 点蚀损伤分布位置对点蚀损伤板最大挠度值的影响数值计算结果 Fig. 7 Variation of the maximum out-of-plane deflection,as a function of DOP in plates with different corrosion patterns |
从图7(a)~图7(c)中可以观察到,在相同的点蚀总深度下,不同的点蚀损伤模式(单面-迎爆面点蚀损伤、单面-背爆面点蚀损伤以及双面点蚀损伤)对板最大挠度值的影响非常小;虽然随着DOP的增大,不同点蚀损伤模式下板最大挠度值的差异呈增大趋势,但是该差异不明显,如图7(c)所示,在点蚀总深度为5 mm,DOP=50.27%时,各损伤模式下板最大挠度值最大相差仅为0.996 mm。由此可见,板最大挠度值对不同的点蚀分布位置很不敏感。
3 结 语本文利用有限元分析软件Ansys/LS-DYNA,研究了点蚀损伤固支钢板在空爆冲击波载荷作用下的动态响应,得到了如下主要结论:
1)本文研究了点蚀损伤深度、点蚀损伤分布密度及点蚀损伤分布位置对钢板动态响应的影响,本文选取最大挠度值增加程度表征板的动态承载能力的降低程度,结果表明,点蚀损伤深度、点蚀损伤分布密度均对板的动态承载能力有较大影响,而点蚀损伤分布位置则影响非常小;
2)保持DOP不变的条件下,随着点蚀深度的增加,板动态承载能力随之降低,且随着DOP的增大,该趋势愈加明显;
3)在特定损伤模式下,随着DOP的增大,板动态承载能力随之增大,且随着点蚀总深度的增加,板动态承载能力增大的效果越来越显著;
4)在相同的点蚀总深度下,不同的点蚀损伤模式:单面-迎爆面点蚀损伤、单面-背爆面点蚀损伤以及双面点蚀损伤,对板动态承载能力的影响非常小,板动态承载能力对点蚀分布位置很不敏感。
| [1] |
吴梵, 滑林. 腐蚀、疲劳损伤下船体结构可靠性研究现状与展望[J]. 中国舰船研究, 2017, 12(5): 52–63.
WU Fan, HUA Lin. Current status and prospects of reliability analysis of hull structures under corrosion and fatigue damage[J]. Chinese Journal of Ship Research, 2017, 12(5): 52–63. |
| [2] | TSCF. Experimental and theoretical investigation of strength of corroded hull elements[R]. Project 300, Report No. 84–3438, Tanker Structure Co-operative Forum, 1984. |
| [3] | DAIDORA J C, PARENTE J, ORISANOLU I R, et al. Residua strength assessment of pitted plate panelsl[R]. SSC-394, Ship Structure Committee, 1997. |
| [4] | FLAKS V Y. Correlation of pitting corrosion of aluminum plates and reduction of load-beating capacity under tension[J]. Fiziko-Khimicheskaya Mekhanika Materialov, 1987, 14(1): 89–93. |
| [5] | PAIK J K. Ultimate strength of ships time-variant risk assessment of aging ship staking account to general/pit corrosion correlation, fatigue cracking and local dent damage[R]. Technical Report RD2002–11, American Bureau of Shipping, 2002. |
| [6] | PAIK J K, LEE J M, KO M J. Ultimate shear strength of plate elements with pit corrosion wastage[J]. Thin-Walled Structures, 2004, 42: 1161–1176. |
| [7] | DUNBAR T E, PEGG N, TAHERI F, et al. A computational investigation of the effects of localized corrosion on plates and stiffened panels[J]. Marine Structures, 2004, 17: 385–402. |
| [8] | NAKAI T, MATSUSHITA H, YAMAMOTO N, et al. Effect of pitting corrosion on local strength of hold frames of bulk carriers (1st report)[J]. Marine Structures, 2004, 17: 403–432. |
| [9] | NAKAI T, MATSUSHITA H, YAMAMOTO N, et al. Effect of pitting corrosion on local strength of hold frames of bulk carriers(2nd report)-lateral distortional buckling and local face buckling[J]. Marine Structures, 2004, 17: 612–641. |
| [10] | NAKAI T, MATSUSHITA H, YAMAMOTO N. Effect of pitting corrosion on the ultimate strength of steel plate subjected to in-plane compression and bending[J]. Journal of Marine Science and Technology, 2006, 11: 52–64. |
| [11] | HUANG Y, ZHANG Y, LIU G, et al. Ultimate strength assessment of hull structural plate with pitting corrosion damnification under biaxial compression[J]. Ocean Engineering, 2010, 37: 1503–1512. |
| [12] |
徐强, 万正权. 含坑点腐蚀的壳板有限元方法[J]. 船舶力学, 2010, 14(1–2): 84–93.
XU Qiang, WAN Zheng-quan. Finite element method of pitting corrosive shell[J]. Journal of Ship Mechanics, 2010, 14(1–2): 84–93. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cblx201001011 |
| [13] | 徐强, 万正权. 含坑点腐蚀的深海耐压球壳有限元分析[J]. 船舶力学, 2011, 15(5): 498–505. http://d.wanfangdata.com.cn/Periodical_cblx201105008.aspx |
| [14] | RAHBAR-RANJI A. Plastic collapse load of corroded steel plates[J]. Sadhana-Academy Proceed. Engineering Science, 2012, 37(3): 341–349. https://link.springer.com/content/pdf/10.1007/s12046-012-0084-2.pdf |
| [15] | RAHBAR-RANJI A. Ultimate strength of corroded steel plates with irregular surfaces under in-plane compression[J]. Ocean Engineering, 2012, 54: 261–269. |
| [16] | RAHBAR-RANJI A. Elastic buckling strength of corroded steel plates[J]. Sadhana-Academy Proceed. Engineering Science, 2013, 38(1): 89–99. https://rd.springer.com/content/pdf/10.1007/s12046-013-0116-6.pdf |
| [17] | CONWEP, Conventional Weapons Effects, US Army TM-855, 1992. |
| [18] | LS-DYNA keyword user's manual[Z] Livermore Software Technology Corporation, 2013. |
| [19] |
吴林杰, 侯海量, 朱锡, 等. 水下接触爆炸下防雷舱舷侧空舱的内压载荷特性仿真研究[J]. 兵工学报, 2017, 38(1): 143–150.
WU Lin-jie, HOU Hai-liang, ZHU Xi, et al. Numerical simulation on inside load characteristics of broadside cabin of defensive structure subjected to underwater contact explosion[J]. Acta Armamentarii, 2017, 38(1): 143–150. http://manu48.magtech.com.cn/Jwk_bgxb/CN/abstract/abstract5308.shtml |
| [20] |
吴有生, 彭兴宁, 赵立本. 爆炸载荷作用下舰船板架的变形与破损[J]. 中国造船, 1995, (4): 55–61.
WU You-sheng, PENG Xing-ning, ZHAO Li-ben. Plastic deformation and damage of naval panels subjected to explosion loading[J]. Shipbuilding of China, 1995, (4): 55–61. http://www.cqvip.com/QK/91784X/199602/2070405.html |
 2018, Vol. 40
2018, Vol. 40
