0 引　言

三体船是近年来发展迅猛的船型，它是一种高性能船，由1个中体和2个片体组成，相比于普通船型，拥有优良的阻力性能和耐波性能，优秀的稳性，较大的甲板面积，以及可以大型化的特点。因此，三体船的应用广泛，性能优异，在军民两用上都具有良好的发展前景^[1]。

而对于三体船舶操纵性能的研究，在国内外都甚少。而操纵性能对于三体船舶又十分重要，尤其对三体船在军事方面的运用十分重要。对于三体船舶操纵性能的研究，其关键在于水动力系数的确定，而想要得到精确的水动力系数，就需要精确计算三体船舶在斜航、旋臂等不同运动状态下的受力情况。在国内外对于水动力导数的求解方法，主要有经验公式、船模试验以及CFD软件以及势流理论求解的方法。

早在1936年Bollay^[2]已将二维的涡格法运用于较少展弦比机翼升力的计算，有着良好的效果。近年来，一些学者将涡格法运用于飞行器、船舶、海洋平台等流体力学相关领域的操纵性分析。Minu Jeona和Seungmin Lee^[3]采用涡格法分析了海上浮动式风力涡轮机在倾斜试验中的操纵性问题。J Gardiner和NA Razak等^[4]利用涡格法对鸟类飞行过程中环翼流场进行仿真分析。Sanghyuk Park^[5]将涡格法应用于固定翼无人机操纵性分析，并考虑了螺旋桨法向力对舵相应的影响，使模型仿真与飞行试验结果较好地吻合。陈材侃等^[6]考虑到非线性的自由液面边界条件，用下潜涡格法求解了水翼绕流问题。詹金林、卢晓平等^{[7 – 8]}对涡格法在船舶横向力以及转首力矩计算中的运用进行了研究。

本文运用势流方法对三体船操纵运动中的斜航运动进行数值模拟^{[9 – 10]}。由于传统源汇模型的诱导速度沿面元的切向连续法相不连续^[11]，对于有升力物体的模拟在满足定解条件的情况下，无法体现升力面两侧的速度差，而恰恰涡环（或偶极）单元的诱导速度沿法向连续而切向不连续^[12]。因此，本文将三体船视作3个有升力机翼，在船体表面布置涡环，采用对叠模的方法，忽略自由面的影响，通过涡环之间的相互诱导速度以及物面不可穿透条件，求解各个涡环的强度，进而得到各个分布点处的速度、压强以及船体的受力情况。并通过计算结果求得相应的水动力系数Yv，Yvvv，Nv，Nvvv。

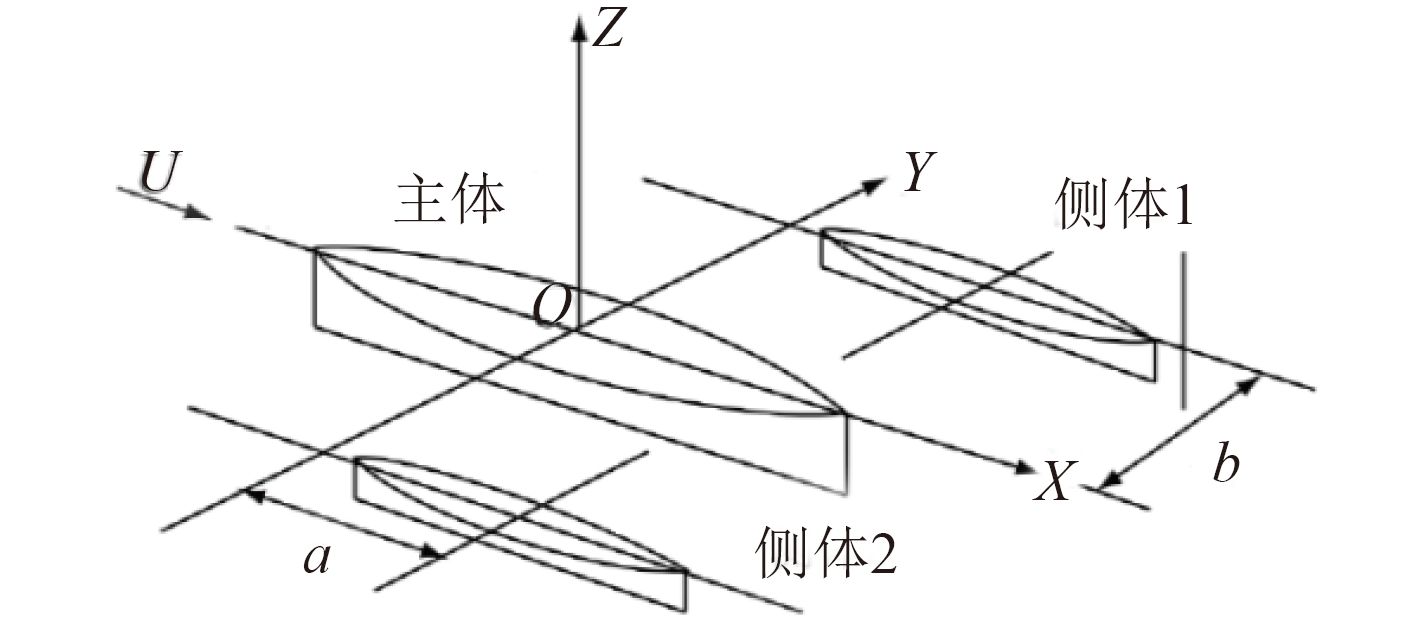
1 数学模型 1.1 坐标系

采用如图1所示的右手坐标系，坐标原点O位于船中，X轴由船首指向船尾，Y轴由船左舷指向右舷，Z轴竖直向上。侧体分布于主体两侧，两侧侧体中心位置对于主体中心位置在X方向的距离同为a，在Y方向的距离同为b。

1.2 控制方程以及边界条件

假定均匀来流速度为 ${{{V}}_0} = {V_{0{{x}}}} \cdot {{i}} + {V_{0y}} \cdot {{j}}$ 。根据势流理论，流场存在速度势Φ，由均匀来流的速度势和扰动速度势φ构成，即：

$\varPhi = x \cdot {V_{0{{x}}}} + y \cdot {V_{0y}} + z \cdot {V_{0z}} + \varphi \text{，}$

(1)

不计自由面兴波，φ应该满足以下定解条件：

$\left \{\begin{array}{l}{\nabla ^2}\varphi = 0\text{，}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{\text{流场中}}} \right)\text{；}\\{{\partial \varphi } / {\partial n}} = - {{{V}}_0} \cdot {{n}}\text{，}\;\;\;\;\;\;\left( {{\text{物面上}}} \right)\text{；}\\{{\partial \varphi } / {\partial n}} = 0\text{，}\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{\text{自由面上}}} \right)\text{；}\\\varphi \to 0\text{，}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{\text{远方辐射条件}}} \right)\text{。}\end{array}\right.$

(2)

对于有升力模型，还应满足：

${p_{TE}}^ + = {p_{TE}}^ - \text{，}\;\;\;\;\;\left( {{\text{船体尾缘库塔条件}}} \right)\text{。}$

(3)

其中， ${p_{TE}}^ + $ 和 ${p_{TE}}^ - $ 分别为尾缘处尾涡面两侧的压力。

1.3 方程的离散与求解

采用在物面和尾涡面上布置涡环的方法进行数值计算。流场中任意一点p的速度势为：

$\varphi (p) = - \frac{1}{{4\pi }}\int_s {m(q)\frac{\partial }{{\partial n}}} \frac{1}{{r(p,q)}}{\rm d}S\text{，}$

(4)

离散处理后得：

$\begin{split}\varphi (p) = & - \frac{1}{{4\pi }}\sum\limits_{j = 1}^N {{m_j}(q)\int_{{s_j}} {\frac{\partial }{{\partial n}}\frac{1}{{r(p,q)}}{\rm d}S} } - \\&\frac{1}{{4\pi }}\sum\limits_{k = 1}^L {{m_k}(q)\int_{{s_k}} {\frac{\partial }{{\partial n}}\frac{1}{{r(p,q)}}{\rm d}S} } \text{。}\end{split}$

(5)

关于式（5）两边求导，可得p点处的诱导速度为：

${{v}}(p) = - \frac{1}{{4\pi }}\sum\limits_{j = 1}^N {{m_j}} \oint_{{l_j}} {\frac{{{{r}} \times {\rm d}l}}{{{r^3}}}} - \frac{1}{{4\pi }}\sum\limits_{k = 1}^L {{m_k}} \oint_{{l_k}} {\frac{{{{r}} \times {\rm d}l}}{{{r^3}}}} \text{。}$

(6)

式中：右边第1项和第2项分别为物面上的涡环单元和尾涡面上的马蹄涡对p点的诱导速度；l_j和l_k分别为物面和尾涡面上面元的周界；m_j和m_k分别为涡环l_j和l_k的强度。涡环走向按由物面外法线方向按右手定则确定。

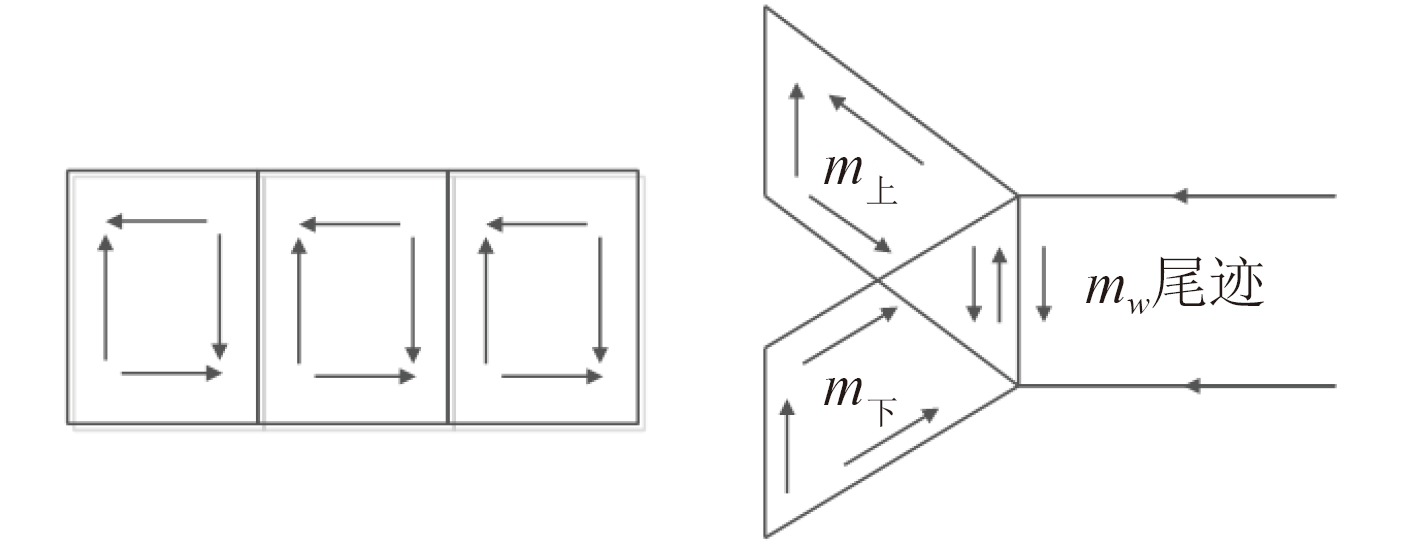
如果要在尾涡面上满足正负方向压强相等的Kutta条件，则需要不断迭代求解得到非线性的尾涡面以满足Kutta条件^[13]，而斜拖运动中船体漂角一般较小，非线性的影响也较小，因此本文参考了文献[14]对Kutta条件进行简化，尾涡面方向与来流方向一致，因为尾涡面上下的压力是连续的，而尾涡面又平行于来流方向，所以尾涡面的每一纵向条带各单元的涡环强度应该相等。如图2所示，这些涡环合在一起相当于一马蹄涡，其尾涡部分平行于来流方向，附着涡部分与物体后缘重合。

根据后缘的Kutta条件，在物体后缘不能有集中涡，于是马蹄涡的强度m_w与相邻物面单元上的涡环强度之间有如下关系式：

${m_w} = {m_{{\text{上}}}} - {{\rm{m}}_{{\text{下}}}}\text{，}$

(7)

流场内任意点p处扰动流场可以写成：

${{v}}(p) = \sum\limits_{j = 1}^N {{m_j}} {{{C}}_j}(p)\text{。}$

(8)

其中：N为物面上的面元总数； ${{{C}}_j}(p)$ 为物面任意单元j对于场点p的诱导速度；物面单元编号为j，而 $j = 1,2.....,N$ 。

当点p趋近于物面某一控制点i时，由物面条件 ${v_n} = - {{n}} \cdot {{{v}}_\infty }$ 得：

${{{n}}_{{p_i}}} \cdot \sum\limits_{j = 1}^N {{m_j}} {{{C}}_j}({p_i}) = - {{{n}}_{{p_i}}} \cdot {{{v}}_\infty }\text{。}$

(9)

其中，p_i为场点趋近于某一物面控制点i， $i = 1,2.....,N$ 。

式（9）可简写为：

$\sum\limits_{j = 1}^N {{K_{ij}}} {m_j} = {B_i} , i = 1,2......,N\text{。}$

(10)

其中：

${{{C}}_j}({p_i}) \!\!=\!\! \left\{\!\! \begin{array}{l}{{C}}_j'({p_i}) \text{，}\!\!\!\!\! {\text{不与马蹄涡相连单元}}\text{；}\\{{C}}_j'({p_i}) \!\!+\!\! {{{H}}_j}({p_i}) \text{，}\!\!\!\!\!{\text{与马蹄涡相连的单元}}\text{。}\end{array} \right.$

(11)

式中： ${{C}}_j'({p_i})$ 为涡环的影响系数， ${{C}}_j'({p_i}) = - \displaystyle\frac{1}{{4\pi }}\oint_{{l_j}} {\frac{{{{{r}}_{ij}} \times {\rm d}{{{l}}_j}}}{{{r_{ij}}^3}}} $ ； ${{{H}}_j}({p_i})$ 为马蹄涡的影响系数。此外， ${K_{ij}} = {{{n}}_i} \cdot {{{C}}_j}({p_i})$ ，n_i为控制点p_i处外法线方向的单位矢量。由式（10）建立N×N的线性代数方程组可以解得涡强m_j。采用薄物体的压力分布计算方法。物面上分布的面偶对其上任一点q_i的诱导速度为：

$\begin{split}{{v}}({p_i}) = & - \frac{1}{2}gradm({p_i}) - \frac{1}{{4\pi }}\int_S {{n}} \times gradm(q) \times \\ &\frac{{{r}}}{{{r^3}}}{\rm d}S - \frac{1}{{4\pi }}\oint_l {m(q)\frac{{{r}}}{{{r^3}}}} \times {\rm d}l\text{，} \end{split}$

(12)

式中：右边第2项为0，第3项之前已求得，对于第1项，解析方法较难计算，本文采用工程上常用的计算方法^[14]，令 $gradm = {h_1}{{{e}}_1} + {h_2}{{{e}}_2}$ ，用m₁，m₂，m₃分别表示物面某一单元处涡强以及单元纵向前方、垂向上方单元处涡强，通过前述方程组求解得到涡强后，则m₁，m₂，m₃为已知量，即可计算：

$\frac{{\partial m}}{{\partial x}} = \frac{{{m_2} - {m_1}}}{{{l_1}}};\;\frac{{\partial m}}{{\partial y}} = \frac{{{m_3} - {m_1}}}{{{l_2}}}\text{。}$

(13)

即

$\begin{align}\frac{{\partial m}}{{\partial x}} \!=\! gradm \cdot {{{e}}_1} \!=\! {h_1} \!+\! {h_2}{{{e}}_1} \cdot {{{e}}_2};\\\frac{{\partial m}}{{\partial y}} = gradm \cdot {{{e}}_2} \!=\! {h_2} \!+\! {h_1}{{{e}}_1} \cdot {{{e}}_2}\text{。}\end{align}$

(14)

记 ${{{e}}_1} \cdot {{{e}}_2} = {g_{12}}$ ，于是联立上式可以解得h₁和h₂，进而得到式（14）第1项。解得各分布点速度后，可得由伯努利方程到物面的压力分布 ${C_{{p_i}}}$ ，再由可控制点的向径p_i，由式（15）和式（16）求得船体受到的横向水动力和转首水动力矩：

${{{Y}}_h} = \sum\limits_{i = 1}^N {{p_i}{S_i}{{{n}}_{yi}}} \text{，}$

(15)

${{{N}}_h} = \sum\limits_{i = 1}^N {{S_i}} {{{p}}_i} \times ({p_i}{{{n}}_{xi}} + {p_i}{{{n}}_{yi}})\text{。}$

(16)

2 三体船斜航数值模拟及计算

选取三体Wigley船型为例，对三体船斜航运动进行数值模拟，进而说明算法的有效性^[15]。船型函数表达式为：

${\rm{y}} = \frac{B}{2}\left[ {1 - {{\left( {\frac{x}{{L/2}}} \right)}^2}} \right]\left[ {1 - {{\left( {\frac{z}{T}} \right)}^2}} \right]\text{。}$

(17)

取主体水线长L=3 m，主体水线宽B=0.3 m，主体吃水z=0.2 m，侧体按主体的0.4倍进行缩放，侧体纵向间距a=0.9 m，横向间距b=0.5 m。对其进行面网格划分，将主体水线划分40份，吃水深度划分5份，侧体水线划分16份，吃水深度划分2份，共划分696个四边形网格，采用正弦分布对船体网格进行划分，如图3所示。

由程序计算可得，在航速为1.625 m/s时斜航运动的受力如表1所示。

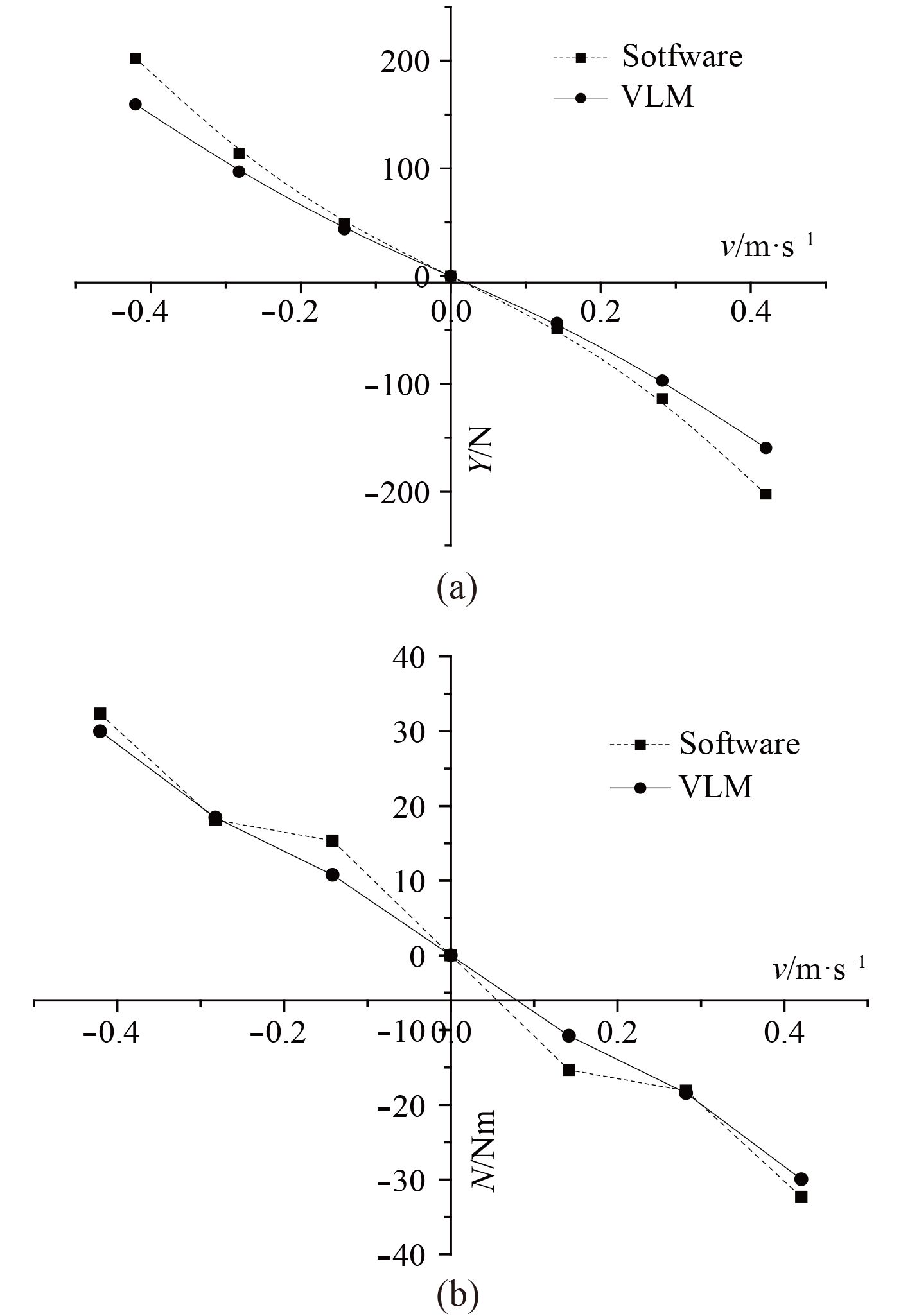
计算结果与商业软件Star-CCM+计算结果进行对比，如图4所示。

水动力系数对比如表2所示。

由计算结果可知，在漂角较小的情况下，程序计算结果与商业软件计算结果相符，但是由于对尾涡面进行了较小漂角下的线性尾涡面假设，因此随着漂角的不断增大，程序计算结果尤其是横向力与商业软件计算结果的差距增大，这与实际相符。由于转首力矩随着漂角的增大，其增幅相对较小，因此模拟较准确，而横向力的增大则非线性程度较大，因此主要的计算误差也体现在Y_vvv上。由于15°的漂角已足以满足工程计算的要求，因此认为对尾涡面的假设可行。

对三体Wigley船型分别采用了正弦分布网格划分。由于船体的受力较变化较大的部位主要在船首尾处，因此正弦网格分布可以在首尾处更好地反应形状变化以及得出更精确的压力分布。也说明对于涡环栅格法的使用，如何正确计算出涡强的分布，对最终压强分布的计算，以及最终横向力以及转首力矩结果的精度起着至关重要的作用。

3 结　语

利用涡格法对于三体船斜航运动的数值模拟，并通过结果回归得到斜拖运动水动力导数的方法可行。由于船体实际操纵运动漂角并不大，因此对于尾涡面的线性假设，在较小漂角情况下适用。但是由于忽略了尾涡面的非线性以及自由面的影响，随着漂角即横向速度的不断增大，受力体现出的弱非线性也更加明显，误差也会随之增大，这符合实际情况。