0 引　言

随着船舶航运业的发展，对船舶航行控制的要求也越来越高，目前针对船舶航向航迹控制的理论研究及工程实践已得到较大发展,国内船舶上已经开始广泛装备航迹自动航行控制系统^{[1 – 3]}。该系统主要对船舶的首向和航迹轨迹进行控制，未对船舶首向与横摇进行综合控制。研究表明船舶操舵控制也可以产生减摇效果，因此只进行首向和航迹控制没有充分发挥操舵和减摇鳍的综合控制效能。由于船舶在大海中航行，风浪流的干扰产生横摇运动会造成船舶航行稳定性下降，直接影响航行安全。如何有效的在船舶航向航迹控制的同时进行舵和鳍的减摇综合控制目前是船舶操纵控制的研究热点之一^{[4 – 5]}。

在20世纪70年代，Cowley和Lambert提出了舵减摇的设想^[6]。随后，舵减摇便在一商船上试验成功，但其减摇效果最多达到50%。由于横摇与首摇存在耦合，1981年，Kallstrom提出舵鳍联合减摇，采用多变量线性二次型控制理论进行控制，取得了更好的减摇效果^[7]。1999年，Sgobbo和Parsons利用美国海岸警卫队901级舰现有的舵/鳍传动机构，对4种控制器进行仿真，发现在不改变现有舵机设备下，舵鳍联合减摇控制器的减摇效果最佳^[8]，该控制器采用的是最优状态反馈控制理论。该文没有深入讨论如何选取最优状态反馈控制的性能指标函数，其给出的权系数矩阵中的参数较多，这些参数的改变会直接影响舵鳍联合减摇控制器的控制性能，现有文献中较少涉及权系数矩阵如何影响舵鳍联合减摇控制性能，因此有必要研究如何选择性能指标函数的问题，以及权矩阵参数影响控制器减摇性能的规律。

本文对船舶运动的三自由度数学模型，根据最优控制理论设计了舵鳍联合减摇控制器并在海浪干扰下进行数字仿真，结果表明控制器减摇性能良好。同时，在工程实际应用中，还没有对设计舵鳍联合减摇控制器时性能指标函数中权矩阵参数如何选取的研究。本文参考船舶航向控制中控制器设计时权矩阵系数的选择范围，经过仿真研究，得到了权矩阵参数对控制器减摇性能的影响，研究内容具有一定的理论意义和工程应用价值。

1 船舶运动三自由度模型

船的运动方程通常需要一个固定在船上的坐标系来表达。其坐标原点选择为船中的设计水线面和中线面处。船舶运动一般有纵荡、横荡、升沉、首摇、横摇、纵摇6个自由度，其中用于研究船舶减横摇中的一般为横荡、首摇和横摇，分别用v，ϕ，ψ，p，r表示横荡速度，横摇角，横摇角速度，纵摇角和纵摇角速度。

根据船舶运动原理，假定纵荡运动的动态特性较其他几个自由度要慢，航速和浪向角不变，将作用在船舶的水动力和力矩泰勒展开后，即可以得到关于横荡、横摇和首摇这3个自由度的方程^[9]：

$\left\{ \begin{array}{l}\left( {m \!-\! {Y_{\dot v}}} \right)\dot v \!-\! \left( {m{z_G} \!+\! {Y_{\dot p}}} \right)\dot p \!+\! (m{x_G} \!-\! {Y_{\dot r}})\dot r \!=\! {{\bar Y}_{hyd}} \!-\! mur \!+\! {Y_r} \!+\! {Y_f}\text{，}\\ - \left( {m{z_G} \!+\! {K_{\dot v}}} \right)\dot v \!+\! \left( {{I_{xx}} \!-\! {K_{\dot p}}} \right)\dot p \!-\! {K_{\dot r}}\dot r \!=\! {{\bar K}_{hyd}} \!+\! m{z_G}ur \!+\! {K_r} \!+\! {K_f}\text{，}\\\left( {m{x_G} - {N_{\dot v}}} \right)\dot v - {N_{\dot p}}\dot p + \left( {{I_{zz}} - {N_{\dot r}}} \right)\dot r = {{\bar N}_{hyd}} \!-\! m{x_G}ur + {N_r} \!+\! {N_f}\text{，}\\\dot \phi = p\text{，}\\\dot \psi = r{\rm cos}\left( \phi \right) \approx r\text{。}\end{array} \right.$

(1)

式中：m为船舶质量；u为船速；x_G，z_G为船舶重心在坐标系中的坐标；I_xx，I_zz为船舶绕x轴，z轴的质量惯性矩； ${Y_{\dot v}}\text{，}{Y_{\dot p}}\text{，}{Y_{\dot r}}\text{，}{K_{\dot v}}\text{，}{K_{\dot p}}\text{，}{K_{\dot r}}\text{，}{N_{\dot v}}\text{，}{N_{\dot p}}\text{，}{N_{\dot r}}$ 为作用在船舶上与加速度项有关的水动力系数； ${Y_r}\text{，}{Y_f}\text{，}{K_r}\text{，}{K_f}\text{，}{N_r}\text{，}{N_f}$ 分别为舵、鳍在3个方向上产生的控制力和力矩，为鳍角α和舵角δ的函数，具体形式可参考文献[9]。 ${\bar Y_{hyd}}\text{，}{\bar K_{hyd}}\text{，}{\bar N_{hyd}}$ 均为水动力泰勒展开式去掉与加速度项有关的系数项后的部分。

令状态向量 $x \buildrel \Delta \over = {\left[ {\begin{array}{*{20}{c}}v&p&r&\phi &\psi \end{array}} \right]^{\rm T}}$ ，输入为 $u = {\left[ {\begin{array}{*{20}{c}}\alpha &\delta \end{array}} \right]^{\rm T}}$ ，对非线性项 ${\bar Y_{hyd}}\text{，}{\bar K_{hyd}}\text{，}{\bar N_{hyd}}$ 在平衡点进行泰勒展开，并取展开式的第1项近似，由式（1）可得

${ M}\dot x = {{ A}_1}x + {{ B}_1}u\text{。}$

(2)

其中：

${ M} = \left[ {\begin{array}{*{20}{c}}{m - {Y_{\dot v}}}&{m{z_G} + {Y_{\dot p}}}&{m{x_G} - {Y_{\dot r}}}&0&0\\{ - \left( {m{z_G} + {K_{\dot v}}} \right)}&{{I_{xx}} - {K_{\dot p}}}&{ - {K_{\dot r}}}&0&0\\{m{x_G} - {N_{\dot v}}}&{ - {N_{\dot p}}}&{{I_{zz}} - {N_{\dot r}}}&0&0\\0&0&0&1&0\\0&0&0&0&1\end{array}} \right]\text{，}$

$\begin{aligned} & {{ A}_1} \!\!\!=\!\!\! \left[\!\!\!\!\!\! {\begin{array}{*{20}{c}}{{Y_{\left| u \right|v}}\left| {\bar u} \right|}\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!{\left( {{Y_{ur}} \!-\! m} \right)\bar u}\!\!\!\!&\!\!\!\!{{Y_{\phi uu}}{{\bar u}^2}}\!\!\!\!&\!\!\!\!0 \\ {{K_{\left| u \right|v}}\left| u \right|}\!\!\!\!&\!\!\!\!{{K_p} \!\!+\!\! {K_{\left| u \right|p}}\left| {\bar u} \right|}\!\!\!\!&\!\!\!\!{\left(\! {{K_{ur}} \!\!+\!\! m{z_G}} \!\right)\bar u}\!\!\!\!&\!\!\!\!{{K_{\phi uu}}{{\bar u}^2} \!\!-\!\! \rho g\nabla GMt}\!\!\!\!&\!\!\!\!0\\{{N_{\left| u \right|v}}\left| u \right|}\!\!\!\!&\!\!\!\!{{N_{\rm{p}}} \!+\! {N_{\left| u \right|{\rm{p}}}}\left| {\bar u} \right|}\!\!\!\!&\!\!\!\!{{N_{\left| u \right|r}}\left| {\bar u} \right| \!-\! m{x_G}\bar u}\!\!\!\!&\!\!\!\!{{N_{\phi u\left| u \right|}}\bar u\left| {\bar u} \right|}\!\!\!\!&\!\!\!\!0\\0\!\!\!\!&\!\!\!\!1\!\!\!\!&\!\!\!\!0\!\!\!\!&0\!\!\!\!&\!\!\!\!0\\0\!\!\!\!&\!\!\!\!0\!\!\!\!&\!\!\!\!1\!\!\!\!&0\!\!\!\!&\!\!\!\!0\end{array}} \!\!\!\!\!\right], \\ & {{ B}_1} = \left[ {\begin{array}{*{20}{c}}{{Y_\alpha }}&{{Y_\delta }}\\{{K_\alpha }}&{{K_\delta }}\\{{N_\alpha }}&{{N_\delta }}\\0&0\\0&0\end{array}} \right]\text{。}\end{aligned}$

式中： ${Y_{\left| u \right|v}}\text{，}{K_{\left| u \right|v}}\text{，}{N_{\left| u \right|v}}\text{，}{K_{\left| u \right|p}}\text{，}{N_{\left| u \right|p}}\text{，}{Y_{ur}}\text{，}{K_{ur}}\text{，}{N_{\left| u \right|r}}\text{，}$ ${Y_{\phi uu}}\text{，}$ ${K_{\phi uu}}\text{，}{N_{\phi u\left| u \right|}} $ 均为作用在船舶上的水动力系数。

所以船舶的三自由度线性化的状态空间模型为：

$\dot x = { A}x + { B}u\text{，}$

(3)

其中 $ { A} = {{ M}^{ - 1}}{{ A}_1},{ B} = {{ M}^{ - 1}}{{ B}_1}\text{。}$

2 最优控制器的设计

当状态方程 $\dot X\left( t \right) = { A}X\left( t \right) + { B}U\left( t \right)$ 表示的系统为可控或可镇定时，令性能指标函数^[10]为

$J=\frac{1}{2}\int_{0}^{\infty }{\left( {{X}^{\text{T}}}QX+{{U}^{\text{T}}}RU \right)}\text{d}t\text{，}$

(4)

则使取极小值的最优控制可表示为

$U = - KX = - {R^{ - 1}}{B^{\rm T}}P\text{。}$

(5)

为黎卡提方程的唯一正数半定解：

$ - {{ A}^{\rm T}}P - P{ A} + P{ B}{R^{ - 1}}{{ B}^{\rm T}}P - Q = 0\text{。}$

(6)

考虑到横荡速度v对控制性能影响不大且难以准确测量，故在控制器设计时选取状态向量时不考虑横荡速度v。即在本文选取的状态向量为 $x \buildrel \Delta \over = {\left[ {\begin{array}{*{20}{c}}p&r&\phi &\psi \end{array}} \right]^{\rm T}}$ ，输入为 $u = {\left[ {\begin{array}{*{20}{c}}\alpha &\delta \end{array}} \right]^{\rm T}}$ ，选取性能指标函数时本文以能量最优为原则，故不能直接反映能量的横摇角速度p，首摇角速度r不纳入到性能指标中，故　　 ${ Q} = \left[ {\begin{array}{*{20}{c}}0&0&0&0\\0&0&0&0\\0&0&{{\lambda _\phi }}&0\\0&0&0&1\end{array}} \right]$ ， ${ R} = \left[ {\begin{array}{*{20}{c}}{{\lambda _\alpha }}&0\\0&{{\lambda _\delta }}\end{array}} \right]$ 。

在设计最优控制器时，本文所选取的性能指标函数为

$J = \frac{1}{2}\int_{0}^{\infty }\left[ {\left( {{\psi ^2} + {\lambda _\delta }{\delta ^2}) + {\lambda _\phi }({\phi ^2} + {\lambda _\alpha }{\alpha ^2}} \right)} \right]{\rm d}t\text{。}$

(7)

控制器性能由横摇减摇效率衡量，定义如下：

${\text{横摇减摇效率}}\eta = \frac{{{{\rm{\sigma }}_{\rm{c}}} - {\rm{\sigma }}}}{{\rm{\sigma }}} \times 100\text{。}$

式中，σ为未安装控制器时的横摇幅值标准差；σ_c为安装了控制器时的横摇幅值标准差。

3 仿真研究

本文主要以美海岸警卫队WMEC910级舰为对象进行实验模拟研究。该舰安装了一对减摇鳍以及配备常规舵。根据文献[9, 11]可得该舰的主要特性参数，对于状态方程有：

$\begin{array}{l}{ A} = \left[ {\begin{array}{*{20}{c}}{ - 0.148\ 7}&{0.189\ 6}&{ - 0.678\ 9}&{1.171\ 4}&0\\{0.021\ 4}&{ - 0.152\ 4}&{ - 1.406\ 4}&{ - 0.956\ 7}&0\\{ - 0.009\ 8}&{0.002\ 9}&{ - 0.292\ 0}&{0.013\ 0}&0\\0&1&0&0&0\\0&0&1&0&0\end{array}} \right],\\{ B} = \left[ {\begin{array}{*{20}{c}}{0.479\ 7}&{0.037\ 6}\\{ - 0.279\ 2}&{0.096\ 3}\\{0.009\ 6}&{0.026\ 0}\\0&0\\0&0\end{array}} \right]\text{。}\end{array}$

鳍机的传递函数表示如下：

${G_f} = \frac{{8.0}}{{{s^2} + 3.4s + 8.0}} = \frac{{{\alpha _a}\left( s \right)}}{{{\alpha _c}\left( s \right)}}\text{，}$

(8)

舵机的传递函数表示如下：

${G_r} = \frac{1}{{6.32s + 1}} = \frac{{{\delta _a}\left( s \right)}}{{{\delta _c}\left( s \right)}}\text{。}$

(9)

本文对海浪干扰采用一种简单的模拟方法，用高斯白噪声驱动1个二阶振荡环节，叠加在船舶数学模型的横摇角输出上。在6级风的情况下，海浪的传递函数为^[12]

${G_f} = \frac{{0.419\ 8s}}{{{s^2} + 0.363\ 8s + 0.367\ 5}}\text{。}$

(10)

设计控制器时的状态方程简化为 ${\dot x_c} = {{ A}_c}x + {{ B}_c}u$ ，

$\begin{array}{l}{{ A}_c} = \left[ {\begin{array}{*{20}{c}}{ - 0.299\ 7}&{ - 1.405\ 1}&{ - 0.956\ 7}&0\\{0.005\ 7}&{ - 0.046\ 6}&{0.013\ 0}&0\\1&0&0&0\\0&1&0&0\end{array}} \right],\\{{ B}_c} = \left[ {\begin{array}{*{20}{c}}{ - 0.279\ 2}&{0.096\ 3}\\{0.009\ 6}&{0.026\ 0}\\0&0\\0&0\end{array}} \right]\text{。}\end{array}$

对于性能指标函数J，令 ${\lambda _\phi } = 20,{\lambda _\alpha } = 1,{\lambda _\delta } = 1$ 可得到最优控制律为

$\begin{split}& {\alpha _c} = - \left(- 2.121\ 4{\rm{*}}\phi - 3.317\ 8{\rm{*}}p \right. + \\& \left. 0.280\ 0{\rm{*}}\psi + 3.117\ 9{\rm{*}}r \right)\text{。} \end{split}$

(11)

$\begin{split}& {\delta _c} = - \left( 0.875\ 9*\phi + 0.945\ 3*p \right. + \\& \left. 0.960\ 0*\psi + 2.659\ 9*r \right)\text{。}\end{split}$

(12)

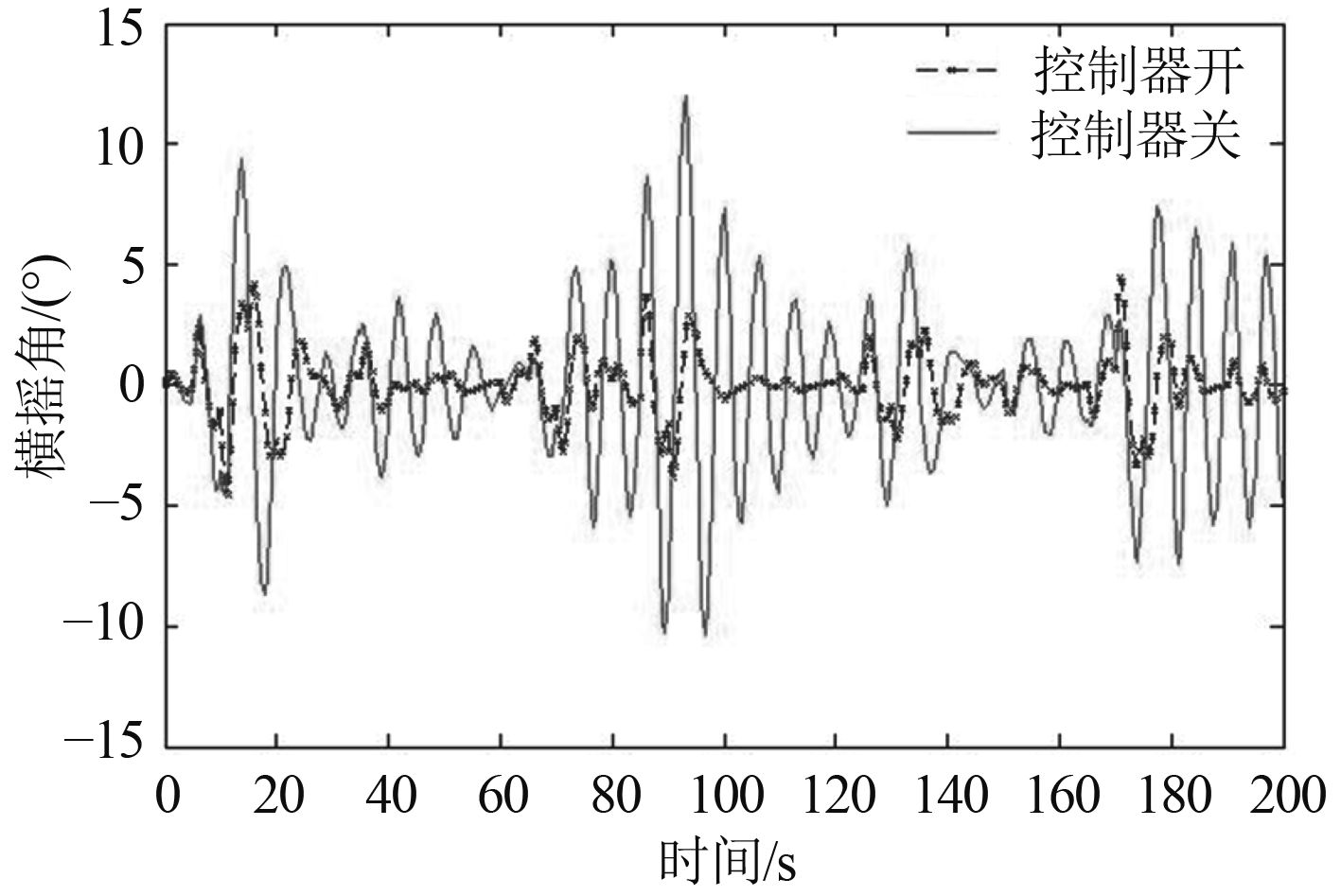
图1表明船舶在有无最优控制器情况下的仿真结果，可以看到有控制器的船舶的横摇角明显减小，说明了控制器具有良好的减摇性能。

为观察 ${\lambda _\phi },{\lambda _\alpha },{\lambda _\delta }$ 对控制器性能的影响，采取控制变量法。

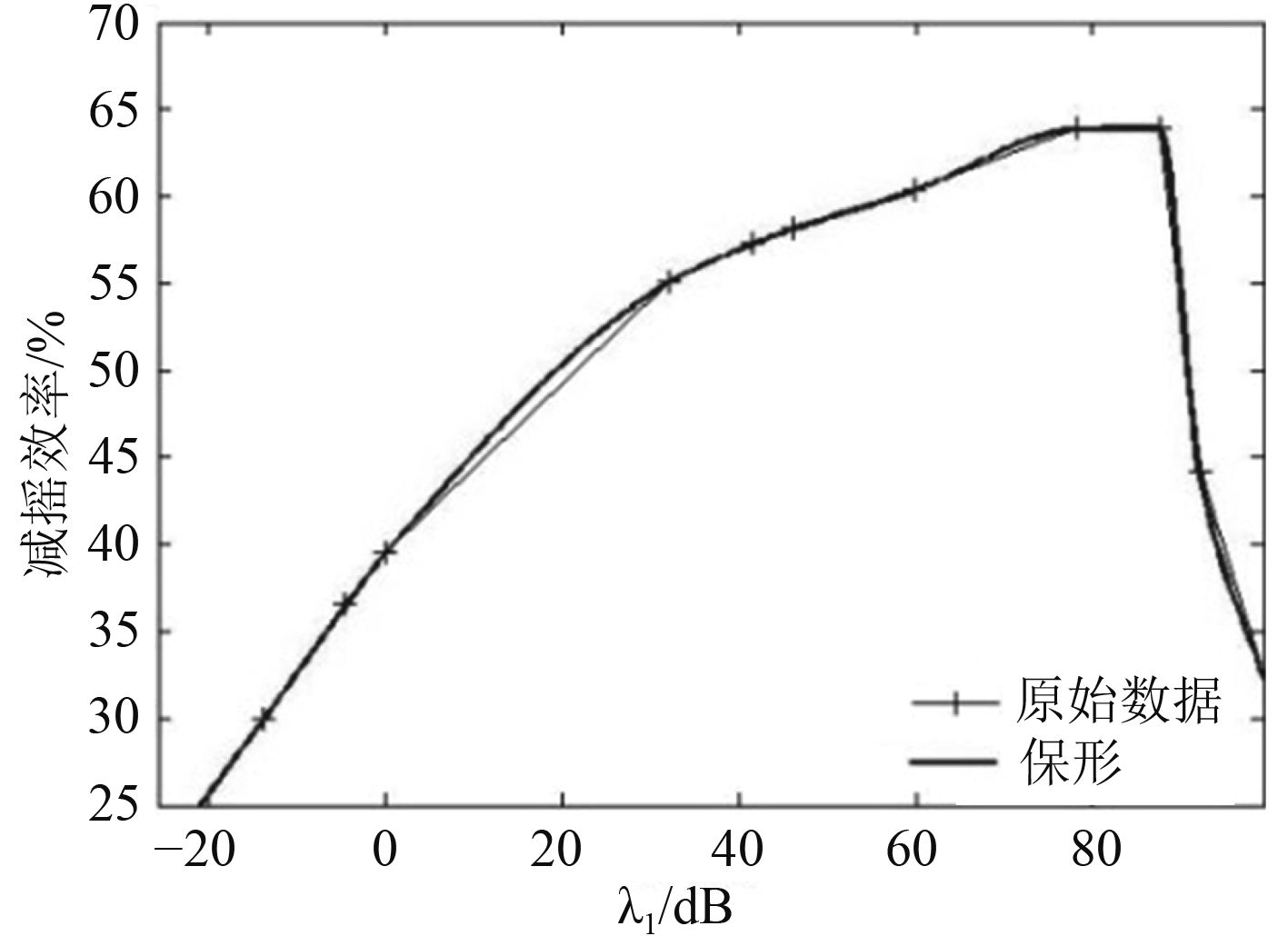
首先，为观察λ_ϕ对控制器性能的影响，令 $ {\lambda _\alpha } = 1,$ ${\lambda _\delta } = 1$ ，则性能指标函数为 $J \!=\! \frac{1}{2}\int_{0}^{\infty } \left[ {\left( {{\psi ^2} \!+\! {\delta ^2}} \right) \!+\! {\lambda _\phi }({\phi ^2} \!+\! {\alpha ^2})} \right]{\rm d}t$ ，对λ_ϕ赋值，得到最优控制律后对控制器进行仿真，控制器减摇效率与 ${\lambda _1}\left( {{\lambda _1} = 20{{\log }_{10}}{\lambda _\phi }} \right)$ 的关系如图2所示，由图可知当 ${\lambda _\phi } = 80$ 时，减摇效率最好；λ_ϕ减小时，减摇效率降低，并λ_ϕ减小到一定值后，反而会加大横摇运动；当λ_ϕ增大时，减摇效率变低，增加到一定值后，也会加大横摇运动。

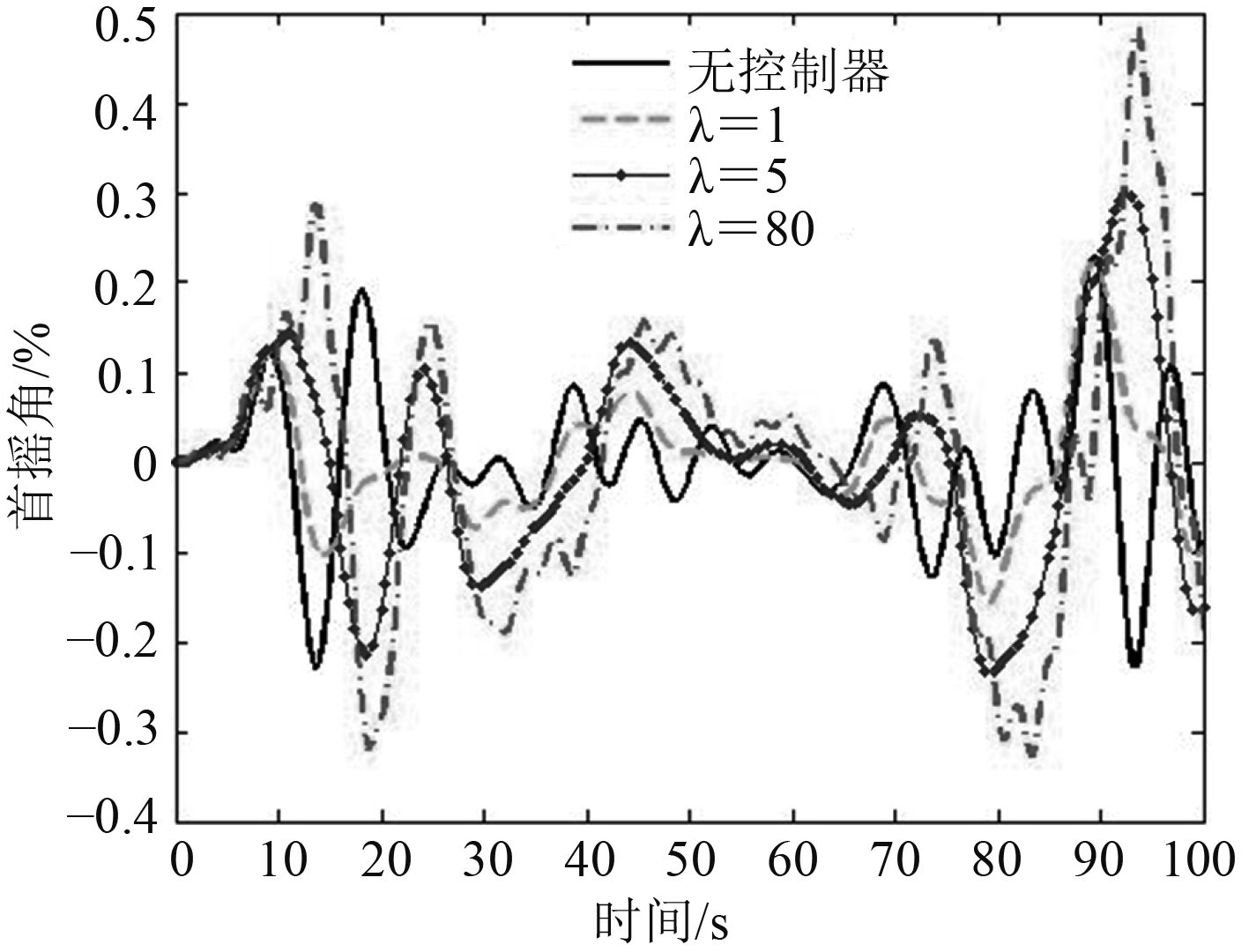
同时，当λ_ϕ变化时，船舶首摇角变化如图3所示，可以看出λ_ϕ增大时，首摇角幅度变大，但总体上对首摇角的影响较小。

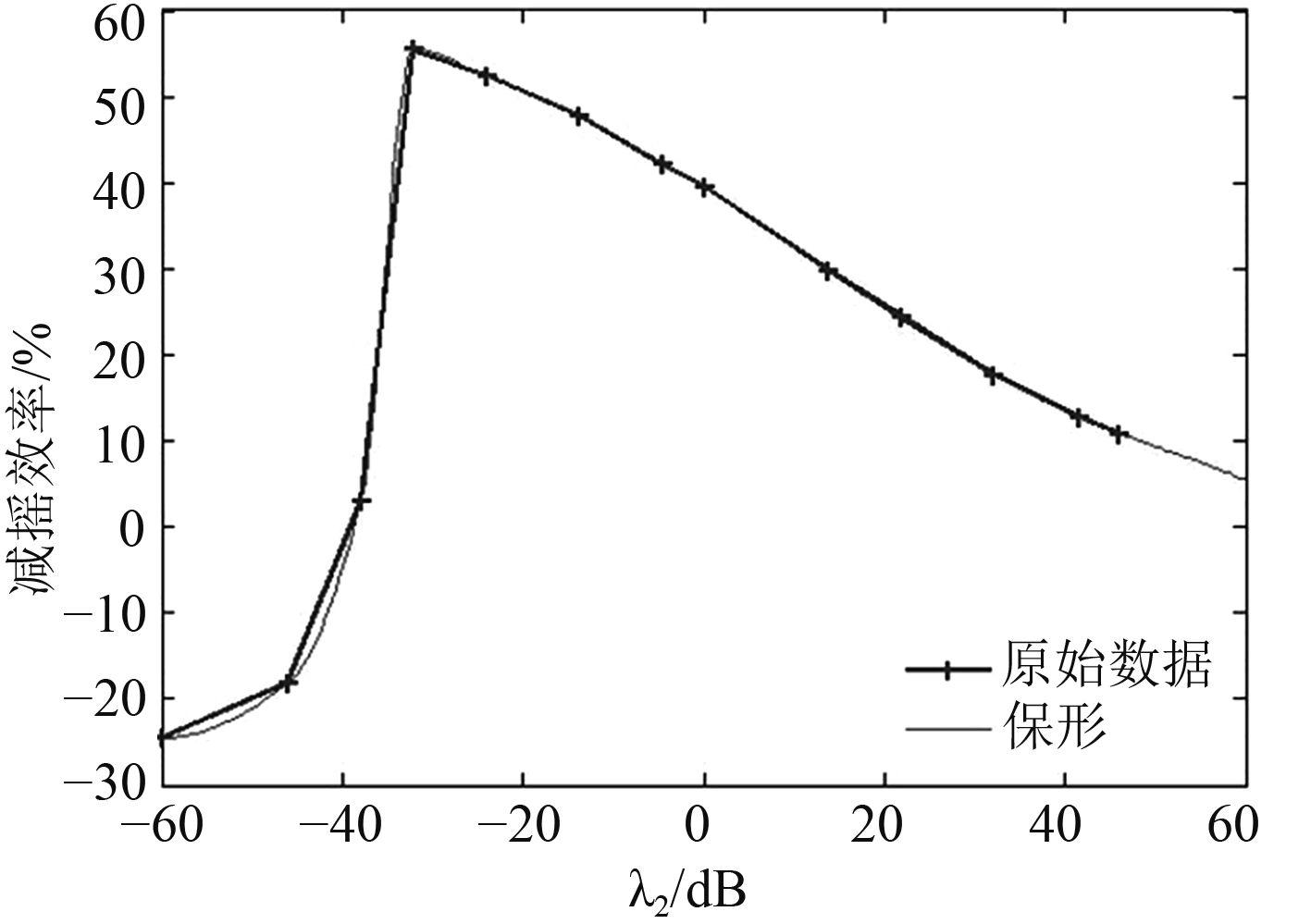
其次，为观察λ_α对控制器性能的影响，令 $ {\lambda _\phi } = 1,$ ${\lambda _\delta } = 1$ ，则性能指标函数为 $J \!=\! \frac{1}{2}\int_{0}^{\infty }\left[ {\left( {{\psi ^2} \!+\! {\delta ^2}} \right) \!+\! ({\phi ^2} \!+\! {\lambda _\alpha }{\alpha ^2})} \right]{\rm d}t$ ，对λ_α赋值，得到最优控制律后对控制器进行仿真，仿真时长t=50 000 s。控制器减摇效率与λ₂（λ₂=20 log₁₀⁡λ_α）的关系如图4所示由图可知当λ_α=0.21时，减摇效率最好；λ_α减小时，减摇效果急剧下降，甚至加大横摇；λ_α增大时，减摇效率逐渐降低。

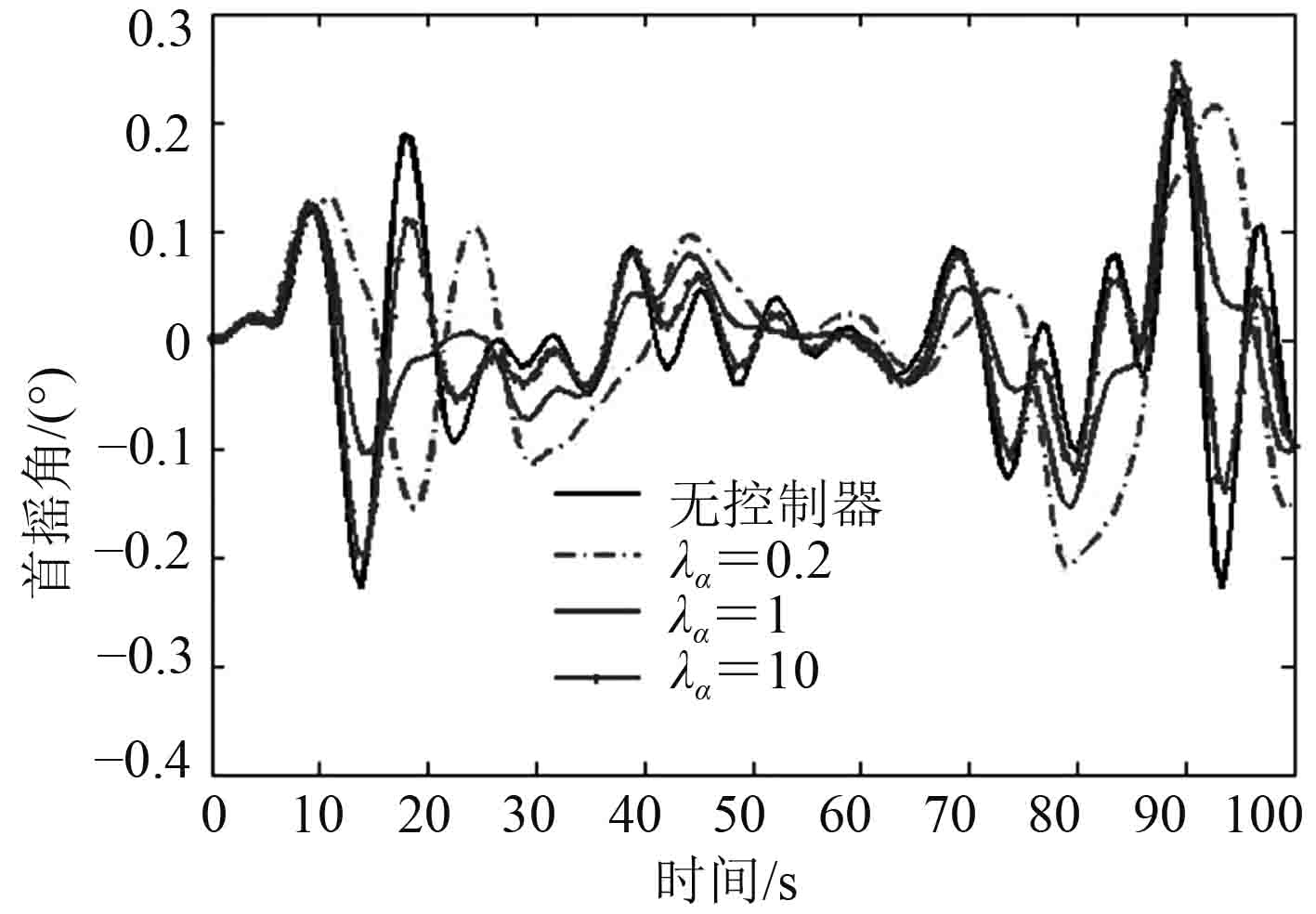
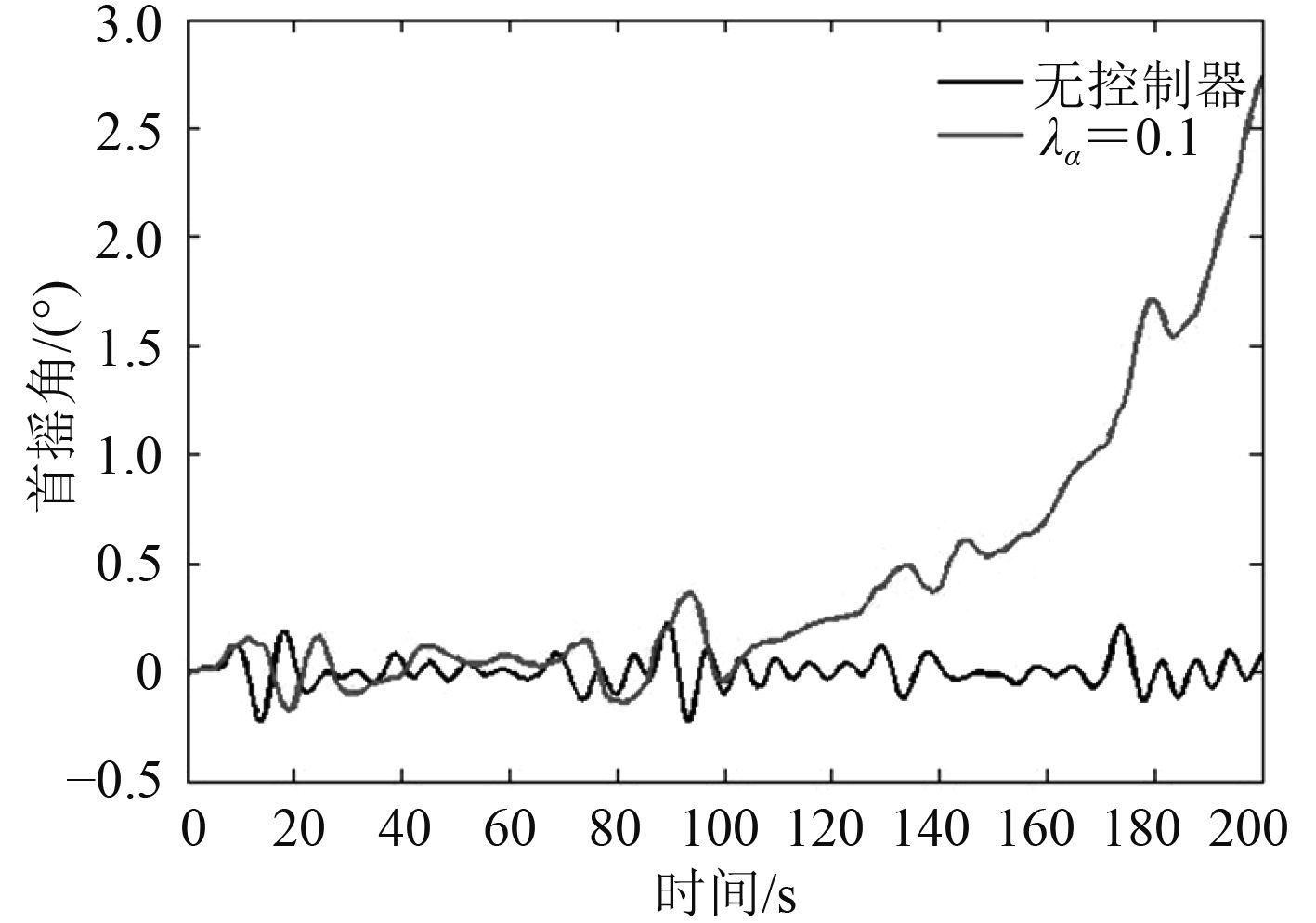
同时，当λ_α变化时，船舶首摇角变化如图5和图6所示，由图5可以看出λ_α减小时，首摇角幅度变大，对首摇角的影响较大；并且当λ_α≤0.20时，由于横摇与横荡之间存在耦合，控制会产生大的横荡速度，进而使船舶横摇运动的加大并造成首摇控制发散。

再者，为观察λ_δ对控制器性能的影响，令 ${\lambda _\phi } = 1, $ ${\lambda _\alpha } =1$ ，则性能指标函数为 $J = \frac{1}{2}\int_{0}^{\infty } \left( {{\psi ^2} + {\lambda _\delta }{\delta ^2}} \right) + ({\phi ^2} + $ ${\alpha ^2}) ]{\rm d}t$ ，对λ_δ赋值，得到最优控制律后对控制器进行仿真,仿真时长t=50 000 s。λ_δ与控制器减摇效率的关系如表1所示，可以看出当λ_δ在3.95～4.20内时，减摇效率最好；λ_δ减小时，减摇效率逐渐降低；λ_δ增大时，无减摇效果，甚至加大横摇运动。

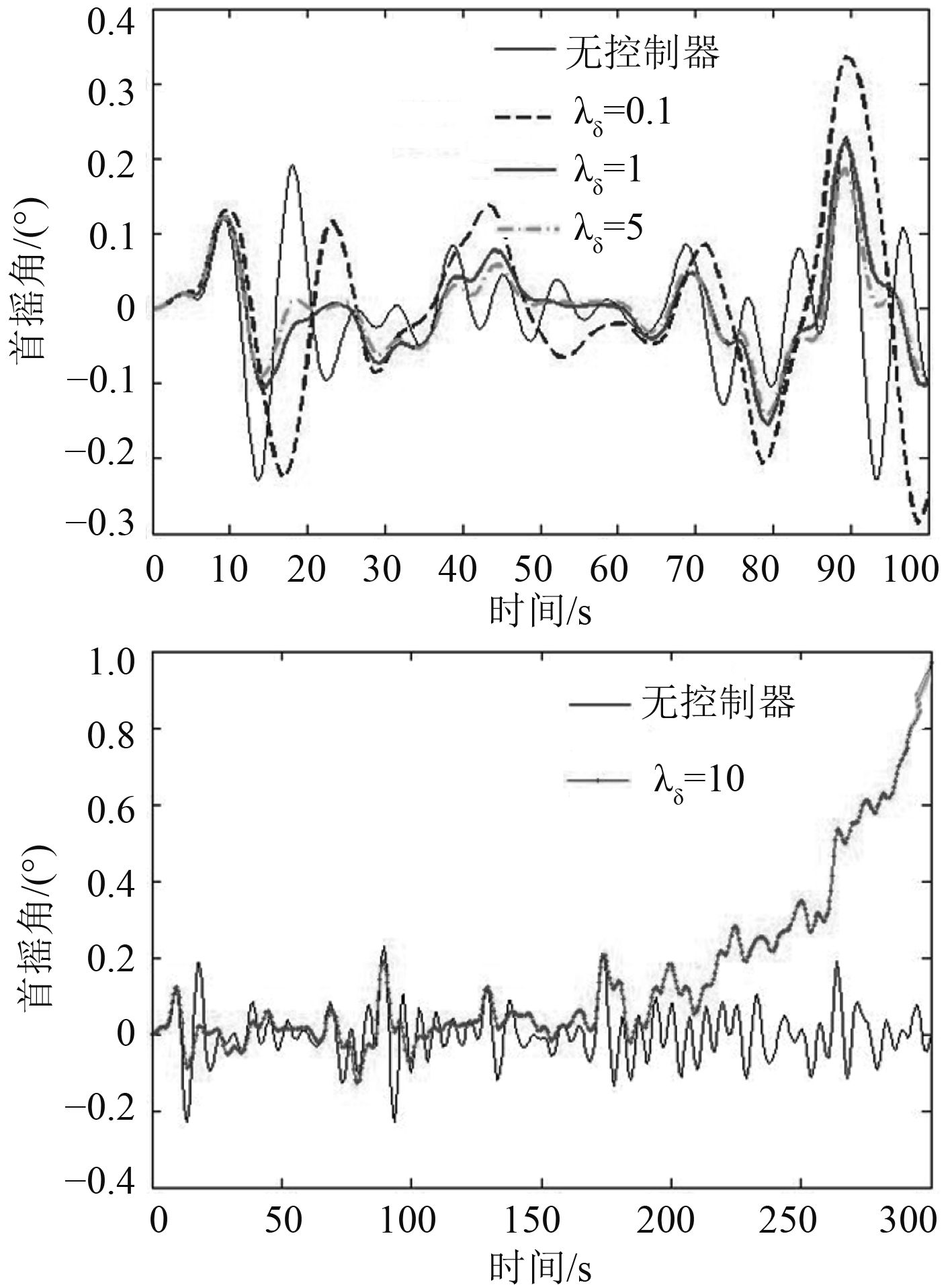
同时，当λ_δ变化时，船舶首摇角变化如图7所示，由于横摇与横荡之间存在耦合，控制会产生大的横荡速度，进而使船舶横摇运动的加大并造成首摇控制发散。

综上所述，权系数λ_ϕ，λ_α，λ_δ对控制器减摇性能的影响为：

1）随着权矩阵参数λ_ϕ的增大，控制器的减摇性能先逐渐提高到最大值而后降低；

2）随着λ_α的减少减摇性能会提高，当减少到一定值时会造成减摇控制系统不稳定。

3）随着λ_δ的增大减摇性能会逐渐提高，当增大到一定值时会造成减摇控制系统不稳定。

为验证上述规律，令性能指标函数 $J = \frac{1}{2}\int_0^\infty {\left[ {({\psi ^2} + } \right.} $ ${\lambda _\delta }{\delta ^2}) + \left. {{\lambda _\phi }({\phi ^2} + {\lambda _\alpha }{\alpha ^2}}) \right]{\rm d}t$ 中的 ${\lambda _\phi }$ =80， ${\lambda _\alpha } = 1.15,{\lambda _\delta } = 1,$ 以此设计得到的最优控制器为

$\begin{split}& {\alpha _c} = - \left( - 5.4462{\rm{*}}\phi - 5.3361{\rm{*}}p \right. + \\& \left. 4.0492{\rm{*}}\psi + 0.2833{\rm{*}}r \right)\text{，}\end{split}$

(13)

$\begin{split}& {\delta _c} = - \left( 1.8166*\phi 2.2427*p \right. + \\& \left. 2.4704*\psi0.9527*r \right)\text{。}\end{split}$

(14)

仿真表明其减摇效率η₁=65.55%，相比 $ {\lambda _\phi } = 1,$ ${\lambda _\alpha } = 1,{\lambda _\delta } = 1$ 得到的控制器减摇效率η=63.89%高1.66个百分点，说明按照所得的规律进行控制器的设计有效。但与此同时首摇角控制精度下降，所以在恶劣海况下对航向要求不高时，可采用此种控制律。

4 结　语

通过对船舶运动的3-DOF的数学模型设计的最优控制器进行仿真，得到了权矩阵参数变化对控制器减摇性能的影响规律，并验证了权矩阵参数对控制器影响规律的有效性。本文只针对美海岸警卫队910级进行仿真，所得到的关于性能指标函数中的 ${{\rm{\lambda }}_\phi },{{\rm{\lambda }}_\alpha },{\lambda _\delta }$ 的变化规律对其他船舶是否适用，这将是下一步研究的重点。