随着船舶向高速化、大型化发展,对螺旋桨的性能要求也越来越高,并且螺旋桨工作在复杂流场中,因此对螺旋桨水动力性能进行准确可靠的预报具有重要意义。随着计算机技术的发展,近20年来计算流体力学方法(CFD)越来越多用在螺旋桨水动力分析上,并且结果可靠性也越来越高[1 – 5]。CFD方法能够克服实验周期长、投入大等缺点,并能分析出螺旋桨各个部位的受力情况,为以后的材料结构性能分析提供参考,这些也是理论方法不具备的优点。目前在螺旋桨水动力方面,多采用多重参考系模型(MRF)来模拟螺旋桨定常水动力性能,其计算精度在一定的进速范围内较高,基本满足研究要求。但是多重参考系模型只能分析螺旋桨定常水动力性能,求解的是螺旋桨周期性转动在某一瞬时的情况,并不能真实模拟螺旋桨的实际转动。为克服这一缺点可采用滑移网格模型(SM)来模拟螺旋桨非定常水动力性能。国内外专家学者针对螺旋桨水动力性能问题做了大量研究。Feneno[6]基于RANS法采用相关软件分别对螺旋桨的定常与非定常水动力性能进行研究,研究结果与实验结果吻合较好,精度较高。Watanabe[7]针对螺旋桨的非定常水动力性能与螺旋桨非定常空泡问题进行研究,得到了较好的仿真结果。Kim[8]基于RANS方程对导管螺旋桨的空泡性能进行分析,并对破裂的球状空泡引起的噪声进行分析,空泡的计算结果与试验值较为吻合。张漫等[9]基于RANS方程的CFD软件对螺旋桨的定常与非定常水动力性能进行计算,结果表明,通过滑移网格技术,计算的螺旋桨非定常水动力性能,相较于定常计算结果更接近试验值。何万国[10]尝试研究用Fluent有限体积方法预测船舶多桨敞水性能的可行性,结果表明此种方法具有较高的计算精度。
首先采用多重参考系(MRF)模型计算螺旋桨的定常水动力性能,得到不同进速下某型螺旋桨的敞水性能曲线、弦向压力分布曲线。以定常水动力性能结果作为初始值并采用滑移网格(SM)模型计算螺旋桨的非定常水动力性能,最后对2种模型所得到的结果进行对比分析,能够较准确预报螺旋桨水动力性能。
1 数学模型 1.1 流体控制方程在研究的螺旋桨流场中假定流体不可压缩,计算中用到质量守恒方程与动量守恒方程分别为:
| $\frac{{\partial {\mu _i}}}{{\partial {x_i}}} = 0, $ | (1) |
| ${\rm{\rho }}\frac{{\partial \left( {{u_i}{u_j}} \right)}}{{\partial {x_j}}} \!=\! - \frac{{\partial p}}{{\partial {x_j}}} \!+\! \rho {g_j} + \rho \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} \!+\! \frac{{\partial {u_j}}}{{\partial {u_i}}}} \right) \!- \!\overline {\mu _i^{'} \mu _j^{'}} } \right]\text{。} $ | (2) |
式中:
根据文献,选用Reliable k-ε模型,其湍动能方程及耗散率运输方程为:
| $\begin{split}&\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\& {G_k} + {G_b} - \rho \varepsilon - {Y_M} , \end{split}$ | (3) |
| $\begin{split}& \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \\& \rho {C_1}E\varepsilon - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }} + {C_{1\varepsilon }}{C_{3\varepsilon }}{C_b}\frac{\varepsilon }{k}\text{。}\end{split}$ | (4) |
式中:
首先将通过坐标转换公式得到的三维坐标点转换为.txt格式然后导入建模软件Solidworks中,用样条曲线拟合各个截面坐标点,采用放样、阵列命令生成桨叶实体,如图1所示,螺旋桨基本参数如表1所示。

|
图 1 螺旋桨实体模型 Fig. 1 Propeller model |
|
|
表 1 螺旋桨主要参数 Tab.1 Main parameters of propeller |
计算螺旋桨水动力性能需要将螺旋桨置于流场中,整个流场域由2部分组成,内部小圆柱体用作旋转域,外部大圆柱体用作静止域,旋转域内边界取在桨叶与桨毂表面;静止域外边界取在大圆柱体表面。静止域内边界与旋转域外边界共用同一个interface(交界面)。
2.2 网格划分及边界条件的设置 2.2.1 网格划分对流场域进行分区网格划分,内部旋转域采用非结构四面体网格,对于流场进口和出口处因其流域变化平缓,所以网格单元可适当增大,使其网格数减少;外部静止域采用结构六面体网格,2个域之间区域采用局部加密[9],如图2所示。

|
图 2 流场网格 Fig. 2 Flow field grid |
进口的边界条件采用速度进口(velocity-inlet),速度进口给定来流速度;出口边界条件采用压力出口(pressure-out),压力值设为0;旋转域命名为rot water,转速设为300 r/min;静止域命名为water;流场域各外围边界设置为壁面(wall),螺旋桨表面设置为无滑移壁面,如图3所示。

|
图 3 流场域边界条件设置 Fig. 3 Flow boundary condition settings |
流场域中存在静止域跟旋转域,可以采用多重参考系模型(MRF)和滑移网格模型(SM)。MRF模型用于螺旋桨定常流计算,计算周期运动的螺旋桨在某一瞬时的运动情况,在使用MRF模型进行计算时,是坐标系在旋转而不是螺旋桨在旋转。SM模型用于螺旋桨非定常计算,螺旋桨是真正在旋转,相比MRF模型,SM模型更能反映螺旋桨的实际运动。
3 螺旋桨水动力性能分析 3.1 螺旋桨定常水动力性能分析为了保证计算结果的准确性,选用SST湍流模型,进速系数J依次取0.3,0.4,0.5,0.6,0.7,计算螺旋桨的推力与转矩,如表2所示。
|
|
表 2 推力T和转矩Q计算结果 Tab.2 Thrust T and torque Q calculation results |
根据推力与转矩计算出螺旋桨的推力系数KT,转矩系数KQ,敞水效率η,与通过武汉理工大学拖曳水池所得到的试验值进行对比如图4所示。
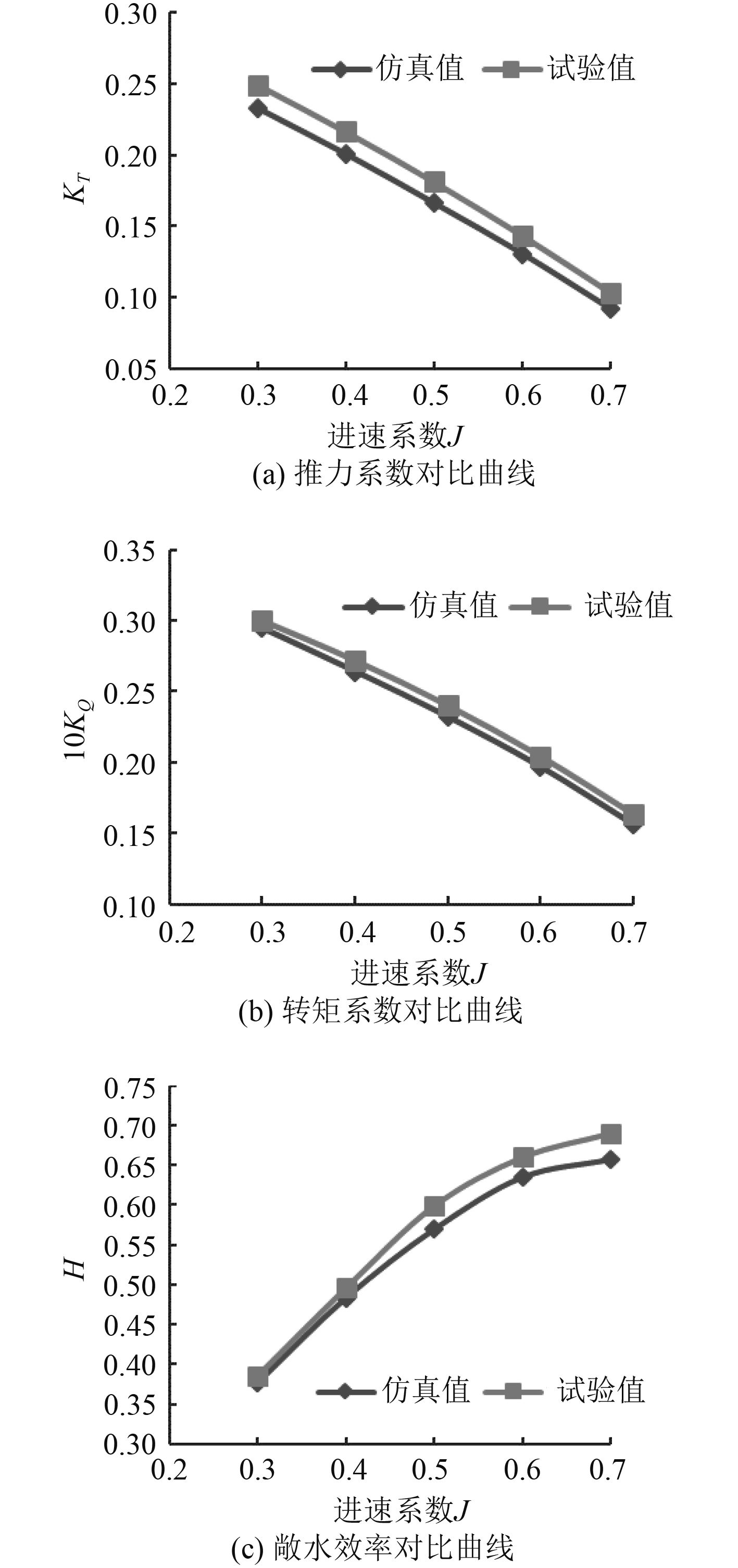
|
图 4 敞水性能对比曲线 Fig. 4 Open water performance comparison curve |
计算得到的推力系数、转矩系数、敞水效率均与试验值吻合较好,计算值均小于理论值,推力系数计算值与试验值之间平均误差为4%。在给定进速范围内,力矩系数计算结果和实验结果非常接近,而且变化趋势也基本一致,两者平均误差在2%以内。敞水效率计算值与试验值变化趋势较为一致,但是随着进速的增加,两者间误差有增大的趋势。
3.2 螺旋桨非定常水动力性能分析首先采用MRF模型,SST湍流模型计算螺旋桨定常水动力性能,并将计算结果作为初始场,然后采用SM模型计算螺旋桨的非定常水动力性能。计算不同进速下螺旋桨的敞水性能。计算结果如表3所示,与试验值的对比曲线如图5所示。
|
|
表 3 螺旋桨敞水性能计算结果 Tab.3 Results of calculation of propeller open water performance |
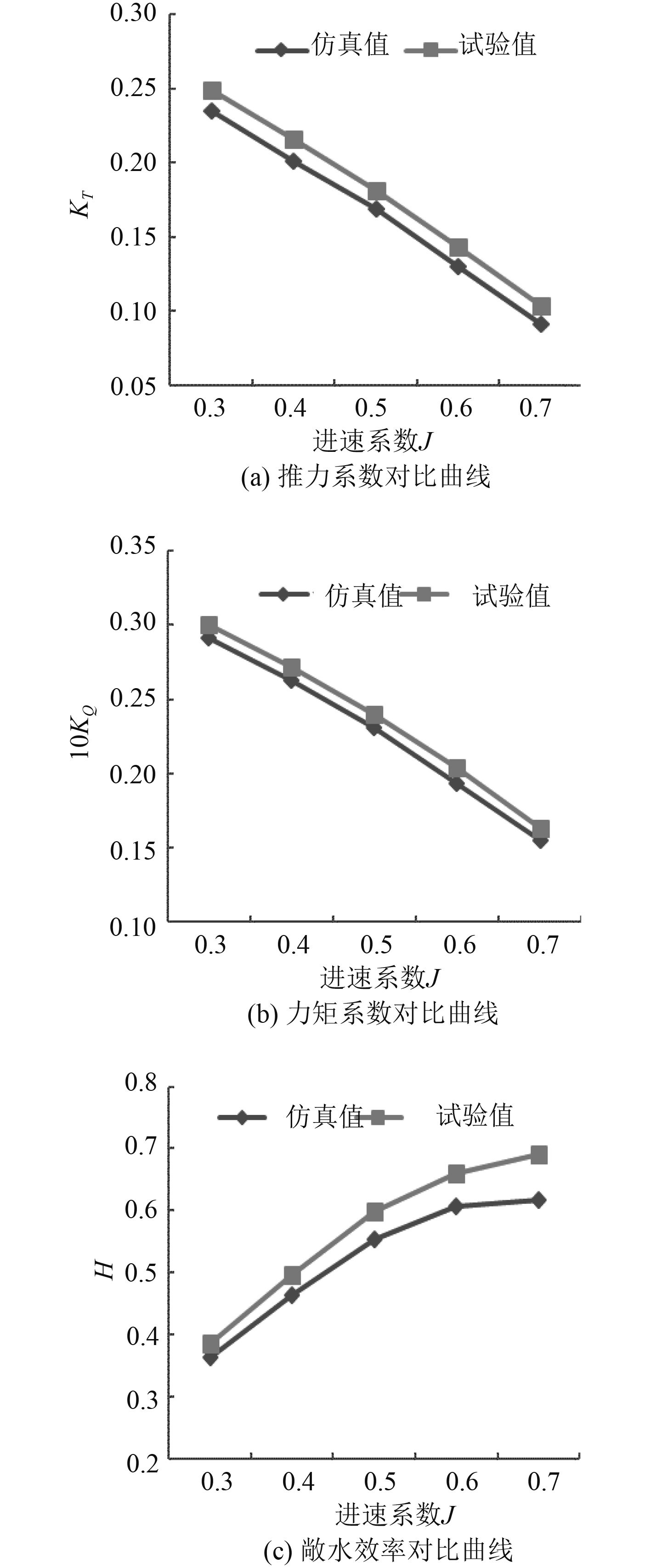
|
图 5 敞水性能对比曲线 Fig. 5 Open water performance comparison curve |
计算结果与试验值的吻合程度较好,推力系数计算值与试验值之间平均误差为3.2%。在给定进速范围内,力矩系数计算结果和实验结果非常接近,而且变化趋势也基本一致,两者平均误差在1.8%以内。在给定的进速范围内,敞水效率计算值与试验值变化趋势较为一致,但是随着进速的增加,两者间误差有增大的趋势。
3.3 不同旋转模型下螺旋桨性能对比分析将MRF模型跟SM模型计算得到的螺旋桨推力系数、转矩系数、敞水效率与试验值进行对比,对比曲线如图6所示。
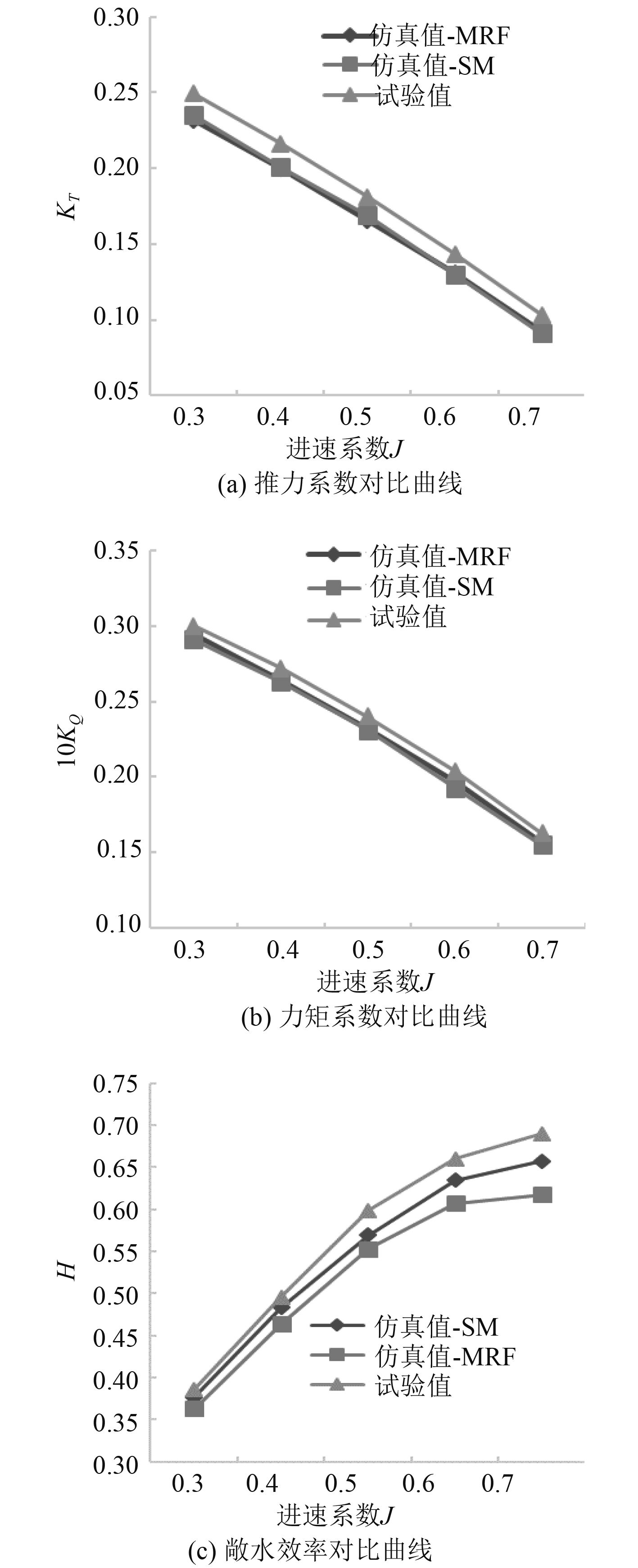
|
图 6 敞水性能对比曲线 Fig. 6 Open water performance comparison curve |
从图6可以观察到不同旋转模型下螺旋桨推力系数、转矩系数和敞水效率在进速系数0.3~0.7范围内与试验值的对比结果。从上述计算结果可以看出,采用SM模型计算的螺旋桨敞水性能曲线相比于MRF模型计算的结果更加接近试验值,采用SM模型使得螺旋桨的推力系数和转矩系数均上升,上升的幅值随着进速系数的增大而逐渐增大;对于敞水效率而言在进速系数0.3~0.7范围内,随着进速的增加,2种模型的计算值与试验值之间的差值越来越大,但SM模型计算的结果差值变化较小。产生这种差别的原因主要是MRF模型产生的旋转只是坐标系的旋转并不是螺旋桨真正的在旋转,计算的仅是周期性旋转在某一瞬时的情况,相当于把非定常的问题当作定常问题来计算;而SM模型模拟的是螺旋桨的真正旋转,是螺旋桨的实际运转情形。
3.4 螺旋桨表面压力情况分布保持螺旋桨转速不变,以进速系数J=0.4时为例,r/R=0.3,0.7,0.9半径处叶切面的弦向压力分布情况如图7所示,对应的压力云图如图8所示。
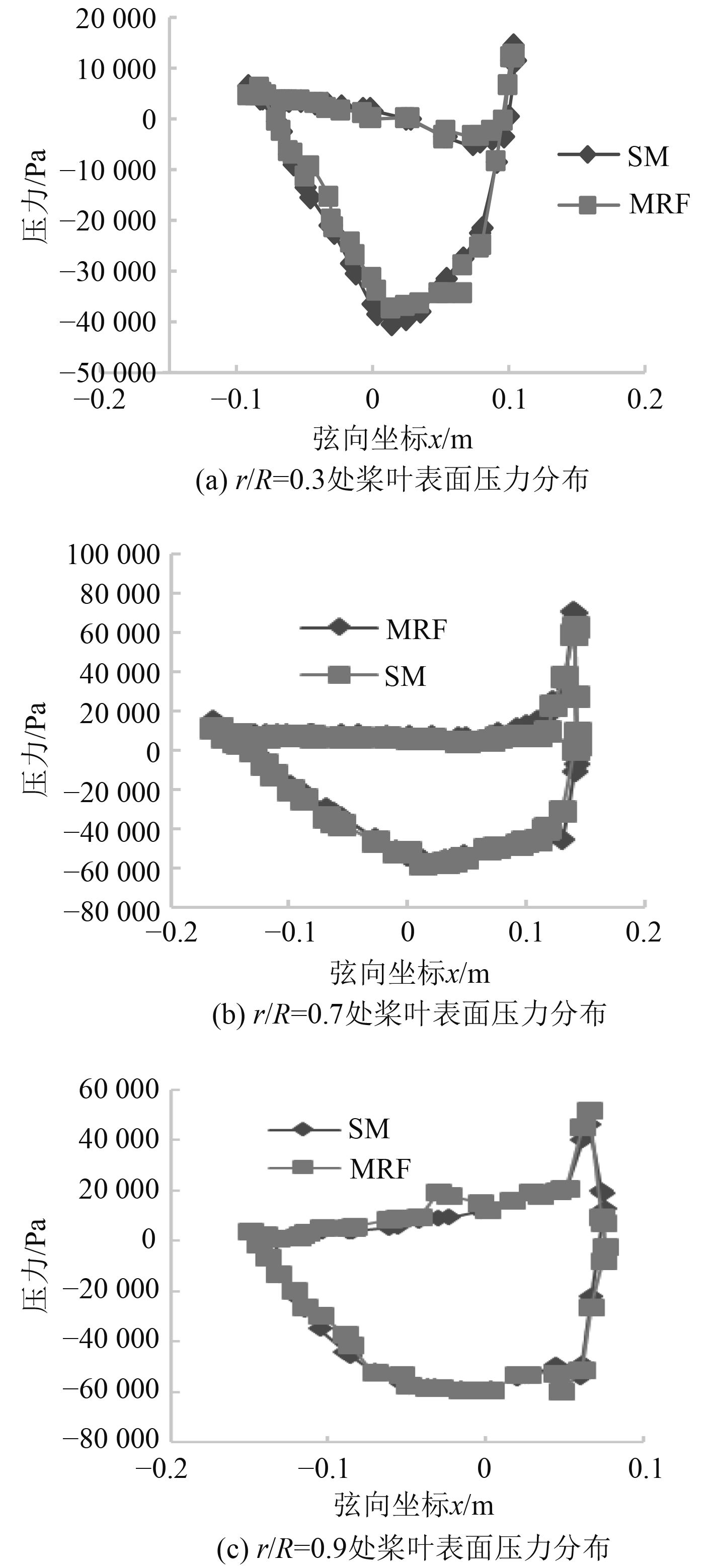
|
图 7 叶切面弦向压力分布曲线 Fig. 7 Tangential pressure distribution curve at leaf section |

|
图 8 桨叶压力分布云图 Fig. 8 Nephogram of blade pressure distribution |
图7给出了通过2种方法所得到的压力分布曲线。通过对2种方法计算结果的对比可以看出,2种方法中叶面处压力分布一致性高于叶背,随着弦向坐标值的增大,叶面处压力分布一致性较好,但是叶背处压力分布偏差有增大的趋势。0.7R处2种方法所得压力分布结果吻合性最好,0.9R次之,在0.3R处偏差最大。
通过图8可以看到采用2种方法桨叶压力分布情况。2种方法中,叶面处高压均处在导边靠近叶梢位置,叶背处负压也处在导边靠近叶梢位置,叶面处导边附近压力高于随边,叶背处导边附近压力低于随边。
4 结 语1)采用结构网格与非结构网格相混合的网格划分方式相比单一网格划分方式更加适合螺旋桨流场域,既能保证结果精度又可以减少网格数量加快计算速度。
2)将通过MRF模型计算的螺旋桨定常水动力性能结果作为初始场,然后采用SM模型计算非定常水动力性能,与定常计算结果相比更加接近试验值。表明采用SM模型更加符合螺旋桨的实际运行情况。
3)对进速系数J=0.4时桨叶表面压力分布情况进行分析,为以后螺旋桨的噪声、振动研究提供依据。
| [1] | 董世汤, 等. 船舶推进器水动力学[M]. 北京: 国防工业出版社, 2009. |
| [2] | 赖华威, 刘月琴, 吴家鸣. 基于CFD方法的螺旋桨性能计算与分析[J]. 船海工程, 2009(4): 131–135. http://www.doc88.com/p-9873795635469.html |
| [3] | CARLTON J S. Marine propellers and propulsion[J]. Marine Propellers & Propulsion, 2012. |
| [4] | 高富东, 潘存云, 蔡汶珊, 等. 基于CFD的螺旋桨敞水性能数值分析与验证[J]. 机械工程学报, 2010, 46(8): 133–139. http://www.cqvip.com/QK/90288X/201008/33626278.html |
| [5] | 王超, 黄胜, 解学参. 基于CFD方法的螺旋桨水动力性能预报[J]. 海军工程大学学报, 2008, 20(4): 107–112. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hjgcdxxb200804023 |
| [6] | FUNENO I. Analysis of unsteady viscous flows around a highly skewed propeller[J]. Journal of the Kansai Society of Naval Architects Japan, 2002(237): 39–45. |
| [7] | WATANADE T, KAWAMURA T, TAKEKOSHI T. Simulation of steady and unsteady cavitation on a marine propeller using a RANS CFD code[C]// Proceedings of 5th International Symposium on Cavitation, Osaka, Japan: CAV2003, 2003. |
| [8] | KIM S E, RHEE S. Toward high-fidelity prediction of tip-vortex around lifting surfaces[C]// Proceedings of the 25th Symposium on Naval Hydrodynamics, St. John, Canada, 2004. |
| [9] | 张漫, 黎胜. 基于滑移网格技术计算螺旋桨水动力性能研究[J]. 船海工程, 2013, 42(5): 25–29. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=whzc201305006 |
| [10] | 何万国. 船舶螺旋桨敞水性能仿真计算分析[J]. 船舶工程, 2014(s1): 48–51. |
 2018, Vol. 40
2018, Vol. 40
