为了防御鱼雷接触爆炸对大型舰船内部重要舱室造成破坏,在大型舰船水下舷侧设有多舱防护结构,其中防护液舱是防御鱼雷爆炸形成的高速破片的重要结构。大型舰船水下舷侧防护结构遭受鱼雷接触爆炸后,在舷侧外板上首先形成直径与鱼雷直径相当的剪切冲塞破片,此破片往舷侧空舱内部高速运动,直至撞击液舱前板。液舱前板在高速破片的撞击下发生剪切冲塞破坏,舷侧外板和液舱前板的冲塞破片以相同入水速度在液舱中运动,在水中形成冲击波,液舱后板在冲击波作用下发生大变形[1]。如果防护液舱结构设计不合理,那么液舱后板轻则变形过大,重则被破片击穿。为了更好地设计防护液舱结构,弄清楚高速破片侵彻防护液舱过程中液舱后板的载荷特性具有重要意义。
国内外研究人员对不同工程背景下弹体或高速破片与液舱的相互作用问题进行了系列研究。国外研究主要针对弹体与航天器燃料舱的相互作用[2 – 6];国内研究主要针对高速破片与大型舰船防护液舱的相互作用[7 – 11],侧重于高速破片在液体中运动时产生的冲击波、压力、气穴、破片速度衰减特性及防护液舱的变形破坏等问题。尽管如此,高速破片侵彻防护液舱过程中液舱后板的载荷特性尚未研究清楚,因此本文对此进行数值仿真研究,旨在为更好地设计防护液舱结构提供参考。
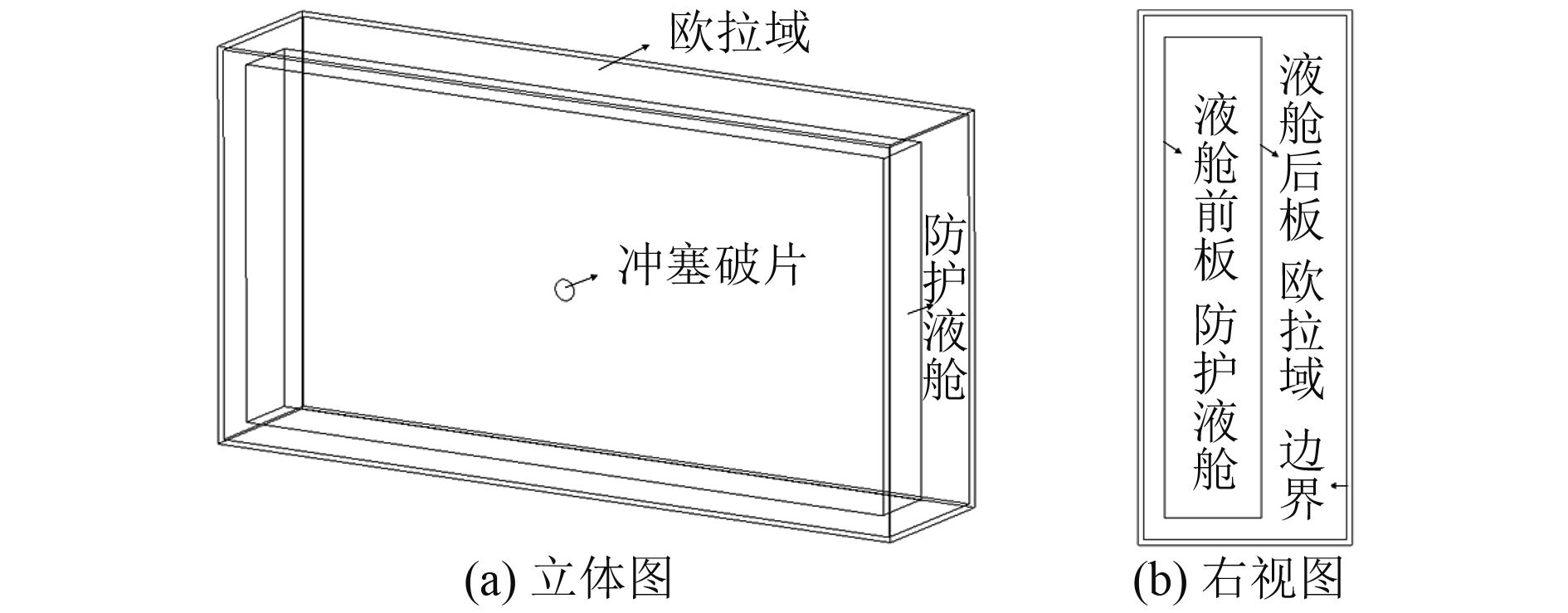
1 有限元数值计算 1.1 有限元模型为了研究高速破片侵彻防护液舱过程中液舱后板的载荷特性,利用LS_DYNA软件,建立如图1所示的有限元模型。
防护液舱的尺寸为18 m×1.8 m×9 m,采用Lagrange壳单元;欧拉域的尺寸为19 m×4 m×10 m,采用Euler单元。有限元网格的划分在中间较密、在四周较疏,Lagrange壳单元的边长约为60~300 mm,Euler单元的边长约为100~300 mm。液舱前板厚14 mm,液舱后板厚36 mm,液舱上下左右的板厚12 mm。防护液舱内为80%的水和20%的空气,防护液舱外为空气。欧拉域边界是1层厚0.1 m的环境单元,其内部压力恒为1.01×105 Pa。
考虑到液舱前板在产自舷侧外板的高速破片撞击下的剪切冲塞过程较难模拟,为便于研究,不考虑液舱前板的剪切冲塞过程,而是直接在液舱前板中央开挖一个直径为533 mm(MK48鱼雷直径)的圆孔,并在此处放置一个直径同为533 mm的圆形破片,此破片的厚度是舷侧外板和液舱前板的厚度之和,在不同工况下破片的速度和厚度见表1。
采用ALE算法模拟空气、水和破片及防护液舱之间的流固耦合作用,采用自动单面接触算法模拟高速破片与液舱后板之间可能的接触作用。
|
图 1 有限元模型 Fig. 1 Finite element model |
此有限元模型涉及空气、水和钢这3种材料。
空气的初始密度为ρ0=1.28 kg/m3,采用Linear_polynomial状态方程,即
| $p = {C_0} + {C_1}\mu + {C_2}{\mu ^2} + {C_3}{\mu ^3} + ({C_4} + {C_5}\mu + {C_6}{\mu ^2})E\text{。}$ | (1) |
式中:p为压力;μ=ρ/ρ0-1,ρ为密度;E为单位体积内能;C0,C1,C2,C3,C4,C5,C6均为常数。各参数取值[12]为:C1=C2=C3=C6=0,C4=C5=0.4,E=0.252 5 MPa。
水的初始密度ρ0=1 000 kg/m3,采用Gruneisen状态方程,即
| $p \!=\! \frac{{{\rho _0}{C^2}\mu \left[ {1 \!+\! \left( {1 \!-\! \frac{{{\gamma _0}}}{2}} \right)\mu \!-\! \frac{\alpha }{2}{\mu ^2}} \right]}}{{{{\left[ {1 \!-\! \left( {{S_1} \!-\! 1} \right)\mu \!-\! {S_2}\frac{{{\mu ^2}}}{{\mu \!+\! 1}} \!-\! {S_3}\frac{{{\mu ^3}}}{{{{\left( {\mu \!+\! 1} \right)}^2}}}} \right]}^2}}} \!+\! \left( {{\gamma _0} \!+\! \alpha \mu } \right)E\text{。}$ | (2) |
式中:p为压力;C为声速;μ=ρ/ρ0-1,ρ为密度;E为单位体积内能;S1,S2,S3,γ0,α均为常数。各参数取值[12]为:C=1 484 m/s,S1=1.979,S2=S3=0,γ0=0.11,α=3,E=0。
高速破片和防护液舱采用钢材,密度为7 800 kg/m3,采用双线性弹塑性本构模型和最大塑性应变失效模型,材料的应变率效应由Cowper-Symonds模型描述,动态屈服强度
| ${\sigma _d} = \left( {{\sigma _0} + \frac{{E{E_h}{\varepsilon _p}}}{{E - {E_h}}}} \right)\left[ {1 + {{\left( {\frac{{\dot \varepsilon }}{D}} \right)}^{\frac{1}{n}}}} \right]\text{。}$ | (3) |
式中:σ0为屈服应力;E为杨氏模量;Eh为硬化模量;εp为等效塑性应变;
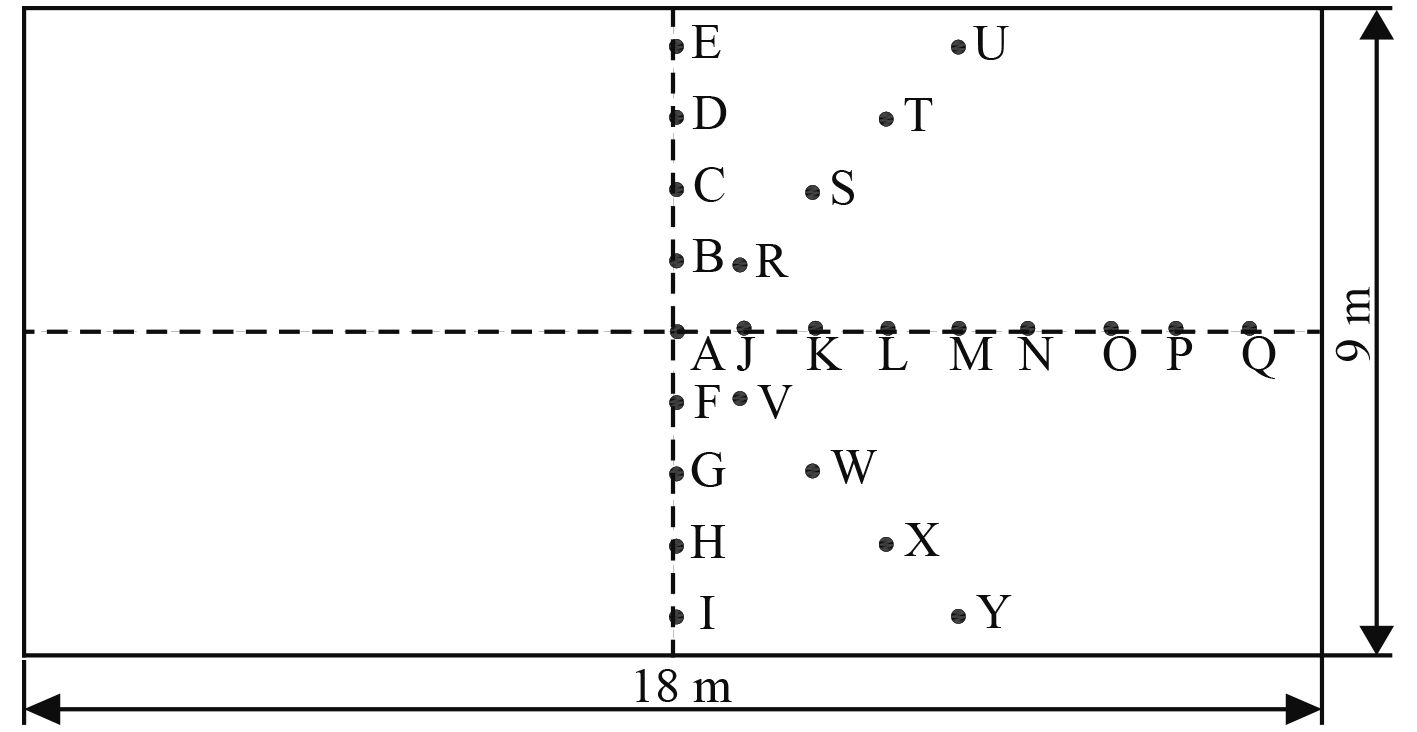
在防护液舱后板上选取如图2所示的25个典型单元作为压力测点,以研究防护液舱后板的载荷传播及衰减特性。
|
图 2 液舱后板的压力测点 Fig. 2 The points on back plate of water cabin for outputting pressure |
计算工况如表1所示。工况1~工况5的破片厚度δ=30 mm,破片速度v在1 000~1 400 m/s范围内变化,以研究破片速度v对防护液舱后板载荷特性的影响。工况1及工况6~工况9的破片速度v=1 200 m/s,破片厚度δ在26~34 mm范围内变化,以研究破片厚度δ对防护液舱后板载荷特性的影响。
|
|
表 1 计算工况 Tab.1 The calculation cases |
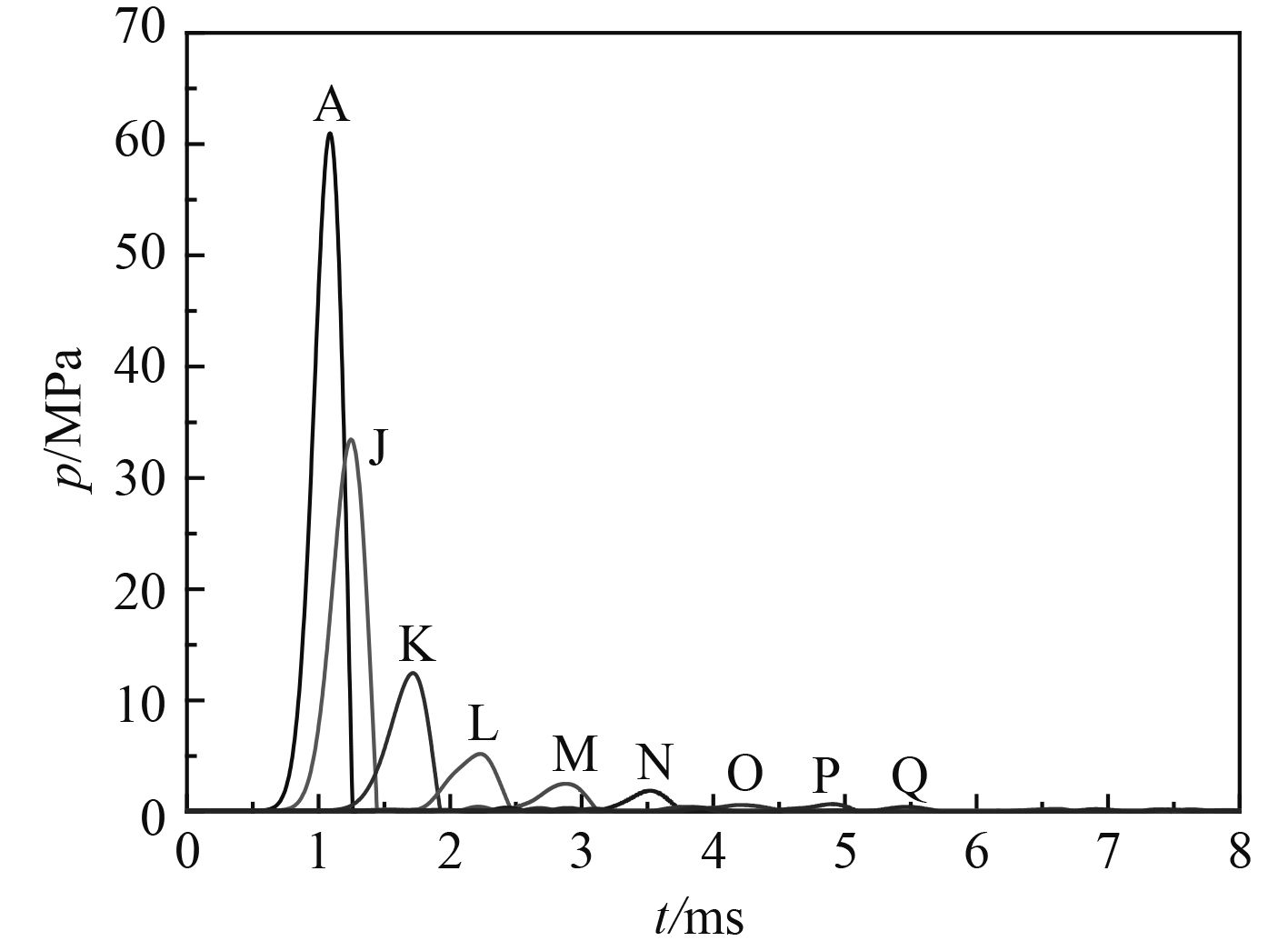
在工况1下,测点A,J~Q(沿液舱后板的长对称轴分布)的压力时程曲线如图3所示,各测点的压力峰值pmax和比冲量i与测点到液舱后板中心距离r的关系分别如图4和图5所示。
|
图 3 工况1下测点A,J~Q的压力曲线 Fig. 3 The pressure curves of points A and J~Q in case 1 |
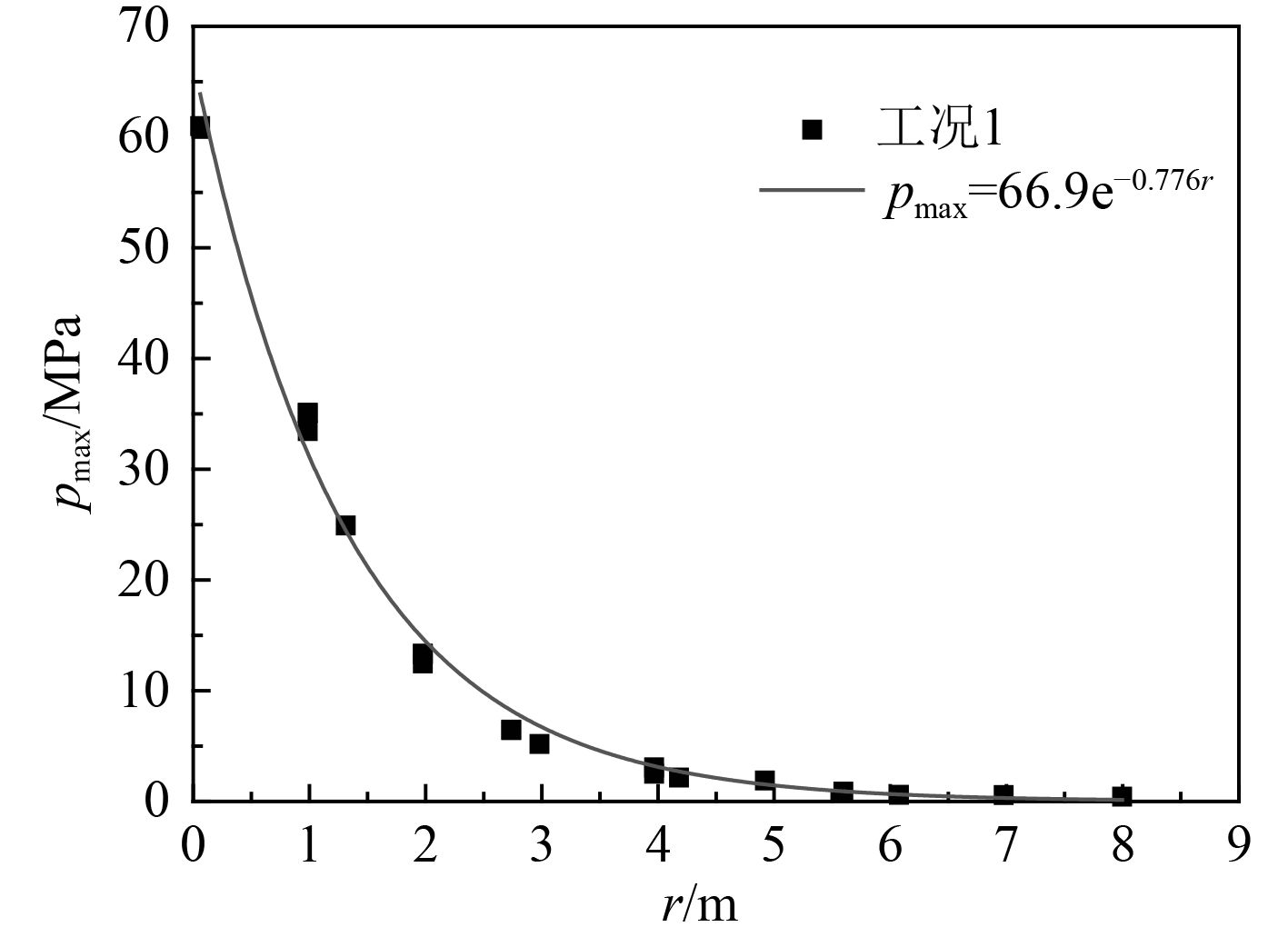
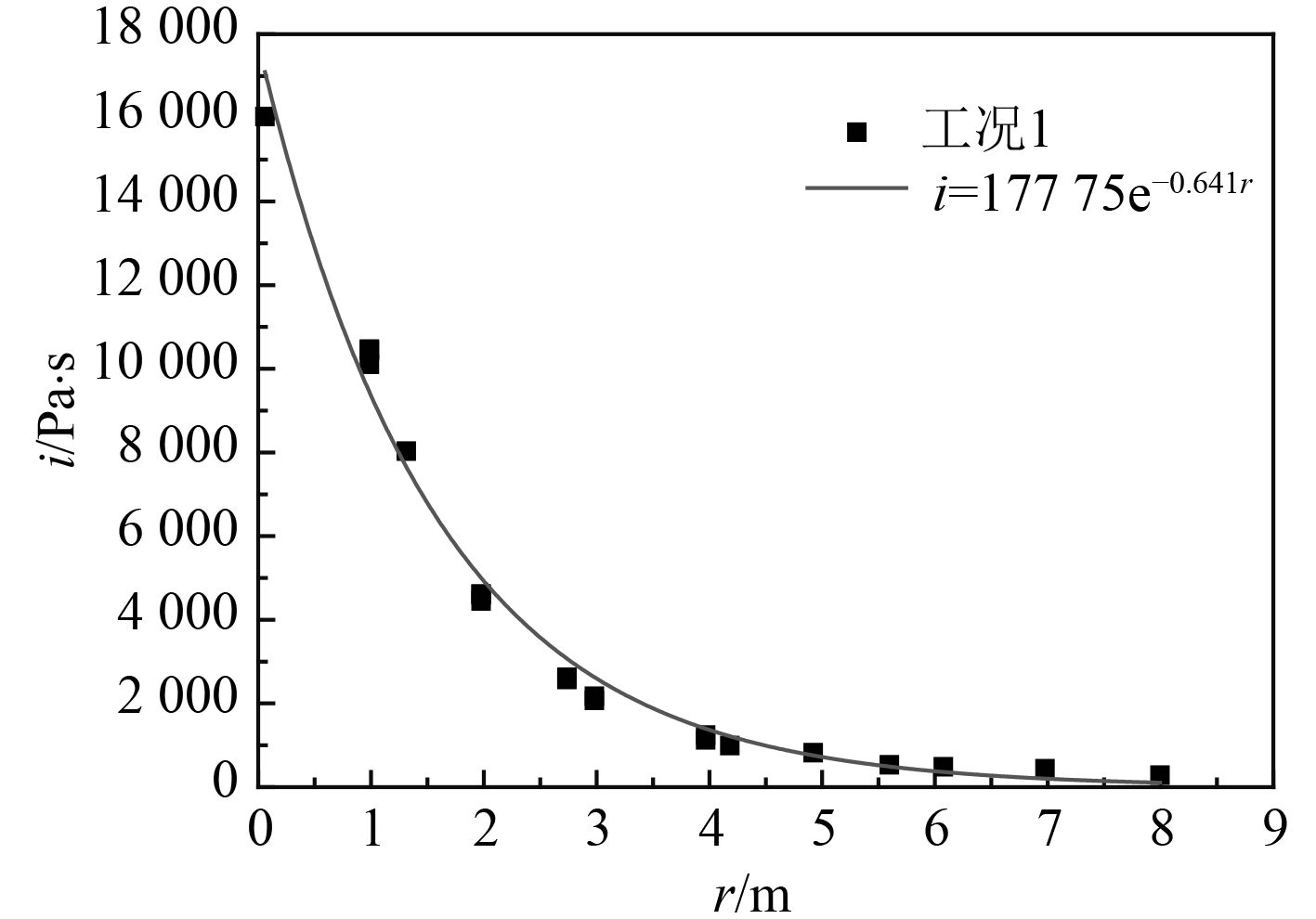
由图3可见,在工况1下,测点A的压力峰值最大,约为61 MPa;随着测点到液舱后板中心的距离r增加,测点的压力峰值逐渐衰减。在以液舱后板中心为起点的其他射线方向上,液舱后板的载荷呈现出类似图3的传播和衰减特性,到液舱后板中心距离相同的几个测点的压力曲线基本重合。由图4和图5可见,在工况1下,各测点的压力峰值pmax和比冲量i随测点到液舱后板中心距离r变化的趋势线呈指数函数形式,经拟合,pmax=66.9E–0.776r MPa,i=17 775E–0.641r Pa·s,其中r以m为单位。
|
图 4 工况1下各测点的压力峰值 Fig. 4 The peak pressure of different points in case 1 |
|
图 5 工况1下各测点的比冲量 Fig. 5 The specific impulse of different points in case 1 |
各测点的压力峰值pmax和比冲量i随测点到液舱后板中心距离r变化的趋势线可取为pmax=K1·eαr和i=K2·eβr形式,其中,pmax,i和r分别以MPa,Pa·s和m为单位。
在各工况下,K1和α值如表2所示,K2和β值如表3所示。由表2和表3可见,破片厚度δ和速度v对K1和K2有显著影响,而对α和β的影响可以忽略不计,α和β的平均值分别为–0.767和–0.641。
|
|
表 2 各工况下趋势线pmax=K1·eαr的K1和α值 Tab.2 The K1 and α values of trend line pmax=K1·eαr in different cases |
|
|
表 3 各工况下趋势线i=K2·eβr的K2和β值 Tab.3 The K2 and β values of trend line i=K2·eβr in different cases |
|
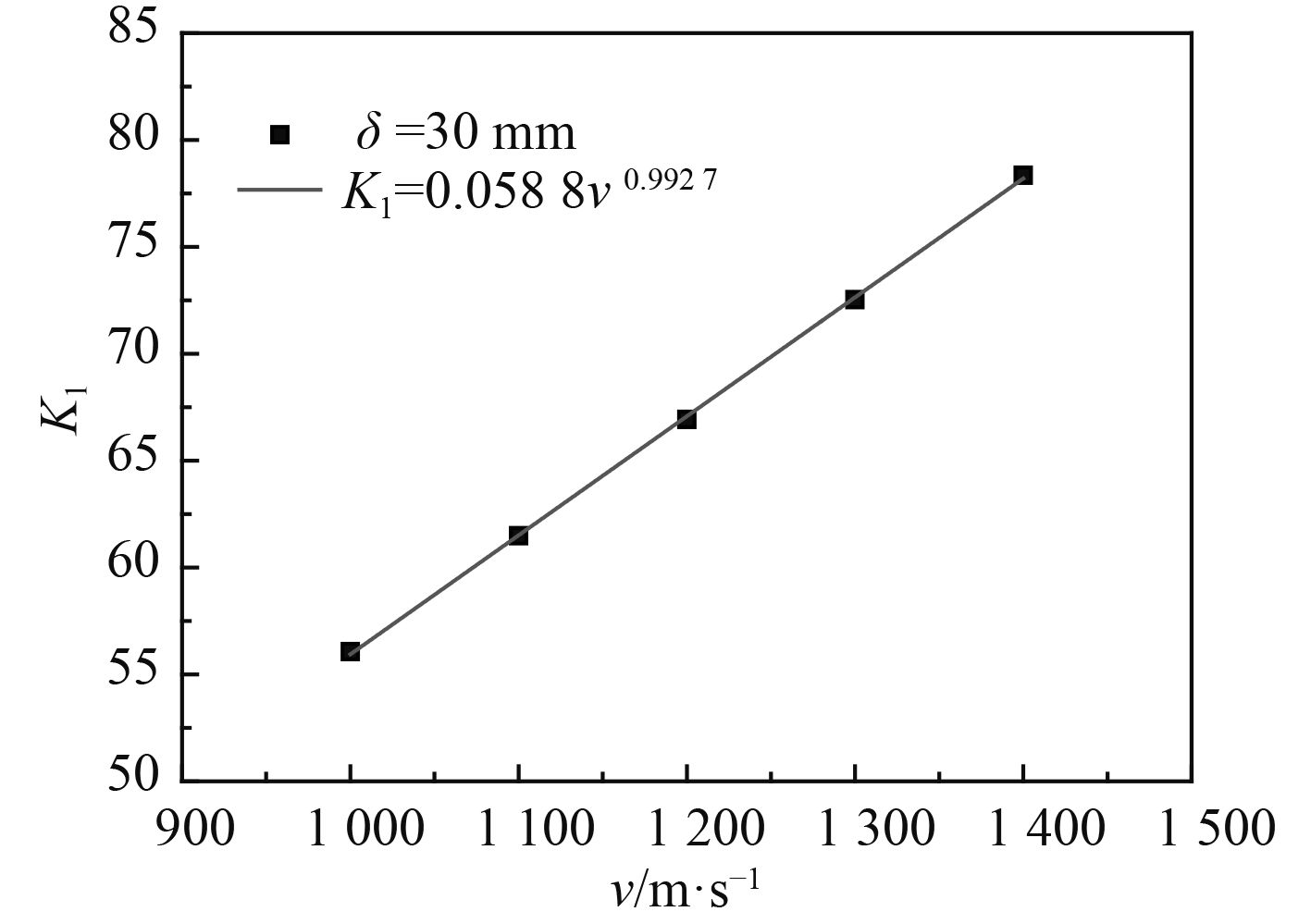
图 6 K1与v的关系 Fig. 6 The relation of K1 and v |
|
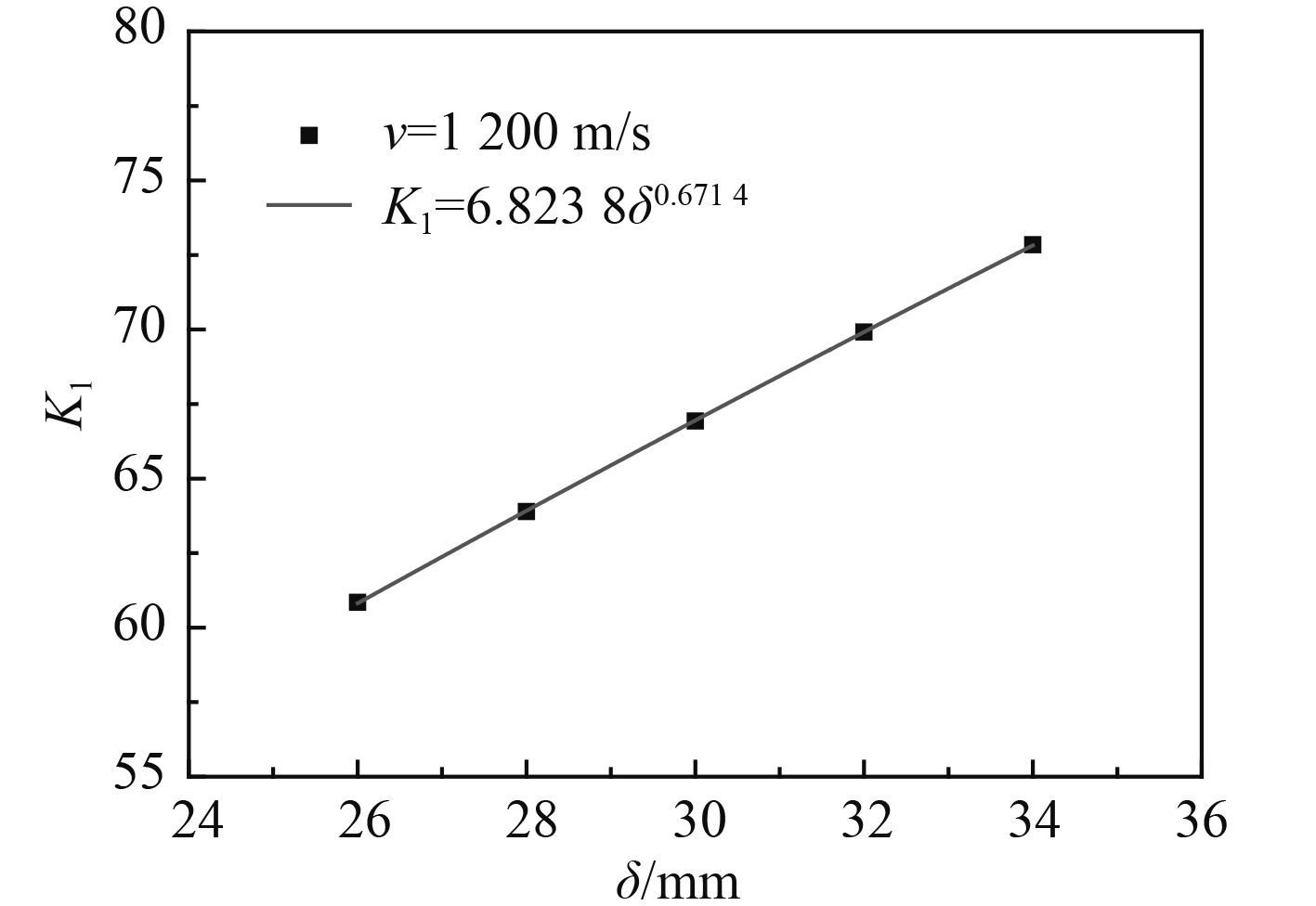
图 7 K1与δ的关系 Fig. 7 The relation of K1 and δ |
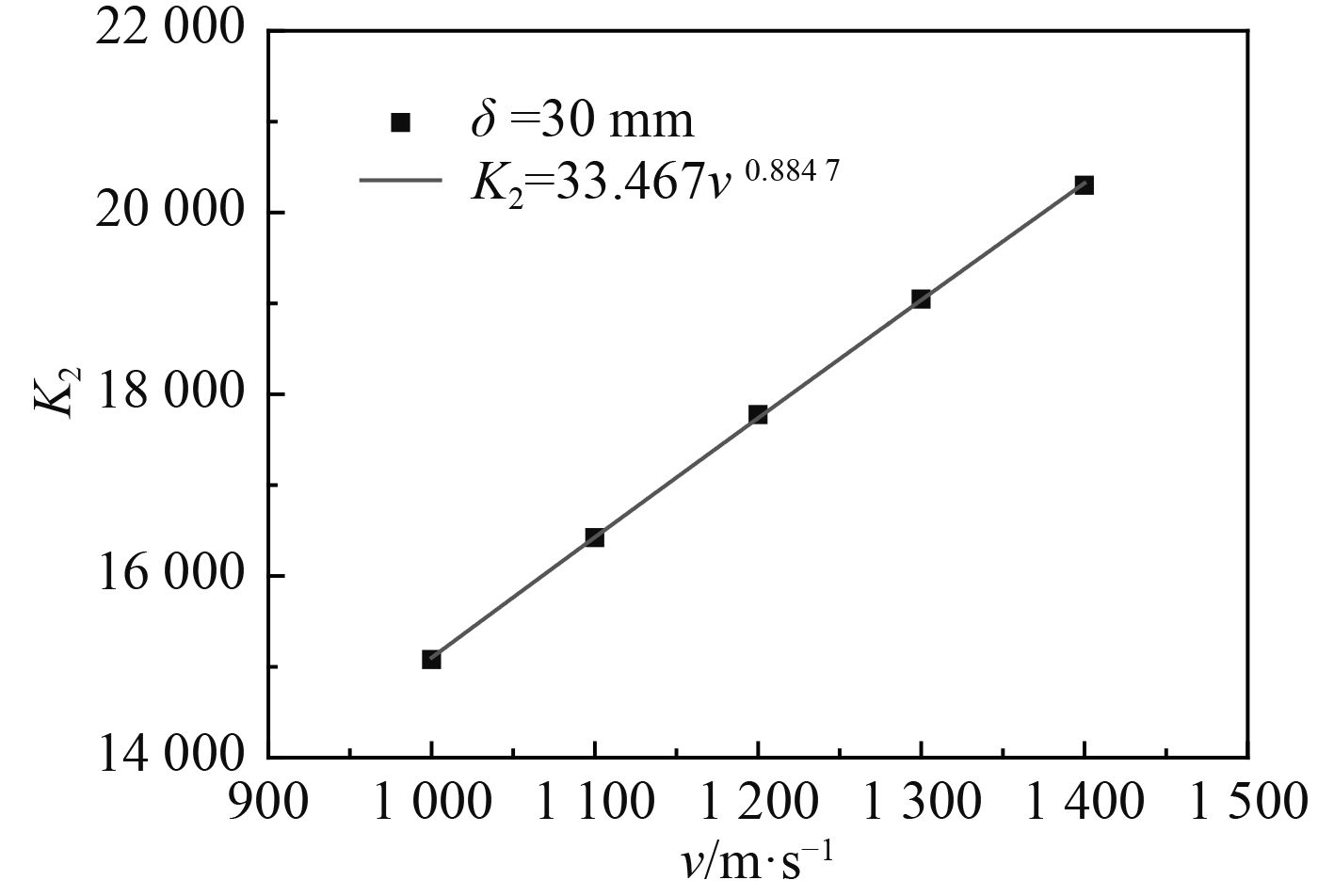
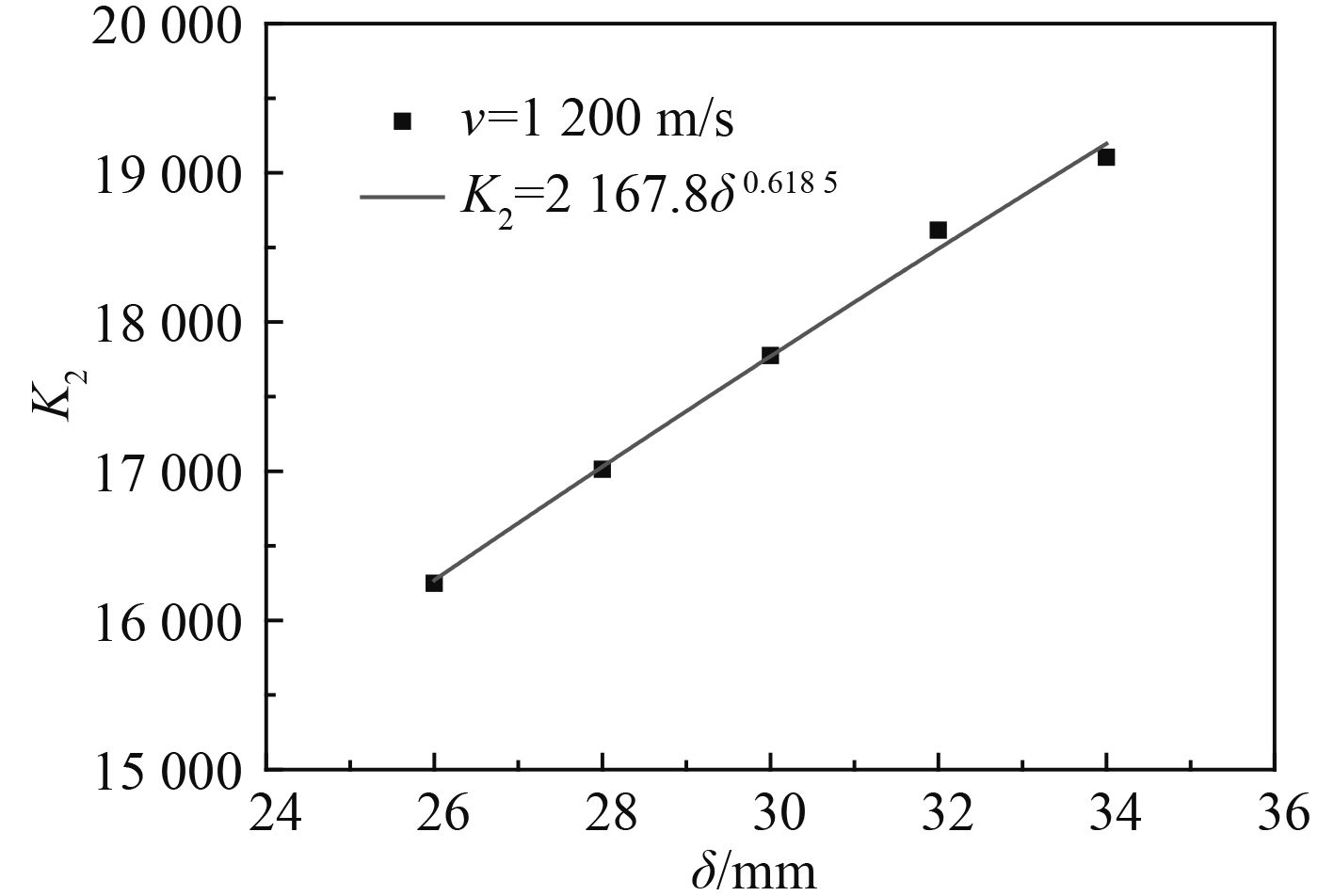
由图6和图8可见,当破片厚度δ不变时,K1和K2均随着破片速度v增加而增加。由图7和图9可见,当破片速度v不变时,K1和K2均随着破片厚度δ增加而增加。当δ=30 mm时,K1和K2与v(以m/s为单位)的拟合关系式分别为K1=0.058 8v0.992 7和K2=33.467v0.884 7。当v=1 200 m/s时,K1和K2与δ(以mm为单位)的拟合关系式分别为K1=6.823 8δ0.671 4和K2=2 167.8δ0.618 5。
|
图 8 K2与v的关系 Fig. 8 The relation of K2 and v |
|
图 9 K2与δ的关系 Fig. 9 The relation of K2 and δ |
基于上述分析,可以将液舱后板上任一点处的压力峰值pmax(以MPa为单位)和比冲量i(以Pa·s为单位)拟合成式(4)和式(5),即
| ${p_{\max }} = 0.006 \cdot {v^{0.9927}} \cdot {\delta ^{0.6714}} \cdot {e^{ - 0.767r}}\text{,}$ | (4) |
| $i = 4.088 \cdot {v^{0.8847}} \cdot {\delta ^{0.6185}} \cdot {e^{ - 0.641r}}\text{。}$ | (5) |
式中:v为破片速度,m/s;δ为破片厚度,mm;r为液舱后板上任一点到其中心点的距离,m。
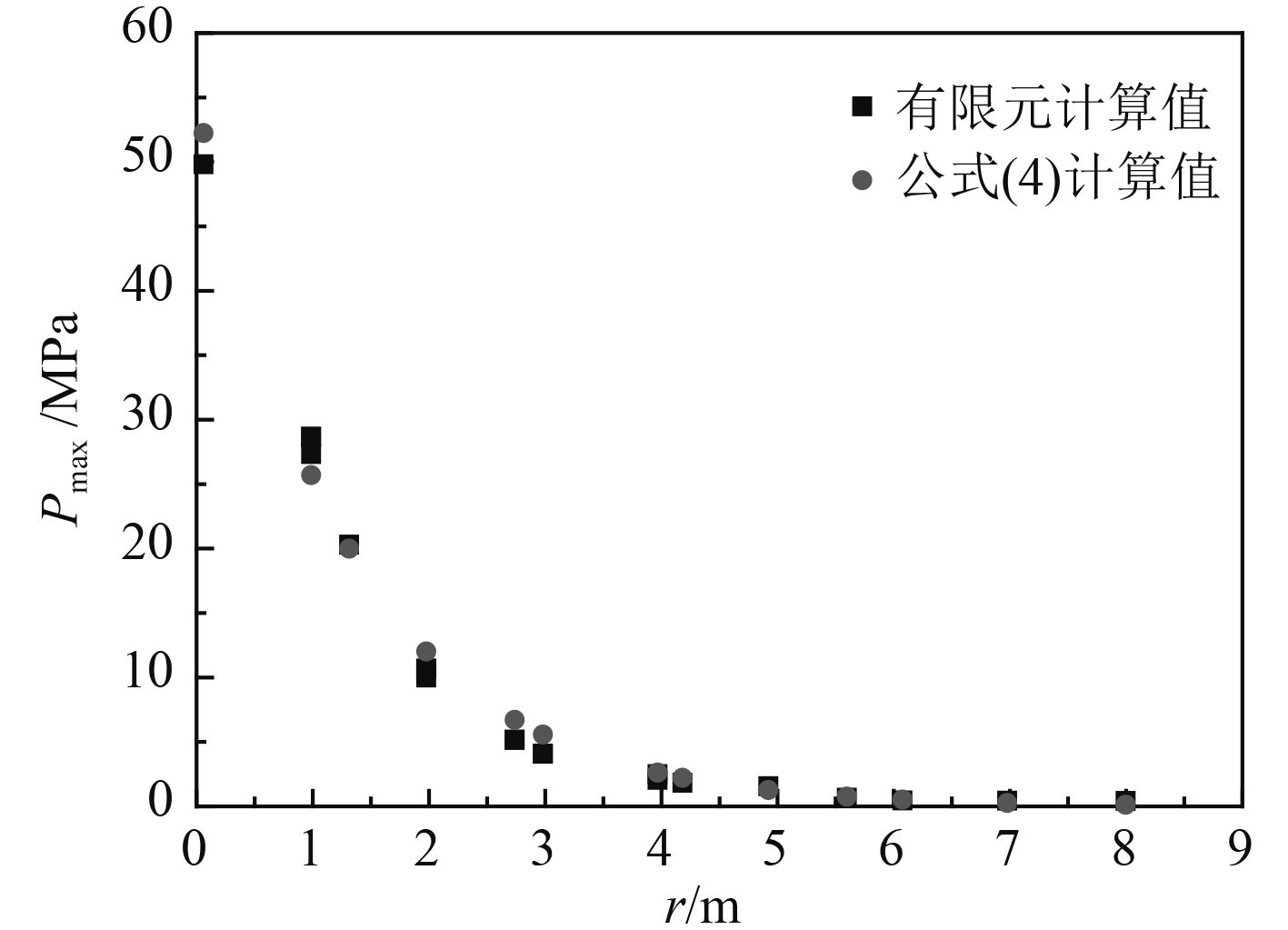
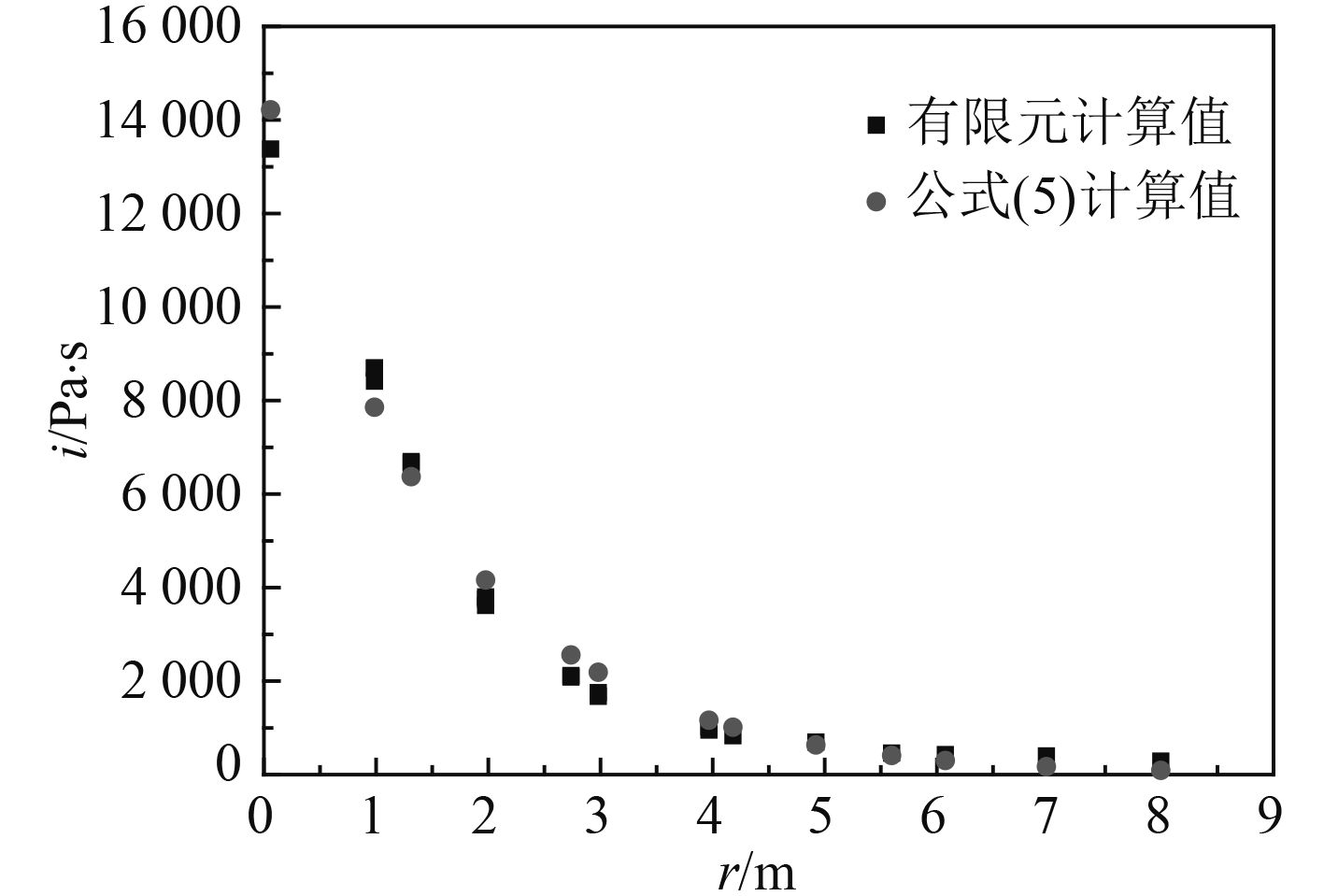
当v=1 050 m/s,δ=27 mm时,液舱后板上各测点的压力峰值pmax和比冲量i的有限元计算值和式(4)、式(5)计算值分别如图10和图11所示,两者吻合较好,从而对式(4)、式(5)进行验证。由式(4)、式(5)可看出,破片的速度v比厚度δ对液舱后板载荷的影响更显著。由于式(4)、式(5)是基于有限元计算结果得出的,并且未考虑液舱的宽度、液舱前后板的厚度及装载水的水位等因素对液舱后板载荷的影响,因此在工程应用上式(4)、式(5)有一定的局限性。尽管如此,对文中的防护液舱结构,当破片的速度v和厚度δ在一定范围内变化时,可以利用式(4)、式(5)对其液舱后板的载荷进行计算。
|
图 10 压力峰值(v=1 050 m/s, δ=27 mm) Fig. 10 The peak pressure (v=1 050 m/s, δ=27 mm) |
|
图 11 比冲量(v=1 050 m/s, δ=27 mm) Fig. 11 The specific impulse (v=1 050 m/s, δ=27 mm) |
利用LS_DYNA软件,本文对不同速度和厚度的高速破片侵彻防护液舱过程中液舱后板的载荷特性进行数值仿真研究。基于仿真计算结果,首先分析了液舱后板载荷的空间分布特性,然后分析了破片速度和厚度对液舱后板载荷的影响,最后得到了液舱后板上任一点的压力峰值和比冲量的拟合计算公式。主要研究结果如下:
1)在空间分布上,液舱后板的载荷在板中心(即破片中心在液舱后板上的投影点)最大,随着到中心点的距离增加而呈指数衰减。
2)增加破片的速度或厚度(或者说增加破片的初始动量),将使液舱后板上任一点的压力峰值和比冲量均增大。
3)文中得到的液舱后板上任一点的压力峰值和比冲量的拟合计算公式可以为防护液舱结构的设计提供参考。
| [1] |
唐廷, 朱锡, 侯海量, 等. 大型水面舰艇防雷舱结构防护机理数值仿真[J]. 哈尔滨工程大学学报, 2012, 33(2): 142–149.
TANG Ting, ZHU Xi, HOU Hai-liang, et al. Numerical simulation study on the defense mechanism of a cabin near the shipboard for large surface vessels[J]. Journal of Harbin Engineering University, 2012, 33(2): 142–149. http://doi.wanfangdata.com.cn/10.3969/j.issn.1006-7043.201012064 |
| [2] | VARAS D, LÓPEZ-PUENTE J, ZAERA R. Experimental analysis of fluid-filled aluminium tubes subjected to high-velocity impact[J]. International Journal of Impact Engineering, 2009, 36: 81–91. |
| [3] | VARAS D, ZAERA R, LÓPEZ-PUENTE J. Numerical modelling of the hydrodynamic ram phenomenon[J]. International Journal of Impact Engineering, 2009, 36: 363–374. |
| [4] | PETER J DISIMILE, LUKE A SWANSON, NORMAN TOY. The hydrodynamic ram pressure generated by spherical projectiles[J]. International Journal of Impact Engineering, 2009, 36: 821–829. |
| [5] | VARAS D, ZAERA R, LÓPEZ-PUENTE J. Numerical modelling of partially filled aircraft fuel tanks submitted to hydrodynamic ram[J]. Aerospace Science and Technology, 2012, 16: 19–28. |
| [6] | ARTERO-GUERRERO J A, PERNAS-SÁNCHEZ J, VARAS D, et al. Numerical analysis of CFRP fluid-filled tubes subjected to high-velocity impact[J]. Composite Structures, 2013, 96: 286–297. |
| [7] |
徐双喜, 吴卫国, 李晓彬, 等. 舰船舷侧防护液舱舱壁对爆炸破片的防御作用[J]. 爆炸与冲击, 2010, 30(4): 395–400.
XU Shuang-xi, WU Wei-guo, LI Xiao-bin, et al. Protective effect of guarding fluid cabin bulkhead under attacking by explosion fragments[J]. Explosion and Shock Waves, 2010, 30(4): 395–400. |
| [8] |
沈晓乐, 朱锡, 侯海量, 等. 高速破片侵彻防护液舱试验研究[J]. 中国舰船研究, 2011, 6(3): 12–15.
SHEN Xiao-le, ZHU Xi, HOU Hai-liang, et al. Experimental study on penetration properties of high velocity fragment into safety liquid cabin[J]. Chinese Journal of Ship Research, 2011, 6(3): 12–15. http://www.cqvip.com/QK/93256A/201103/38474331.html |
| [9] |
孔祥韶, 吴卫国, 李俊, 等. 爆炸破片对防护液舱的穿透效应[J]. 爆炸与冲击, 2013, 33(5): 471–478.
KONG Xiang-shao, WU Wei-guo, LI Jun, et al. Effects of explosion fragments penetrating defensive liquid-filled cabins[J]. Explosion and Shock Waves, 2013, 33(5): 471–478. |
| [10] |
孔祥韶, 吴卫国, 刘芳, 等. 舰船舷侧防护液舱对爆炸破片的防御作用研究[J]. 船舶力学, 2014, 18(8): 996–1004.
KONG Xiang-shao, WU Wei-guo, LIU Fang, et al. Research on protective effect of guarding fluid cabin under attacking by explosion fragments[J]. Journal of Ship Mechanics, 2014, 18(8): 996–1004. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cblx201408015 |
| [11] |
张元豪, 陈长海, 侯海量, 等. 高速破片侵彻防护液舱后的水中运动特性试验研究[J]. 兵器材料科学与工程, 2016, 39(5): 44–48.
ZHANG Yuan-hao, CHEN Chang-hai, HOU Hai-liang, et al. Experimental study on kinetic characteristic of high velocity fragments in water after penetration of protecting liquid cabin[J]. Ordnance Material Science and Engineering, 2016, 39(5): 44–48. http://www.cnki.com.cn/Article/CJFDTOTAL-BCKG201605013.htm |
| [12] | 张婧. 舰船结构在爆炸作用下的非线性响应及可靠性研究[D]. 哈尔滨: 哈尔滨工程大学, 2009. |
| [13] |
吴林杰, 朱锡, 侯海量, 等. 空中近距爆炸下加筋板架的毁伤模式仿真研究[J]. 振动与冲击, 2013, 32(14): 77–81.
WU Lin-jie, ZHU Xi, HOU Hai-liang, et al. Simulations for damage modes of a stiffened plate subjected to close-range air-blast loading[J]. Journal of Vibration and Shock, 2013, 32(14): 77–81. |
 2018, Vol. 40
2018, Vol. 40
