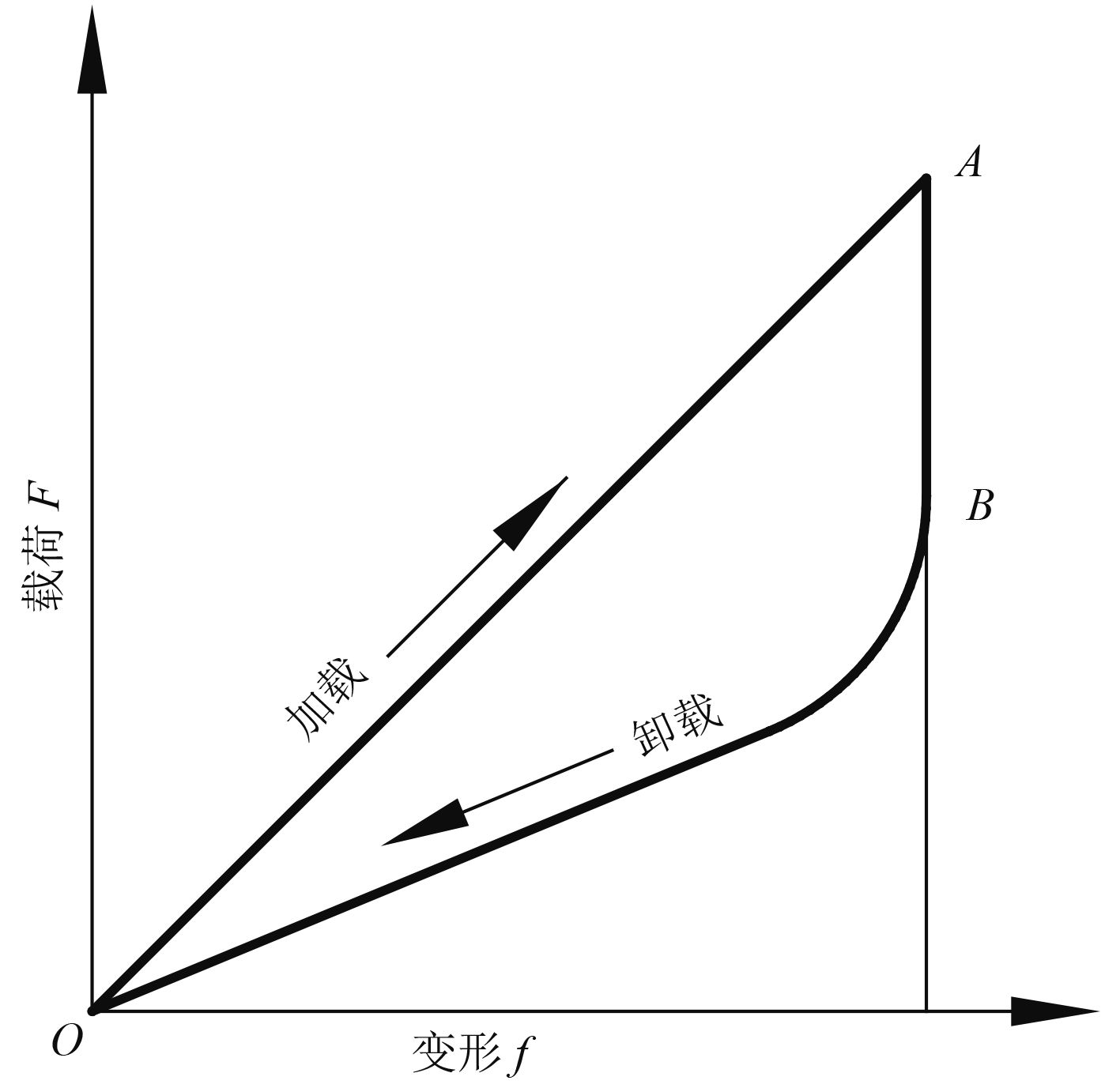
环形弹簧由多个带有内锥面的外圆环和带有外锥面的内圆环配合组成,由于接触表面具有很大的摩擦力,加载时增大弹簧作用力,卸载时减小弹簧作用力。环形弹簧再加载和卸载循环中,由摩擦力转化为热能所消耗的功,其大小几乎可以达到加载过程所作功的60%~70%[1],其常应用在空间尺寸受限而又需要强力缓冲的场合。
|
图 1 环形弹簧力学性能曲线 Fig. 1 Annular spring mechanical property curve |
在不需利用自动机复进能量完成机构动作的小口径火炮(大口径机枪)中,特别是转管自动机,应用环形弹簧进行后坐缓冲优势比较明显,不仅可以减小自动机后坐能量,也可以减轻复进对炮架的冲击,提高射击精度。
ADAMS软件是功能强大的动力学仿真软件,在ADAMS中的弹簧刚度只能是固定值,不能设置不同的加载和卸载刚度直接模拟环形弹簧,本文用ADAMS中的一维作用力的表达式来模拟环形弹簧缓冲,勿需编写用户子程序[3]。
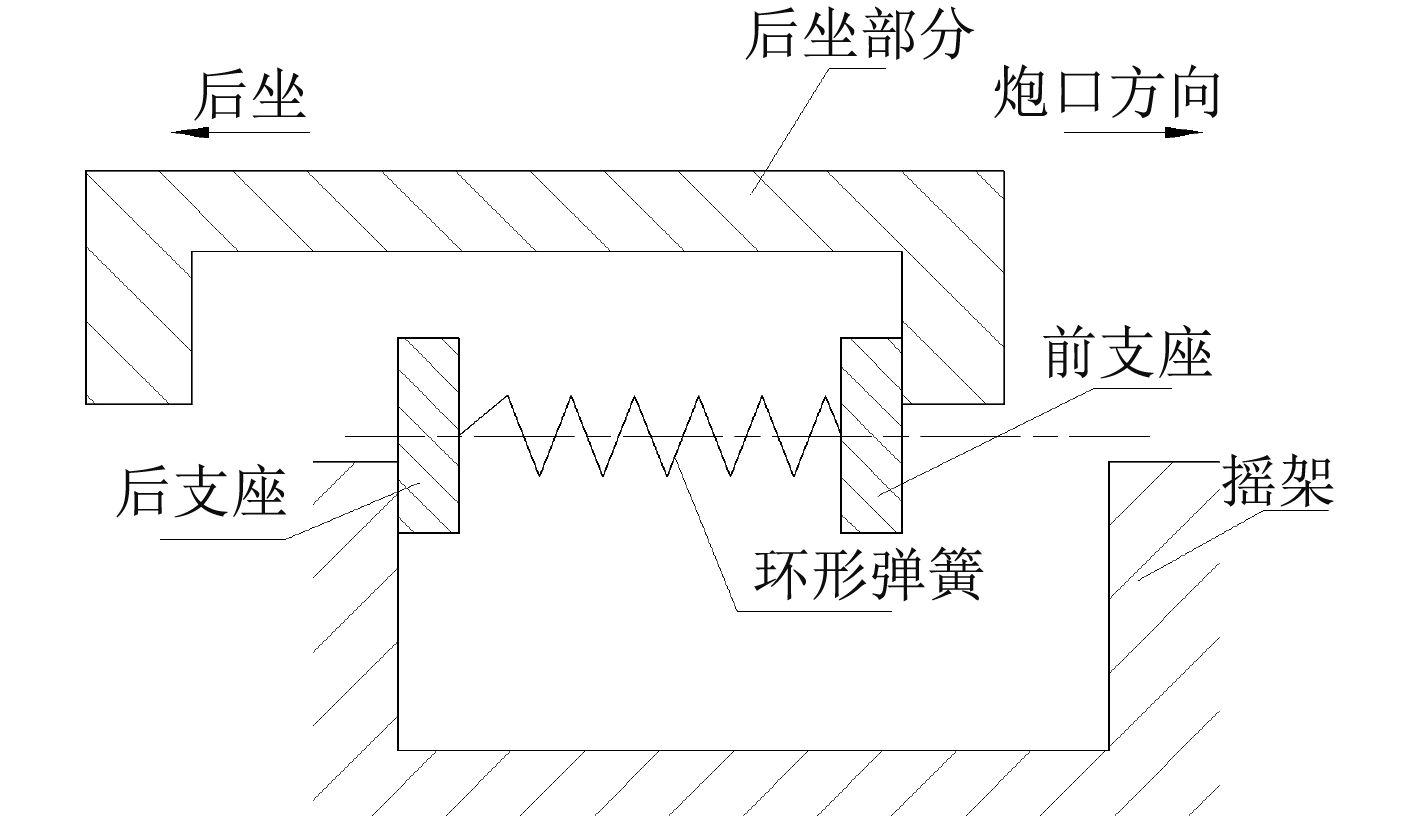
1 转管炮后坐缓冲受力分析本文以某转管炮为对象,利用ADAMS软件,对自动机后坐复进运动进行模拟仿真。后坐缓冲模型如图2所示,后坐部分受到发射冲击力火药气体作用向后运动,压缩环形弹簧进行缓冲并存储复进能量,后坐到某平衡点后(即后座速度为0时),在环形弹簧作用下开始复进,在自动机复进过程中发射下一发炮弹,后座能量被自动机前冲能量抵消一部分后,自动机继续后坐,如此连发时,实现了自动机浮动,后坐力峰值降低,大小稳定。在高射速射击过程中,自动机复进一般不会出现前冲状态,即前支座不会碰撞摇架,有利于减小复进冲击力。
|
图 2 后坐缓冲模型示意图 Fig. 2 Structure chart of the recoiling buffer |
以后坐部分为研究对象,其受力如图3所示。后坐部分主要承受炮膛合力、弹簧力和摩擦力。

|
图 3 后坐部分受力图 Fig. 3 force diagram of the Recoiling Buffer |
设后坐部分质量为
| $F = m\ddot x = F(t) - k \cdot x - c \cdot \dot x - \mu \cdot m \cdot g\text{。}$ |
式中:
弹簧阻尼与速度方向相反,摩擦力与速度方向相反。
2 ADAMS下环形弹簧力学特性实现方法在ADAMS环境下实现环形弹簧力学特性模拟的方法,如图2所示,首先,在前支座和后支座之间添加SFORCE力,该力的值项用函数表达式表示;其次,为判断环形弹簧受力方向变化,需调用逻辑函数IF判断,以实现后坐复进过程的转变;最后,通过后座位移仿真数据得出环形弹簧受力大小,即后坐力。
逻辑依据是:
1)当前支座处于后坐运动时:作用力=弹簧变形力+阻尼+摩擦力;
2)当前支座处于复进运动时:作用力=弹簧变形力×比例系数+阻尼×比例系数-摩擦力;
3)当后支座处于复进运动时:作用力=弹簧变形力+阻尼-摩擦力;
4)当后支座处于后坐运动时:作用力=弹簧变形力×比例系数+阻尼×比例系数+摩擦力。
在ADAMS软件环境下,以前、后支座的运动速度作为后坐复进判断条件,而不直接以后坐部分运动作为判断条件,是因为后坐部分不能准确的反映弹簧的反向压缩情况。以炮口方向为正,具体如下:
若后支架不动,前支架运动
若前支架不动,后支架运动
式中:
需要说明的是,由于弹簧力的存在,前、后支座不可能存在同时运动情况。由于在仿真软件下,开始仿真段存在振荡情况,因此增加判断前、后支座运动的条件。下面列出ADAMS软件下的环形弹簧表达式。
2.1 按设计参数仿真按照ADAMS函数表达式的IF嵌套语句写出该力,IF函数的各式为IF(表达式1:表达式2,表达式3,表达式4),表示当表达式1<0,执行表达式2,当表达式1=0,执行表达式3,表达式1>0,执行表达式4。
IF(后支座位移:
IF(前支座位移:
IF(前支座速度:
),
),
IF(前支座位移:
IF(前支座速度:
),
),
IF(后支座速度:
)
)
2.2 用弹簧测试数据仿真在环形弹簧生产出来后,要进行压力测试,根据测试数据也可以进行后坐仿真,下面以环形弹簧的测试数据为条件的函数表达式。要用到AKISPL函数,该函数返回根据Akima样条曲线的拟合值。AKISPL 格式为AKISPL(第1独立变量,第2独立变量,样条函数名,求导阶数),其中第1独立变量代表样条中第1个实数变量,如弹簧压缩量;第2独立变量表示第2个实数变量,如曲面;求导阶数合法值:0-返回曲线坐标值,1-返回一阶导数值,2-返回二阶导数值,SPLINE_1是环形弹簧测量加载曲线,SPLINE_2是环形弹簧测量卸载曲线。
IF(后支座位移:
IF(前支座位移:
IF(前支座速度:
AKISPL(
AKISPL(
AKISPL(
),
AKISPL(
),
IF(前支座位移:
IF(前支座速度:
AKISPL(
AKISPL(
AKISPL(
),
AKISPL(
),
IF(后支座速度:
AKISPL(
AKISPL(
AKISPL(
)
)
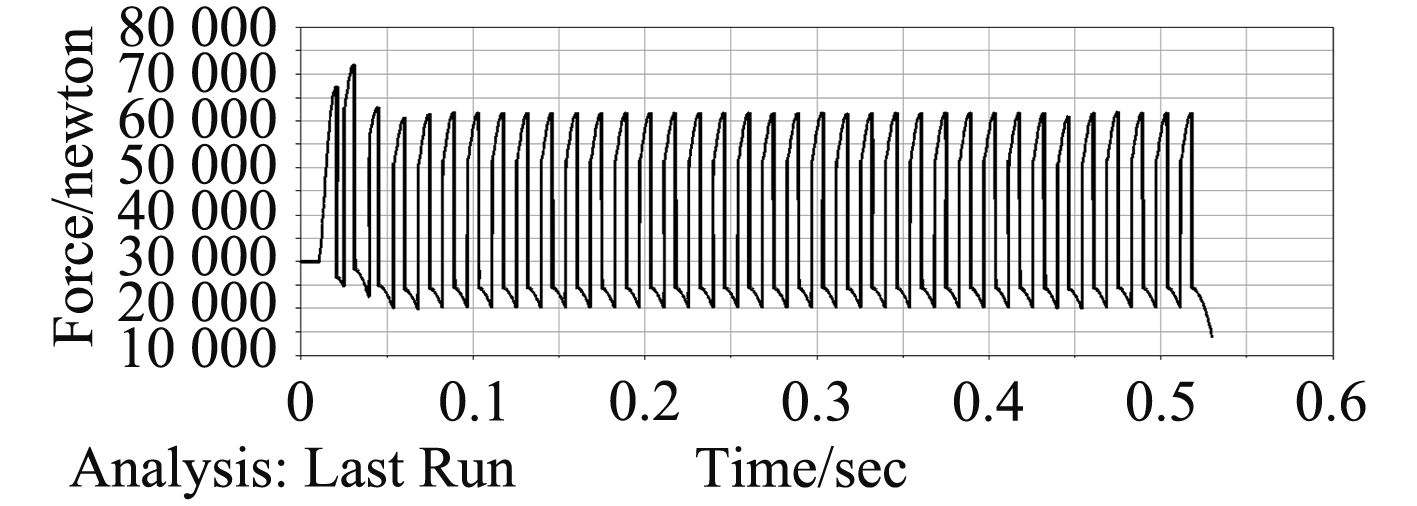
3 仿真结果 3.1 依据设计参数仿真根据设计参量,编写ADAMS函数表达式,并进行仿真,得到如下结果。可以看到设计满足后坐缓冲要求,自动机射击过程可以“浮动”起来。
|
图 4 弹簧力-时间曲线 Fig. 4 Spring force-time curve |
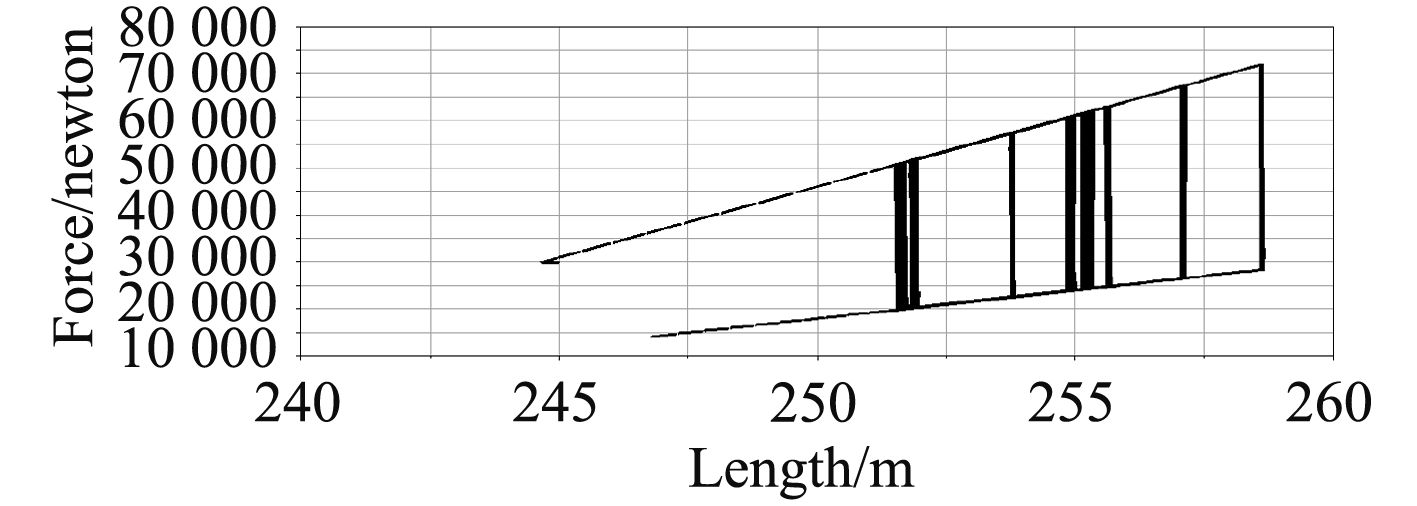
|
图 5 弹簧力-位移曲线 Fig. 5 Spring force-displacement curve |
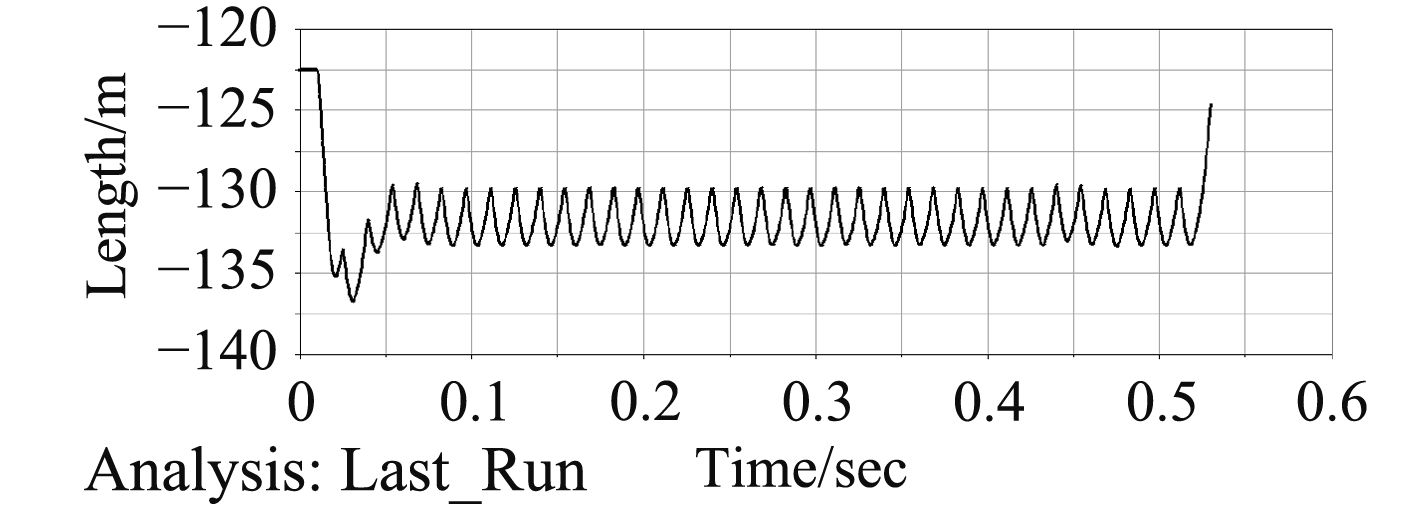
|
图 6 自动机后坐位移-时间曲线 Fig. 6 Recoil displacement-time curve |
在实际生产中,弹簧并不能完全符合技术设计要求,因此需对弹簧测试数据进行仿真,结果见图8。本文的环形弹簧测试数据是已经射击了几千发后的数据,因此可见弹簧有压缩到极限位的情况。
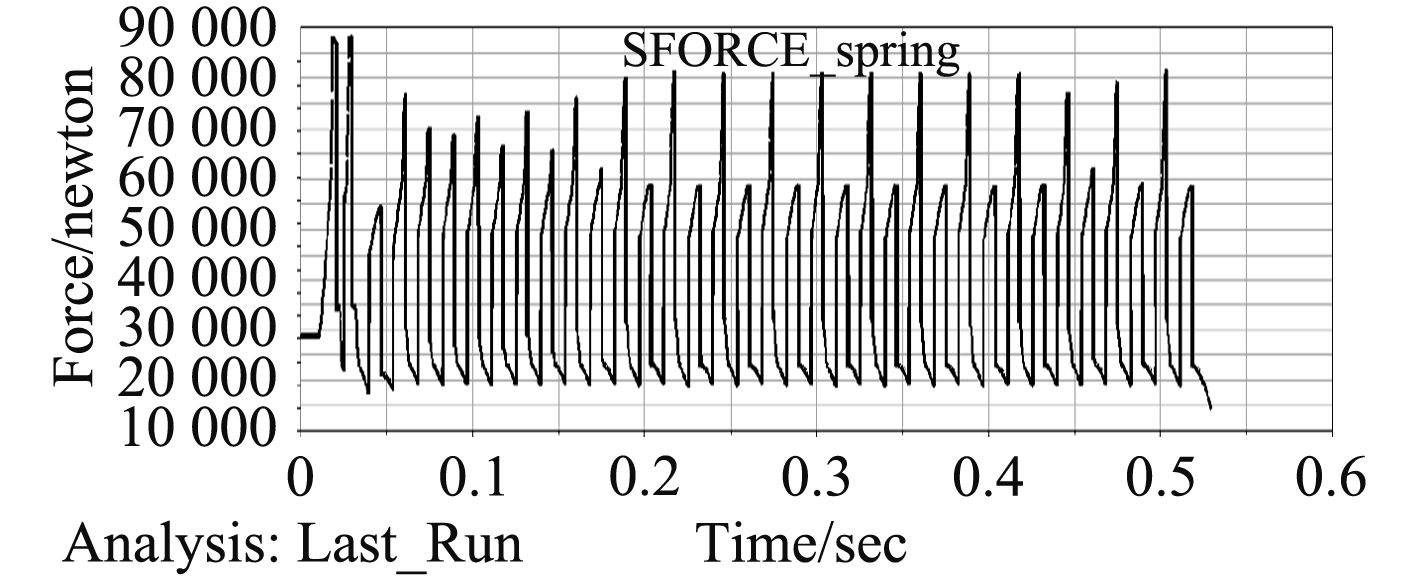
|
图 7 弹簧力-时间曲线 Fig. 7 Spring force-time curve |
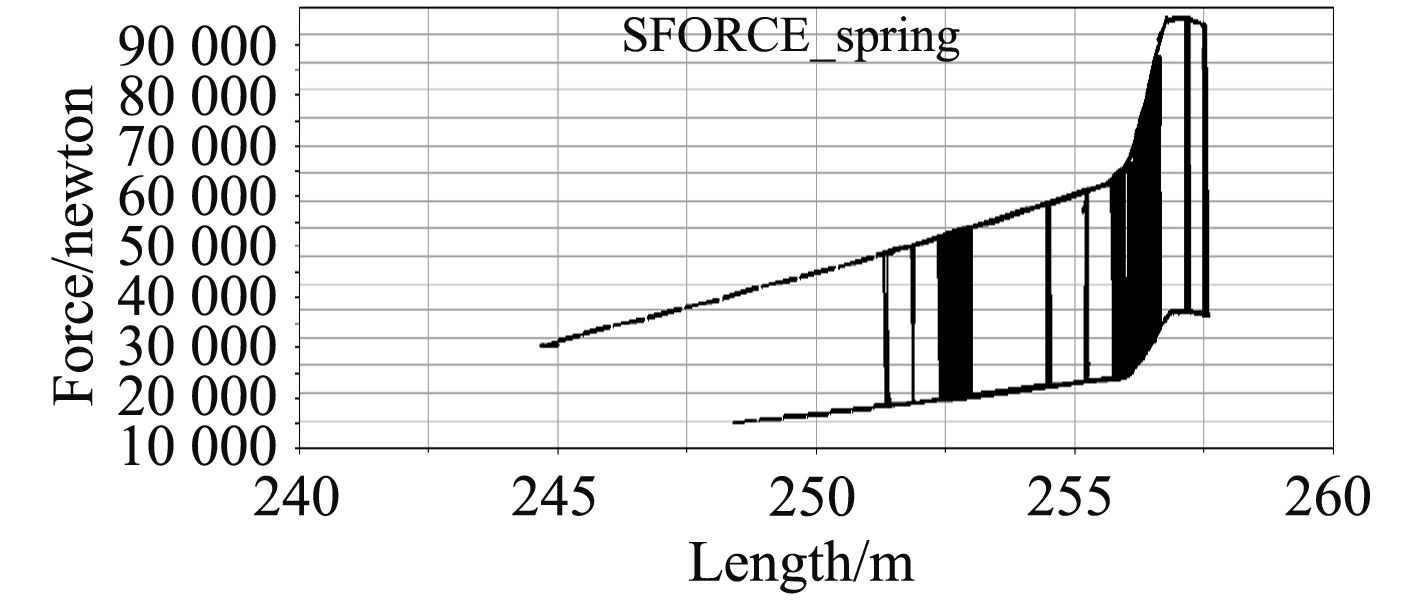
|
图 8 弹簧力-位移曲线 Fig. 8 Spring force-displacement curve |
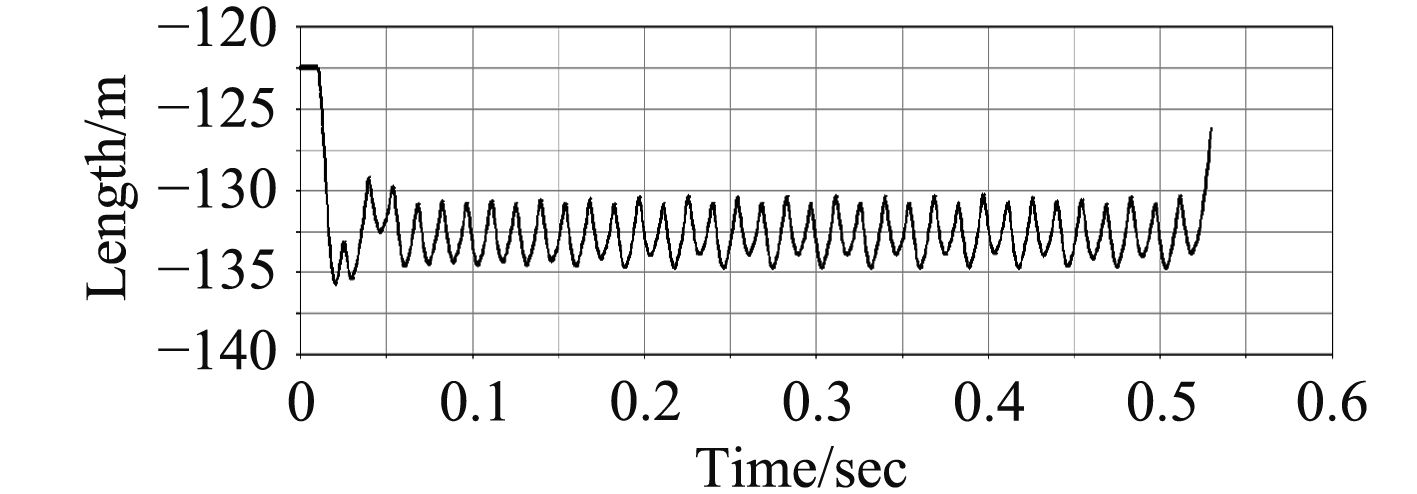
|
图 9 后坐位移曲线(发射率4 200发/分) Fig. 9 Recoil displacement-time curve |
把仿真的后坐位移曲线与实际测试的位移曲线进行对比,可以发现曲线较一致,特别是用测试弹簧数据仿真的后坐位移曲线,其趋势与测试后坐位移曲线比较一致(见图9和图10)。由于仿真时对实际情况进行了大量简化,仿真结果和实际结果并不完全一致。
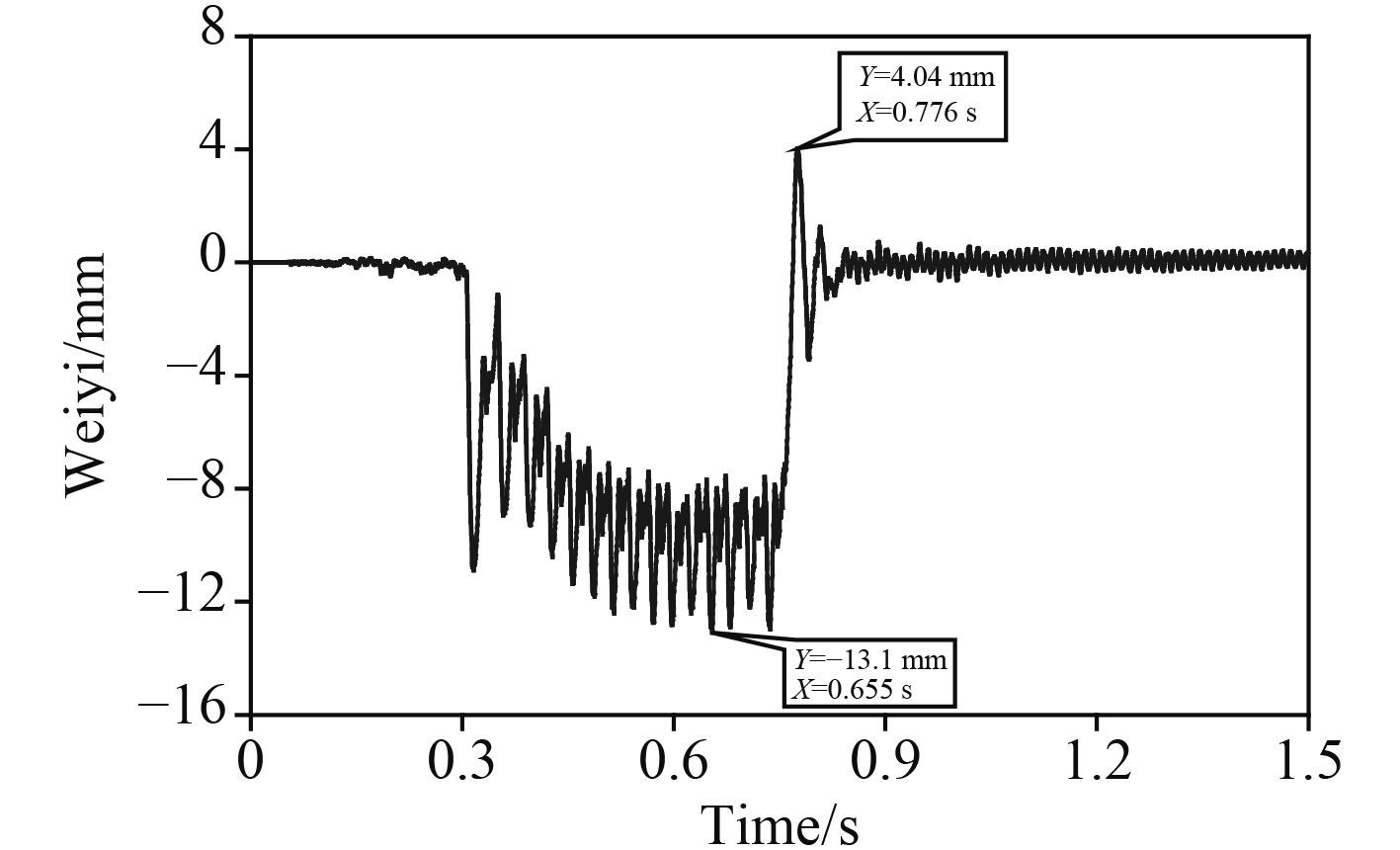
|
图 10 实际射击测试后坐位移曲线(发射率4 200发/分) Fig. 10 Test dadta of recoil displacement-time curve |
通过运行函数表达式,在ADAMS软件下实现了环形簧特性的后坐缓冲运动仿真,通过与试验数据比对,结果较吻合。该方法可以用到火炮设计的数字仿真中,简化了仿真过程,对提高设计手段具有积极意义。
| [1] |
成大先. 机械设计手册(第3卷)[M]. 第五版. 第11篇第9章环形弹簧. 北京: 化学工业出版社, 2014.
CHENG Da-xian. Mechanical design handbook(3)[M]. Version 5. Chapter 9. Annular Spring. Beijing: Chemical Industry Press, 2014. |
| [2] |
刘明敏, 张蔚峰, 朱延飞. 2种缓冲簧反后坐效能分析[J]. 舰船科学技术, 2014, 36(11): 157–161.
LIU Ming-min, ZHANG Wei-feng, ZHU yan-fei. Efficiency analysis about two kinds of counter recoil equipment[J]. Ship Science and Technology, 2014, 36(11): 157–161. |
| [3] |
周发明, 王宝元, 霍文妮, 等. 环形弹簧特性的RecurDyn子程序实现方法[J]. 火炮发射与控制学报, 2007(2): 21–23.
ZHOU Fa-ming, WANG Bao-yuan, HUO Wen-ni, et al. Implementation of recurdyn subprogram with characteristics of ring spring[J]. Journal of Gun Launch and Control, 2007(2): 21–23. |
| [4] |
贾长治, 杜秀菊, 刘广生, 等. 火炮冲击缓冲装置动态特性影响仿真分析与改进方法[J]. 机械工程学报, 2012, 48(19): 156–162.
JIA Chang-zhi, DU Xiu-ju, LIU Guang-sheng, et al. Simulation and improvement of dynamic characteristics of impact buffering mechanism of guns based on virtual prototyping technology[J]. Journal of Mechanical Engineering, 2012, 48(19): 156–162. |
| [5] |
申江森, 高跃飞, 徐凤军. 基于ADAMS的某突击炮发射动力学仿真[J]. 机械工程与自动化, 2015(2): 105–107.
SHEN Jiang-sen, GAO Yue-fei, XU Feng-jun. ADAMS based dynamic simulation of assault gun firing[J]. Mechanical Engineering & Automation, 2015(2): 105–107. http://doi.wanfangdata.com.cn/10.3969/j.issn.1672-6413.2015.02.042 |
 2018, Vol. 40
2018, Vol. 40
