海军工程大学 导航工程系,湖北 武汉 430000
收稿日期: 2016-12-01, 修回日期: 2017-01-16.
基金项目: 国家自然科学基金资助项目(4150622)
作者简介: 鲁鑫(1995 – ),男,硕士研究生,研究方向为惯性技术及其应用
Attitude estimation analysis under different attitude representation methods
Navigation Engineering Department, Naval University of Engineering, Wuhan 43000, China
0 引 言 对于基于捷联惯导系统的组合导航来说[1-2],关键是构建姿态转换矩阵,即所谓的“数字平台”。而构建精准、高效的姿态转换矩阵的前提就是有效的姿态估计算法[3-4]。从理论上讲,姿态估计算法的提出主要基于2个方面,即信息融合技术和姿态表示方法[5]。在信息融合技术方面,随着现代滤波技术和组合导航模式的发展,使得高精度、快速的姿态估计成为可能,其主要成就体现为Kalman滤波技术的不断革新与发展,涌现出了线性Kalman滤波(KF),扩展Kalman滤波(EKF),无味Kalman滤波(UKF)以及粒子滤波(PF)等滤波算法,极大地推动了组合导航姿态估计领域研究的发展。另外,随着卫星姿态控制、航天器交会对接等问题的提出,对于姿态估计算法的性能要求更高,尤其体现为精度更高而计算量更小的高性能姿态估计算法的提出,将姿态估计从“姿态确定”阶段(即只对姿态单参量估计)推向了“姿态估计”阶段(即实现了导航全参量的估计)。在这方面,Crassidis、Markley等提出了乘性EKF滤波算法(MEKF)、四元数无味估计器(USQUE),Choukroun等提出新型四元数姿态估计滤波算法[6-7],以上算法采用的姿态参数表示均是采用四元数。而Karlgaard等于2009年提出的修正罗德里格斯参数(MRP)姿态估计算法,解决了MRP奇异值问题,相比于基于四元数的姿态估计算法来说计算量更小。后续研究中,针对以上算法在精度、稳定性和计算量等方面,学者们也进行了比较深入的研究[8, 9]。
然而,从姿态表达角度将多种姿态估计算法比较分析的研究却相对缺乏,因此本文重点开展了不同姿态方法下的姿态估计分析的研究。对四元数无味估计器、基于修正罗德里格斯参数和高阶罗德里格斯参数所构成的姿态估计算法进行研究分析,比较三者在计算量和精度的各方面的差异。
1 基于USQUE的姿态估计算法研究 假设一个非线性离散系统模型为
|
$\left\{ \begin{gathered} {x_k} = f({x_{k - 1}}) + {q_{k - 1}} \hfill \text{,}\\ {y_k} = h({x_k}) + {v_k} \text{。} \hfill \\ \end{gathered} \right.$
|
(1) |
式中:
${x_k} \in {{R}^n}\text{;}{y_k} \in {{R}^m}$
;
$f( \cdot )$
和
$h( \cdot )$
分别为状态函数和量测函数,
${q_{k - 1}} \sim N(0,{Q_{k - 1}})$
,
${v_k} \sim N(0,{R_{k - 1}})$
。USQUE算法的提出是由于UKF[10 – 12]无法直接应用于直接式,重点在于解决状态方程中的四元数规范性约束问题。
下面结合直接式,简单推导USQUE的计算流程。在USQUE算法中采用广义误差Rodrigues参数作为局部变量,而乘性误差四元数作为中间变量,定义误差四元数
$\delta q = {[\delta {q_0}\;\;\delta \rho ]^{{T}}}$
,
$\delta q$
的广义误差Rodrigues参数形式
$\delta \sigma $
表示为
|
$\delta \sigma = f\frac{{\delta \rho }}{{a + \delta {q_0}}}\text{。}$
|
(2) |
其中
$f$
和
$a$
为可变参数,一般取
$f = 1$
,
$a = 0$
。
在直接式中
$k - 1$
时刻有状态量
$ {\hat x_{k - 1|k - 1}} =[\delta {\hat \sigma _{k - 1|k - 1}}, $
$ \hat x_{k - 1|k - 1}^e]^{{T}}$
,其中
$\hat x_{k - 1|k - 1}^e$
是非姿态状态量。滤波方差矩阵为
${{{P}}_{k - 1|k - 1}}$
,全局变量姿态四元数的估计量为
$\hat q_{b,k - 1|k - 1}^n$
。具体步骤如下:
时间更新
首先根据上步状态估计量和滤波方差矩阵计算相应的Sigma点
|
${\chi _{k - 1}}(i) = \left[ \begin{gathered} \chi _{k - 1}^{\delta \sigma }(i) \hfill \\ \chi _{k - 1}^e(i) \hfill \\ \end{gathered} \right] = {{sig}}ma({\hat x_{k - 1|k - 1}},{P_{k - 1|k - 1}}),i = 0,1, \cdots 2n\text{,}$
|
(3) |
其中
$\chi _{k - 1}^{\delta \sigma }(i)$
对应的误差四元数形式为
|
$\chi _{k - 1}^{\delta q}(i) = {[\delta {q_{k - 1,0}}(i)\;\;\delta {\rho _{k - 1}}(i)]^{{T}}}\text{,}$
|
(4) |
$\chi _{k - 1}^{\delta q}(i)$
可由式(2)的逆形式求得,即
|
$\delta {q_{k - 1,0}}(i) = \frac{{ - a||\chi _{k - 1}^{\delta q}(i)|{|^2} + f\sqrt {{f^2} + (1 - {a^2})||\chi _{k - 1}^{\delta q}(i)|{|^2}} }}{{{f^2} + ||\chi _{k - 1}^{\delta q}(i)|{|^2}}}\text{,}$
|
|
$\delta {\rho _{k - 1}}(i) = {f^{ - 1}}[a + \delta {q_{k - 1,0}}(i)]\chi _{k - 1}^{\delta q}(i)\text{。}$
|
(5b) |
根据
$k - 1$
时刻的四元数估计值
${\hat q_{k - 1|k - 1}}$
计算四元数对应的Sigma点
|
$\chi _{k - 1}^q(i) = \chi _{k - 1}^{\delta q}(i) \otimes {\hat q_{k - 1|k - 1}}\text{,}$
|
(6) |
$ \otimes $
表示四元数相乘,将
$\chi _{k - 1}^q(i)$
和构造一组新的Sigma点,即
|
${\chi '_{k - 1}}(i) = \left[ \begin{gathered} \chi _{k - 1}^q(i) \hfill \\ \chi _{k - 1}^e(i) \hfill \\ \end{gathered} \right]\text{,}$
|
(7) |
将
${\chi '_{k - 1}}(i)$
在滤波中进行传递得到
${\chi '_{k|k - 1}}(i)$
,将
${\chi '_{k|k - 1}}(i)$
写成分解形式
|
${\chi '_{k|k - 1}}(i) = \left[ \begin{gathered} \chi _{k|k - 1}^q(i) \hfill \\ \chi _{k|k - 1}^e(i) \hfill \\ \end{gathered} \right]\text{,}$
|
(8) |
为了计算状态预测均值和滤波方差,根据乘性四元素公式得
|
$\chi _{k|k - 1}^{\delta q}(i) = \chi _{k|k - 1}^q(i) \otimes {[\chi _{k|k - 1}^q(0)]^{ - 1}}\text{,}$
|
|
$\chi _{k|k - 1}^{\delta q}(i) = {[\delta {q_{k|k - 1,0}}(i)\;\;\delta {\rho _{k|k - 1}}(i)]^{{T}}}\text{,}$
|
(9b) |
|
$\chi _{k|k - 1}^{\delta \sigma }(i) = f\frac{{\delta {\rho _{k|k - 1}}(i)}}{{a + \delta {q_{k|k - 1,0}}(i)}}\text{,}$
|
将
$\chi _{k|k - 1}^{\delta \sigma }(i)$
和
$\chi _{k|k - 1}^e(i)$
组合构造一步预测后的状态传递Sigma点
|
${\chi _{k|k - 1}}(i) = \left[ \begin{gathered} \chi _{k|k - 1}^{\delta \sigma }(i) \hfill \\ \chi _{k|k - 1}^e(i) \hfill \\ \end{gathered} \right]\text{,}$
|
(10) |
则状态预测均值和滤波方差分别为
|
${\hat x_{k|k - 1}} = \sum\limits_{i = 0}^{2n} {w(i){\chi _{k|k - 1}}(i)} \text{,}$
|
(11) |
|
$\begin{split}{P_{k|k - 1}} = & \sum\limits_{i = 0}^{2n} {w(i)({\chi _{k|k - 1}}(i) - {{\hat x}_{k|k - 1}})}\\& {{({\chi _{k|k - 1}}(i) - {{\hat x}_{k|k - 1}})}^{{T}}} + {Q_{k - 1}}\end{split}\text{。}$
|
(12) |
其中
$w(i)$
为Sigma点的权值;
${Q_{k - 1}}$
为系统噪声方差。
量测更新
采用松组合模式,量测方程是线性的,直接采用线性Kalman滤波量测更新过程进行。写出相应的量测转移矩阵形式,即
|
${y_k} = {{{H}}_k}{x_k} + {\eta _k},$
|
(13) |
根据观测量的不同,
${{{H}}_k}$
不同,即采用位置作为外界辅助信息的位置松组合量测转移矩阵:
|
${{{H}}_{p,k}} = [{0_{3 \times 6}}\;\;{I_{3 \times 3}}\;\;{0_{3 \times 6}}]\text{,}$
|
(14) |
由于量测方程是线性的,因此量测更新直接采用线性Kalman滤波量测更新过程
|
${\hat x_{k|k}} = {\hat x_{k|k - 1}} + {K_k}({y_k} - {H_k}{\hat x_{k|k - 1}})\text{,}$
|
|
${P_{k|k}} = [{I_n} - {K_k}{H_k}]{P_{k|k - 1}}\text{,}$
|
|
${K_k} = {P_{k|k - 1}}H_k^{ T}{[{H_k}{P_{k|k - 1}}H_k^{ T} + {R_k}]^{ - 1}}\text{。}$
|
(15c) |
姿态更新
在量测更新后姿态部分得到了局部变量
$\delta {\hat \sigma _{k|k}}$
,而直接式姿态估计的结果需要的是全局变量
$\hat q_{b,k|k}^n$
,因此,姿态更新的目的正是为了得到
$\hat q_{b,k|k}^n$
。
记
${\hat x_{k|k}} = {[\delta {\sigma _{k|k}},\hat x_{k|k}^e]^{{T}}}$
,则
$\delta {\sigma _{k|k}}$
对应的四元数形式为
|
$\hat x_{k|k}^{\delta q} = {[\delta {q_{k,0}}\;\;\delta {\rho _k}(i)]^{{T}}}\text{,}$
|
(16) |
其中
|
$\delta {q_{k,0}} = \frac{{ - a{{\left\| {\delta {\sigma _{k|k}}} \right\|}^2} + f\sqrt {{f^2} + (1 - {a^2}){{\left\| {\delta {\sigma _{k|k}}} \right\|}^2}} }}{{{f^2} + {{\left\| {\delta {\sigma _{k|k}}} \right\|}^2}}}\text{,}$
|
|
$\delta {\rho _k} = {f^{ - 1}}[a + \delta {q_{k,0}}]\delta {\sigma _{k|k}}\text{,}$
|
(17b) |
则四元数的更新根据乘性四元数公式得
|
$\hat q_{b,k|k}^n = \hat x_{k|k}^{\delta q} \otimes \chi _{k|k - 1}^q(0)\text{。}$
|
(18) |
最后将
${\hat x_{k|k}}$
中姿态部分即
$\delta {\sigma _{k|k}}$
置0,释放积累的过程姿态误差,并进入下一时刻的滤波周期。
2 基于MRP和HOMRP的姿态估计算法研究 Rodrigues参数族本质上是四元数在三维超平面上的投影。Rodrigues参数族并不存在四元数在非线性滤波中的约束问题,同时,Rodrigues参数少了一个冗余的标量,所以在理论上Rodrigues参数族要比四元数在姿态表示上的计算量更小,但存在着奇异性问题。Rodrigues参数族统一可表示为
|
$R{P_{family}} = e\tan (\frac{\vartheta }{{2N}})\text{。}$
|
(19) |
式中:
$R{P_{family}}$
为Rodrigues参数族的姿态表示参数;
$\vartheta $
为旋转矢量;N为正整数。当
$N = 1$
时,为RP;当
$N = 2$
时,为MRP;当
$N > 2$
时,一般称为HOMRP。MRP和HOMRP分别在
$2\pi \pm 4n\pi $
和
$4N\pi \pm 8Nn\pi $
处奇异。
相比四元数在直接式中姿态更新方程,Rodrigues参数族的姿态更新方程只有3个参数表达量,表达形式更简单。基于MRP的姿态更新方程如下所示:
MRP姿态更新方程
|
$\sigma {{ = }}\frac{{1{{ + }}{{\left\| \sigma \right\|}^2}}}{4}\left( {{I_3} + 2\frac{{{{[\sigma \times ]}^2} + [\sigma \times ]}}{{1 + {{\left\| \sigma \right\|}^2}}}} \right)\omega \text{,}$
|
(20) |
其姿态转移矩阵表示式为
|
${{C}}(\sigma ) = {I_3}{{ + }}\frac{{8{{[\sigma \times ]}^2} - 4(1 - {{\left\| \sigma \right\|}^2})[\sigma \times ]}}{{1 + {{\left\| \sigma \right\|}^2}}}\text{,}$
|
(21) |
将以上基于MRP的姿态更新方程构建入直接式中,即可实现基于MRP的直接式姿态的估计。
对于基于HOMRP的姿态估计算法,本文重点研究4阶HOMRP,即
|
$\tau = e\tan (\frac{\vartheta }{8})\text{,}$
|
(22) |
其中HOMRP为
$\tau = [{\tau _1}\;\;{\tau _2}\;\;{\tau _3}] \in {{R}^3}$
。
由于HOMRP定义的特殊形式,一般的三角函数无法对其进行分解表示,采用Cayley变换的数学手段将HOMRP与其他姿态表示方法联系起来,以下为HOMRP与MRP和四元数姿态切换关系:
与MRP的关系:
|
$\sigma = \pm \frac{{2\tau }}{{1 - {{\left\| \tau \right\|}^2}}}\text{,}$
|
(23) |
其中
$\left\| \tau \right\| = \sqrt {\tau _1^2 + \tau _2^2 + \tau _3^2} \text{。}$
与四元数的关系:
|
$\tau = \frac{\rho }{{1 + {q_0} \pm \sqrt {2(1 + {q_0})} }}\text{,}$
|
(24) |
式(24)中的分母中含加减,一般取正,因此,用HOMRP表示四元数为
|
$\rho = 4\tau \frac{{1 - {{\left\| \tau \right\|}^2}}}{{{{(1 + {{\left\| \tau \right\|}^2})}^2}}}\text{,}$
|
|
${q_0} = \frac{{1 - 6{{\left\| \tau \right\|}^2} + {{\left\| \tau \right\|}^4}}}{{{{(1 + {{\left\| \tau \right\|}^2})}^2}}}\text{。}$
|
(25b) |
HOMRP姿态更新方程
|
$\frac{{{{d}}\tau }}{{{{d}}t}} = G(\tau )\omega \text{,}$
|
|
$\begin{split} G(\tau ) = & \frac{1}{{8(1 - {{\left\| \tau \right\|}^2})}}[2(3 - {\left\| \tau \right\|^2})\tau {\tau ^{ T}} - 4(1 - {\left\| \tau \right\|^2})[\tau \times ]+ \\& (1 - 6{\left\| \tau \right\|^2} + {\left\| \tau \right\|^4}){I_3}] \text{。}\end{split}$
|
(26b) |
其中:
${{d}}\tau /{{d}}t = \tau $
表示HOMRP对时间求导。这里需要重点对式(26)进行研究,式(26)是基于HOMRP的姿态更新方程。
3 基于MRP、HOMRP和USQUE的姿态估计结果分析 采用标准的基于捷联惯导的状态方程为组合导航模型,比较USQUE、MRP和HOMRP的姿态估计的效果。仿真真实运动轨迹的姿态
$trj({q_k})$
、速度
$trj({v_k})$
和位置
$trj({p_k})$
信息,仿真周期
${T_s}$
为0.1 s,运动轨迹的仿真时间T=1 050 s。
初始化参数为
|
${x_0} = {[trj({q_0})\;\;trj({v_0})\;\;trj({p_0})]^{{T}}}\text{,}$
|
|
${P_0} = { diag}({[{I_{3 \times 1}} \cdot \deg \;\;0.1 \cdot {I_{3 \times 1}} \cdot \deg \;\;10/{\mathop{ Re}\nolimits} \;\;10/{\mathop{ Re}\nolimits} \;\;5]^{{T}}})\text{,}$
|
|
${R_0} = { diag}{({[10/glv \cdot {\mathop{ Re}\nolimits} \;\;10/glv \cdot {\mathop{ Re}\nolimits} \;\;10]^{{T}}})^2}\text{,}$
|
|
${Q_0} = {{diag}}{({[{w_{eb}}\;\;{w_{db}}\;\;{0_{3 \times 3}}]^{{T}}})^2}\text{。}$
|
(28d) |
式中:
$trj( \cdot )$
表示真实运动轨迹情况;
${I_{3 \times 1}} = {[1\;\;1\;\;1]^{{T}}}$
;
$\deg = \pi /{180^ \circ }$
;
${R_e}$
为地球半径(6 378 137 m)(WGS-84)。
|
${w_{eb}} = {[0.29 \times {10^{ - 4}}\;\;0.29 \times {10^{ - 4}}\;\;0.29 \times {10^{ - 4}}]^{{T}}}\text{,}$
|
|
${w_{db}} = {[0.97 \times {10^{ - 4}}\;\;0.97 \times {10^{ - 4}}\;\;0.97 \times {10^{ - 4}}]^{{T}}}\text{。}$
|
(29b) |
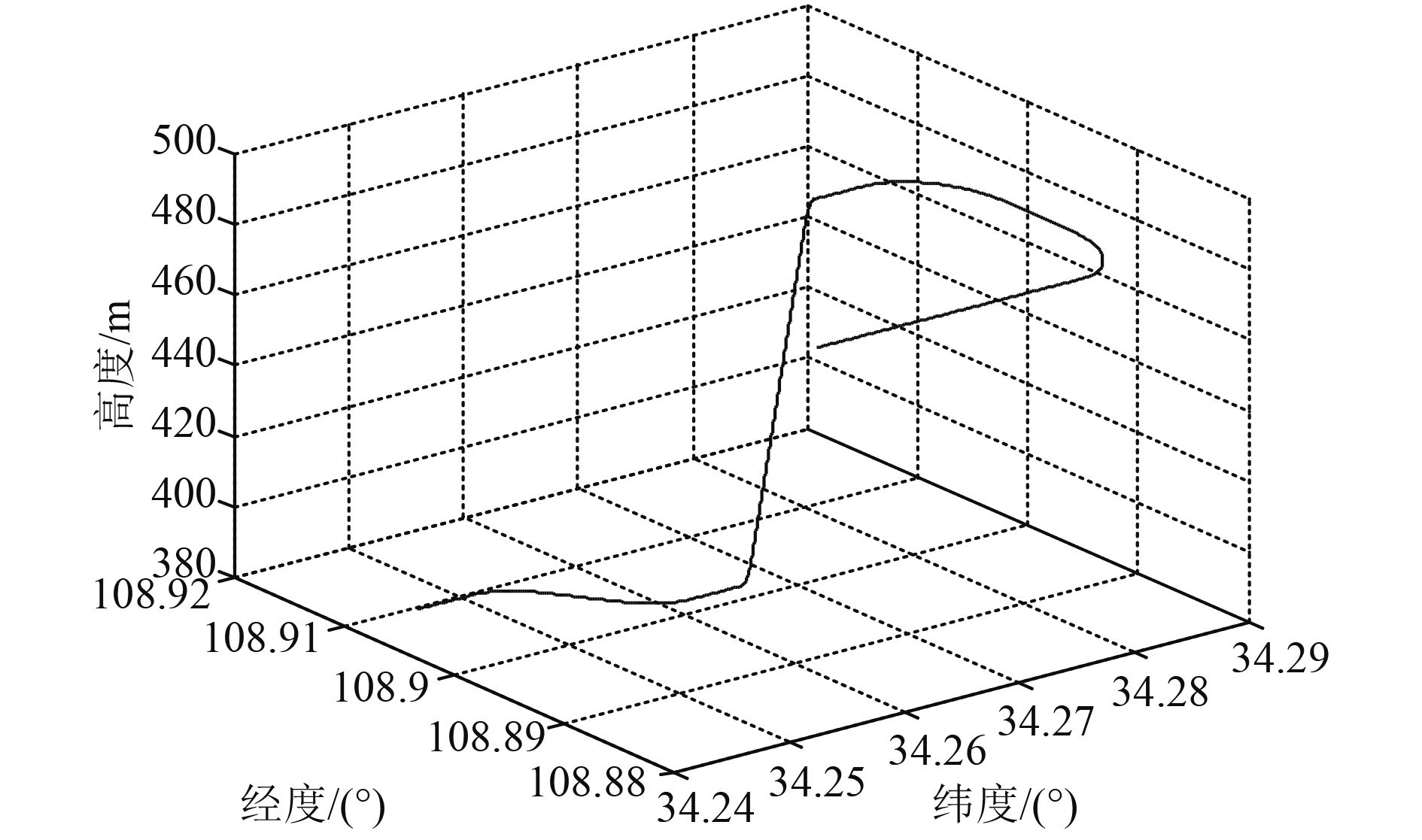
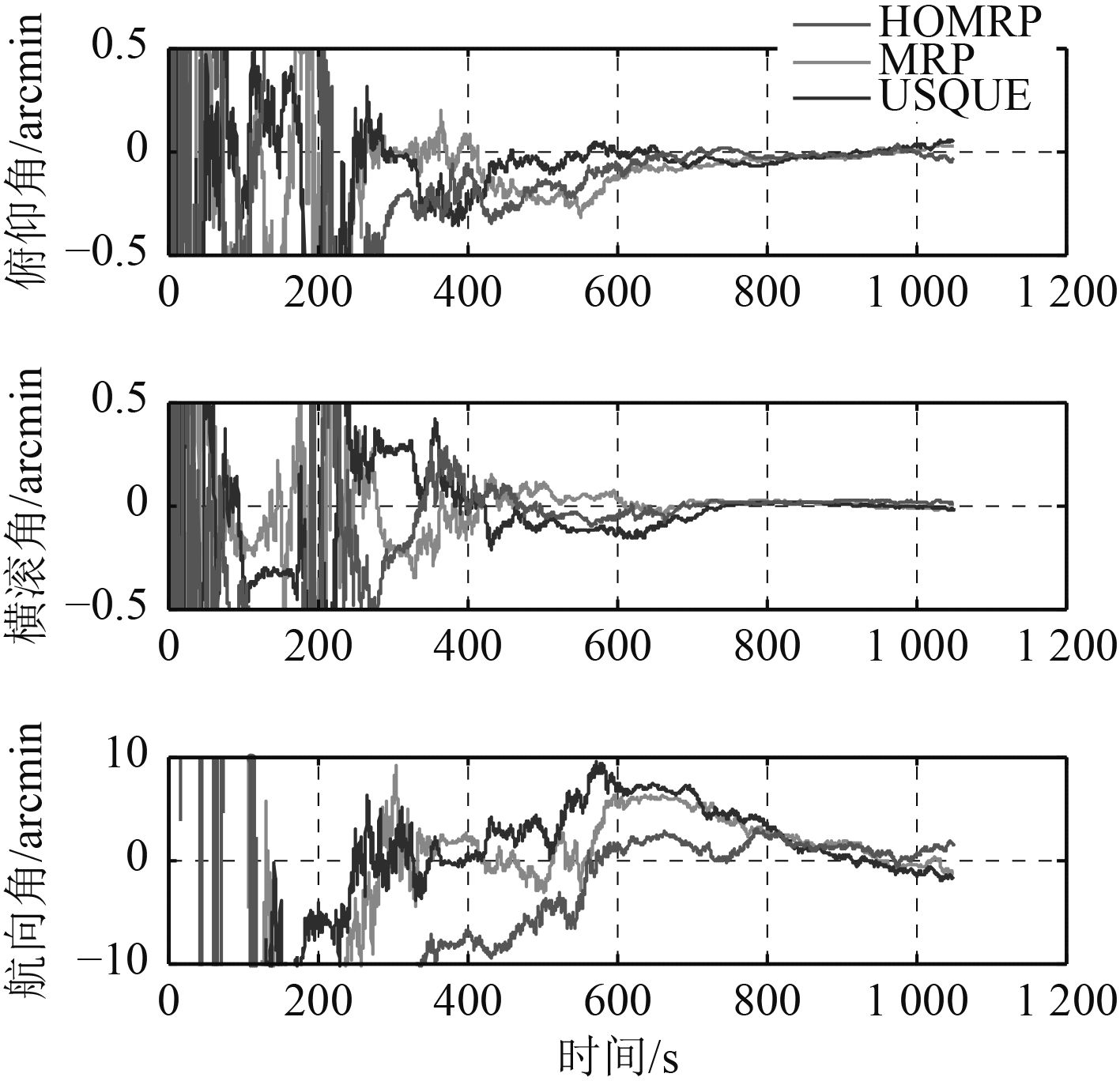
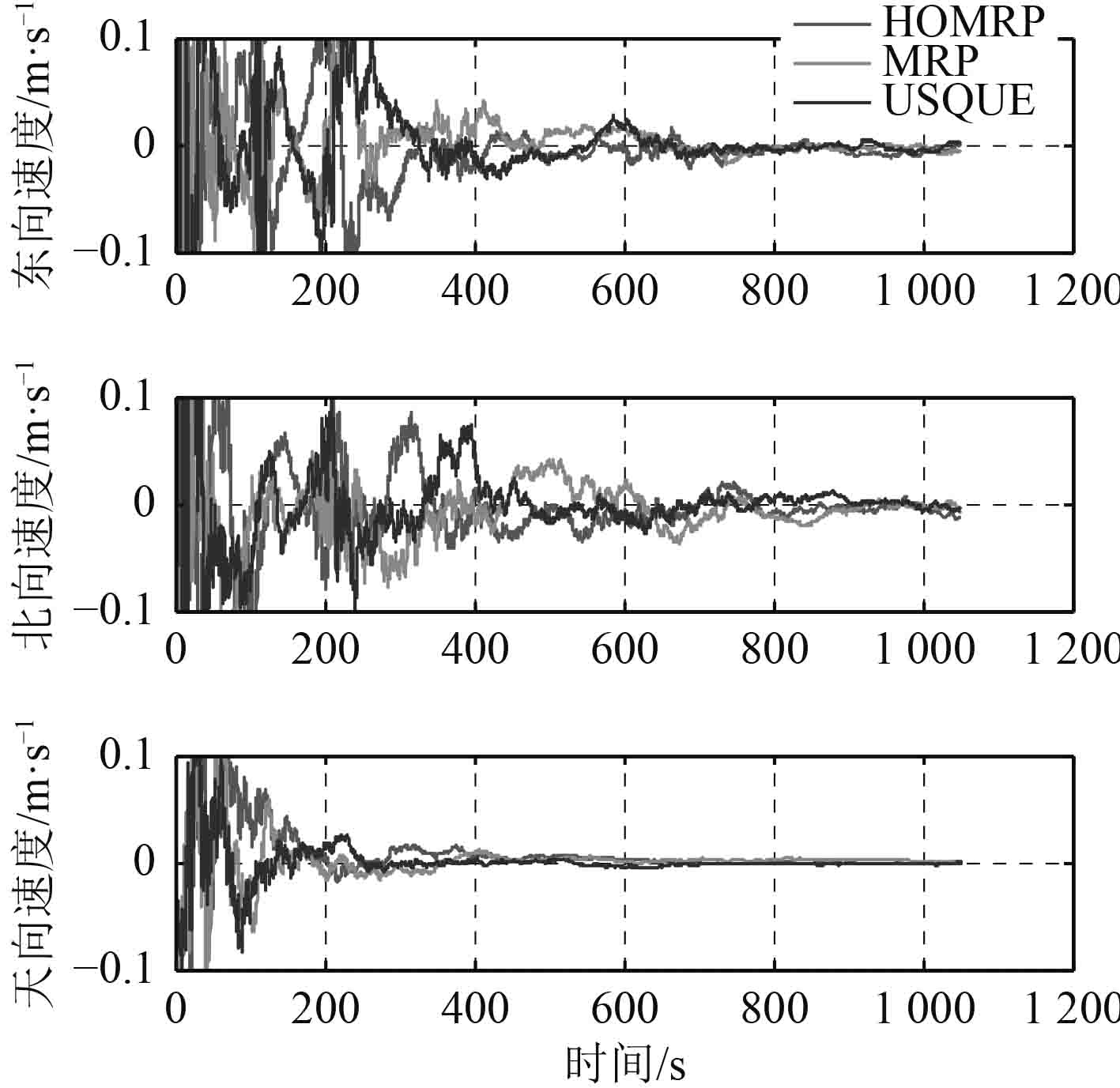
图1为假设运动轨迹,3种姿态参数比较结果如图2~图4所示。
图2~图4主要从姿态、速度、位置比较了基于USQUE、MRP和HOMRP的姿态估计效果。无论是在姿态、速度还是位置估计,都是呈渐进稳定的趋势,并且走势基本相同。在姿态估计结果中,USQUE前期震荡明显小于HOMRP和MRP,但同时达到稳定。在速度和位置估计结果中,USQUE的整体震荡也较小,但是收敛时间较长。为了给大家更直接的感觉,更为清晰的分辨出三者间的效果以及优缺点,下面将其以数值的形式呈现。表格中数据为算数平均数。
|
$y = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {x_i^2} } \text{。}$
|
(30) |
表 1(Tab. 1)

表 1 HOMRP下估计结果均值
Tab. 1 Mean value of the estimated results under HOMRP
姿态(俯仰、横滚、
航向)/arcmin
|
速度(东、
北、天)/m·s–1 |
位置(纬度、
经度、高度)/m
|
时间/s |
| 0.925 4 |
0.030 4 |
0.585 9 |
115.280 9 |
| 0.735 1 |
0.034 1 |
0.586 3 |
| 18.612 |
0.017 1 |
0.399 4 |
|
表 1 HOMRP下估计结果均值
Tab.1 Mean value of the estimated results under HOMRP
|
表 2(Tab. 2)

表 2 MRP下估计结果均值
Tab. 2 Mean value of the estimated results under MRP
姿态(俯仰、横滚、
航向)/arcmin
|
速度(东、
北、天)/m·s–1 |
位置(纬度、
经度、高度)/m
|
时间/s |
| 1.113 2 |
0.025 1 |
0.644 9 |
119.844 5 |
| 1.000 5 |
0.028 2 |
0.541 0 |
| 20.816 6 |
0.009 5 |
0.388 4 |
|
表 2 MRP下估计结果均值
Tab.2 Mean value of the estimated results under MRP
|
表 3(Tab. 3)

表 3 USQUE下估计结果均值
Tab. 3 Mean value of the estimated results under USQUE
姿态(俯仰、横滚、
航向)/arcmin
|
速度(东、
北、天)/m·s–1 |
位置(纬度、
经度、高度)/m
|
时间/s |
| 0.665 9 |
0.026 9 |
0.569 2 |
142.741 6 |
| 0.575 7 |
0.024 9 |
0.593 1 |
| 15.132 9 |
0.007 4 |
0.291 2 |
|
表 3 USQUE下估计结果均值
Tab.3 Mean value of the estimated results under USQUE
|
从表可以看出USQUE在姿态、速度以及经度、高度的均值均小于MRP和HOMRP,证明其在这些方面的估计效果较好,但是时间在三者中最长。同时可以看出在姿态的结果估计中HOMRP的均值要明显小于MRP,但是在速度和位置方面MRP有明显小于HOMRP,可以得到在对姿态的估计HOMRP的效果要好于MRP,而速度和位置方面MRP则要好于HOMRP,三者间HOMRP所用时间最短。结果表明基于USQUE的姿态估计算法的估计精度最高,同时具有全局非奇异性,而基于MRP和HOMRP的姿态估计算法需要设计奇异值避免方法,但计算量要明显小于四元数。
4 结 语 本文重点针对四元数无味估计器、基于修正罗德里格斯参数和高阶罗德里格斯参数所构成的姿态估计算法进行理论推导与性能比较分析。结果表明四元数无味估计器精度最优,但计算量较大,而基于高阶罗德里格斯参数的姿态估计算法计算量最小,相对精度较高。目的是为了在不同环境要求下选择最优算法,从而获得更高效益。

 2018, Vol. 40
2018, Vol. 40
