声呐浮标的作用距离与具体的海洋环境、潜艇的目标特性以及声呐浮标的工作深度等密切相关[1]。在不同的声速剖面下,声呐浮标工作深度不同,其对潜艇的探测距离不同。因此,研究声呐浮标如何根据海洋水声环境进行探测目标,对于提高其环境适应性、探测性具有重要意义。水声学通常把水深200 m以内的海域划分为浅海,而我国近海最显著的特点是200 m以内的浅海水域比较多,多在60~80 m,南海近海海域也鲜有超过100 m的区域。因此,本文重点介绍浅海水文环境的声传播特性、潜艇的目标特性,分析不同水文条件下的声传播损失,提出声呐浮标如何根据实际水文条件合理使用的方法。
1 潜艇辐射噪声模型潜艇的辐射噪声来源于许多方面,主要包括机械噪声和螺旋桨噪声。当潜艇达到一定航速时螺旋桨表面会形成气泡,产生螺旋桨空化噪声,这时,潜艇的辐射噪声急剧增大。该速度称为临界速度。随着潜艇的下潜,临界速度逐渐增大,计算公式如下[2]:
| ${V_c} = {V_{c100}}\sqrt {\frac{{p + \rho gH - p_d^{}}}{{p + 100\rho g - {p_{d100}}}}} \text{,}$ | (1) |
式中:Vc为临界速度,kn;H为潜艇航行深度,m;Vc100为潜艇航行在100 m深度时的临界速度,kn;p为海平面上的标准大气压力,Pa;pd为潜艇航行深度处水的饱和蒸汽压力,Pa,其值远远小于标准大气压力,计算时可忽略;pd100为100 m深度时水的饱和蒸汽压力,Pa,其值远远小于标准大气压力,计算时可忽略;ρ为海水密度,kg/m3;g为重力加速度,m/s2。
本文采用文献[3]中的潜艇辐射噪声仿真模型,如下式:
| $SL = \left\{ \begin{array}{l}25\lg {V_m} + 77 + 20a\;\;\text{,}\;\;\;\;\;\;\;\;\;\;\;{V_m} < {V_c}\text{,}\\104 + 20a + \Delta \;\;\text{,}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{V_m} = {V_c}\text{,}\\104 + 20a + \Delta + b({V_m} - {V_c})\;\;\text{,}\;{V_m} > {V_c}\text{。}\end{array} \right.$ | (2) |
式中:Vm为潜艇的航速,kn;a为潜艇类别,a=1表示极安静潜艇,a=2表示安静潜艇,a=3表示潜艇速度超过临界航速后辐射噪声随航速的变化,按潜艇类型取1.5~2;Δ为潜艇速度超过临界航速后辐射噪声声源级的增量,按潜艇类型取25~50 dB。
以安静型潜艇为例,令b=1.7,Δ=35,通过仿真计算得到潜艇的辐射噪声随航行深度和航行速度的变化规律,如图1所示。从图中可以看出,当潜艇的航速超过其临界速度时,辐射噪声会急剧增大,不利于潜艇的隐蔽,所以潜艇通常都会根据其所处的深度,选择在临界速度以下航行。
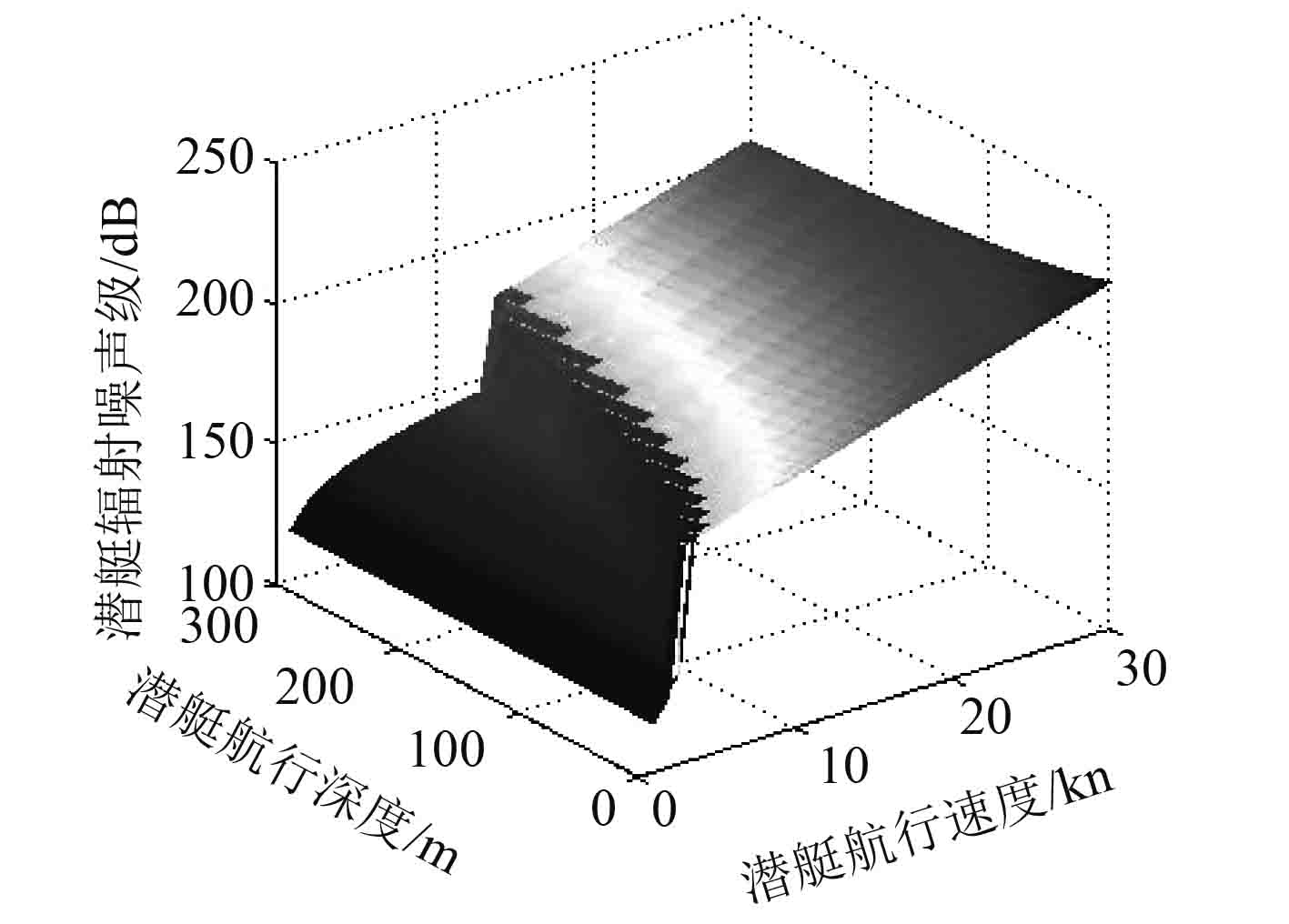
|
图 1 潜艇的辐射噪声与航深和航度的关系 Fig. 1 The relationship of the submarine’s radiated noise and the depth and speed |
浅海环境噪声主要源于海面,主要受海况或海面风速影响[4 – 5],可以通过下式估算噪声谱级。
| $N{L_f} = 10\lg {f^{ - 1.7}} + 6S + 55\text{,}$ | (3) |
式中:f为频率,kHz;S为海况等级(S=0,1,…,9)。则环境噪声级为:
| $\begin{split}NL = 10\lg \left( {\int_{{f_1}}^{{f_2}} {{{10}^{\frac{{N{L_f}}}{{10}}}}{ d}f} } \right) =& 10\lg \left( {f_1^{ - 0.7} - f_2^{ - 0.7}} \right) + \\& 6S + 56.5\text{。}\end{split}$ | (4) |
浅海声场的计算一直是水声领域研究的难点问题,目前国内外都有若干技术比较成熟的声场计算模型,不同的海区条件和声呐参数需要采用不同的模型。本文采用BELLHOP模型来计算水声场。与传统射线模型相比,该模型能够较好地处理声线能量焦散和完全影区等问题,其可靠性在近年来的研究中得到了较充分的验证。
假设一声线的声压p为:
| $p\left( {s,n} \right) = A\left( s \right)\phi \left( {s,n} \right){e^{j\omega \tau }}\text{。}$ | (5) |
式中:ω为圆频率;A为沿声线方向的振幅;ϕ为垂直于声线方向的影响函数;s为沿声线方向的弧长;n为垂直于声线中心方向的位移;τ为沿声线的传播时间。
在柱面坐标系下,控制方程为:
| $\begin{split}& \displaystyle\frac{{{ d}r}}{{{ d}s}} = c\xi \left( s \right),\;\displaystyle\frac{{{ d}\xi }}{{{ d}s}} = - \frac{1}{{{c^2}}}\frac{{{ d}c}}{{{ d}r}}\text{,}\\& \displaystyle\frac{{{ d}z}}{{{ d}s}} = c\zeta \left( s \right),\;\displaystyle\frac{{{ d}\zeta }}{{{ d}s}} = - \frac{1}{{{c^2}}}\frac{{{ d}c}}{{{ d}z}}\text{。}\end{split}$ | (6) |
式中:r和z分别表示水平距离和深度;ξ和ζ为与掠射角有关的2个中间变量,
在射线追踪过程中,通过引入2个变量u和v来控制高斯射线束的能量分布:
| $\frac{{{ d}v}}{{{ d}s}} = cu\left( s \right),\;\frac{{{ d}u}}{{{ d}s}} = - \frac{{{c_{nn}}}}{{{c^2}\left( s \right)}}v\left( s \right)\text{。}$ | (7) |
式中:cnn为声线法线方向的二阶微分。由此,ϕ,A可表示为高斯声线宽度W的函数:
| $\phi \left( {n,s} \right) = \exp \left[ { - {{\left( {n/W} \right)}^2}} \right]\text{,}$ | (8) |
| $A\left( s \right) = \frac{1}{{{{\left( {2\pi } \right)}^{1/4}}}}\sqrt {\frac{c}{{c\left( 0 \right)}}\frac{{\delta \alpha }}{r}\frac{{2\cos \alpha }}{W}} \text{,}$ | (9) |
| $W = v\left( s \right)\delta \alpha /c\left( 0 \right)\text{。}$ | (10) |
式中,δα为临近声线夹角的微分。
传播时间τ可表示为声速倒数的积分:
| $\tau \left( s \right) = \tau \left( 0 \right) = \int_0^S {\frac{1}{{c\left( {s'} \right)}}{ d}s'} \text{。}$ | (11) |
将
| ${p_c}\left( {r,z} \right) = \sum\limits_{j = 1}^N {{p_j}\left( {r,z} \right)} \text{。}$ | (12) |
式中,N为特征声线的个数。
4 典型声速剖面下的声传播及声传播损失 4.1 正梯度声速剖面声速正梯度条件下,声线向海面弯曲,如图2所示。
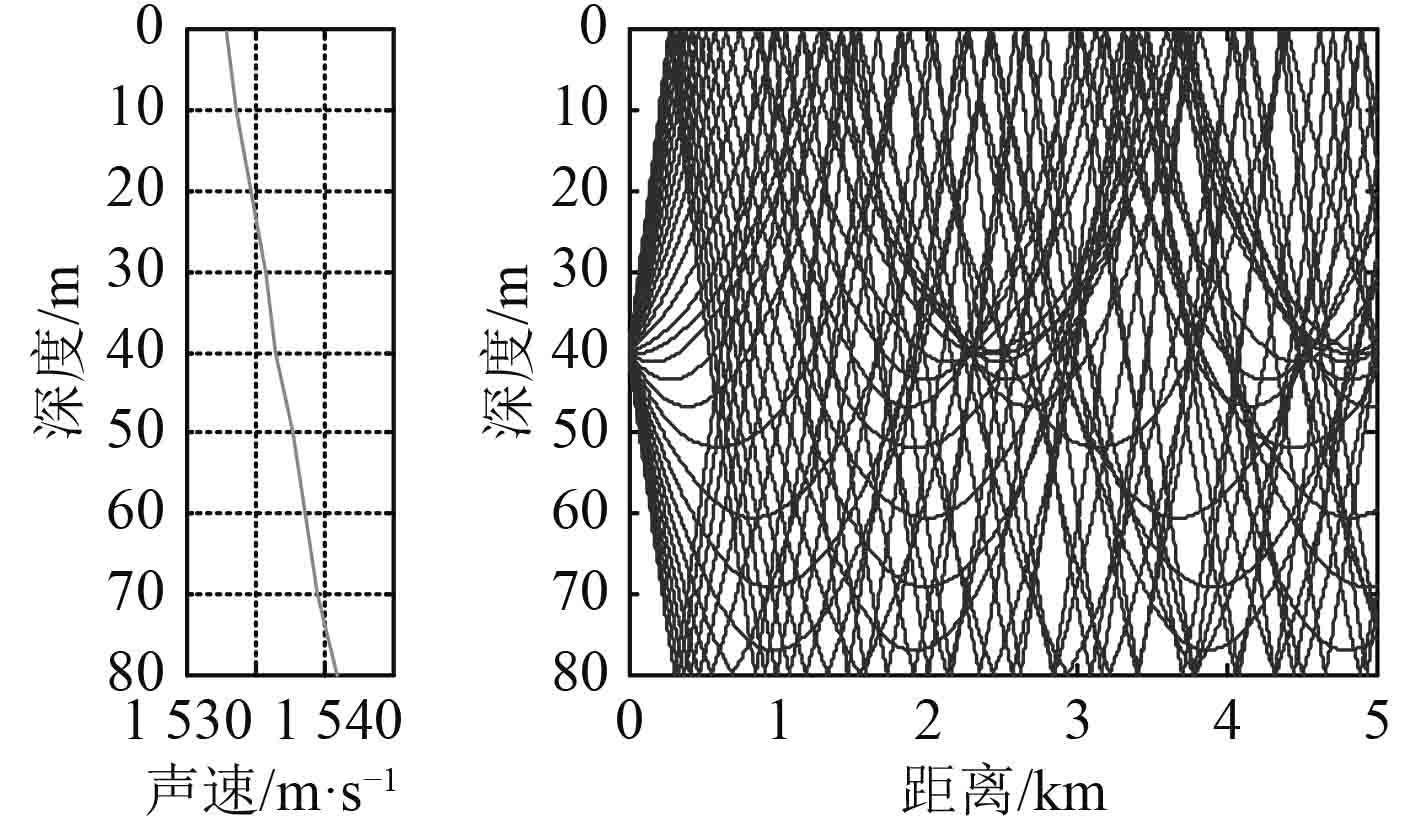
|
图 2 正梯度声速剖面时的声传播特性 Fig. 2 Acoustic propagation characteristic existing positive gradient sound speed profile |
传播损失如图3所示。
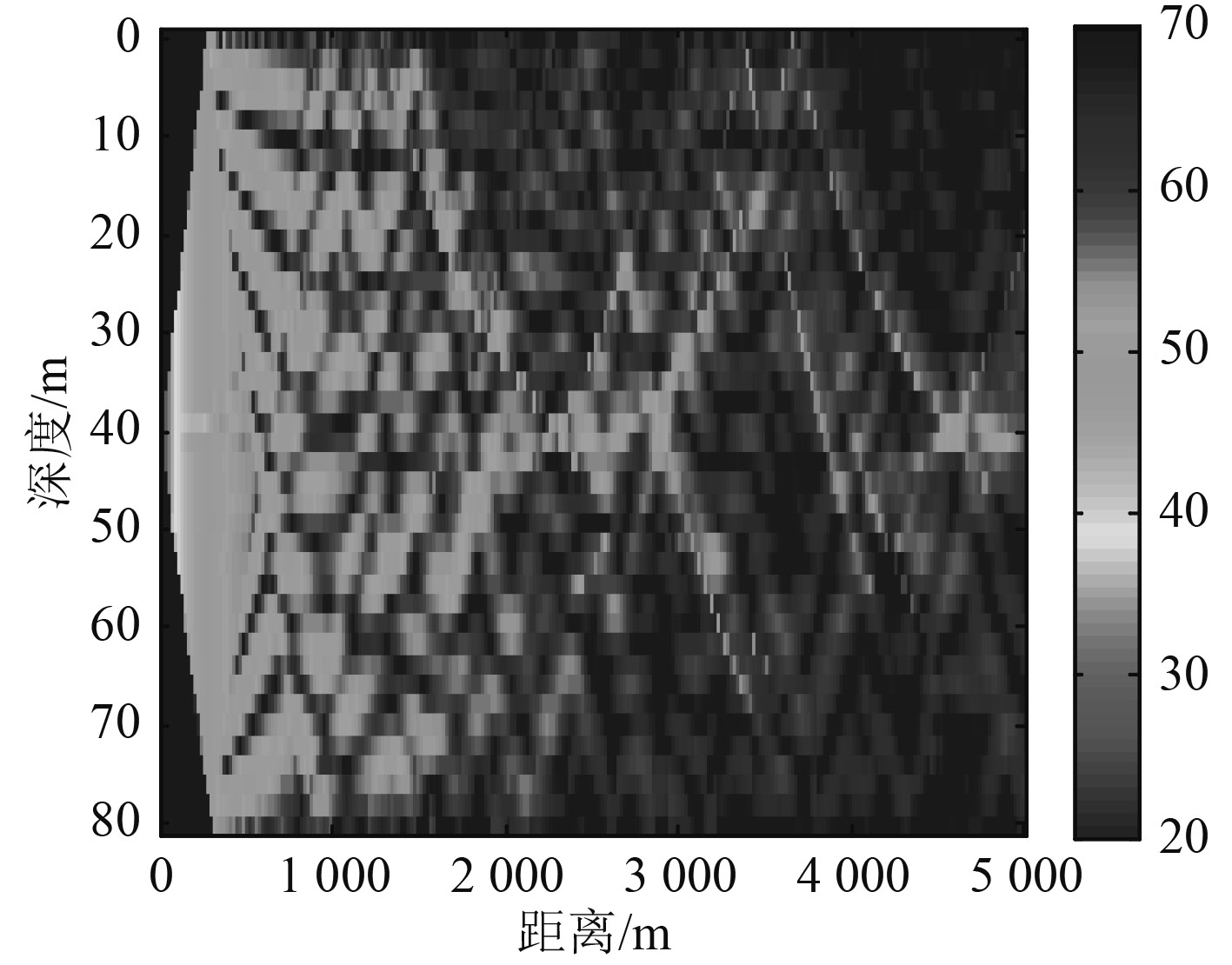
|
图 3 正梯度声速剖面时的声传播损失 Fig. 3 Transmission loss existing positive gradient sound speed profile |
声速负梯度条件下,声线向海底弯曲,如图4所示。

|
图 4 负梯度声速剖面时的声传播特性 Fig. 4 Acoustic propagation characteristic existing negative gradient sound speed profile |
传播损失如图5所示。
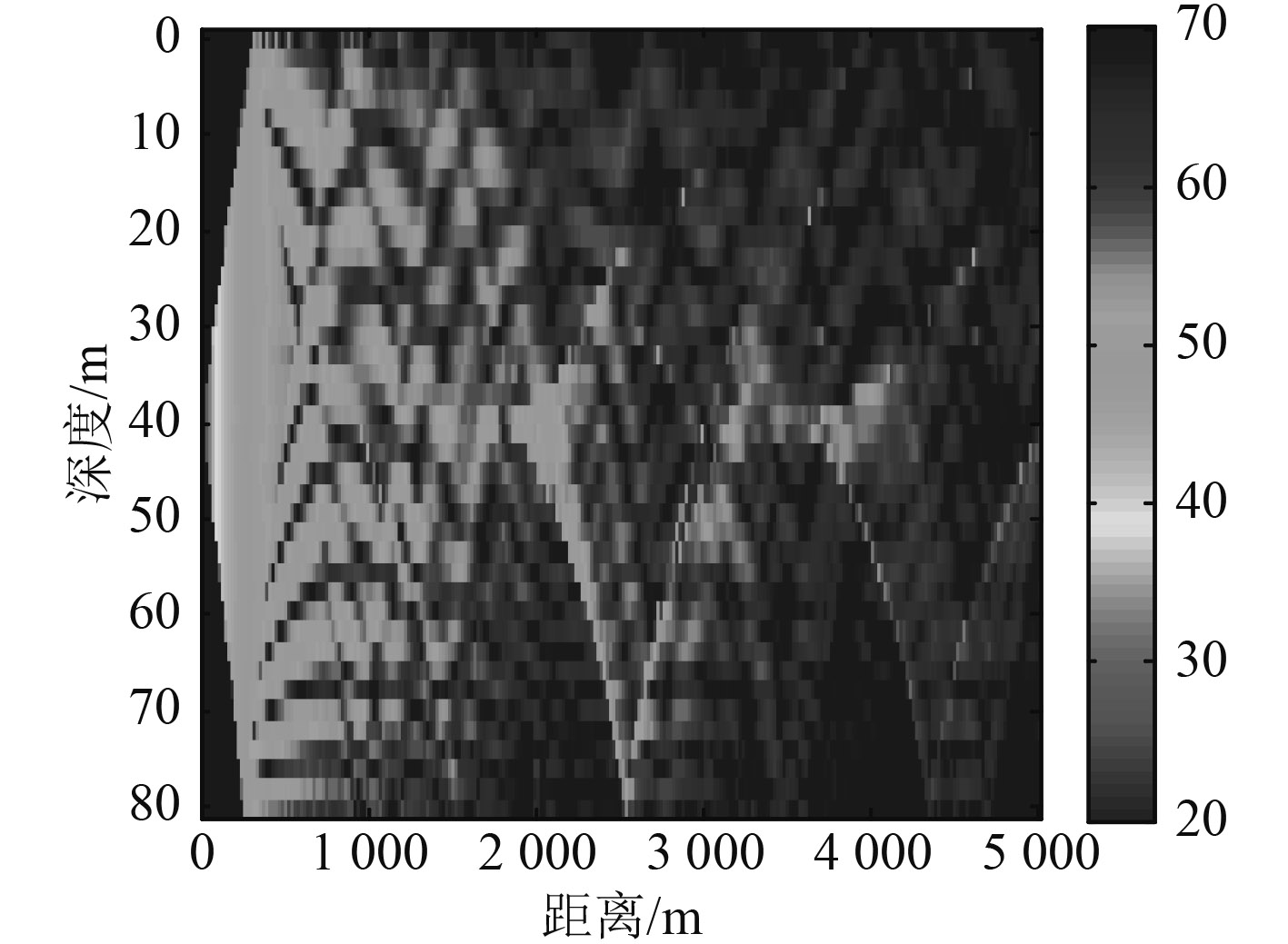
|
图 5 负梯度声速剖面时的声传播损失 Fig. 5 Transmission loss existing negative gradient sound speed profile |
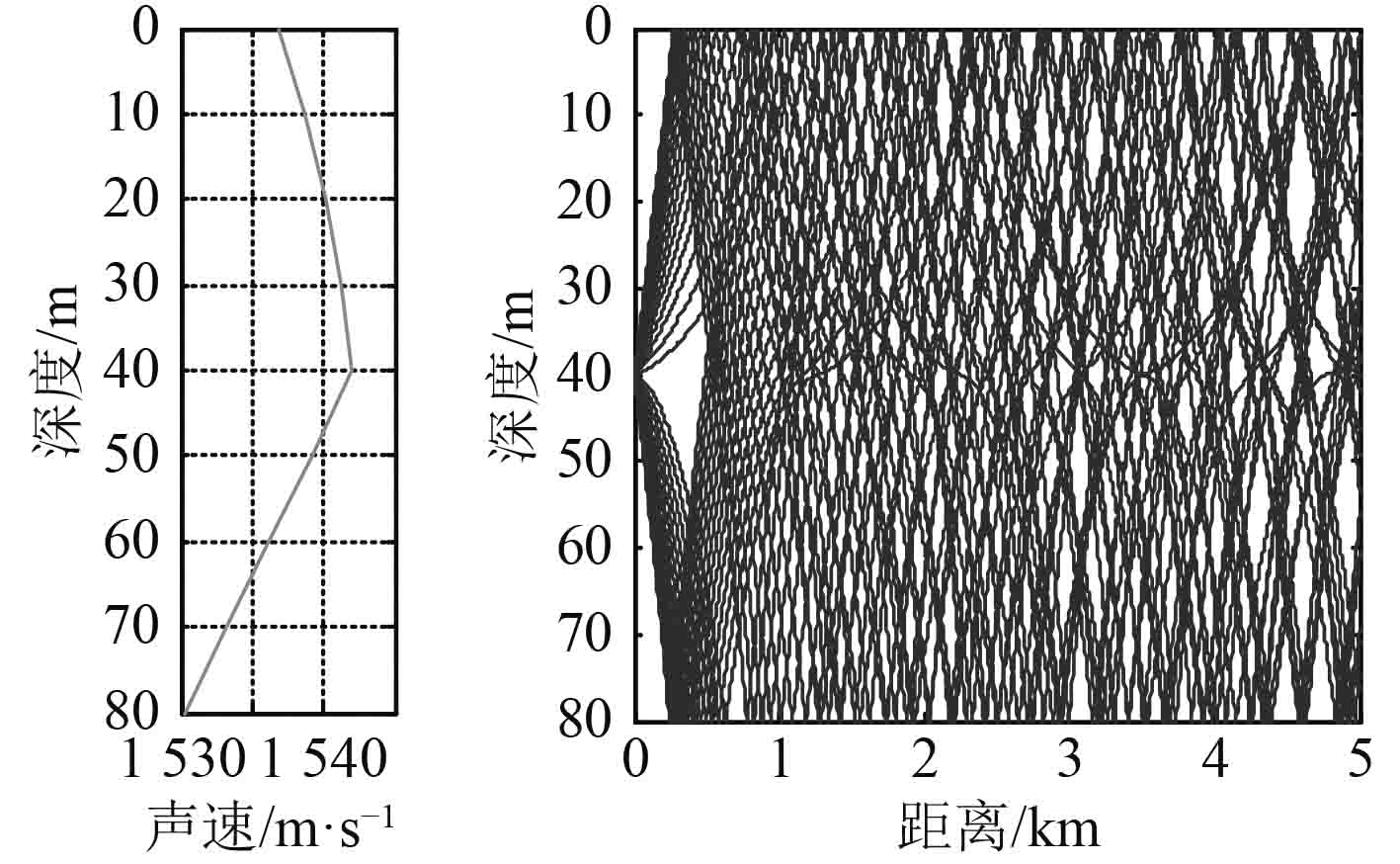
该声速梯度条件下,在跃变层以上,声线向海面弯曲,在跃变层以下,声线向海底弯曲,如图6所示。
|
图 6 反声道声速剖面时的声传播特性 Fig. 6 Acoustic propagation characteristic existing negative sound channel sound speed profile |
传播损失如图7所示。

|
图 7 反声道声速剖面时的声传播损失 Fig. 7 Transmission loss existing negative sound channel sound speed profile |
被动声呐方程为
| $SE = SL - NL - TL - DT + DI\text{,}$ | (13) |
式中:SL为目标声源级,dB;NL为海洋环境噪声,dB;TL为传播损失,dB;DT为检测阈,dB;DI为接收指向性指数,dB;SE为信号余量,dB,通常当SE>0时,认为能检测到目标[4, 7]。
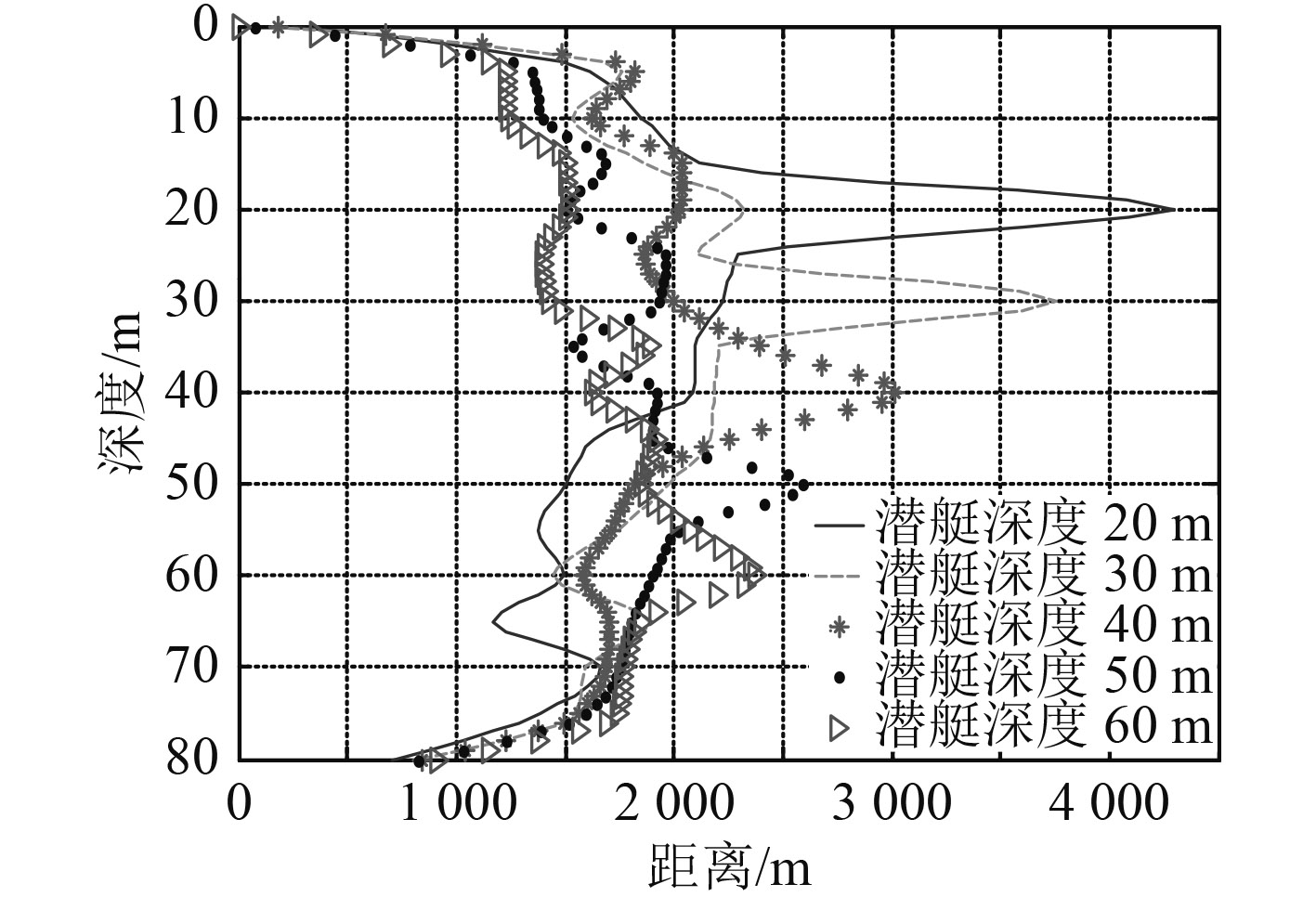
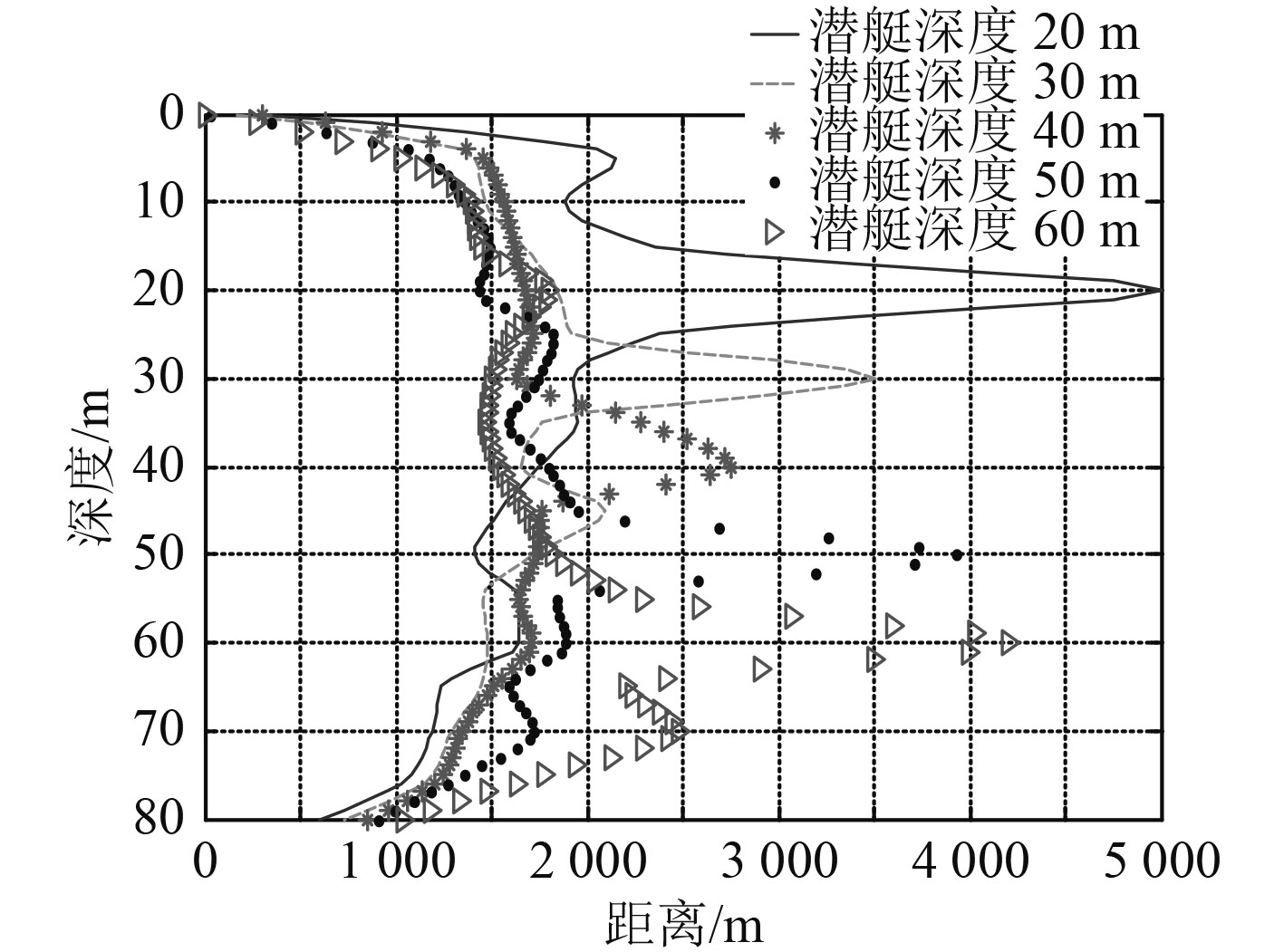
潜艇在海中航行,出于对自身安全的考虑,通常不会距离海面和海底太近,以安静型潜艇为例,假设海区深度为80 m,3级海况,海底平坦,沉积层为砂-泥-粘土,沉积层厚度为20 m,被动全向声呐浮标的接受指向性指数为0,工作带宽为10 Hz~10 kHz,检测阈为10 dB,潜艇航行速度为4 kn,在海区深度上每5 m选一个点,分别仿真计算在3种声速剖面下,潜艇航行深度在20 m(临界速度为4.2 kn)、30 m(临界速度为4.8 kn)、40 m(临界速度为5.4 kn)、50 m(临界速度为5.9 kn)、60 m(临界速度为6.4 kn)时被动声呐浮标在不同深度的探测距离,进而分析声呐浮标的最佳使用深度。如图8~图10所示。
|
图 8 正梯度声速剖面下被动声呐浮标探测距离 Fig. 8 The detection range of passive sonobuoy when positive gradient sound speed profile |

|
图 9 负梯度声速剖面下被动声呐浮标探测距离 Fig. 9 The detection range of passive sonobuoy when negative gradient sound speed profile |
|
图 10 反声道声速剖面下被动声呐浮标探测距离 Fig. 10 The detection range of passive sonobuoy when negative sound channel sound speed profile |
从图8~图10中可以得出一致的结论,即当浮标与潜艇处于同一深度时,均能达到最佳的探测距离。
但通常情况下,潜艇在海中的航行深度未知,从图8中可以看出,当浮标深度处于20 m和30 m时,探测效果最好,最大探测距离能够达到4.3 km。这是由于在正梯度声速剖面下,海面附近会形成表面声道,有利于声信号的远距离传播,因此,在正梯度声速剖面下,可以选择将浮标置于20~30 m之间。
从图9中可以看出,当浮标深度处于50 m和60 m时,探测效果最好,最大探测距离能够达到3.3 km。这是由于负梯度声速剖面下,声线向海底弯曲,经过海底反射后向远距离传播,但声信号经过海底的反射会损失一部分能量,所以在此条件下取得的探测效果不如在表面声道下的探测效果好。因此,在负梯度声速剖面下,可以选择将浮标置于50~60 m之间。
从图10中可以看出,当浮标深度处于20 m,30 m和50 m,60 m时,都能取得较好的探测效果,唯独在40 m时,探测距离较近,这是由于在跃变层以上,声速呈正梯度分布,会在海面附近形成表面声道,有利于声信号的传播,而在跃变层以下,声速呈负梯度分布,声线向海底弯曲,经过海底的反射,向远距离传播。因此,在反声道声速剖面下,可以选择将浮标置于20~30 m之间或者50~60 m之间。
6 结 语本文利用BELLHOP模型计算了浅海水声场。在充分考虑潜艇辐射噪声、海洋环境噪声的情况下,对被动声呐浮标在不同深度的探测效果进行了仿真分析,结果表明,声呐浮标处于不同深度时,对潜艇的探测效果有明显差别,找到浮标的最佳的探测深度,能够充分发挥装备自身的性能,得到最佳的探测效果。
| [1] | 张纪铃, 胡鹏涛. 浅海声速剖面对声呐作用距离的影响研究[J]. 电声技术, 2014, 38(10): 36–38. |
| [2] | 高守勇, 王升, 马力, 等. 潜艇辐射噪声近场特性研究[J]. 声学技术, 2011, 30(3): 7–9. http://industry.wanfangdata.com.cn/dl/Detail/Thesis?id=Thesis_Y936989 |
| [3] | 高学强, 杨日杰. 潜艇辐射噪声声源级经验公式修正[J]. 声学与电子工程, 2007, 87: 17–18. https://www.wenkuxiazai.com/doc/1e5ef1e27c1cfad6195fa7cf.html |
| [4] | 刘伯胜, 雷家煜. 水声学原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2010. |
| [5] | 孟春霞, 李桂娟, 张 亮. 浅海环境噪声垂直指向性获取与分析[J]. 声学技术, 2013, 32(5): 37–39. http://www.cnki.com.cn/Article/CJFDTotal-SCXH197710009.htm |
| [6] | 刘盂庵, 连立民. 水声工程[M]. 杭州: 浙江科学技术出版社, 2002: 72–73. |
| [7] | 梁民赞, 孟华, 陈迎春, 等. 水声环境复杂性对声呐探测距离的影响[J]. 船舶科学技术, 2013, 35(4): 45–48. http://wuxizazhi.cnki.net/Sub/wqjs/a/JCKX201304012.html |
 2018, Vol. 40
2018, Vol. 40
