机械噪声是舰艇水下辐射噪声主要噪声源,是降低舰艇水下辐射噪声水平的主要控制方向。精确定位机械声源艇体表面强辐射区域,是深入研究机械声源传递特性、定量分离机械噪声贡献的前提和基础[1, 2]。
近场声全息是一种有效的机械声源定位技术,首先由Williams[3]基于Fourier声学提出。针对空间离散域Fourier变换存在严重的空间频率泄露问题,后续研究人员相继提出比较有效的近场声全息信息处理方法,主要包括:基于边界元法近场声全息[4]、基于等效源法近场声全息[5]、基于Helmholtz最小二乘近场声全息[6]和统计最优近场声全息[7 – 9]。
统计最优近场声全息是利用叠加原理,通过全息面到重构面的曲线拟合实现声场反演,最终达到辐射声场重构或预测。统计最优近场声全息是利用叠加原理,通过全息面到重构面的曲线拟合实现声场反演,最终达到辐射声场重构或预测。由于不受测量数据数量的限制,可以对基波函数进行任意高阶次截断,统计最优近场声全息能够获得高精度的声场投影,是全局最优的声场重构方法。根据舰艇结构特征,采用基于柱面坐标的多参考统计最优近场声全息算法,可实现机械声源艇体表面强辐射区域定位。实际结构近场声全息测量一般采用扫描法,该测量方法简便易行。本文针对扫描法测量全息面复声压的获取方式,重点研究柱面统计最优算法定位精度的影响因素及关系,为实艇机械声源近场声全息定位提供实用化参数选择依据。
1 柱面统计最优近场声全息算法 1.1 测量模型在圆柱坐标系(r,φ,z)中,

|
图 1 柱面全息面及声源重构面网格剖分 Fig. 1 Mesh reconstruction of cylindrical holographic surface and sound source |
在全息面划分测量节点和网格过程中,连续信号将在空间上被离散。在空间采样过程,全息面测量网格剖分,决定着柱面波函数计算所引入截断误差的大小,影响着声源面的重构精度。测量信号若以采样间隔
| ${k_{z,N}} = \frac{1}{2}\left( {\frac{{2\pi }}{\Delta }} \right)\text{。}$ | (1) |
在圆柱坐标系下,全息面
| $\begin{aligned}&{k_{s,N}} = \frac{1}{2}{\left. {\left( {\frac{{2\pi }}{{\Delta s}}} \right)} \right|_{\Delta s = \frac{{2\pi {r_h}}}{{P - 1}}}} = \frac{{P - 1}}{{2{r_h}}}\text{,}\\ &{k_{z,N}} = \frac{1}{2}{\left. {\left( {\frac{{2\pi }}{{\Delta z}}} \right)} \right|_{\Delta z = \frac{{2L}}{{Q - 1}}}} = \frac{{\pi (Q - 1)}}{{2L}}\text{。}\end{aligned}$ | (2b) |
在空间采样过程,空间截断频率不得高于相应的Nyquist波数,否则由采样定理可知信号将出现混叠失真。因此,根据Nyquist波数计算式(2),能够选择适当的空间截断频率,并借助空间截断频率能够指导全息面测量网格的剖分。
1.2 多参考全息面复声压全息面复声压用声压幅值和相位描述。声压幅值通过在全息面上测量节点信号自谱直接获得,声压相位通过参考点与测量节点信号互谱获得。当声源仅为一个或不相干时,采用单参考点;当声源为多个相干源时,采用多参考点。
针对单参考点情况,采用J元阵进行K次扫描实现全息面的声压逐点扫描测量,其中
| ${\left[ {\begin{array}{*{20}{c}}{{y_{1k}}} \!\!&\!\! {{y_{2k}}}\!\! &\!\! \cdots & {{y_{Jk}}}\end{array}} \right]^{{T}} } = {r_{1k}}{\left[ {\begin{array}{*{20}{c}}{{h_{1k}}} \!\! & \!\! {{h_{2k}}} \!\! & \!\! \cdots \!\! &\!\! {{h_{Jk}}}\end{array}} \right]^{{T}}\text{,} }$ |
其向量格式为
| ${{{Y}}_k} = {R_k}{{{H}}_k}\text{,}$ | (3b) |
若
| ${\overline{\overline Y} _{jk}} = \sqrt {{C_{{y_{jk}}{y_{jk}}}}} {e^{j\angle {C_{{y_j}_k{r_{1k}}}}}}\text{。}$ | (4) |
针对多参考点情况,采用上述单参考点相同的全息面声压逐点扫描测量方式。其中,
| $\left[ {\begin{array}{*{20}{c}}{{y_1}} \\{{y_2}} \\\vdots \\{{y_N}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{h_{11}}} & {{h_{12}}} & \cdots & {{h_{1M}}} \\{{h_{21}}} & {{h_{22}}} & \cdots & {{h_{2M}}} \\\vdots & \vdots & \ddots & \vdots \\{{h_{N1}}} & {{h_{N2}}} & \cdots & {{h_{NM}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{r_1}} \\{{r_2}} \\\vdots \\{{r_M}}\end{array}} \right]\text{,}$ |
其矩阵格式为
| ${{y}} = {{{H}}_{{yr}}}{{r}}\text{,}$ | (5b) |
对方程(5),等式两边乘
| ${{{H}}_{{yr}}} = {{E}} \{ {{y}}{{{r}}^{{H}} }\} \cdot {{{E}} ^{ - 1}}\{ {{r}}{{{r}}^{{H}} }\} = {{{C}}_{{yr}}}{{C}}_{{rr}}^{ - 1}\text{,}$ | (6) |
参考点声压信号自谱矩阵
| ${{{C}}_{{rr}}} = {{U\Sigma }}{{{V}}^{{H}} } = {{U\Sigma }}{{{U}}^{{H}}\text{,} }$ | (7) |
若定义局部场
| ${{Y}} = {{{H}}_{{yr}}}{{U}}{{{\Sigma }}^{1/2}} = {{{C}}_{{yr}}}{{U}}{{{\Sigma }}^{ - 1/2}}\text{。}$ | (8) |
综合单参考点和多参考点情况,能够基于逐点声压扫描测量方式建立全息面的复声压场。
1.3 柱面统计最优数学模型在圆柱坐标下,声场介质中坐标位置
| $\left( {{\nabla ^2} - \frac{1}{{{c^2}}}\frac{{{\partial ^2}}}{{\partial {t^2}}}} \right)p = 0\text{,}$ | (9) |
其中,
| ${\nabla ^2} = \frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{r}\frac{\partial }{{\partial r}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {\varphi ^2}}} + \frac{{{\partial ^2}}}{{\partial {z^2}}}\text{,}$ |
Helmholtz方程(9)的自由场行波解
| $\begin{array}{l}p(r,\varphi ,z) = \sum\limits_{n = - \infty }^{ + \infty } {{e^{jn\varphi }}\frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty } {{ d}{k_z}{P_n}({r_s},{k_z})} } \text{,}\\{e^{j{k_z}z}}\left\{ {\begin{array}{*{20}{c}}{\frac{{{{H}}_n^{(1)}({k_r}r)}}{{{{H}}_n^{(1)}({k_r}{r_s})}},{k_r} = \sqrt {{k^2} - k_z^2} }\text{,}\\[5pt]{\frac{{{{{K}}_n}({k_r}^\prime r)}}{{{{{K}}_n}({k_r}^\prime {r_h})}},{k_r}^\prime = \sqrt {k_z^2 - {k^2}} }\text{,}\end{array}} \right.\end{array}$ | (10) |
式中:
根据波动方程解的结构,柱面统计最优算法定义柱面波函数
| ${\varPhi _{n,{k_z}}}(r,\phi ,z) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{\mathop{ H}\nolimits} _n^{(1)}({k_r}r)}}{{{\mathop{ H}\nolimits} _n^{(1)}({k_r}{r_s})}}{e^{jn\varphi }}{e^{j{k_z}z}},\;\;{k_r} = \sqrt {{k^2} - k_z^2} }\\{\frac{{{{\mathop{ K}\nolimits} _n}({k_r}'r)}}{{{{\mathop{ K}\nolimits} _n}({k_r}'{r_s})}}{e^{jn\varphi }}{e^{j{k_z}z}},\;\;{k_r}' = \sqrt {k_z^2 - {k^2}} }\end{array}} \right. \!\! \text{,}r \geqslant {r_s}\text{。}$ | (11) |
将方程(11)利用求和计算积分,并进行截断处理,得
| $p(r,\varphi ,z) \! \approx \! \frac{1}{{2\text{π} }}\sum\limits_{n = 0}^N {\sum\limits_{m = 0}^M {{P_n}({r_s},m \cdot \Delta {k_z}){\varPhi _{n,m}}(r,\varphi ,z)} } \Delta {k_z}\left| {_{{k_z} = m \cdot \Delta {k_z}}} \right.\text{,}$ | (12) |
为了便于实现理论推导,将全息面、重构面的二维柱面网格映射到一维数据结构,即
| $({r_t},{\varphi _p},{z_q})\xrightarrow{{l = (q - 1)P + p}}\left( {{{\vec r}_{t,j}}} \right)\text{,}$ | (13) |
利用全息面上PQ个测量节点的声压信息进行最小二乘拟合,重构面的声压预测[11],即
| $p({\vec r_{t,j}}) = \sum\limits_{l = 1}^{PQ} {{c_l}({{\vec r}_{h,j}})p({{\vec r}_{h,l}})}\text{。} $ | (14) |
在重构面
| ${\varPhi _{n,m}}({\vec r_{t,j}}) = \sum\limits_{l = 1}^{PQ} {{c_l}({{\vec r}_{h,j}}){\varPhi _{n,m}}({{\vec r}_{h,l}})} \left| {_{{k_z} = m \cdot \Delta {k_z}}} \right.\text{,}$ | (15) |
方程(15)写成矩阵形式
| ${{b}} = {{Ac}}\text{,}$ | (16) |
其中,
| ${ b} \!=\! {\left[ {{b_{kl}}} \right]_{MN \times PQ}}\mathop \equiv \limits^{l = (q - 1)P + p,k = (n - 1)M + m} {\left[ {{\varPhi _{n,m}}(r,{\varphi _p},{z_q})} \right]_{MN \times PQ}}\text{,}$ |
| ${{A}} \!=\! {\left[ {{a_{kl}}} \right]_{MN \times PQ}}\mathop \equiv \limits^{l = (q - 1)P + p,k = (n - 1)M + m} {\left[ {{\varPhi _{n,m}}({r_h},{\varphi _p},{z_q})} \right]_{MN \times PQ}}\text{,}$ |
| ${{c}} \!=\!\! {\left[ {{c_{kl}}} \right]_{PQ \times PQ}}\mathop \equiv \limits^{l = (q - 1)P + p,k = (n - 1)M + m} {\left[ {{c_l}(r,{\varphi _p},{z_q})} \right]_{PQ \times PQ}}\text{。}$ |
所以权系数矩阵为
| ${{c}} = {({{{A}}^{{H}} }{{A}} + \Theta {{I}})^{ - 1}}{{{A}}^{{H}} }{{b}}\text{,}$ | (17) |
其中,正则化因子
将权系数矩阵(17)代入方程(14),并以矩阵形式表述重构面上声压
| $\begin{split}&{\left[ {{p_{r(j)}}} \right]_{1 \times PQ}} = {\left[ {{p_h}_{(j)}} \right]_{1 \times PQ}}{\left[ {{c_{lk}}} \right]_{PQ \times PQ}}=\\& {{p}}_h^{\mathop{ T}\nolimits} {({{{A}}^{\mathop{ H}\nolimits} }{{A}} + \Theta {{I}})^{ - 1}}{{{A}}^{\mathop{ H}\nolimits} }{{b}}\text{。}\end{split}$ | (18) |
其中全息面测量声压由式(8)给出。
2 定位精度影响因素分析根据近场声全息测量方法与柱面统计最优近场声全息算法,通过仿真研究,分析信息处理参数与测量阵参数对声源定位精度影响关系,为柱面统计最优近场声全息定位方法参数实用化选择提供依据。
2.1 信息处理参数根据柱面统计最优近场声全息算法的理论推导可知,影响重构面声压计算结果的因素主要包括正则化因子、倐逝波截断波数,而柱面函数的截断阶次因其高阶累计量相对较小而在选取一定阶次以后对算法影响不大。
倐逝波截断波数由倐逝波信噪比D和k-space指数窗函数共同决定。根据轴向倐逝波条件方程可得[9]:
轴向波数
| $\left| {{k_{z,c}}} \right| < \frac{{\pi D}}{{27.3({r_h} - {r_s})}}\text{,}$ | (19) |
周向波数上限
| $\left| {{k_{s,c}}} \right| = \frac{n}{{{r_s}}} < \frac{{\pi D}}{{27.3({r_h} - {r_s})}}\text{,}$ | (19b) |
于是,波数k-space指数窗函数为
| ${W_{{{k - space}}}} = \left\{ \begin{array}{l}1 - \displaystyle\frac{1}{2}{e^{ - \left( {1 - \left| {{k_t}} \right|/{k_c}} \right)/{\alpha _k}}}\;\;\text{,}\;\;\left| {{k_t}} \right| < {k_c}\text{,}\\\displaystyle\frac{1}{2}{e^{\left( {1 - \left| {{k_t}} \right|/{k_c}} \right)/{\alpha _k}}}\;\;\;\;\text{,}\;\;\;\;\;\left| {{k_t}} \right| > {k_c}\text{。}\end{array} \right.$ | (20) |
其中,
设在圆柱坐标系,全息面半径rh=0.414 5 m,左端z0=0 m,右端zh=0.85 m的圆柱面,声源面与重构面半径分别为rc=0.075 m和rs=0.09 m,在全息面上进行32×34个节点的网格剖分,声源频率fr=1 000 Hz,声源坐标(0.075 m,180°,0.65 m)。
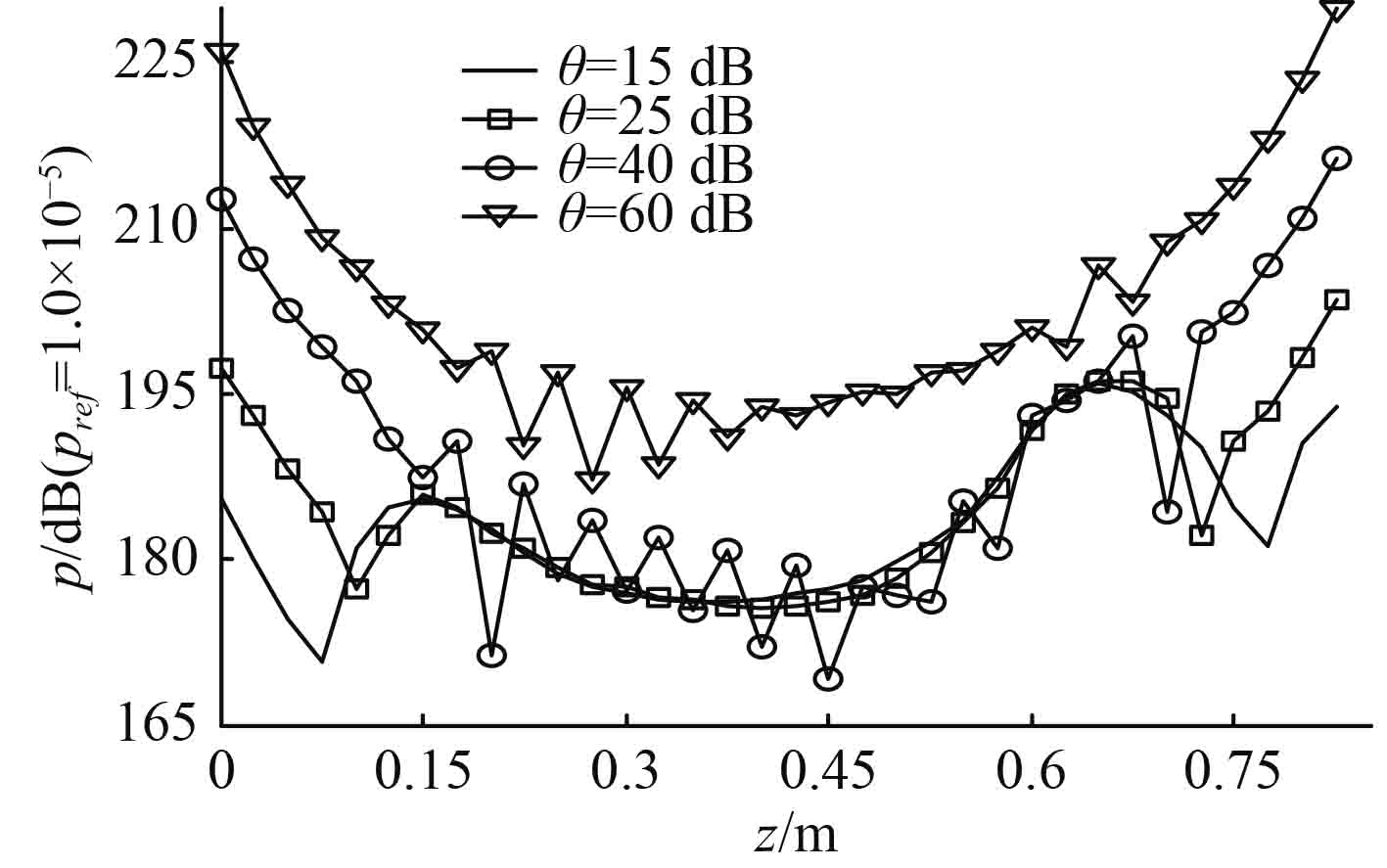
在图2中,通过选择不同的
|
图 2 正则化因子对重构声压沿轴向分布影响 Fig. 2 Influence of regularization factor on the distribution of reconstructive sound pressure along the axial diretion |
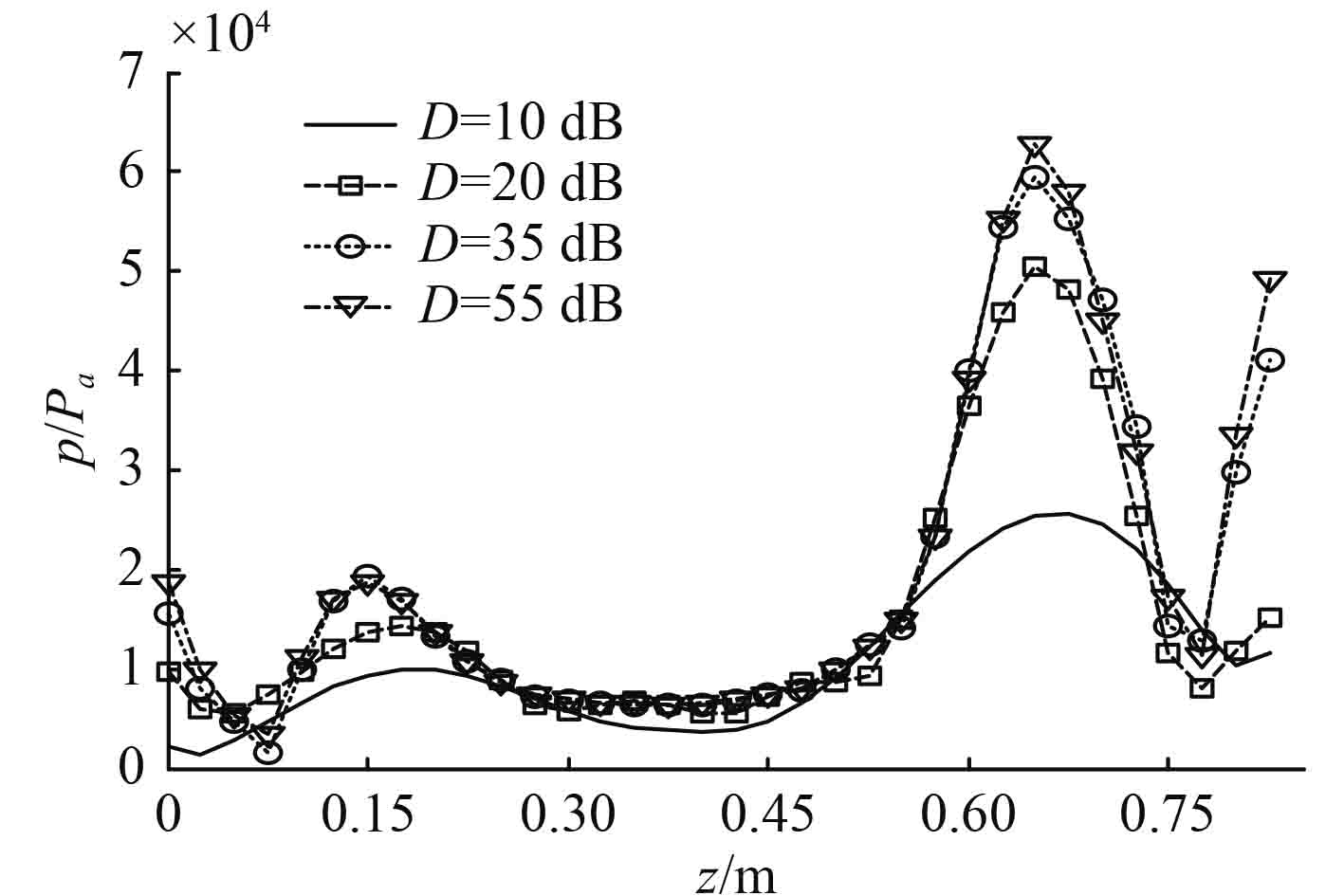
在图3中,倏逝波信噪比D分别为10 dB,20 dB,35 dB和55 dB。在确定的测量距离
|
图 3 倏逝波信噪比对重构声压沿轴向分布影响 Fig. 3 Influence of evanescent wave sing-to-noise ratio on the distribution of reconstructive sound pressure along the axial diretion |
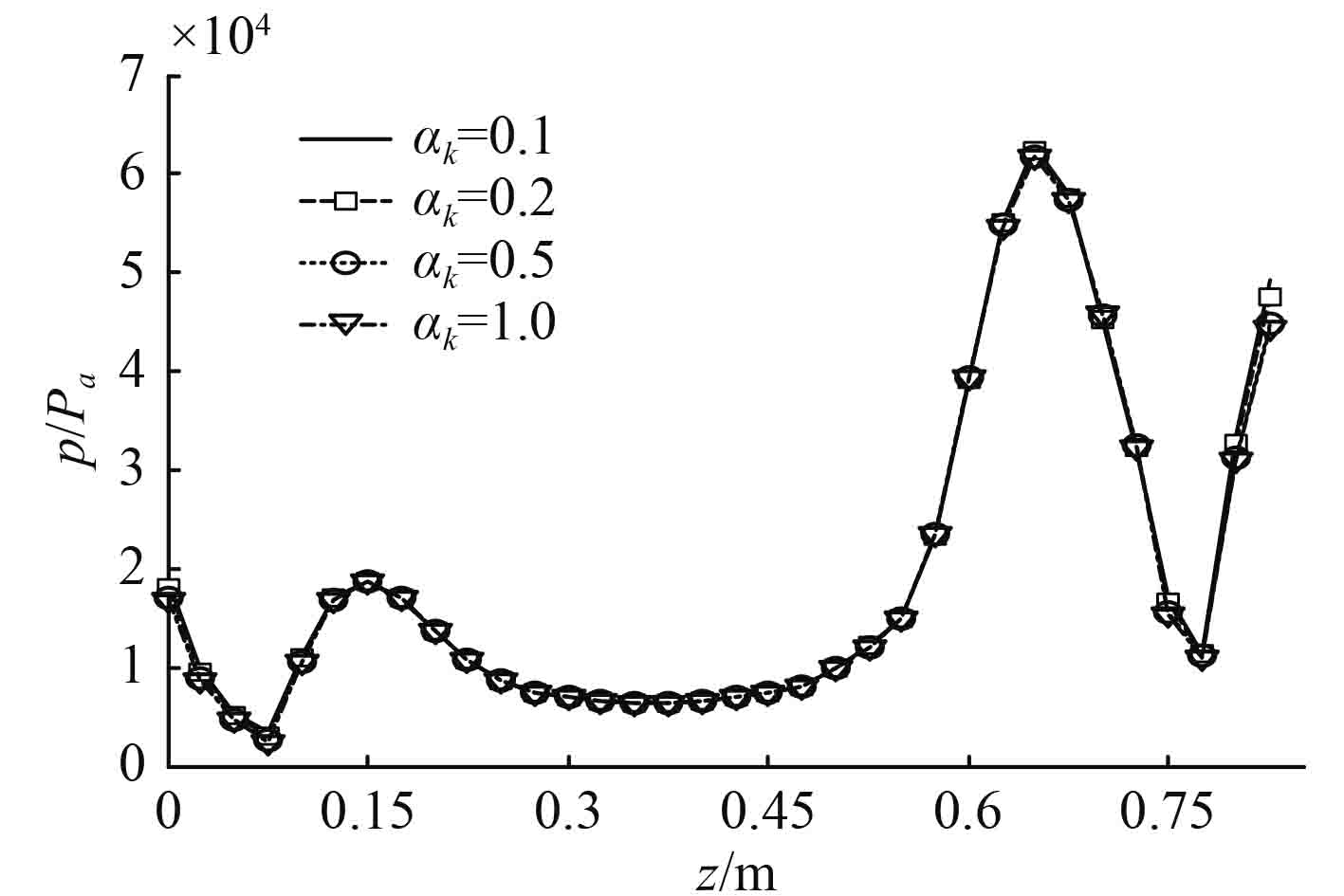
在图4中,选择不同的窗型参数
|
图 4 窗型参数对重构声压沿轴向分布影响 Fig. 4 Influence of window parameter on the distribution of reconstructive sound pressure along the axial direction |
根据柱面全息面测量方法,影响定位精度的测量系统参数主要包括阵元间距l、全息面尺寸L和测量距离ds。对于实际测量系统,声压的测量不可能遍布整个全息面,而只能是覆盖于全息面上一个特定二维尺寸的表面积上,这个特定尺寸的表面积称为测量孔径。对于柱面结构,测量孔径在轴向方向有限,导致测量信号的不连续性,存在着空间频率泄露,最终造成边缘节点上的重构声场数值的发散和无意义。为此,采用将Tukey窗函数应用于轴向滤波,能够有效抑制空间频率泄露,有效地消除了有限测量孔径效应。
Tukey窗函数
| ${W_{{{Tukey}}}} = \left\{ {\begin{array}{*{20}{c}}\begin{array}{l}\displaystyle\frac{1}{2} + \displaystyle\frac{1}{2}\cos \left[ {\frac{{2\pi }}{\alpha }\left( {z - {z_R}/2} \right)/{L_{w,T}} - \pi } \right]\text{,}\\{z_R}/2 - {L_{w,T}} \leqslant z \leqslant {z_R}/2\text{,}\\1\quad\text{,} z < {z_R}/2 - {L_{w,T}}\text{,}\\0\quad\text{,} z > {z_R}/2\text{。}\end{array}\end{array}} \right.$ |
式中:
仿真条件与2.1节相同,根据柱面统计最优算法,以下分别给出声源定位偏差与测量阵参数及

|
图 5 阵元间距对定位精度影响 Fig. 5 Influence of array element spacing on positioning accuracy |
从图5仿真结果可以看出,重建位置偏差随阵元间距增大,且当其他测量参数取值比较理想时,阵元间距小于波长的1/3时阵元间距的改变对声源重建位置的影响并不大。由所取的几组测量参数值的结果可以得出,当取
|
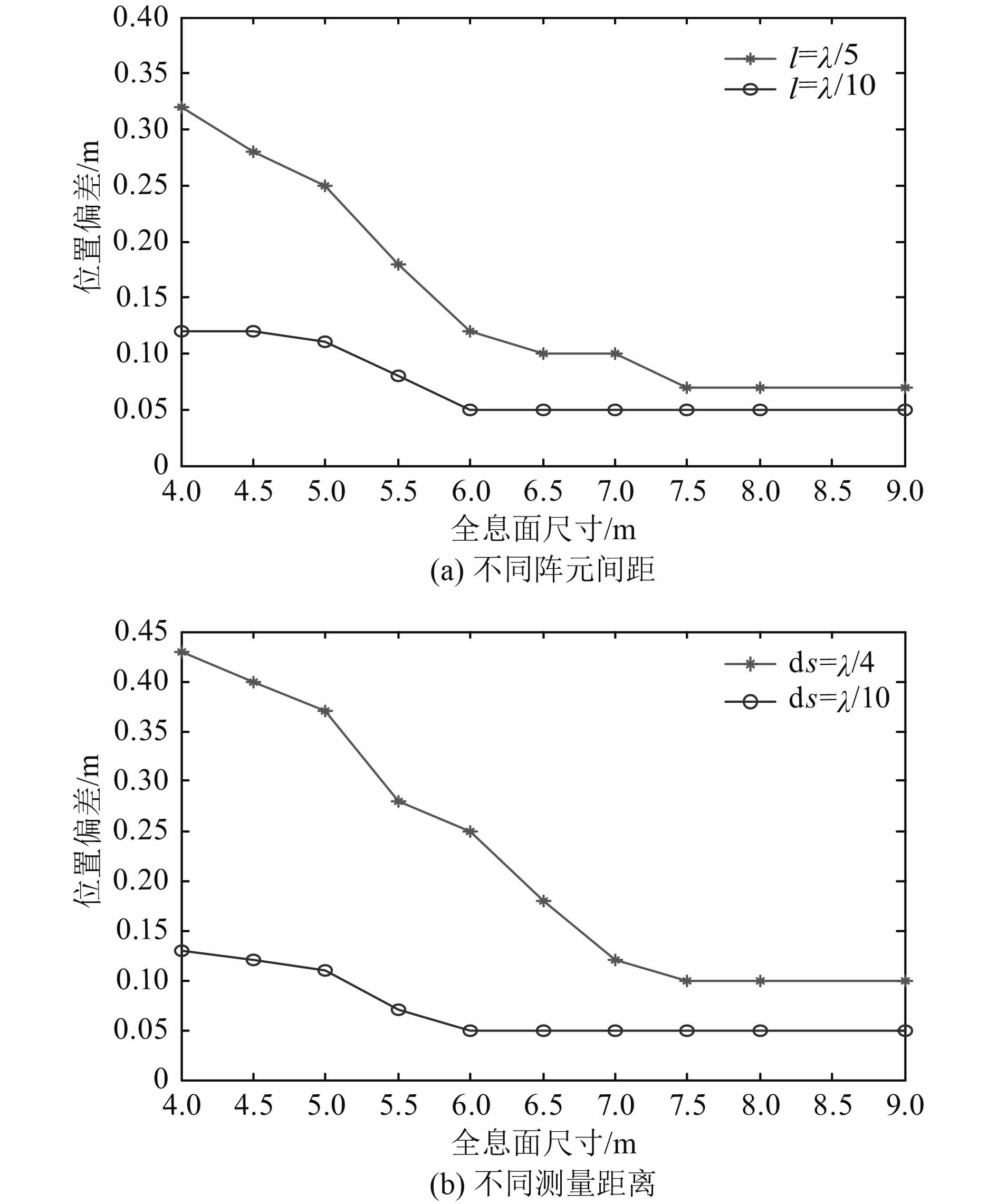
图 6 全息面尺寸对定位精度影响 Fig. 6 Influence of holographic size on positioning accuracy |
从图6的仿真结果可以看到,重建位置偏差随全息测量面尺寸增大而减小,且当其他测量参数取值比较理想时,测量面边长大于3倍波长的重建结果已经很准确。

|
图 7 测量距离对定位精度影响 Fig. 7 Influence of measuring distance on positioning accuracy |
从图7可知,全息测量距离增大时,重建位置偏差随之增大。当其他测量参数选取比较理想,测量距离小于波长的1/5时,重建位置偏差随全息测量距离变化不很明显。而其他测量参数的选取不够理想时,测量面与声源面间的距离是一个比较敏感的参数,因此在实际测量中,需要优先考虑全息测量距离。

|
图 8 重构面上声压沿轴向分布曲线 Fig. 8 The distribution of sound pressure along the axial direction of the reconstructed surface |
在图8中,窗函数参数
针对柱面统计最优算法,进行多源数值仿真研究,验证参数选取方法的有效性。在该仿真过程中,采用3个脉动小球噪声源和8个参考点,均布置在声源面内部,噪声源和参考点参数在表1中给出,其中小球振动频率fR=1 000 Hz,参数选取方法按照第2部分研究结果给出。
|
|
表 1 多点噪声源及参考点参数 Tab.1 Multi point nosie source and reference point parameters |
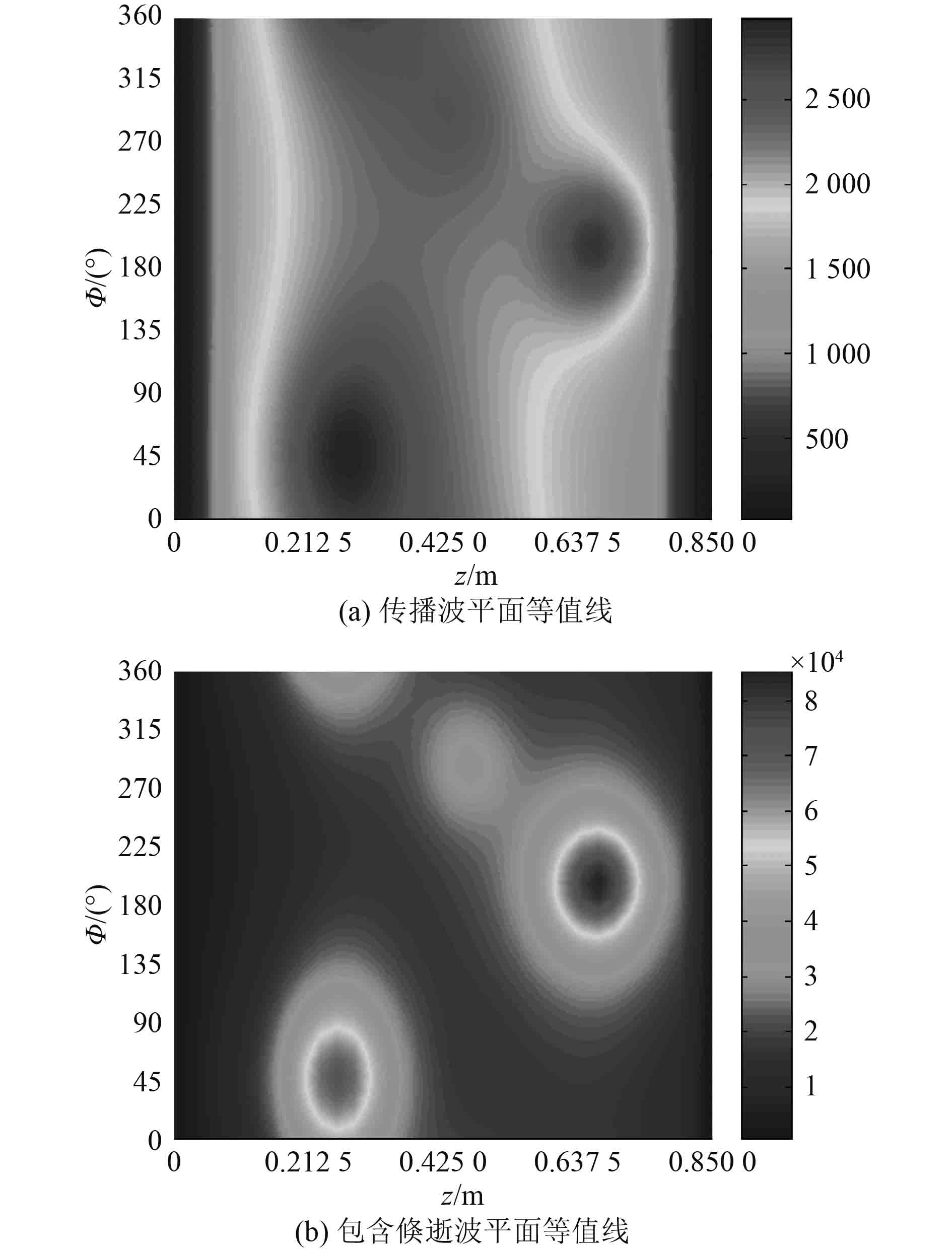
图9给出逐点扫描获得的全息面复声压谱。其中,图9(a)为传播波复声压谱平面等值线分布图,而图9(b)中的复声压谱平面等值线分布图包含传播波和非传播波(倏逝波)2种波成分。由图可知,在测量孔径方面,周向声压幅值谱连续,没有测量孔径效应;轴向存在有限测量孔径效应,Tukey窗函数滤波使得声压幅值在轴向两边缘产生平顺下降,能够消除轴向有限测量孔径效应;当复声压谱包含倏逝波成分时,声源部位近场特性明显,复声压谱的分辨率显著提高。
图10就重构面声压幅值对比给出了计算结果和柱面统计最优算法重构的结果。由图可见,柱面统计最优算法由于在近场捕捉到了非传播的倏逝波,声场的测量和重构结果均考虑到了高空间波数谱成分,使得声源表现为集中分布,实现了声源向中心的聚焦,实现噪声源的精确定位。重构结果在量级上明显区别于计算的结果,是由轴向和周向波数频率的截断和大的离散长度,以及频域和波数域滤波造成的,没有修正这一量级差异显然并不影响噪声源的定位结果。
|
图 9 多点源全息面声压幅值谱 Fig. 9 Sound pressure amplitude spectrum of multi sound holographic surface |

|
图 10 多点源重构面声压幅值谱 Fig. 10 Sound pressure amplitude spectrum of multi point source reconstruction surface |
为验证柱面统计最优近场声全息参数选取方法的有效性,在消声水池进行了近场声全息模型试验。试验模型采用2.2 m×Φ0.65 m×0.008 m普通碳钢材质圆柱壳体,在圆柱壳结构内部水平单侧极点母线上布置2个复合棒振子,作为双源激励振源,复合棒振子纵向间距为0.7 m。同时在圆柱壳结构内部均匀布置振动传感器,其轴向间距约为0.35 m,周向间隔约为45°,作为结构振动响应测量。
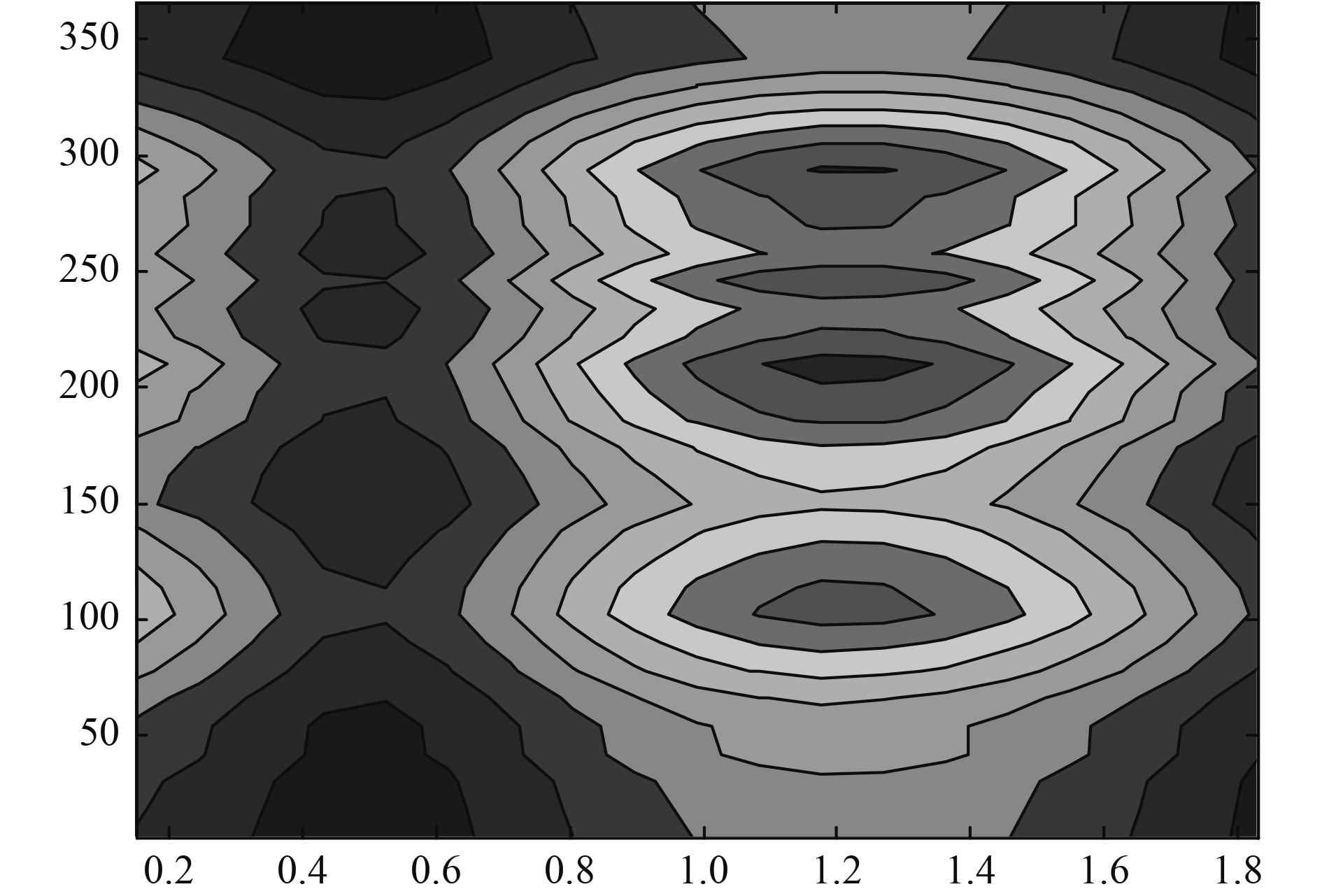
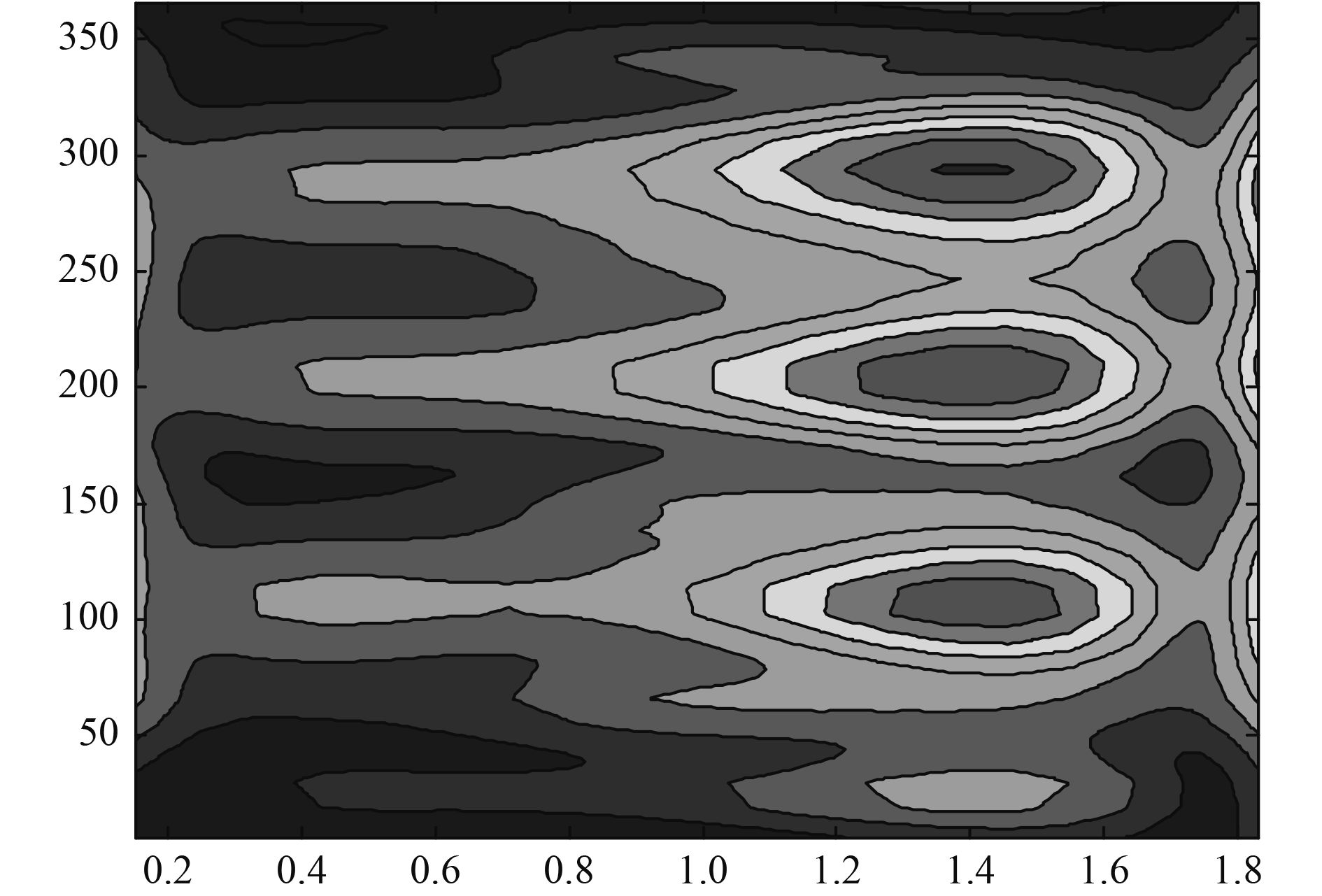
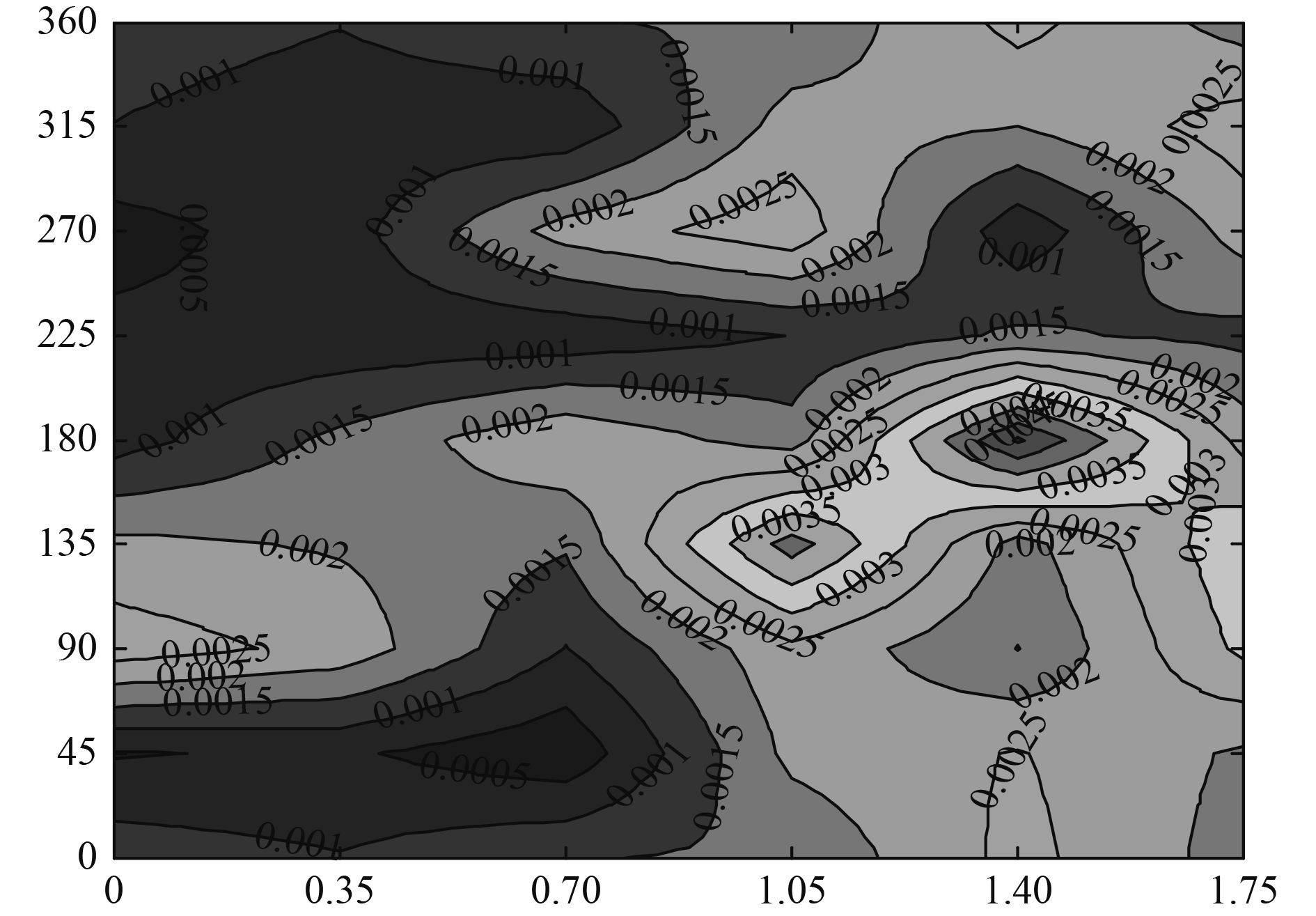
振源激励频率为1 kHz,声全息面测量半径为rH=0.635 m,声源重构面半径为rs=0.355 m。采用本文研究建立的近场声全息参数选取方法,给出近场声全息模型试验结果。图11~图13分别为全息面复声压测量结果、声压重构结果和壳体振动测量结果。
从全息面复声压测量结果可以看出,轴向1.2 m、周向100°~300°位置附近声压值较高。从声压重构结果与壳体振动测量结果可以看出,重构声场在(1.4 m,100°),(1.4 m,200°),(1.4 m,300°)位置中心聚集,亮点分辨率小于0.3 m,且与壳体强振动位置相近,为声源存在位置。因此,模型试验结果验证了柱面统计最优近场声全息参数选取方法的有效性。
|
图 11 复声压测量结果 Fig. 11 Complex sound pressure measurement results |
|
图 12 声压重构结果 Fig. 12 Sound pressure reconstruction results |
|
图 13 壳体振动测量结果 Fig. 13 Shell vibration measurement results |
针对舰艇圆柱壳结构,通过对柱面统计最优近场声全息参数选取方法研究,获取了基于扫描法近场声全息测量系统参数及信息处理参数与声源定位精度影响关系,且通过数值仿真与模型试验,验证参数选取方法的有效性,得到如下结论:
1)利用Tukey窗函数应用于轴向滤波,可有效消除轴向有效测量孔径效应,窗函数参数
2)算法实现过程,正则化因子应采用较低的信噪比参数,倏逝波信噪比参数应采用较高值,同时考虑有效测量孔径效应要求进行优化选取;
3)实际测量时,测量系统阵元间距小于1/3倍声源波长、轴向测量孔径大于3倍声源波长、测量距离小于声源1/5倍波长。
| [1] |
周东旺, 李舜酩, 江星星. 基于传递函数估计的近场声全息的噪声源识别[J]. 仪器仪表学报, 2015, 36(12): 2874–2880.
ZHOU Dong-wang, LI Shun-mei, JIANG Xing-xing. Non-field sound holography based on transfer function estimation [J]. Journal of Instrumentation, 2015, 36(12): 2874–2880. |
| [2] |
杨超. 基于局部近场声全息的机械噪声源特征提取技术[D]. 上海: 上海交通大学, 2009: 87–112.
YANG Chao. Feature extraction of mechanical noise sources based on local near-field acoustic holography [D]. Shanghai: Shanghai Jiaotong University, 2009: 87–112. |
| [3] | WILLIAMS E G. Fourier acoustics: sound radiation and nearfield acoustical holography [M]. London: Academic Press, 1999: 115–148. |
| [4] |
陈心昭, 毕传兴, 李卫兵. 近场声全息技术及其在噪声源识别中的应用[J]. 现代振动与噪声技术, 2005, 4(1): 1–13.
CHEN Xin-zhao, BI Chuan-xing, LI Wei-bing. Near-field acoustic holography and its application in noise source identification [J]. Modern Vibration and Noise Technology, 2005, 4(1): 1–13. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZDZD200510001004.htm |
| [5] |
张海滨, 蒋伟康, 万泉. 适用于循环平稳声场的基于波叠加法的近场声全息技术[J]. 物理学报, 2008, 57(1): 313–321.
ZHANG Hai-bin, JIANG Wei-kang, WAN Quan. No-field acoustic holography based on wave superposition method for cyclostationary sound field [J]. Journal of Physics, 2008, 57(1): 313–321. |
| [6] | SEMENONA T, WU S F. The helmholtz equation least-squares method and rayleigh hypothesis in near-field acoustical holography[J]. Journal of the Acoustical Society of America, 2004, 115(4): 1632–1640. |
| [7] | CHO Y T, BOLTON J S, HALD J. Source visualization byusing statistically optimized nearfield acoustical holography in cylindrical coordinates[J]. Journal of the Acoustical Society of America, 2005, 118(4): 2355–2364. |
| [8] |
李卫兵, 陈剑, 于飞. 统计最优柱面近场声全息[J]. 机械工程学报, 2005, 41(4): 123–127.
LI Wei-bing, CHEN Jian, YU Fei. Statistics on optimal cylindrical near-field sound holography [J]. Journal of Mechanical Engineering, 2005, 41(4): 123–127. |
| [9] |
程广福, 肖斌, 王志伟. 柱面多参考统计最优近场声全息研究[J]. 哈尔滨工程大学学报, 2011, 32(1): 90–97.
CHENG Guang-fu, XIAO Bin, WANG Zhi-wei. Cylindrical multi-reference statistical optimal near-field acoustic holography[J]. Journal of Harbin Engineering University, 2011, 32(1): 90–97. http://www.oalib.com/paper/4856820 |
| [10] | KIM Y, BOLTON J S, KWON H. Partial sound field decomposition in multi-reference near-field acoustical holography by using optimally located virtual references[J]. Journal of the Acoustical Society of America, 2004, 115(4): 1641–1652. |
| [11] | HALD J. Basic theory and properties of statistically optimized near-field acoustical holography[J]. Journal of the Acoustical Society of America, 2009, 125(4): 2105–2120. |
 2018, Vol. 40
2018, Vol. 40
