1. 武汉理工大学 高性能船舶技术教育部重点实验室,湖北 武汉 430063;
2. 武汉理工大学 能源与动力工程学院,可靠性工程研究所,湖北 武汉 430063;
3. 武汉理工大学 物流工程学院,湖北 武汉 430063
收稿日期: 2017-04-14, 修回日期: 2017-06-12.
基金项目: 国家自然科学基金资助项目(51479152)
作者简介: 徐立(1975 – ),男,副教授,研究方向为船舶动力装置性能分析及优化
Phase change simulation of ice particles-seawater two-phase flow in heat exchanger of polar ship
1. Key Laboratory of High Performance Ship Technology (Wuhan University of Technology), Ministry of Education, Wuhan 430063, China;
2. Reliability Engineering Institute, School of Energy and Power Engineering, Wuhan University of Technology, Wuhan 430063, China;
3. School of Logistics Engineering, Wuhan University of Technology, Wuhan 430063, China
0 引 言 北极航道是沟通东亚、北美和欧洲的最方便的路线。与通过苏伊士运河或巴拿马运河的传统商业路线相比,北极航道具有明显的优势,因为北极航道具有缩短航线,减少二氧化碳排放和降低运输成本等优点。近年来,由于全球气温的上升,北极地区海冰面积陆续减少。以往的卫星观测数据表明,过去几十年北极海冰每10年下降约3%,其中夏季海冰融化最为显著[1]。每年夏天,北极航道都有无冰期,这为北极商船提供了机会,与传统的航道不同,商船在北极航道受到北极冰区的影响。当船舶在冰区航行时,船舶海底吸入口过滤器将被大块冰覆盖,并且冰晶颗粒将与海水一起进入海水系统,海水和冰晶粒子将形成固-液两相流。两相流的特性比单相流复杂得多,当海水和冰晶两相流进入极地船舶的热交换器时,冰晶会熔化,这对海水的传热特性有一定的影响。目前,大多数对极地船的研究主要集中在海冰的融化,航行的可行性分析,法律问题和对极地船舶运行的建议。对海水和冰晶两相流的流动和相变特性研究的很少。
由于计算流体动力学(CFD)方法的经济性和有效性以及实验测量技术的局限性,CFD方法用于研究冰晶粒子在极地船壳管式换热器的分布和相变特性。欧拉-欧拉模型是描述固液两相流的有效模型[2]。Zhang成功用相间传热传质模型研究了水平管道中氮浆熔融特性[3]。本文采用欧拉-欧拉模型与界面传热传质模型研究冰晶的融化。随着北极航道的开通,对极地船换热器中冰晶的分布和熔化特性的研究具有重要意义,这也为极地船海水冷却系统的稳定性提供了保障。
1 几何模型 船舶经常使用的管壳式换热器如图1所示。本文研究了壳管式换热器单个海水管中冰晶的熔化和分布,对整个热交换器的研究起到了指导作用。常用的海水管是直管和U管。根据GB151-1999行业标准[4],建立了直管和U管的三维几何模型。管的直径为24 mm,其长度为1 000 mm。
表 1(Tab. 1)

表 1 直管和U形管的相关参数
Tab. 1 Parameters of straight and U-shaped tubes
| 参数 |
直管 |
U形管 |
| 长度/mm |
1 000 |
1 000 |
| 管口直径/mm |
12 |
12 |
| 管壁厚度/mm |
2.5 |
2.5 |
| 圆弧半径/mm |
~ |
100 |
|
表 1 直管和U形管的相关参数
Tab.1 Parameters of straight and U-shaped tubes
|
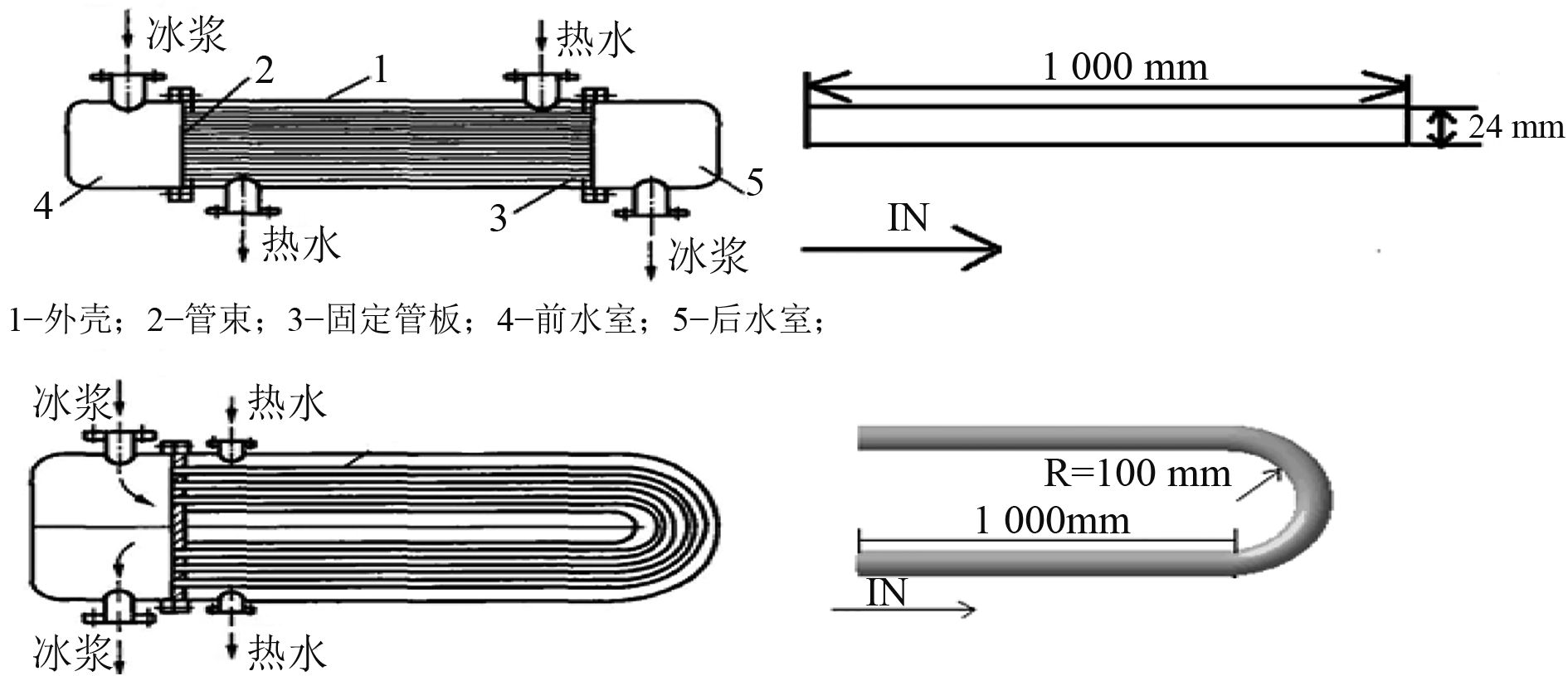
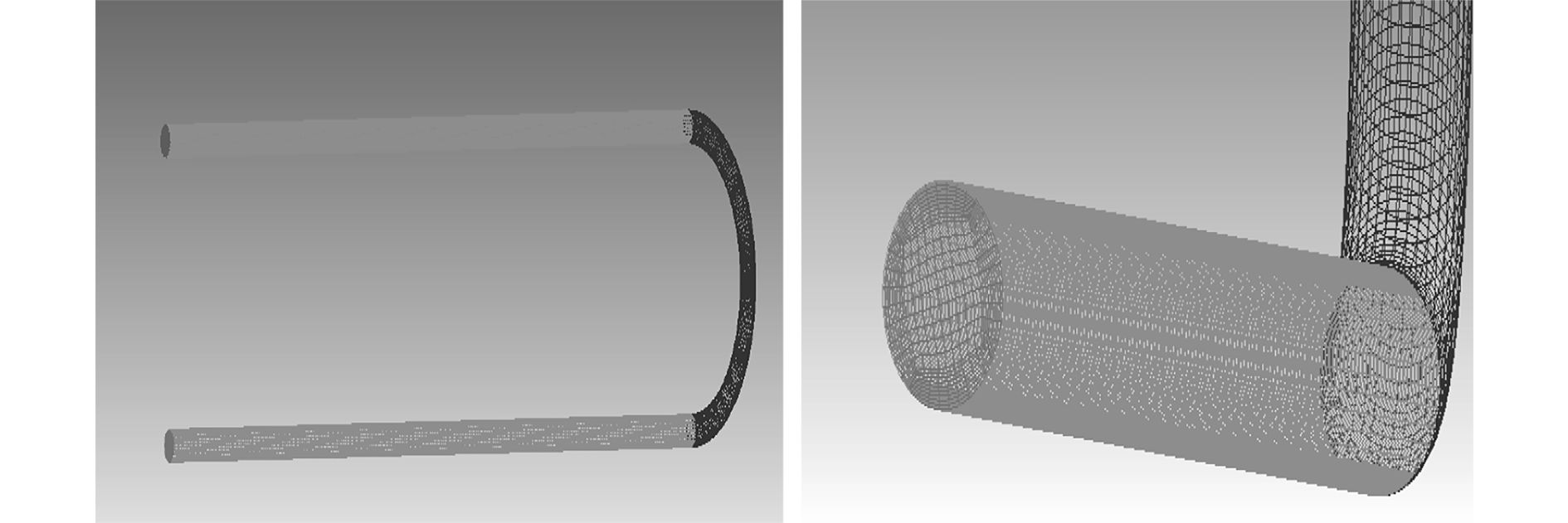
2 网格模型 在本研究中,使用商业计算流体动力学软件Ansys ICEM15.0来研究冰晶-海水两相流的流动和相变特性。首先,创建直管和U形管的三维模型。然后在模型中进行网格生成,直管和U形管的计算域分为六面体结构的网格单元。将直管分成114 915 6个网格单元,将U形管分成210 296 5个网格单元,模型进行网格划分后网格质量大于0.65,符合仿真的网格质量要求。如图2和图3所示,为U型管和直管的网格模型。
3 数学模型 本研究中使用的CFD模型利用粒状流动力学理论来描述粒子相互作用。为了简化数学模型,冰晶颗粒被假定为球形,非弹性和光滑的,体积分数为15%,可以认为是牛顿流体[5]。在本研究中,用欧拉-欧拉模型研究管道中冰晶的分布,相间传热传质模型模拟冰晶的相变。欧拉-欧拉双流体模型中固相和液相的守恒方程包括连续性方程、动量守衡方程等。
3.1 连续性方程
|
$\frac{\partial }{\partial }\left( {{{{\alpha }}_{{i}}}{{{\rho }}_{{i}}}} \right) + \nabla \cdot \left( {{{{\alpha }}_{{i}}}{{{\rho }}_{{i}}}{{{{\vec v}}}_{{i}}}} \right) = {{{\dot m}}_{{{pi}}}},$
|
(1) |
式中:i表示固相或液相,当i=l时为液相,i=s时为固相,下标p表示i的相对相。在式(1)中,ai为每个相的体积分数;
$\overrightarrow {{{{v}}_{{i}}}} $
为每个相的速度;
${{{\rho }}_{{i}}}$
为每个相的密度;
${{{\dot m}}_{{{pi}}}}$
为相间传质系数。每相的体积分数的关系可以表示为
${{{\alpha }}_{{s}}} + {{{\alpha }}_{{l}}} = 1$
。
3.2 动量守恒方程 固液两相流,每个相都有自己的动量守恒方程。固相和液相的动量守恒方程略有不同。因此,本文分别描述了它们的动量守恒方程。
3.2.1 海水动量守恒方程
|
$\frac{\partial }{\partial }\left( {{{{\alpha }}_{{l}}}{{{\rho }}_{{l}}}{{{{\vec v}}}_{{l}}}} \right) + \nabla \cdot \left( {{{{\alpha }}_{{l}}}{{{\rho }}_{{l}}}{{{{\vec v}}}_{{l}}}{{{{\vec v}}}_{{l}}}} \right) = - {{{\alpha }}_{{l}}}\nabla {{P}} + \nabla \cdot {{{\tau }}_{{l}}} + {{{m}}_{{{sl}}}}{{{\tilde v}}_{{s}}} + {{{F}}_{{l}}},$
|
(2) |
|
${{{\tau }}_{{l}}} = {{{\alpha }}_{{l}}}{{{\mu }}_{{l}}}\left[ {\nabla {{{{\vec v}}}_{{l}}} + {{\left( {\nabla {{{{\vec v}}}_{{l}}}} \right)}^{{T}}}} \right] - \frac{{2{{{\alpha }}_{{l}}}{{{\mu }}_{{l}}}\left( {\nabla {{\overrightarrow { \cdot {{v}}} }_{{l}}}} \right){{I}}}}{3},$
|
(3) |
|
${{{F}}_{{l}}} = {{{\alpha }}_{{l}}}{{{\rho }}_{{l}}}{{g}} + {{{F}}_{{{sl}}}} = {{{\alpha }}_{{l}}}{{{\rho }}_{{l}}}{{g}} + {{{F}}_{{{drag}}.{{l}}}} + {{{F}}_{{{td}}.{{l}}}}\text{。}$
|
(4) |
式中:
${{{\mu }}_{{l}}}$
为海水的粘度;P为固相和液相共用的压力;
${{{\tau }}_{{l}}}$
为海水的应力张量,可以用方程式(3)表示;
${{{m}}_{{{sl}}}}$
为冰粒融化而穿过固相和液相界面的质量;
${{{F}}_{{{sl}}}}$
为海水和冰晶之间的作用力;
${{{F}}_{{{drag}}.{{l}}}}$
为两相间的拖曳力;
${{{F}}_{{{td}}.{{l}}}}$
为湍流扩散力。由于冰晶颗粒直径小,省略虚拟质量力和升力以简化数学模型。
3.2.2 冰晶的动量守恒方程
|
$\frac{\partial }{\partial }\left( {{\alpha _s}{\rho _s}{{\vec v}_s}} \right) \!+\! \nabla \cdot \left( {{\alpha _s}{\rho _s}{{\vec v}_s}{{\vec v}_s}} \right) \!=\! - {\alpha _s}\nabla {{P}} + \nabla \cdot {\tau _s} \! -\! {m_{sl}}{\vec v_s} + {F_s},$
|
(5) |
|
${\tau _s} \!=\! \left( { - {P_s} \!+\! {\xi _s}\nabla \cdot {{\vec v}_s}} \right) \!+\! {\mu _s}\left\{ {\left[ {\nabla {{\vec v}_s} + {{\left( {\nabla {{\vec v}_s}} \right)}^T}} \right] - \frac{2}{3}\left( {\nabla \cdot {{\vec v}_s}} \right)I} \right\},$
|
(6) |
|
${F_s} = {\alpha _s}{\rho _s}g + {F_{drag.s}} + {F_{td.l}}\text{。}$
|
(7) |
在方程(5)中,
${{{\tau }}_{{s}}}$
为固相的应力张量,其可以表示为方程(6);
${{{P}}_{{s}}}$
为固体压力,
${{{\xi }}_{{s}}}$
为冰晶粒子的体积粘度;
${{{\mu }}_{{s}}}$
为冰晶粒子的剪切粘度。
3.3 能量守恒方程
|
$\begin{split}& \frac{\partial }{\partial }\left( {{\alpha _i}{\rho _i}{h_i}} \right) + \nabla \cdot \left( {{\alpha _s}{\rho _s}{{\vec v}_s}{h_i}} \right) = \\& \nabla \cdot \left( {{\lambda _i}\nabla {T_i}} \right) + {\tau _i}:\nabla {{\vec v}_i} \pm {m_{sl}}{h_s} - {h_v}\left( {{T_i} - {T_p}} \right)\end{split},$
|
(8) |
式中:
${{{h}}_{{i}}}$
为焓;
${{{\lambda }}_{{i}}}$
为热导率;
${{{T}}_{{i}}}$
为每个相的温度;
${{{h}}_{{v}}}$
为界面传热系数。当i=s或l时,±为+或-。
3.4 相间传热传质 在本文中,相间传热传质模型用于模拟由冰晶融化引起的相间热和质量传递。在能量方程中,
${{{m}}_{s{{l}}}}{{{\vec v}}_{{s}}}$
表示由冰晶相变引起的动量交换,
$ \pm {{{m}}_{s{{l}}}}{{{h}}_{{s}}} - {{{h}}_{{v}}}\left( {{{{T}}_{{i}}} - {{{T}}_{{p}}}} \right)$
表示冰晶相变引起的热量交换。通过计算特定界面面积的单个颗粒与流体之间的传热系数到相间传热系数
${{{h}}_{{v}}}$
,该系数可由下式表示:
|
${h_v} = \frac{{6{\alpha _s}{h_{sl}}}}{{{d_s}}},$
|
(9) |
其中
${{{d}}_{{s}}}$
表示冰粒子的直径,并且
${{{h}}_{{{sl}}}}$
是可以通过Gunn’s[6]方法获得的相间传热系数。
|
$\begin{split}& {h_{sl}} = \frac{{{\lambda _l}}}{{{d_s}}}[\left( {7 + 10{\alpha _l} + 5\alpha _l^2} \right)\left( {1 + 0.7Re_s^2P{r^{1/3}}} \right) + \\& \left( {1.33 - 2.4{\alpha _l}1.2\alpha _l^2} \right)Re_s^{0.7}P{r^{1/3}}]\text{。}\end{split}$
|
(10) |
式中:
${{Pr}}$
为普朗特数;
${{R}}{{{e}}_{{s}}}$
为雷诺数,
${{R}}{{{e}}_{{s}}} = \frac{{{{{\rho }}_{{{l}}{{{d}}_{{{s}}\left| {\mathop {{{v}}_{{s}}}\limits^ \rightharpoonup - \overrightarrow {{{{v}}_{{l}}}} } \right|}}}}}}{{{{{\mu }}_{{l}}}}}$
。
冰晶融化向海水传递的质量
|
${{{m}}_{{{sl}}}} = \frac{{{{{h}}_{{{sl}}\left( {{{{T}}_{{l}}} - {{{T}}_{{s}}}} \right)}}}}{{\Delta {{H}}}},$
|
(11) |
其中ΔH表示冰晶颗粒的潜热。
3.5 相间作用力 相间作用力包括拖曳力和湍流扩散力。拖曳力可以表示为
|
${F_{drag.l}} = {k_{sl}}\left( {{{\vec v}_s} - {{\vec v}_l}} \right),$
|
(12) |
其中,
${{{k}}_{{{sl}}}}$
为动量交换系数,可表示为
|
${{{k}}_{{{sl}}}} = \frac{{3{{{C}}_{{D}}}{{{\rho }}_{{l}}}{{{\alpha }}_{{s}}}{{{\alpha }}_{{l}}}}}{{4{{{d}}_{{s}}}\left| {{{{{\tilde v}}}_{{s}}} - {{{{\tilde v}}}_{{l}}}} \right|}},$
|
(13) |
CD为拖曳力系数,可表示为
|
${C_D} = {\left( {0.63 + \frac{{4.8}}{{\sqrt {R{e_s}/\left| {{{\vec v}_s} - {{\vec v}_l}} \right|} }}} \right)^2}{\text{。}}$
|
(14) |
湍流扩散力
${{{F}}_{{{td}},{{l}}}}$
常用Burns et al.模型计算[7]
3.6 颗粒流动力学理论 因为离散相被认为是连续相,离散相具有与连续相相似的性质,如体积粘度
${{{\xi }}_{{s}}}$
,剪切粘度
${{{\mu }}_{{s}}}$
, 颗粒压力等,这些性质也被称为“假流体性质”。颗粒流动力学理论用于描述冰晶颗粒的假流体性质,该理论基于气体的动力学理论提出,并且颗粒被认为是致密的空气分子。颗粒温度
${\theta _s}$
被提出来描述颗粒的波动能量,其被定义为
|
${\theta _s} = \frac{1}{3}{v'_s}{v'_s},$
|
(15) |
其中
${{{v'}}_{{s}}}$
表示颗粒波动速度。
从动力学理论导出的方程表示为
|
$\begin{split}& \frac{3}{2}\left[ {\frac{\partial }{\partial }\left( {{\alpha _s}{\rho _s}{\theta _s}} \right) + \nabla \cdot \left( {{\alpha _s}{\rho _s}\overrightarrow {{v_s}} {\theta _s}} \right)} \right] = \\& \left( { - {p_s}I + {\tau _s}} \right) \cdot \nabla \overrightarrow {{v_s}} + \nabla \cdot \left( {k{\theta _s}\nabla {\theta _s}} \right) + {\delta _{{{ls}}}} - \gamma {\theta _s}\end{split},$
|
(16) |
式中:
$\left( { - {p_s}I + {\tau _s}} \right)\cdot\nabla \overrightarrow {{v_s}} $
表示粒子的应力张量;
$k{\theta _s}$
为扩散系数;
$k{\theta _s}\nabla {\theta _s}$
为扩散能;
$\gamma {\theta _s}$
为由颗粒碰撞而消耗的能量;
${\delta _{{{ls}}}}$
为相间转换的能量。此外,颗粒压力可以表示为
|
${P_s} = {\alpha _s}{\rho _s}{\theta _s} + 2{\rho _s}\left( {1 + {e_{ss}}} \right)\alpha _s^2{g_o}{\theta _s},$
|
(17) |
式中:
${{{e}}_{{{ss}}}}$
为粒子碰撞恢复系数,设置为0.9;
${g_o}$
为颗粒径向分布函数。该函数常用模型由Gidaspow[8]给出。
$k{\theta _s}$
常用Gidaspow et al模型进行计算。
$\gamma {\theta _s}$
的计算表达式由Lun et al.[9]给出。
${\delta _{{{ls}}}} = - 3{k_{s{{l}}}}{\theta _s}$
。
体积粘度ξs用于表征颗粒抵抗变形的能力,其可以计算为
|
${\xi _s} = \frac{4}{3}\alpha _s^2{\theta _s}{d_s}\left( {1 + {e_{{{ss}}}}} \right)\sqrt {\frac{{{\theta _s}}}{\pi }} ,$
|
(18) |
颗粒剪切粘度由2部分组成。
|
${\mu _s} = {\mu _{s.c}} + {\mu _{s.k}},$
|
(19) |
${\mu _{s.c}}$
为颗粒间碰撞引起的颗粒粘性。
|
${\mu _{s.c}} = \frac{4}{5}\alpha _s^2{\theta _s}{\rho _s}{d_s}\left( {1 + {e_{ss}}} \right)\sqrt {\frac{{{\theta _s}}}{\pi }} ,$
|
(20) |
${{{\mu }}_{{{s}}.{{k}}}}$
为动力粘度,可表示为
|
${\mu _{s.k}} = \frac{{10{\rho _s}{d_s}\sqrt {{\theta _s}\pi } }}{{6\left( {3 - {e_{ss}}} \right)}}\left[ {1 + \frac{2}{5}\left( {1 + {e_{ss}}} \right)\left( {3{e_{ss}} - 1} \right){\alpha _s}{g_o}} \right]\text{。}$
|
(21) |
3.7 湍流模型 大量的工程实验表明,k-
${{\varepsilon }}$
湍流模型对于研究管流是有效的,并且因为冰晶粒子和海水的密度相似。混合物k-
${{\varepsilon }}$
湍流模型用于捕获冰晶-海水两相流的湍流特征,该模型对两相的密度、速度、湍流粘度等项做加权平均, 然后用一个k-
${{\varepsilon }}$
方程进行描述,比较适合于捕捉离散项和连续相密度接近的两相流的湍流特性。控制方程如下所示:
|
$\frac{\partial }{{\partial {{t}}}}\left( {{{{\rho }}_{{m}}}{{k}}} \right) + \nabla \cdot \left( {{{{\rho }}_{{m}}}{{k}}{{{{\vec v}}}_{{m}}}} \right) = \nabla \cdot \left( {\frac{{{{{\mu }}_{{{t}}.{{m}}}}}}{{{{{\sigma }}_{{k}}}}}\nabla {{k}}} \right) + {{{G}}_{{{k}},{{m}}}} - {{{\rho }}_{{m}}}{{\varepsilon }},$
|
(22) |
|
$ \frac{\partial }{{\partial {{t}}}}\left( {{{{\rho }}_{{m}}}{{\varepsilon }}} \right) \!+\! \nabla \!\cdot\! \left( {{{{\rho }}_{{m}}}{{\varepsilon }}{{{{\vec v}}}_{{m}}}} \right)\left(\! {\frac{{{{{\mu }}_{{{t}}.{{m}}}}}}{{{{{\sigma }}_{{\varepsilon }}}}}\nabla {{\varepsilon }}} \!\right) \!+\! \frac{{{\varepsilon }}}{{{k}}}\left( {{{{C}}_{1{{\varepsilon }}}}{{{G}}_{{{k}},{{m}}}} \!-\! {{{C}}_{2{{\varepsilon }}}}{{{\rho }}_{{m}}}{{\varepsilon }}} \right), $
|
(23) |
|
${{{\rho }}_{{m}}} = {{{\alpha }}_{{l}}}{{{\rho }}_{{l}}} + {{{\alpha }}_{{s}}}{{{\rho }}_{{s}}},$
|
(24) |
|
${{{\vec v}}_{{m}}} = \frac{{{{{\alpha }}_{{l}}}{{{\rho }}_{{l}}}{{{{\vec v}}}_{{l}}} + {{{\alpha }}_{{s}}}{{{\rho }}_{{s}}}{{{{\vec v}}}_{{s}}}}}{{{{{\alpha }}_{{l}}}{{{\rho }}_{{l}}} + {{{\alpha }}_{{s}}}{{{\rho }}_{{s}}}}},$
|
(25) |
|
${{{\mu }}_{{{t}}.{{m}}}} = \frac{{0.09\left( {{{{\alpha }}_{{l}}}{{{\rho }}_{{l}}} + {{{\alpha }}_{{s}}}{{{\rho }}_{{s}}}} \right){{{k}}^2}}}{{{\varepsilon }}},$
|
(26) |
${G_{k,m}}$
为湍流动能。
|
${G_{k,m}} = {\mu _{t.m}}\left( {\nabla {{\vec v}_m} + {{\left( {\nabla {{\vec v}_m}} \right)}^{ T}}} \right):\nabla {\vec v_m}\text{。}$
|
(27) |
k-
${{\varepsilon }}$
方程中的系数
${{{\sigma }}_{{k}}}$
=1,
${{{\sigma }}_{{k}}}$
=1.3,
${C_{1\varepsilon }} = 1.44$
,
${C_{2\varepsilon }} = 1.92$
。
4 数值参数设置 海水和冰晶的热物性与海水的盐度有很大的关系。海水的平均盐度为35‰。由于海冰的融化,北极海水的盐度必须降低。在本研究中,海水的盐度被分配为15‰。海水和冰晶的热物性如表2所示,盐度为15‰[10, 11]。
在本研究中,采用速度入口边界条件,速度设置为1 m/s,1.5 m/s和2 m/s。冰晶的体积分数为15%。根据王治[12]的计算,在取海水管与被冷却水之间的换热系数为759 W·m–2·K–1和被冷却水的温度为50℃。使用自由流出口边界条件。管道入口处冰粒和海水的温度分别为272.34 K和273.15 K。为了求解控制方程,使用有限体积方法来离散这些方程,并且使用二阶方案。相耦合SIMPLE算法用于求解这些离散方程。时间步长设为0.005 s,当残差小于1.0×10–3时,数值结果被认为是收敛的。在本研究中,实现了网格独立性。
表 2(Tab. 2)

表 2 海水和冰晶的热物性
Tab. 2 Thermophysical properties of seawater and ice crystals
| 热物性 |
密度/kg·m–3 |
导热系数/W·m–1·K–1 |
比热/J·kg–1·K–1 |
潜热/kJ·kg–1 |
颗粒直径/mm |
温度/K |
粘度/kg/m·s |
| 冰晶 |
860 |
2.21 |
69740 |
62.379 |
0.5 |
272.34 |
~ |
| 海水 |
1011.93 |
0.56 |
4160 |
~ |
~ |
273.15 |
0.00156 |
|
表 2 海水和冰晶的热物性
Tab.2 Thermophysical properties of seawater and ice crystals
|
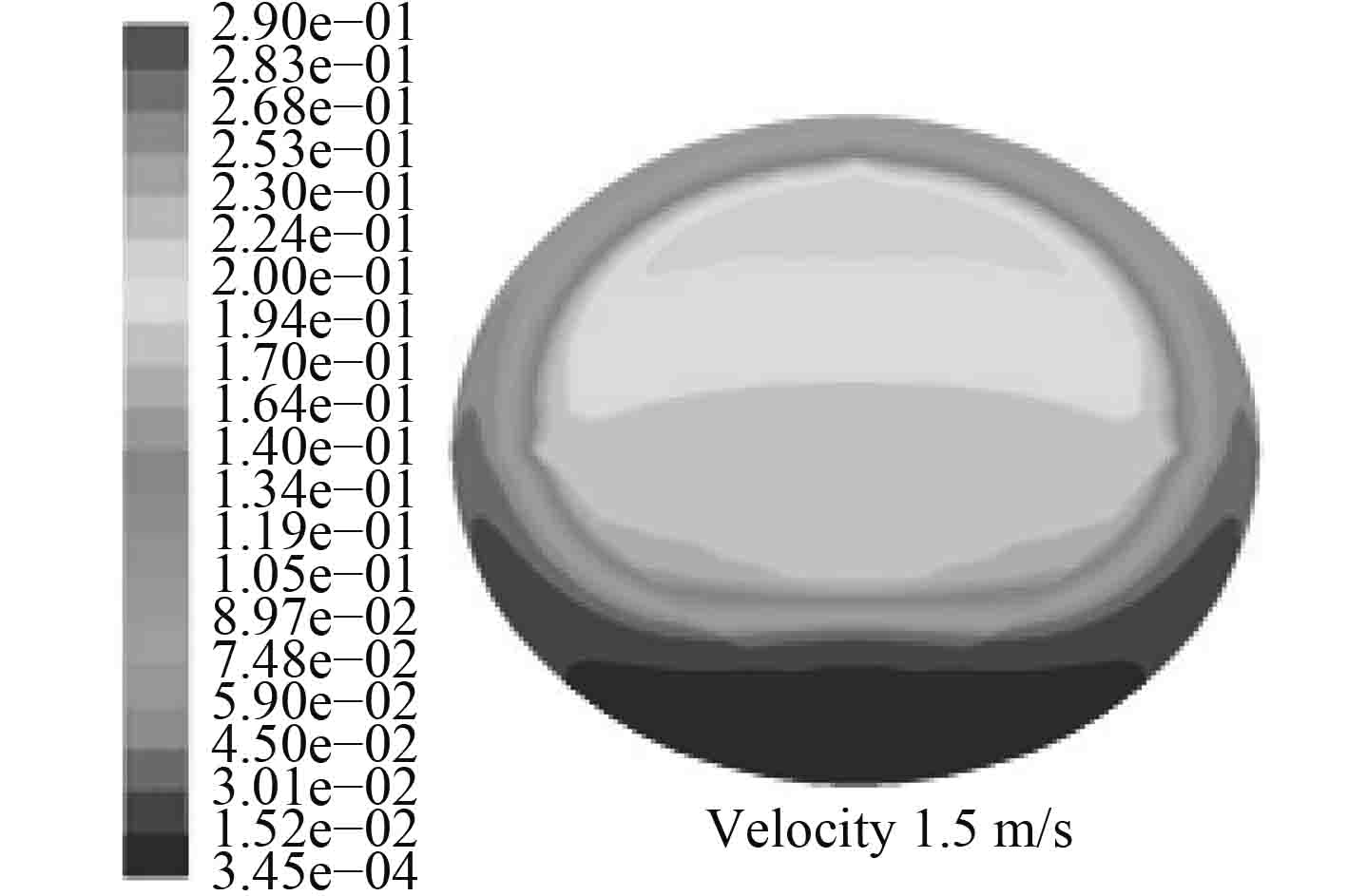
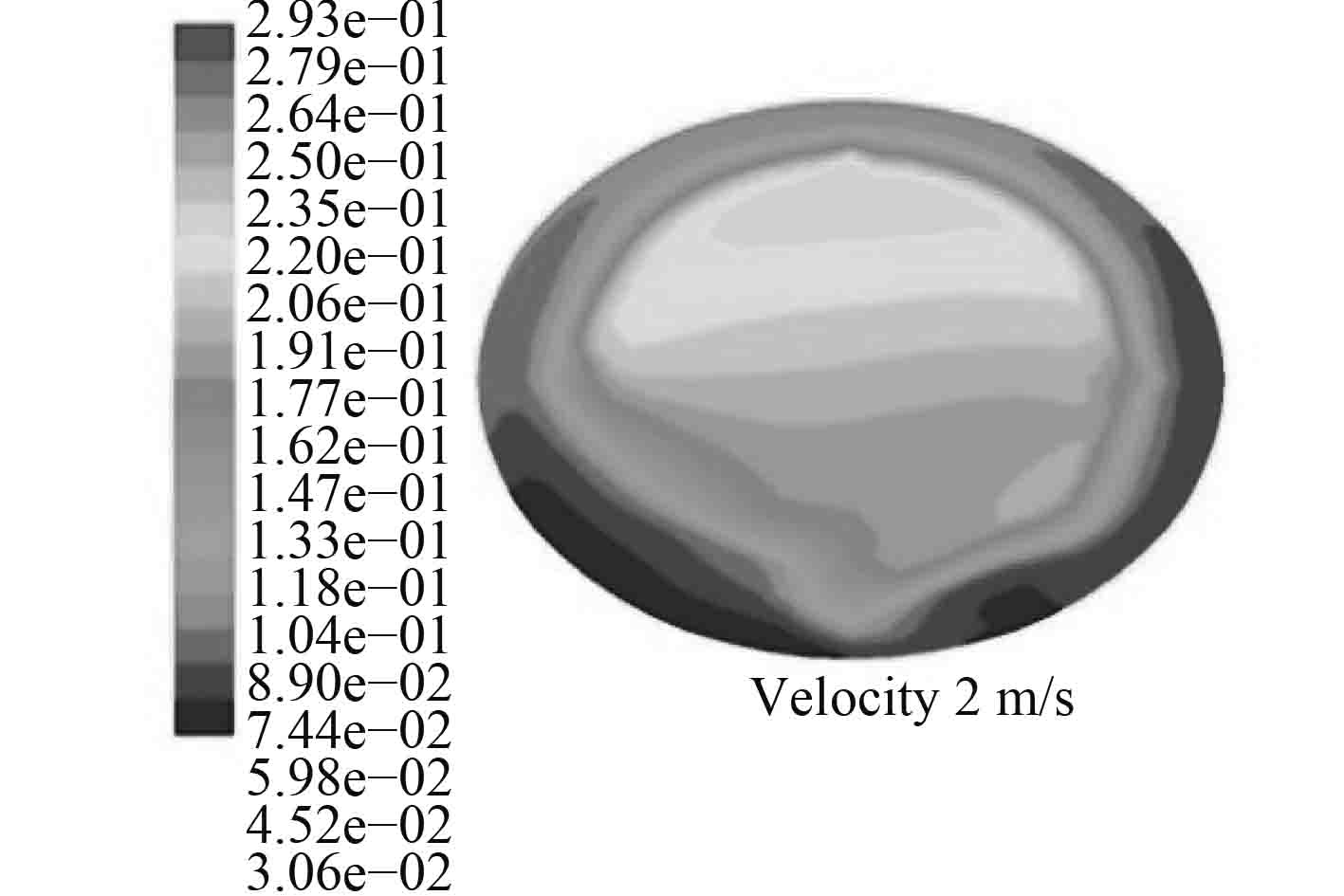
5 仿真分析 5.1 直管和U管中冰晶颗粒的分布 从图4~图7可以看出直管中冰晶颗粒的体积分数特性,冰晶颗粒主要集中在主流区。由于冰晶颗粒的密度较小,在直管的上部有更多的冰颗粒。从图7中可以看出随着入口速度的增加,湍流强度更强,分布情况受冰晶颗粒密度影响变小,冰晶颗粒的分布更加均匀。在边界层区域中,由于冰晶颗粒和壁之间的碰撞和冰晶颗粒的熔化,导致冰晶颗粒减少,这种现象在入口速度增加时更为明显。
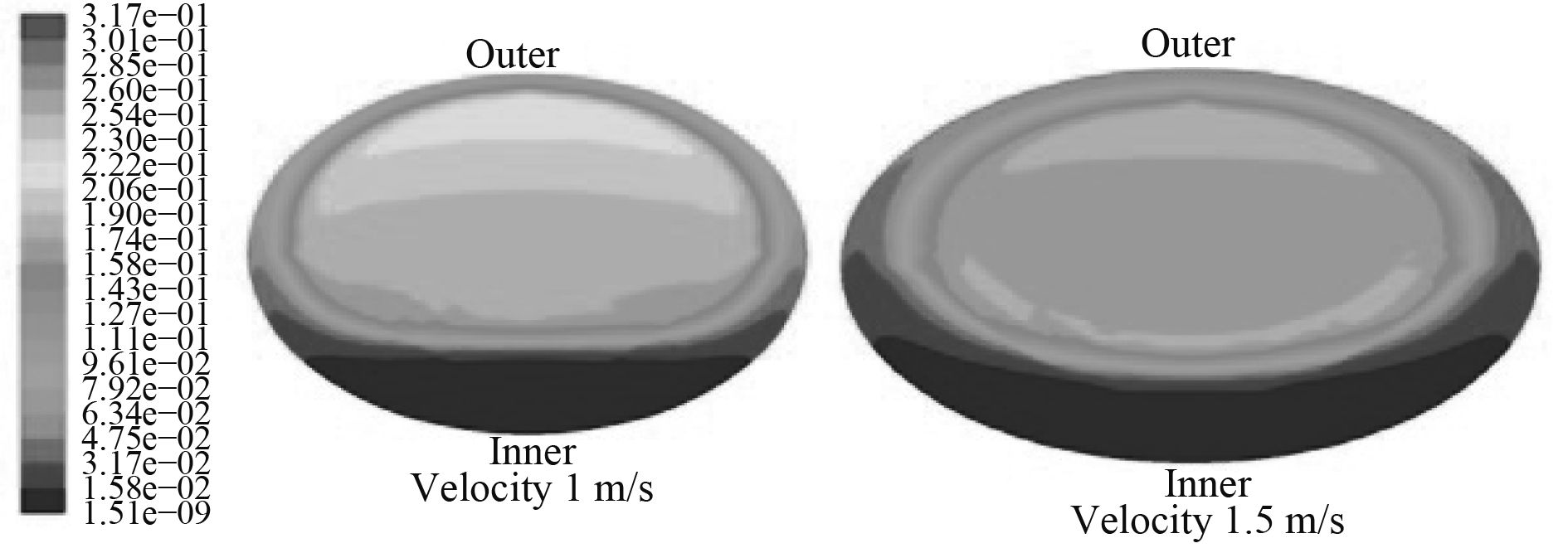
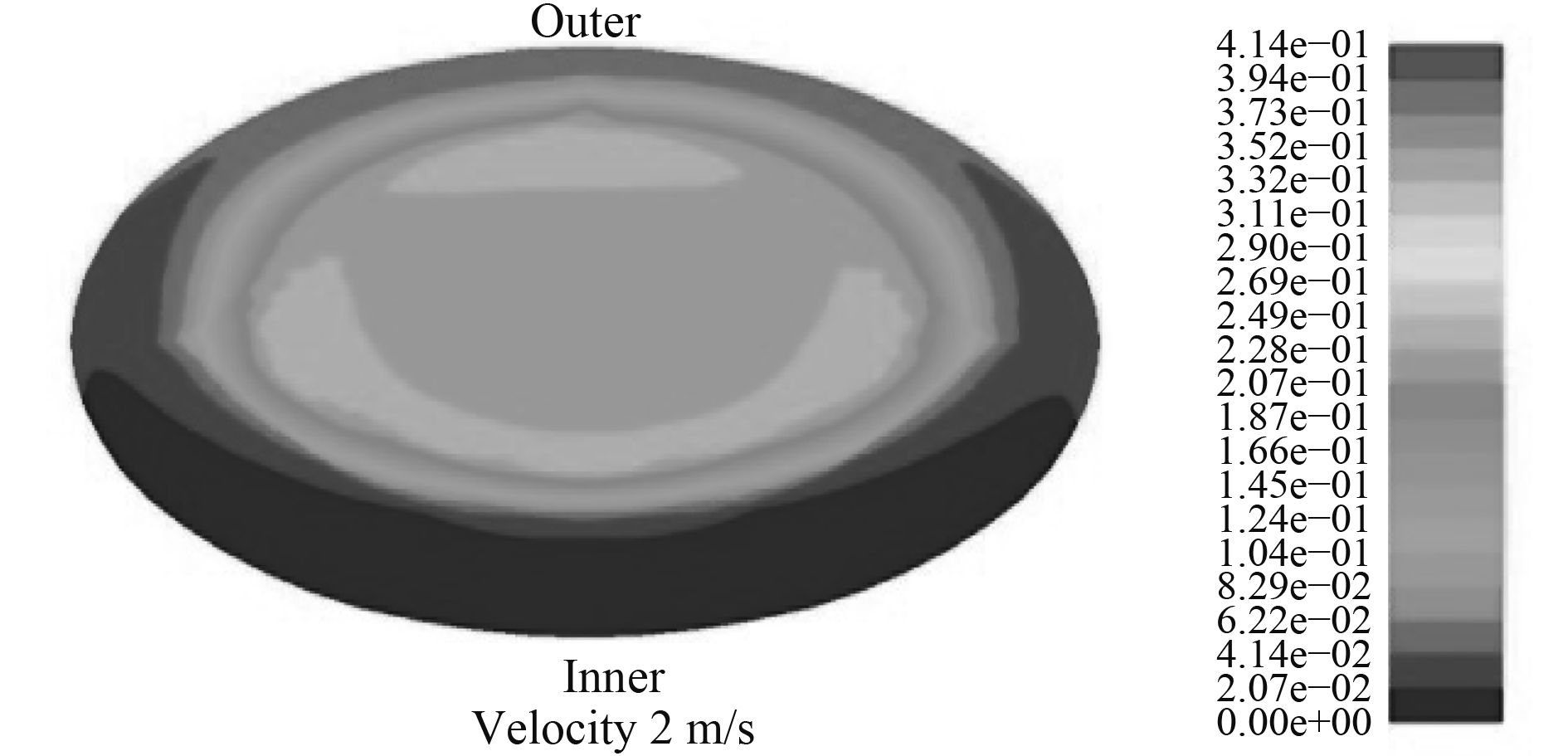
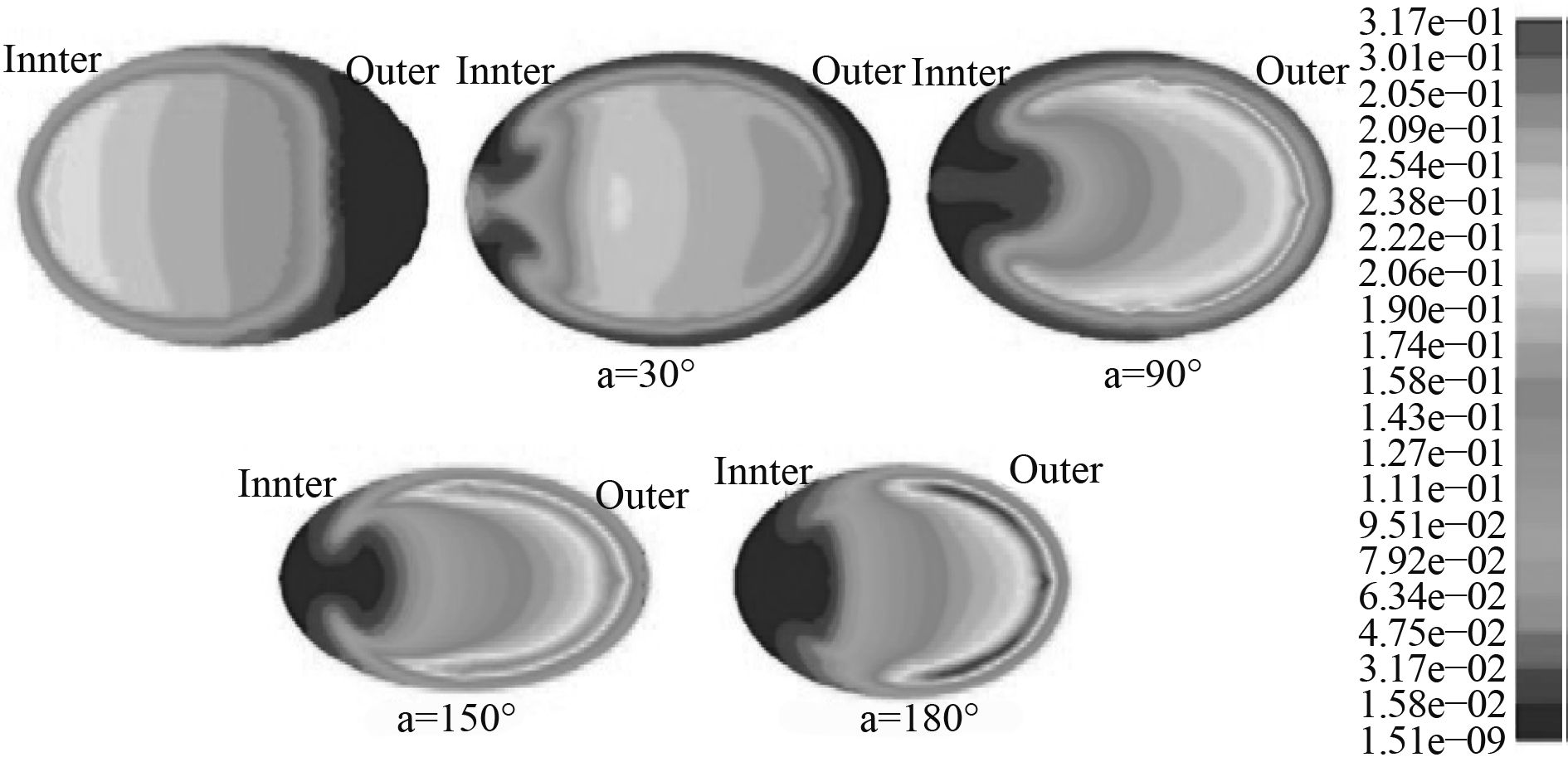
图8~图13描述了U型管中冰晶颗粒的体积分数。从图9和图10比较中可看出,由于湍流的影响,冰颗粒的分布更加均匀。从图11可以看出,由于离心力的作用,更多的冰晶颗粒集中在U形管的拐弯处外侧,随着海水速度的增加,离心力的影响更加明显,更多的冰粒子移动到外侧。从图8、图9和图10看出,由于颗粒和管壁之间的碰撞,冰晶颗粒通过U型管的拐角处时,颗粒逐渐移动到流场的主流场。
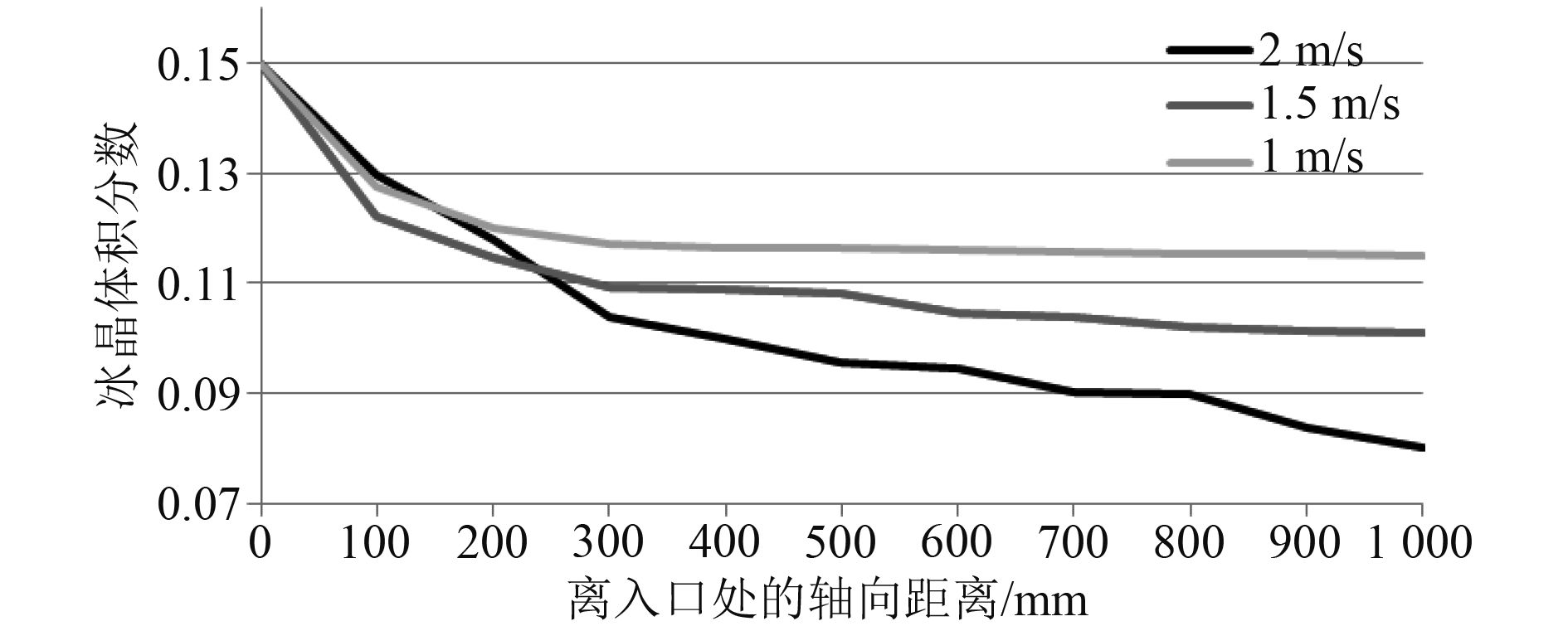
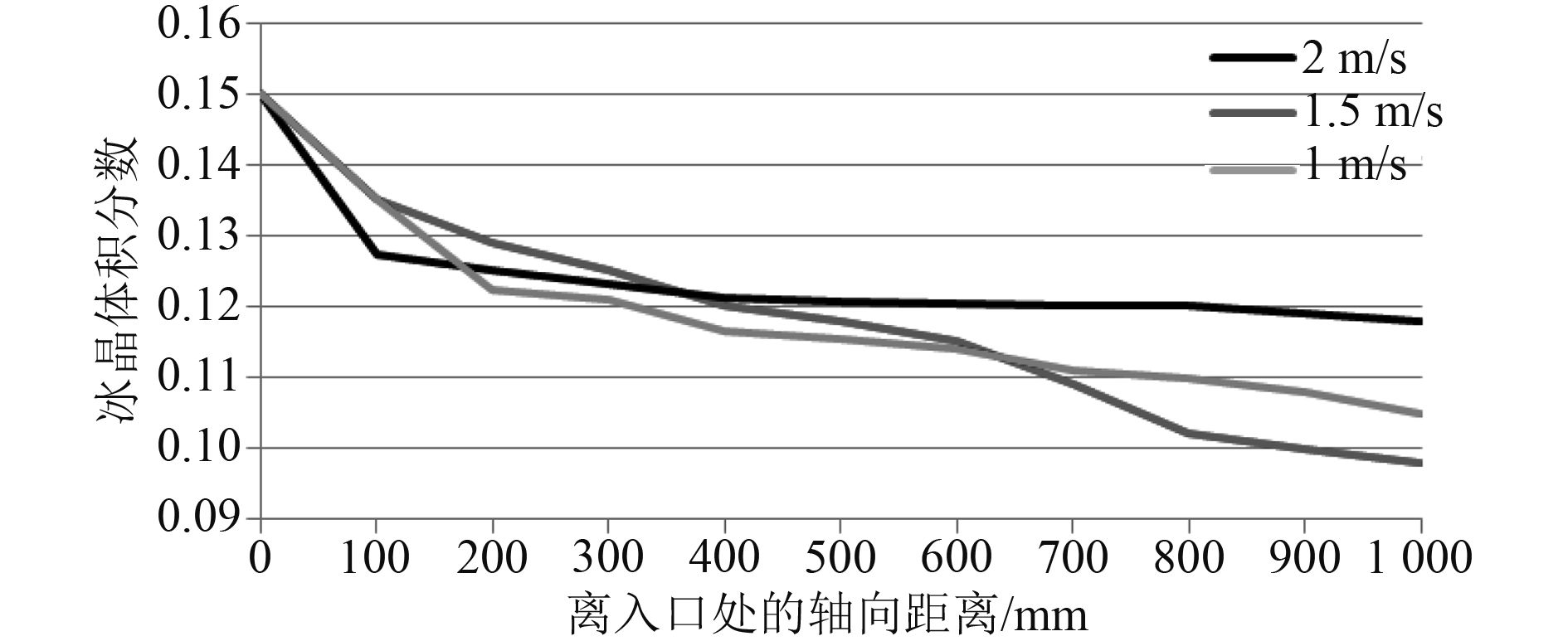
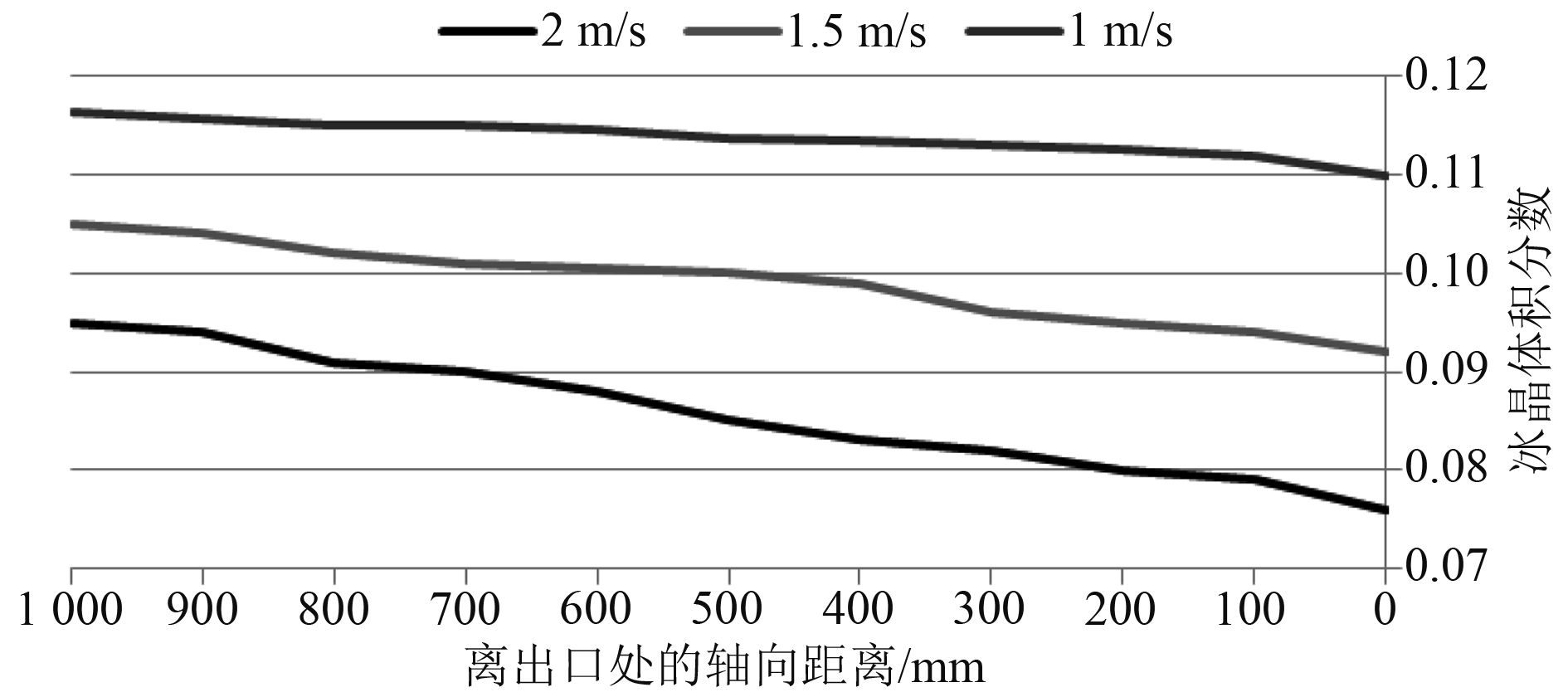
5.2 冰晶颗粒的熔化特性 在本研究中,冰晶颗粒的熔融特性可用冰晶从入口处到出口处的体积分数来表示。图14至16描述了直管和U管中的冰晶颗粒的融化特性。在图14中,由于冰晶颗粒和海水之间的温度差的增加,冰晶的体积分数沿轴向方向逐渐减小,并且在直管的入口区域中的海水的温度比在中心区域中增加地更快,因此,在入口区域时,冰晶的体积分数变化的最快,曲线下降的最快,并且随着入口速度的不同,冰晶的体积分数变化情况不同,速度越大,湍流波动增加,导致更多的冰粒随着管道入口速度的增加而融化。而在图15和图16中,分别描述了U型管下部和上部的冰晶颗粒的体积分数变化情况,并表明U型管扁平部分的冰晶颗粒融化特性与直管类似。但是,在入口速度相同时,直管和U管中的冰晶的融化特性不同,计算结果表明,由于更多的热量传入U形管中,U形管中有更多的冰粒融化,并随着入口速度的增加,冰晶的融化速度加快。
6 结 语 本次研究调查了极性船舶热交换器海水管中冰粒的分布和相变特性,可以得出冰晶-海水两相流的流动模式是悬浮的,随着入口速度的增加,湍流强度增强,冰晶颗粒的分布更加均匀。冰晶颗粒在U型管的拐角处受到离心力的作用,会从U型管内壁流到U型管角部的外壁。通过比较出口处冰晶的体积分数,发现在进口速度相同的情况下,U型管中有更多的冰粒融化,并且融化的冰晶颗粒量随入口速度的增加而增加。





 2018, Vol. 40
2018, Vol. 40
