FPSO(浮式生产储卸油装置)作为集生产处理、储存外输及生活、动力供应等多功能于一体的综合大型海上生产设施,已逐渐成为海上石油资源开发中不可或缺的重要装备[1 – 2]。然而,FPSO在海上运营过程中长期处于复杂的海洋环境中,其船体和舱内的构件通常会发生较为严重的腐蚀,从而将导致船体结构强度尤其是总纵强度降低[3 – 4]。因此,对老旧FPSO进行考虑腐蚀影响的总纵强度分析,对保证其安全性具有极其重要的意义[5]。
近年来,各国船级社及一些相关科研机构已开始在船舶设计阶段考虑腐蚀对船舶结构强度的影响,但对于受腐蚀影响的老旧船舶尤其是老旧FPSO的研究则较为少见。本文中的FPSO自1993年开始投产,已累计运营近20年,其船体遭受了不同程度的腐蚀,而其使用年限已接近25年的设计寿命;然而,若对达到设计寿命的 FPSO 即进行报废将会造成巨大的资源浪费和经济损失[6]。本文对该FPSO进行考虑腐蚀影响的总纵强度分析和校核,作为其延寿改造评估的重要内容,将对改造方案的确定具有重要的指导作用。
1 船体总纵外载荷计算本文中FPSO于1993年8月在上海江南造船厂建成交船,为单底双舷侧钢质结构型式,其主要技术参数为:总长218.13 m,垂线间长210 m,型宽32.8 m,型深18.2 m,满载吃水11.7 m,满载排水量7 5524 t,载重量57 624 t,货油舱容58 598 m3。
1.1 静水载荷计算基于静水剪力和弯矩的直接计算方法,利用水动力分析软件MOSES对FPSO在满载和压载状态下的静水剪力和弯矩进行计算,在Moses环境中建立的静水载荷计算模型如图1所示。

|
图 1 静水载荷计算模型 Fig. 1 Hydrostatic load calculation model |
将MOSES中的计算结果根据CCS《油船结构直接计算分析指南》中的规定,对端点处的剪力和弯矩计算值进行修正[7],可得满载和压载时的剪力和弯矩沿船长分布如图2和图3所示。
由图2和图3可知,FPSO在满载和压载时的重量分布不同导致其在2种载况下的静水剪力和弯矩的纵向分布不同。
|
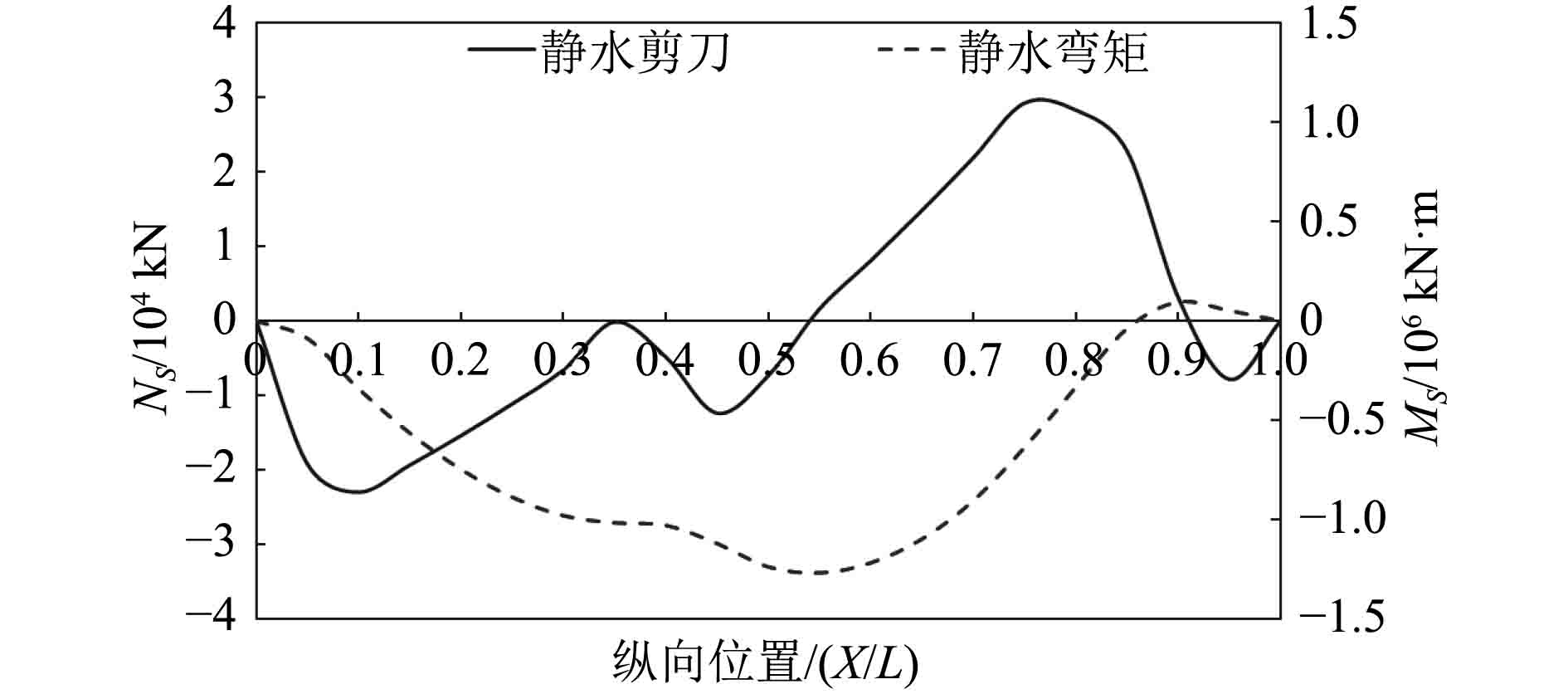
图 2 满载时的静水剪力和弯矩沿船长分布 Fig. 2 Distribution of hydrostatic shear force and bending moment along ship length in full load condition |
|
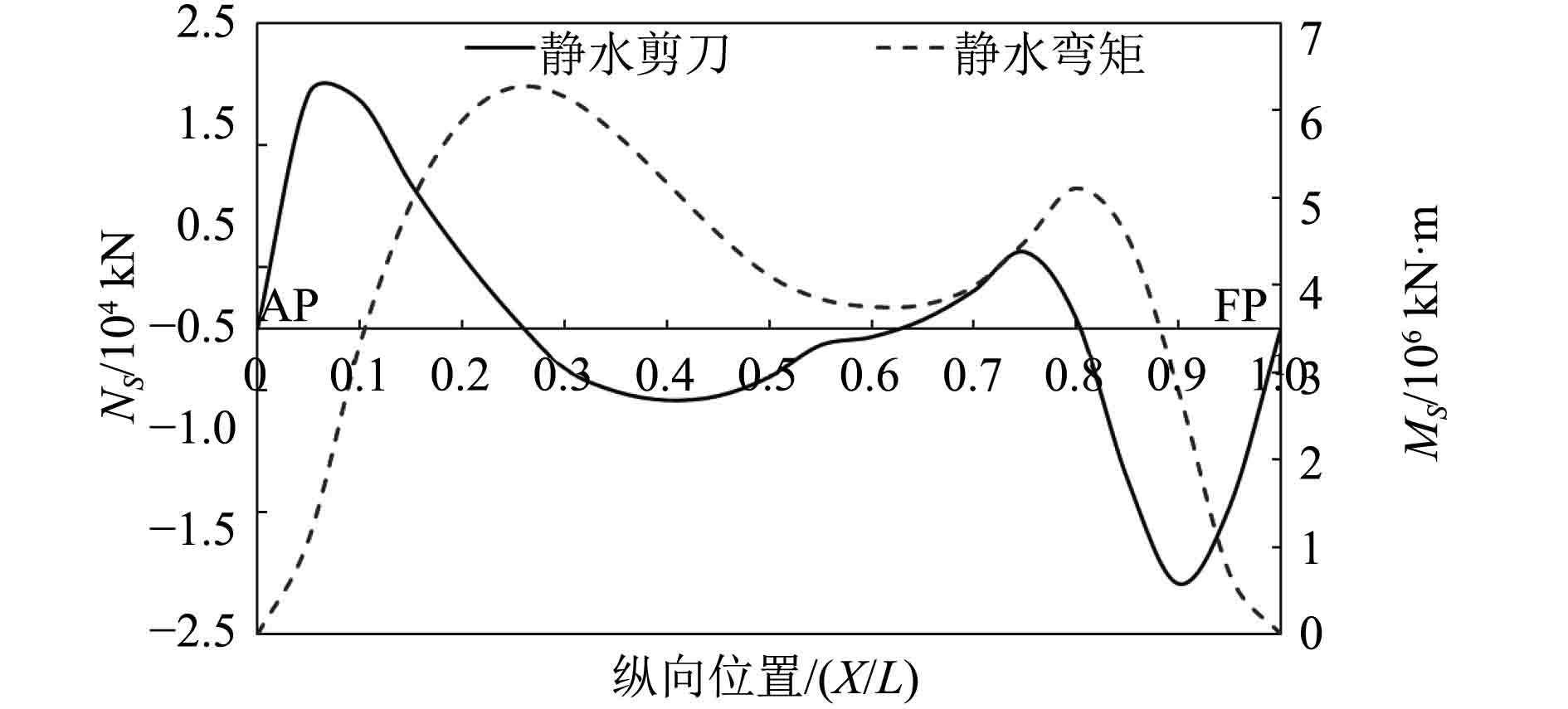
图 3 压载时的静水剪力和弯矩沿船长分布 Fig. 3 Distribution of hydrostatic shear force and bending moment along ship length in ballast condition |
满载时的静水弯矩基本都为负值,即此时船体处于中垂状态,最大弯矩位于船中附近;静水剪力在船尾至船中区域为负值,在船中至船首区域为正值,最大分别位于距船尾0.2 L和0.75 L附近。压载时静水弯矩都为正值,即此时船体处于中拱状态,在距船首和船尾1/4 L处的静水弯矩相对较大,而船中的静水弯矩相对较小,此时的最大弯矩位于距船尾1/4 L处。
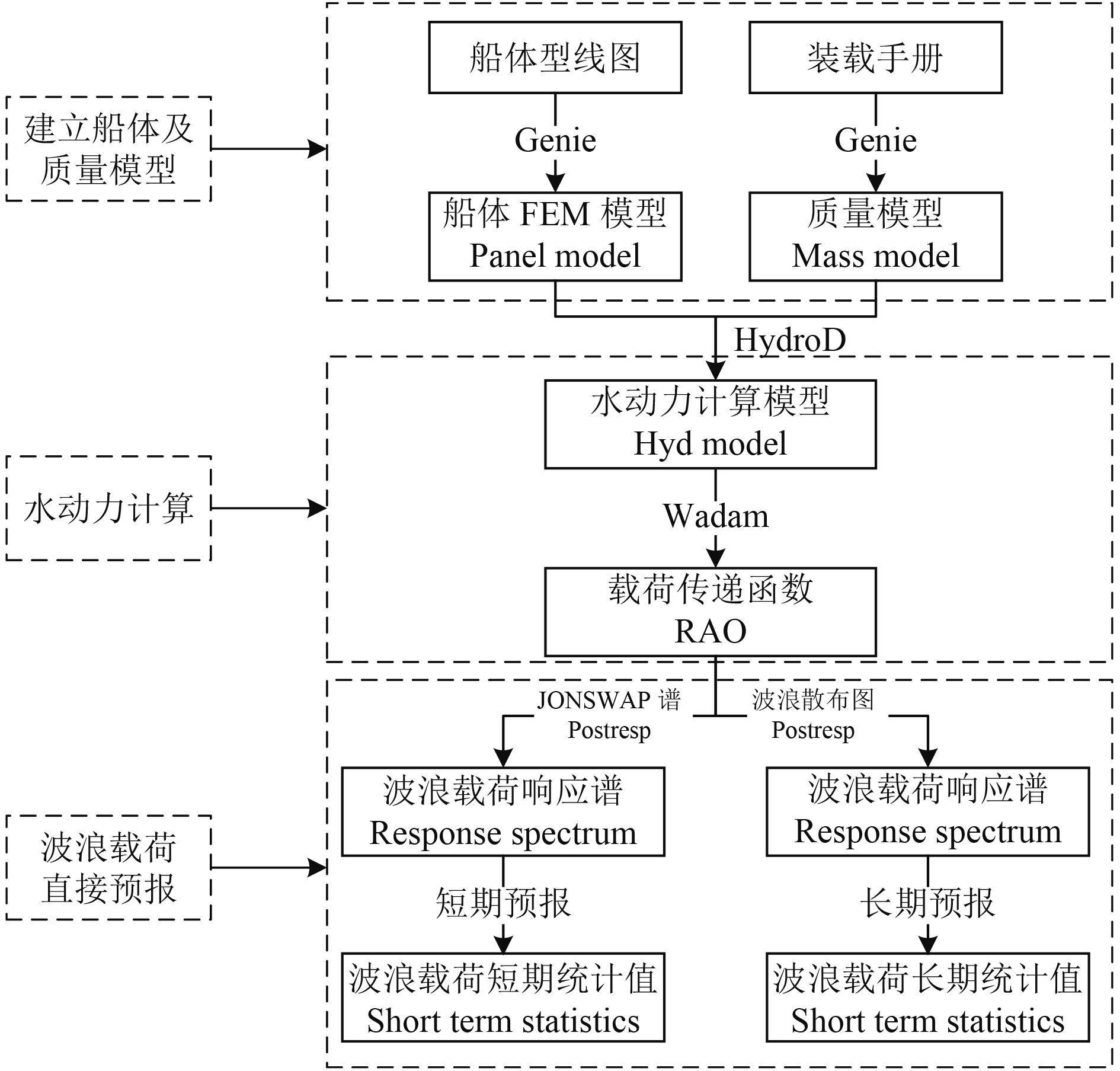
1.2 波浪载荷计算本文基于三维势流理论,通过水动力分析软件Sesam的Wadam分析模块对FPSO在满载和压载状态下分别进行水动力分析,并以计算的规则波中波浪载荷响应为基础,应用随机过程理论,对其在渤海某油田海域的波浪载荷特性进行长期和短期预报,具体的计算流程如图4所示。
|
图 4 波浪载荷计算流程图 Fig. 4 Flow chart of wave load calculation |
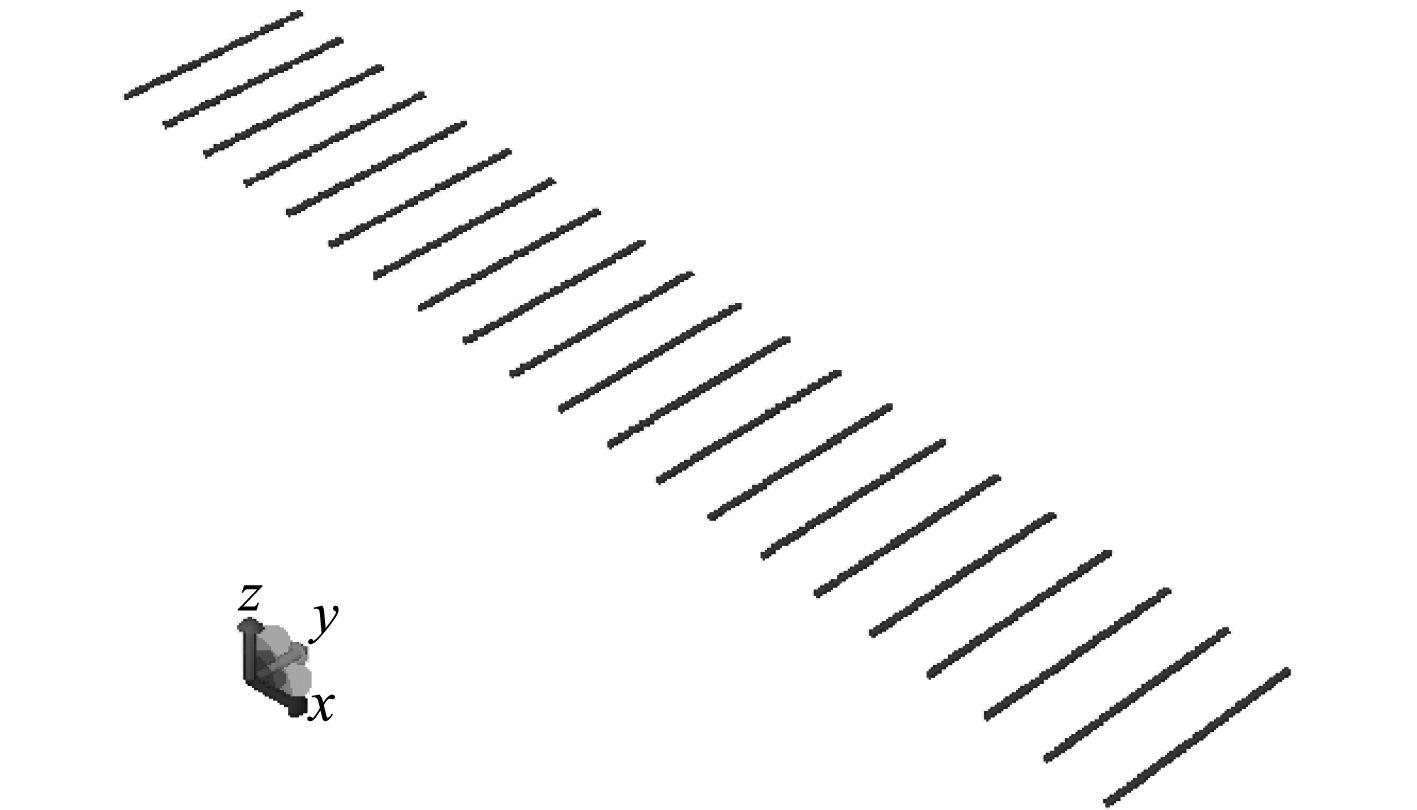
在Sesam-Genie环境中建立FPSO船体湿表面有限元模型如图5所示,整个船体的单元数量约为1 600个。同时,采用“质量棒”的方式定义船体及装载的质量模型,每个站位上定义重量等于该站等效重量的“质量棒”,如图6所示。

|
图 5 船体有限元模型 Fig. 5 Finite element model of hull wet surface |
|
图 6 质量模型 Fig. 6 Mass model |
计算波浪载荷时的载况同样选为满载和压载2种状态;波浪频率取0.2~3 rad/s,间隔0.05 rad/s,共57个频率;浪向角取0°~180°,间隔15°,共13个浪向;水深约为18 m。
1.2.2 波浪载荷直接预报由于船体外表面形状变化多样,波浪成分复杂和波形的不规则以及船舶和波浪相互作用的随机性等因素,使得波浪载荷的准确计算变得非常困难。目前,通常采用谱分析法计算船体所受的波浪载荷。把载荷传递函数与实际工作海况对应的波浪谱相结合,便可得到船体受到的载荷谱,通过波浪统计预报方法便可得出船体波浪载荷的统计值[8]。本文分别采用波浪统计预报方法的短期预报和长期预报对船体波浪载荷的统计值进行预报。
1)短期预报
海洋工程中一般采用3 h短期预报,载荷平均循环次数为n=10 800/Tz,计算时可取超越概率水平为Q=1/n=Tz/10 800,则可计算出此概率下的响应值。本文在进行FPSO船体波浪载荷响应短期预报中采用JONSWAP谱,其谱密度函数表达式为[9]:
| $S(\omega ) = \alpha {g^2}{\omega _{{p}}}^{ - 5}\exp \left[ { - \frac{5}{4}{{(\frac{\omega }{{{\omega _p}}})}^{ - 4}}} \right]{\gamma ^{\exp \left[ { - \frac{1}{{2{\sigma ^2}}}{{(\frac{{\omega - {\omega _p}}}{{{\omega _{{p}}}}})}^2}} \right]}}\text{,}$ | (1) |
式中:
| $\left\{ \begin{gathered} \gamma {{ = }}5{{ }}{T_P}/\sqrt {{H_S}} \leqslant 3.6 \text{,}\hfill \\ \gamma = \exp (5.75 - \frac{{1.15{T_P}}}{{\sqrt {{H_S}} }}){{ 3}}{{.6 < }}{T_P}/\sqrt {{H_S}} < 5 \text{,}\hfill \\ \gamma = 1{{ }}{T_P}/\sqrt {{H_S}} \geqslant 5 \text{。}\hfill \\ \end{gathered} \right.$ | (2) |
2)长期预报
通常规定船舶一生中遭到的波浪载荷循环次数为n=108,则计算时可取概率水平为Q=1/n=10–8。由长期超越概率即可得出对应响应变量的设计值。本文在进行波浪载荷长期预报时根据渤海某油田海域的波浪数据定义波浪散布图,各浪向以等概率作用在船体上。
3)直接预报结果
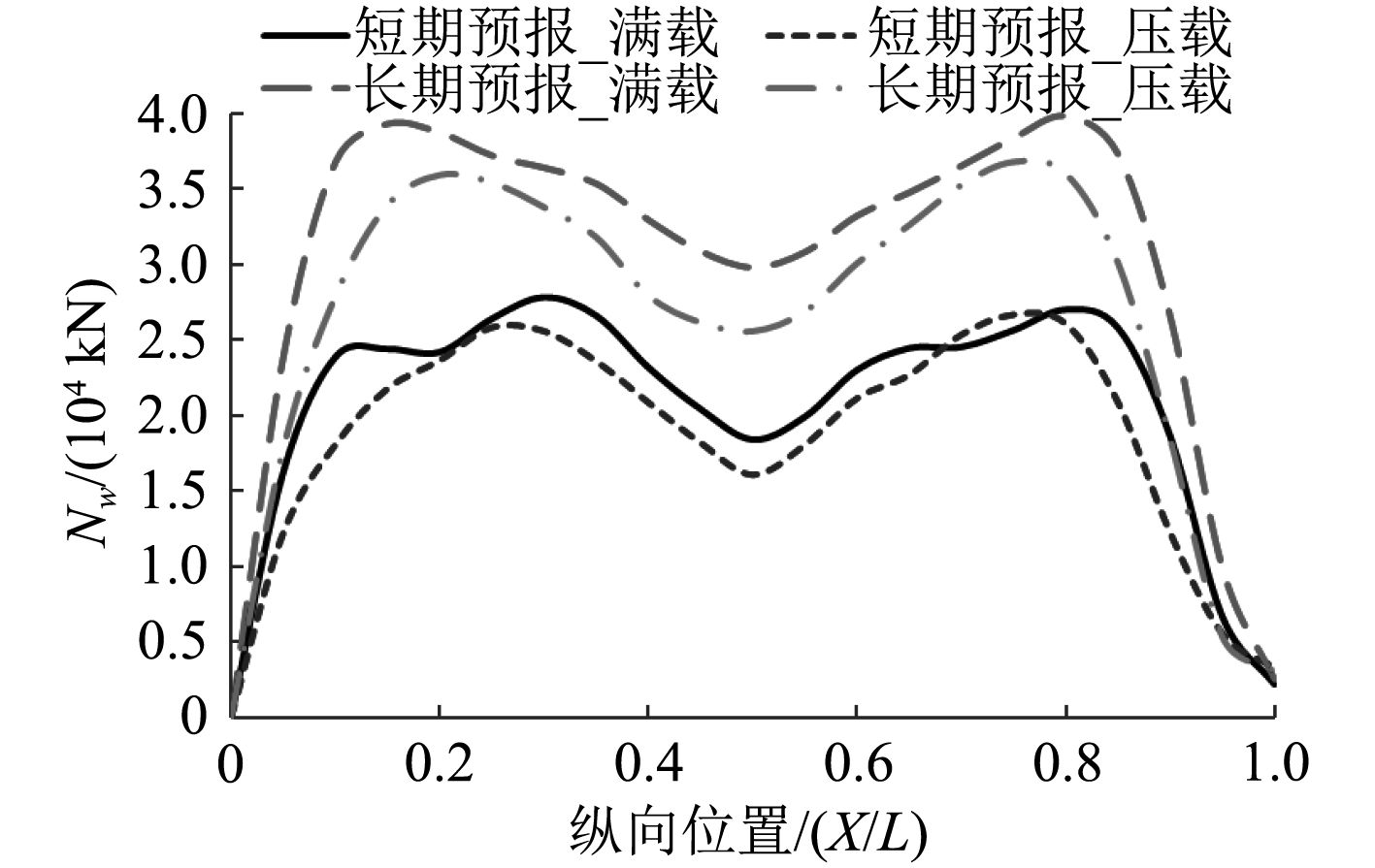
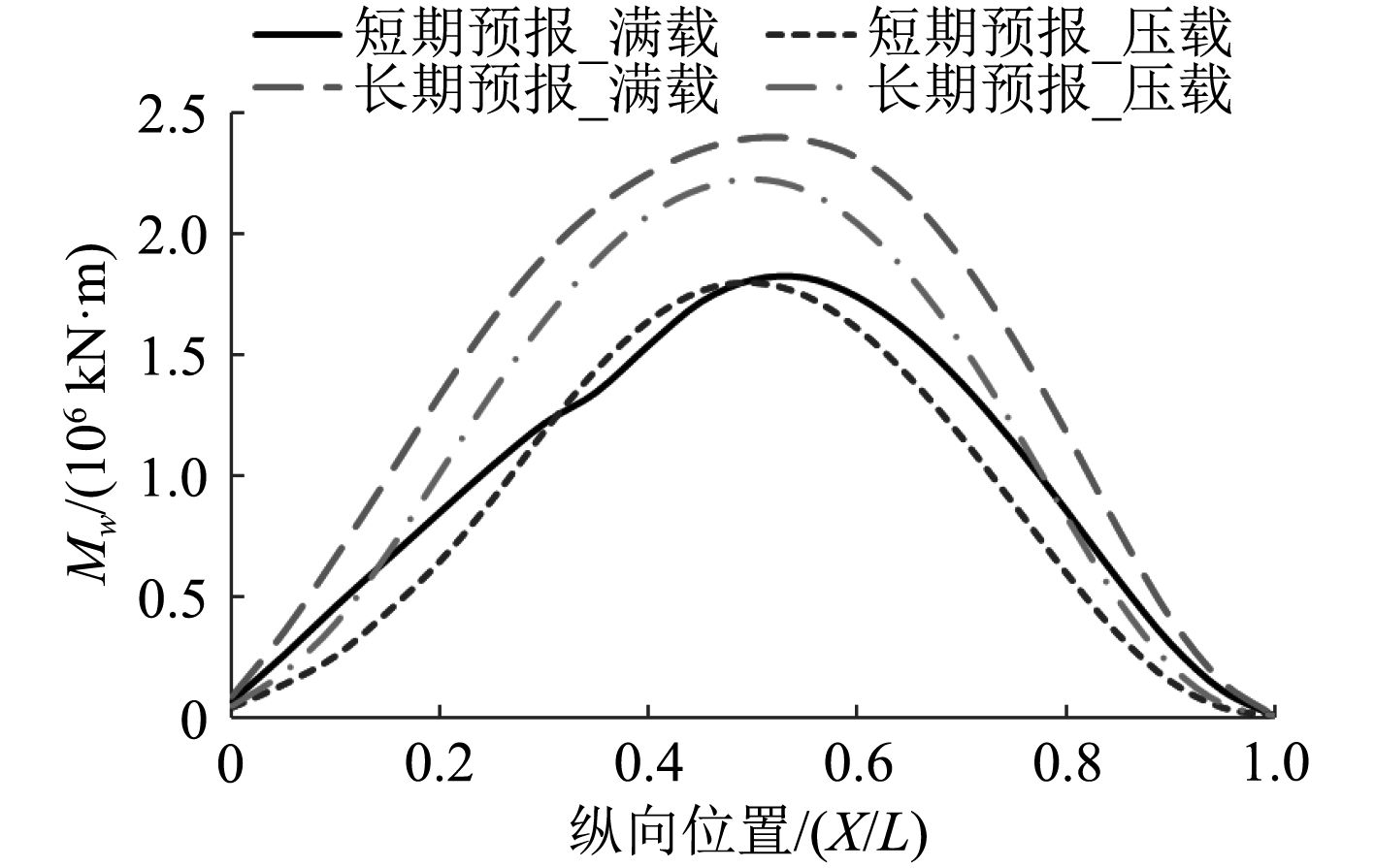
计算得到FPSO在满载和压载状态下的波浪剪力和弯矩长短期预报曲线如图7和图8所示。分析图7和图8可知,FPSO在满载和压载状态时波浪剪力和弯矩的长期和短期预报值沿船长的分布趋势均是关于船中呈对称分布;但波浪剪力在船中位置的预报值最小,在距船首和船尾1/4 L附近的预报值均最大,而波浪弯矩的预报值均是在船中附近最大。同时,满载时波浪载荷预报值基本都要比压载时预报值大,而长期预报值也都大于短期预报值。
|
图 7 波浪剪力直接预报值沿船长分布曲线 Fig. 7 Distribution curve of wave shear force direct forecast value along ship length |
|
图 8 波浪弯矩直接预报值沿船长分布曲线 Fig. 8 Distribution curve of wave bending moment direct forecast value along ship length |
由于1.2.2节计算得到的波浪剪力和弯矩为各参考截面的剖面剪力和弯矩,不能直接用于总纵强度的分析。因此,本文根据CCS《油船结构强度直接计算分析指南》对剖面剪力和弯矩进行修正,以得到FPSO在满载和压载时的中拱和中垂剪力和弯矩沿船长的分布。由于波浪载荷长期预报值都大于短期预报值,故本文根据式(3),将FPSO的长期预报值修正结果与静水载荷合成得到总纵外载荷沿船长分布曲线如图9和图10所示。
| $\left\{ \begin{gathered} N( + ) = {N_S} + {N_V}( + ) \text{,}\hfill \\ N( - ) = {N_S} + {N_V}( - ) \text{,}\hfill \\ M( + ) = {M_S} + {M_V}( + ) \hfill \text{,}\\ M( - ) = {M_S} + {M_V}( - ) \hfill \text{。}\\ \end{gathered} \right.$ | (3) |
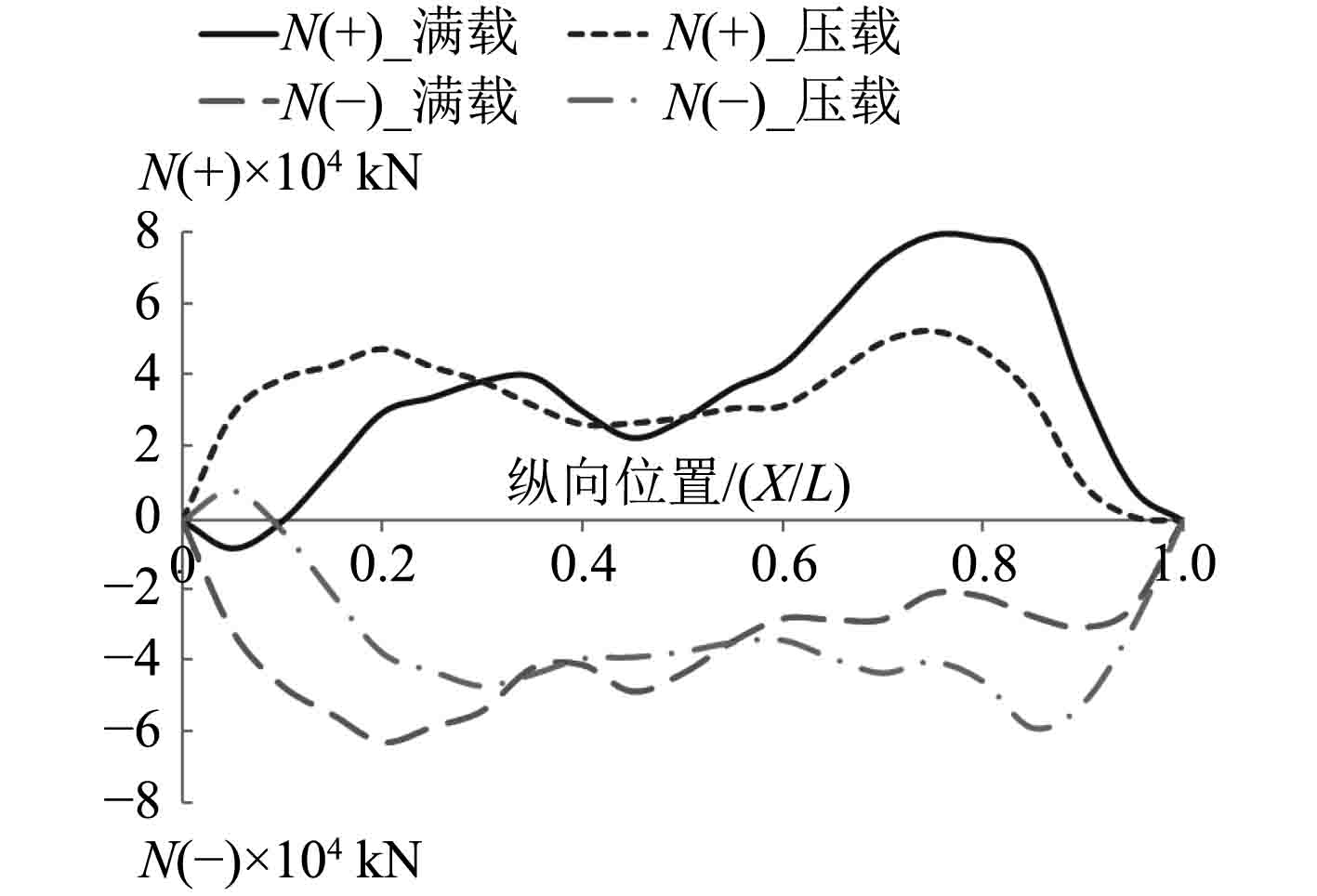
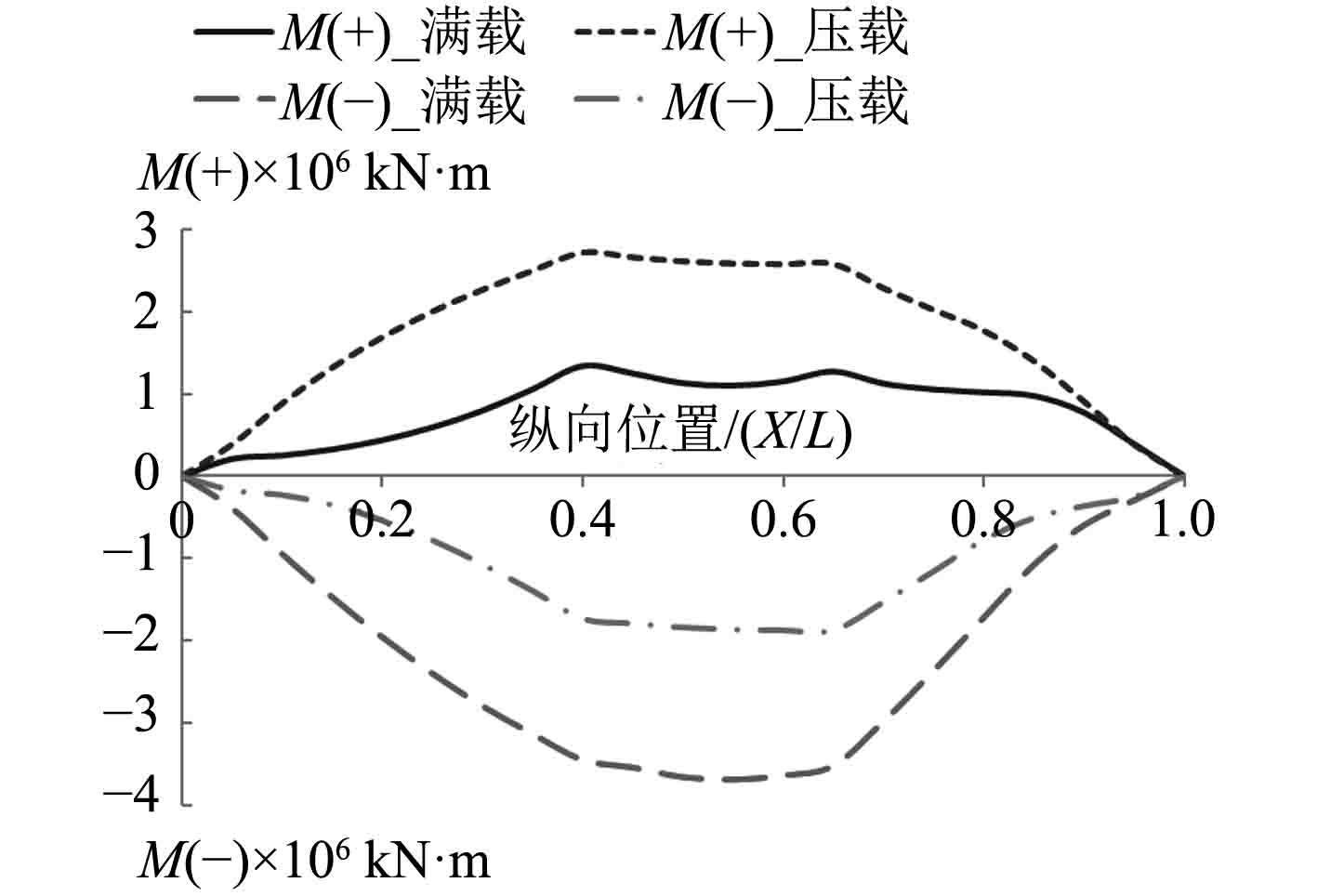
式中:N(+)和N(-)分别为船体剖面中拱剪力和中垂剪力,M(+)和M(-)分别为船体剖面中拱弯矩和中垂弯矩。
|
图 9 总纵剪力沿船长分布曲线 Fig. 9 Distribution curve of longitudinal shear force along ship length |
|
图 10 总纵弯矩沿船长分布曲线 Fig. 10 Distribution curve of longitudinal bending moment along ship length |
由图9和图10可知,FPSO在满载和压载时的中拱和中垂剪力沿船长分布均是在船中附近的剪力值最小,而在距船首和船尾的0.2 L~0.25 L附近的区域剪力值相对较大。满载和压载时的中拱和中垂弯矩沿船长分布均是关于船中呈对称分布,且都是在0.4 L~0.6 L区域内的弯矩值最大。
另外,由于满载时船体在静水中为中垂状态,而压载时船体在静水中呈中拱状态,导致满载中拱弯矩小于压载中拱弯矩,在船中区域(0.4 L~0.6 L)弯矩相对较大的位置满载中拱弯矩比压载中拱弯矩约小50%~57%;而满载中垂弯矩要大于压载中垂弯矩,在船中区域(0.4 L~0.6 L)弯矩相对较大的位置满载中垂弯矩比压载中垂弯矩约大50%。
2 考虑腐蚀影响的船体总纵强度分析 2.1 船体剩余剖面模数 2.1.1 构件腐蚀量计算方法确定船舶腐蚀量的准确方法是通过采用无损检测的方式现场勘验和测厚来确定,但对于没有船体测厚报告的情况,可参考相关规范中关于腐蚀余量的规定估算腐蚀量。本文即参照《海上浮式装置入级与建造规范》(以下简称《规范》)[10]中关于腐蚀速率的规定来估算FPSO服役近20年的腐蚀量,进而得到腐蚀后各构件的厚度。《规范》中规定腐蚀量tcorr由构件两面所处环境的年腐蚀速率和涂层寿命决定,按照下式计算:
| ${t_{corr}} = {N_r}({t_{c1}} + {t_{c2}})\text{,}$ | (4) |
式中:Nr为腐蚀年限,即涂层失效后腐蚀的年限;tc1,tc2为单面腐蚀速率,取值如表1所示。
|
|
表 1 结构构件单面腐蚀速率 Tab.1 Corrosion rate of single side of structural member |
根据船体中横剖面图,对纵向强力构件进行编号,并选定参考轴,分别求出各构件的剖面积Ai,其形心距参考轴的距离为Zi,静矩为AiZi,惯性矩为AiZi2。对于高度较大的垂向构件,如舷侧板等,还需计算其自身惯性矩i0=Aihi2/12(hi为该构件的垂直高度),则得:
| $\left\{ \begin{gathered} A = \sum {{A_i}} {{ }} \text{,}\hfill \\ B = \sum {{A_i}{Z_i}{{ }}} \text{,}\hfill \\ C = \sum ( {A_i}{Z_i}^2 + {i_0}){{ }} \hfill \text{。}\\ \end{gathered} \right.$ | (5) |
则水平中和轴至参考轴的距离为:
| $\varepsilon = \frac{B}{A}{{ }}\text{。}$ | (6) |
根据平行移轴定理可得,船体中横剖面对水平中和轴的惯性矩为:
| $I = 2\left( {C - {\varepsilon ^2}A} \right){{ = }}2(C - \frac{{{B^2}}}{A}){{ }}\text{。}$ | (7) |
任意构件至中和轴的距离为:
| ${Z_i}^\prime = {Z_i} - \varepsilon \text{,}$ | (8) |
则甲板和船底的剖面模数Wd和Wb分别为:
| $\left\{ \begin{gathered} {W_d} = I/{Z_{^d}}^\prime = ({Z_d} - \varepsilon ) \hfill \text{,}\\ {W_b} = I/{Z_{^b}}^\prime = ({Z_b} - \varepsilon ) \hfill \text{。}\\ \end{gathered} \right.$ | (9) |
根据式(4)计算得不同部位构件腐蚀厚度,再根据式(5)~式(9)计算得FPSO腐蚀后的剩余剖面模数如表2所示。
|
|
表 2 剩余剖面模数 Tab.2 Residual section modulus |
根据《钢质海船入级与建造规范》(以下简称《钢规》)中的规定,船舶总纵弯曲应力应满足[11]:
| $\sigma ( \pm ) \leqslant \left[ \sigma \right]\text{,}$ | (10) |
式中:[σ]为许用弯曲应力,[σ]=175/KL(MPa);KL为总纵强度材料系数,对于Q235钢,《钢规》中规定KL=1,即[σ]=175 MPa。σ(±)为中拱或中垂总纵弯曲应力,MPa,可按照下式进行弯曲应力的计算:
| $\sigma ( \pm ) = \frac{{\left| {M( \pm )} \right|}}{W}\text{,}$ | (11) |
式中:M(±)为中拱或中垂总纵弯矩;W取Wd与Wb中小者。计算得到FPSO服役20~40年后的船体最大总纵弯曲应力如表3所示。
|
|
表 3 FPSO服役20~40年后最大总纵弯曲应力 Tab.3 Maximum longitudinal bending stress of FPSO after operating 20 to 40 years |
从表3中数据可知,现阶段(服役20年后)的FPSO船体最大总纵弯曲应力比许用弯曲应力小,此时船体总纵弯曲强度满足《钢规》的要求。在FPSO船体不进行任何维护的前提下,继续服役至25年时,总纵弯曲强度虽满足《钢规》的要求,但富裕量很小。当继续服役至40年时,其最大总纵弯曲应力将严重不满足《钢规》的要求,所以FPSO在延期服役过程中应定期进坞进行换板加强,以提高船体剖面模数,从而提高总纵弯曲强度。
2.2.1 总纵剪切强度根据《钢规》中的规定,船舶总纵剪应力应满足:
| $\tau ( \pm ) \leqslant \left[ \tau \right]\text{,}$ | (12) |
式中:[τ]为许用剪切应力,[τ]=110/KL(MPa);KL为总纵强度材料系数,对于Q235钢,《钢规》中规定KL=1,即[τ]=110 MPa。τ(±)为中拱或中垂时的剪切应力,MPa,可按照下式进行船体剖面剪切应力的计算:
| $\tau = \frac{{\left| {N( \pm )} \right|S}}{{I\delta }} \times {10^2}{{ MPa}}{\text{。}}$ | (13) |
式中:N(±)为中拱或中垂时的剪力,kN;S为静矩,cm3;I为计算剖面对水平中和轴的惯性矩,cm4;δ根据规范确定。由式(13)计算可得FPSO服役20~40年后的最大总纵剪应力如表4所示。
|
|
表 4 FPSO服役20~40年后的最大总纵剪应力 Tab.4 Maximum longitudinal shear stress of FPSO after operating 20 to 40 years |
由表4中数据可得,现阶段(服役20年后)的FPSO船体最大总纵剪应力比许用剪应力小近50%,满足《钢规》的要求。在FPSO船体不进行任何维护的前提下,继续服役至40年时,最大剪切应力仍比许用剪应力小近35%,裕量仍很大。所以,对于本文的FPSO,其总纵剪切强度不是主要的强度问题,应主要关注其总纵弯曲强度。
3 结 语本文以已服役近20年的FPSO为研究对象,通过水动力分析软件MOSES和SESAM计算了其满载和压载时的总纵外载荷,并对其进行了总纵强度的分析与校核,得到主要结论如下:
1)满载状态时FPSO船体处于中垂状态,最大静水剪力和弯矩分别位于距船尾0.75 L和0.55 L附近;而压载时船体处于中拱状态,最大静水剪力和弯矩分别位于距船尾0.9 L和0.25 L附近。
2)FPSO在满载和压载状态时的波浪剪力和弯矩的长短期预报值均是关于船中呈对称分布,只是最大值的位置不同。波浪剪力预报值在船中附近最小,而在距船首尾1/4 L附近最大;波浪弯矩的预报值均是在船首尾位置为0,而在船中附近最大。此外,满载时的波浪载荷预报值基本要比压载时大,而且长期预报值均大于短期预报值。
3)FPSO目前状态的总纵弯曲与剪切强度均满足《钢规》的要求,但船体在目前状态不进行任何维护的前提下,继续服役至40年时,船体总纵弯曲强度将严重不满足《钢规》的要求,而总纵剪切强度仍满足《钢规》的要求。对于本文中的FPSO,其总纵剪切强度不是主要的强度问题,应主要关注其总纵弯曲强度,在延期服役过程中应定期进坞进行除锈涂漆维护和换板加强。
| [1] |
周守为, 曾恒一, 范模. 我国浮式生产储油装置的研制与开发[J]. 中国海上油气, 2006, 18(2): 73–78.
ZHOU Shou-wei, ZENG Heng-yi, FAN Mo. Floating production, storage and offloading system researched and developed in China [J]. China Offshore Oil and Gas, 2006, 18(2): 73–78. http://d.wanfangdata.com.cn/Periodical_zghsyq-gc200602001.aspx |
| [2] |
《海洋石油工程设计指南编委会》. 海洋石油工程FPSO与单点系泊系统设计[S]. 北京: 石油工业出版社, 2007.
Editorial Board of Guidelines for Offshore Oil Engineering Designing. Design of offshore oil engineering FPSO and single point mooring system [S]. Beijing: Petroleum Industry Press, 2007. |
| [3] |
唐文勇, 张道坤, 刘坤, 等. 考虑腐蚀影响的FPSO风险接受准则研究[J]. 船舶力学, 2013, 17(5): 502–512.
TANG Wen-yong, ZHANG Dao-kun, LIU Kun, et al. Study on risk acceptance criterion of FPSO considering influence of corrosion [J]. Journal of Ship Mechanics, 2013, 17(5): 502–512. http://www.cnki.com.cn/Article/CJFDTOTAL-CBLX201305008.htm |
| [4] | JOEM K P. Ship hull ultimate strength reliability considering corrosion [J]. Journal of Ship Research, 1998, 42(2): 154–165. |
| [5] |
马巍巍, 范模, 李达, 等. 提高老旧船形浮体总纵强度探讨[J]. 中国海上油气, 2011, 3(1): 66–70.
MA Wei-wei, FAN Mo, LI Da, et al. Research on raising longitudinal strength of old ship shape naval architecture [J]. China Offshore Oil and Gas, 2011, 3(1): 66–70. |
| [6] |
邱世欣, 赵胜涛, 胡楠, 等. FPSO 延期服役评估方法[J].中国修船, 2013, 26(1): 52–54.
QIU Shi-xin, ZHAO Sheng-tao, HU Nan, et al. Extended service evaluation method for FPSO [J]. China Shiprepair, 2013, 26(1): 52–54. |
| [7] |
中国船级社. 油船结构直接计算分析指南[S]. 北京: 人民交通出版社, 2003.
China Classification Society. Guide for directing calculation of oil tanker structure [S]. Beijing: China Communications Press, 2003. |
| [8] | 戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007. |
| [9] | 刘水庚译. BEREARD MOLIN著. 海洋工程水动力学[M]. 北京: 国防工业出版社, 2012. |
| [10] | 中国船级社. 海上浮式装置入级与建造规范[S]. 北京: 人民交通出版社, 2013. |
| [11] | 中国船级社. 钢质海船入级与建造规范[S]. 北京: 人民交通出版社, 2006. |
 2018, Vol. 40
2018, Vol. 40
