0 引　言

锚泊系统在船舶与海洋工程中的应用十分广泛。而传统的永久或半永久多点锚泊定位系统，其给定的锚链预张力在随后的环境扰动下不再改变，即锚泊系统各个方向上将被动地响应外界干扰（风，浪，流），承受不同的环境力而间接地造成锚链张力的分布不平衡。而且，随着船舶水平位移的不断累积，最终会导致单根或多根锚链张力过大或过小，造成锚链的疲劳断裂或能量的浪费^[1]。若船舶在受到外界环境载荷作用时，其锚泊系统的锚链张力阈值能够随扰动进行合理地优化分配^[2]，则船舶就能发挥各锚链的定位能力而避免其安全隐患。因此，在以保证船舶误差范围内定位为前提^[3]，研究环境扰动下张力的合理分配问题对于工程船舶作业的安全性很有必要。

遗传算法（GA）作为全局随机概率搜索算法，其本身具有较强的鲁棒性，扩展性和高效的并行计算处理能力，为解决复杂优化问题提供了一种有效地途径。但是，算法固有的缺陷，如早熟、收敛速度缓慢和稳定性差等问题难以有效地应用于实际工程中。国内外许多学者通过对算法不断研究改进来提高算法的性能。文献[4]在配对个体中以精英策略防止早熟；文献[5]研究了编码类型的不同对遗传算法性能的影响；文献[6]采用模拟退火和免疫混合算法来实现全局最优，保证种群多样性以提高软件测试效率；文献[7]从全局角度提出一种改进自适应算法（IAGA）提高全局搜索和收敛能力。以上方法分别从不同方面改善了算法性能，但忽略了选择交叉个体间的相似性，搜索解方向性的保持以及交叉和变异率选择的盲目性。因此，本文基于张力优化模型，利用非线性规划局部搜索特点，结合相似度选择交叉配对的个体并改进交叉、变异自适应操作策略以及将量子变异和灾变作为自适应辅助算子引入遗传算法的2种改进算法来提高系统的运行效率和定位要求。并将其应用于船舶实际作业环境的张力分配问题中，比较相同工况下，张力分配算法在收敛性，稳定性方面的变化。仿真结果表明:改进算法具有更好地优化精度和收敛性能。

1 锚链张力优化模型

对于传统的锚泊定位系统，当船舶受到环境扰动力与锚链的总回复力相平衡时^[8]，船舶处于新平衡位置，但此时船舶的各锚链张力可能分布极不平衡。为防止由此产生的锚泊定位安全问题，可利用锚机收放锚链改变张力大小，确保船舶定位与作业安全要求。那如何随作业环境要求而改变张力呢？这就是张力分配问题。张力分配应保证各锚链张力合理分布^{[9, 10]}。定义锚链张力优化的目标函数：两两锚链张力差的平方和为最小，其数学模型如式（1）所示，实际应用中数学模型需要附加约束条件。

$\min {\kern 1pt} {\kern 1pt} {\kern 1pt} F = {\sum\limits_{i = 1}^8 {{\kern 1pt} \sum\limits_{j = 1}^8 {({T_i} - {T_j})^2} } }\text{。}$

(1)

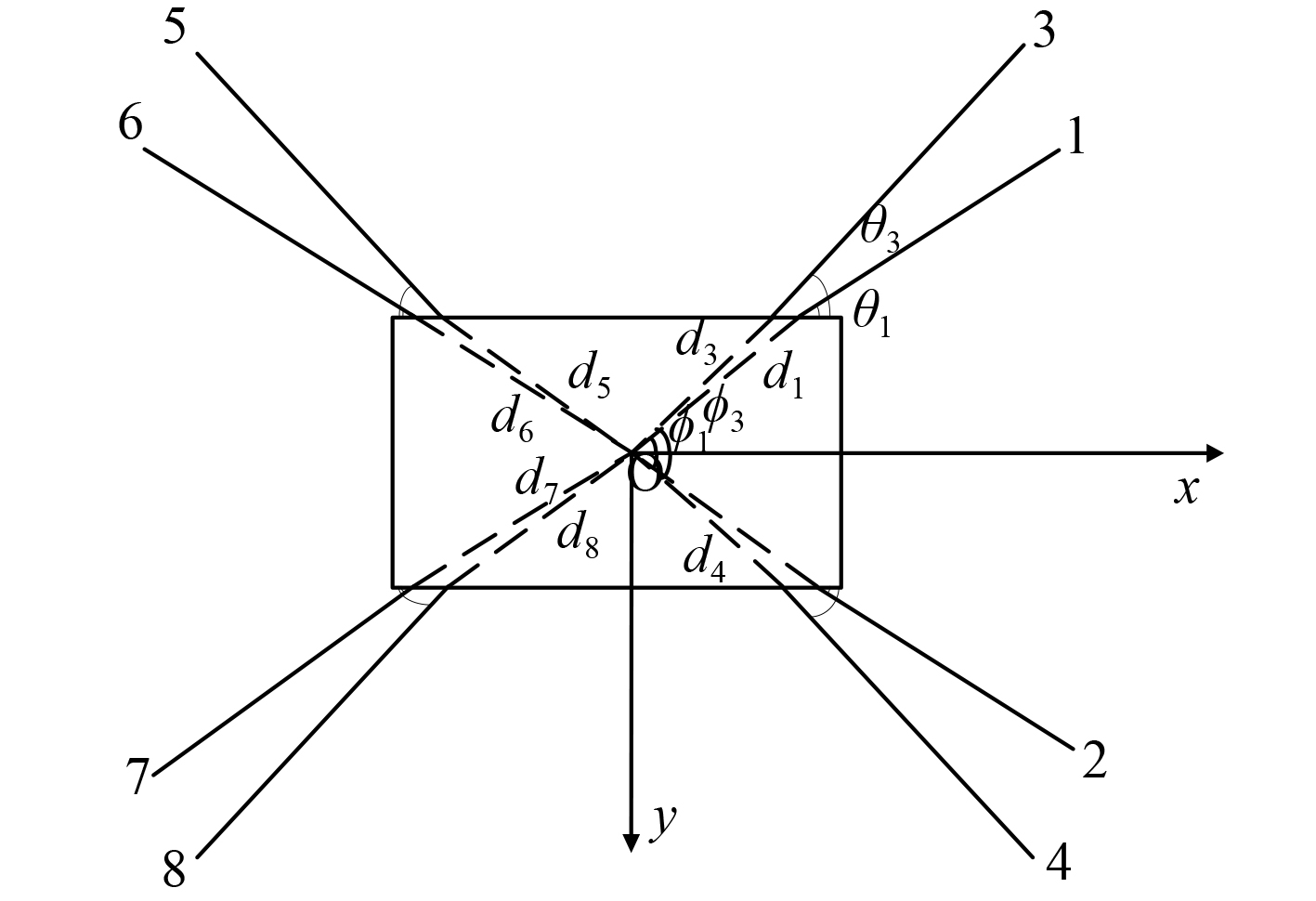
以图1所示8根锚链工程船为例，约束条件由船舶定位要求与锚链安全确定。船舶位置约束^[11]如等式（2）所示，锚链安全约束如不等式（3）所示。

$\left\{ \begin{gathered} \sum\limits_{i = 1}^8 {{T_i}\cos {\phi _i} = {F_{{x}}}}, \; \hfill \\ \sum\limits_{i = 1}^8 {{T_i}\sin {\phi _i} = {F_{{y}}}}, \hfill \\ \sum\limits_{i = 1}^8 {{T_i}{d_i}( - \cos {\phi _i}\sin {\theta _i} + \sin {\phi _i}\cos {\theta _i}) = N}\text{。} \hfill \\ \end{gathered} \right.\;\;\;\;\;\;\;\;\;\;\;\;\;$

(2)

${T_{\min }} \leqslant {T_i} \leqslant {T_{{{max}}}},1 \leqslant i \leqslant {{8}},$

(3)

式中： ${F_{{x}}}$ ， ${F_{{y}}}$ ， $N$ 分别为纵荡、横荡控制力及首摇方向的控制力矩； ${T_i}$ 为各锚链的张力值； ${\theta _i}$ 为锚链布置角度； ${\phi _i}$ 为 $x$ 轴与船舶中心到系缆点的连线间的夹角； ${d_i}$ 为着链点到船舶中心的距离； ${T_{\min }}$ 为锚链最小张力值； ${T_{\max }}$ 为锚链最大安全的可承受力值。

2 改进遗传算法

遗传算法（GA）由于不依赖于优化函数本身的特性而被广泛应用。但在实际工程优化应用中，往往存在高维变量和复杂的约束条件，使得标准遗传算法很容易陷入早熟收敛，后期进化缓慢和多样性保持不好的问题。针对这些缺陷，本文进行改进。

2.1 改进遗传算法1（IGA1） 2.1.1 算法改进思路

通过分析知，张力优化模型实际是求解非线性规划问题，所以本算法利用非线性规划具有较强局部搜索能力的特点，将其应用于全局性遗传算法，并在遗传算法中引入个体相似度概念，交叉配对策略选择交叉对象，同时从宏观和微观上调控交叉和变异率来平衡算法空间深度和广度，弥补局部搜索差的缺陷，提高全局寻优的能力。

2.1.2 个体相似度与交叉配对策略

为避免盲目地选择交叉个体，提高交叉操作效率，这里提出以个体相似度为依据选择交叉配对的父代个体。

1）个体相似度

个体相似度是指2个体具有相同等位基因的数量^{[12 – 13]}。利用三维空间向量余弦定理可推导出多维空间向量的夹角，其夹角大小可表示个体相似程度，夹角越小，个体越相似。为此，将 $m$ 位二进制编码的个体 ${{{X}}_i}$ 和 ${{{X}}_j}$ 记成向量，即 ${{{X}}_i} = {({x_{i1}},{x_{i2}},{x_{i3}}, \cdots {x_{im}})^{{T}}}$ ， ${{{X}}_j} = {({x_{j1}},{x_{j2}},{x_{j3}}, \cdots ,{x_{jm}})^{{T}}}$ ，其中 ${x_{ik}},{x_{jk}} \in \{ 0,1\} $ ， $k = 1,2,3 \cdots ,m$ 。则向量 ${{{X}}_i}$ 和 ${{{X}}_j}$ 的夹角 $\theta $ 可由式（4）计算得到，余弦值越大，向量夹角越小，个体越相似。这里定义遗传算法 ${{{X}}_i}$ ， ${{{X}}_j}$ 个体相似度如式（5）所示。当 $S({{{X}}_i},{{{X}}_j}) = 1$ 代表2个体一样； $S({{{X}}_i},{{{X}}_j}) = 0$ 代表2个体完全不同。

$\begin{split} \cos \theta =& \frac{{({{{X}}_i},{{{X}}_j})}}{{\left| {\left| {{{{X}}_i}} \right|} \right|\;\left| {\left| {{{{X}}_j}} \right|} \right|}} = \frac{{{{{X}}_j}^{{T}}{{{X}}_i}}}{{\sqrt {{{{X}}_i}^{{T}}{{{X}}_i}} \sqrt {{{{X}}_j}^{{T}}{{{X}}_j}} }}=\\ & \frac{{\sum\limits_{k = 1}^m {{x_{ik}}{x_{jk}}} }}{{\sqrt {(\sum\limits_{k = 1}^m {{x_{ik}}^2} )(\sum\limits_{k = 1}^m {{x_{jk}}^2} )} }}, \end{split} $

(4)

$S({{{X}}_i},{{{X}}_j}) = \frac{{1 + \cos \theta }}{2} \in \left[ {0,1} \right]\text{。}$

(5)

2）交叉配对策略

将个体按适应度大小进行非线性降序排序，排序后对应的个体序列记为 ${{X'}_i},i = 1,2,3 \cdots N$ 。由式（4）和式（5）计算 ${{{X}}_i}^\prime $ 与其余个体的相似度 $S\left( {{{{X'}}_i},{{{X'}}_j}} \right),j = 1,2,3, \cdots ,N$ 且 $j \ne i$ 。固定 ${{{X}}_i}^\prime $ ，对 $S\left( {{{{X'}}_i}{,}{{{X'}}_j}} \right)$ 按数值升序排序，并在末个数后添加 $\max (S\left( {{{{X'}}_i},{{{X'}}_j}} \right))$ ，记为 ${S'_k}\left( {{{{X'}}_i},{{{X'}}_j}} \right),$ k=1,2,3,···N, 取 ${S'_k}\left( {{{{X'}}_i},{{{X'}}_j}} \right)$ 中 $k = i$ 对应的 ${{{X}}_i}^\prime $ 与 ${{{X}}_j}^\prime $ 交叉配对。

2.1.3 交叉、变异自适应操作的改进

改变标准遗传算法中交叉与变异率选择固定而引起的缺陷，将种群整体进化效果考虑进去，对任子武的IAGA算法^{[7, 14]}进行改进。根据指数函数的性质，从宏观上以增加种群多样性来防止早熟收敛，对群体设置较大的 ${P_c}$ ， ${P_m}$ ；微观上根据个体适应度大小调整 ${P_c}$ ， ${P_m}$ 。假设 ${f_{\min }}$ 为群体的最小适应度值；以 $\alpha = \frac{{{f_{\max }} - {f_{avg}}}}{{{f_{avg}} - {f_{\min }} + \lambda }}$ 判断未成熟收敛， $\lambda $ 为避免分母是0的无穷小正数； ${U_a}$ 为各代适应度值大于平均适应度值的个体数目，而 ${U_b}$ 正好相反。具体表达式描述如式（6），式（7）。其中 ${P_{{{c}}1}},{P_{{{c}}2}},{P_{{{m}}1}},{P_{{{m}}2}} \in (0,1)$ ，其余参数定义见文献[7]。

${p_{{c}}} = \left\{ \begin{array}{l}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{0.9^{{\kern 1pt} \alpha }}\;\;\;\;\;\;\;\;,\alpha < 1\text{且}{U_a} > {U_b},\\{p_{{{c1}}}} - \displaystyle\frac{{({p_{{{c1}}}} - {p_{{{c2}}}})(f - {f_{{{min}}}})}}{{{f_{{{max}}}} - {f_{{{min}}}}}},\text{其他}\text{。}\end{array} \right.$

(6)

${p_{{m}}} = \left\{ \begin{array}{l}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{0.15^\alpha }\;\;\;\;\;\;\;\;\;\;,\alpha < 1\text{且}{U_a} > {U_b},\\{p_{{{m1}}}} - \displaystyle\frac{{({p_{{{m1}}}} - {p_{{{m2}}}})(f' - {f_{\min }})}}{{{f_{{{max}}}} - {f_{{{min}}}}}},\text{其他}\text{。}\end{array} \right.$

(7)

2.1.4 非线性规划

对非线性函数 $f(x)$ 具有 $\left\{ \begin{gathered} {{A}} \cdot {{x}} \leqslant {{b}} \hfill \\ {{Aeq}} \cdot {{x}} = {{Beq}} \hfill \\ {{LB}} \leqslant {{x}} \leqslant {{UB}} \hfill \\ \end{gathered} \right.$ 约束，其中 ${{A}}$ 和 ${{Aeq}}$ 为矩阵， ${{x}}$ ， ${{b}}$ ， ${{Beq}}$ ， ${{LB,UB}}$ 为矢量，求解 $\min f(x)$ 就是带约束的多维非线性规划问题。遗传算法中以相隔固定代数作为进行非线性规划寻优的条件。非线性规划中的等式约束，采用降维与排序处理^[15]。文献[15]假设线性等式约束方程组 ${{Ax}} = {{b}}$ （ $n \geqslant m$ ）有 $n$ 个原变量， $m$ 个等式约束，则 $n - m$ 个变量就为设计变量，其余 ${T_i}/KN$ 个变量由线性方程组解得，从而降低了维数，也使等式约束严格成立。张力优化模型中有 8个变量，3个等式约束，这里选 ${T_{1,}}{T_2}, \cdots {T_5}$ 作为设计张力变量， ${T_6},{T_7},{T_8}$ 由线性方程组解出，由此保证严格满足等式约束。算法流程如下：

1）初始化种群数 $N$ ，编码长度 $L$ ， ${P_{c{{max}}}} = {P_{{{c1}}}}$ ， ${P_{c{{min}}}} = {P_{{{c2}}}}$ ， ${P_{m{{max}}}} = {P_{{{m1}}}}$ ， ${P_{{m{ min}}}} = {P_{{{m2}}}}$ ，迭代结束条件等参数；

2）产生满足式（3）约束边界的 $N$ 个均匀分布的个体为初始种群；

3）计算个体适应度；

4）根据个体相似度交叉配对策略，选出父代配对交叉个体，以式（6）和式（7）式交叉和变异率进行操作形成子代个体新种群；

5）判断是否需要非线性寻优。若否，进入步骤6；若是，将得到满足约束的结果作为非线性寻优的初始条件进行局部搜索，并让得到的最优值作为新的种群进行全局搜索；

6）判断进化是否终止。若否，返回步骤3。

2.2 改进遗传算法2（IGA2）

改进算法2是将量子计算引入遗传算法中，采用旋转门动态调整策略并以自适应量子变异和灾变算子为辅助，使遗传算法（GA）的搜索解有更好的多样性和方向性，提高收敛性能。

2.2.1 量子比特编码

作为量子计算存储信息单元的介质是一个两态量子体系，叫量子比特（量子位）。用0或1态，或其任意叠加状态表示一个量子位。其叠加态表示为：

$\left| \varphi \right\rangle = \alpha \;\left| {\;0\;} \right\rangle \beta \;\left| {\;1\;} \right\rangle, $

(8)

其中： $(\alpha ,\beta )$ 是2个比特概率幅； $\left| 0 \right\rangle $ 和 $\left| 1 \right\rangle $ 分别为自旋向下，向上态，且满 ${\left| \alpha \right|^2} + {\left| \beta \right|^2} = 1$ ， ${\left| \alpha \right|^2},{\left| \beta \right|^2}$ 分别是上述2个态对应概率。求解张力优化模型时用含 $c$ 个量子位表示控制变量 ${T_{1,}}{T_2}, \cdots {T_8}$ ，编码如下：

${{{q}}_j}^t = \left[ \begin{gathered} {\alpha _{11}}^t \cdots {\alpha _{1c}}^t{\alpha _{21}}^t \cdots {\alpha _{2c}}^t \cdots {\alpha _{m1}}^t \cdots {\alpha _{mc}}^t\; \hfill \\ {\beta _{11}}^t \cdots \;{\beta _{1c}}^t{\beta _{21}}^t \cdots {\beta _{2c}}^t \cdots {\beta _{m1}}^t \cdots {\beta _{mc}}^t\; \hfill \\ \end{gathered} \right]\;,$

(9)

式中： ${{{q}}_j}^t$ 为第 $t$ 代，第 $j$ 个染色体； $m$ 为染色体基因数； $c$ 为每个基因包含的量子位数。对群体中每个染色体，量子位编码 $({\alpha _i},{\beta _i})$ 都初始化为 $\left( {\frac{1}{{\sqrt 2 }},\frac{1}{{\sqrt 2 }}} \right),i = 1,2, \cdots m$ 。

2.2.2 旋转门动态调整策略

种群多样性的维持一般使用如式（10）的量子旋转门^[16]作为量子遗传进化操作的执行机构，利用其对叠加的量子态作用，动态改变量子旋转门旋转方向和角度，从而更新种群，加快收敛。

${{U}}({\theta _i}) = \left[ \begin{gathered} \cos ({\theta _i}) \hfill \\ \sin ({\theta _i}) \hfill \\ \end{gathered} \right.\;\;\left. \begin{gathered} - \sin ({\theta _i}) \hfill \\ \;\;\cos ({\theta _i}) \hfill \\ \end{gathered} \right]\;\;,{\theta _i} = s({\alpha _i},{\beta _i}) * \Delta {\theta _i},$

(10)

其中： ${\theta _i}$ ， $s({\alpha _i},{\beta _i})$ 分别为旋转角和方向。为了使旋转角改变幅度 $\Delta \theta $ 更加符合实际应用，使最优值与当下值较远时增大 $\Delta \theta $ ，扩大搜索范围，加快收敛；反之，减小 $\Delta \theta $ 。因此作如下调整：

$\Delta \theta = {\theta _{\min }} + \frac{{{f_{{x}}} - {f_{\min }}}}{{{f_{\min }}}} \times ({\theta _{\max }} - {\theta _{\min }}),$

(11)

式中： ${\theta _{\min }}$ ， ${\theta _{\max }}$ 分别是 $\Delta \theta $ 为 $0.001\pi \sim 0.05\pi $ 最小及最大值； ${f_{\min }}$ 为最优个体适应度； ${f_{{x}}}$ 为当下个体适应度。

2.2.3 量子变异与灾变

由式（11）知，随着进化代数不断推进，进化后期个体间差别减小，调整操作很难发挥作用。为防止演化搜索停止不前，算法中引入自适应量子变异和灾变算子以提高后期收敛的速度。

借鉴自适应遗传算法的思想，以式（12）作为变异操作的公式。

${P_m} = \left\{ \begin{array}{l}\quad 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; f' > {f_{avg}},\\{P_0} + \frac{{f' - {f_{\min }}}}{{{f_{avg}} - {f_{\min }}}},f' < {f_{avg}}{\text{且}}f' \ne {f_{\min }},\\\quad {P_0},\;\;\;\;\;\;\;\;\;\;\;\; f' = {f_{\min }}\text{。}\end{array} \right.$

(12)

其中 ${P_0} = 0.01$ ，其余参数描述见文献[7]。式（12）以适应度大小进行量子变异，既保证较优个体得以保存，提高种群多样性，又加快了收敛速度。同时为了防止算法后期搜索迟钝，引入灾变算子，当未产生最优解的代数达到设定值时，对部分个体加大扰动，重新生成新个体。

3 仿真与分析 3.1 参数选取

根据1 000 t应急打捞起重船的基本参数，选取以下使用环境：风浪流入射角为 ${45^ \circ }$ ，风速7.9 m/s,有义波高1 m，流速3.087 m/s；船长为105 m，垂线间长103.8 m，船宽为31.2 m，型深为7 m，8台工作负载350 kN定位锚机近似的分布在长方形的4个角；锚链预张力50 kN,破断载荷1 080 kN；其中环境扰动力矩： ${F_{{x}}}$ = 236.71 kN， ${F_{{y}}}$ = 1 315.5 kN， $N$ =2 553 kN·m。

GA初始参数：种群数100，最大代数200，代沟0.9，染色体长度20；交叉和变异率分别为0.7,0.01；IGA1初始参数： ${P_{c{{max}}}}$ = 0.9， ${P_{c{{min}}}}$ = 0.4， ${P_{m{{max}}}}$ = 0.1， ${P_{m{{min}}}}$ = 0.01，其他参数同GA。IGA2初始参数：种群数100，染色体长度20，最大代数200。

3.2 仿真结果及分析

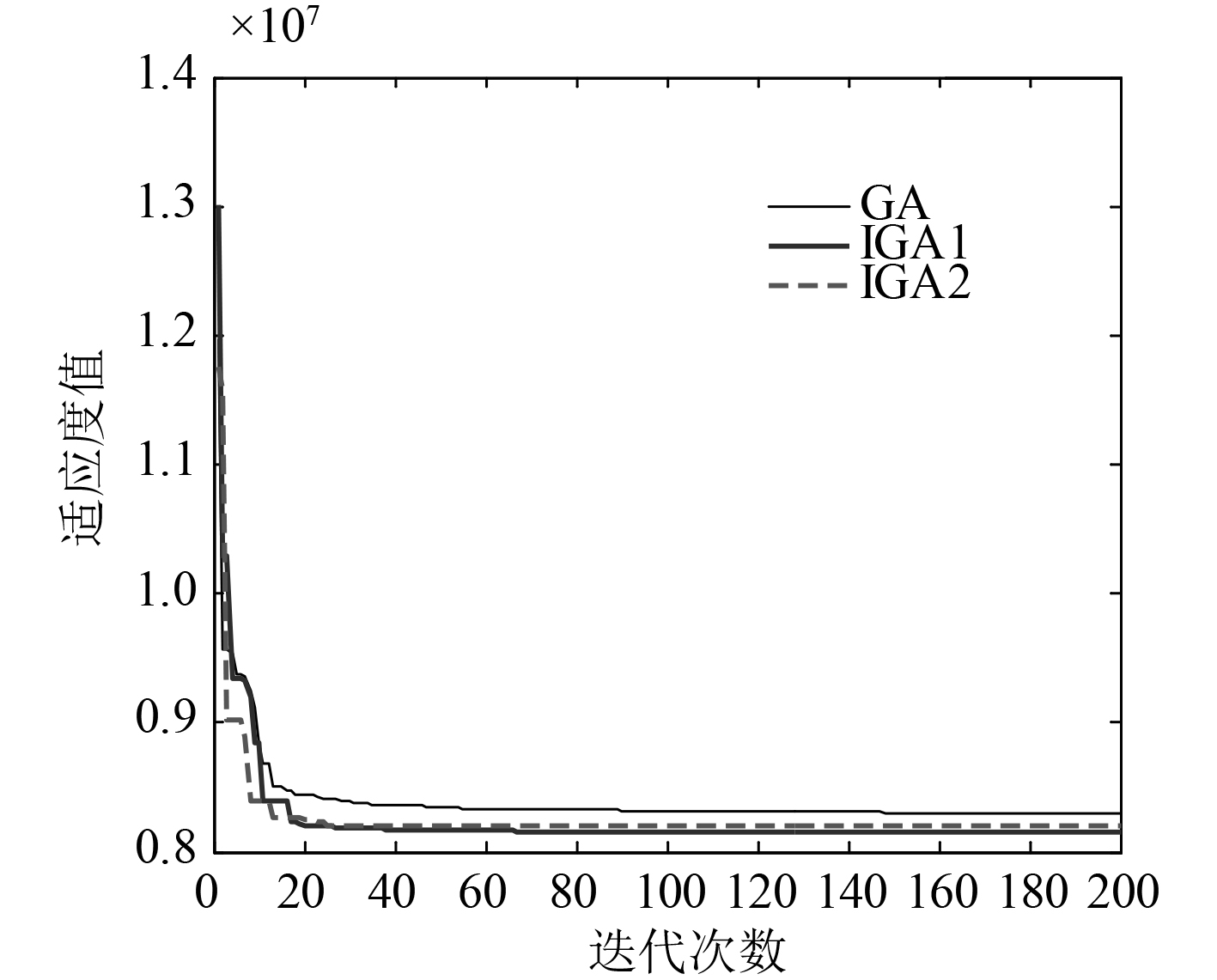
图2分别为用标准遗传及改进算法对张力模型进行张力分配适应度值变化情况。表1为3种遗传算法锚链张力优化结果。表2是算法各执行10次的平均收敛代数，最小收敛代数，平均计算时间和平均最优适应度值的比较。

IGA1算法依据相似度选择交叉配对个体，提高了算法操作效率和搜索空间，使得算法在10～20代能快速收敛。GA算法在60～65代停滞于局部最优，但IGA1算法由于非线性规划局部搜索作用使之很快找到全局最优解。IGA2算法由于动态旋转门始终保持最优解进化的方向，并在适当的时机进行灾变，提高了收敛速度，加快了全局和局部搜索过程。

4 结　语

在研究锚链张力优化模型、遗传算法的基础上，采用个体相似度交叉配对，动态改变交叉与变异率，非线性规划及约束边界处理，量子化编码，旋转门动态调整及自适应变异等措施改进遗传算法，并用改进的算法对锚泊定位系统的张力进行优化仿真，仿真结果验证了改进算法张力分配的合理性和有效性，改进算法的优化能力强于标准遗传算法。不足之处是改进算法增加了计算时间。