随着海洋经济的快速发展,人类对海洋的探索越来越重视,而深海环境的复杂多变,使得作业的船舶或平台需要更高的定位精度,传统的作业工具由于其自身的局限性,如锚泊操作复杂、机动性能差等缺点,已经不能满足现代定位精度的要求,因此,具有智能控制的动力定位系统应运而生[1]。
动力定位系统(Dynamic Positioning System,DPS)是指在不借助外界的辅助下,依靠自身的动力装置来对船舶进行定位的控制系统;主要有测量系统、控制系统和推进系统3部分组成,其中控制系统是核心[2],其工作原理如图1所示。
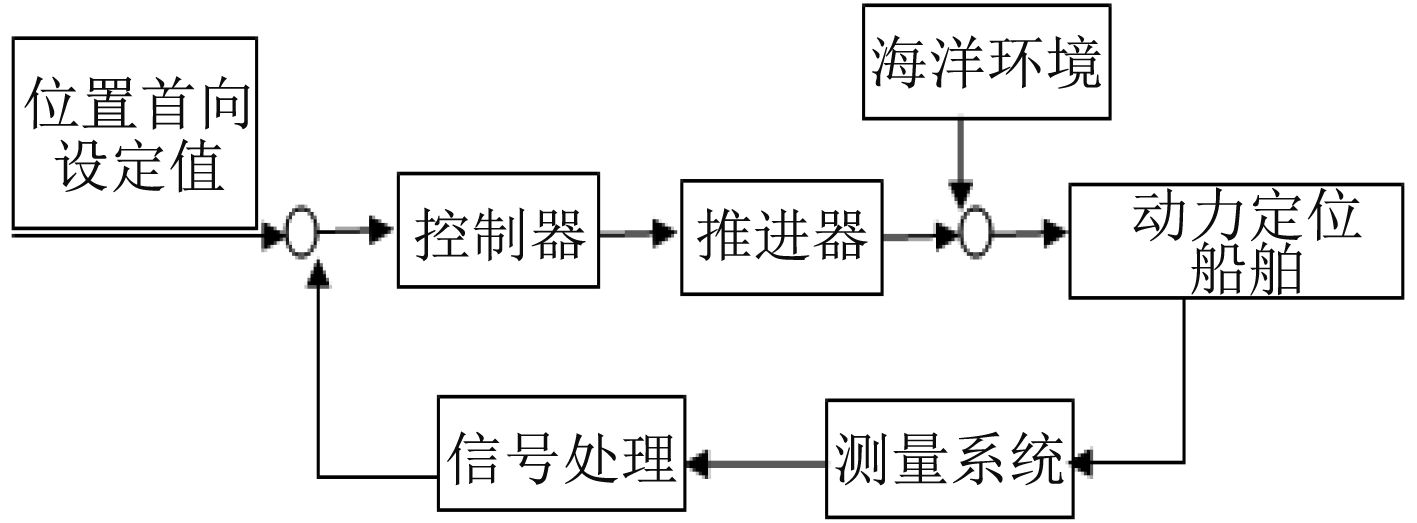
|
图 1 船舶动力定位系统框图 Fig. 1 Block diagram of DPS |
工作原理为:DPS根据测量系统获得的船舶运动信息及当前环境参数,将船舶当前的位置和首向与设定值比较,经过信号处理剔除噪声、船舶干扰信号;控制器根据得到的偏差和控制算法计算出所需推力;船舶的推进器形成一个足以抵消外界环境干扰的主动力和转矩,最终使船舶保持目标位置或设定的航迹[3]。
本文在前人研究的基础上,对动力定位船舶的控制系统进行研究,采用滑模变结构控制(Sliding Model Control,SMC)方法设计一种新型的控制器,使其具有较好的控制效果,具有更好的稳定性和鲁棒性。
1 船舶动力定位系统的数学模型船舶在海上的运动极其复杂,包括横摇(Rolling)、纵摇(Pitching)、首摇(Yawing)、横荡(Swaying)、纵荡(Surging)和垂荡(Heaving)六自由度的运动[4]。本文为了简化船舶运动的数学模型,只考虑水平面上横荡、纵荡和首摇三自由度的运动。
1.1 建立坐标系首先建立坐标系,包括大地坐标系EON和随船坐标系XOY,如图2所示,船舶的位置和首向的矢量式为
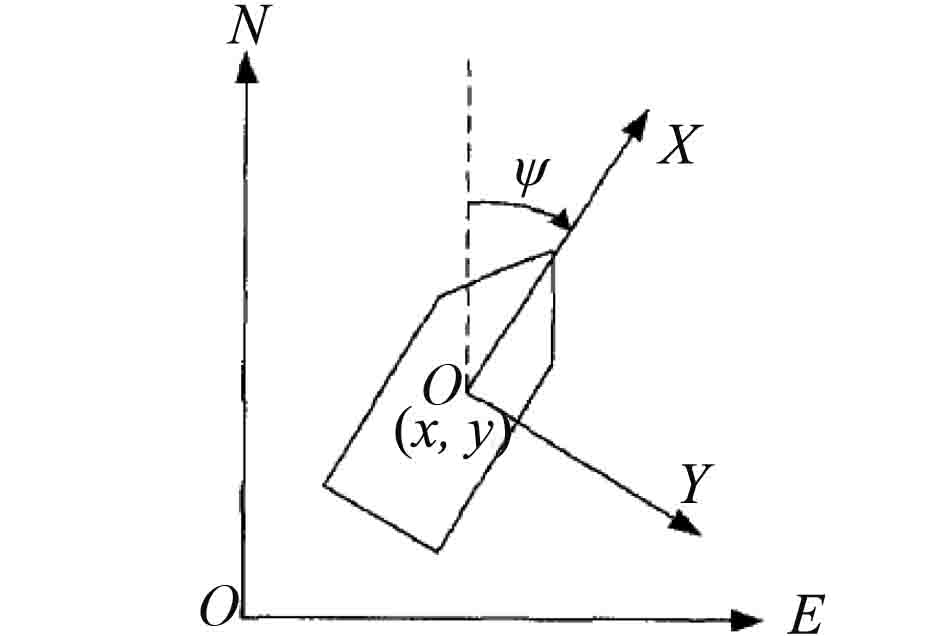
|
图 2 大地坐标系和随船坐标系 Fig. 2 Earth-fixed frame and body frame |
2种坐标系的转换关系为[5]:
| $\dot \eta = { J}\left( \varphi \right)\upsilon \text{,}$ | (1) |
式中,转换矩阵:
| ${ J}\left( \varphi \right) = \left[ {\begin{array}{*{20}{c}}{{{cos}}\varphi } & { - {{sin}}\varphi } & 0\\{{{sin}}\varphi } & {{{cos}}\varphi } & 0\\0 & 0 & 1\end{array}} \right]\text{。}$ | (2) |
船舶运动包括低频运动和高频运动,高频运动仅表现为周期性的振荡而不会引起平均位置的改变,一般从测得的综合信息分离出低频信号加以控制,而不对高频信号进行控制;为便于描述船舶运动,本文假设船舶质量分布均匀、左右对称且视为刚体,忽略海洋环境的高频干扰,只考虑风、流、浪等引起的低频干扰,得到经简化的三自由度船舶低频运动的数学模型[6]:
| $\begin{aligned}{ M}\dot \upsilon + & { D}\left( \upsilon \right)\upsilon = {\tau _c} + {\tau _s}\text{,}\\ & \dot \eta = { J}\left( \varphi \right)\upsilon \text{。}\end{aligned}$ |
式中:M为惯性矩阵,且满足
| $\begin{array}{l}{ M} = \left[ {\begin{array}{*{20}{c}}{m - {X_{\dot u}}} & 0 & 0\\0 & {m - {Y_{\dot \nu }}} & 0\\0 & 0 & {{I_z} - {N_{\dot r}}}\end{array}} \right]\text{,}\\[10pt]{ D}\left( \upsilon \right) = \left[ {\begin{array}{*{20}{c}}{ - {X_u}} & 0 & 0\\0 & { - {Y_v}} & 0\\0 & 0 & { - {N_r}}\end{array}} \right]\text{。}\end{array}$ |
式中:m为船舶质量,IZ为船舶转动惯量;
传统的DPS控制器很难满足现代船舶定位精度的要求,故要采用更加适宜的控制方法来设计控制器。滑模变结构控制理论的提出,对解决系统的不确定性问题具有很强的鲁棒性,对非线性系统的控制具有良好的控制效果。滑模控制理论以其独特的优点,广泛应用于各类控制器的设计当中[8]。
2.1 滑模变结构控制理论变结构控制是一类特殊的非线性控制,其非线性表现为控制的不连续性;其控制原理为,根据系统所期望的动态特性来设计系统的切换超平面,通过滑动模态控制器使系统状态从超平面之外向切换超平面收束;系统一旦到达切换超平面,控制作用将保证系统沿切换超平面到达系统原点,这一沿切换超平面向原点滑动的过程称为滑模控制;其优点是能够克服系统的不确定性,对干扰和未建模动态具有很强的鲁棒性,尤其是对非线性系统具有良好的控制效果;该方法的缺点在于当状态轨迹到达滑模面后,难于严格地沿着滑模面向平衡点滑动,而是在滑模面两侧来回穿梭,从而产生抖振[9]。
2.2 滑模变结构控制器的设计本文采用双环滑模控制的方法来设计控制律,采用积分器来设计切换函数。外环控制是将船舶的实际位置和首向
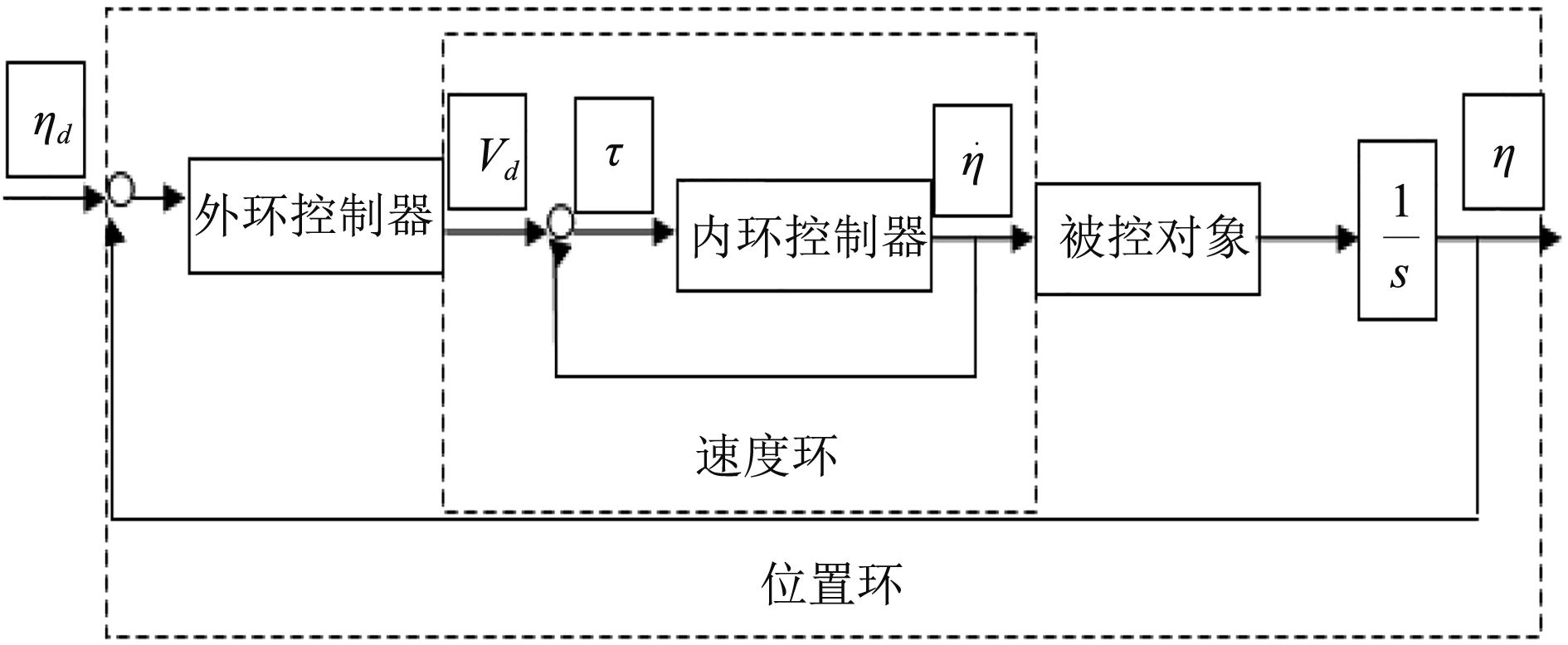
|
图 3 双环滑模动力定位系统框图 Fig. 3 Block diagram of bicyclic SMC system |
本文设计的控制目标:设计控制向量τc,使船舶的实际位置和首向η保持在期望的位置和首向ηd上。
设系统的位置和首向误差为e,定义:
| $e = \eta - {\eta _d}\text{,}$ | (4) |
则其速度误差
| $\dot e = \dot \eta - {\dot \eta _d} = \upsilon - {\upsilon _d}\text{,}$ | (5) |
对其求一阶导数得:
| $\ddot e = \dot \upsilon - {\dot \upsilon _d}\text{,}$ | (6) |
定义系统的外环滑模面so:
| ${s_o} = \eta + { \varLambda _1}\mathop \smallint \nolimits_0^t \eta {{d}}t,\;\;\;\;{s_0} \in {R^3}\text{,}$ | (7) |
其中,对角矩阵Λ1特征值为正。
对式(7)求一阶导数得:
| ${\dot s_o} = \dot \eta + {\varLambda _1}\eta $ | (8) |
将式(3)、式(5)代入式(7)得:
| ${\dot s_o} = { J}\left( \varphi \right)\dot e + { J}\left( \varphi \right){\upsilon _d} + {\varLambda _1}\eta \text{,}$ | (9) |
定义期望值vd:
| ${\upsilon _d} = {{ J}^{ - 1}}\left( \varphi \right)\left( { - {\varLambda _1}\eta - {\rho _1}{{sgn}}\left( {{s_o}} \right)} \right)\text{,}$ | (10) |
式中:ρ1>0,将vd代入式(8)得
| ${\dot s_o} = { J}\left( \varphi \right)\dot e - {\rho _1}{{sgn}}\left( {{s_o}} \right)\text{。}$ | (11) |
定义系统的内环滑模面si:
| ${s_i} = \dot e + {\varLambda _2}\mathop \smallint \nolimits_0^t \dot e{{d}}t\text{,}$ | (12) |
其中,对角矩阵Λ2特征值为正。
对式(12)求一阶导数得:
| ${\dot s_i} = \ddot e + {\varLambda _2}\dot e \text{,}$ | (13) |
将式(3)、式(6)代入式(12)得:
| ${\dot s_i} = - {{ M}^{ - 1}}{ D}\upsilon + {{ M}^{ - 1}}\left( {{\tau _c} + {\tau _s}} \right) - {\dot \upsilon _d} + {\varLambda _2}\dot e\text{,}$ | (14) |
得控制律τc:
| ${\tau _c} = M\left( {{{\dot s}_i} + {{\dot \upsilon }_d} - {\varLambda _2}\dot e} \right) + D\upsilon - {\tau _s}\text{,}$ | (15) |
可令
| ${\dot s_i} = {\tau _s} - {\rho _2}{{sgn}}\left( {{\tau _{\max}}{s_i}} \right)\text{,}$ | (16) |
其中ρ2>0。
则控制律τc:
| ${\tau _c} = { M}\left( {{{\dot s}_i} + {{\dot \upsilon }_d} - {\varLambda _2}\dot e} \right) + { D}\upsilon - {\dot s_i} - {\rho _2}{{sgn}}\left( {{\tau _{\max}}{s_i}} \right)\text{。}$ | (17) |
Lyapunov函数常作为判断系统稳定性的重要工具,本文用来判断所设计控制器的稳定性[11]。
对外环滑模面so,构造Lyapunov函数Vo:
| ${V_o} = \frac{1}{2}{s_o}^{{T}}{s_o}\text{,}$ | (18) |
对上式求一阶导数:
| ${\dot V_o} = {s_o}^{{T}}{\dot s_o}\text{,}$ | (19) |
将式(11)代入式(19)得:
| ${\dot V_o} = {s_o}^{{T}}{ J}\left( \psi \right)\dot e - {\rho _1}{s_o}^{{T}}{{sgn}}\left( {{s_o}} \right)\text{。}$ | (20) |
当系统的实际速度趋近于期望速度,即
| ${\dot V_o} = - {\rho _1}{s_o}^{{T}}{{sgn}}\left( {{s_o}} \right) \leqslant 0\text{。}$ | (21) |
根据Lyapunov函数的稳定性理论可知,所设计的外环滑模的控制系统趋于稳定。
对内环滑模面si,构造Lyapunov函数Vi:
| ${V_i} = \frac{1}{2}{s_i}^{{T}}{s_i}\text{,}$ | (22) |
对上式求一阶导数:
| ${\dot V_i} = {s_i}^{{T}}{\dot s_i}\text{,}$ | (23) |
将式(16)代入上式得:
| ${\dot V_i} = {s_i}^{{T}}{\tau _s} - {\rho _2}{s_i}^{{T}}{{sgn}}\left( {{\tau _{\max}}{s_i}} \right)\leqslant 0 \text{。}$ | (24) |
根据Lyapunov函数的稳定性理论可知,所设计的内环滑模的控制系统趋于稳定[12]。
3 仿真试验为了验证所设计的滑模变结构控制器的控制效果,采用的船舶模型为经简化的动力定位船舶三自由度模型,为了便于仿真,将式(3)进一步简化得:
| $\dot \nu = - {{ M}^{ - 1}}{ D}\left( \upsilon \right)\upsilon + {{ M}^{ - 1}}\left( {{\tau _c} + {\tau _s}} \right)\text{,}$ | (25) |
式中,令
| $\dot \upsilon = { A}\upsilon + { B}\left( {{\tau _c} + {\tau _s}} \right)\text{,}$ | (26) |
本文以某动力定位船舶为对象进行仿真研究[13],该动力定位船舶的主要参数如表1所示。
|
|
表 1 动力定位船舶的主要参数 Tab.1 Main parameters of dynamic position ship |
公式(3)中的惯性矩阵M,线性阻尼矩阵
| $\begin{aligned}{ M} = \left[ {\begin{array}{*{20}{c}}{1.127 \ 4} & 0 & 0\\0 & {1.890 \ 2} & 0\\0 & 0 & {0.127 \ 8}\end{array}} \right]\text{,}\\{ D} = \left[ {\begin{array}{*{20}{c}}{0.035 \ 8} & 0 & 0\\0 & {0.118 \ 3} & 0\\0 & 0 & { - 0.030 \ 8}\end{array}} \right]\text{。}\end{aligned}$ |
由计算出的惯性矩阵M,线性阻尼矩阵
| $\begin{aligned}{ A} = \left[ {\begin{array}{*{20}{c}}{ - 0.031 \ 8} & 0 & 0\\0 & { - 0.062 \ 8} & 0\\0 & 0 & {0.250 \ 6}\end{array}} \right],\\{ B} = \left[ {\begin{array}{*{20}{c}}{ - 0.887 \ 0} & 0 & 0\\0 & { - 0.541 \ 5} & 0\\0 & 0 & { - 8.008 \ 2}\end{array}} \right]\end{aligned}$ |
仿真中,取船舶的期望位置和首向
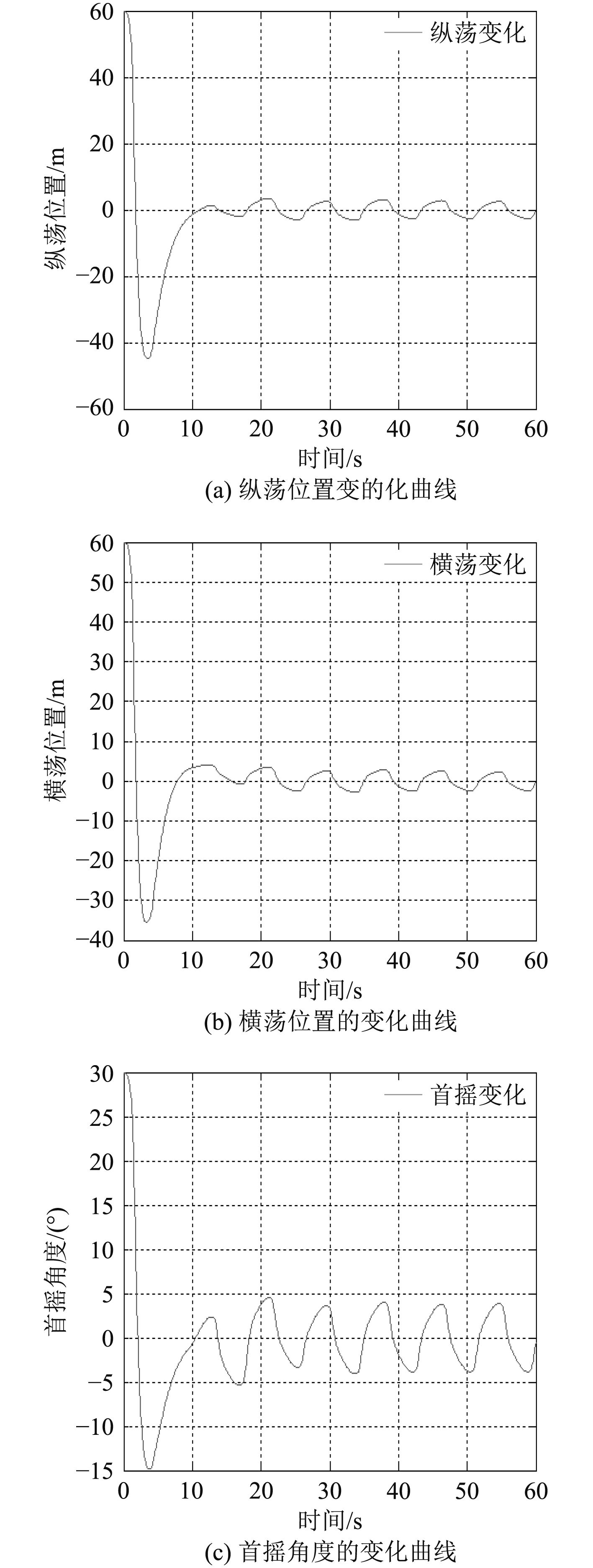
|
图 4 船舶位置和艏向的变化曲线 Fig. 4 Curve of ship positioning and heading |
|
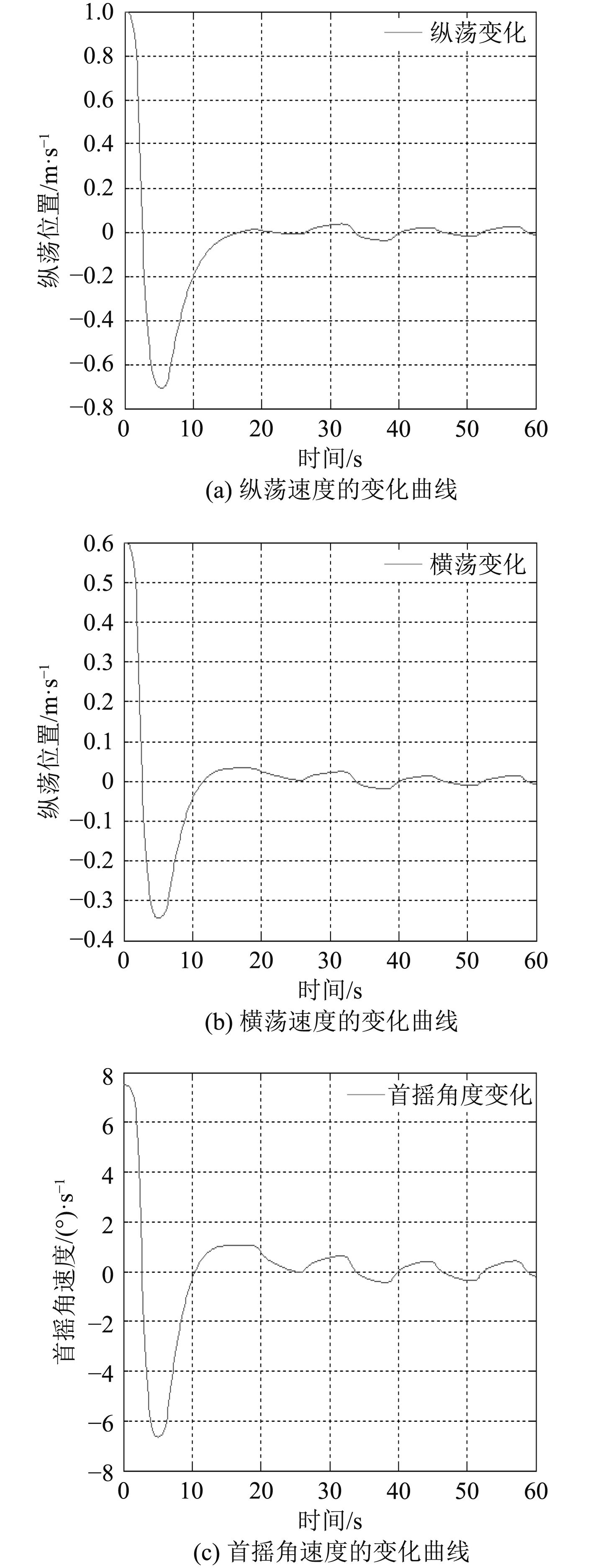
图 5 船舶速度的变化曲线 Fig. 5 Curve of ship speed |

|
图 6 控制律的变化曲线 Fig. 6 Curve of control law |
从仿真结果来看,所设计的滑模变结构控制器表现出了良好的控制效果。由图4船舶位置和首向的变化曲线可知,所设计的控制律能使船舶位置和首向渐进稳定到期望值;由图5船舶速度的变化曲线可知,所设计的控制律能使船舶速度渐进稳定到目标值,并保持该状态;由图6控制律的变化曲线可知,所设计的控制律在经过一段时候,能趋于稳定状态,说明该控制律具有较好的控制效果。
4 结 语本文基于动力定位船舶简化的三自由度数学模型,借助滑模变结构控制方法,设计一种滑模变结构控制的动力定位控制器,并对所设计的控制器进行了稳定性分析,最后借助某动力定位船舶作为仿真对象,通过Matlab编程对控制器进行仿真验证,结果表明,在有外界环境的干扰下,该控制器能较好地保持稳定性和鲁棒性,控制精度较高,对今后进行动力定位控制器的设计研究具有一定的参考意义。
| [1] | 赵志高, 杨建民, 王磊. 动力定位系统发展状况及研究方法[J]. 海洋工程, 2002, 20(1): 91–97. http://www.oalib.com/paper/4328778 |
| [2] | 史斌杰, 吴辙莹. 动力定位系统的最新技术进展分析[J]. 上海造船, 2011, 87(3): 43–45. http://www.cqvip.com/QK/83201X/201103/39335947.html |
| [3] | 边信黔, 付明玉, 王元慧. 船舶动力定位[M]. 科学出版社, 2011, 5. |
| [4] | 童进军, 何黎明, 田作华. 船舶动力定位系统的数学模型[J]. 船舶工程, 2002, 5: 27–29. http://d.wanfangdata.com.cn/Periodical_cbgc200205006.aspx |
| [5] | LIN Yong-yi, DU Jia-lu, HU Xin, et al. Design of neural network observer for ship dynamic positioning system[C]// Proceedings of the 33rd Chinese Control Conference. 2014. 7: 28-30. |
| [6] | E A TANNURI, A C AGOSTINHO, H M MORISHITA, et al. Dynamic positioning systems: an experimental analysis of sliding mode control[J]. EI Control Engineering Practice. 2010 (18) : 1121–1132. |
| [7] | 郭娟. 不同海况条件下船舶动力定位混合控制系统设计[D]. 上海: 上海交通大学, 2012. |
| [8] | 王祝炯. 滑模变结构控制系统设计研究[D]. 杭州: 浙江工业大学, 2003. |
| [9] | 刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2005. |
| [10] | 刘洋. 船舶动力定位的智能控制及推力分配研究[D]. 大连: 大连海事大学, 2013. |
| [11] | 罗利军, 李银山, 李彤. 李雅普诺夫指数谱的研究与仿真[J]. 计算机仿真, 2005, 22(12): 285–288. |
| [12] | YAN Ming, YI Jin-hui, LIU Yang, et al. Sliding mode control algorithm based on T-S fuzzy model for a class of nonlinear systems[C]// IEEE International Conference on Automation and Logistics Shenyang, China. 2009, 8. |
| [13] | T I FOSSEN, S I SAGATUN, A J SRENSRN. Identification of dynamically positioned ships [J]. Journal Control Engineering Practice. 1996, 4 (3): 369–376. |
| [14] | 刘胜. 现代船舶控制工程[M]. 北京: 科学出版社, 2010: 32–33. |
| [15] | 管自新, 温智宁. 基于MATLAB常微分算子ode45的RLC电路状态轨迹的描绘[J]. 中国科技信息, 2008, 13: 34–35. http://d.wanfangdata.com.cn/Periodical_zgkjxx200813016.aspx |
 2018, Vol. 40
2018, Vol. 40
