20世纪70年代以来,船舶的耐波性理论计算方法迅速的发展,出现了例如新切片法、保角变换法和三维流体动力计算法等船舶耐波性理论计算的方法。
耐波性衡准主要包括造成船舶子系统性能下降的衡准和造成子系统能够工作的极限运动水平的衡准。现在采用的衡准一般是船舶作业的极限衡准,指的是船舶在受到波浪的影响下,人员、船体或者船上的子系统能否进行作业或完成任务的极限指标[1]。
20世纪50年代初期,Denis与Pierson等把平稳随机过程与线性迭加理论用于预报船舶在不规则海浪中的响应后,使得船舶在海浪中的性能可以从工程应用的角度去研究探讨。现如今船舶耐波性理论尽管发展迅速,但是切实的把耐波性理论实际应用的还是为数不多,本次研究希望通过对海洋数据的收集整理,通过数据来探究船舶的耐波性以达到能够对船舶的航行进行辅助的目的[2]。
1 耐波性基本理论船舶在实际海浪中运动是船舶受到海洋环境(主要是风、浪)干扰后所产生的运动,对于船舶的航行、甲板上浪和船体弯矩有着很大的影响。1957年Korvin-Kroukovskyr提出了计算船舶纵摇升沉运动的切片理论。
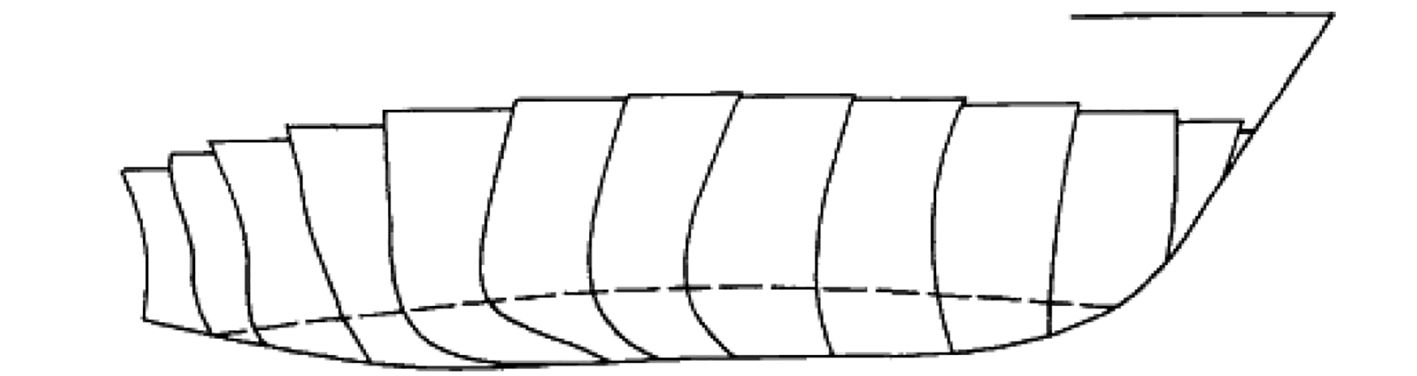
切片理论将三维的船体看成一个细长体,然后分成一系列二维横向片体,如图1所示,而对于每一个片体,其性能都可以被计算与预测。这样,把船体周围三维的流动简化为二维的,船体的水动力性能就可以通过在船体长度方向的二维片体的数值的积分(迭加)来计算[3]。
|
图 1 船体切片近似示意图 Fig. 1 The approximation schematic diagram of the hull microtome section |
Seakeeper模块是隶属于Maxsurf软件中的耐波性分析模块,是基于Salvesen等的切片理论来计算船舶升沉与纵摇的响应,基于横摇阻尼理论对横摇响应进行计算,由于使用切片理论,Seakeeper模块可以提供非常精确地耐波性预测,尤其是针对肥大型船舶的计算上更是有其得天独厚的优势[4]。
Seakeeper中的切片理论(linear strip theory)假定船舶的运动是线性谐波,在这种情况下,对于给定波的频率与速度船舶升沉与纵摇的响应将正比于波幅。
切片理论提出了以下假设:
1)流体是无粘性的,粘性阻尼被忽略;
2)船体是细长的;
3)船体是刚体,没有发生结构弯曲;
4)速度适中;
5)运动幅值小(至少与波幅线性相关);
6)水深比波长大得多;
7)船体的刨面是直壁的;
8)船体的存在对波没有影响(Froude-Krilov假设)。
2 seakeeper数值模拟 2.1 参数设置船长108 m,水线面长度100 m,宽18 m,吃水深度为6.6 m,标准排水量为7 700 t;横稳心高0.74 m;横摇衰减系数为0.15,横摇惯性半径为船宽的40%,纵摇惯性半径为船长的25%。
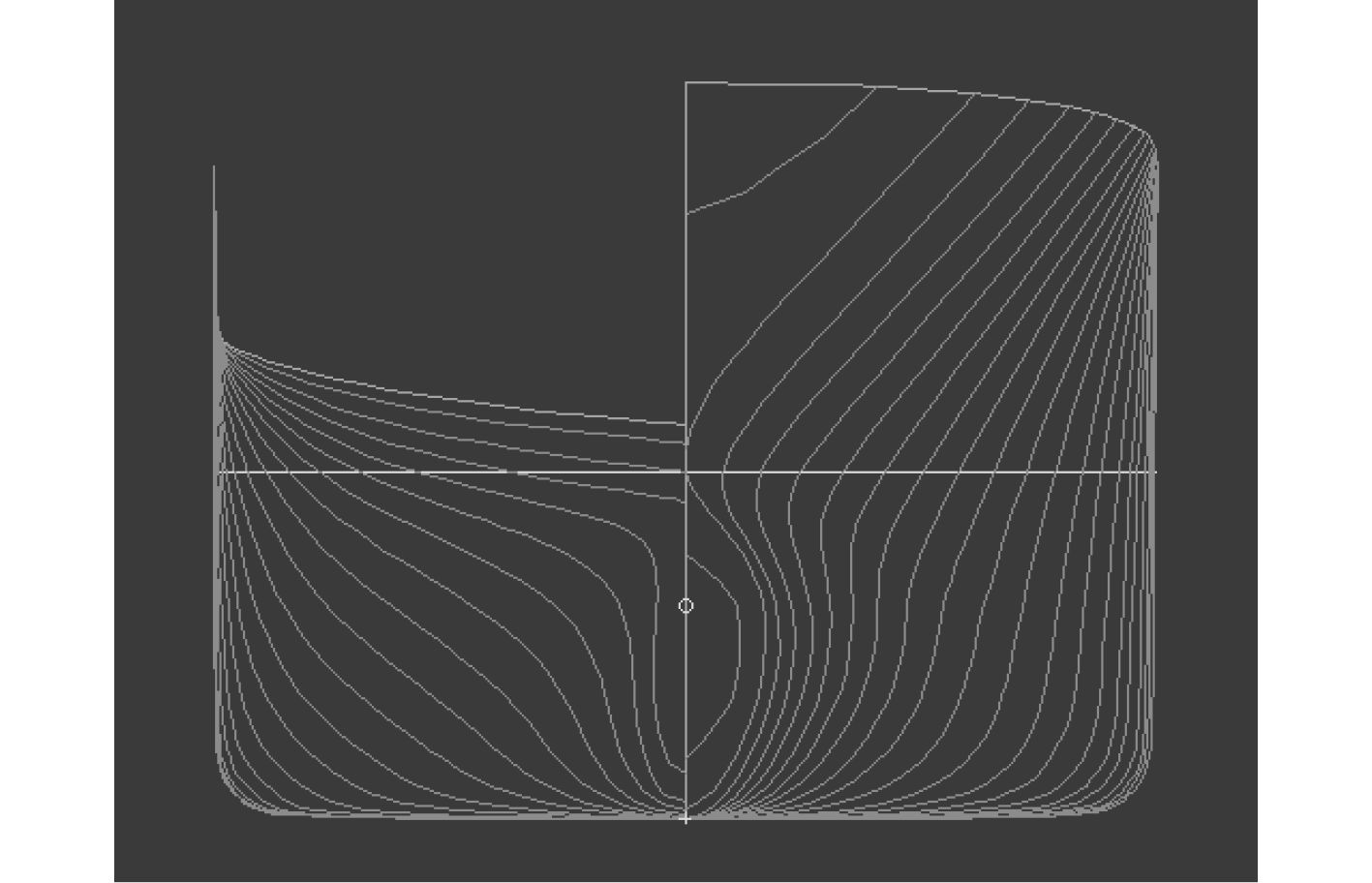
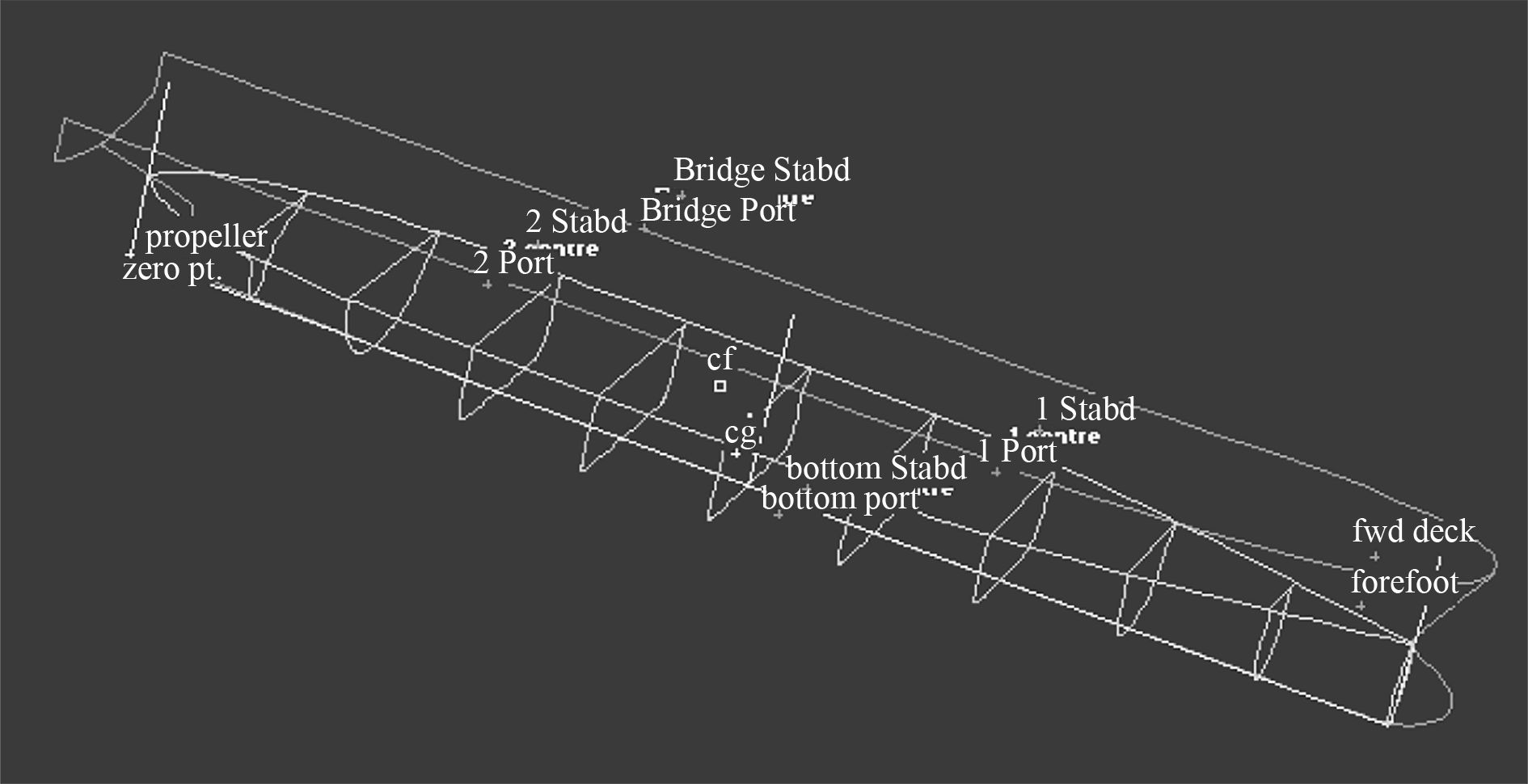
通过Maxsurf主体程序建立船舶的船体模型,其横剖面图以及Seakeeper仿真软件切片示意图如图2和图3所示。
|
图 2 横剖面图 Fig. 2 Cross-sectional view |
|
图 3 切片示意图 Fig. 3 Ship section chart |
对于局部海域的海洋环境对船舶耐波性指标影响参数如下:
风速范围:8~22 m/s;有义波高范围:0.5~11 m;平均波周期范围:2~13 s;仿真时长:t=300 s;仿真步长:tb=0.01 s。
按照风速范围取5,6,7,8,9级风,波浪力的方向是任意波方向,在进行横摇、纵摇以及升沉的计算时,不规则波面由100个波分量组成,设定水的密度为1.025×103 kg/m3。
2.2 仿真结果对于船舶来说,影响其运动的因素有很多,当确定了船型以及其航行区域时,浪向角、浪高与航速等因素对于船舶的运动尤其是纵向运动也有很大影响。而对于船舶的运动而言,分析其传递函数尤其是在规则波中的传递函数是较好的分析方式。
本次研究以4种航向和不同航速下的船舶运动采用Seakeeper软件进行计算。分别以迎浪(首向与波浪行进方向夹角为180°)、首斜浪(首向与波浪行进方向夹角为135°)、横浪(首向与波浪行进方向夹角为90°)、尾斜浪(首向与波浪行进方向夹角为45°)姿态进行匀速直线航行,并且不做滚转、偏航与俯仰等机动,只是在海浪的作用下进行横摇、纵摇与升沉运动[5]。
Seakeeper对不同条件的计算结果如下,其中Za,φa,θa分别为垂荡、横摇与纵摇的幅值;ζa,k,λ,Lwl,Fr分别为波幅,波数,波长,水线长(设计水线长)与傅汝德数。
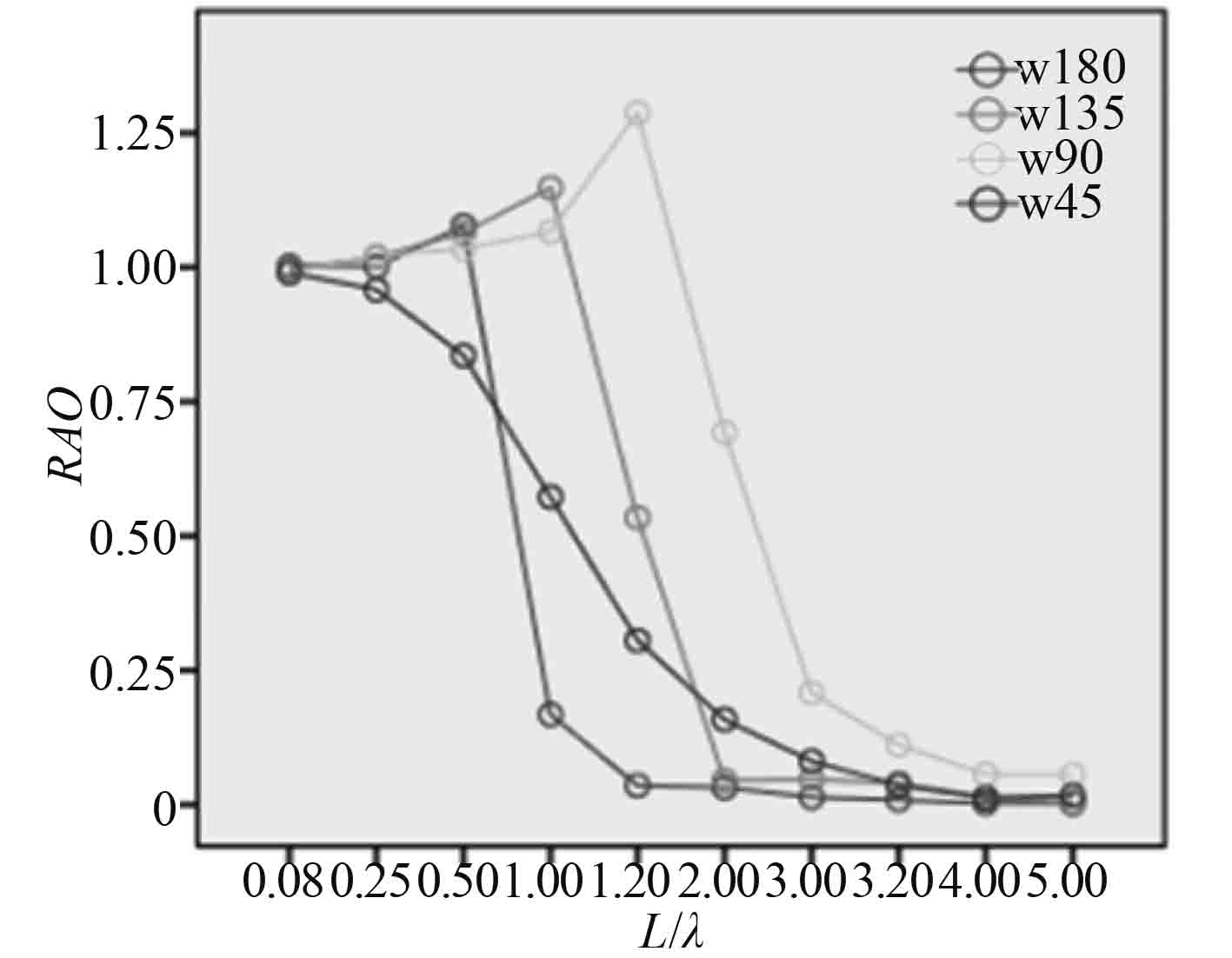
用Seakeeper软件对船舶以不同航速不同航向计算的结果如图4~图9所示,w180~w45分别表示船舶航向:
|
图 4 升沉(Fr=0.37) Fig. 4 Heave (Fr=0.37) |
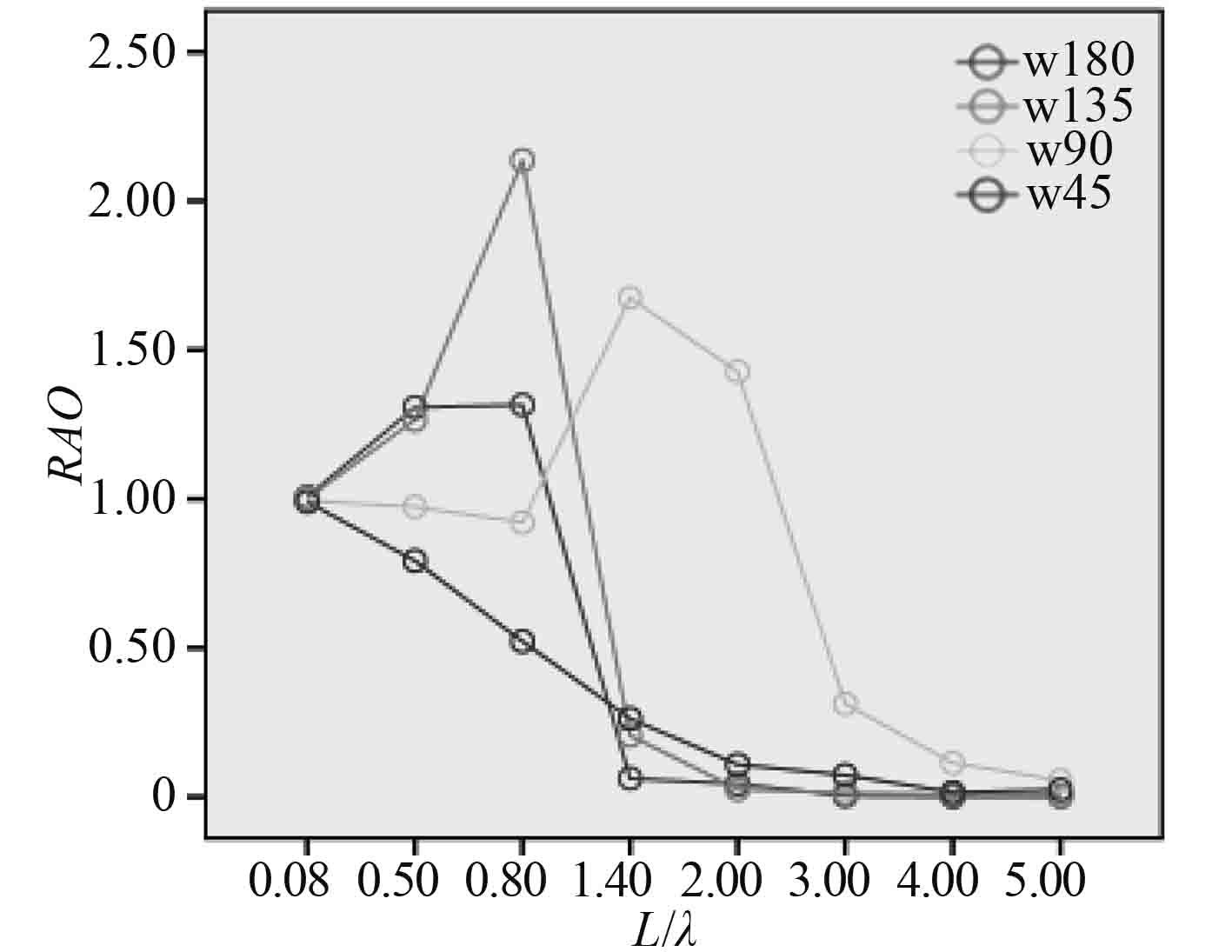
|
图 5 升沉(Fr=0.55) Fig. 5 Heave (Fr=0.55) |
图4~图5中,
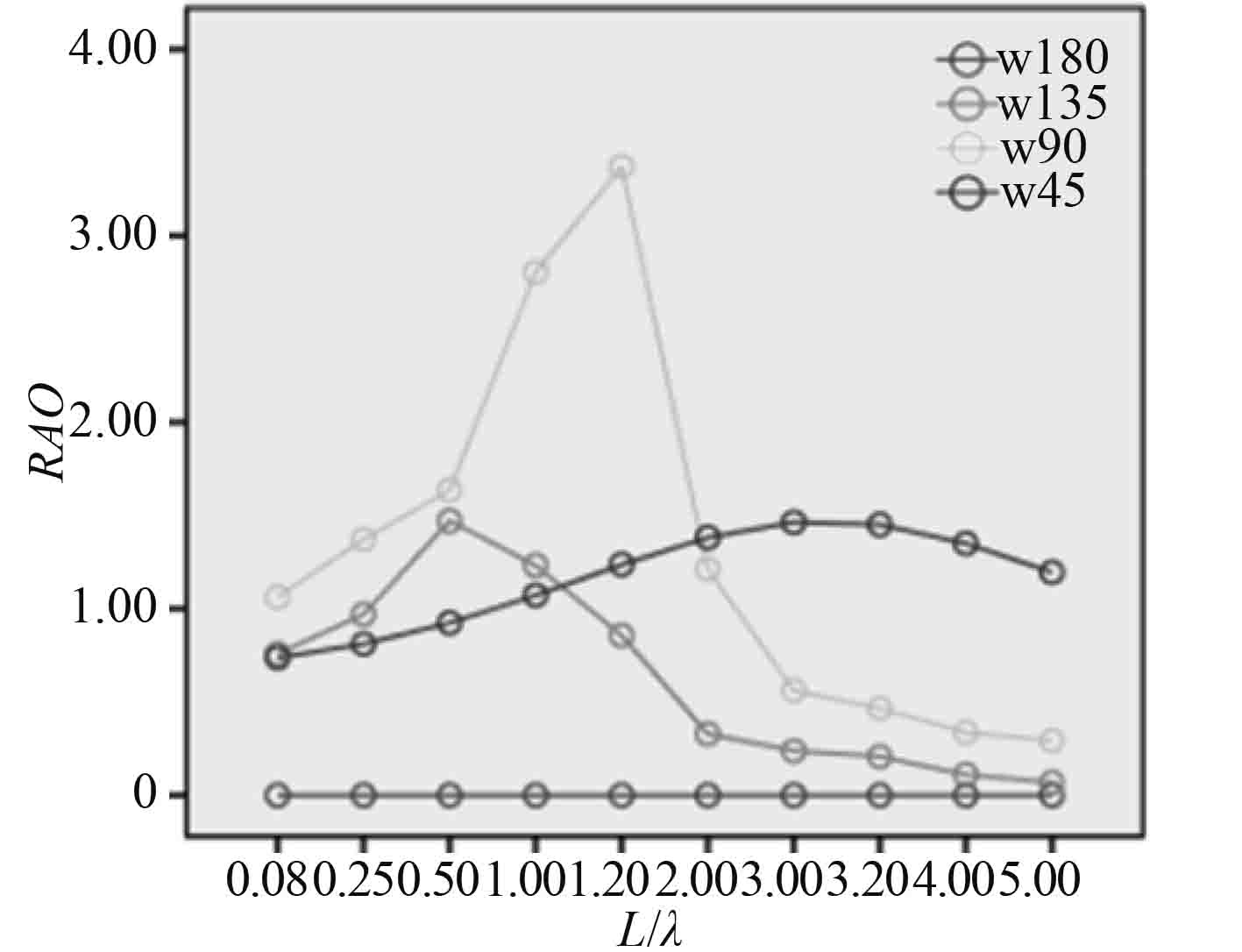
|
图 6 横摇(Fr=0.37) Fig. 6 Roll (Fr=0.37) |
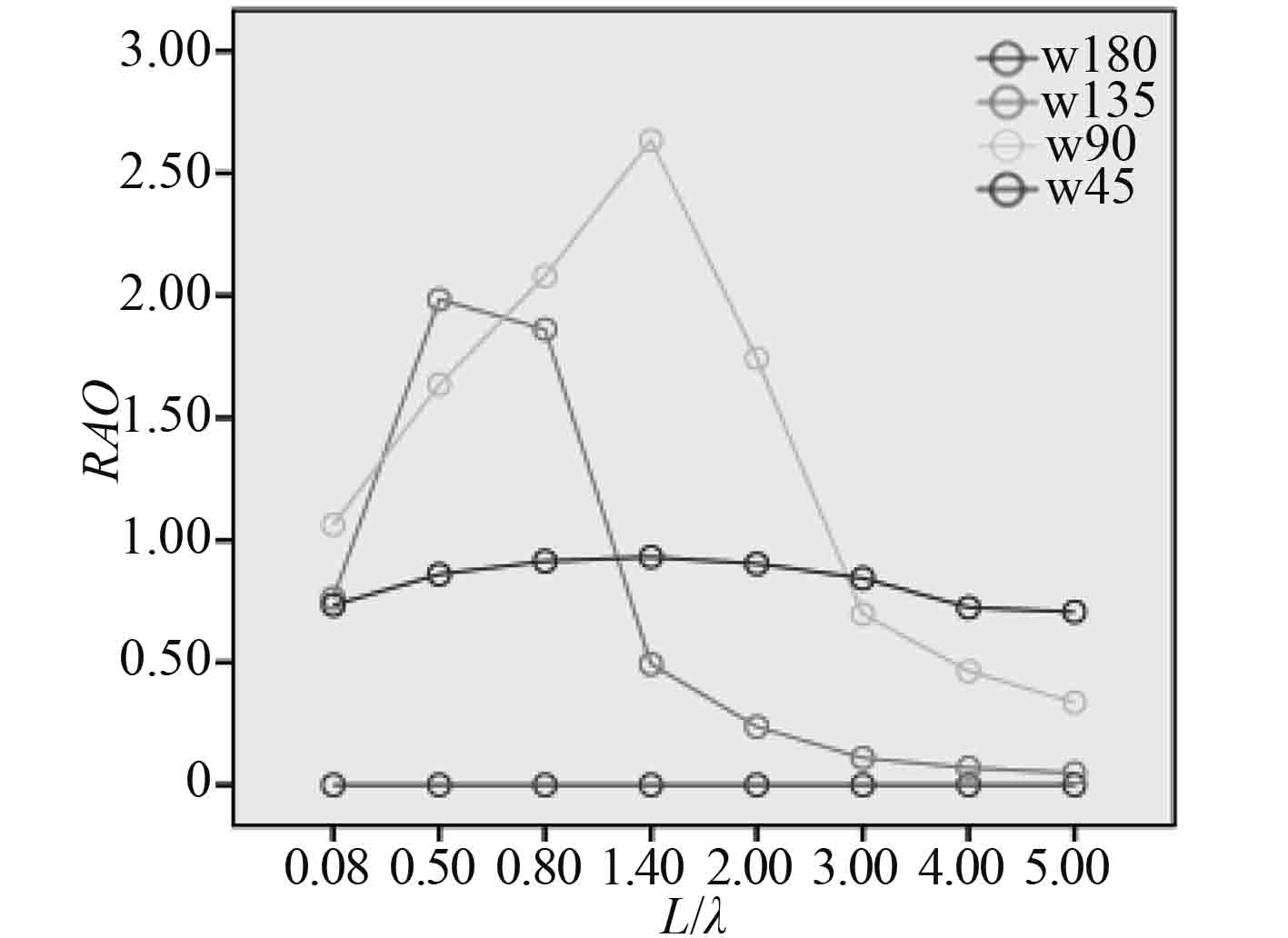
|
图 7 横摇(Fr=0.55) Fig. 7 Roll (Fr=0.55) |
图6~图7中,
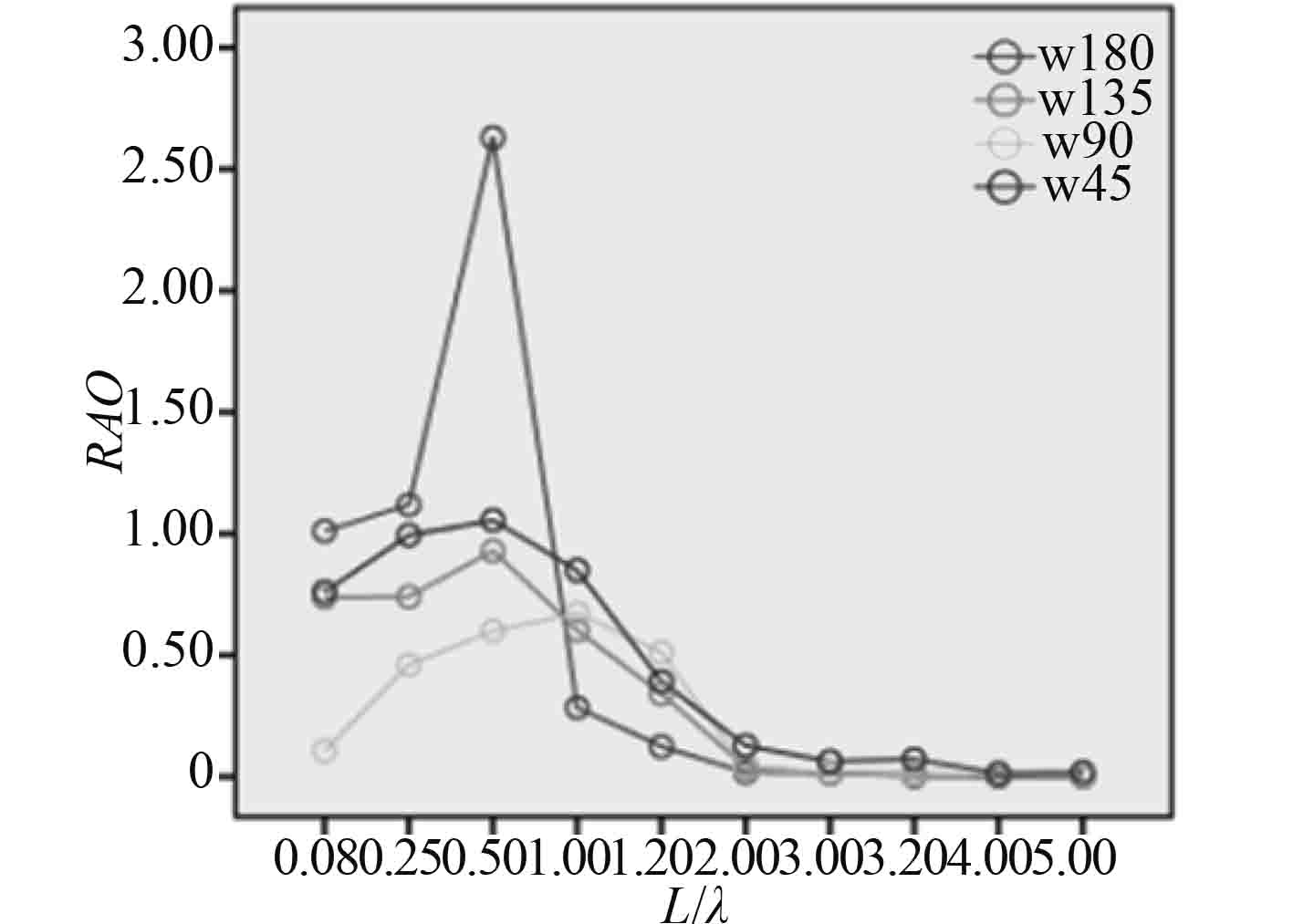
|
图 8 纵摇(Fr=0.37) Fig. 8 Pitch (Fr=0.37) |
|
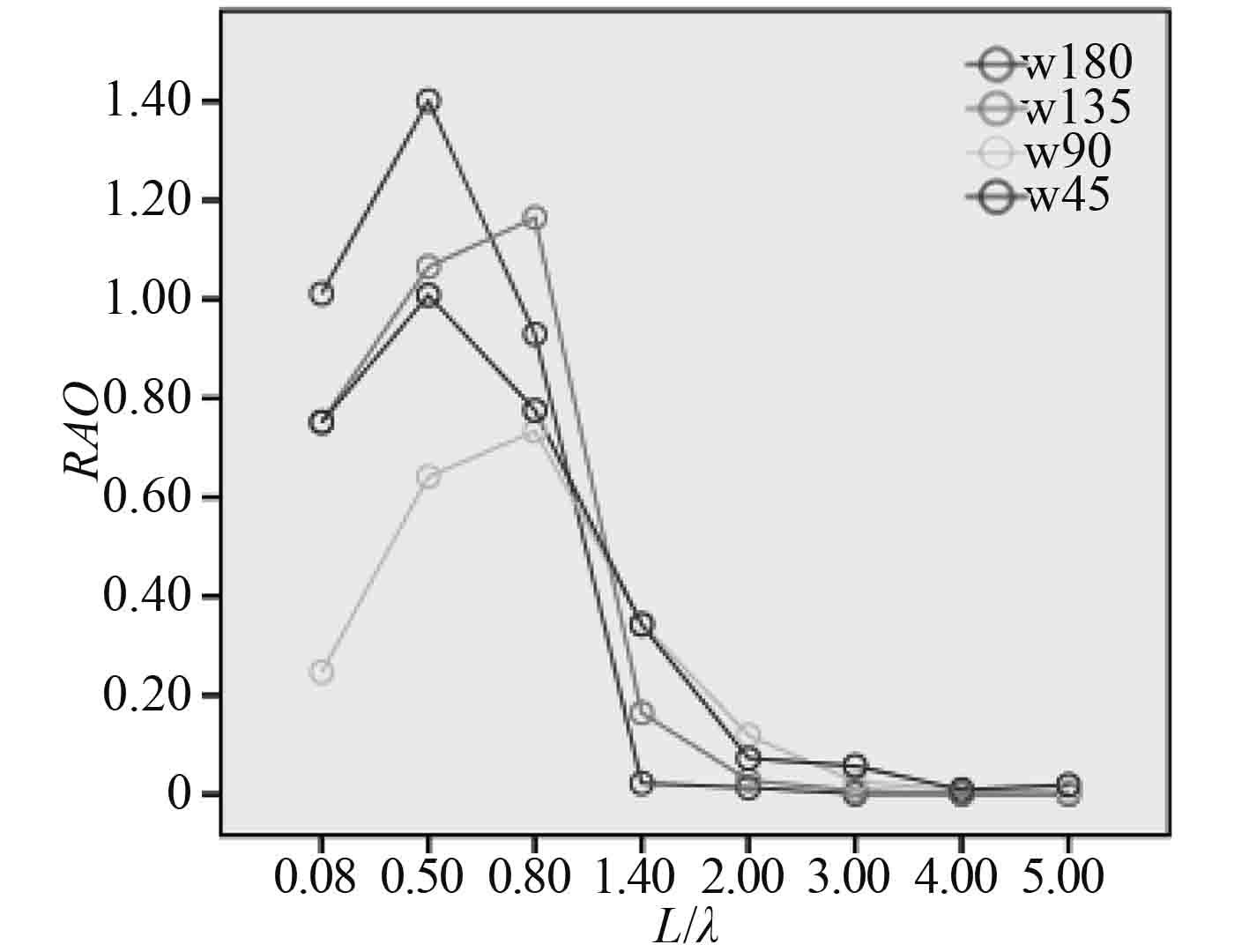
图 9 纵摇(Fr=0.55) Fig. 9 Pitch (Fr=0.55) |
图8~图9中,
本文采用莫尔公式进行估算船舶纵摇和升沉运动的幅值。纵摇角有义值与升沉有义值分别如下式所示:
| $\begin{split}{(2\theta )_{1/3}} =& {A_0} + {A_1}{C_w} + {A_2}{C_b} + {A_3}\frac{{{l_w}}}{{{b_w}}} + {A_4}\frac{{{l_w}}}{t} + {A_5}{l_{cb}}+\\& {A_6}\frac{{{R_{yy}}}}{{{l_w}}} + {A_7}\frac{{0.5520v}}{{\sqrt {{l_w}} }} + {A_8}{\left( {\frac{{0.5520v}}{{\sqrt {{l_w}} }}} \right)^2},\end{split}$ | (1) |
| ${(2z)_{1/3}} = 0.3048 \times \left[ \begin{array}{l}{A_0} + {A_1}{C_w}\\ + {A_2}{C_b} + {A_3}\displaystyle\frac{{{l_w}}}{{{b_w}}} + {A_4}\frac{t}{{{l_w}}}\\[3pt] + {A_5}{l_{cb}} + {A_6}\displaystyle\frac{{{R_{yy}}}}{{{l_w}}} + {A_7}\frac{v}{{\sqrt {{l_w}} }}\end{array} \right],$ | (2) |
式中:lcb为浮心在中横剖面前的纵向位置,以相对船长得百分数表示,近似取为lcb=0.05;Ryy为船的纵向质量惯性半径,以船长的百分数表示,近似取为Ryy=0.25lw;v为船舶运动的航速,kn。系数A0~A8与风级、船长有关。
|
|
表 1 船舶在波高4 m单幅有义纵摇值 Tab.1 Pitch significative value in 4 m wave height |
|
|
表 2 船舶在波高4 m单幅有义升沉值 Tab.2 Heave significative value in 4 m wave height |
通过对比可得,seakeeper计算得出的纵摇与升沉的有义虽然与预估公式有一定的偏差,但是其总体趋势还比较准确。计算结果与回归公式的计算结果大体趋势与数值接近,计算结果具有其可行性。
3 耐波性影响因素分析 3.1 指标分析根据中国船舶科学研究院中心提出的耐波性衡准以及其他相关文献参考资料,选择耐波性衡准如表3所示[6 – 7]。
|
|
表 3 耐波性衡准(有义值) Tab.3 Seakeeping criteria (significant) |
在局部海域内以15 kn航速135°航向不同风浪条件下耐波性指标所能达到的最大值如表4所示(耐波性指标为单幅有义值)。
|
|
表 4 船舶耐波性 Tab.4 Seakeeping individual indicators |
|
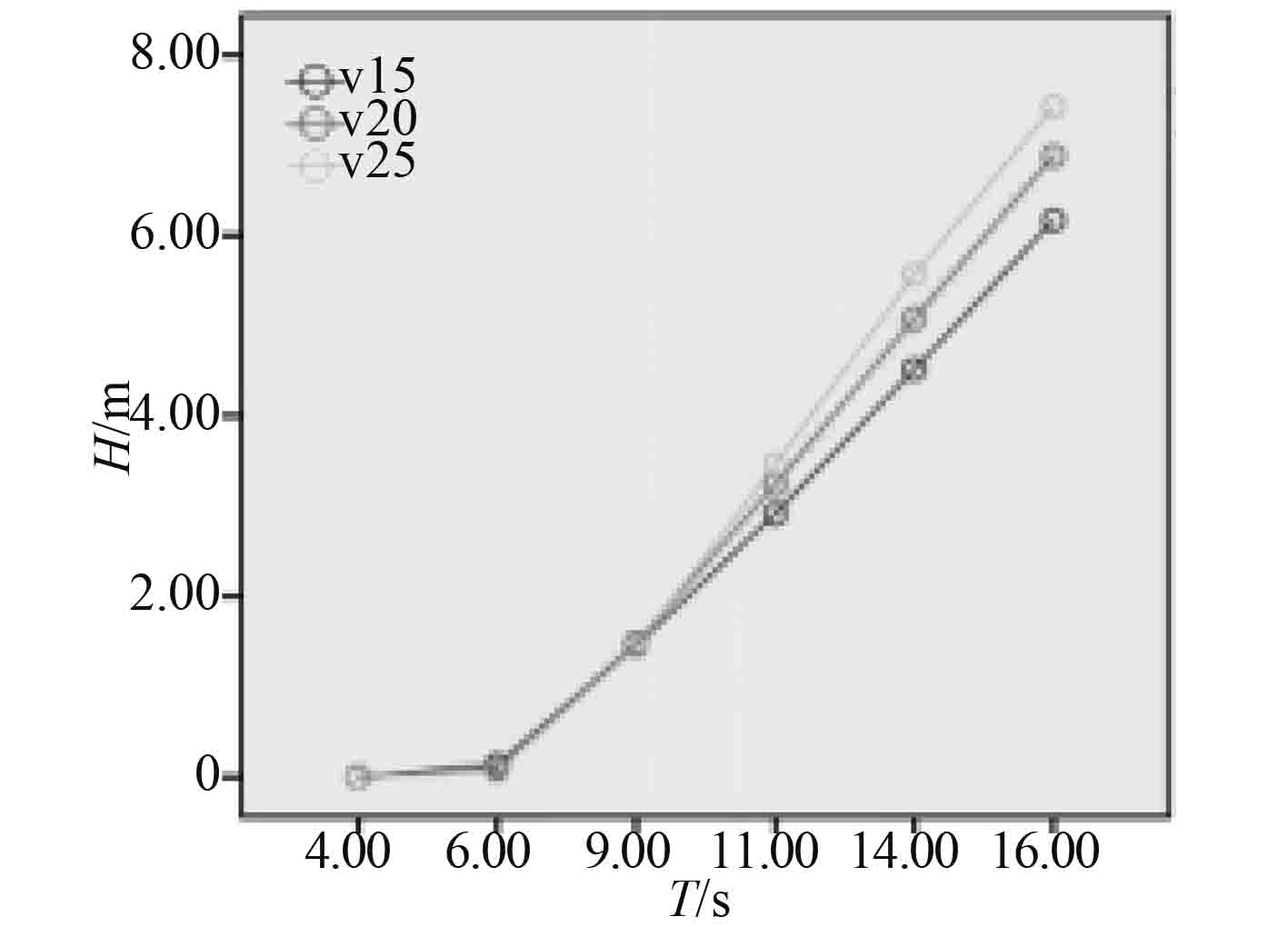
图 10 航向为135°时升沉随航速、波周期变化 Fig. 10 Heading 135° heave with speed, wave periodchange |
|
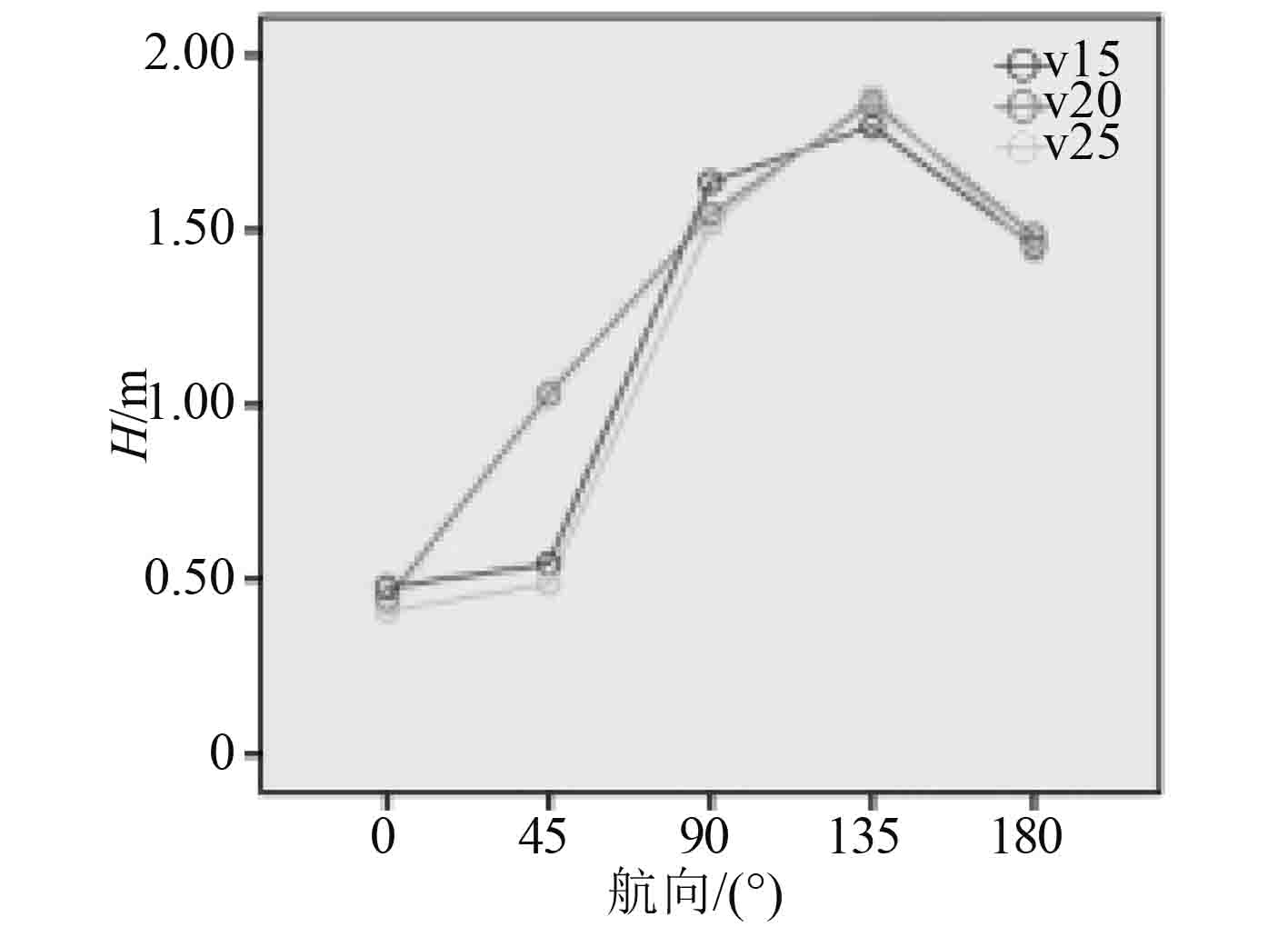
图 11 波周期为9 s时升沉随航速、航向变化 Fig. 11 Wave period 9 sheave with Speed anddirection change |
由图10可以看出海洋环境的变化对船舶的耐波性有显著影响;由图11得出航向对升沉、横摇与纵摇有显著影响,在考虑耐波性时不能忽视其影响。
从表3和表4可以看出当波周期大于9 s时横摇与船首垂向加速度还可以在衡准值之内,而纵向的运动(包括纵摇与升沉)均已大于耐波性衡准的有义值,在判断船舶耐波性指标时已经可以认为大于波周期9 s时候的海洋环境对船舶航行造成影响[8 – 9]。
4 耐波性影响因素分析 4.1 正交试验正交试验以及其分析方法是目前为止非常常见的优化试验和分析方法,用于研究多因素多水平的方法[10]。正交试验主要以概率论和数理统计思想做基础,利用标准正交来进行试验的安排,通过对结果的分析找到优化方案,正交试验采用以部分代表整体的方式,挑选出有代表性的试验点,通过对代表性的分析对全面试验的情况进行了解。
本次研究局部海域海洋环境对耐波性指标的影响,由于Seakeeper软件的计算原理,需要至少提供航速、航向以及风浪数值这3个因素,每个因素分为若干水平,如果应用全因素试验一种船型至少要进行125种左右的试验。所以设计正交试验来找出因素中对耐波性指标影响较大的因素,设计正交试验组,来减少试验组数与时间。
4.2 正交试验设计通过SPSS软件进行正交试验设计,因素为航速、航向、风速与空白列,空白列又称误差列是用来在正交试验后的分析中减小误差。通过Seakeeper软件对设计好的正交试验表中的条件进行仿真计算,并把得到的数据结果填写到正交试验表中,具体设计如表5所示。
|
|
表 5 正交试验设计表 Tab.5 Orthogonal design table |
通过SPSS软件进行分析。分析采用多变量分析,分析各个因素主要项或者说主效应之间的关系,本次研究中还选用Ducan显著性检验法进行检验(Ducan检验法指多范围检查,能指定a为0.05,0.01或0.1,默认值为0.05)[11]
通过SPSS进行正交分析结果如表6所示。
|
|
表 6 试验A正交试验分析表 Tab.6 Test A Orthogonal analysis table |
试验中,heave,roll与pitch的校正的模型统计量F分别为25.353,18.833,19.047,显著性p值都近似于0,因此所用的模型具有统计学意义,p值可以用其来判断模型中的系数有无统计学意义。
试验A中变异来源为航速时,因变量heave的p值为0.533在显著水平a=0.05或a=0.1上无统计学意义,roll的p值为0.205在显著水平a=0.05或a=0.1上无统计学意义,因变量pitch的p值为0.830在显著水平a=0.05或a=0.1上无统计学意义,说明航速的变异来源在显著性水平为0.05与0.1上无统计学意义,也就是说因子航速不显著。
试验A中变异来源为风速时,因变量heave的p值接近于0在显著水平a=0.05上有统计学意义,roll的p值为0.008在显著水平a=0.05上有统计学意义,因变量pitch的p值接近于0在显著水平a=0.05上有统计学意义,这说明因子风速有统计学意义。
试验A中变异来源为航向时,因变量heave的p值为0.010在显著水平a=0.05上有统计学意义,roll的p值接近0在显著水平a=0.05上有统计学意义,因变量pitch的p值为0.126在显著水平a=0.05或a=0.1上无统计学意义。
通过试验A对其进行方差分析可以得知以上结论,对上述结论进行总结后可以得知,航速对升沉、横摇与纵摇的有一定的影响但并不是太显著;风速对升沉、横摇与纵摇有显著的影响,对升沉与纵摇影响略大于横摇;航向对升沉、横摇与纵摇有显著影响,其中横摇与升沉的影响略大于纵摇。
由正交试验分析结果可知,对于船舶而言环境因素对其纵摇、横摇与升沉有很大影响,并且纵摇与升沉略大于横摇,于本次研究中可以证明通过海洋环境有关风、浪的数据去简单估计、衡量与判断船舶的耐波性可行,通过局部海洋环境数据库对海洋环境数据的检索可以来判断船舶在所选海域内的耐波性。
5 结 语本文从切片理论入手,采用seakeeper软件进行船舶耐波性数值模拟,并通过莫尔回归公式验证了数值模拟的可靠性,从数值模拟结果可以看出海洋环境的变化对船舶的耐波性有显著影响,而且航向变化对升沉、横摇与纵摇都有显著影响,在考虑耐波性时不容忽略。通过参考文献给出的耐波性衡准可以看出,文中的船舶当波周期大于9 s时其纵摇和升沉都已经大于耐波性衡准的有义值,已经严重影响航行。并应用到统计学上的正交试验的方法对耐波性的影响因素进行分析,并得知航速对升沉、横摇与纵摇有一定的影响但并不是太显著;风速对升沉、横摇与纵摇有显著的影响,对升沉与纵摇影响略大于横摇;航向对升沉、横摇与纵摇有显著影响,其中横摇与升沉的影响略大于纵摇。
| [1] | 戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007. |
| [2] |
刘大刚, 解以扬, 刘斌贤. 大风浪条件下船舶风险状况动态评估预警系统[J]. 中国航海, 2015, 38(1): 63–67.
LIU Da-gang, XIE Yi-yang, LIU Bin-xian. Dynamic risk evaluation and early warning system for vessels under rough sea condition[J]. Navigation of China, 2015, 38(1): 63–67. http://mall.cnki.net/magazine/Article/ZGHH201501027.htm |
| [3] |
韩晓光, 杨艳明, 郭航. 基于切片法的高速船摇荡运动预报研究[J]. 广州航海高等专科学校学报, 2009, 17(4): 7–10.
HAN Xiao-guang, YANG Yan-ming, GUO Hang. High-speed craft’s swaying motion forcecast based on strip theory[J]. Journal of Guangzhou Maritime College, 2009, 17(4): 7–10. |
| [4] |
董文才, 左文锵, 吴晓光. 水面舰船耐波性指标及对Seakeeper软件的评价[J]. 中国舰船研究, 2006, 1(2): 1–6.
DONG Wen-cai, ZOU Wen-qiang, WU Xiao-guang. Seakeeping index and valuation of the seakeeper software for surface ships[J]. Chinese Journal of Ship Research, 2006, 1(2): 1–6. http://d.wanfangdata.com.cn/Periodical_zgjcyj200602001.aspx |
| [5] | LI Dong-qin, PHILIP A W, ZHAO Xin. Establishment of effective metamodels for seakeeping performance in multidisciplinary ship design optimization[J]. Journal of Marine Science and Technology, 2016, 24(2): 233–243. |
| [6] | 王银. 舰船方案设计中的耐波性预报模型研究[D]. 哈尔滨: 哈尔滨工程大学, 2012. |
| [7] |
熊文海, 毛筱菲, 李毓江. 船舶耐波性衡准及其评价方法浅析[J]. 船海工程, 2007, 36(4): 42–45.
XIONG Wen-hai, MAO Xiao-fei, Li Yu-jiang. Review on evaluation methods and criteria for sea-keeping of ships[J]. Ship&Ocean Engineering, 2007, 36(4): 42–45. |
| [8] |
董亚力. 船舶耐波性研究及其在航海中的应用[J]. 舰船科学技术, 2016, 38(5A): 13–15.
DONG Ya-li. Resaerch on ship seakeeping and its application in the navigation[J]. Ship Science and Technology, 2016, 38(5A): 13–15. http://www.cnki.com.cn/Article/CJFDTOTAL-DLHS199904005.htm |
| [9] | 熊文海. 船舶耐波性评价及其在航海安全中的应用[D]. 武汉: 武汉理工大学, 2004. |
| [10] | 张娴, 刘琳. 科技论文中正交试验结果分析方法的使用[J]. 编辑学报, 2007. 19(5): 340–341. http://www.doc88.com/p-28771517055.html |
| [11] |
刘瑞江, 张业旺, 闻崇炜, 等. 正交试验设计和分析方法研究[J]. 实验技术与管理, 2010. 27(9): 52–55.
LIU Rui-jiang, ZHANG Ye-wang, WEN Chong-wei, et al. Study on the design and analysis methods of orthogonal experiment[J]. Experimental Technology and Management, 2010. 27(9): 52–55. http://www.docin.com/p-489865329.html |
 2018, Vol. 40
2018, Vol. 40
