自20世纪50年代苏联将潜艇电场信号作为引信制造出非触发反潜锚雷(KCM),证实这种来源于船、艇腐蚀或防腐电流的新型信号源可用于水中兵器开发后,各海洋大国纷纷开展该领域的研究[1 – 4]。传统研究根据其产生机理采用最基本的电结构——电偶极子对场源进行建模,将空气—海水—海床构成的浅海环境简化成理想无限大三层平行分层导电媒质[5 – 7],利用镜像法推导位于海水中的静态电偶极子在三层平行分层环境中的场分布表达式,进而达到分析场的分布特征的目的 [8 – 9]。目前已取得了一定的研究成果,可初步应用于水雷引信,舰船探测与定位,舰船隐身与防护等方面[10 – 11]。
但是,实际海洋环境相当复杂[12],各水域情况不一,在边界影响不能忽略的情况下,传统理想无限大平行分层环境下的研究成果不能直接应用;并且打击准确、定位精确、隐身完美等军方需求的不断增长也要求研究者需要针对复杂水域开展研究。据此,本文将海床倾斜水域作为切入点,在前人研究基础上[13 – 17],以水平直流电偶极子模拟场源,在推导出海水中的水平直流电偶极子在全空间产生的标量电位分布表达式的基础上,对海床倾斜水域中潜艇水下标量电位的分布特征进行了仿真分析,并与传统平行分层环境下电位分布进行对比。工作为进一步研究更为复杂水域环境下潜艇腐蚀相关电场的场分布问题奠定了基础。
1 海床倾斜水域水平直流电偶极子水下标量电位分布表达式的推导电偶极子作为最基本的电结构,其产生的场可以直接用来模拟某些辐射场,一定分布的电偶极子的组合理论上可以用来模拟任意电流分布产生的场。现有研究表明可用水平直流电偶极子模拟潜艇水下电场分布[18 – 21]。本文正是以水平直流电偶极子对场源进行模拟,并运用镜像法推导出了潜艇水下标量电位的表达式。推导过程如下:
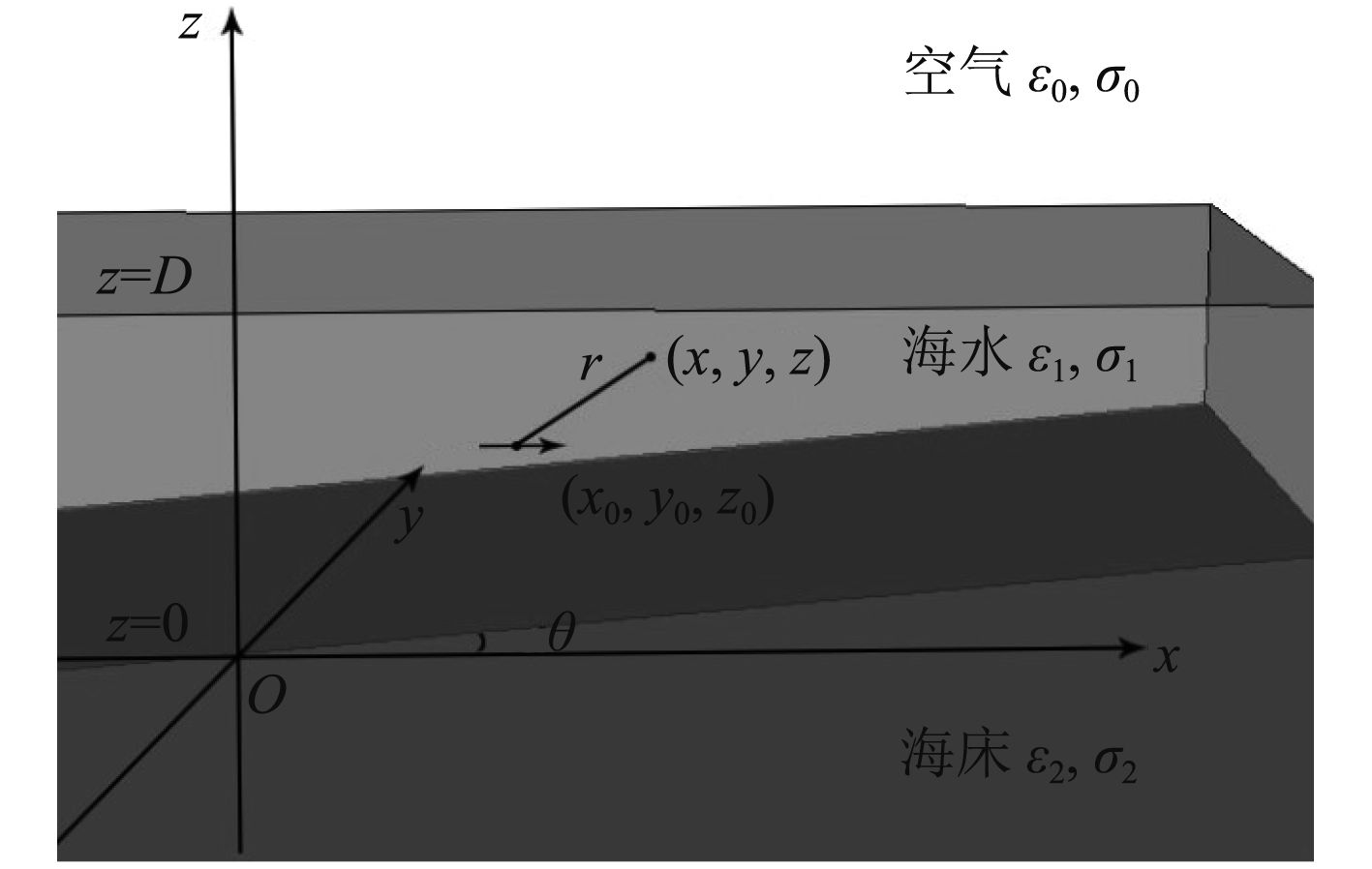
空气—海水—倾斜海床环境可由图1所示的3层媒质模型来表示。建立直角坐标系如图1所示,
|
图 1 空气—海水—倾斜海床三层媒质模型 Fig. 1 Three-layered conductive media model of air, seawater and inclined seabed |
设
| $\small \begin{align}& \left( {{x_{k{{a}}}},{y_{ka}},{z_{ka}}} \right) = {\left(\!\!\! \begin{array}{l}{x_0}\cos {\theta _k} + {\left( { - 1} \right)^{k + 1}}{z_0}\sin {\theta _k} + 2D\sum\limits_{l = 0}^{{m_k}} {\sin 2l\theta } \\{y_0}\\{x_0}\sin {\theta _k} + {\left( { - 1} \right)^k}{z_0}\cos {\theta _k} - 2D\left( {\sum\limits_{l = 0}^{{m_k}} {\cos 2l\theta } - 1} \right)\end{array} \!\!\! \right)^{ T}},\\& {{P}_{ka}} = {\eta _k}Idl\cos {\theta _k}{i} + {\eta _k}Idl\sin {\theta _k}{k},k = 0,1,2,3 \cdots {\text{;}}\end{align}$ |
| $\scriptsize\begin{array}{l}\left( {{x_{kb}},{y_{kb}},{z_{kb}}} \right) = {\left(\!\! \begin{array}{l}{x_0}\cos {\theta _{k - 1}} + {\left( { - 1} \right)^k}{z_0}\sin {\theta _{k - 1}} + 2D\sum\limits_{l = 0}^{{m_{k{{ - }}1}}} {\sin 2l\theta } \\{y_0}\\2D - \left\{ {{x_0}\sin {\theta _{k - 1}} + {{\left( { - 1} \right)}^{k - 1}}{z_0}\cos {\theta _{k - 1}} - 2D\left( {\sum\limits_{l = 0}^{{m_{k{{ - }}1}}} {\cos 2l\theta } - 1} \!\!\right)} \right\}\end{array} \right)^{ T}}\! ,\\{{ P}_{kb}} = {\eta _{k - 1}}Idl\cos {\theta _{k - 1}}i - {\eta _{k - 1}}Idl\sin {\theta _{k - 1}}{ k}, k = 1,2,3 \cdots {\text{。}}\end{array}$ |
则水平直流电偶极子在海水中产生的标量电位可表示为:
| $\begin{array}{l} {\mathit{\Phi }_1} = \sum\limits_{k = 0}^n {\frac{{{\eta _k}Idl\cos {\theta _k}(x - {x_{ka}}) - {\eta _k}Idl\sin {\theta _k}(z + {z_{ka}} - 2D)}}{{4\pi {\sigma _1}{r_{(k + 1)b}}^3}}} + \\ \sum\limits_{k = 0}^n {\frac{{{\eta _k}Idl\cos {\theta _k}(x - {x_{ka}}) + {\eta _k}Idl\sin {\theta _k}(z - {z_{ka}})}}{{4\pi {\sigma _1}{r_{ka}}^3}}} , \end{array}$ | (1) |
同理可求出场点在空气及海床中时的标量电位分别为:
| ${{{\varPhi }}_0} = \sum\limits_{k = 0}^n {\frac{{\frac{{2{\varepsilon _0}}}{{{\sigma _1}}}{\eta _k}Idl\cos {\theta _k}(x - {x_{ka}}) + \frac{{2{\varepsilon _0}}}{{{\sigma _1}}}{\eta _k}Idl\sin {\theta _k}(z - {z_{ka}})}}{{4\pi {\varepsilon _0}{r_{ka}}^3}}}, $ | (2) |
| $ \small\begin{align}& {\varPhi _2} = \frac{{\frac{{2{\sigma _2}}}{{{\sigma _1} + {\sigma _2}}}Idl(x - {x_0})}}{{4\pi {\sigma _2}{r_1}^3}} + \\&\sum\limits_{k = 1}^n {\frac{{\frac{{2{\sigma _2}}}{{{\sigma _1} \!+\! {\sigma _2}}}{\eta _{k - 1}}Idl\cos {\theta _{k - 1}}(x \!-\! {x_{kb}}) \!+\! \frac{{2{\sigma _2}}}{{{\sigma _1} \!+\! {\sigma _2}}}{\eta _{k - 1}}Idl\sin {\theta _{k \!-\! 1}}(z \!-\! {z_{kb}})}}{{4\pi {\sigma _2}{r_{kb}}^3}}} {\text{。}}\end{align}$ | (3) |
其中:
上述表达式的正确性可通过将之代入边界条件验证是否满足来说明。得到空气—海水—倾斜海床环境下水平直流电偶极子产生的电位分布表达式后,便可以此为基础分析海床倾斜水域潜艇水下标量电位分布特征,下文即采用数值仿真方法对此进行分析。
2 海床倾斜水域潜艇水下标量电位的特征分析真实海洋环境中,海床虽然是以一定的坡度向海洋底延伸的,但坡度一般较小。世界范围内,大陆架平均坡度只有0°07′,Sherpard(1973)计算的大陆坡的平均坡度为4°17′[12]。因此本文在对海床倾斜水域中的潜艇水下标量电位分布特征进行仿真分析时,假定海床倾斜角度均为5°以下的小角度。
2.1 海床倾斜水域标量电位的分布特征采用水平直流电偶极子对潜艇水下电位分布进行模拟,仍采用如图1所示的坐标系。设水平直流电偶极子的偶极矩为10 A·m,方向沿
|
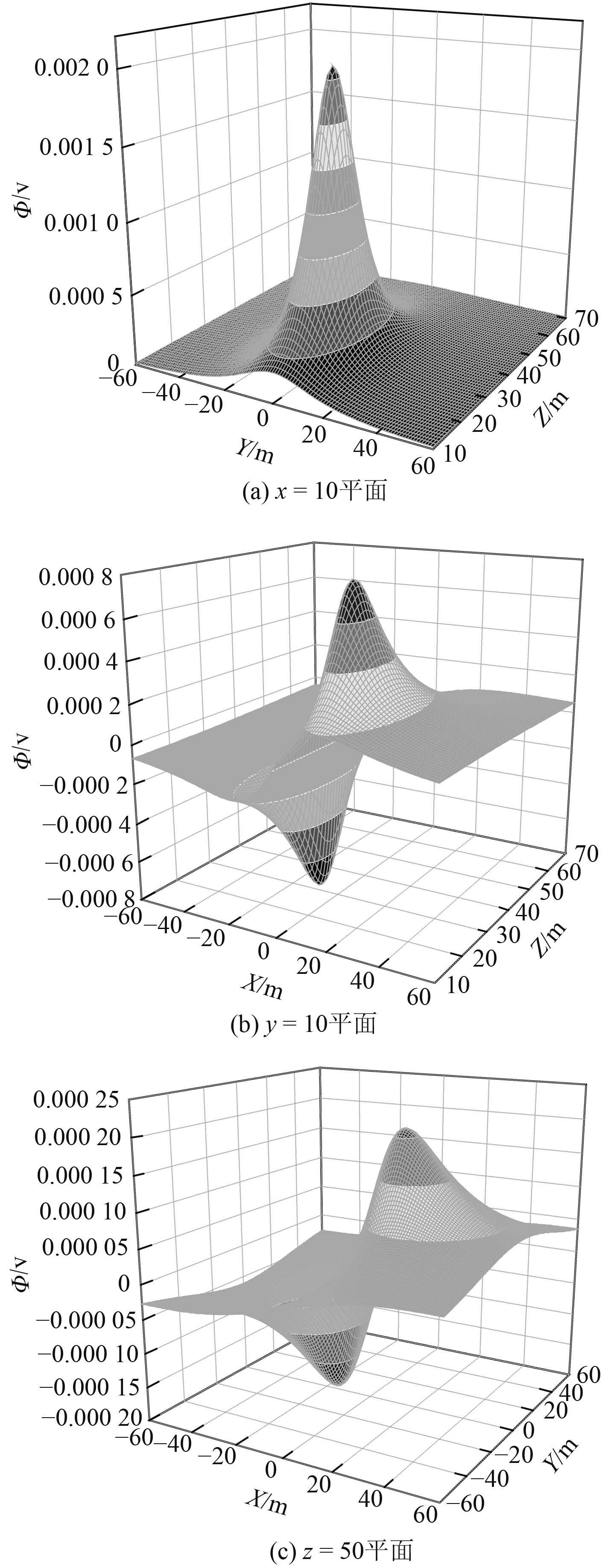
图 2 x=10,y=10及z=50平面上水下标量电位分布 Fig. 2 Underwater electric scalar potential distribution at x=10, y=10 and z=50 |

|
图 3 标量电位随x、y、z的变化 Fig. 3 Variation of electric scalar potential with x、y、z |
由图2可看出,潜艇水下标量电位分布有明显的区域特征:场点相对于潜艇纵向偏移量
同时由图3可知,随着场点相对于潜艇垂直偏移量
电位在
上述分布特征可用于潜艇探测与定位:某深度平面上电位两峰值点连线,线上各场点均满足
综上所述,海床倾斜水域潜艇水下标量电位分布特征明显,且量值可观。特别是根据其分布特征,可提出实现潜艇探测与定位的新思路,具有重大应用价值。
2.2 海水电导率对电位分布的影响在前述海洋环境、源参数条件下,为分析海水电导率对电位分布的影响,用Matlab编程,计算不同电导率时电位随

|
图 4 不同海水电导率时标量电位随x的变化 Fig. 4 Variation of electric scalar potential with x at different electrical conductivity of seawater |
|
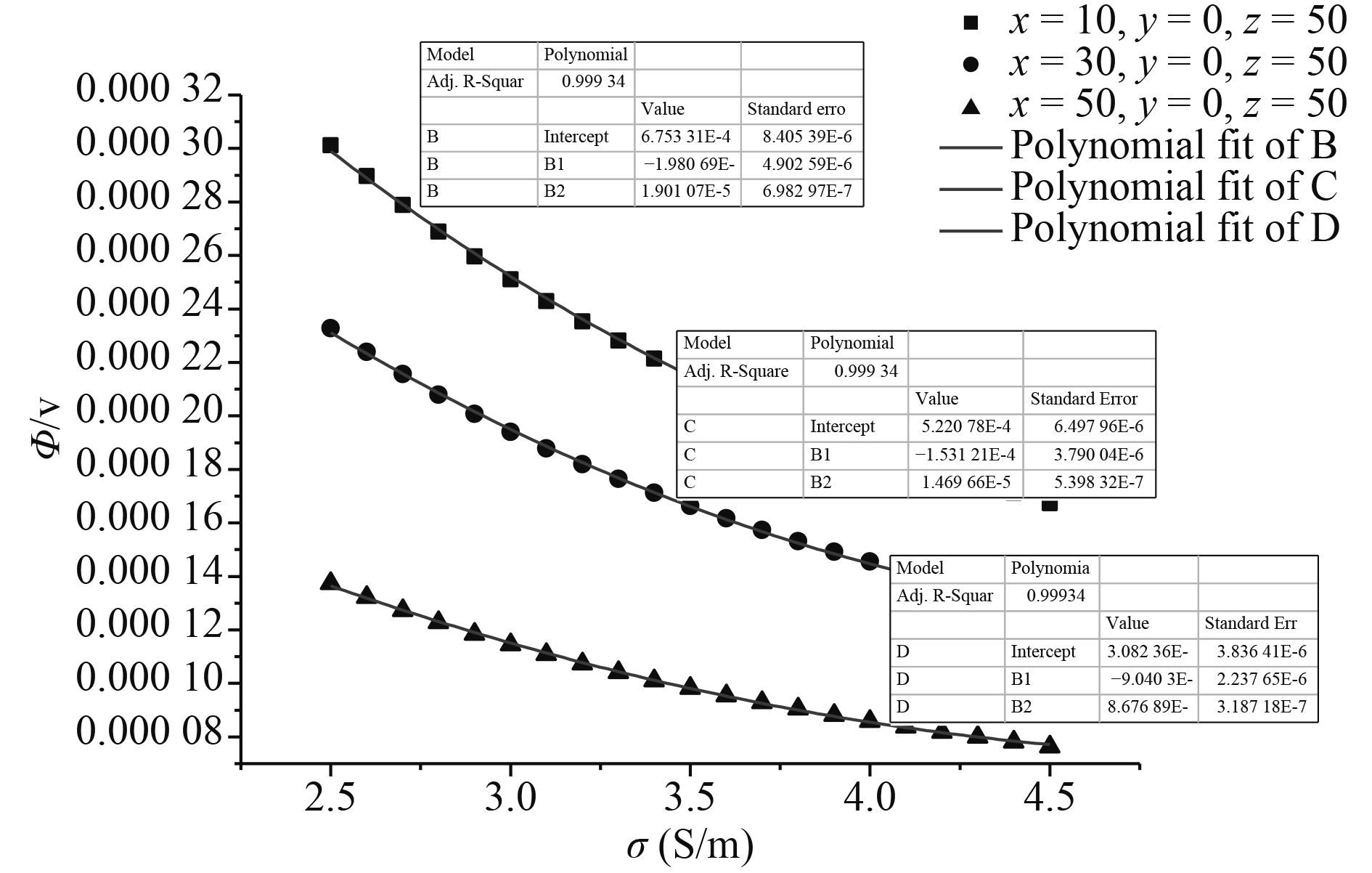
图 5 标量电位随海水电导率的变化 Fig. 5 Variation of electric scalar potential with the electrical conductivity of seawater |
由图可见:在海床倾斜水域,场源各参数不变时海水电导率不改变水下标量电位分布特征的区域性,但对具体场点会影响其标量电位大小,本文所研究区域标量电位的绝对值随海水电导率的增大,呈非线性衰减。
2.3 标量电位随海床倾斜角度的变化特征在前述海洋环境、源参数条件下,为分析海床倾斜角度对电位分布的影响,用Matlab编程,分别计算不同倾斜角度时电位随
|
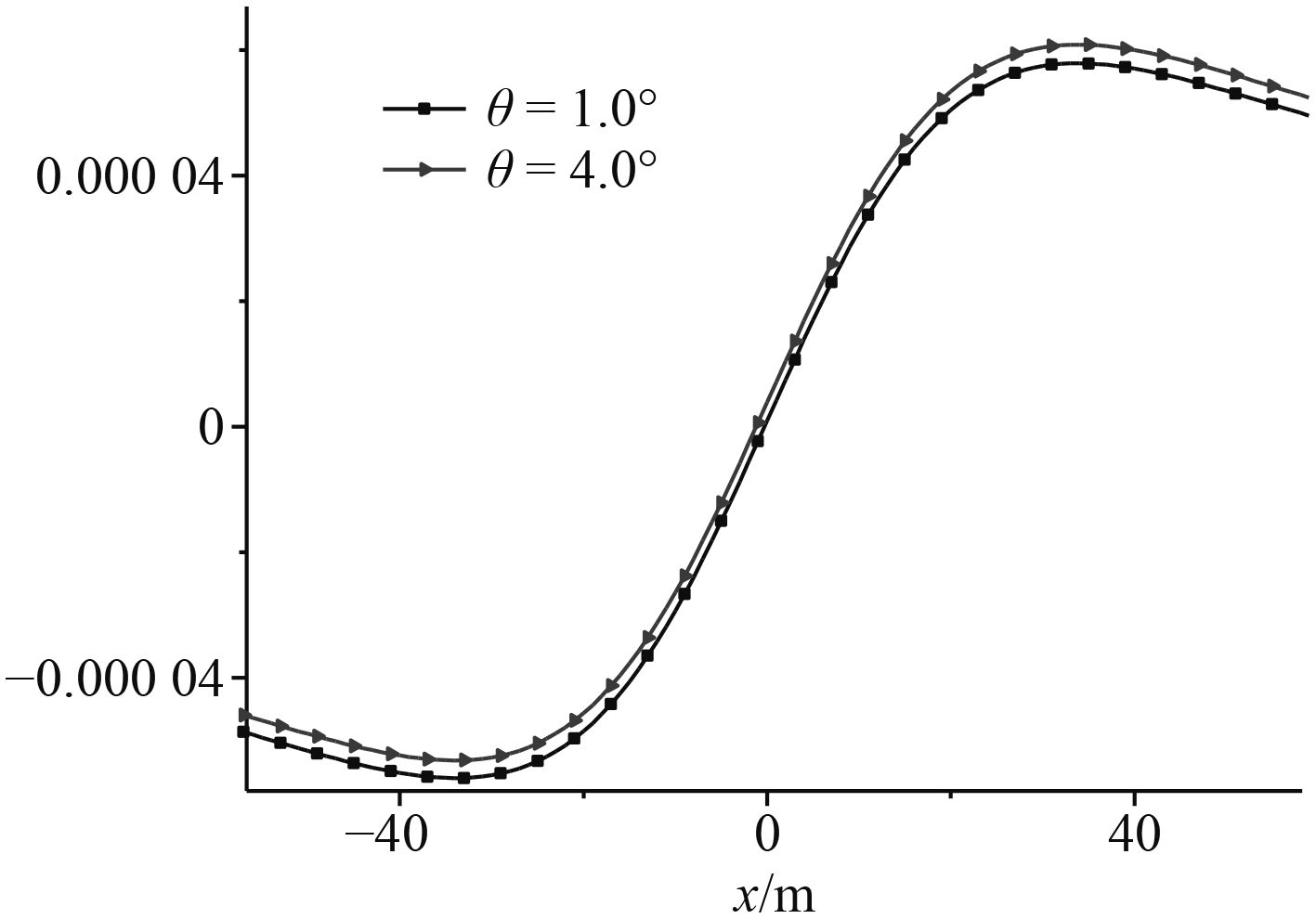
图 6 不同海床倾斜角度时标量电位随x的变化 Fig. 6 Variation of electric scalar potential with x at different inclined angle of seabed |

|
图 7 标量电位随海床倾斜角度的变化 Fig. 7 Variation of electric scalar potential with the inclined angle of seabed |
由图可见:在海床倾斜水域,海床倾斜角度不改变水下标量电位分布特征的区域性,但对具体场点会影响其标量电位大小。在本文研究的小角度范围内,各场点处电位随海床倾斜角度的增加,近似呈线性单调递增。
3 倾斜海床水域与传统平行海床水域电位分布的对比在前述海洋环境、源参数条件下,为与传统平行海床条件下电位分布做对比,分别令

|
图 8 倾斜海床水域与平行海床水域电位分布的比较 Fig. 8 Electric scalar potential distribution comparisons between the inclined seabed waters and parallel seabed waters |
由图8可看出,倾斜海床水域域与平行海床水域相比:
1)电位分布特征的区域性相同;
2)平行海床时存在电位为0的场点,而海床倾斜时无;
3)平行海床时电位分布关于源的投影点,沿偶极矩方向反对称,而倾斜海床时该对称性丧失。
另外,本文将
本文针对海床倾斜水域,采用水平电偶极子模拟潜艇水下电场场源,进而对潜艇水下标量电位分布特征进行分析。主要内容如下:1)推导出了海床倾斜水域水平电偶极子水下标量电位的分布表达式;2)仿真分析了海床倾斜水域潜艇水下标量电位的分布特征,并分析了海水电导率变化和海床倾斜角度变化对电位分布的影响;3)将海床倾斜水域与传统理想平行海床水域的潜艇水下标量电位分布做了对比。
研究表明:海床倾斜水域潜艇水下电位分布特征明显,量值可观,可用于潜艇的探测与定位;小角度范围内,改变海床倾斜角度和海水电导率,所研究水域电位分布特征的区域性不变,量值随海床倾斜角度增大呈线性增加,随海水电导率增大呈二次方衰减;与传统平行海床水域电位分布相比,海床倾斜水域不存在零电位,沿偶极矩方向的对称性丧失。未来研究工作主要从以下2个方面进行:1)实验验证本文提出的潜艇探测与定位方法的可行性;2)研究海床倾斜水域潜艇腐蚀相关电场的场分布特征问题。
| [1] | WU Jian-hua, XING Shao-hua, LIANG Cheng-hao, et al. The influence of electrode position and output current on the corrosion related electro-magnetic field of ship[J]. Advances in Engineering Software, 2011, 42 (10): 902–909. |
| [2] | FALLAH M A, ABIRI H. Electromagnetic fields induced by the motion of di-hull bodies in a conducting fluid[J]. IEEE Transactions on Magnetics, 2013, 49(10): 5257–5263. |
| [3] | BIRSAN M. Measurement of the extremely low frequency (ELF) magnetic field emission from a ship[J]. Measurement Science and Technology, 2011, 22(8): 085709. |
| [4] | HE F, WANG X, ZHOU G. Feature extraction of shaft-rate electric field in the far field[C]// Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications (MAPE), 2013 IEEE 5th International Symposium on. IEEE, 2013: 189–192. |
| [5] | LIN G H, ZHANG Y R, LI K, et al. Electromagnetic field of a horizontal electric dipole buried in a medium covering one-dimensionally anisotropic medium[J]. AEU-International Journal of Electronics and Communications, 2013, 67(8): 708–716. |
| [6] | LUO Y, LI Q M, HE H Y. Study on electric field detection of ship based on character of gradient[C]// Consumer Electronics, Communications and Networks (CECNet), 2011 International Conference on. IEEE, 2011: 3576–3579. |
| [7] |
陈聪, 蒋治国, 姚陆锋, 等. 浅海中潜艇腐蚀相关静态电磁信号特征[J]. 海军工程大学学报, 2014, 26(3): 1–6.
CHEN Cong, JIANG Zhi-guo, YAO Lu-feng, et al. Characteristic analysis of corrosion-related static electromagnetic field produced by a submarine in shallow sea[J]. Journal of Naval University of Engineering, 2014, 26(3): 1–6. |
| [8] |
陈聪, 李定国, 龚沈光. 浅海中静态电偶极子电场分布的镜像法研究[J]. 武汉理工大学学报, 2010, 34(4): 716–720.
CHEN Cong, LI Ding-guo, GONG Shen-guang. Research on the electric field produced by static electric dipole located in shallow sea with mirror image theory[J]. Journal of Wuhan University of Technology, 2010, 34(4): 716–720. http://www.cnki.com.cn/Article/CJFDTOTAL-HEBG201406006.htm |
| [9] |
卢新城, 王婷, 陈新刚, 等. 海船轴频电场建模方法研究[J]. 武汉理工大学学报, 2012, 36(1): 168–170.
LU Xin-cheng, WANG Ting, CHEN Xin-gang, et al. Research on the modeling method of a sea gong vessel’s shaft-rate electric fields[J]. Journal of Wuhan University of Technology, 2012, 36(1): 168–170. |
| [10] |
杨国义. 舰船水下电磁场国外研究现状[J]. 舰船科学技术, 2011, 33(12): 140–142.
YANG Guo-yi, Situation on underwater electromagnetic field researches of ships abroad[J]. Ship Science and Technology, 2011, 33(12): 140–142. http://d.wanfangdata.com.cn/Periodical_jckxjs201112033.aspx |
| [11] | RODRIGO F J, MARÍA-DOLORES B, SÁNCHEZ A. Underwater threats detection based on electric field influences[J]. Undersea Defence Technology Conference Europe, Hamburg(Germany), 2010. |
| [12] | 冯士筰, 李凤歧, 李少菁. 海洋科学导论[M]. 北京: 高等教育出版社, 1999. |
| [13] |
陈聪, 李定国, 蒋治国, 等. 二次等效法求三层媒质中静态电偶极子的场分布[J]. 物理学报, 2012, 61 (24): 244101.
CHEN Cong, LI Ding-guo, JIANG Zhi-guo, et al. Electric field of a static electric dipole in three layer medium model using secondary equivalent method[J]. Acta Physica Sinica, 2012, 61(24): 244101. |
| [14] | ADEY R, BAYNHAM J M W. Predicting corrosion related signatures [J]. Simulation of Electro-chemical Processes II. WIT Transactions on Engineering Sciences, 2007, 54: 213–223. |
| [15] | KEDDIE A J, POCOCK M D, DEGIORGI V G. Fast solution techniques for corrosion and signatures modeling[J]. Simulation of Electro-chemical Processes II. WIT Transactions on Engineering Sciences, 2007, 54: 225–234. |
| [16] | ALLAN P J. Investigations of the magnetic fields from ships due corrosion and its countermeasures [D]. Glasgow: University of Glasgow, 2004: 101–116. |
| [17] | 谭浩, 贾亦卓, 龚沈光. 基于径向基神经网络回归预测的船舶轴频电场实时检测方法[J]. 应用基础与工程科学学报, 2013, 21(1): 167–173. http://d.wanfangdata.com.cn/Periodical_yyjcygckxxb201301018.aspx |
| [18] | LIN G H, ZHANG Y R, LI K, et al. Application of electromagnetic wave in the 1-D medium from a horizontal electric dipole in an isotropic region[J]. Journal of Electromagnetic Waves and Applications, 2015, 29 (1): 50–59. http://www.tandfonline.com/doi/pdf/10.1080/09205071.2014.981295 |
| [19] | KING R W P. The electromagnetic field of a horizontal electric dipole in the presence of a three layered region: Supplement[J]. J. Appl. Phys., 1993, 74(8): 4845–4848. |
| [20] | 陈聪, 李定国, 蒋治国, 等. 等效源法求分层导电媒质中水平直流电偶极子的磁场[J]. 应用基础与工程科学学报, 2015, 23(5): 1001–1009. http://www.cnki.com.cn/Article/CJFDTOTAL-YJGX201505014.htm |
| [21] |
陈聪. 舰船电磁场的模型研究和深度换算[D]. 武汉: 海军工程大学, 2008.
CHEN Cong. Research on the modeling and the extrapolation of electromagnetic field of ships[D]. Wuhan: Navy University of engineering, 2008. |
 2018, Vol. 40
2018, Vol. 40
