2. 中船重工船舶设计研究中心有限公司, 辽宁 大连 116001
2. China Ship Design and Research Center Corporation, Dalian 116001, China
船舶在高海况下航行时,船体首部的外飘区域往往承受剧烈的砰击载荷。准确地预报外飘砰击载荷是合理地设计船首抗砰击结构的前提。Von Karman[1]采用动量守恒方法计算了楔形体进入静水面时所受的砰击载荷。Wagner[2]在Von Karman研究的基础上,考虑了楔形体入水时引起的波面升高,并给出了楔形体表面的压力分布公式。Dobrovol'skaya[3]基于解析公式给出楔形体恒速入水时的自相似解。Zhao,Sun等[4 – 6]采用非线性边界元法计算了二维剖面的入水砰击载荷,并进一步分析了发生流动分离后剖面砰击载荷的变化。Sun[6]采用非线性边界元法和模态叠加法对圆壳入水过程中的砰击载荷与结构响应进行预报,结果与试验值吻合较好。陈震等[7 – 8]采用MSC.Dytran软件仿真了楔形体和平底结构的入水砰击载荷。Aquelet等[9]讨论了在采用任意欧拉拉格朗日算法预报砰击载荷时,接触阻尼对数值噪声的影响。Stenius等[10]通过改变参数对楔形体入水问题进行了大量计算,分析了网格密度、接触刚度、接触阻尼、时间步长对局部砰击压力载荷的影响。张晓波[11],骆寒冰[12],Wang [13]等针对小尺度的楔形体模型或外飘模型在自由落体时所受的砰击载荷进行预报,并将预报值与试验值进行比较。
船体外飘剖面随船体运动时,剖面底部入水后流体与剖面可能发生分离,分离后的液面再次砰击到外飘区域,这一过程中会捕捉一定的气体从而导致二次砰击问题更为复杂。过往的研究普遍针对小尺度的楔形体模型和外飘模型,而且模型的运动状态为自由落体运动或匀速运动。由于模型型线和模型运动速度的影响,很难反映出实船外飘剖面的二次砰击现象。本文利用耐波性理论确定的船波相对运动规律,对实船尺度的外飘剖面砰击载荷进行预报,分析二次砰击现象、网格密度和接触刚度参数对砰击载荷的影响。
1 基本理论 1.1 控制方程在任意欧拉拉格朗日算法(ALE)中,除拉格朗日坐标和欧拉坐标之外,引入参考坐标系进行控制方程的描述。若物质的速度为
| $\frac{{\partial \rho }}{{\partial t}} = - \rho \frac{{\partial {v_i}}}{{\partial {x_i}}} - {w_i}\frac{{\partial \rho }}{{\partial {x_i}}}\text{,}$ | (1) |
| $\rho \frac{{\partial {v_i}}}{{\partial t}} = \frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}} + \rho {b_i} - \rho {w_i}\frac{{\partial {v_i}}}{{\partial {x_j}}}\text{,}$ | (2) |
| $\rho \frac{{\partial E}}{{\partial t}} = {\sigma _{ij}}\frac{{\partial {v_i}}}{{\partial {x_j}}} + \rho {b_i}{v_i} - \rho {w_j}\frac{{\partial E}}{{\partial {x_j}}}\text{。}$ | (3) |
式中:
由流体材料的本构方程,应力张量
| ${\sigma _{ij}} = - p{\delta _{ij}} + \mu (\frac{{\partial {v_i}}}{{\partial {x_j}}} + \frac{{\partial {v_j}}}{{\partial {x_i}}})\text{。}$ | (4) |
式中:
当网格速度为
船体结构砰击现象中涉及空气、水和船体3种材料。其中,本文对于空气和水采用NULL材料模型进行模拟,采用刚体模型对船体的外飘型线进行模拟。对于流体材料需要结合相应的流体状态方程来实现控制方程的求解。状态方程描述了体积变形与压力的关系。本文采用线性多项式状态方程来表达空气,采用Gruneisen方程来表达水,具体的参数取值参照文献[11]。
1.3 耦合算法采用罚函数耦合方法来模拟砰击现象中结构与流体的耦合现象。罚函数耦合方法类似于一个弹簧系统,弹簧的一端与结构网格(主物质)的节点相连,弹簧的另一端与流体网格(从物质)的节点相连。当流体节点浸入结构网格表面时,在界面处产生耦合力会分布到欧拉流体的节点上来保证结构表面的物面条件。耦合力与结构网格进入流体网格中的深度成正比,可以表达为:
| ${{P}} = {{kd}}{\text{。}}$ | (5) |
式中:P为耦合力;k为接触刚度;d为浸入深度。
与文献[11 – 13]不同,本文给出耦合力与浸入深度的变化关系。当浸入深度d=0时,P=0;当d=dmax时,P=pmax。dmax和pmax分别为所允许的最大浸入深度和砰击时达到的最大砰击压力。本文后续均采用上述2点给出耦合力与浸入深度的线性关系,此时接触刚度相当于pmax与dmax的比值。
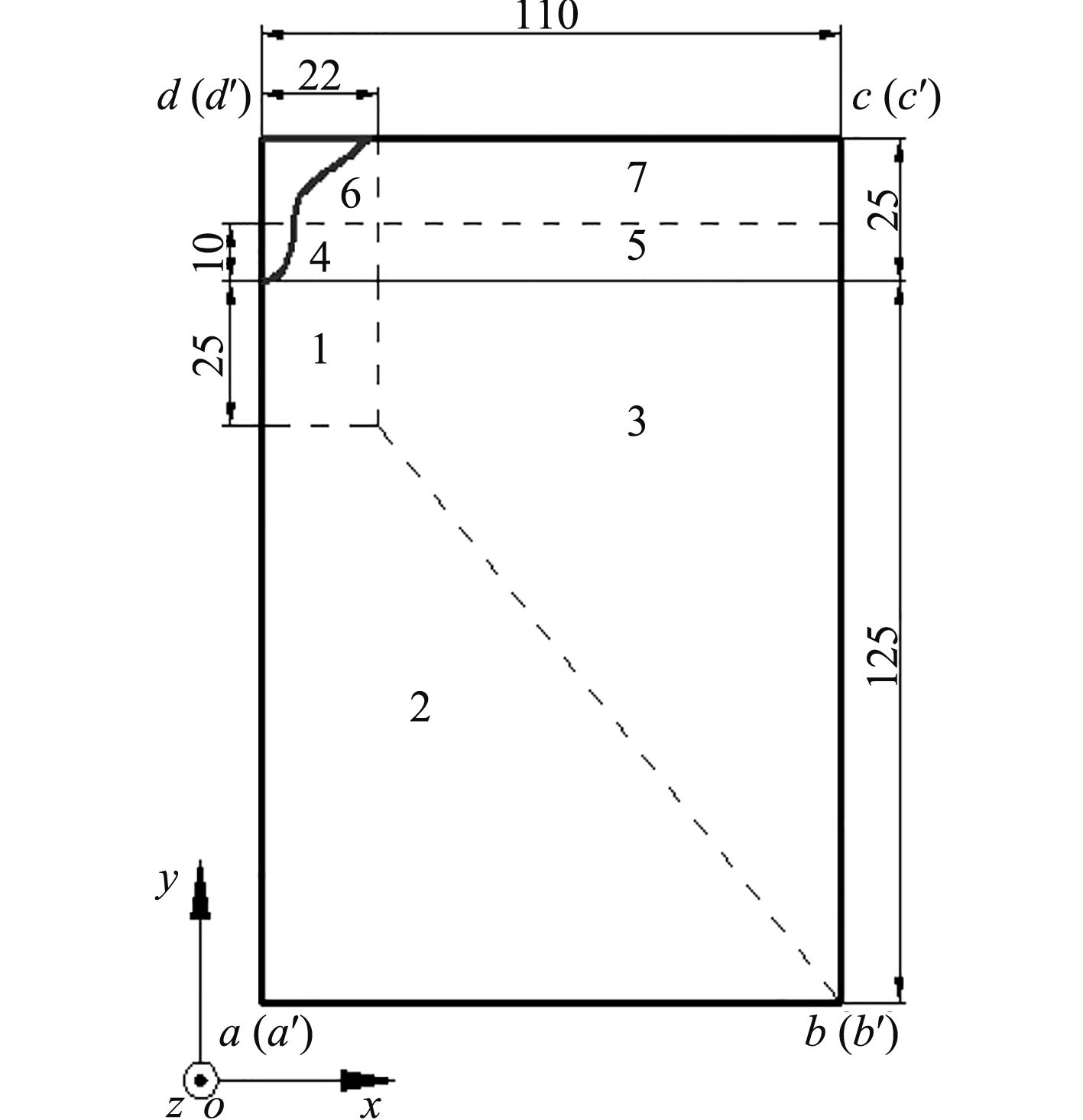
2 数值模型 2.1 网格域建立如图1所示的砰击载荷数值预报模型,图中流体域的尺度代表各自之间的长度比例,可根据结构剖面的大小确定流体域的大小。区域1到区域3为水域,区域4–区域7为空气域,曲线为外飘剖面结构。区域1、区域4为结构与流体的主要作用区域,采用细网格进行划分。区域2–区域3,5–区域7采用尺度渐变的网格进行过渡。XOY面内结构网格的长度是区域1网格在x方向上网格长度的1.5倍。模型在z方向(垂直于纸面向外)的尺度为1个网格的长度。网格密度的示意如图2所示。
|
图 1 数值模型 Fig. 1 Numerical model |

|
图 2 网格密度示意图 Fig. 2 Schematic diagram of mesh density |
在add’a’面施加对称条件,采用一半模型进行船体外飘剖面砰击入水的模拟。在abb’a’,bcc’b’,cdd’c’平面添加无反射边界条件,来模拟无限尺度的流域。约束abcd,a’b’c’d’平面内节点z方向的线位移和绕x,y方向的角位移,模拟二维砰击现象。通过添加负y方向的加速度,实现重力加速度。给定剖面初速度或强制位移,实现不同运动规律下砰击载荷的预报。
3 数值模拟中的主要影响因素 3.1 网格密度网格密度是影响数值仿真计算的重要参数,网格尺寸过大会导致仿真结果不真实,不能很好地表达结构与流体之间的耦合作用;网格尺寸过小会影响计算效率,导致工程应用性差。因此网格密度的选取至关重要。
3.2 接触刚度接触刚度(PFAC)是用来描述耦合系统之间刚度的参数,它用来计算流体和结构之间的耦合力。接触刚度的大小会影响穿透现象的发生,如果接触刚度太大,会使物质产生钢化现象,物质表面过分刚硬会影响程序计算的稳定。
3.3 二次砰击由于船体首部各剖面形状均不同,在曲率变化大的剖面可能会有二次砰击现象发生,而且发生二次砰击的剖面计算所得的砰击压力峰值要远大于首次砰击产生的砰击压力峰值,因此在船首一些特殊剖面必须考虑二次砰击的现象并且对二次砰击的砰击压力峰值进行计算,才能够完整的模拟整个砰击过程。
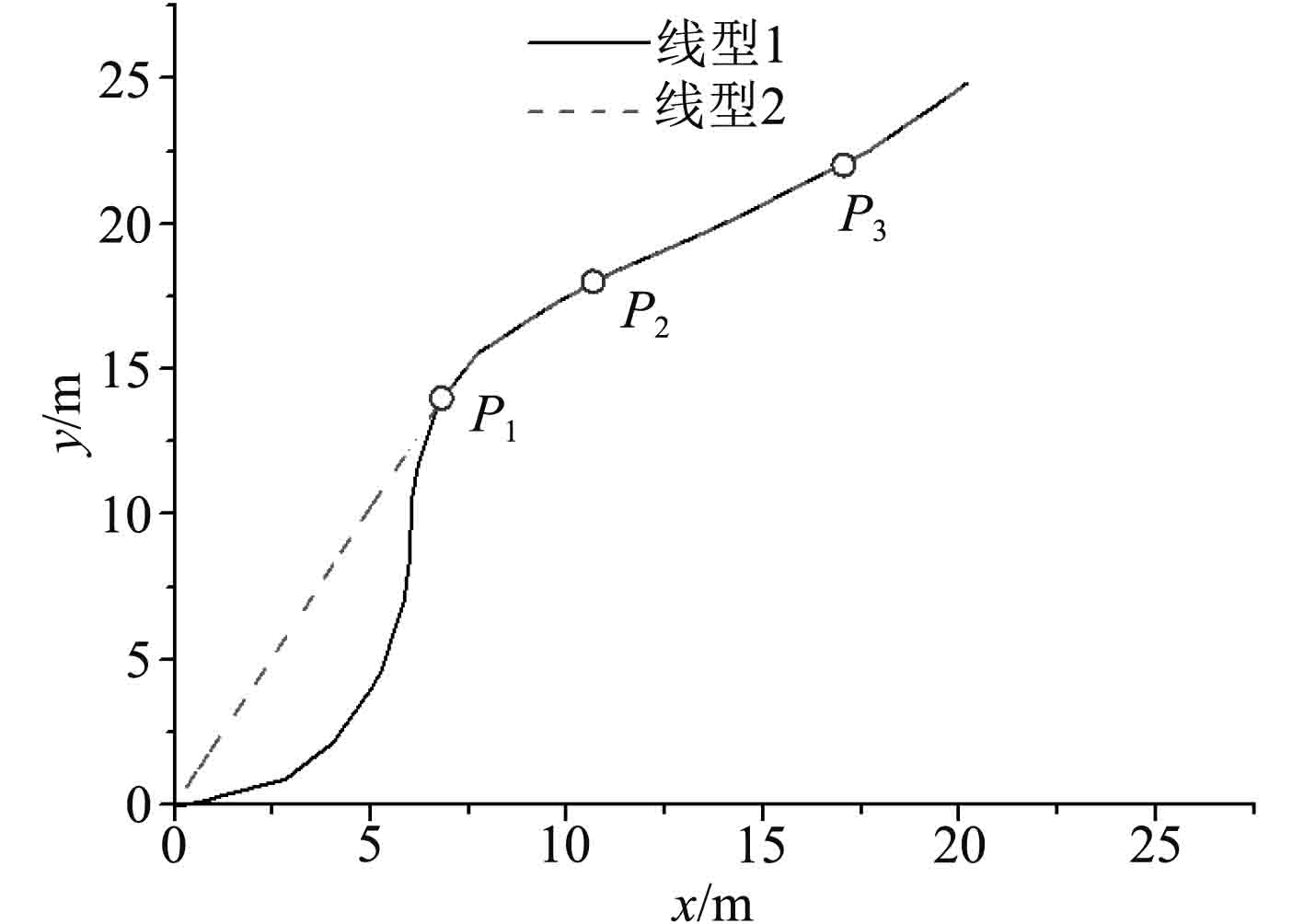
4 算例分析对2种外飘型线,进行船舶与波浪相对运动规律下的砰击载荷的预报,讨论了网格密度、接触刚度和剖面形式对砰击载荷的影响,并将数值预报得到的砰击压力系数与规范值进行对比。型线1与型线2仅在P1以下形状不同,外飘区域的形状完全相同。依照剖面的尺度确定仿真模型区域1的x,y,z方向尺度分别为22 m,25 m,0.5 m,其他区域按照图3给定的比例进行确定。接触阻尼取为0.9倍的临界阻尼。
|
图 3 实船尺度剖面 Fig. 3 Section of an actual ship |
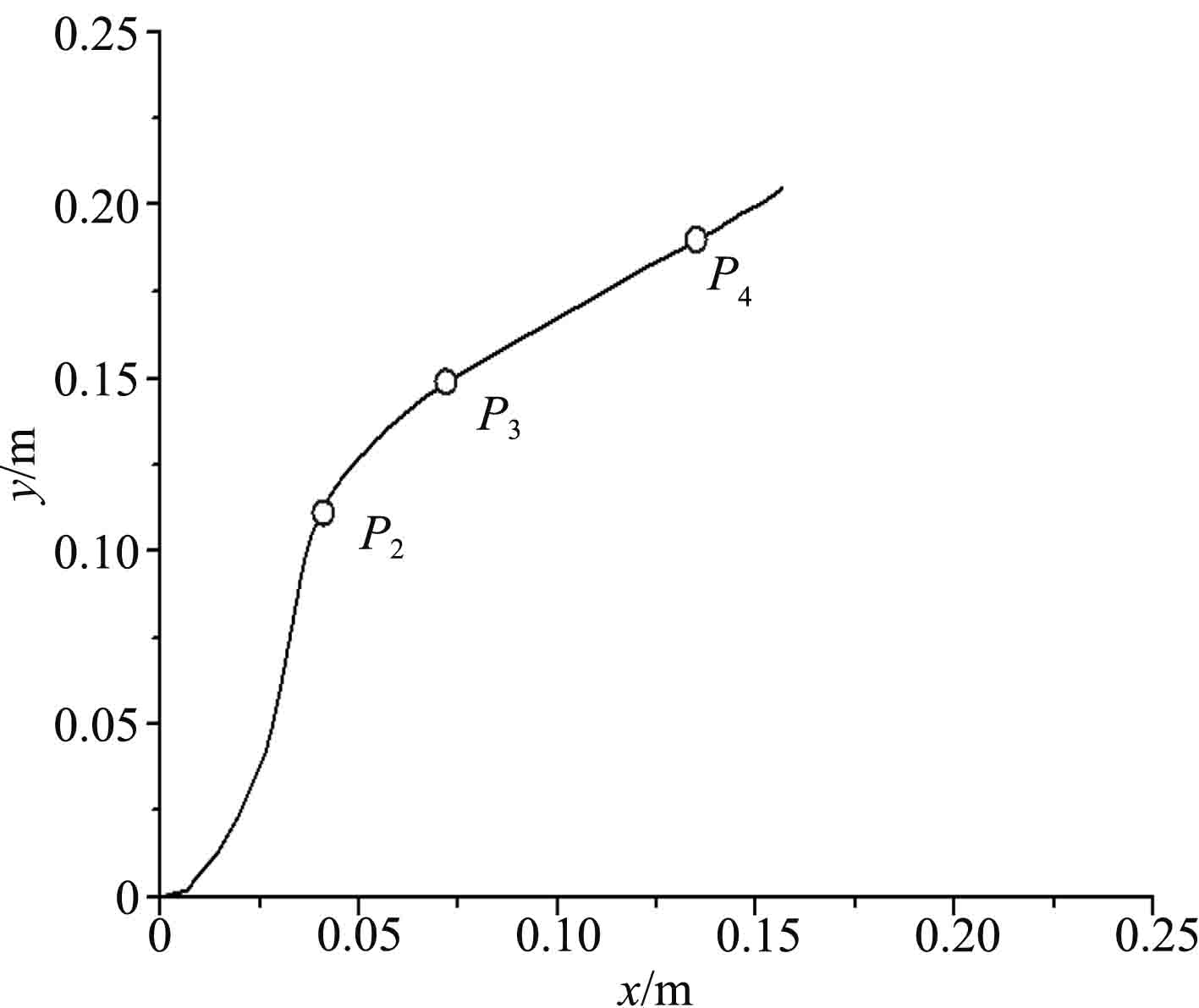
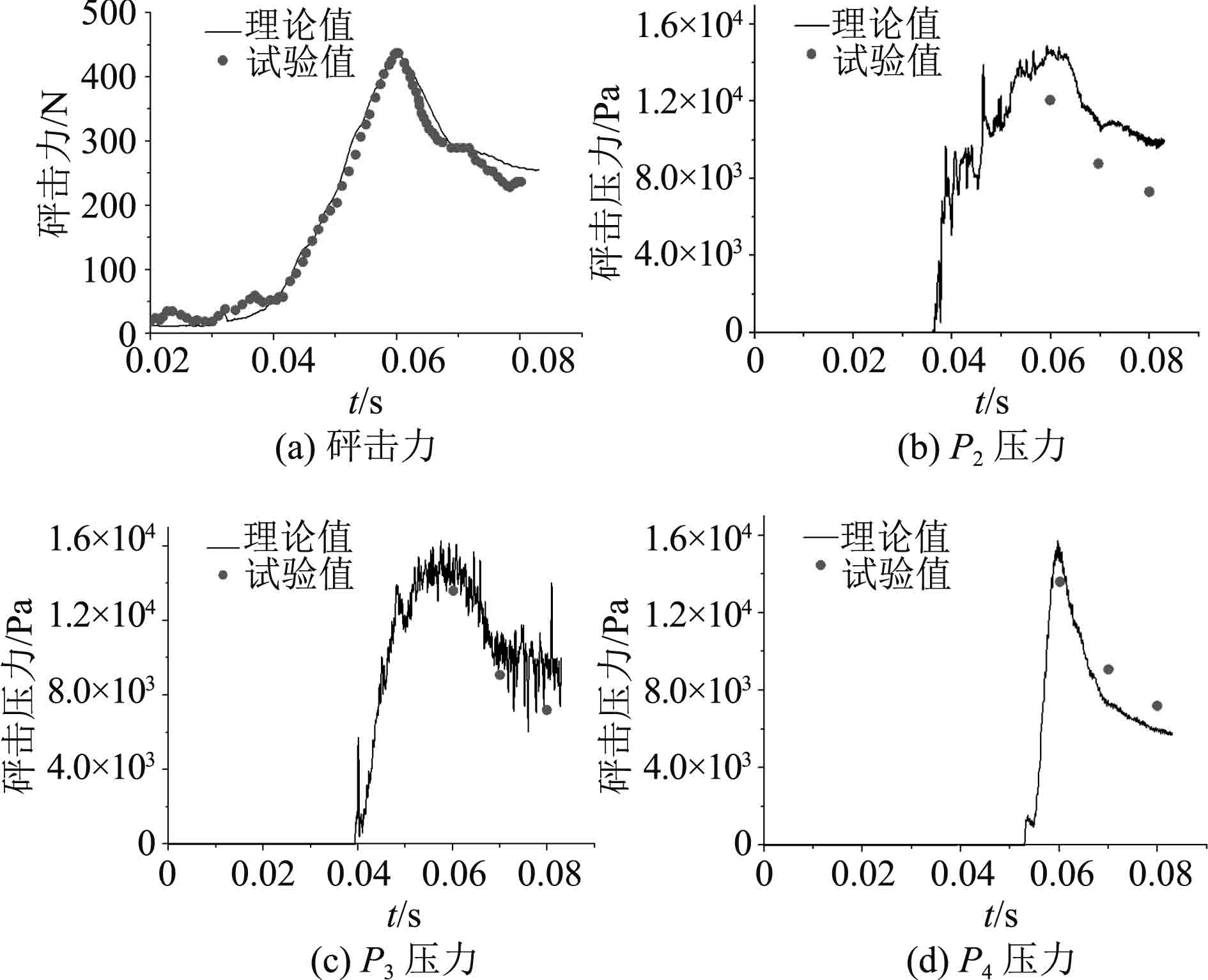
针对落体砰击试验中的外飘砰击力和砰击压力载荷进行预报,由试验模型尺度确定仿真模型区域1的x,y,z方向尺度分别为0.22 m,0.25 m和0.005 m,其他区域按照图4给定的比例进行确定。其中,细网格区域1、区域4的网格在x、y方向的尺度分别为0.001 1 m和0.001 25 m。接触刚度相关的参数dmax=0.000 3 m和pmax=17 000 Pa。接触阻尼取为0.9倍临界阻尼。通过与公开发表的文献[6]进行对比,如图5所示。可以看出理论值与试验值吻合较好,验证本文采用的数值模型和计算参数的正确性。
|
图 4 落体模型剖面 Fig. 4 Section of the free-drop model |
|
图 5 理论值与试验值对比 Fig. 5 Comparison between numerical results and experimental results |
|
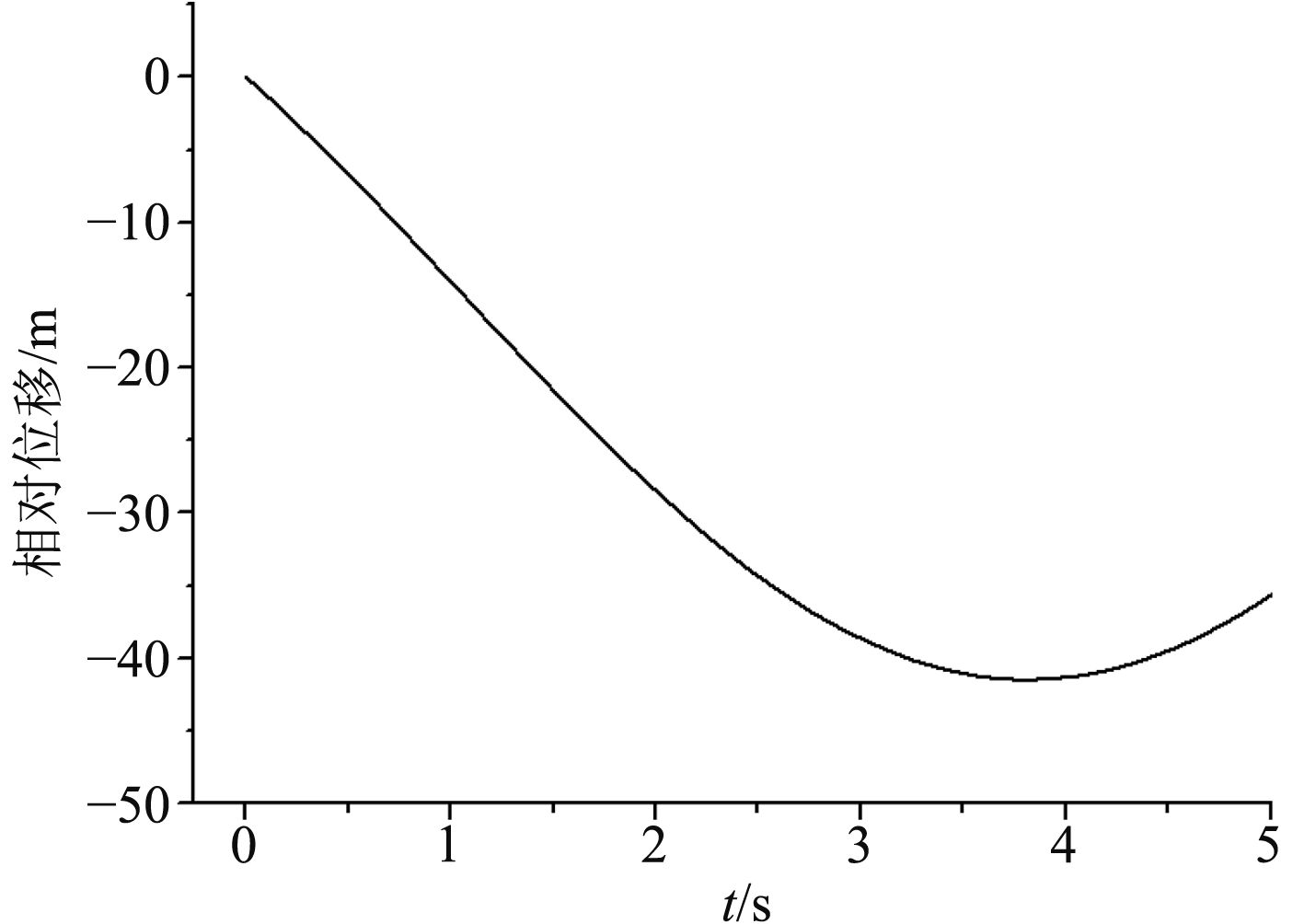
图 6 船舶与波浪相对运动 Fig. 6 Relative motion between the ship and the wave |
在与接触刚度相关的参数dmax=0.04 m和pmax=2.40×106 Pa时,改变网格的密度,针对2种型线进行船舶相对运动关系下的砰击载荷预报。不同网格密度下对应细网格区域在x,y方向的尺度dx,dy如表1所示。砰击力与砰击压力的对比如图7和图8所示,为了节省空间仅给出P1位置的砰击压力随时间变化曲线。砰击力与砰击压力的峰值如表2所示。
|
|
表 1 细网格区域的网格尺度 Tab.1 Mesh size in fine grid region |
|
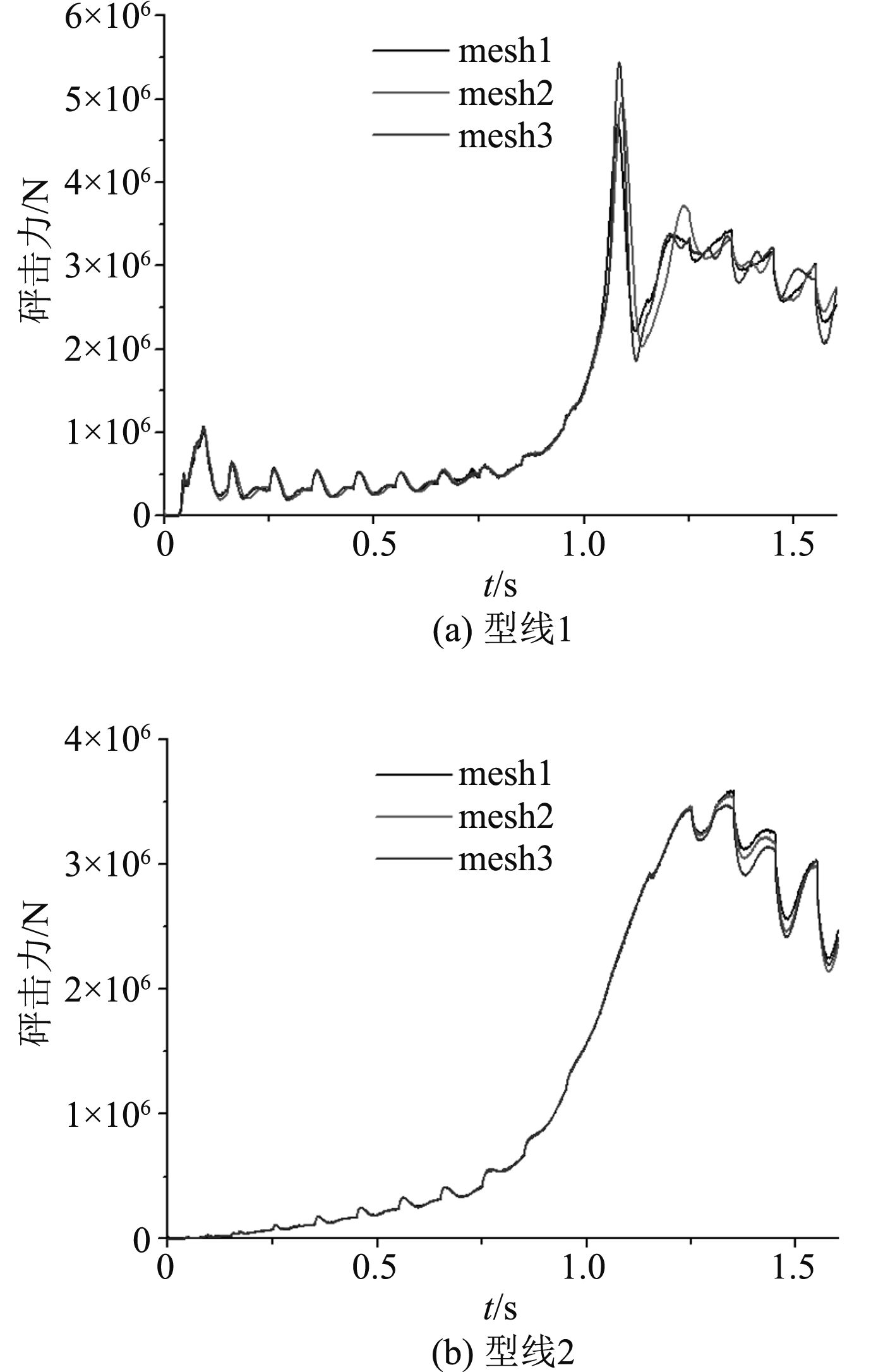
图 7 不同网格密度下砰击力 Fig. 7 Slamming forces with different mesh densities |
|
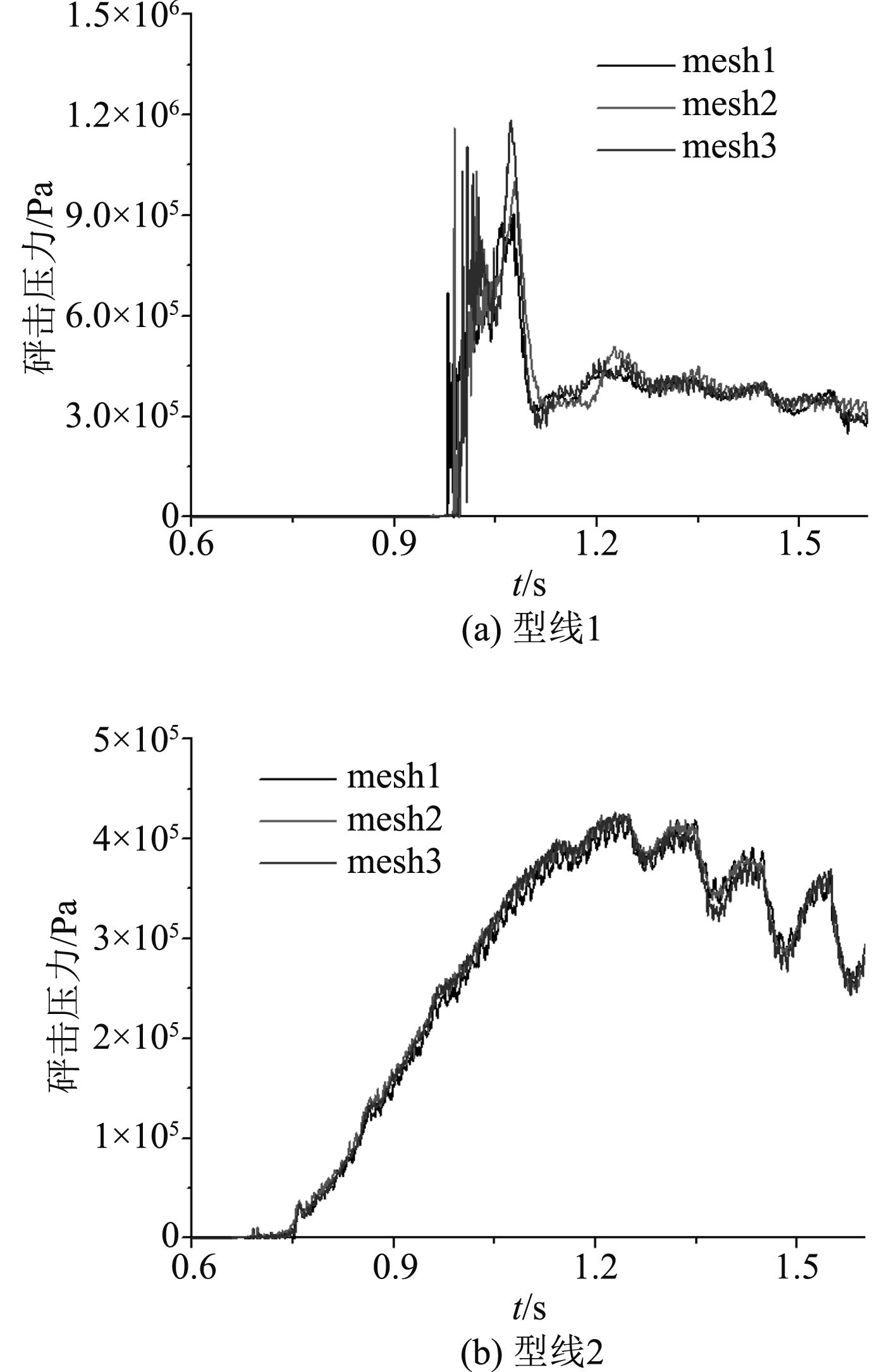
图 8 不同网格密度下P1处砰击压力 Fig. 8 Slamming pressure of P1 with different mesh densities |
|
|
表 2 不同网格密度下砰击载荷峰值 Tab.2 Peak values of slamming loads with different mesh densities |
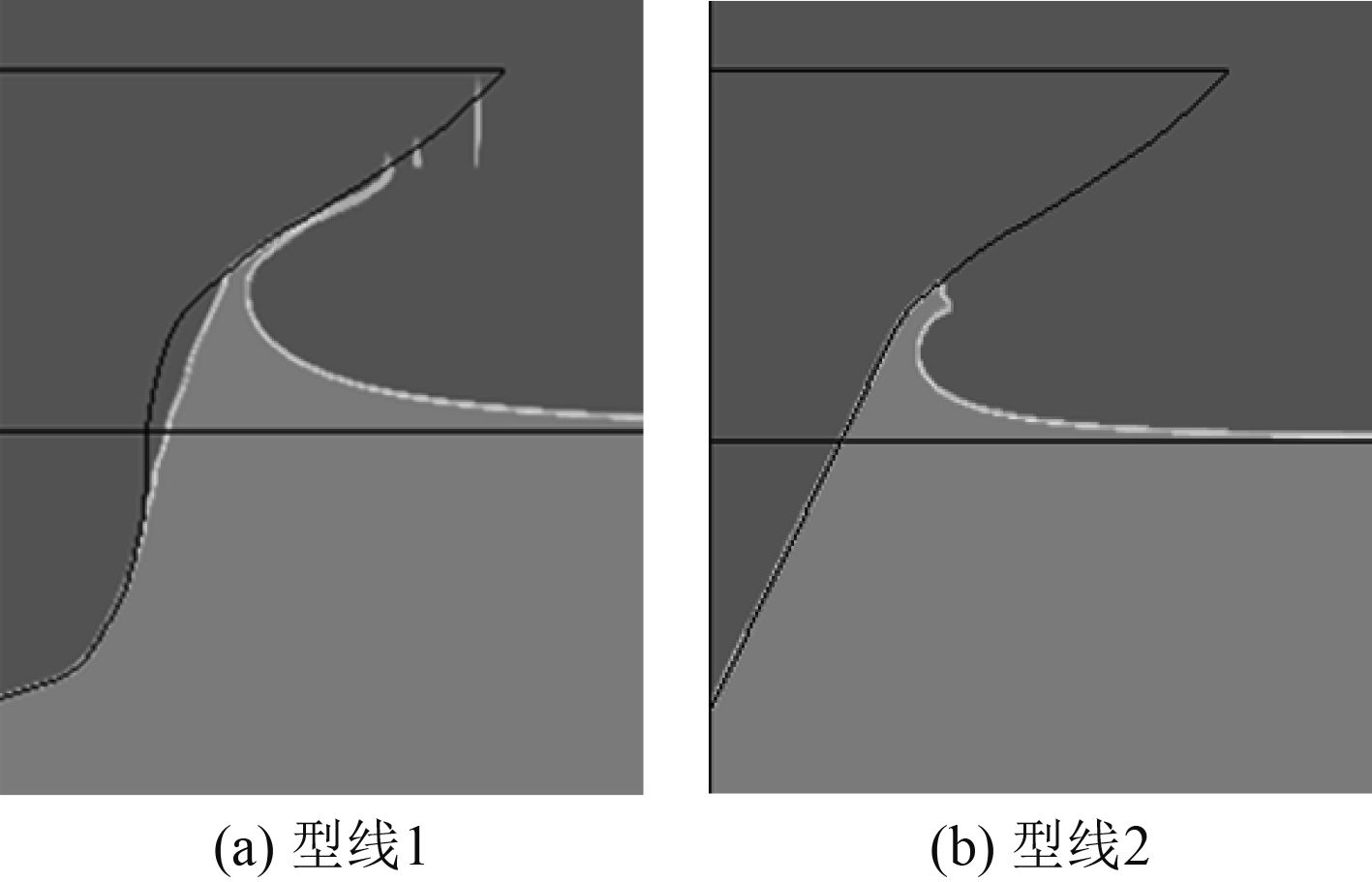
可以看出,对于型线1和型线2,不同网格下的砰击力和砰击压力变化趋势一致;当网格尺度从mesh1到mesh3逐渐减小时,型线1的砰击力和砰击压力的峰值有增大的趋势,而型线2砰击力和砰击压力的峰值变化不大。由图9可以看出型线1出现了液面与剖面分离后二次砰击现象,分析正是由于此种现象,导致不同网格下,型线1的砰击力与砰击压力的峰值更难达到收敛。
|
图 9 t=0.8 s时流场液面 Fig. 9 Water elevation of the fluid at t=0.8 s |
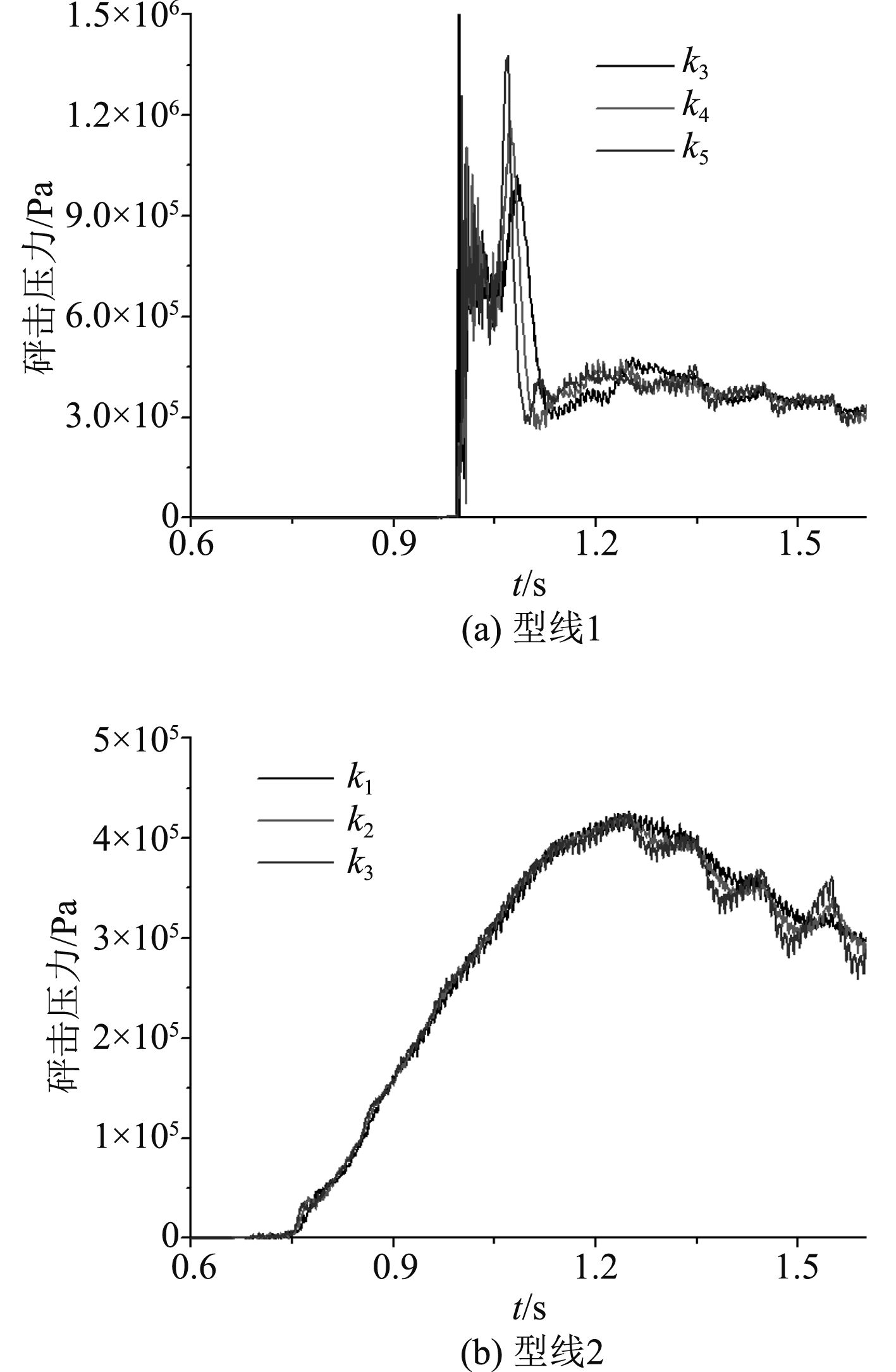
在网格密度为mesh3时,改变与接触刚度相关的参数dmax和pmax,针对2种型线进行船舶相对运动关系下的砰击载荷的预报,参数dmax和pmax如表3所示。砰击力与砰击压力的对比如图10和图11所示。砰击力与砰击压力的峰值如表4所示。
|
|
表 3 接触刚度参数 Tab.3 Parameters of the contact stiffness |

|
图 10 不同接触刚度下砰击力 Fig. 10 Slamming pressures with different contact stiffness |
|
图 11 不同接触刚度下的砰击压力 Fig. 11 Slamming forces with different contact stiffness |
|
|
表 4 不同接触刚度下砰击载荷峰值 Tab.4 Peak values of slamming loads with different contact stiffness |
可以看出,对于型线1和型线2,不同接触刚度下的砰击力和砰击压力变化趋势一致;对于型线2,当接触刚度从k1到k3逐渐增大时,砰击力和砰击压力的峰值变化不大,已经收敛,但在载荷下降时间段内(1.2 s以后),数值噪声有增大的趋势;由型线2的砰击峰值和接触刚度收敛范围,推断当接触刚度从k3到k5时,型线1砰击力和砰击压力峰值也收敛。但计算结果表明,当接触刚度从k3到k5时,砰击力和P1,P2砰击压力峰值有增大的趋势, 分析原因为二次砰击后,砰击力与砰击压力的峰值受接触刚度的影响更为敏感。文献[14]在平底结构入水问题中说明持续时间较短的砰击压力峰值的差别并不会导致应力响应的差别,在理论预报的砰击压力峰值与试验值存在差别的情况下,结构应变与试验依然吻合较好,因而后续可从结构应变响应的角度对型线1的接触刚度的收敛性进行研究。
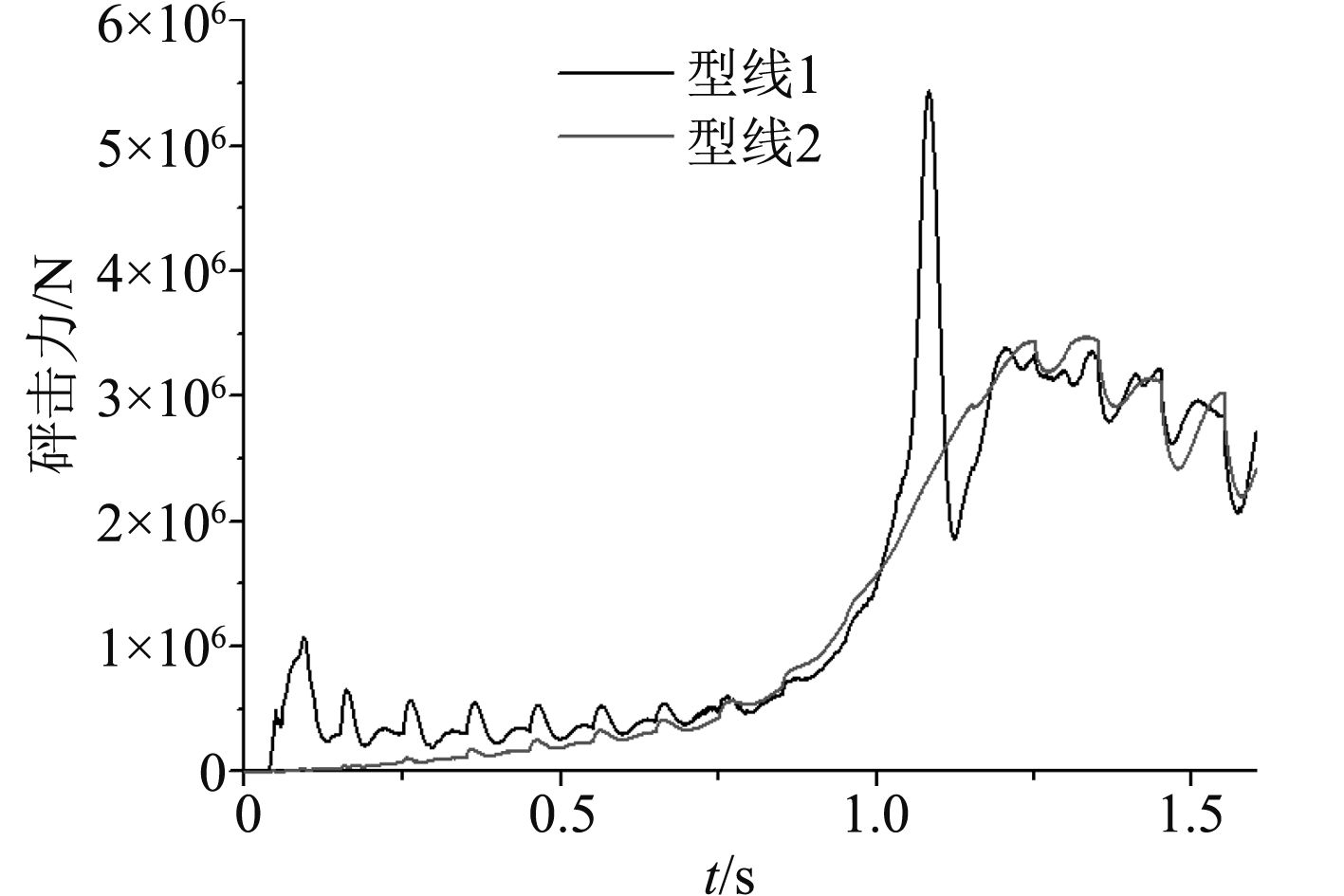
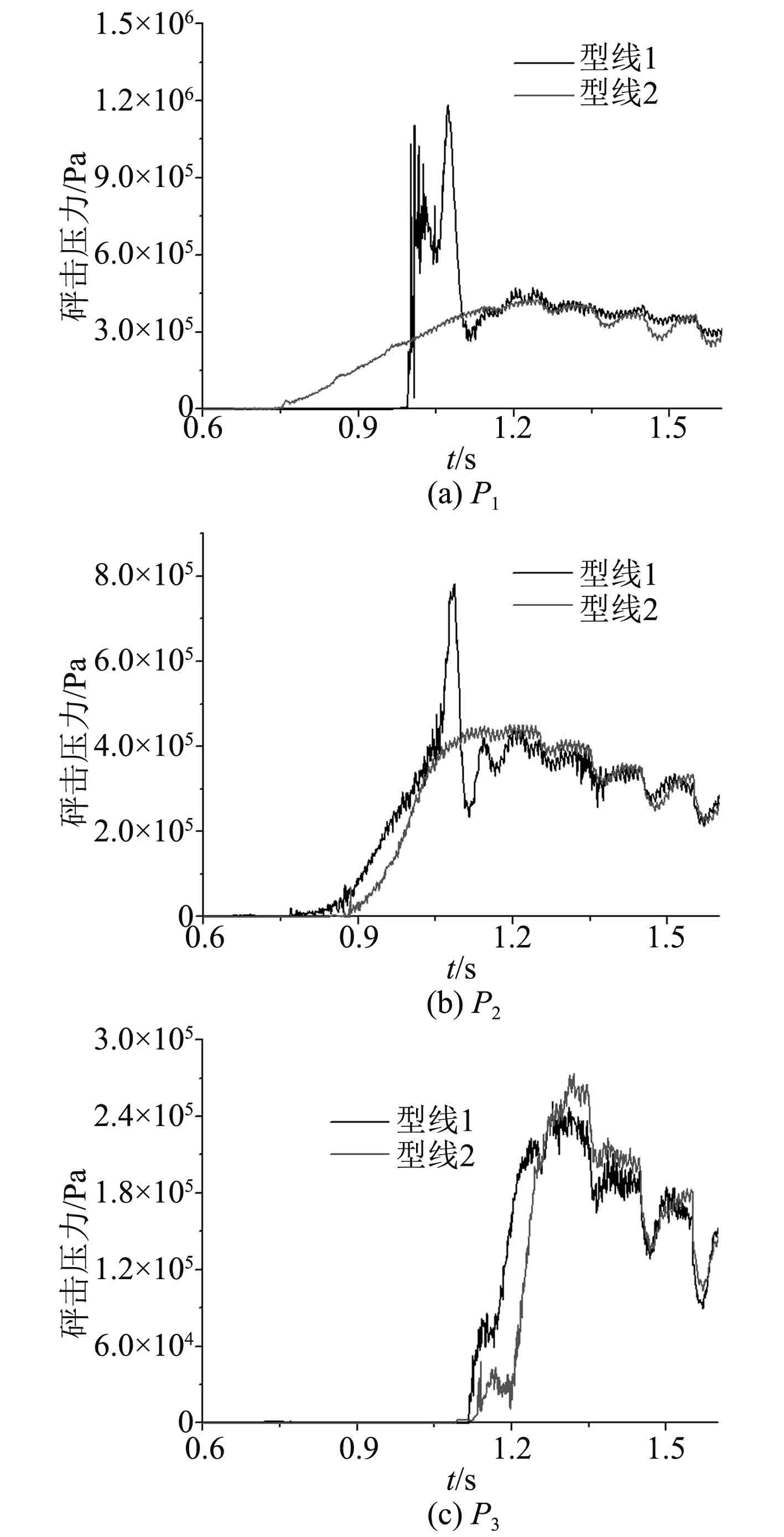
4.4 不同剖面形状计算结果在接触刚度为k4、网格密度为mesh3时,对2种不同剖面砰击载荷的对比如图12和图13所示。可以看出,2种剖面形式在时间从1.0 s到1.2 s之间,由于二次砰击的影响,导致型线1的砰击力和P1,P2处砰击压力比型线2多一个很大的峰值。在1.2 s之后,2种型线的砰击载荷相差不大。
|
图 12 不同型线下的砰击力 Fig. 12 Slamming forces of different sections |
|
图 13 不同型线下的砰击压力 Fig. 13 Slamming pressures of different sections |
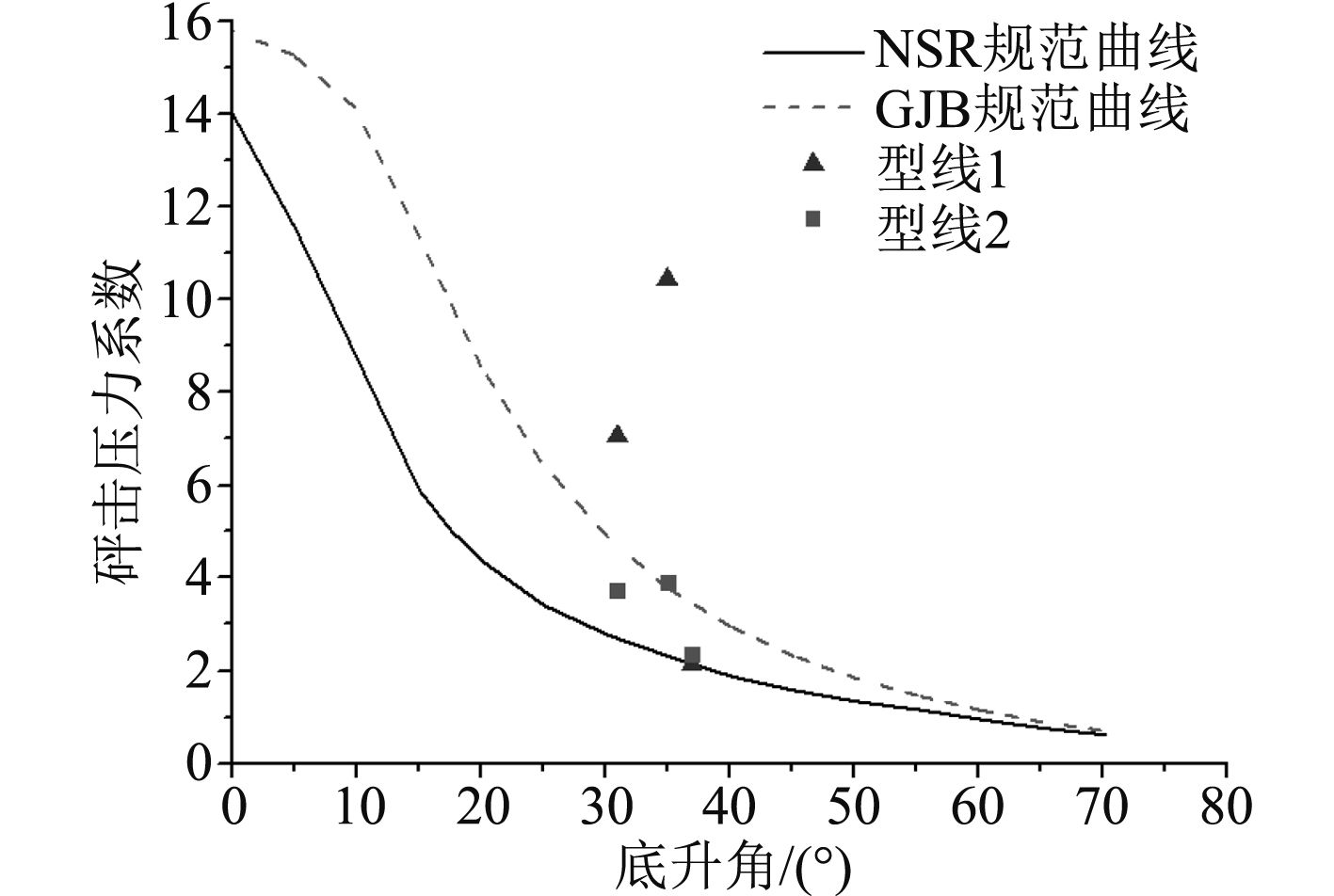
在接触刚度为k2、网格密度为mesh3时,利用2种不同剖面确定砰击压力和砰击速度换算得到砰击压力系数,如表5所示。P1恰好位于曲率变化比较大的位置,考虑到剖面入水后的液面升高,单纯依据P1局部位置的底升角确定砰击压力是不合理的,这里选取P1位置上部曲率变化平稳位置确定P1的底升角。由图14可以看出,型线2各点对应的砰击压力系数恰好位于2种规范曲线[15]之间,而型线1的P1,P2对应的砰击压力系数则明显大于规范值,可见目前规范曲线尚未考虑到二次砰击引起砰击压力峰值的增大。
|
|
表 5 砰击压力系数的数值预报结果 Tab.5 Numerical results of the slamming pressure coefficient |
|
图 14 砰击压力系数理论值与规范值 Fig. 14 Numerical and rule results of the slamming pressure coefficient |
本文通过对船首外飘砰击载荷的预报得到如下结论:
1)通过对比数值预报结果与落体砰击模型试验结果,验证本文在网格划分和接触刚度等参数选取的合理性。
2)通过研究不同网格密度、接触刚度下2种型线的砰击力与砰击压力载荷的数值预报,可以看出对于型线2,在网格密度相对稀疏,dmax约为模型宽度的0.002,pmax约为剖面可达到的最大砰击压力时,即可得到稳定的砰击载荷数值结果;由于二次砰击现象,导致型线1砰击力和砰击压力载荷的峰值受网格密度和接触刚度的参数影响更加敏感,但不同参数下,砰击力与砰击压力载荷的变化趋势一致,后续可从结构响应的角度对二次砰击现象中的网格密度和接触刚度的收敛性进行研究。
3)在相同网格密度和接触刚度参数下,型线1在二次砰击发生时(1.0~1.2 s),砰击力和砰击压力P1、P2明显要大于型线2的值,1.2 s之后2种型线砰击载荷变化几乎一致。可见,二次砰击现象会导致局部位置砰击载荷的增加,应该引起结构设计的关注。
4)由砰击压力系数与规范值的比较看出,对于未发生二次砰击(型线2的P1,P2,P3)和不受二次砰击影响的位置(型线1的P3),砰击压力系数与规范值相差不大。但对于受二次砰击压力较大的位置(型线1的P1,P2),砰击压力系数明显大于规范值,可见当前规范仍需更合理地考虑二次砰击现象对砰击载荷的影响。
| [1] | VON KARMAN T. The impact on seaplane floats during landing[R]. NACA TN321, oct. 1929. |
| [2] | WAGNER H. Uber stass-und gleitvorgange und der oberflache von flussigkeiten[J]. ZAMM, 1932, 12(4): 193–215. |
| [3] | DOBROVOL’SKAYA Z N. On some problems of similarity flow of fluids with a free surface[J]. Journal of Fluid Mechanics, 1969, 36: 805–829. |
| [4] | ZHAO R, FALTINSEN O M. Water entry of two-dimensional bodies[J]. Journal of Fluid Mechanics, 1993, 246: 593–612. |
| [5] | ZHAO R, FALTINSEN O M, AARSNES J V. Water entry of arbitrary two-dimensional sections with and without flow separation [C]// Proc. 21st Symposium on Naval Hydrodynamics, 1996: 408–423. |
| [6] | SUN Hui. A boundary element method applied to strongly nonlinear wave-body interaction problems [D]. Norway: Norwegian University of Science and Technology, 2007: 15–100. |
| [7] | 陈震, 肖熙. 二维楔形体入水砰击仿真研究[J]. 上海交通大学学报, 2007, 41(9): 1425–1428. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_shjtdxxb200709008 |
| [8] | CHEN Zhen, XIAO Xi. The simulation study on water entry of 2D wedge bodies[J]. Journal of Shanghai Jiaotong University, 2007, 41(9): 1425–1428. https://www.researchgate.net/publication/34361756_Slipping_of_wedge_bodies |
| [9] | 陈震, 肖熙. 平底结构砰击压力峰值分析[J]. 上海交通大学学报, 2006, 40(6): 983–987. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_shjtdxxb200606024 |
| [10] | CHEN Zhen, XIAO Xi. Analysis about the slamming pressure peak value on a flat bottom structure[J]. Journal of Shanghai Jiaotong University, 2006, 40(6): 983–987. |
| [11] | AQUELET N, SOULI M, OLOVSSON L. Euler-lagrange coupling with damping effects: application to slamming problems[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195: 110–132. |
| [12] | STENIUS I, ROSN A, KUTTENKEULER J. Explicit FE-modeling of fluid-structure interaction in hull-water impacts[J]. Int Shipbuild Prog, 2006, 53, 1031–1121. |
| [13] | 张晓波. 船底结构砰击时的流固耦合数值模拟[D]. 大连: 大连理工大学, 2007. |
| [14] | 骆寒冰, 吴景健, 王珊, 等. 基于显式有限元方法的二维楔形刚体入水砰击载荷并行计算预报[J]. 船舶力学, 2012, 16(8): 907–913. https://www.wenkuxiazai.com/doc/8b2512393968011ca300911a.html |
| [15] | LUO Hang-bing, WU Jing-jian, WANG Shan, et al. Parallel computing simulation of water entry of a 2D rigid wedge using an explicit finite element method [J]. Journal of Ship Mechanics, 2012, 16(8): 907–913. |
| [16] | WANG S, GUEDES S C. Slam induced loads on bow-flared sections with various roll angles[J]. Ocean Eng, 2013, 67: 45–57. |
| [17] | FALTINSEN O M. Hydrodynamics of high-speed marine vehicles[M]. New York: Cambridge University Press, 2005. |
| [18] | 王辉. 船体结构局部强度设计中的砰击载荷确定方法[J]. 中国造船, 2010, 51(2): 68–77. http://www.cnki.com.cn/Article/CJFDTOTAL-JTKJ201006025.htm |
| [19] | WANG Hui. Slamming load determination in local structure design of ships[J]. Shipbuilding of China, 2010, 51(2): 68–77. |
 2018, Vol. 40
2018, Vol. 40
