入水砰击问题涉及流体与固体相互耦合作用,是水弹性力学研究领域中的一个热点。当冲击发生时,水弹性力学的相关特性主要取决于流体物理特性、结构物几何特性和物理特性以及入水的初速度及入水角度等因素。
由于实尺度试验成本太高、操作困难等原因,模型试验更受研究者的青睐[1 – 8]。张岳青等[9]进行了楔形体垂直入水冲击实验,通过滤波消除高频信号,得到了合理的加速度响应值。在数值方法方面,早期入水问题的研究对象多为刚体,但是随着理论知识的丰富,研究弹性体入水也逐渐增多[10 – 12]。张智[13]用Fluent软件模拟了楔形体垂直入水砰击和转角度入水砰击的2种情况,并得到了加速度、速度和砰击压力等随时间变化的曲线,同时,他还对砰击影响进行了敏感性分析。
本文数值模拟部分主要采用Ansys软件中Fluent和Workbentch模块,外加自主编程,结合动网格技术来模拟和计算刚性和弹性楔形体的入水过程。
1 入水问题的数学模型和数值模型 1.1 结构入水水弹性力学的微分控制方程考虑一个弹性体,其区域为Vs,入水的流体区域为VL,弹性体表面为Sp,弹性体和流体的交界面为S(见图1)。

|
图 1 弹性体与液体耦合图 Fig. 1 The sketch diagram of a plastic structure coupled with liquid |
设弹性体是各向同性且为线变形,弹性体的运动微分方程为:
| ${\rho _s}\frac{{{\operatorname{D} ^2}{u_i}}}{{\operatorname{D} {t^2}}} = {\sigma _{ij,j}} + {F_i}\text{。}$ | (1) |
式中:
应变-位移关系为:
| ${e_{ij}} = \frac{1}{2}\left( {{u_{i,j}} + {u_{j,i}}} \right)\text{。}$ | (2) |
式中:
各向同性弹性体的应力-应变关系为:
| ${\sigma _{ij}} = {{\lambda }}{e_{kk}}{\delta _{ij}} + 2\mu {e_{ij}}\text{。}$ | (3) |
式中:
| ${{\lambda }} = \frac{{E{{\nu }}}}{{\left( {1 + {{\nu }}} \right)\left( {1 - 2{{\nu }}} \right)}}{{,}}\;{{\mu }} = \frac{E}{{\left( {1 + 2{{\nu }}} \right)}}\text{。}$ | (4) |
式中,
对于流体部分的区域
| ${\rho _L}\frac{{{D^2}{u_i}}}{{D{t^2}}} = {\rho _L}\left( {\frac{\partial }{{\partial t}} + {u_j}\frac{\partial }{{\partial {x_j}}}} \right){u_i} = {F_i} + \frac{{\partial {p_{ij}}}}{{\rho \partial {x_j}}}\text{。}$ | (5) |
式中:
| ${p_{ij}} = - p{\delta _{ij}} + 2\mu \left( {{s_{ij}} - \frac{1}{3}{s_{kk}}{\delta _{ij}}} \right)\text{。}$ | (6) |
式中:
连续方程为
| $\frac{{D{\rho _L}}}{{{D_t}}} + {\rho _L}{u_{i,i}} = 0\text{,}$ | (7) |
对于不可压缩的液体,其状态方程可取
| ${\rho _L} = {\text{常数}}\text{。}$ | (8) |
若考虑压缩性,对于纯液体,其压强与密度间的关系可由下列半经验的公式给出:
| ${\left( {\frac{{p + B}}{{{p_0} + B}}} \right)^{\frac{1}{A}}} = \frac{{{\rho _L}}}{{{\rho _{{L_0}}}}}\text{。}$ | (9) |
式中:A,B为与液体性质有关的常数,对于A=7,B=3 000大气压,下标0表示未经扰动时的量。
若考虑水的微量可压缩性,则有
| $p = \frac{{k\left( {\rho - {\rho _0}} \right)}}{{{\rho _0}}}\text{。}$ | (10) |
式中:K为体积弹性系数;
在弹性体和流体的交界面S上应满足压强相等和法向速度相等的条件:
| ${\left( {{{\dot u}_i}{n_i}} \right)_s} = {\left( {{{\dot u}_i}{n_i}} \right)_L}\;\; \text{。}$ | (11) |
式中:
1)控制方程的离散方法
本文流体域采用有限体积法,结构域采用有限元法。
关于有限体积法对流域控制方程进行离散的过程如下:
首先将连续方程和运动方程统写为
| $\frac{\partial }{{\partial t}}\left( {\rho \varphi } \right) + \nabla \cdot \left( {\rho {{u}}\varphi } \right) = \nabla \cdot \left( {{\Gamma _\varphi }\nabla \varphi } \right) + {{{S}}_\varphi }\text{,}$ | (12) |
其中,左侧第1项是瞬态项,第2项是对流项,右侧依次代表扩散项和源项。假定
| $\int\nolimits_{\Delta V} {\nabla \cdot \left( {\rho {{u}}\varphi } \right)} { d}V = \int\nolimits_{\Delta V} {\nabla \cdot \left( {{\Gamma _\varphi }\nabla \varphi } \right)} { d}V + \int\nolimits_{\Delta V} {{{{S}}_\varphi }{ d}V}\text{,} $ | (13) |
通过高斯公式:
| $\int\nolimits_{\Delta V} {\nabla \cdot {{a}}{ d}V} = \int\nolimits_A {{{n}} \cdot {{a}}{ d}A} \text{,}$ | (14) |
变换得到:
| $\int\nolimits_A {{{n}} \cdot \left( {\rho {{u}}\varphi } \right)} { d}A = \int\nolimits_A {{{n}} \cdot \left( {{\Gamma _\varphi }\nabla \varphi } \right)} { d}A + \int\nolimits_{\Delta V} {{{{S}}_\varphi }} { d}V\text{。}$ | (15) |
最后由耦合界面条件得到:
| $\sum\limits_f^{{N_{faces}}} {{\rho _f}{{{u}}_f}{\varphi _f} \cdot {A_f} = \sum {{\Gamma _\varphi }{{\left( {\nabla \varphi } \right)}_n} \cdot {A_f}} } + {{{S}}_\varphi }V{\text{。}}$ | (16) |
式中:
2)流场的求解方法
本文选用了SIMPLEC算法。该方法考虑了SIMPLE算法中省略掉的速度修正方程中的
3)流场与结构耦合方程
流体方程表示为
| ${{F}}\left[ {{X}} \right] \equiv \left[ {\begin{array}{*{20}{c}} {{{{F}}_f}\left[ {{{{X}}_f},{{\underline {{d}} }_s}\left( {{{{X}}_s}} \right)} \right]} \\ {{{{F}}_s}\left[ {{{{X}}_s},{{{\tau }}_f}\left( {{{{X}}_f}} \right)} \right]} \end{array}} \right] = 0\text{。}$ | (17) |
式中:
自主设计模型结构,自主设计试验装置。通过布置在楔形体结构内的传感器,全程实时监测楔形体结构的下落的压力变化,为研究楔形体结构物入水砰击问题的模型试验方法提供补充和改进,也为该问题的数值模拟方法进行验证。
2.2 试验模型为研究结构入水砰击过程中的砰击压力,结构模型为铝制模型。模型如图2所示。
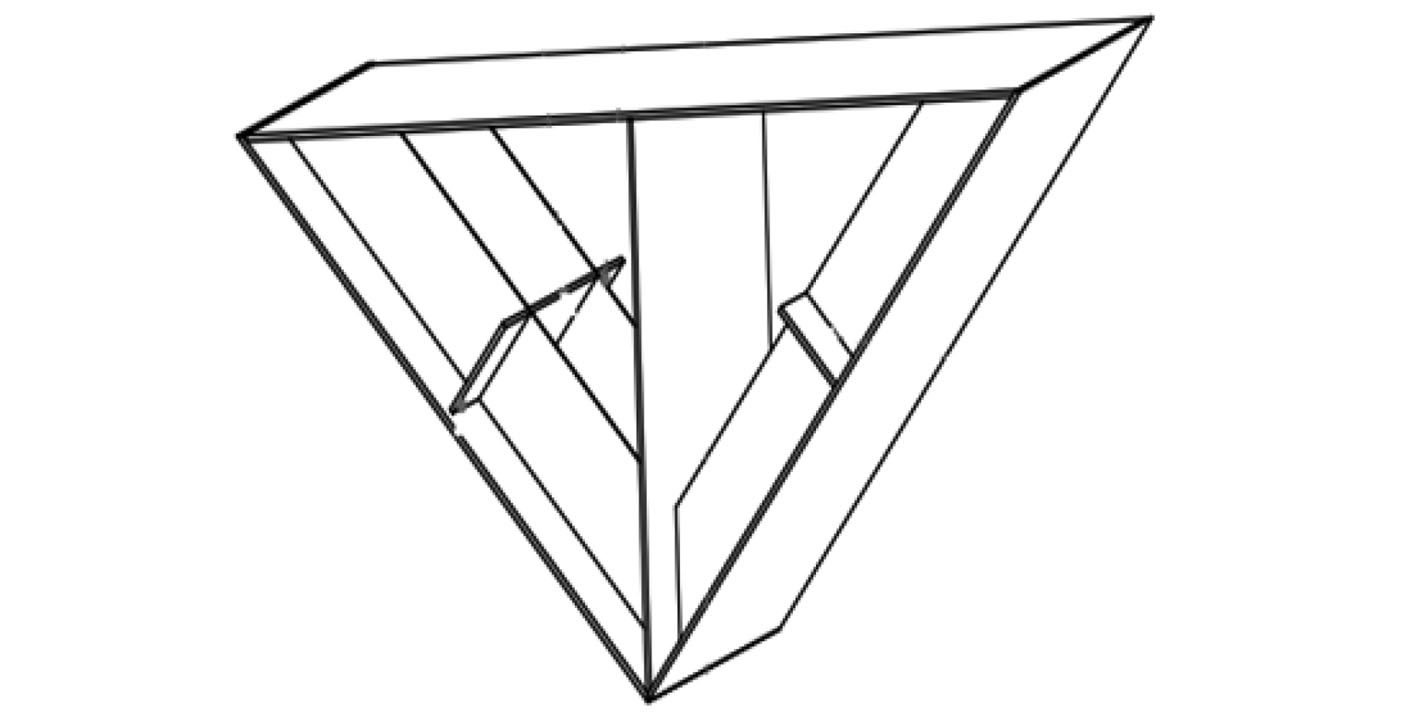
|
图 2 模型正视图 Fig. 2 Model front view |

|
图 3 模型成品图 Fig. 3 Figure of finished mode |
图3是模型成品图,在图3中,为保证传感器的引线能够顺利牵出,在楔形体顶部开一个孔。左右2个开孔,是为了保证楔形体重心仍位于结构中心处。在图5中,考虑到楔形体水密性,并为了保护传感器,在楔形体左右两端用有机玻璃进行密封。模型的主要参数如下:
楔形体主尺度为:1 m×1 m×0.5 m,肋骨2道,纵骨3道(其中1道主龙骨)。
楔形体底升角:45°。
楔形体厚度:4 mm。
2.3 测点布置该试验中的模型是轴对称结构,因此只布置一边测点即可。如图4所示,其中图4(a)为测点示意图,图4(b)表示测点在模型中的真实位置。
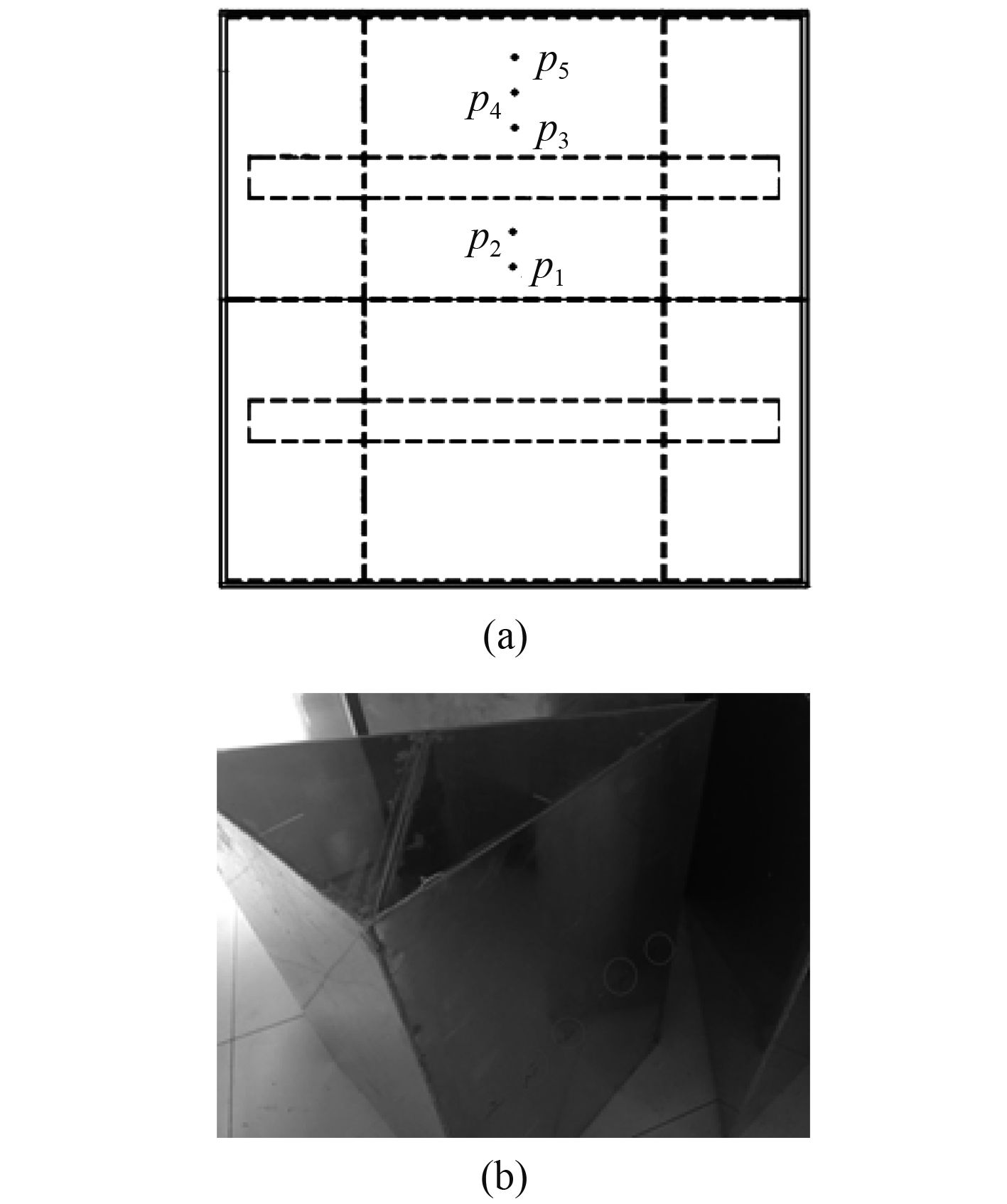
|
图 4 测点布置图 Fig. 4 Measuring point layout |
该实验中总共布置了5个测试点,全部位于楔形体中垂面上,P1距顶部10 cm,随后每2个点之间间距10 cm,考虑到中间加强筋结构,所以P2和P3之间间隔20 cm。
2.4 试验仪器试验仪器包括高灵敏压力传感器、数据信号采集器、计算机、相关仪器电源和导线等。
压力传感器:若干个,量程为–10 kPa~2 MPa。该传感器要满足可以遇水的需求。
信号采集器:1台,用来采集分析系统测量到的结构入水瞬间的砰击压力值。
计算机:1台,用来与信号采集器连接,接收与存储信号采集器的数据。
该试验的采集工作由以上仪器配合完成,压力传感器测量得到结构入水的砰击压力值,后经数据信号采集器接收与储存,最后通过计算机读取。
实验开始前,先将压力传感器进行标定。
2.5 试验装置和试验方案试验水池的尺寸为5 m×2.5 m×3 m。砰击试验塔架的高度为5m,塔架的横梁中端固定一小型起重机。试验中采用电动葫芦和手动脱钩相结合的方式,并在横梁上润滑油,目的是为了尽量减少由起吊装置造成的速度损失。为了减少砰击的离散性,将人为因素降到最低,减小偶然误差对测量结果的影响,每组试验都进行5次重复试验,2次试验之间大约间隔25 min。与此同时,等待水面重新平静,模型充分干燥以及准备下一次的入水试验。图5为模型入水装置示意图。
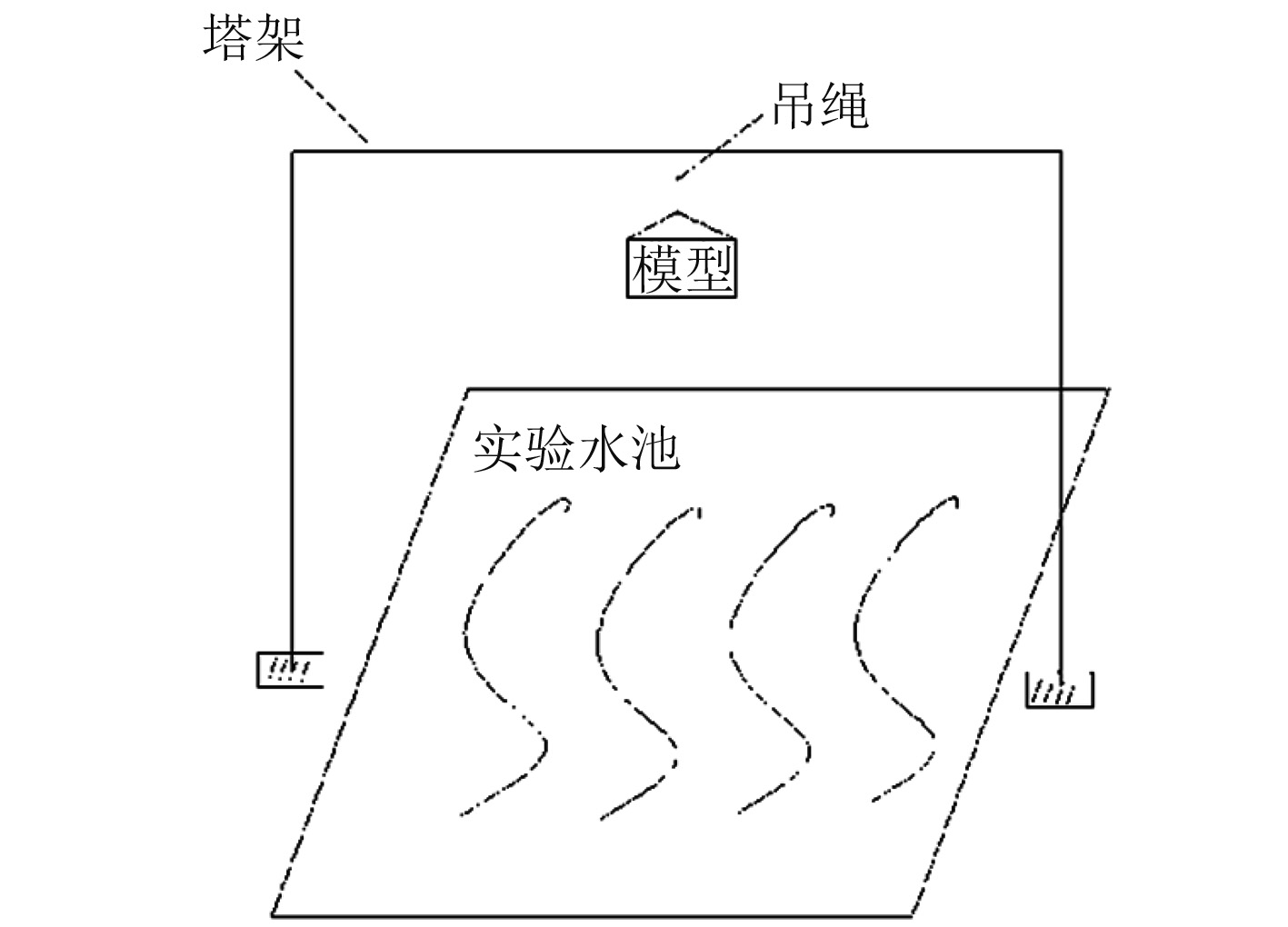
|
图 5 模型入水装置示意图 Fig. 5 Schematic diagram of the model into water |
试验开始时,用电动葫芦将模型拉升至指定高度,然后剪断吊绳使其自由下落。
2.6 实验过程及结果分析本次试验主要是模拟结构物自由落体的入水砰击试验。实验开始时,首先将模型吊于空中悬臂梁上,然后让结构在距离自由液面0.5 m,0.8 m和1 m的高度自由下落。
|
|
表 1 模型入水试验工况表 Tab.1 Model test conditions into the water |
表1为模型入水试验工况表。每次试验开始时,先将各个测试仪器归零,移动起重机,将模型提升到所在工况的高度,然后用剪刀剪断吊绳,让模型自由落下。模型入水过程中,底部首先与水面发生碰撞,溅射出来的水花沿着中部向两边扩散,此时,数据采集仪器会自动将压力传感器的电压信号历程记录下来。每一次试验结束后,将模型重新提升至下一个目标高度,等待水面平静后进行下一次试验。

|
图 6 模型落水过程 Fig. 6 Model drowning process |
由图6的模型落水过程图可以发现,模型落入水中后,在其两侧激起水花。随着下落高度的增加,水花成喷射状。
|
|
表 2 模型中心处各点的砰击压力峰值试验值 Tab.2 The test slamming peak of each pointat the center of the model |
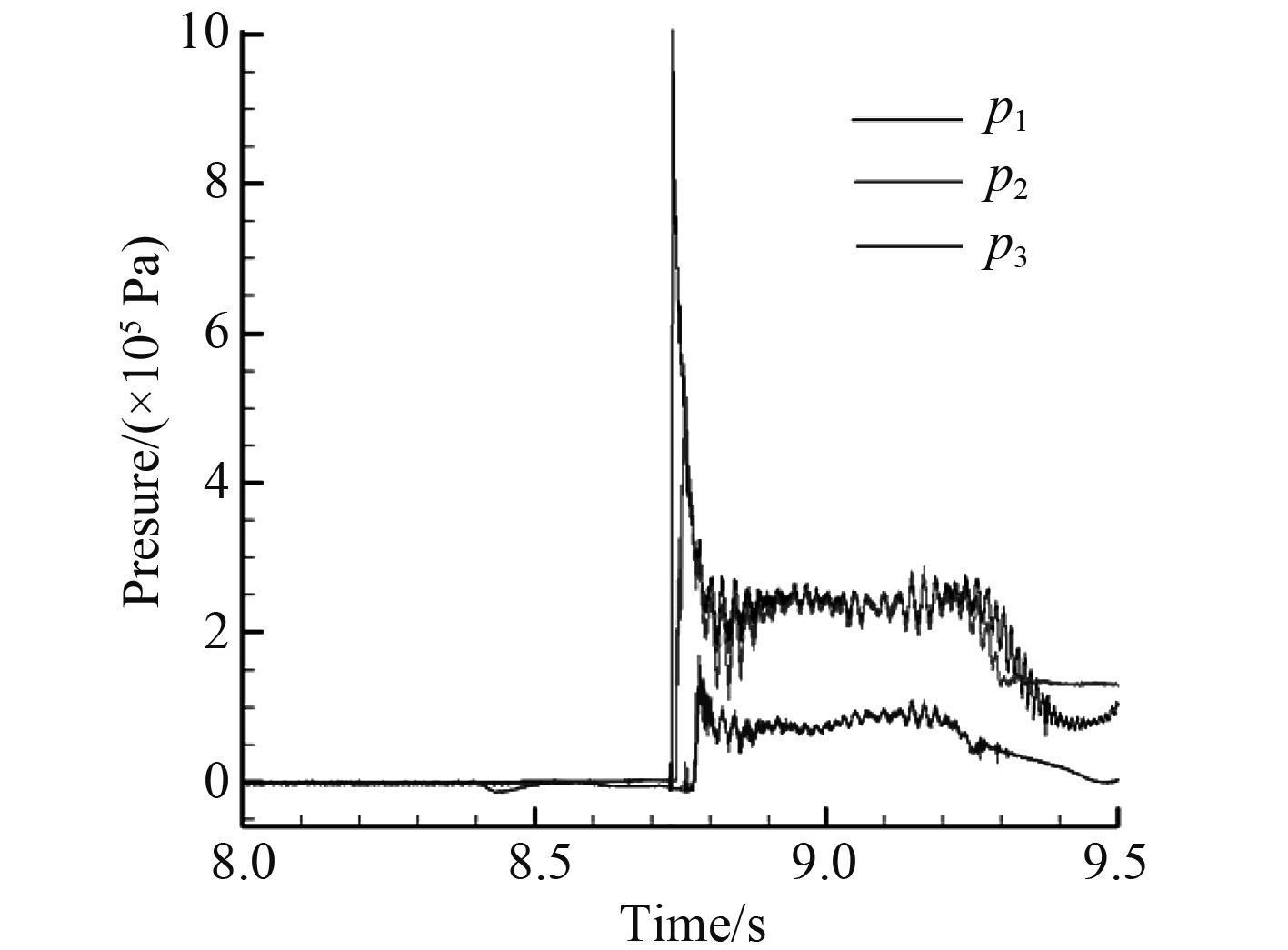
|
图 7 0.5 m高度各点落水砰击压力时间历程图 Fig. 7 The pressure time history diagram of each pointfrom 0.5 m height |
表2表示不同高度下有压力传感器测得的在模型中心处各点的砰击压力峰值。图7和图8分别表示0.5 m和1 m高度各点落水砰击压力历程图。由图表可知,随着下落高度的增加,即砰击入水速度的增大,砰击压力峰值逐渐增大。在楔形体下落过程中,越靠近楔形体底部的点越早接触水面,得到的砰击压力值也越大。由于测点布置时,未充分考虑浮力与重力的关系,模型落水瞬间,水流未来得及冲击到P5点时,浮力已经大于重力,因而P5点未有监测值。
|
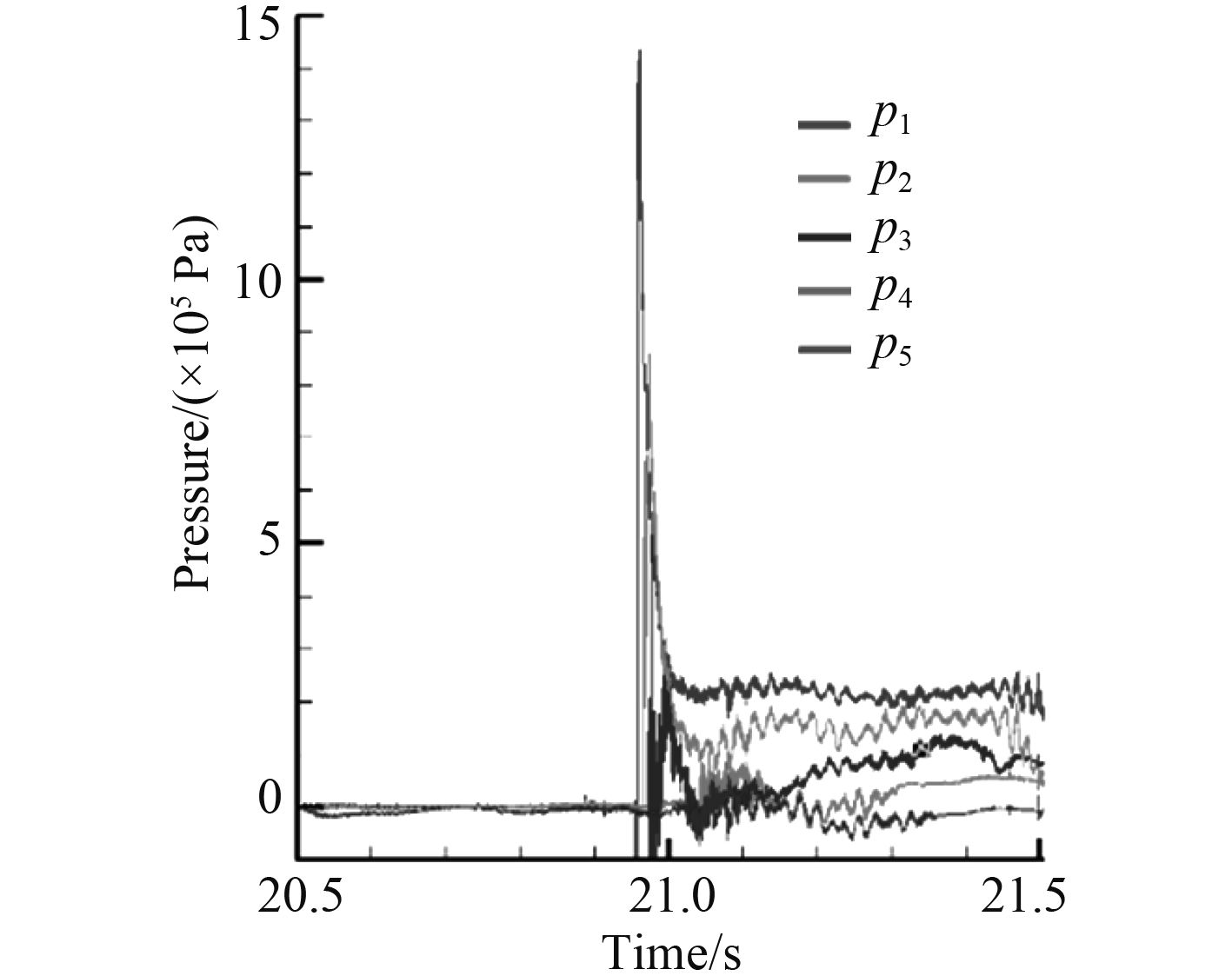
图 8 1 m高度各点落水砰击压力时间历程图 Fig. 8 The pressure time history diagram of each pointfrom 1 m height |
综上所述,随着下落高度的增加,入水砰击速度的增大,砰击压力峰值逐渐增大;砰击发生时,即底部刚接触水面的时候,模型的砰击压力迅速增大到峰值,因而越靠近底部受到的砰击压力也越大,随着入水深度地增加,砰击压力逐渐减小,直至水面平静。
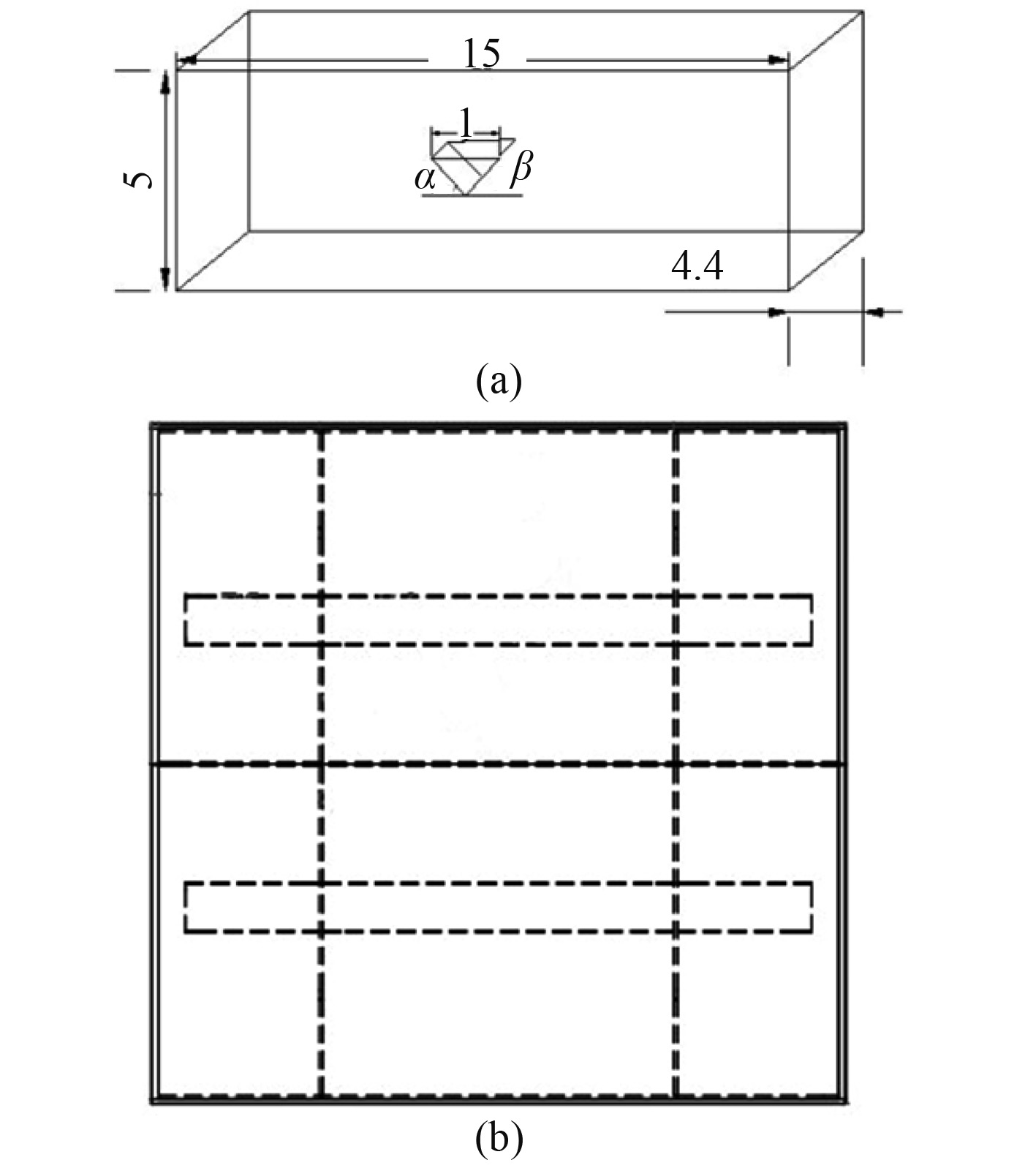
3 三维柔性楔形体入水 3.1 几何建模及网格划分本节研究的三维楔形体结构如图9所示,图9(a)表示计算域,图9(b)表示三维对称楔形体平面图。其中对称楔形的底边长为1 m,高度1 m,α=β=45°。计算域尺寸为:高5 m,长15 m,宽度4.4 m,基本满足不反射边界条件。此时楔形体结构完全按照试验模型来模拟,即与上述刚性楔形体模型不同的是,楔形体主体有2道肋骨,3道纵骨。
|
图 9 计算域和结构平面图 Fig. 9 The sketch diagram of computational domain and structure plan |
与模拟三维刚性楔形体入水近似,对液面附近网格进行加密。网格单元总数为102 453。采用六面体网格能够减少网格数量,并且不需要进行网格重构,极大地减少了计算量。楔形体结构全部采用四面体网格划分。网格划分如图10所示。

|
图 10 网格划分 Fig. 10 Meshing |
本节选用3D压力基求解器,流动为非定常流,考虑重力加速度大小为9.81 m/s2。物理求解模型选择VOF多相流模型,同时打开Implicit Body Force,以提高解的稳定性。选择标准壁面函数(Standard Wall Functions)。边界条件作如下设置,将整个区域的最上面设置成压力出口,其他边界均设置为无滑移壁面边界。在这里采用弹簧光滑模型和网格重构模型,同时开启6DOF模型。在运动属性中,将楔形体定义为刚体(rigid body),楔形体的质量及转动惯量在udf中设置。
3.3 弹性体入水的响应分析本节研究三维弹性对称楔形体距自由液面1 m高度下落的情况。
|
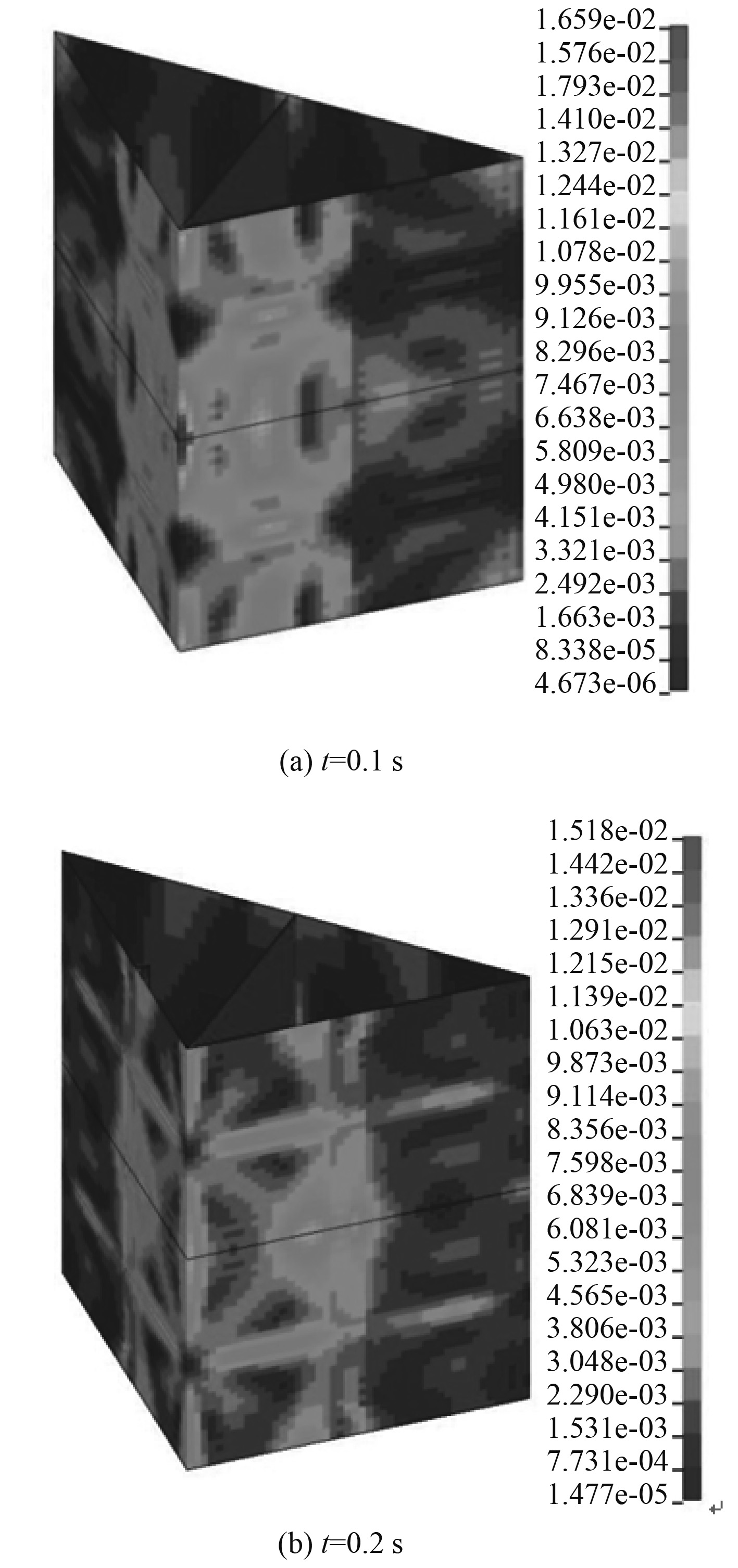
图 11 楔形体不同时刻的压力分布云图(h=1 m) Fig. 11 Contours of surface pressure of wedge in different time (h=1 m) |
图11是非对称楔形体从1 m高度自由落下不同时刻楔形体表面压力分布云图。从压力分布云图可以看出,在入水过程中,楔形体的高压区主要分布在楔形体头部,随着楔形体下落深度的增加,高压波逐渐传播出去,楔形体表面的压力趋于平稳。

|
图 12 楔形体不同时刻的等效应力云图(h=1 m) Fig. 12 Contours of von mises stress of wedge in different time (h=1 m) |
从图12楔形体不同时刻的等效应力云图中可以看出,应力最大区域依然是楔形体头部区域,在t=0.1 s时刻,达到了15 520 Pa。随着楔形体下落深度的增加,应力在楔形体表面逐渐趋于稳定。
图13是不同时刻流体的速度云图。从图中可以看出,在楔形体下落过程中,流体的速度增大,在t=0.5 s时速度达到了10.06 m/s,最大速度在楔形体底端两侧顶角处。随着楔形体下落深度的增加,流体速度逐渐减小。在t=0.2 s时,速度又增大,此时是因为楔形体的下落造成了流体飞溅,飞溅的速度较楔形体下落时流体的速度大,最大速度处仍在楔形体底端两侧顶角处。
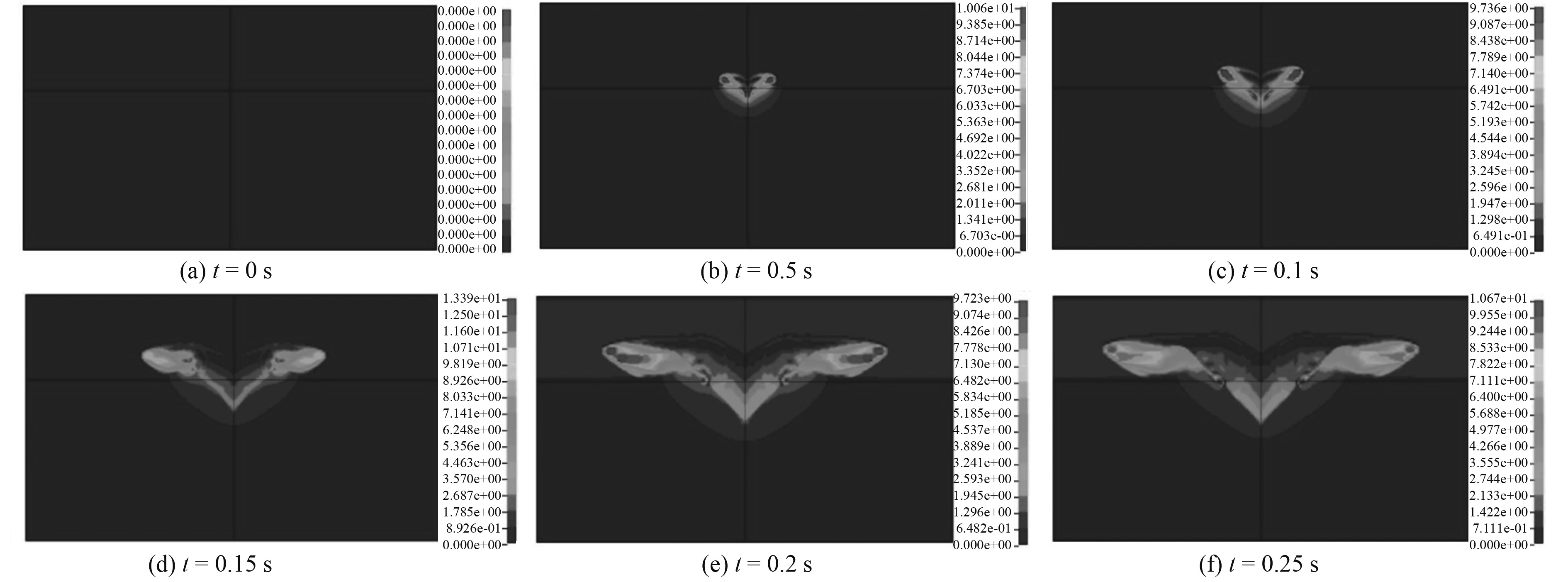
|
图 13 流体不同时刻的速度云图(h=1 m) Fig. 13 Contours of velocity of fluid in different time (h=1 m) |
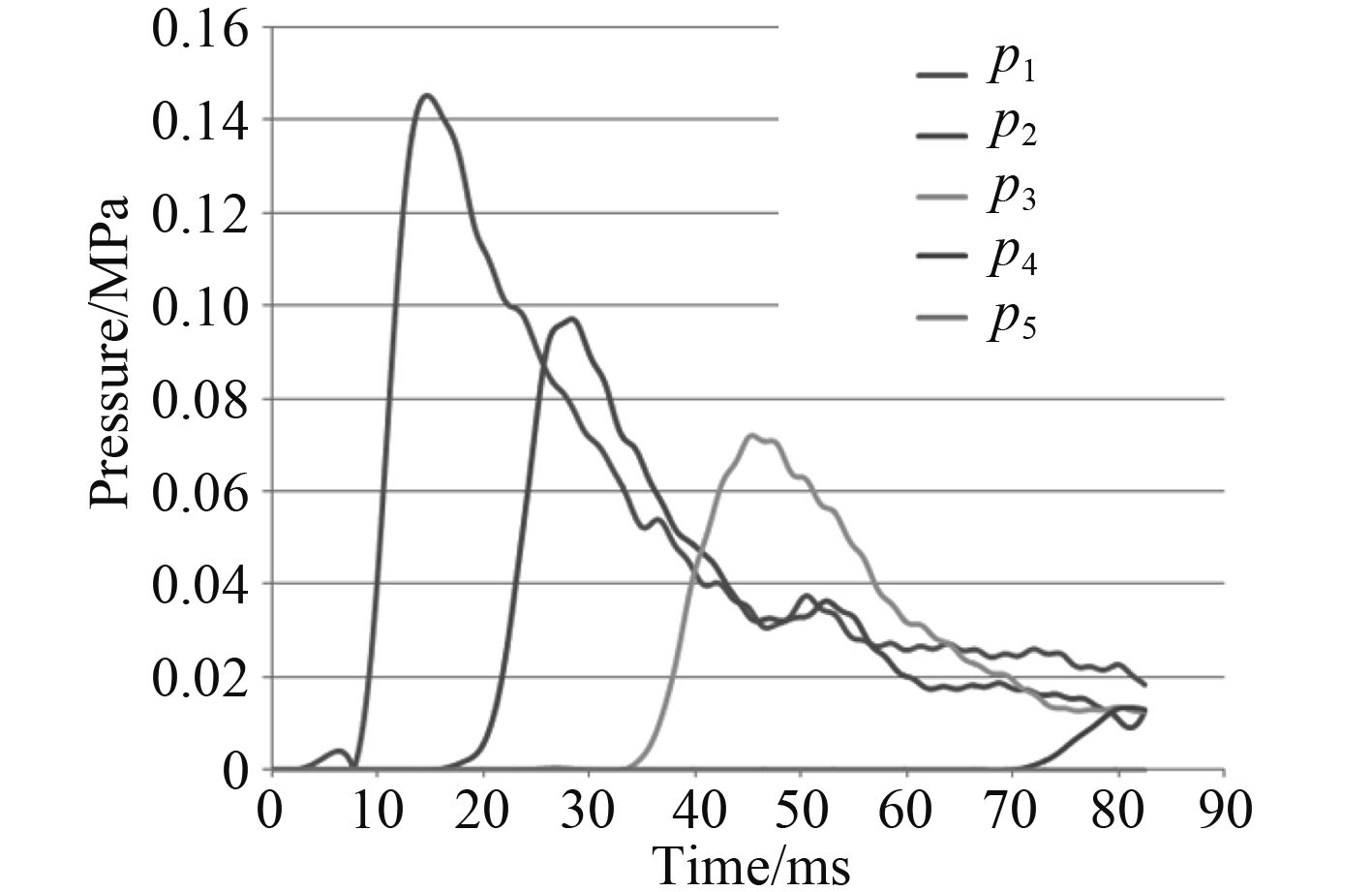
为更全面验证上述试验的可行性与有效性,本文在柔性楔形体入水的计算中加入了5个测点,这5个测点位置与试验模型的测点位置相匹配,如图7(a)所示。
|
图 14 测点的砰击压力图 Fig. 14 Slamming pressure peak of test points |
图14是测点的砰击压力图。从图中可以看出,最大的砰击压力为P1点,依次减小,P5因位置原因,未得到水流的冲击,因而没有数据,与试验中测点的趋势相符。
|
|
表 3 数值模拟测点试验值和模型试验测点砰击压力峰值对比 Tab.3 Contrast of slamming pressure peak between numerical simulation and model test points |
表3是数值模拟测点试验值和模型试验测点砰击压力峰值对比。以上4组对比数据中,误差范围在10%以内,排除空气阻力等,本次数值模拟结果基本符合实际。
从表3中4组对比数据中,可以看出考虑弹性体的数值模拟的砰击压力值均大于模型实验得到的砰击压力值,这是由于在考虑弹性体的数值模拟中,默认选择了先进行耦合计算,然后考虑固体的弹性形变,但是在实际试验中,耦合与形变同时发生。固体变形,相当于一个卸力的效果,使压力有效降低,考虑弹性体计算短暂的忽略了这个变形,所以数值稍微高一点。
4 结 语本文自行设计了楔形体入水试验,以便验证改数值模拟方法的正确性。自行设计了试验模型和试验装置,完成对试验模型的加工制造,调试完整个水池试验系统后进行了不同高度的入水砰击试验。试验完整记录了模型入水砰击的过程,得到了模型在不同高度下入水砰击过程中的砰击压力。最后,进行三维弹性体入水的数值模拟,数值模拟模型完全参照试验模型,得到了砰击压力云图、等效应力云图以及流体的速度云图,对比分析了弹性体测点与试验中测点的砰击压力,验证了该数值模拟方法的可行性与有效性。
| [1] | OCHI M K, MOTTER L E. Prediction of slamming characteristics and hull responses for ship design[J]. Transactions SNAME, 1973, Vol. 81, 144–177. |
| [2] | PUKHNACHOV V V. Linear approximation in the problem on a blunt body entry in water [J]. Din. Sploshnoi Sredy. 1979, 38: 143–150. https://link.springer.com/article/10.1007/BF01054755 |
| [3] | TAKAGI K, 1994, Influence of e1asticity on hydrodynamic impact problem[J], J. Kansai Soc. N. A., Japan, Sep. 1994, No. 222, pp. 97–106. |
| [4] | A. EL MALKI ALAOUI, A. NÊME, A. TASSIN, et al. Experimental study of coefficients during vertical water entry of axisymmetric rigid shapes at constant speeds[J]. Applied Ocean Research. 2012, 37: 183–197. |
| [5] | SUN S Y, SUN S L, WU G X. Oblique water entry of a wedge into waves with gravity effect[J]. Jounal of Fluids and structures, 2015, 52: 49–64 (IF, 2.021). |
| [6] | 张伟, 郭子涛, 肖新科, 等. 弹体高速入水特性实验研究[J]. 爆炸与冲击. 2011, 31(6): 579–584. http://www.cqvip.com/QK/94778X/201106/40751656.html |
| [7] | 何春涛, 王聪, 魏英杰, 等. 圆柱体垂直入水空泡形态试验[J]. 北京航空航天大学学报, 2012(11): 1542–1546. http://www.oalib.com/references/16438451 |
| [8] | 杨衡, 张阿漫, 龚小超, 等. 不同头型弹体低速入水空泡试验研究[J]. 哈尔滨工程大学学报, 2014, 09: 1060–1066. |
| [9] | 张岳青, 徐绯, 金思雅, 等. 楔形体入水冲击响应的试验研究及应用[J]. 机械强度, 2015, 37(2): 226–231. http://www.cnki.com.cn/Article/CJFDTotal-JXQD201502007.htm |
| [10] | 杨衡, 孙龙泉, 龚小超, 等. 弹性结构入水砰击载荷特性三维数值模拟研究[J]. 振动与冲击, 2014, 33 (19): 28–33. http://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201419006.htm |
| [11] | 张伟伟, 金先龙, 刘涛. 正交异性复合材料储液容器入水过程数值分析[J]. 计算力学学报, 2015, 32(15): 633–638, 698. |
| [12] | SUN P, MING F, ZHANG A. Numerical simulation of interactions between free surface and rigid body using a robust SPH method[J]. Ocean Engineering, 2015, 98: 32–49. |
| [13] | 张智. 基于CFD技术的三维楔形体入水砰击试验和数值预报研究[D]. 天津: 天津大学. 2013. |
 2018, Vol. 40
2018, Vol. 40
