舰船抗冲击性能研究首先要解决作用在船体结构上的爆炸冲击载荷,爆炸冲击载荷的准确描述是保证舰船爆炸冲击动响应分析精度的基础。爆炸冲击载荷由设备安装处船体基础的运动引起。爆炸冲击载荷是船体结构动特性、隔振系统频率和爆炸冲击强度三者的函数。爆炸冲击强度是与爆炸冲击环境有关的。在一定深度下实施的水中爆炸,对于舰船有2种效应:一种是水中冲击波;另一种是爆炸产物在水中形成膨胀收缩气泡的脉动压力对舰船产生的冲荡(Whipping)或称气泡脉动[1 – 2]。前者引起继续时间短而加速度值很高的运动,容易造成舰船结构局部的严重破损;而后者容易引起船体低频但幅值较大的振荡,对低频结构和低频安装的设备有显著的影响[3]。由于气泡脉动对舰船的影响相对较小,所以本文仅研究水下非接触爆炸冲击波作用下舰船的抗冲击性能。本文通过运用MSC.Dytran建立舰船、水域和炸药的有限元模型,并利用Dytran软件进行有限元分析,准确模拟出了中远场爆炸冲击波在水中的传播过程以及舰船结构的动态响应,为舰船的抗冲击性能分析提供了前提条件,为深入开展舰船抗冲击研究奠定了基础。
1 球形炸药水下爆炸冲击载荷的理论分析本文采用JWL炸药状态方程来模拟炸药的爆炸过程[4],TNT的状态方程采用标准的JWL状态方程。JWL状态方程描述爆压P和单位体积内能e及爆炸产物体积V之间的关系,即
| $P = A\left( {1 - \frac{\omega }{{{R_1}V}}} \right){e^{ - {R_1}V}} + B\left( {1 - \frac{\omega }{{{R_2}V}}} \right){e^{ - {R_2}V}} + \omega \eta {\rho _0}e{\text{。}}$ | (1) |
式中:A=373.77 GPa;B=3.747 1 GPa;R1=4.15;R2=0.9;ω=0.35;η=ρ/ρ0,ρ0=1.63 g/cm3,ρ为爆炸产物密度;TNT的e=6.0 GJ/m3。爆速为6 930 m/s,爆压为21 GPa。
水下爆炸冲击波在深水中传播时会基本保持球对称波峰面。而在无限水域情况下,针对一定的炸药当量,水下爆炸冲击波阵面的压力峰值随距离之间的规律可以采用经典的库尔公式计算:
| ${p_m} = {\left( {\frac{{{W^{\frac{1}{3}}}}}{R}} \right)^\alpha } \cdot k{\text{。}}$ | (2) |
式中:Pm为压力峰值,Pa;W为炸药当量,kg;R为距爆心距离。对于TNT炸药而言,α与k分别为1.13和5.33E7。对于其他炸药,可根据能量等效原理来估算冲击波的压力峰值。
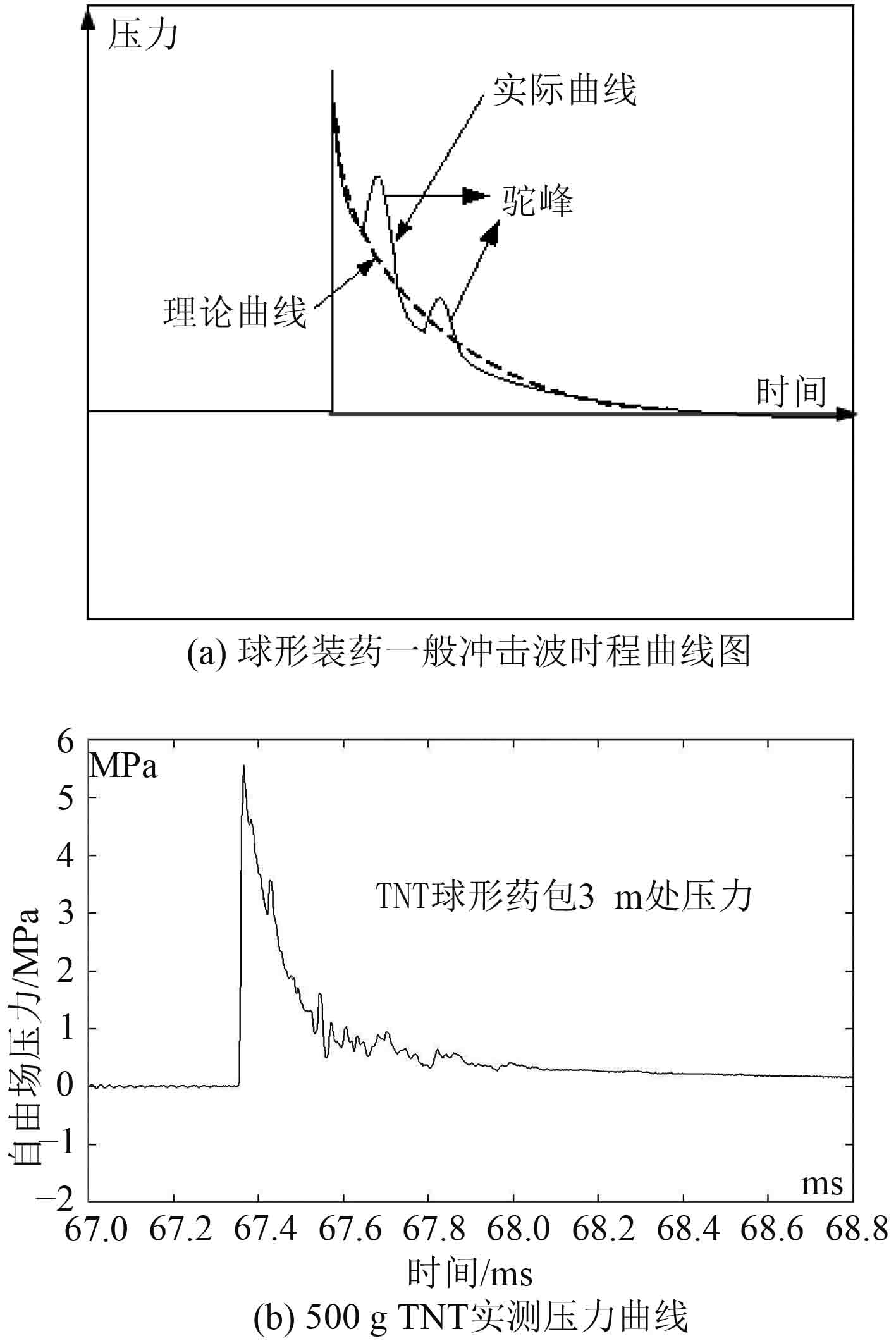
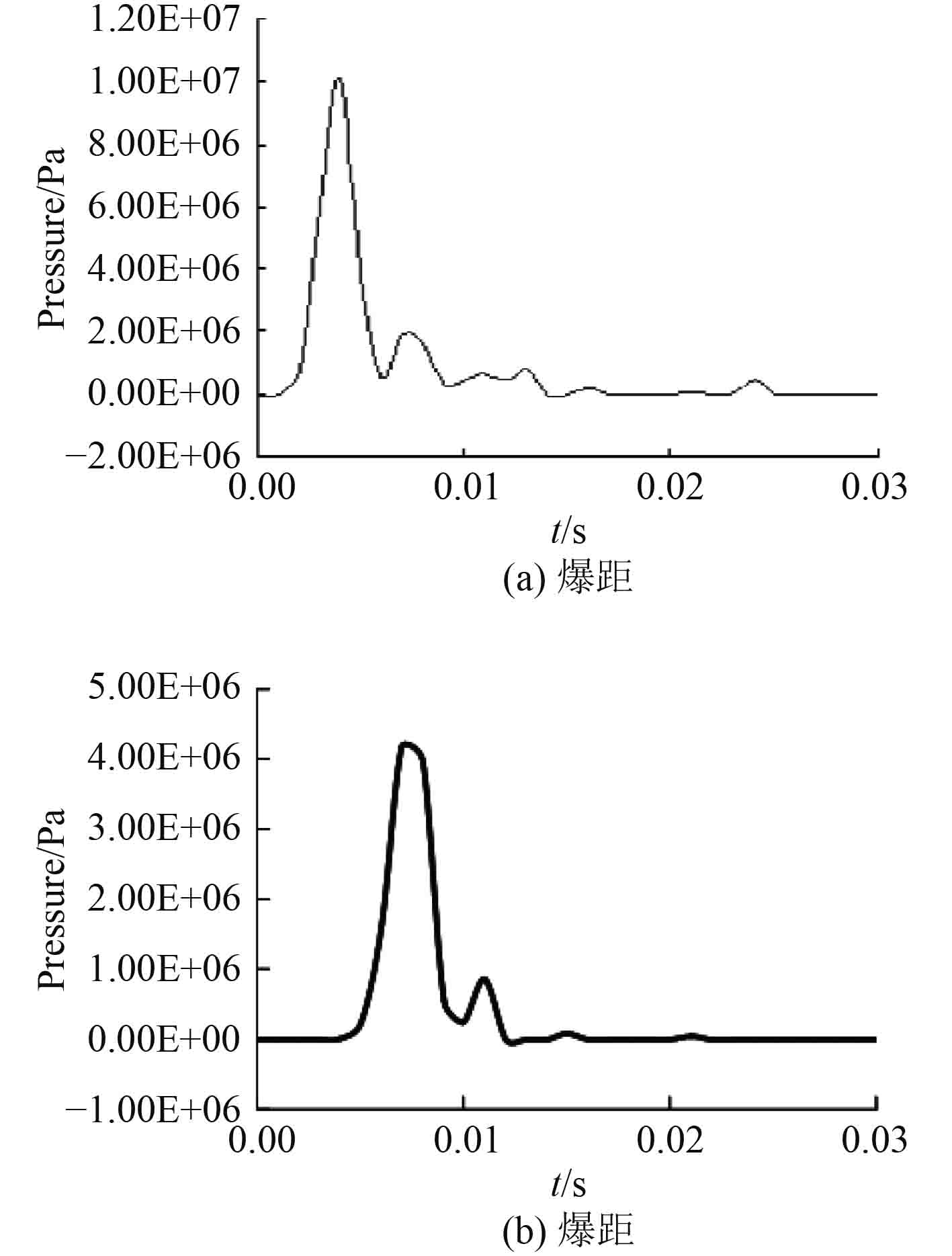
球形炸药在中心起爆时,所产生的冲击波压力波形不会是一条平滑曲线,而会产生数个振荡波峰,如图1(a)所示。因为炸药在水下爆炸以后,水下爆炸冲击波会向外辐射,反射稀疏波则向药球中心集中,多个方向的反射稀疏波聚集后就会产生压缩波,叠加后又形成了爆炸冲击波,此爆炸冲击波向外辐射后追赶第1个冲击波(First shock),再与它叠加后又会产生第2次波峰(Second shock),在一些情况下还可能会产生多次波峰(Third shock)。图1(b)是500 g TNT球形装药在水下10 m爆炸时在距爆源3 m处测量的压力波形,图中出现了多个波峰。
|
图 1 球形装药冲击波时程曲线图 Fig. 1 Time-step curves of Spherical charge shock wave |
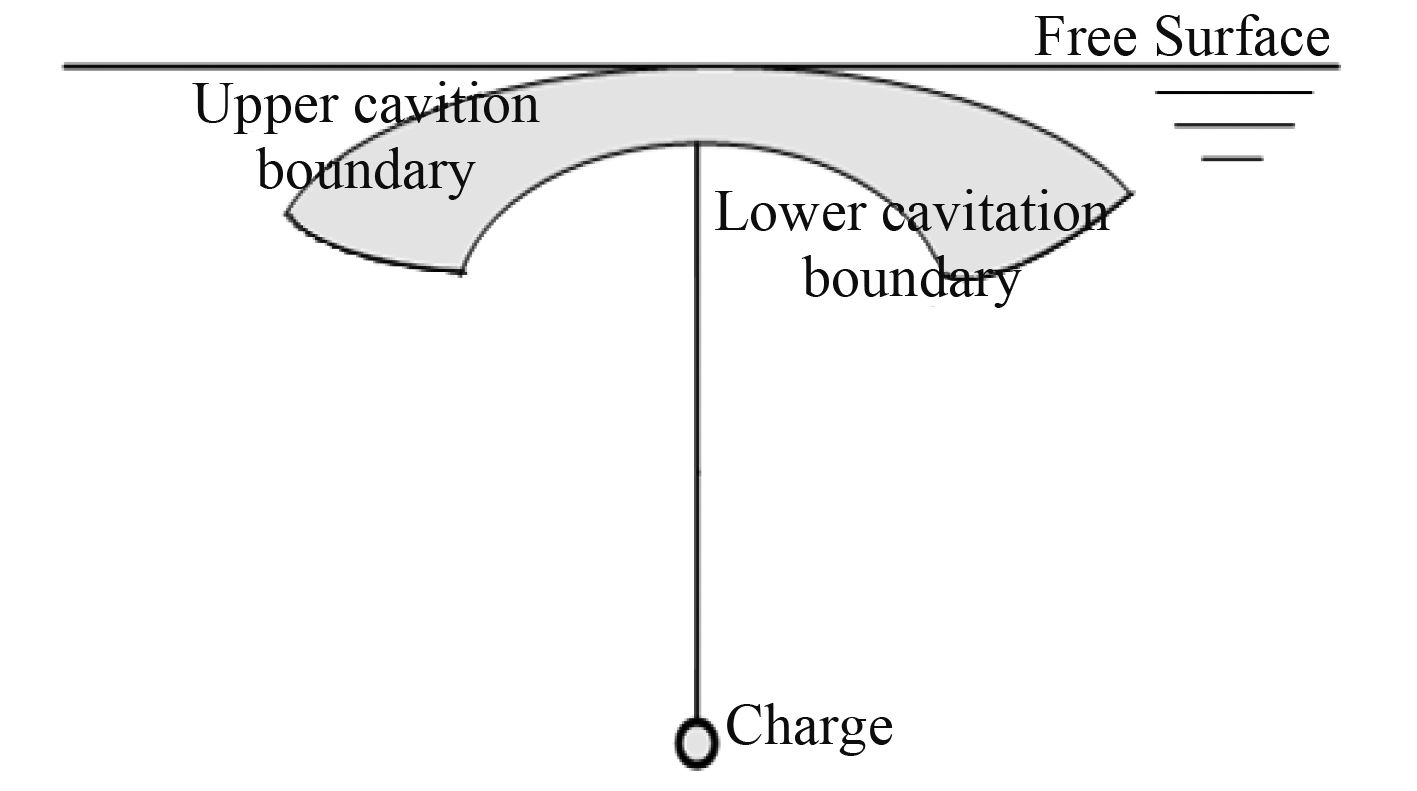
水下爆炸产生的空化效应发生在爆炸冲击波作用的初期,原因是水下爆炸初始冲击波打到结构边界或者自由边界以后都会发生反射作用,而反射冲击波与入射冲击波叠加起来以后就会产生负压区[5],由于水中往往含有部分杂质使得水能承受的张力大大降低(一般认为约为0.5 MPa左右),从而产生空化现象。区域空化如图2所示,整个区域由上下边界构成。
|
图 2 水下爆炸产生的空化区域 Fig. 2 Cavitation area produced by underwater explosion |
|
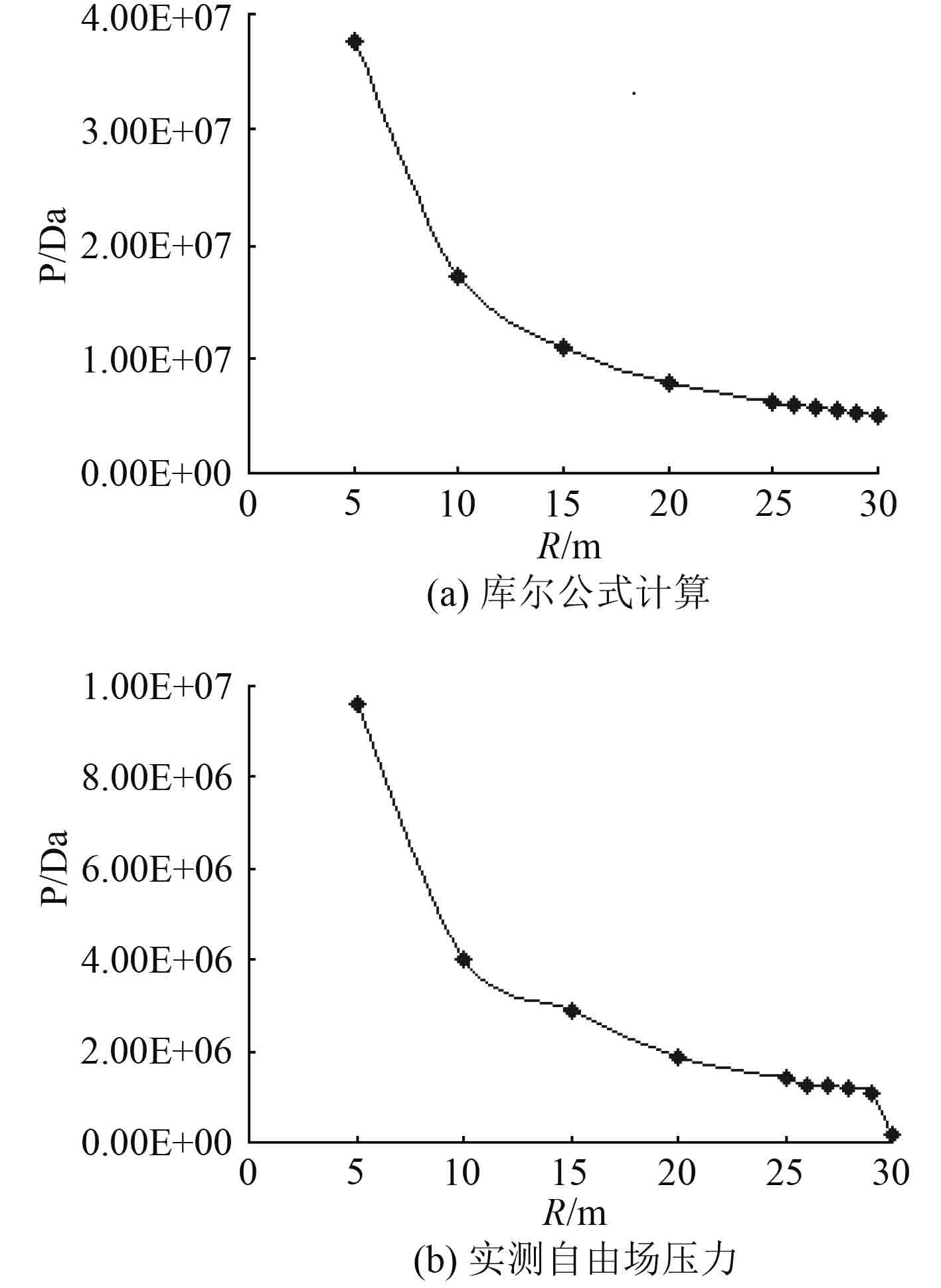
图 3 冲击波压力峰值库尔公式计算结果与实测自由场压力的对比 Fig. 3 The comparison between the cole formula computing results of shock wave pressure and the measured free field pressure |
图3为50 kg TNT炸药爆炸以后实测自由场压力峰值与库尔公式计算结果的对比。从图3中可以看出当爆距接近30 m时,空化区的压力峰值明显低于规则区的,空化效应减弱了水下爆炸冲击波的作用力,导致冲击波压力在水面附近迅速衰减,这即为文献中常提及的空化效应或水面截断效应[6],通过本文的数值模拟就可以清晰地捕捉到这个不易观察到的现象。
2 球形炸药水下爆炸冲击载荷的数值模拟 2.1 舰船、水域和炸药有限元模型的建立 2.1.1 水域有限元模型的建模方法舰船及舰载设备受到的水下爆炸冲击一般都发生在无限水域,但在数值仿真过程中不可能也没有必要来模拟这种无限水域。Song-Gab Lee等采用LS-DYNA软件针对水爆作用对舰船动态响应数值模拟的流场模型开展了较为深入的研究,研究结果认为流场区域的尺寸在船宽方向取约3倍的船体型宽,在船长方向略大于船长即可,深度方向可取爆炸深度,并将流场底面边界设定为刚性壁以模拟无限水域[7]。文献[7]中所研究的为舰艇垂直迎爆的工况,而本文则在舰艇舷侧迎爆时的计算工况下,也借鉴了它的研究成果,在流场深度方向取爆距R,底面边界设为流出边界以模拟无限水深,上边界设为流出边界并考虑一个大气压;同时水域四周的边界视炸药位置而定,如炸药位于边界上就设为刚性壁以模拟完整的炸药在无限水域中爆炸,否则设为流出边界。
水域单元会采用六面体单元,因为主要为考察船中结构的动态响应,同时也为了节省计算周期,会在水域单元的中间位置采用0.5 m单元尺寸的较细网格,而在其他的部位则会采用较粗的网格,网格属性用MM/HYDRO(PEULER1)卡定义。
常规的水下爆炸实验中,水下爆炸产生的冲击波压力往往小于2.5×109 Pa,其属中等强度的爆炸冲击波。此时水下爆炸冲击波穿过介质后的熵值变化较小,基本可作为等熵过程,水的Tait等熵状态方程为[8]
| $P = B\left[ {{{\left( {\frac{\rho }{{{\rho _0}}}} \right)}^n} - 1} \right],$ | (3) |
其中B=3.045×108 Pa,n=7.15。
但是MSC.Dytran程序中用NonlinFluid(DMAT)卡定义水材料时,并无形如式(3)的状态方程。程序中水材料是通过多项式方程来描述的,具体形式如下:
| $p = {a_1}\mu + {a_2}{\mu ^2} + {a_3}{\mu ^3} + ({b_0} + {b_1}\mu + {b_2}{\mu ^2} + {b_3}{\mu ^3}){\rho _0}e{\text{。}}$ | (4) |
式中:μ=ρ/ρ0–1;ρ0为水的初始密度;ρ为材料密度。
式(3)按Taylor公式展开得:
| $p = 2.18 \times {10^9}\mu + 6.69 \times {10^9}{\mu ^2} + 1.15 \times {10^{10}}{\mu ^3}{\text{。}}$ | (5) |
对比式(4)和式(5)可得:a1=2.18×109 Pa,a2=6.69×109 Pa,a3=1.15×1010 Pa;b0=b1=b2=b3=0。水的初始密度ρ0=1 000 kg/m3,初始比内能e0=83.950 kJ/kg。
2.1.2 炸药有限元模型的建模方法炸药水下爆炸后,爆轰产物的压力可根据JWL状态方程进行计算。JWL状态方程由美国的3位学者(Jones,Wilkins,Lee)研究得到的,其表达式为本文式(1)中所示。MSC.Dytran中通过JWL Explosive(DMAT)卡定义炸药材料的本构关系,并通过定义DETSPH卡来确定炸药的起爆时间、位置以及爆轰波的传播速度。
2.1.3 舰船有限元模型的建模方法船体有限元建模时,对骨材进行了等效简化,全船采用Lagrangian三节点单元(Tria3)和四节点单元(Quad4)划分,共划分为1 680个三节点单元和86 248个四节点单元,网格属性可通过Default(PSHELL)卡定义。为消除计算中船体结构的刚体位移,对全船进行了有效约束。船体的钢材为高强度船用低碳钢,材料本构模型采用ElasPlas(DMATEP)卡定义,具体参数为:材料密度ρ=7 800 Kg/m3,弹性模量E=2.1×1011 Pa,剪切模量G=81.8 MPa,屈服应力2.35×108 Pa,泊松比0.3,失效应变0.4。
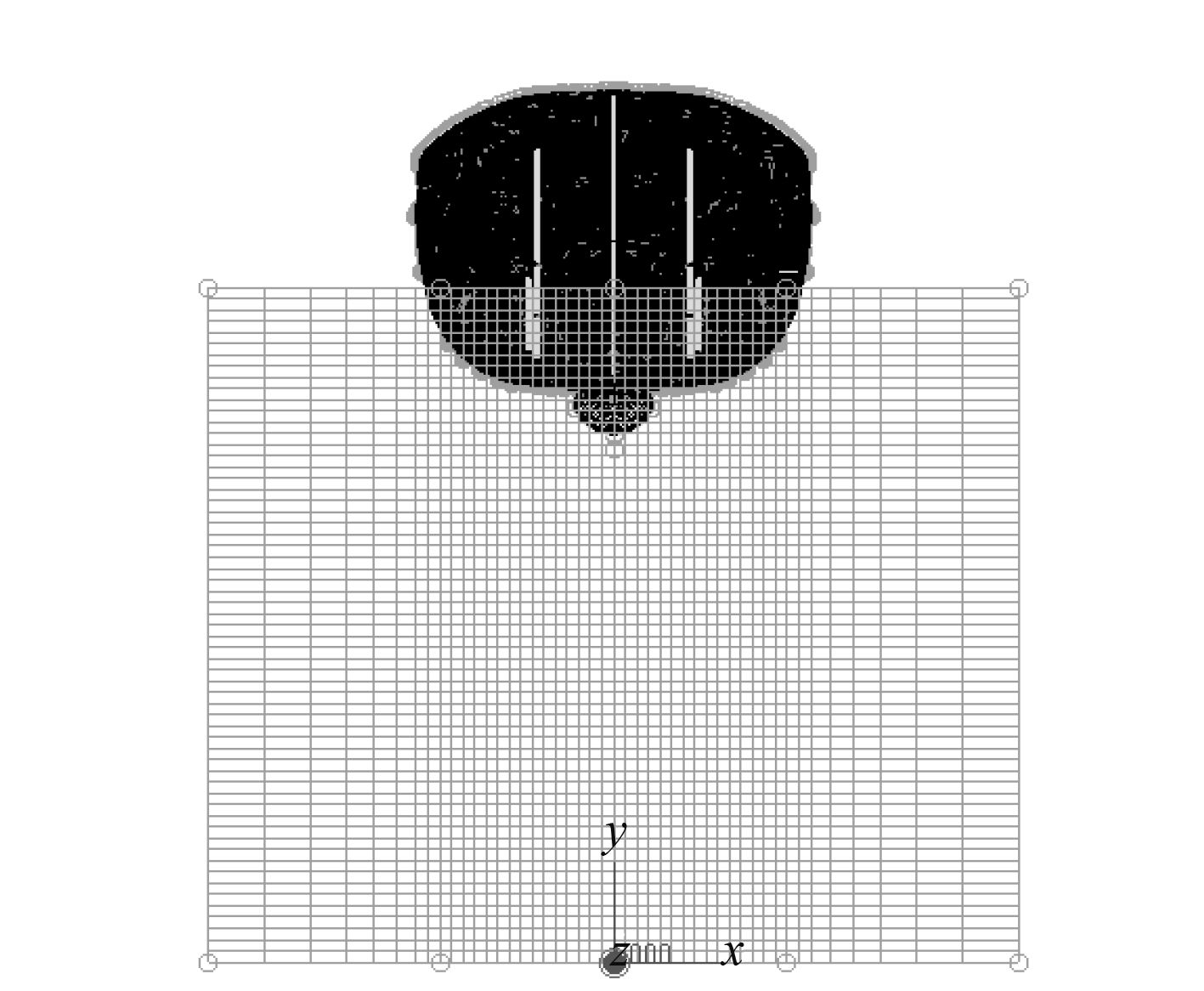
计算时流固耦合算法采用一般耦合算法,炸药水深30 m,当量50 kg TNT,处于中部正龙骨下方。图4给出了舰船、水域和炸药的有限元模型。
|
图 4 舰船、水域和炸药的有限元模型 Fig. 4 Finite element models of warship, water and charge |
|
图 5 水下爆炸后流场中某点的压力时历曲线图 Fig. 5 The pressure of a point in the flow field after underwater explosion |
水下爆炸后流场中某点的压力时历曲线如图5所示。由图可知,水下爆炸产生的冲击波速度和水的声速基本相同。水下爆炸冲击波经过这个点时,它的瞬时压力时程曲线会呈指数衰减,与经典的库尔理论基本保持一致。从数值仿真结果可以看出,距爆炸中心附近的冲击波会产生数个波峰,这应是水下爆炸冲击波产生的剩余能量的扩散所导致,致使周围流场压力发生一次或者数次的迅速上升,波形趋势与图1(b)中的实测数据也非常接近。
|
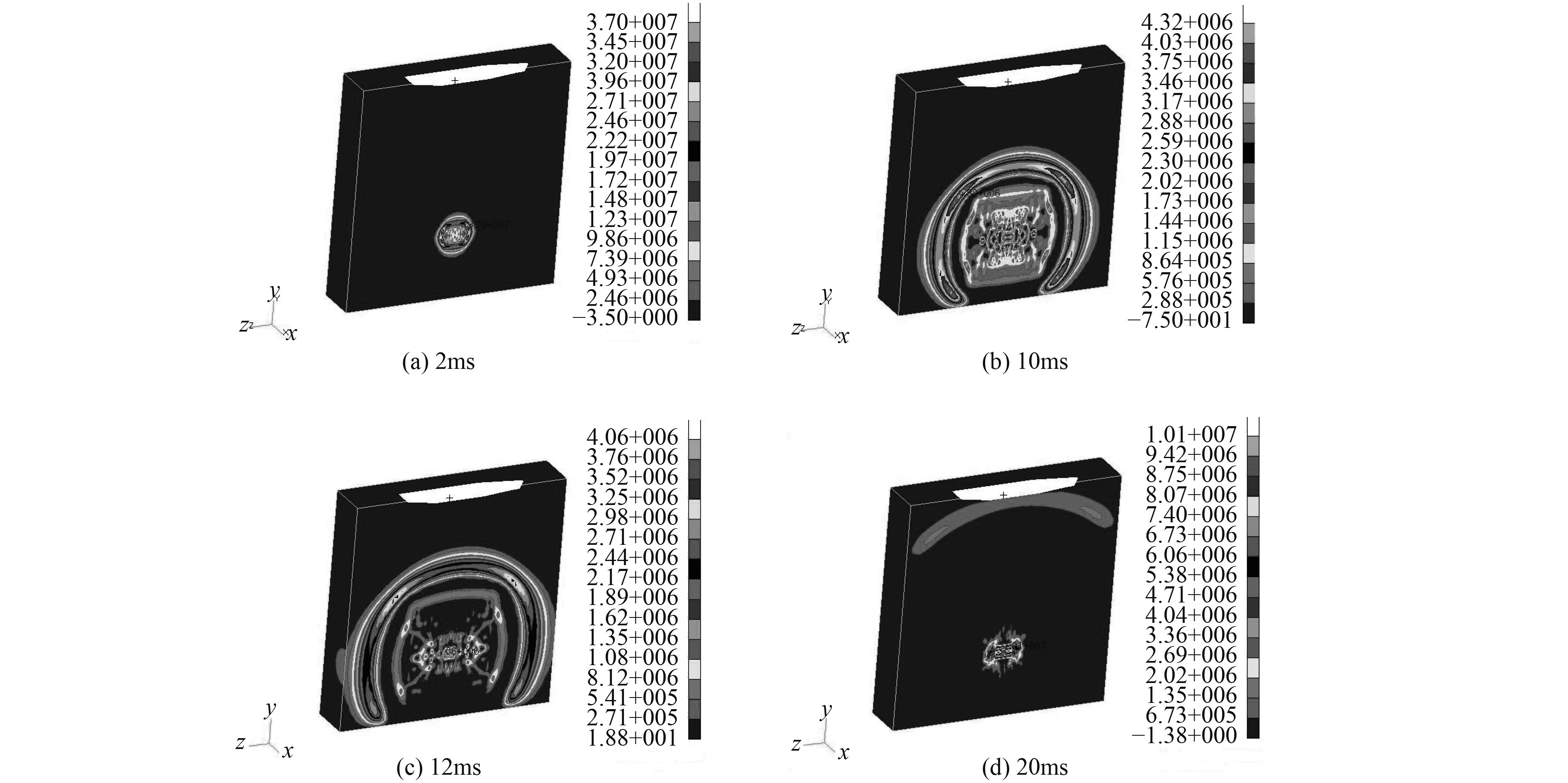
图 6 水下爆炸球形冲击波扩散时历云图 Fig. 6 The spread of cloud map by the spherical shock wave of underwater explosion |
水下爆炸球形冲击波扩散时历云图如图6所示。可以看出,球形炸药在水下爆炸后,冲击波以球面波的形式快速传播,爆炸初始阶段峰面压力非常大,随着冲击波的扩散,在接近船体时已经大幅度衰减。

|
图 7 水下爆炸冲击波作用下舰艇结构应力响应云图(单位:Pa) Fig. 7 The structural stress response of the warship under the action of underwater explosion shock wave |
图7是当量为50 kg TNT,爆距为30 m的球形炸药爆炸后船体受冲击波作用下的应力云图。可以看出,水下非接触爆炸作用后,水中爆炸产生的冲击波是影响舰船冲击响应的主要因素,尤其是冲击波的垂向作用影响更大;冲击载荷主要作用集中在舰底,其所承受的应力要比上层建筑大很多,全船的最大应力就集中在船中的迎爆面位置。水下爆炸产生的冲击波最先作用到舰底,接着冲击振动通过舰船的垂向结构会向上层快速传递,一直传到甲板和上层建筑为止,与此同时垂向结构也会降低冲击振动的强度,所以舰船上层构件所受到的冲击响应会小于舰船底部或舰船舭部,并呈逐步减小的趋势。
3 结 语本文运用通用软件MSC.Dytran建立舰船、水域和炸药的有限元模型,并利用Dytran软件进行有限元分析,准确地模拟出了水下爆炸冲击波在水中的传播过程、空化效应以及整个舰船结构的动态响应,为舰船结构的抗冲击性能分析提供了输入条件,为深入开展舰船抗冲击研究打下了基础。球形炸药在水下爆炸后,爆炸冲击波以球面波的形式传播,冲击波的速度约为水的声速。冲击波经过流场中某点时,该点的瞬时压力与时间的关系呈指数分布,但在水面附近由于流-固耦合面处的空化效应而迅速衰减,与库尔理论基本吻合。爆炸冲击波的垂向作用是船体冲击响应的主要影响因素,冲击载荷主要作用集中在舰底,其所承受的应力要比上层建筑大很多,全船的最大应力就集中在船中的迎爆面位置。水下爆炸产生的冲击波最先作用到舰底,接着冲击振动通过舰船的垂向结构会向上层快速传递,一直传到甲板和上层建筑为止,与此同时垂向结构也会降低冲击振动的强度,所以舰船上层构件所受到的冲击响应会小于舰船底部或舰船舭部,并呈逐步减小的趋势。
| [1] | 陈建平. 二次脉动压力下舰船抗爆性能研究[D]. 哈尔滨: 哈尔滨工程大学. 2000, 3. |
| [2] | 姚熊亮, 陈建平. 水下爆炸二次脉动压力下舰船抗爆性能研究[J]. 中国造船, 2001, 10(2): 48–55. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU200908003040.htm |
| [3] | 姚熊亮, 徐小刚, 张凤香. 流场网格划分对水下爆炸结构响应的影响[J]. 哈尔滨工程大学学报, 2003, 6(3): 238–244. http://d.wanfangdata.com.cn/Periodical_hebgcdxxb200303001.aspx |
| [4] | 顾文彬, 阳天海, 叶序双, 等. 单个装药浅层水中沉底爆炸的数值模拟[J]. 解放军理工大学学报(自然科学版), 2000, 1(7): 51–55. http://d.wanfangdata.com.cn/Periodical_jfjlgdxxb200003011.aspx |
| [5] | ZONG Z. Dynamic plastic response of a submerged free-free beam to underwater gas bubble[J]. Acta Mechanica, 2003, 161: 179–194. |
| [6] | 张朋祥, 顾文彬, 叶序双. 浅层水中爆炸冲击波切断现象浅探[J]. 爆炸与冲击, 2002, 7(3): 221–228. http://d.wanfangdata.com.cn/Periodical_bzycj200203006.aspx |
| [7] | Sang-Gab Lee. Fluid mesh modeling on surface ship shock response under underwater explosion[J]. Practical Design of Ships and other Floating Structures, 2001: 1315–1322. https://www.sciencedirect.com/science/article/pii/S0029801808000322 |
| [8] | 张振华, 朱锡, 白雪飞. 水下爆炸冲击波的数值模拟研究[J]. 爆炸与冲击, 2004, 3(2): 182–188. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU201206002006.htm |
 2018, Vol. 40
2018, Vol. 40
