2. 哈尔滨工程大学,黑龙江 哈尔滨 150001
2. Harbin Engineering University, Harbin 150001, China
舰载直升机的起降面临许多陆基环境下不曾遇到的挑战[1]。气流绕过舰船上层建筑物在机库后方的飞行甲板起降区形成非定常紊流,其特征频率往往低于2 Hz,而驾驶员操纵响应频率的范围是0.2~1.6 Hz[2],因此,在直升机着舰过程中,起降区的紊流将直接影响驾驶员的操纵。
起降区空气流场的研究,一般采用实船测量、PIV风洞试验和CFD仿真计算3种方法[3]。当前,CFD仿真方法发展迅速,且因其成本低廉等优势被越来越多地应用于舰载直升机起降区空气流场研究。例如,利物浦大学[4 – 5]已使用Fluent软件对孤立SFS2舰船(Simple Frigate Shape 2[6])的尾流场进行数值模拟,首先使用定常模型进行分析,发现计算得到的流场和气动载荷偏低,接着换成非定常的模型,得到了比较符合实际的结果。Alpman[7]则对舰船/直升机的动态干扰进行计算,并添加了飞行动力学模型,虽然采用的是简化的LHA舰船(Landing Helicopter Assault[8])模型以及叶素理论,但其计算结果依然表明了舰船/直升机耦合流场分析的重要性。国内也开展了一些针对起降区空气流场的CFD研究。如,陆超等[9]使用
虽然有关舰船尾流场的CFD模拟已经开展了不少工作,但是真正耦合舰船/直升机流场的研究还较少。其困难在于除了要考虑舰船尾流对直升机的影响外,还需要计入旋翼下洗流对舰船尾流的作用,这是一个双向耦合的过程[10]。之前的研究大多采用“简单叠加法”,即把孤立舰船的流场信息提取出来,再添加到旋翼流场的计算当中,这种方法只是简单地将舰船尾流和旋翼下洗流叠加,没有考虑两者流场的相互耦合关系[11]。
鉴于此,本文分别使用作用盘和运动嵌套网格技术建立了2种可用于分析舰船/直升机耦合流场的方法,先采用作用盘模型代替旋翼以模拟舰船/直升机耦合流场。然后,运用“运动嵌套网格方法”来获得更为细节的耦合流场特性,并与“作用盘方法”计算的耦合流场结果进行对比。通过对孤立舰船、孤立旋翼以及舰船/旋翼耦合流场的计算分析,得到了一些有实际意义的结论。
1 计算方法与模型 1.1 流场控制方程和计算网格本文分别使用“作用盘方法”和“运动嵌套网格方法”来模拟旋翼,均采用非定常N-S方程作为主控方程,具体表达式分别为:
作用盘方法:
| $\frac{\partial }{{\partial t}}\iiint_V {\vec W}{\rm d}V + \iint_{\partial V} {\left( {{{\vec F}_c}\left( {\vec W} \right) - {{\vec F}_v}\left( {\vec W} \right)} \right)}{\rm d}S = \iiint {{R} {\rm d}V}\text{,}$ | (1) |
运动嵌套网格方法:
| $\frac{\partial }{{\partial t}}\iiint_V {\vec W}{\rm d}V + \iint_{\partial V} {\left( {{{\vec F}_c}\left( {\vec W} \right) - {{\vec F}_v}\left( {\vec W} \right)} \right)}{\rm d}S = \iiint {\vec T{\rm d}V}\text{。}$ | (2) |
式中:
| $\vec W = \left[ \begin{gathered} \rho \\ \rho u \\ \rho v \\ \rho w \\ \rho E \\ \end{gathered} \right]\text{,}$ | (3) |
| ${\vec F_c} = \left[ \begin{gathered} \rho U \\ \rho uU + {n_x}p \\ \rho vU + {n_y}p \\ \rho wU + {n_z}p \\ \rho HU \\ \end{gathered} \right]\text{,}$ | (4) |
| ${\vec F_v} = \left[ \begin{gathered} 0 \\ {n_x}{\tau _{xx}} + {n_y}{\tau _{xy}} + {n_z}{\tau _{xz}} \\ {n_x}{\tau _{yx}} + {n_y}{\tau _{yy}} + {n_z}{\tau _{yz}} \\ {n_x}{\tau _{zx}} + {n_y}{\tau _{zy}} + {n_z}{\tau _{xzz}} \\ {n_x}{\varPhi _x} + {n_y}{\varPhi _y} + {n_z}{\varPhi _z} \\ \end{gathered} \right]\text{,}$ | (5) |
| $\vec R = \left[ \begin{gathered} 0 \\ {R_x} \\ {R_y} \\ {R_z} \\ 0 \\ \end{gathered} \right]\text{,}$ | (6) |
| $\vec T = \left[ \begin{gathered} 0 \\ \rho v\Omega \\ - \rho u\Omega \\ 0 \\ 0 \\ \end{gathered} \right]\text{。}$ | (7) |
式中:
| $\rho E = \frac{p}{{\gamma - 1}} + \frac{{\rho \left( {{u^2} + {v^2} + {w^2}} \right)}}{2}\text{,}$ | (8) |
| $\rho H = \rho E + p\text{。}$ | (9) |
式中:Ω为旋翼转动角速度;U为桨叶在计算位置上与流体的相对速度;
以“作用盘方法”模拟旋翼桨盘时,其实质是在桨盘位置处添加了一个准定常的分布力:
| $\vec R = - N \cdot \frac{{{\rm d}\vec F}}{{2\pi r{\rm d}r}} \cdot {S'}\text{。}$ | (10) |
式中:
本文使用的舰船模型是LPD-17舰船。为了方便计算,对舰船上层建筑物进行简化处理,并以1∶2比例对原模型进行缩放,缩小后模型舰船甲板的长L为32 m,宽W为16 m,机库门的高度H为8 m。选取“海豚”直升机的旋翼作为算例,其基本参数如表1。
|
|
表 1 “海豚”直升机旋翼参数 Tab.1 The rotor parameters of Dolphin helicopter |
采用切割体网格进行网格划分,该网格具有数据结构简单、通量计算便捷、自适应处理能力较强等诸多优点,既保证了计算所需的精度,又减少了计算资源的耗费。由于本文涉及作用盘和运动嵌套网格2种方法,因此需要生成2种网格。
“作用盘方法”网格:以圆柱体代替桨盘平面,同时,为提高计算精度,对旋翼、舰船表面都进行了附面层加密,整个计算域网格数量为520万。
“运动嵌套网格方法”网格:与“作用盘方法”保持一致的网格尺寸,但是还需要对每片桨叶单独划分网格,其最终网格数量为700万。2种方法对应网格示意图分别如图1所示。

|
图 1 两种方法网格示意图对比 Fig. 1 The comparison of grid diagram in two methods |
选取SFS2舰船模型作为验证算例,其外形简单且形成的涡与典型的舰船产生的涡比较相似,所以国内外关于该模型的风洞和水洞的实验数据较多,从而便于CFD方法的验证。该模型主要尺寸为138.7 m
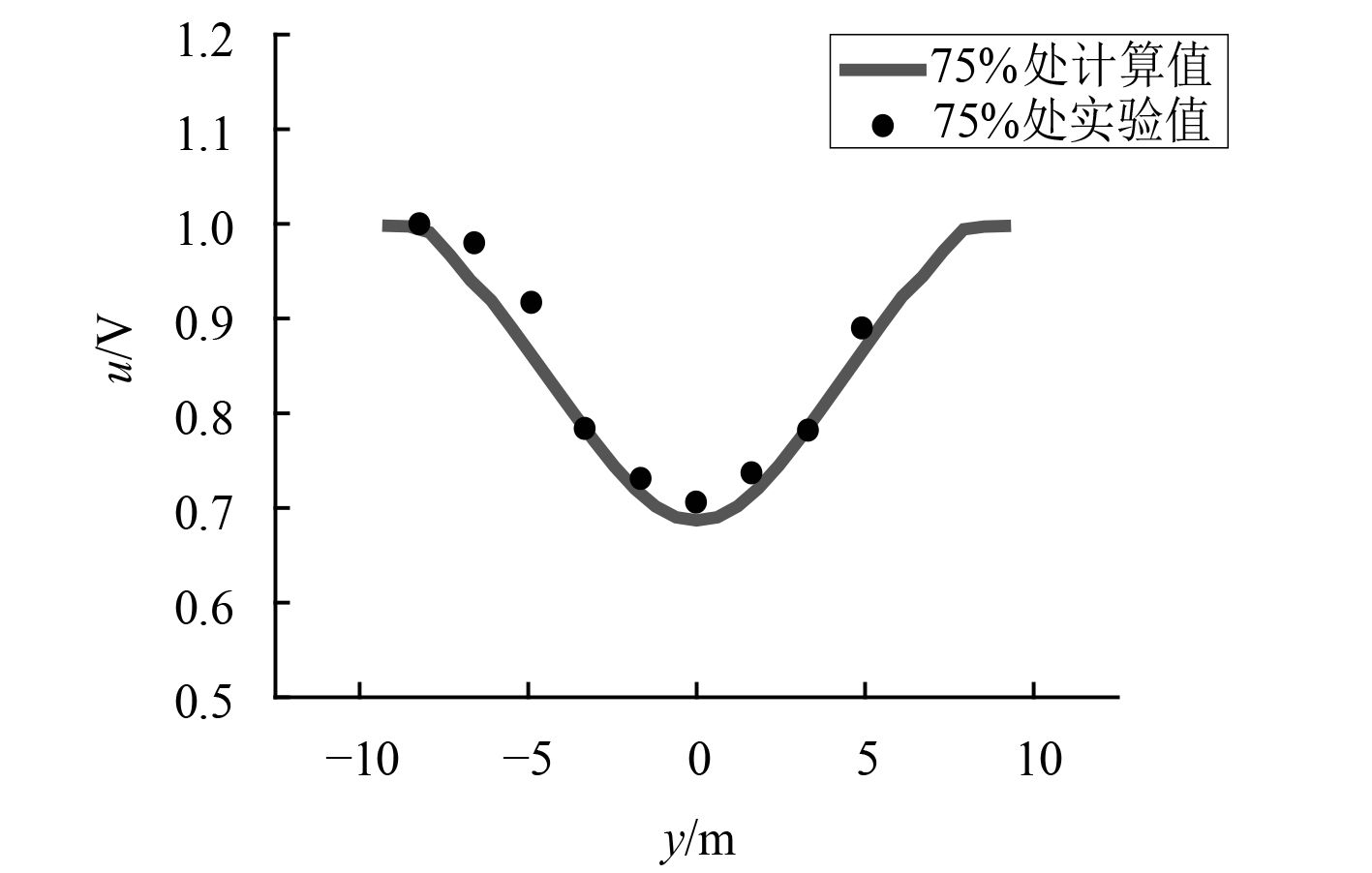
以0°风向角、12 m/s航行速度的工况为例,在甲板上方选取一系列监测点(距离甲板10.668 m,距离机库20.4 m),监测甲板上方气流速度分量u(平行前方来流的方向)的大小,其结果如图2所示。
|
图 2 甲板上方气流速度分量对比图 Fig. 2 The comparison diagram of air velocity components above deck |
从图中可以看到,本文的计算数值与实验数据结果总体吻合较好,个别点处稍有差别。
2.2 “作用盘方法”验证为验证本文“作用盘方法”的有效性,以Robin旋翼悬停状态作为算例,其桨叶的相关参数如表2所示。
|
|
表 2 Robin旋翼参数 Tab.2 Robin rotor parameters |
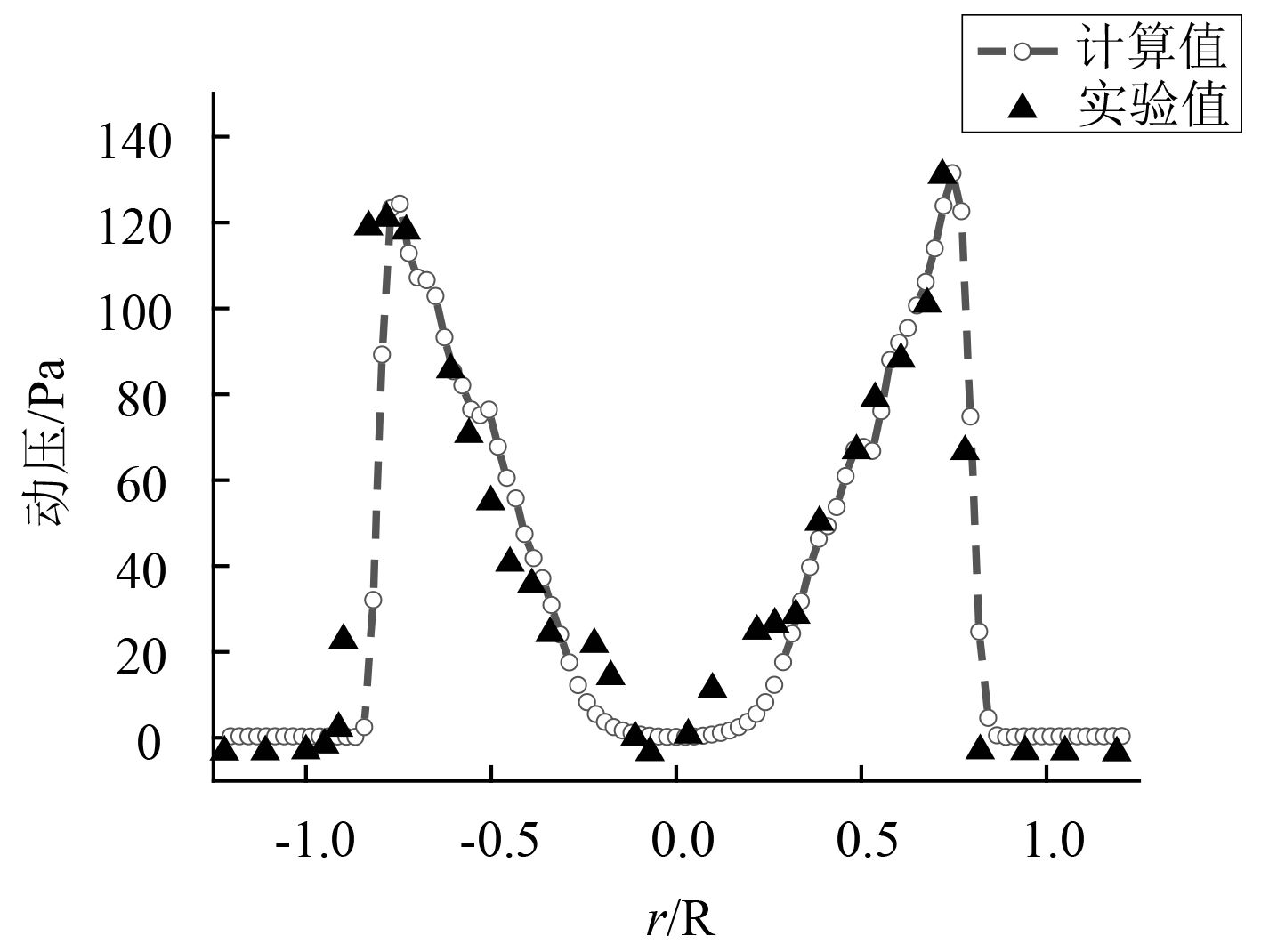
为更贴近实验条件,设置计算域底面为壁面边界条件,保持旋翼桨盘离地面的高度为3.6R(其中R为桨叶半径)。测量桨盘下方距离桨盘平面0.326R处的动压大小。并与实验值[12]进行对比,结果如图3所示。
|
图 3 桨盘下方0.326R处动压分布 Fig. 3 The dynamic pressure distribution of 0.326R under the paddles |
由图可见,使用“作用盘方法”捕捉到的旋翼桨盘下方压强的变化沿旋翼轴呈对称分布,大致符合悬停状态下旋翼流场的分布特征,并且计算得到的压强值与实验值吻合得很好,虽然稍有误差,但总体趋势保持一致。可以认为“作用盘方法”有效。
2.3 “运动嵌套网格方法”验证选取Caradonna-Tung旋翼(简称C-Tung旋翼)的悬停状态作为算例,由于该旋翼的相关实验数据比较充分,而且桨叶外形简单,因此被广泛应用于直升机旋翼CFD方法的验证之中。
本文分别计算了在0.612和0.727桨尖马赫数下旋翼桨叶剖面压强系数的分布,现仅摘取几个典型剖面的计算结果与实验值进行对比,图4为总距8°时计算值与实验值的对比。

|
图 4 旋翼桨叶剖面压强系数的分布对比 Fig. 4 The distribution of pressure coefficients in rotor blade profile |
从图中的对比数据可以看出,在0.612和0.712桨尖马赫数状态下,无论是桨尖部分还是主要升力段部分,计算结果与实验值都比较吻合,表明本文的“运动嵌套网格方法”能够有效地模拟桨叶表面的压力分布,且计算结果的精度符合实际工程应用的要求。
3 孤立舰船流场研究 3.1 上层建筑物对起降区空气流场的影响一般舰船上要安装桅杆、雷达等设备,气流绕过这些建筑物会在其后方产生气流分离,形成复杂的流动现象。紊乱的气流跟随来流往舰船后方运动,直接影响到舰载直升机的起降区,会增加驾驶员着舰操纵的负担。
为了分析舰船上层建筑物对直升机起降区空气流场的影响,对航行的舰船进行以下对比研究:规定舰船航行速度为15 m/s,不考虑侧向风的影响,分别对有无上层建筑物时2艘舰船的流场进行计算。
图5是舰船流场纵向剖面的流线图(重点关注起降区区域),由图可见,2种情况下甲板上方的涡流区漩涡中心位置均发生了变化。相比于无上层建筑物的舰船流场,有上层建筑物的流场其漩涡中心更加贴近甲板表面,即受到上层建筑物的影响,原本甲板上方的涡流区被向下压缩了,这说明甲板上方的流场可能出现了额外的向下的速度分量。

|
图 5 舰船流场纵向剖面流线图 Fig. 5 Longitudinal profile flow chart of ship flow field |
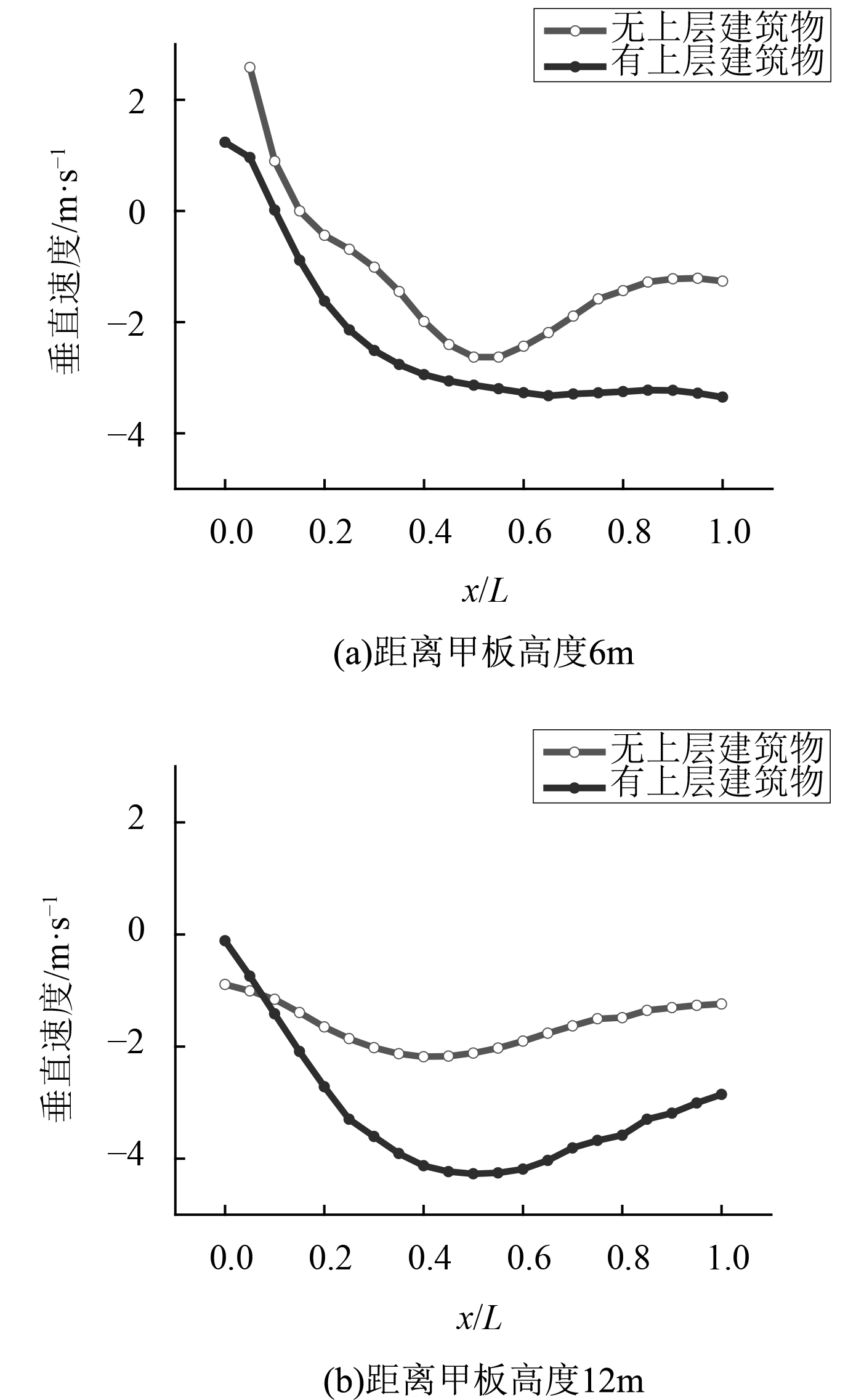
众所周知,垂向方向的速度分量对直升机桨盘平面拉力的影响最为明显。因此,需要对舰船流场中垂向方向的速度分量进行具体研究。
|
图 6 不同高度处流场垂向方向的速度变化 Fig. 6 The velocity change of vertical direction at different height |
图6给出了纵向剖面内2个不同高度处流场垂向方向的速度变化曲线图。与无上层建筑物的舰船流场相比,上层建筑物的存在引起了甲板上方垂向方向的速度增量,并且该影响区域一直延伸到甲板末端。因此可以得出结论,舰船上层建筑物会对直升机安全着舰产生不利的影响。
后文中的算例均为包含上层建筑物的LPD-17舰船模型。
3.2 风向角对起降区空气流场的影响舰船在航行过程中往往会受到侧向风的影响。侧向角越大,甲板上方气流受到的影响越明显,直至整个甲板区域全部处于侧向风之中,因而有必要对侧向风影响下的起降区空气流场进行分析。
这里分别选取了0°风向角和右舷15°风向角2种不同工况下舰船的尾流场作为研究对象,设置来流的速度为15 m/s。
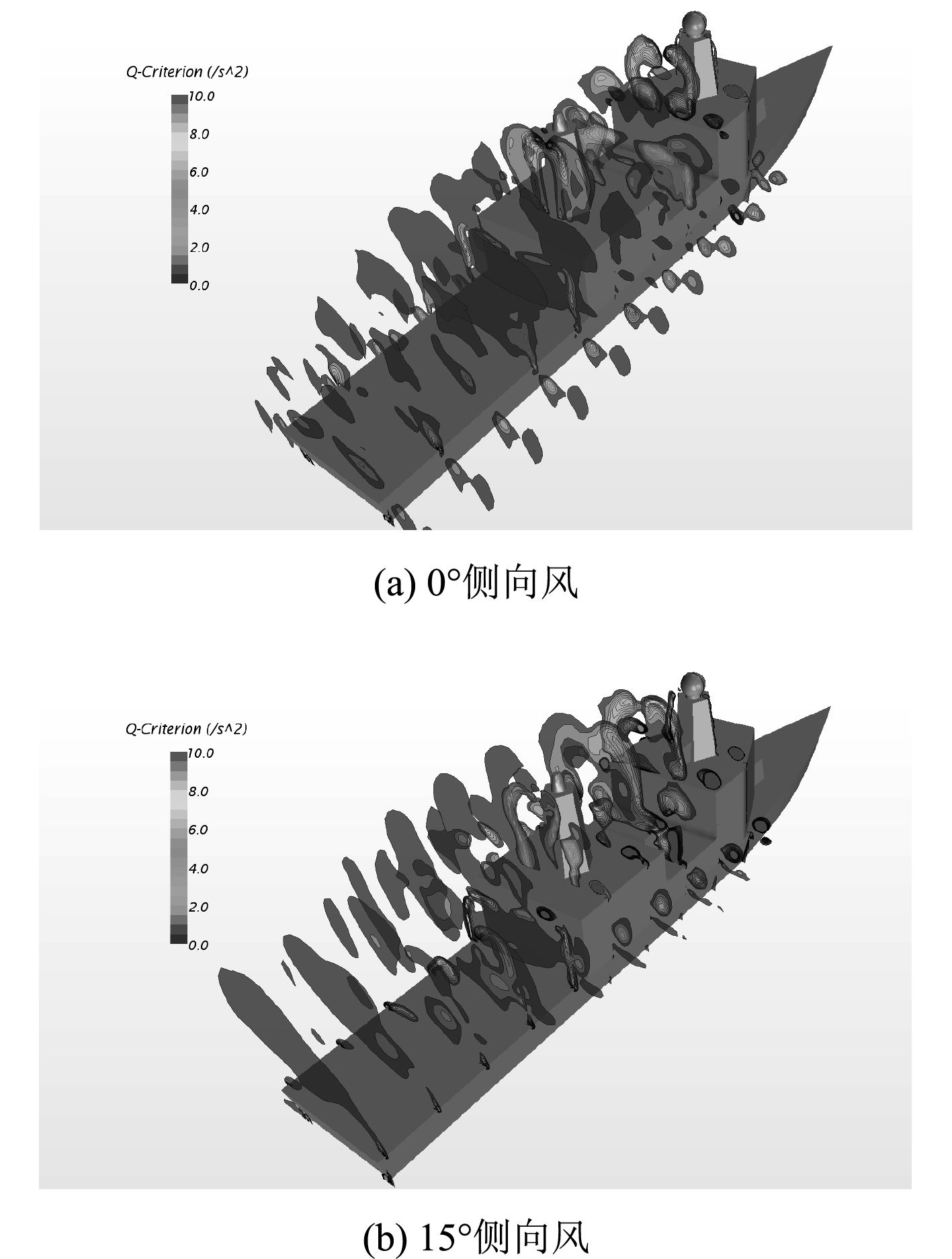
为了清楚地观察起降区空气流场的漩涡结构,在该区域选取多个等距离的截面,并计算出其涡量云图,如图7所示。通过图7(a)和图7(b)的对比可见,在右舷侧向风的作用下,整个流场出现明显的向左的分量,机库右舷边缘分离的漩涡开始往甲板中间脱落,同时甲板区域的右后方形成一块没有大漩涡结构的近似三角形区域,此处气流渐渐不受舰船上层建筑物的影响,有利于直升机着舰。为了验证该结果,下面做进一步分析。
|
图 7 不同侧向风下截面涡量云图 Fig. 7 The vortex flow chart of different lateral wind |
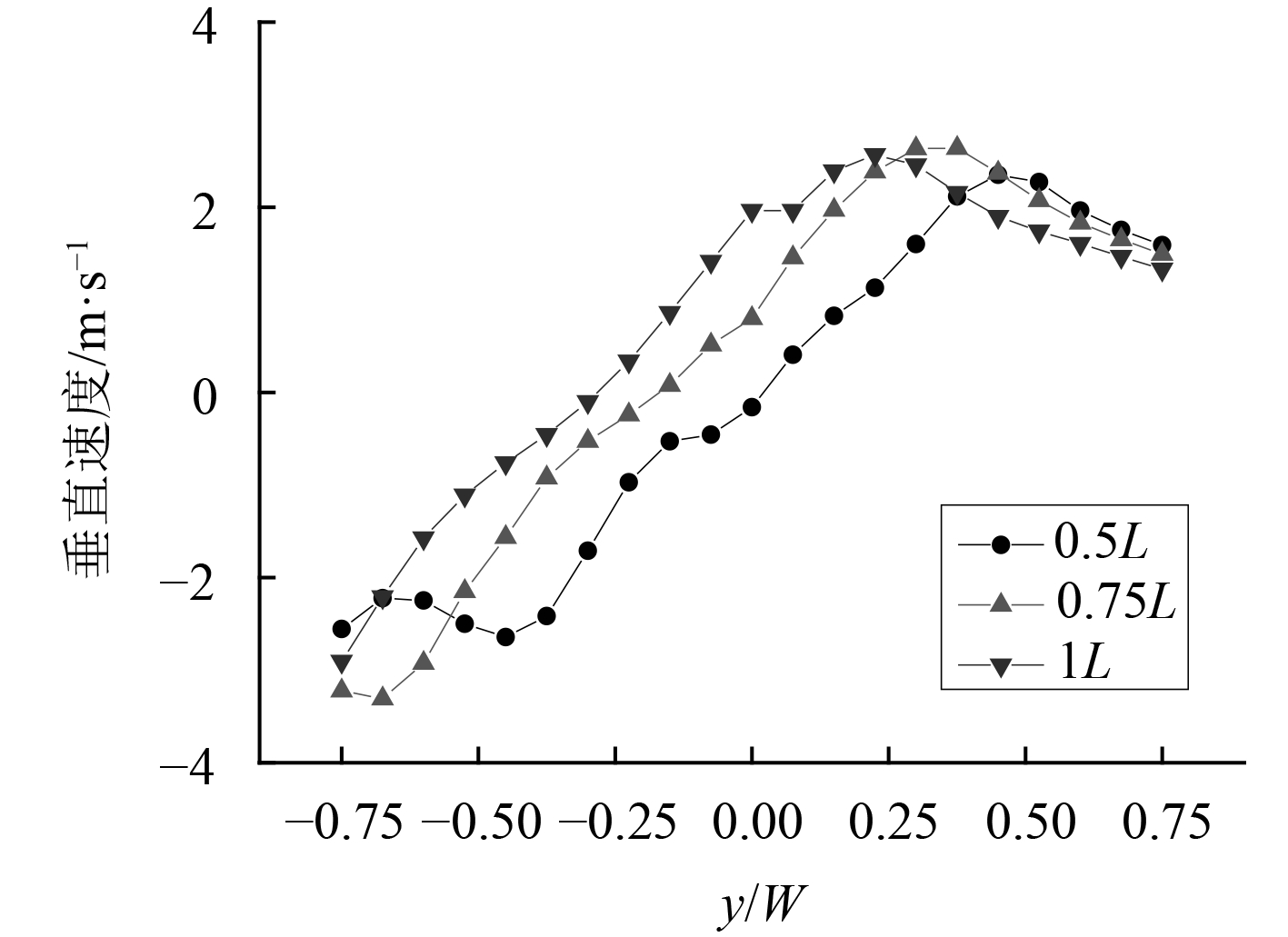
在距离甲板9 m高度处,设置3条水平监测线,离机库的距离分别为0.5 L,0.75 L和1 L,监测该位置处的垂向速度分量,计算结果如图8所示。
|
图 8 右舷15°侧向风下不同监测点垂向速度分量 Fig. 8 The vertical velocity component wind in different monitoring points under starboard 15 ° |
由图可以看出,在右舷15°侧向风工况下,甲板上方右半部分流场不仅没有下洗速度分量,反而有向上的速度分量,并且越往甲板后方,上洗气流影响范围越广,也就是说在右舷风工况下,甲板的右后方是比较合理的安全着舰点。
4 直升机/舰船耦合流场研究 4.1 “作用盘方法”的耦合流场计算分析为了对比耦合后流场与孤立流场的差别,这里分别对比计算了孤立舰船、孤立旋翼和舰船/旋翼耦合3种算例。其中,旋翼中心位于舰船纵向剖面内,距离甲板9 m,距离机库12 m。并针对该3种算例分别计算0°风向角工况下的流场信息。
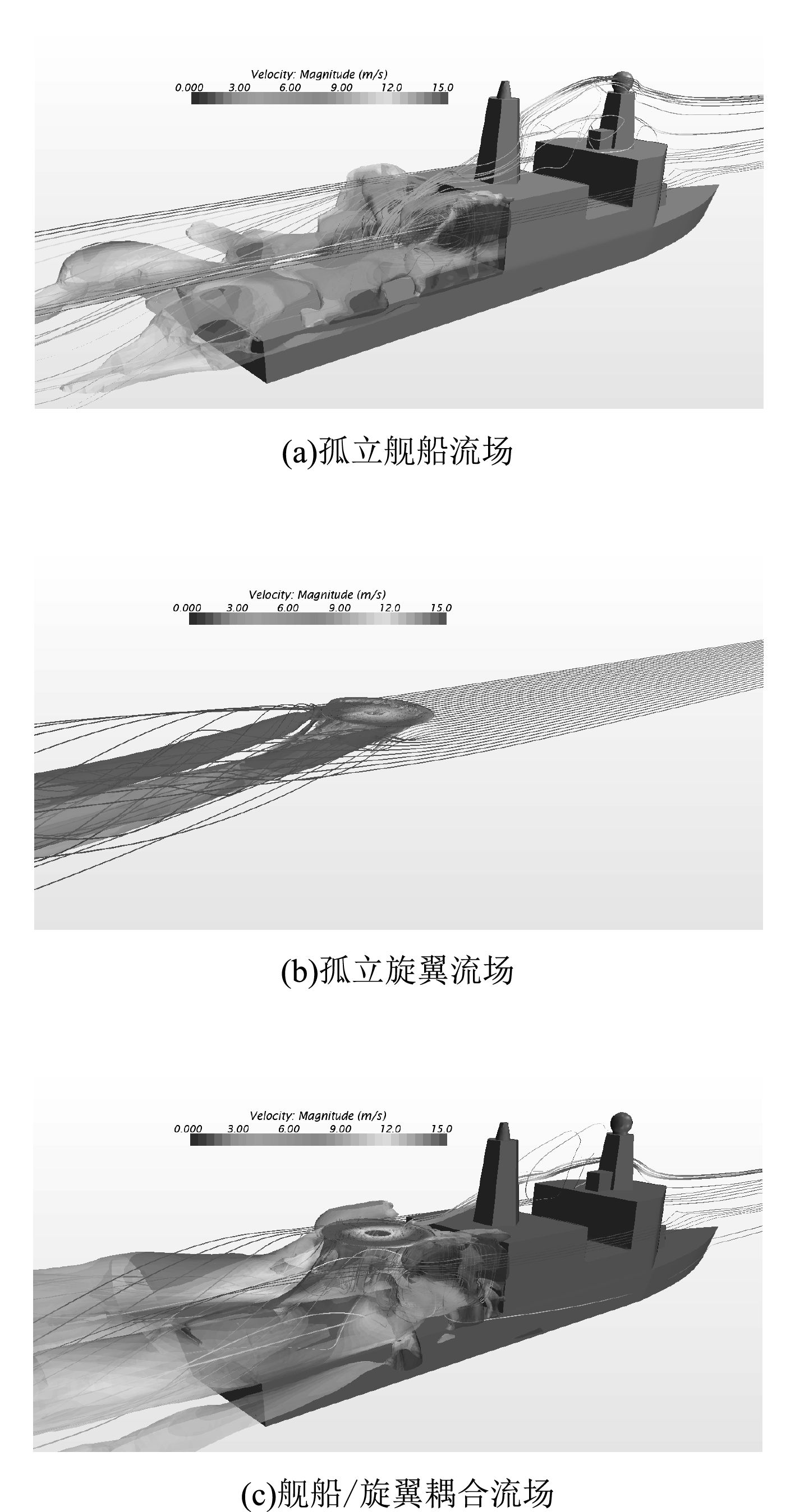
图9是Q判据等于0.5时3种算例对应的等值涡量和速度流线图。
|
图 9 三种算例流场等值涡量和速度流线图 Fig. 9 The equivalent vorticity and velocity flow chart of three examples |
在孤立舰船算例中(见图9(a)),气流经过机库顶端和侧面分别向下和向内偏斜,在紧贴机库的后方形成了明显的涡流区,同时甲板两侧的上方也有一对旋转方向相反的漩涡,不过该漩涡的强度相对较小。而在孤立旋翼时(见图9(b)),从桨盘平面脱出来一对长长的漩涡,一直向后方延伸。
在耦合旋翼和舰船的流场算例中(见图9(c)),整个起降区空气流场显示出明显的相互干扰特性,而不是单独旋翼流场和单独舰船流场的简单相加。首先,在加入旋翼流场的作用后,舰船流场中紧贴机库的后方的涡流区明显增强,这从流线图的疏密程度可以看出,而且原本甲板上方两侧较弱的反向漩涡在旋翼尾流的作用下也得到了增强,并拓宽了漩涡影响范围。其次再看旋翼尾涡的变化,原本旋翼的后方脱出一对很长的漩涡,但是在舰船尾流的影响下,旋翼尾涡迅速向下方偏斜,并快速到达舰船甲板位置。
为进一步验证耦合流场与简单叠加流场的区别,在桨盘下方3 m选取2条水平线作为监测点,距离机库为0.125 L和0.625L,分别计算出叠加流场与耦合流场垂向方向速度分量,如图10所示。在甲板上方区域(–0.5W~0.5W)两者的差别比较明显,耦合方法得到的结果显示出良好的对称性,与实际情况比较吻合。由此也表明,通过简单叠加法得到的起降区空气流场并不可靠。

|
图 10 叠加流场和耦合流场垂向方向速度对比图 Fig. 10 The comparison of vertical velocity between the superimposed flow field and the coupled flow field |
由4.1节的结论可知“作用盘方法”可有效地模拟舰船/旋翼耦合干扰问题,但其也有一定的局限性,因为在计算过程中没有出现具体的桨叶外形,无法捕捉桨叶转动的细节,为了弥补这一缺陷,接下来将使用“运动嵌套网格方法”来实现旋翼的转动。
图11给出了Q判据等于1时“作用盘方法”和“运动嵌套网格方法”计算得到的流场等值涡量图。

|
图 11 两种方法流场等值涡量对比图 Fig. 11 The comparison diagram of equivalent vorticity in two methods |
由于“运动嵌套网格方法”模拟的是实际桨叶旋转的过程,为了使舰船尾流和旋翼下洗流充分耦合,本文模拟实际10 s的时间跨度,其完整计算时间是“作用盘方法”计算时间的10多倍。但使用“运动嵌套网格方法”捕捉到的桨尖涡要比“作用盘方法”更为精确,从图11(b)中可以看到旋翼桨尖涡一层层向后方脱落的痕迹,而“作用盘方法”并不能捕捉到这些细节。
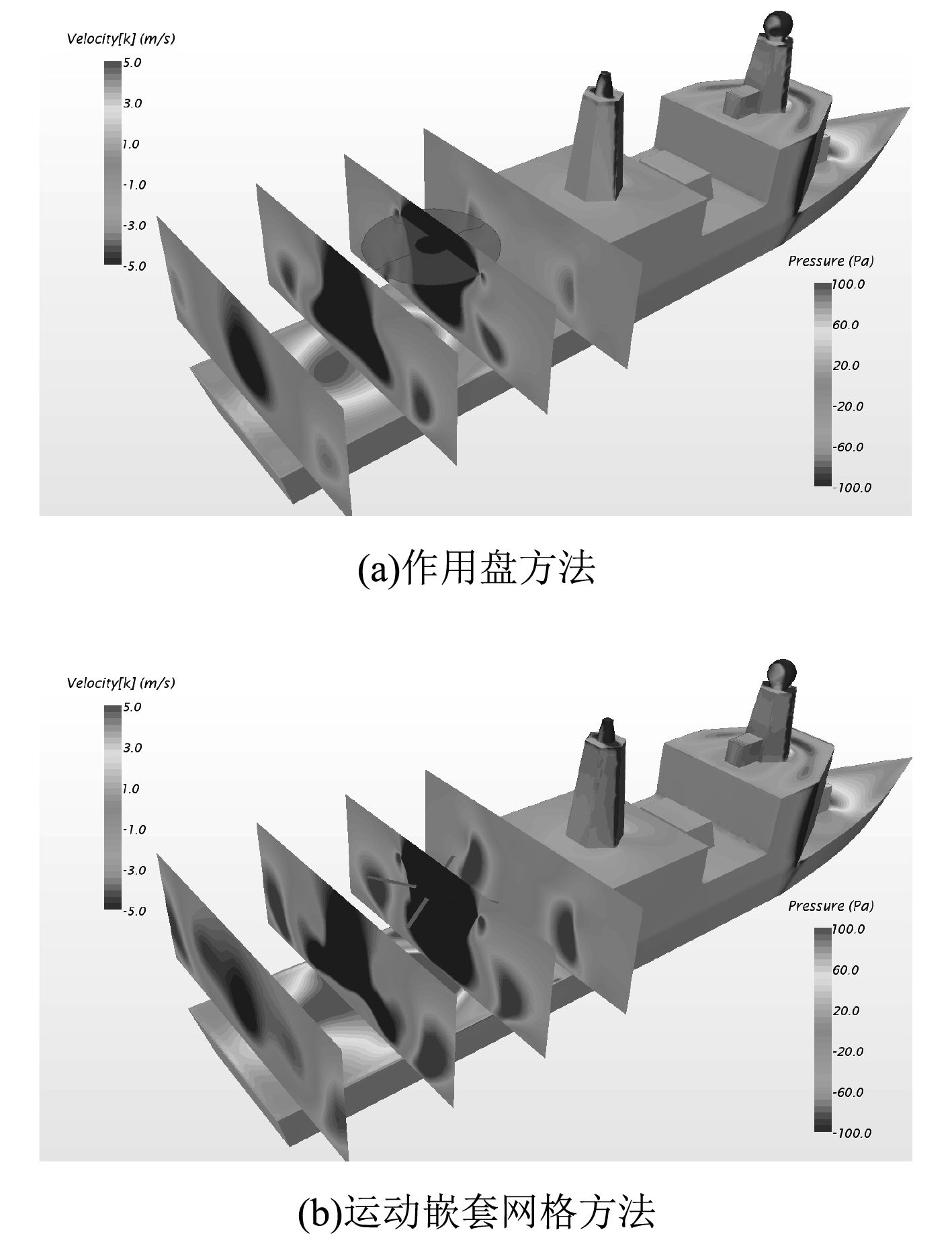
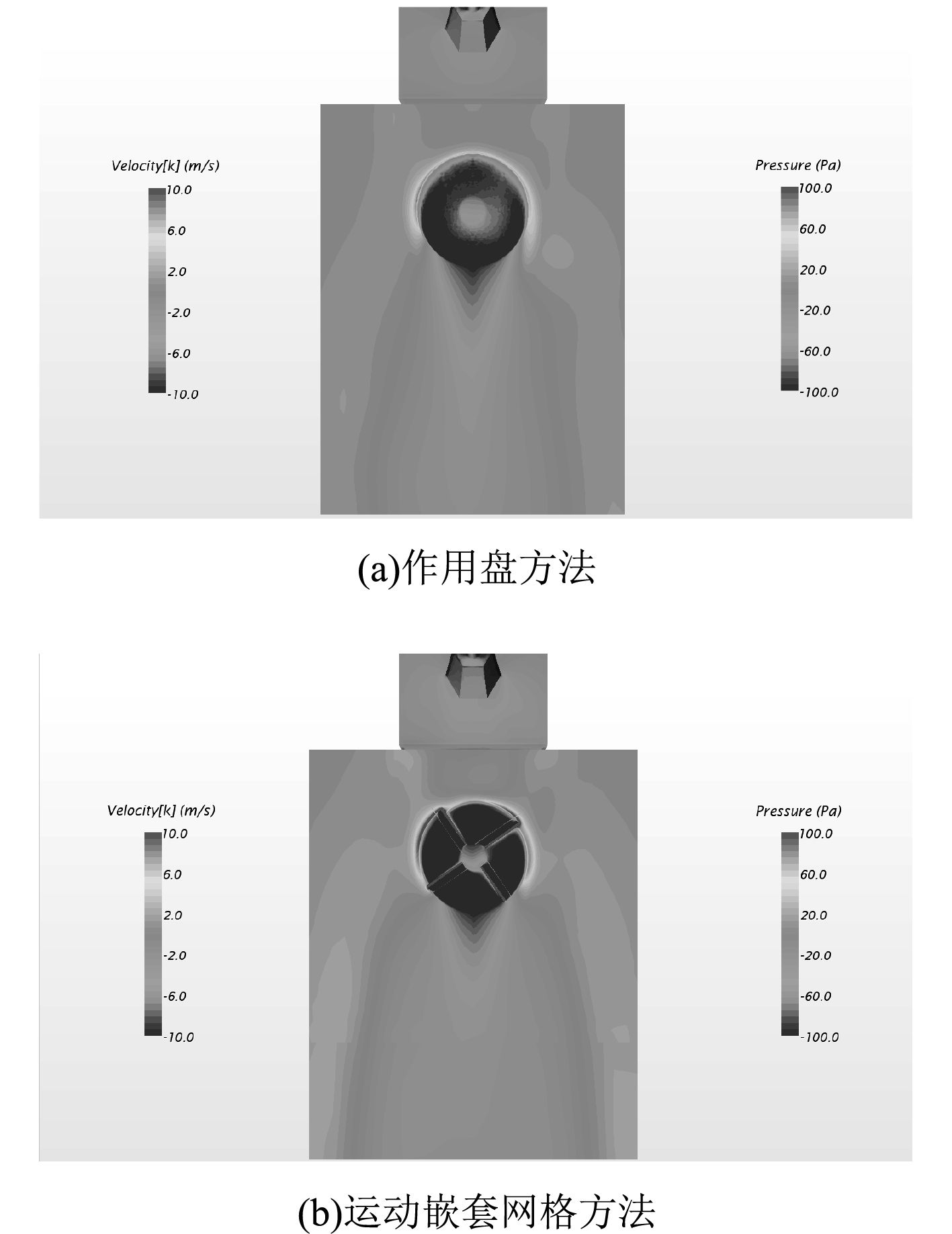
为了进一步分析和对比这2种方法得到的起降区空气流场,图12和图13分别给出了2种方法计算的起降区竖直和水平截面内垂向速度分布云图。
|
图 12 两种方法计算的起降区横截面垂向速度分布云图 Fig. 12 The vertical velocity distribution of Cross section used in two methods |
|
图 13 两种方法计算的起降区水平面垂向速度分布云图 Fig. 13 The vertical velocity distribution of horizontal plane used in two methods |
虽然“作用盘方法”对旋翼流场细节的捕捉不够充分,不过从整个起降区空气流场中漩涡的大小以及速度的分布来看,“作用盘方法”还是能够得到与“运动嵌套网格方法”相似的结论。
5 结 语本文充分考虑了舰船/直升机流场之间的耦合问题,分别运用“作用盘方法”和“运动嵌套网格方法”对孤立舰船、孤立旋翼以及舰机耦合等流场问题进行了数值模拟,并进行对比分析,得出以下结论:
1)舰船上层建筑物的存在会引起起降区下洗速度增大,使得直升机旋翼拉力减小,这种拉力变化会增加驾驶员操纵负担。
2)在右舷风工况下,甲板右后方会形成一块没有较强漩涡结构的近似三角形区域,是比较合理的安全着舰点。
3)“作用盘方法”一定程度上可以有效地用来研究舰船/直升机双向耦合流场,相比于“简单叠加法”得到的起降区空气流场可靠性更高。
4)“运动嵌套网格方法”可以捕捉到起降区空气流场的细节,得到的流场结果更加准确,但对于模拟时间跨度较大起降区空气流场需要耗费巨大的计算量。
| [1] | 郜冶, 刘长猛. 护卫舰气流场数值计算研究[J]. 哈尔滨工程大学学报, 2013, 34 (5): 599–603. |
| [2] | ZAN S J. On aerodynamic modelling and simulation of the dynamic interface[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2005, 219 (5): 393–410. DOI: 10.1243/095441005X30315 |
| [3] | LEE Y, SILVA M. CFD modeling of rotor flow field aboard ship[C]//48th AIAA Aerospace Sciences Meeting, Orlando, Florida. 2010. |
| [4] | HODGE S J, ZAN S J, ROPER D M, et al. Time‐accurate ship airwake and unsteady aerodynamic loads modeling for maritime helicopter simulation[J]. Journal of the American Helicopter Society, 2009, 54 (2): 22005–22005. DOI: 10.4050/JAHS.54.022005 |
| [5] | ROPER D M, OWEN I, PADFIELD G D, et al. Integrating CFD and piloted simulation to quantify ship-helicopter operating limits[J]. Aeronautical Journal, 2006, 110 (1109): 419–428. DOI: 10.1017/S0001924000001329 |
| [6] | ZHANG F, XU H, BALL N G. Numerical simulation of unsteady flow over SFS2ship model[C]//47th AIAA Aerospace Sciences Meeting, Orlando, Florida. 2009. |
| [7] | ALPMAN E, LONG L N, BRIDGES D O, et al. Fully-coupled simulations of the rotorcraft/ship dynamic interface[C]// 63rd American Helicopter Society Annual Forum. American Helicopter Society, inc, 2007: 1367. |
| [8] | CZERWIEC R M, POLSKY S A. LHA airwake wind tunnel and CFD comparison with andwithout bow flap[C]//22nd Applied Aerodynamics Conference and Exhibit, Providence, Rhode Island, 2004. |
| [9] | 陆超, 姜治芳, 王涛. 不同工况条件对舰船舰面空气流场的影响[J]. 舰船科学技术, 2009, 31 (9): 38–42. |
| [10] | RAJMOHAN N, ZHAO J G, HE C G. An efficient POD based technique to model rotor/ship airwake interaction[C]//68th American Helicopter Society Annual Forum, Fort Worth, Texas, 2012. |
| [11] | CROZON C, STEIJL R, BARAKOS G N. Numerical study of helicopter rotors in a ship airwake[J]. Journal of Aircraft, 2014, 51 (6): 1813–1832. DOI: 10.2514/1.C032535 |
| [12] | MCKEE J W, NAESETH R L. Experimental investigation of the drag of flat plates andcylinders in the slipstream of a hovering rotor[M]. NACA, 1958. |
 2018, Vol. 40
2018, Vol. 40
