2. 黄海造船有限公司,山东 荣成 264309
2. Huanghai Shipbuilding Co., Ltd., Rongcheng 264309, China
舰船在航行时,由于风浪或拐弯等因素,船体的姿态时刻发生变化,而测量、目标跟踪等设备需要良好的稳定姿态,因此需要借助舰载稳定平台来维持被控对象的平稳[1 – 2]。稳定平台的应用十分广泛:汽车上使用稳定平台,可以隔离因道路不平造成对运输物品的摇晃;航拍飞行器上使用稳定平台,可以隔离因气流冲击而造成对相机等设备的影响;舰船上使用稳定平台,能够消除船体在风浪或拐弯航行时受到的扰动,稳定舰船上的手术床、雷达等设备[3 – 5]。
1 舰载稳定平台的动态结构模型本文研究的舰载稳定平台为包含航向轴和俯仰轴的双轴转台,使用的是永磁直流力矩电机。永磁直流力矩电机,假设电流连续,则动态电压方程为:
| ${U_{{d}0}} = R{I_{d}} + L\frac{{{\rm d}{I_{d}}}}{{{\rm d}t}} + E \text{。}$ | (1) |
忽略粘性摩擦和弹性转矩,电机轴上的运动方程为:
| ${T_e} - {T_L} = \frac{{G{D^2}}}{{375}}\frac{{{\rm d}n}}{{{\rm d}t}}\text{,}$ | (2) |
式中:TL为含空载转矩在内的负载转矩,N·m;GD2为电力拖动装置折算到电机机轴上的飞轮矩,N·m2。
定义电枢回路的电磁时间常数(s):
| ${T_l} = \frac{L}{R}\text{,}$ | (3) |
电力拖动系统的机电时间常数(s):
| ${T_m} = \frac{{G{D^2}R}}{{375{C_e}{C_m}}}\text{。}$ | (4) |
将式(3)和式(4)代入式(1)和式(2),得
| ${U_{d0}} - E = R({I_d} + {T_l}\frac{{{\rm d}{I_{d}}}}{{{\rm d}t}})\text{,}$ | (5) |
| ${I_{d}} - {I_{{d}L}} = \frac{{{T_m}}}{R}\frac{{{\rm d}E}}{{{\rm d}t}}\text{。}$ | (6) |
式中,IdL为负载电流,A。
在零初始条件下,对式(5)和式(6)两侧进行拉氏变换,可得电压与电流的传递函数为:
| $\frac{{{I_{d}}(s)}}{{{U_{{d}0}}(s) - E(s)}} = \frac{{1/R}}{{{T_l}s + 1}}\text{,}$ | (7) |
电流与电动势间的传递函数为:
| $\frac{{E(s)}}{{{I_{d}}(s) - {T_L}/{C_m}}} = \frac{R}{{{T_m}s}}\text{。}$ | (8) |
将直流电机用于伺服控制系统,角速度对时间积分后变成位置信号θ(rad),再将位置单位转换为“度”,将角速度转换为转速,即
| $\theta = \frac{{180}}{\pi }\int {\omega {\rm{d}}t} = \frac{{180}}{\pi } \cdot \frac{{2\pi }}{{60}}\int {n{\rm{d}}t} = 6\int {n{\rm{d}}t} \text{。}$ | (9) |
将式(9)拉氏变换可得:
| $\theta (s) = \frac{6}{s}n(s)\text{。}$ | (10) |
额定励磁下,由直流力矩电动机组成的舰载稳定平台动态结构模型如图1所示。
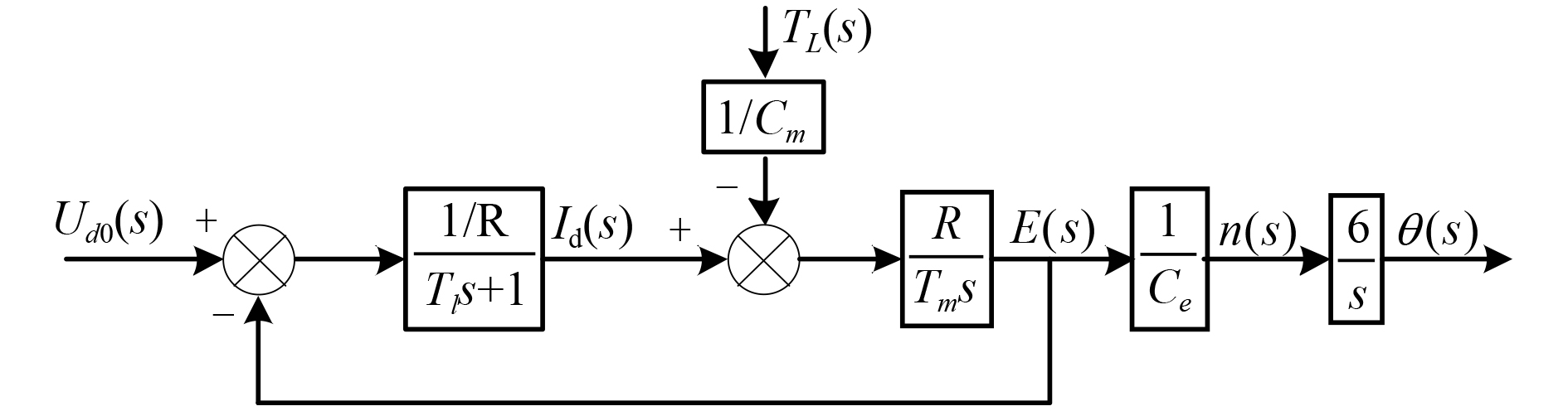
|
图 1 舰载稳定平台的动态结构模型 Fig. 1 Dynamic structure model of shipborne stable platform |
如图1所示,直流电机动态模型的电压与电流关系为:
| $\left[ {\frac{{{U_{{d}0}}(s) - E(s)}}{R} - {I_{d}}(s)} \right]\frac{1}{{{T_l}s}} = {I_{d}{\rm d}}(s)\text{。}$ | (11) |
直流力矩电机模型变为如图2所示。
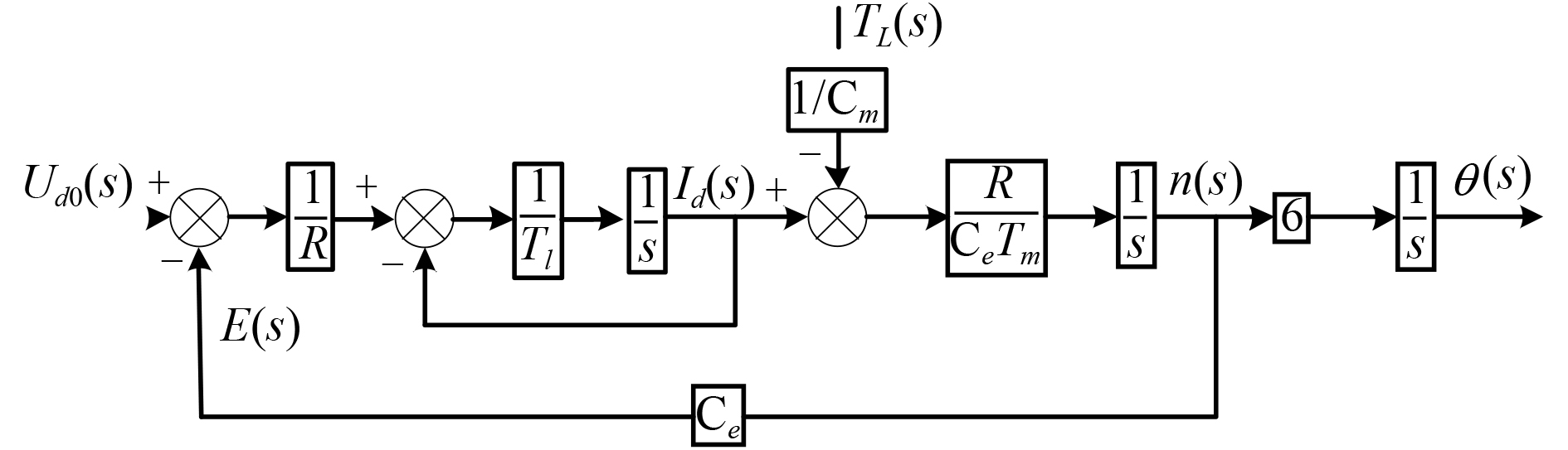
|
图 2 直流电机模型展开图 Fig. 2 DC motor model development diagram |
取位置、转速、电流为状态变量,输入电压、负载转矩为输入变量,则图2可转换为状态框图,如图3所示。
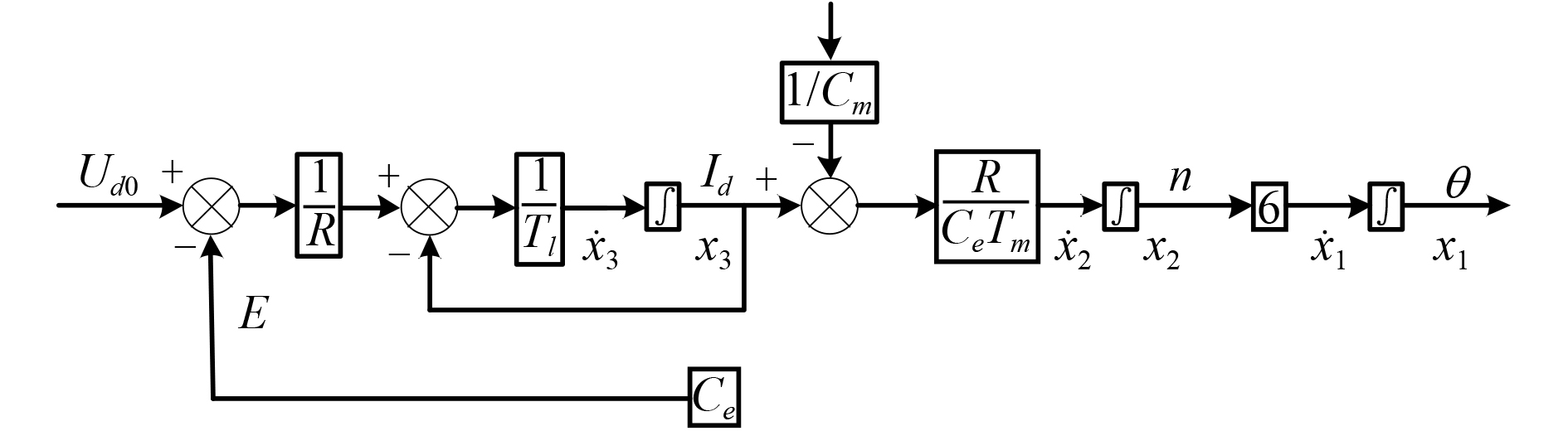
|
图 3 直流电机的状态转换图 Fig. 3 State transition diagram of DC motor |
由图3可写出状态方程,如式(12)所示。
| $\begin{split}&\left[ {\begin{array}{*{20}{c}}{{{\dot x}_1}}\\{{{\dot x}_2}}\\{{{\dot x}_3}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}0 & 6 & 0\\0 & 0 & {\frac{R}{{{C_e}{T_m}}}}\\0 & { - \frac{{{C_e}}}{L}} & { - \frac{1}{{{T_l}}}}\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}{{x_1}}\\{{x_2}}\\{{x_3}}\end{array}} \right] + \\&\left[ {\begin{array}{*{20}{c}}0 & 0\\0 & { - \frac{R}{{{C_m}{C_e}{T_m}}}}\\{\frac{1}{L}} & 0\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}{{U_{d0}}}\\{{T_L}}\end{array}} \right]\text{。}\end{split}$ | (12) |
忽略摩擦阻力和空载转矩时,状态方程如式(13)所示。
| $\left[ {\begin{array}{*{20}{c}}{{{\dot x}_1}}\\{{{\dot x}_2}}\\{{{\dot x}_3}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}0 & 6 & 0\\0 & 0 & {\frac{R}{{{C_e}{T_m}}}}\\0 & { - \frac{{{C_e}}}{L}} & { - \frac{1}{{{T_l}}}}\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}{{x_1}}\\{{x_2}}\\{{x_3}}\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}0\\0\\{\frac{1}{L}}\end{array}} \right]{U_{{d}0}}\text{。}$ | (13) |
该系统的一般形式为:
| $\left[ {\begin{array}{*{20}{c}}{{{\dot x}_1}}\\{{{\dot x}_2}}\\{{{\dot x}_3}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{A_{11}}} & {{A_{12}}} & {{A_{13}}}\\{{A_{21}}} & {{A_{22}}} & {{A_{23}}}\\{{A_{31}}} & {{A_{32}}} & {{A_{33}}}\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}{{x_1}}\\{{x_2}}\\{{x_3}}\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}0\\0\\{{B_3}}\end{array}} \right] \cdot u\text{。}$ | (14) |
设滑模切换函数为:
| $\sigma {\rm{ = }}{\mathit{\boldsymbol{Sx}}}\text{,}$ | (15) |
式中,
选择指数趋近律[6]:
| $\dot \sigma = - k\sigma - \eta {\mathop{\rm sgn}} (\sigma )\text{,}(k > 0,\eta > 0)\text{,}$ | (16) |
根据滑模切换函数的定义,得
| $\dot \sigma = {\mathit{\boldsymbol{S}}}{\dot{x}} = {\mathit{\boldsymbol{S}}}({\mathit{\boldsymbol{Ax}}} + {\mathit{\boldsymbol{B}}}u)\text{,}$ | (17) |
整理后,控制器表达式:
| $u = - {({\mathit{\boldsymbol{SB}}})^{ - 1}}\left[ {{\mathit{\boldsymbol{SAx}}} + k\sigma + \eta {\mathop{\rm sgn}} (\sigma )} \right]\text{。}$ | (18) |
传统的滑模算法会导致控制器输出时,产生高频电流抖动,使转台电机电流在设定值附近有高频振荡,转台的稳定性不好。
取
| $\left\{ \begin{array}{l}{{\dot x}_1} = {x_2}\text{,}\\{{\dot x}_2} = {x_3}\text{,}\\{{\dot x}_3} = f\left( {\mathit{\boldsymbol{x}}} \right) + b\left( {\mathit{\boldsymbol{x}}} \right)u\text{。}\end{array} \right.$ | (19) |
式中:
给出新的滑模切换函数如下:
| $\begin{split}S =& \displaystyle {\dot x_3} + {a_1}{\mathop{\rm sgn}} \left( {{x_1}} \right){\left| {{x_1}} \right|^{{\beta _1}}} + {a_2}{\mathop{\rm sgn}} \left( {{x_2}} \right){\left| {{x_2}} \right|^{{\beta _2}}} + \\&{a_3}{\mathop{\rm sgn}} \left( {{x_3}} \right){\left| {{x_3}} \right|^{{\beta _3}}}\text{。}\end{split}$ | (20) |
式中:
| ${\beta _2} = \frac{{{\beta _1}{\beta _3}}}{{2{\beta _3} - {\beta _2}}}\text{。}$ | (21) |
设计新的控制器:
| $u = b{\left( {\mathit{\boldsymbol{x}}} \right)^{ - 1}}\left( {{u_{eq}} + {u_n}} \right)\text{,}$ | (22) |
| $\begin{split}{u_{eq}} = & - \left( {f\left( {\mathit{\boldsymbol{x}}} \right) + {a_3}{\mathop{\rm sgn}} \left( {{x_3}} \right){{\left| {{x_3}} \right|}^{{\beta _3}}} + {a_2}{\mathop{\rm sgn}} \left( {{x_2}} \right){{\left| {{x_2}} \right|}^{{\beta _2}}}} \right.\\&\left. { + {a_1}{\mathop{\rm sgn}} \left( {{x_1}} \right){{\left| {{x_1}} \right|}^{{\beta _1}}}} \right)\text{,}\end{split}$ | (23) |
| ${\dot u_n} + T{u_n} = v\text{,}$ | (24) |
| $v = - \left( {{k_T} + \eta } \right){\mathop{\rm sgn}} \left( s \right)\text{,}$ | (25) |
| ${u_n}\left( {{t_0}} \right) = 0\text{。}$ | (26) |
式中:T,kT,η为大于0的常数。
根据式(19)和式(20),滑模切换函数改写为:
| $\begin{align}S = & f\left( x \right) + b\left( x \right)u + {a_3}{\mathop{\rm sgn}} \left( {{x_3}} \right){\left| {{x_3}} \right|^{{\beta _3}}} + \\ &{a_2}{\mathop{\rm sgn}} \left( {{x_2}} \right){\left| {{x_2}} \right|^{{\beta _2}}} + {a_1}{\mathop{\rm sgn}} \left( {{x_1}} \right){\left| {{x_1}} \right|^{{\beta _1}}}\text{。}\end{align}$ | (27) |
把式(22)代入式(27),得
| $\begin{align}{l}S =& f\left( x \right) + {u_{eq}} + {u_n} + {a_3}{\mathop{\rm sgn}} \left( {{x_3}} \right){\left| {{x_3}} \right|^{{\beta _3}}} +\\ & {a_2}{\mathop{\rm sgn}} \left( {{x_2}} \right){\left| {{x_2}} \right|^{{\beta _2}}} + {a_1}{\mathop{\rm sgn}} \left( {{x_1}} \right){\left| {{x_1}} \right|^{{\beta _1}}}\text{,}\end{align}$ | (28) |
把式(23)代入式(28),得
| $S = {u_n}\text{,}$ | (29) |
根据式(24)、式(25)和式(26),得
| $\begin{array}{l}{u_n}\left( t \right) = \left( {{u_n}\left( {{t_0}} \right) + \frac{1}{T}\left( {{k_T} + \eta } \right){\mathop{\rm sgn}} \left( s \right)} \right){e^{ - T\left( {t - {t_0}} \right)}} - \\\;\;\;\;\;\;\;\;\;\;\; \frac{1}{T}\left( {{k_T} + \eta } \right){\mathop{\rm sgn}} \left( s \right)\text{。}\end{array}$ | (30) |
构造李雅普诺夫函数为:
| $V = \frac{1}{2}{s^2}\text{,}$ | (31) |
则函数导数为:
| $\begin{array}{l}\dot V = s\dot s =\\ \;\;\;s{{\dot u}_n} =\\ \;\;\;s\left( {{{\dot u}_n} + T{u_n} - T{u_n}} \right) = \\ \;\;\;s\left( { - \left( {{k_T} + \eta } \right){\mathop{\rm sgn}} \left( s \right) - T{u_n}} \right) = \\ \;\;\;\left( { - T{u_n}s - {k_T}\left| s \right|} \right) - \eta \left| s \right|\text{,}\end{array}$ | (32) |
根据式(30)和条件
| ${k_T} \geqslant T\left| {{u_n}\left( t \right)} \right|\text{。}$ | (33) |
将不等式(33)代入式(32),得
| $\dot V = s\dot s \leqslant\leqslant - \eta \left| s \right| \leqslant 0\text{。}$ | (34) |
由式(34)可知系统满足李雅普诺夫稳定条件,系统可以在有限时间内进入稳定状态[7]。
新的控制方法通过非奇异终端滑模控制,消除了控制器输出的高频电流抖动,克服了传统滑模控制的缺点。
4 仿真分析 4.1 传统滑模控制仿真分析为了验证算法的有效性,使用Matlab对舰载稳定平台的模型进行传统滑模控制的仿真分析。
舰载稳定平台采用的电机是宇捷直流力矩电机,型号:NH250LYX-M300-E60,其参数如表1所示。
|
|
表 1 舰载稳定平台NH250LYX-M300-E60型电机参数 Tab.1 Ship-borne stability platform NH250LYX-M300-E60 motor parameters |
使用极点配置方法设计滑模平面,得到滑模切换函数:
| $\sigma = 0.396{x_1} + 0.548{x_2} + {x_3}\text{,}$ | (35) |
代入数据得到控制器的表达式如下:
| ${U_{d0}} = \displaystyle - 0.007 \times [ - 169.053{x_2} - 296.964{x_3} + k\sigma + \eta {\mathop{\rm sgn}} (\sigma )]\text{。}$ | (36) |
取k=20时,系统具备良好的趋近速度,由于滑模切换函数使用的是偏差量,整体抖动不大此处取η=5。电力电子变换器的放大倍数为6,故控制器输出应缩小1/6并限幅输出±10 V。用Matlab进行阶跃特性仿真,给定36°时的仿真结果如图4所示。
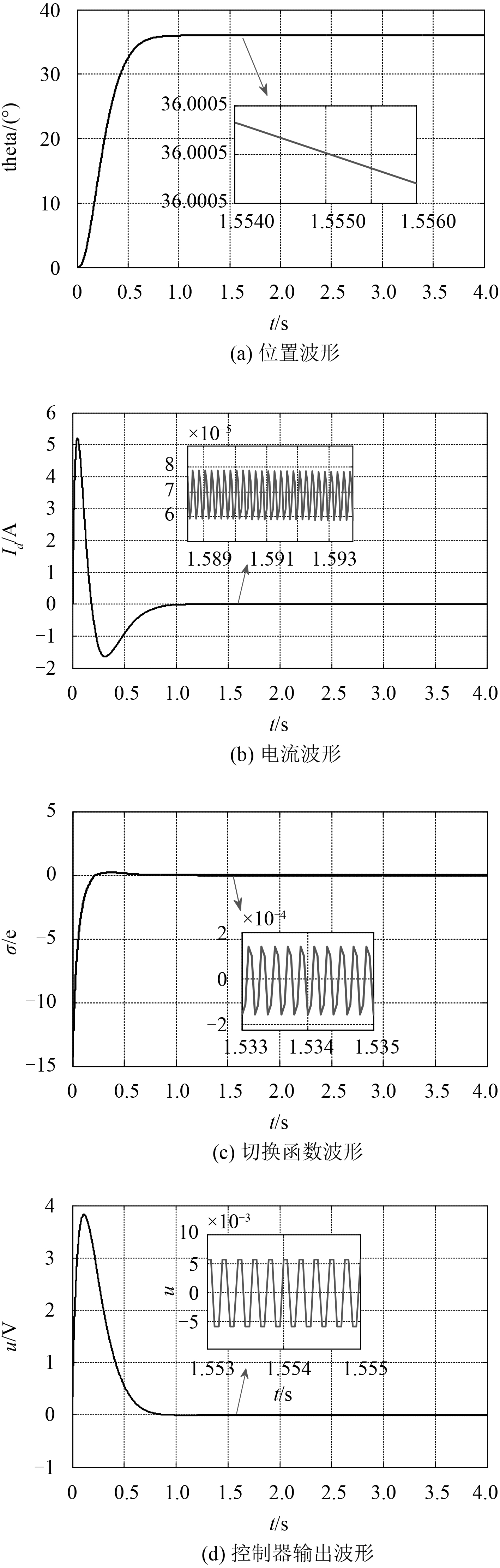
|
图 4 滑模控制下的转台阶跃特性仿真结果 Fig. 4 Simulation results of turntable step characteristic under sliding mode control |
从图4可以看出,传统滑模控制器可以使位置达到设定目标,并且在稳态值附近只有微幅低频摆动。但是电流波形、切换函数、控制器输出形成了高频抖动,这种高频抖动可能损坏舰载稳定平台的机械结构,大大降低了稳定平台的寿命。
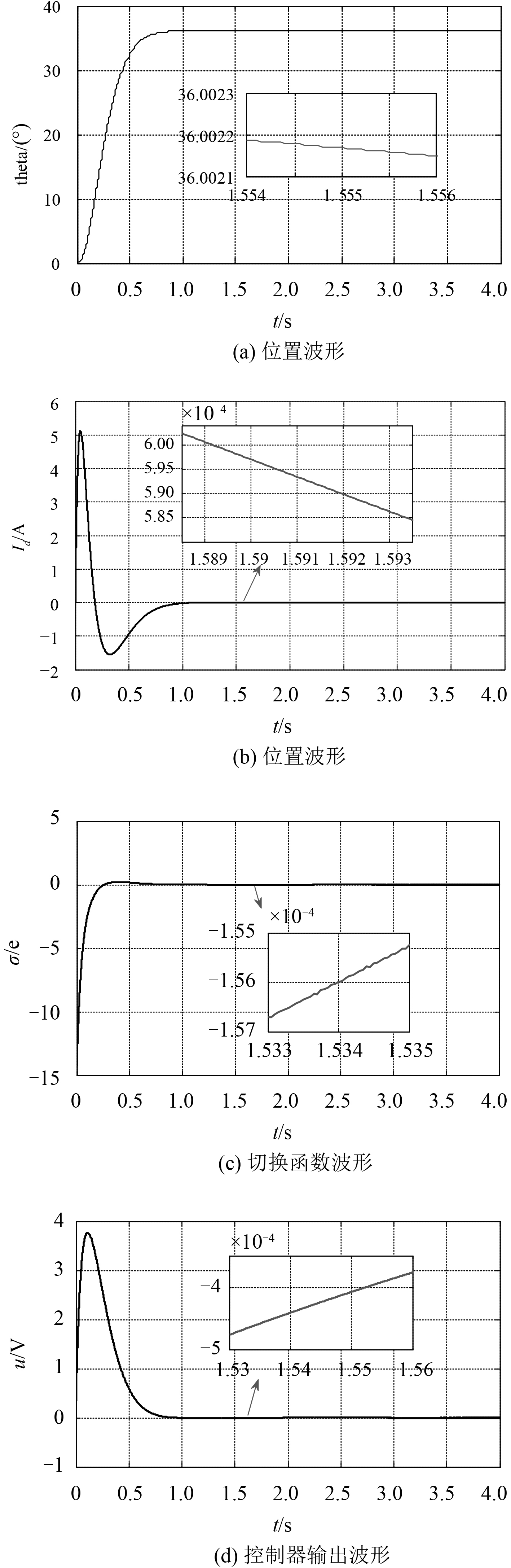
4.2 无抖动滑模控制仿真分析选择无抖动滑模切换函数的参数为:
|
图 5 无抖动滑模控制仿真结果 Fig. 5 Simulation results of chatting-free sliding mode control |
对比图4和图5,图4(c)中,系统状态在滑模面上快速穿梭,形成高频的滑模抖动,而图5(c)中,系统缓慢地逼近、穿越、远离滑模切换平面,消除了高频抖动,通过图5(b)和图5(d)可以看出,电流波形和控制器输出波形也消除了高频抖动,通过图5(a)可以看出,在新的滑模控制中系统依然可以稳定在给定位置。
5 双轴舰载稳定平台试验研究舰载稳定平台如图6所示,包含航向轴和俯仰轴2个电机。当船体随着波浪或拐弯发生倾斜时,通过调节平台2个轴,维持平台水平和稳定。舰载稳定平台要求伺服系统有较好的快速性和稳定性。平台采用的电机参数如表1所示,平台伺服控制器基于STM32F407VET6设计,上位机基于Labview平台设计。

|
图 6 双轴舰载稳定平台 Fig. 6 Biaxial ship-borne stability platform |
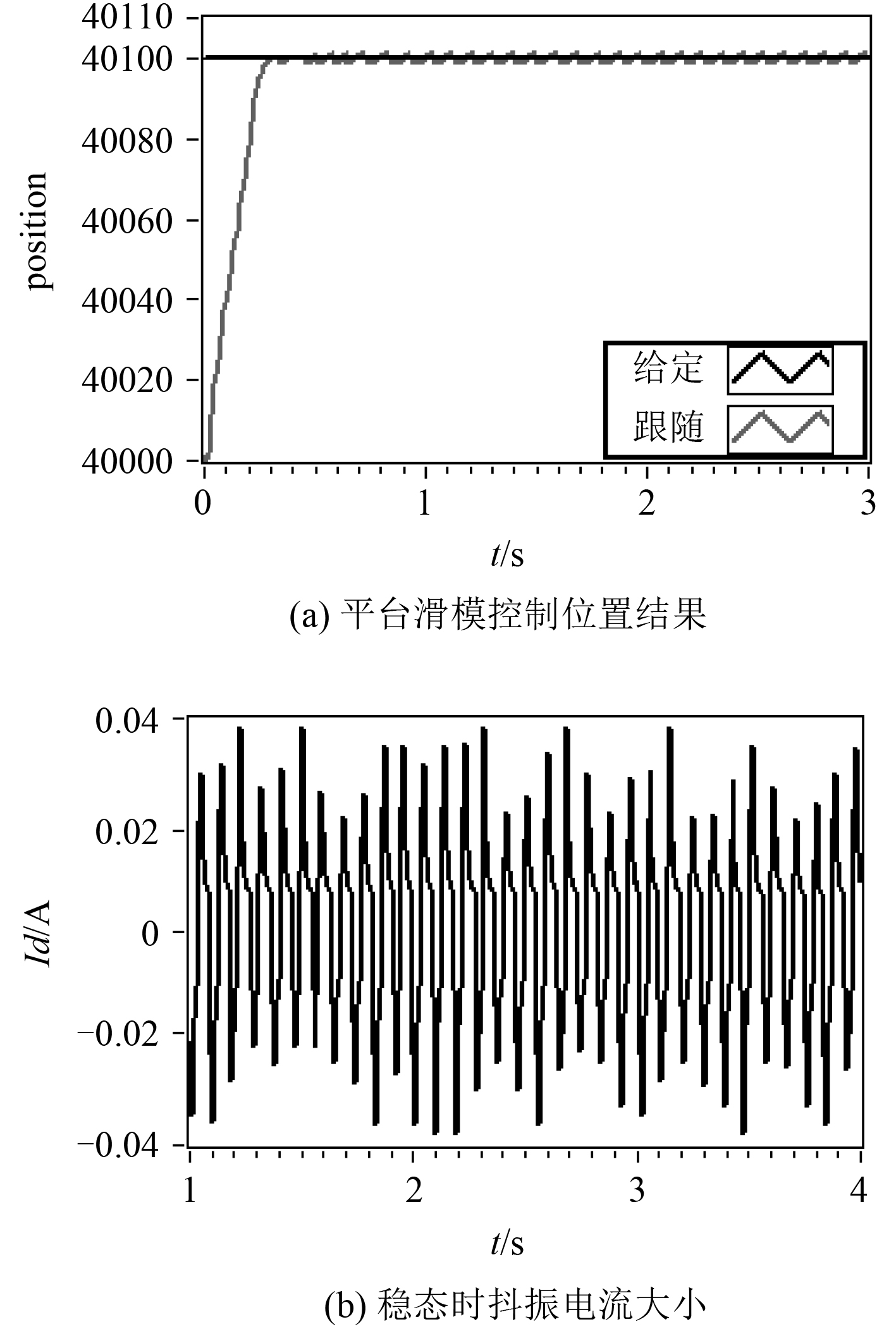
由于高频抖动会对舰载稳定平台造成一定程度的损坏,因此,只对无抖动滑模控制进行试验研究。给定转台一个阶跃位置信号,测量得到其响应波形如图7所示[8]。
|
图 7 转台滑模控制阶跃响应调试结果 Fig. 7 Turntable sliding mode control step response debug result |
平台旋转一周编码器输出的脉冲数量是80 000,从图7 (a)中可以看出,位置相应可以快速达到给定目标,在给定值附近的抖动不会超过10个脉冲(合0.045°),电流的抖动只有小于0.04 A的低频抖动,对于转台的影响基本可以忽略。
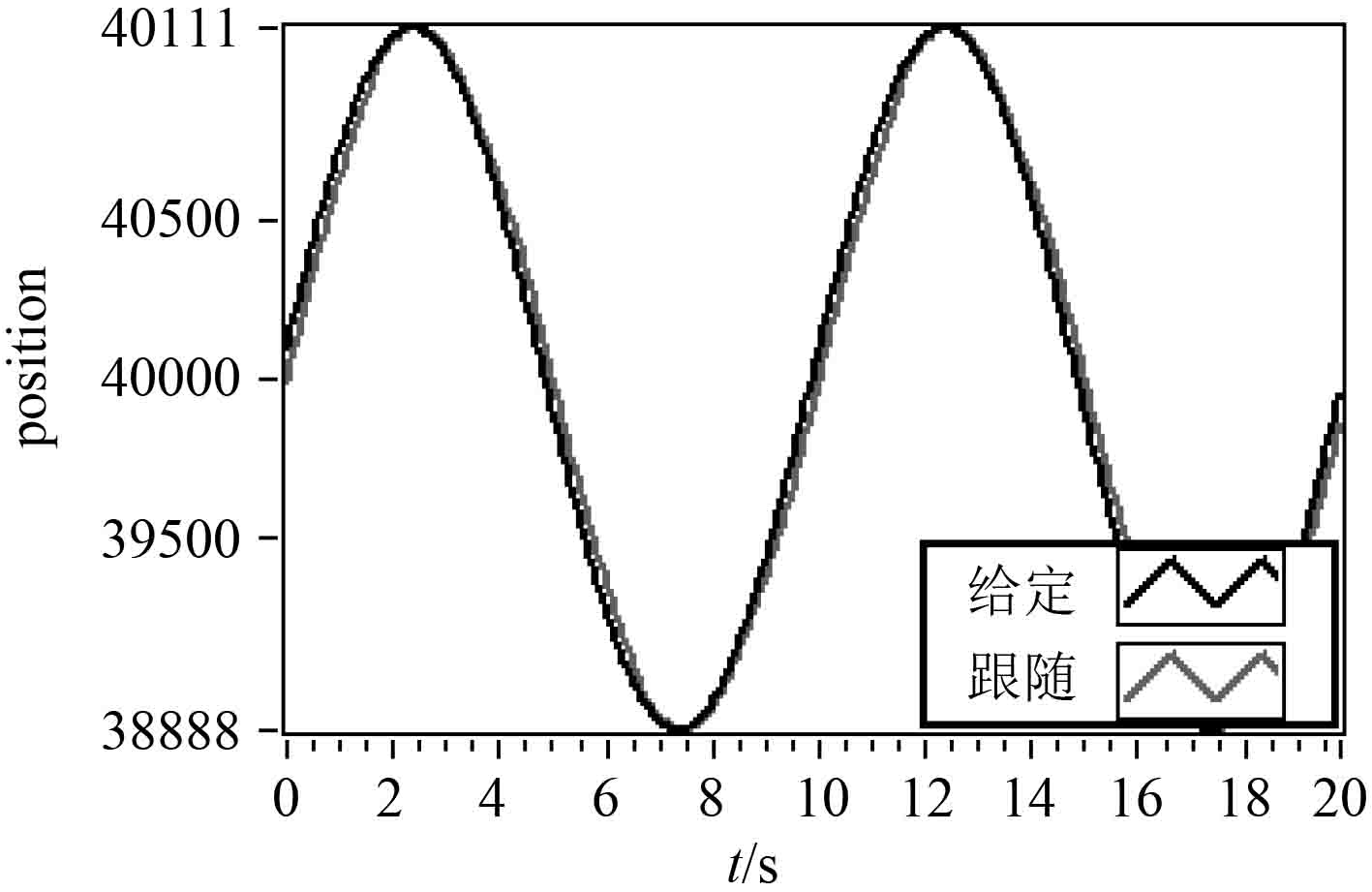
海洋波浪的平均周期大约在1~10 s[9],为了模拟舰载平台在波浪中的稳定特性,使平台航向轴和俯仰轴同时在无抖动滑模控制算法下,跟随周期为10 s、幅度为5°的正弦波信号。由于2个轴的试验结果相同,故只给出航向轴的试验结果,如图8所示[8]。
从图8中可以看出,航向轴最大跟随误差约为80(合0.36°),即稳态误差为0.1%。基于非奇异终端的滑模控制具有快速的跟随性能和良好的稳定性能。
当船舶在海浪中航行时,船体随着波浪摆动,舰载稳定平台通过反向调整,跟随转动,使平台维持水平状态,并且消除了高频抖动,保护了舰载稳定平台的机械结构,增加其寿命。
6 结 语本文建立了舰载稳定平台的数学模型,基于STM32F407VET6和Labview设计了双轴舰载稳定平台伺服控制系统,通过仿真验证了非奇异终端滑模控制的理论可行性,通过双轴舰载稳定平台试验研究验证了非奇异终端滑模控制可以解决平台的高频抖动问题,并且具有良好的精度和跟踪性。
|
图 8 转台滑模控制模拟跟随调试结果 Fig. 8 Turntable sliding mode control simulation follow the debugging results |
| [1] | 陈松林, 单梅林, 王丽斌. 基于干扰观测器的飞行仿真转台完全跟踪控制[J]. 电机与控制学报, 2015, 19 (1): 113–118. |
| [2] | HILKERT J M. Inertially stabilized platform technology concepts and principles[J]. IEEE Control System Magazine, 28, Febrary 2008: 26–46. |
| [3] | 李猛. 两轴船载稳定平台控制系统设计与研究[D]. 哈尔滨: 哈尔滨工业大学, 2015: 1–5. |
| [4] | EYYUP S, TUNA B, BULENT E P. Compensation of friction effects in gyro-stabilized motion platforms[C]// American Control Conference. Chicago, IL, 1–3 July. 2015: 3242–3248. |
| [5] | 余珊珊, 夏军. 光纤陀螺在机载光电稳定平台中的应用[J]. 电子质量, 2015 (5): 30–32. |
| [6] | 齐亮. 基于滑模变结构方法的永磁同步电机控制问题研究及应用[D]. 上海: 华东理工大学, 2013: 7–10. |
| [7] | Y FENG, X YU, Z MAN. Nonsingular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159–2167. |
| [8] | 史普帅. 基于船载稳定平台的伺服控制系统研究[D]. 威海: 哈尔滨工业大学, 2016. |
| [9] | 毕凡. 波浪对环流输运影响和涌浪传播耗散特征研究[D]. 青岛: 中国海洋大学, 2013. |
 2018, Vol. 40
2018, Vol. 40
