近年来,随着海洋资源勘探与开发,海洋安全越来越受到人们的高度重视。无人艇由于在海洋科研、海洋安全等方面具有广泛的应用潜力,逐渐成为国际研究热点。因为欠驱动无人艇具有非常复杂的非线性特性,使其成为非线性控制的一个重要研究领域,所以欠驱动无人艇的研究具有很大的挑战和实际意义。
早期的无人艇协同控制问题主要是针对编队控制。2009年,Burger等[1]针对模型中非对角惯性矩阵和阻尼矩阵,在设计时考虑洋流对船舶运动的影响,设计了一种欠驱动船舶直线路径跟踪编队控制器。2010年,彭周华等[2]在领导-跟随模式下,利用神经网络对领航船动态进行逼近,设计一种仅需要领航船位置信息的鲁棒自适应编队控制器,无需领航船的速度信息且有效地补偿了不确定性问题。
对于协同路径跟踪和协同目标跟踪问题,2007年,Bibuli等[3]结合Lyapunov直接法与反步法设计了鲁棒控制器,实现了欠驱动船舶的有效路径跟踪控制。2010年,Oh等[4]基于视线法(line of sight,LOS),利用预测控制设计了当舵角控制输入满足一定约束条件的欠驱动船舶路径跟踪控制。2012年,R.Yu等[5]研究了一个具有参数不确定性的欠驱动船舶鲁棒跟踪控制问题。提出了一种滑模控制律并实现了欠驱动自主水面舰艇的轨迹跟踪。2014年,Thomas Glotzbach等[6]研究了多无人艇编队LOS协同目标跟踪的理论与实践。为了实现LOS协同目标跟踪,开发单一的自主海洋航行器协同编队是控制体系。在控制体系中,解决了跟踪移动水下目标和无人艇编队问题。
包含控制是指存在多个领导者,通过设计控制协议,驱使所有跟随者进入有领导者围成区域内。包含控制可以应用于许多实际问题。比如,一组不同类型的机器人要从一个地点转移到另一个地点。其中只有一部分机器人有能力来探测途中的危险障碍,这些机器人就被设计为领导者,其他机器人为跟随者。跟随者只需要在领导者所包围的安全区域内运动,就可以安全的到达目的地。
2011年,Meng等[7]研究了多智能体为Lagrange系统的包含控制问题,以及多刚体系统的有限时间包含控制问题。2011年[14],李建祯研究了多智能体系统一致性若干问题研究,以及有多个领导者的二阶多智能体系统的包含控制问题。
2014年,彭周华等[8]研究了基于神经DSC方法的多领导者水下机器人的网络化包含控制方法。研究多领导者水下机器人在包含控制中存在的模型不确定性和海风、海浪、海流的环境干扰。基于一种预测神经动态面控制设计方法,提出了自适应包含控制器,使跟随者进入领导者的凸包范围内。
2015年,彭周华等[9]研究了在模型不确定性和洋流干扰情况下的多领导者水下航行器的网络化包含控制。提出了基于预测的神经动态面控制设计方法,开发的自适应包含控制器,使得跟随者的运动轨迹收敛到有领导者形成的凸包。
然而,与各位学者研究的内容相比,对于欠驱动无人艇的包含控制问题并未涉及。因此,本文研究了具有多个动态领航船的欠驱动无人艇的包含控制问题,提出了一种基于虚拟领航船的包含控制方法。然后为虚拟领航船设计了相应的包含控制算法,并基于滑模控制理论为跟随船设计了目标跟踪算法。使得每个跟随者都至少有一个领导者到该跟随者有一条有向路径,在通过合理的配置参数,所有的跟随者就能进入领导者组成的凸包内。
1 准备知识与问题描述 1.1 图论的概念本文采用图
一条有向路径是由一系列
图
定义1令
本文考虑由
|
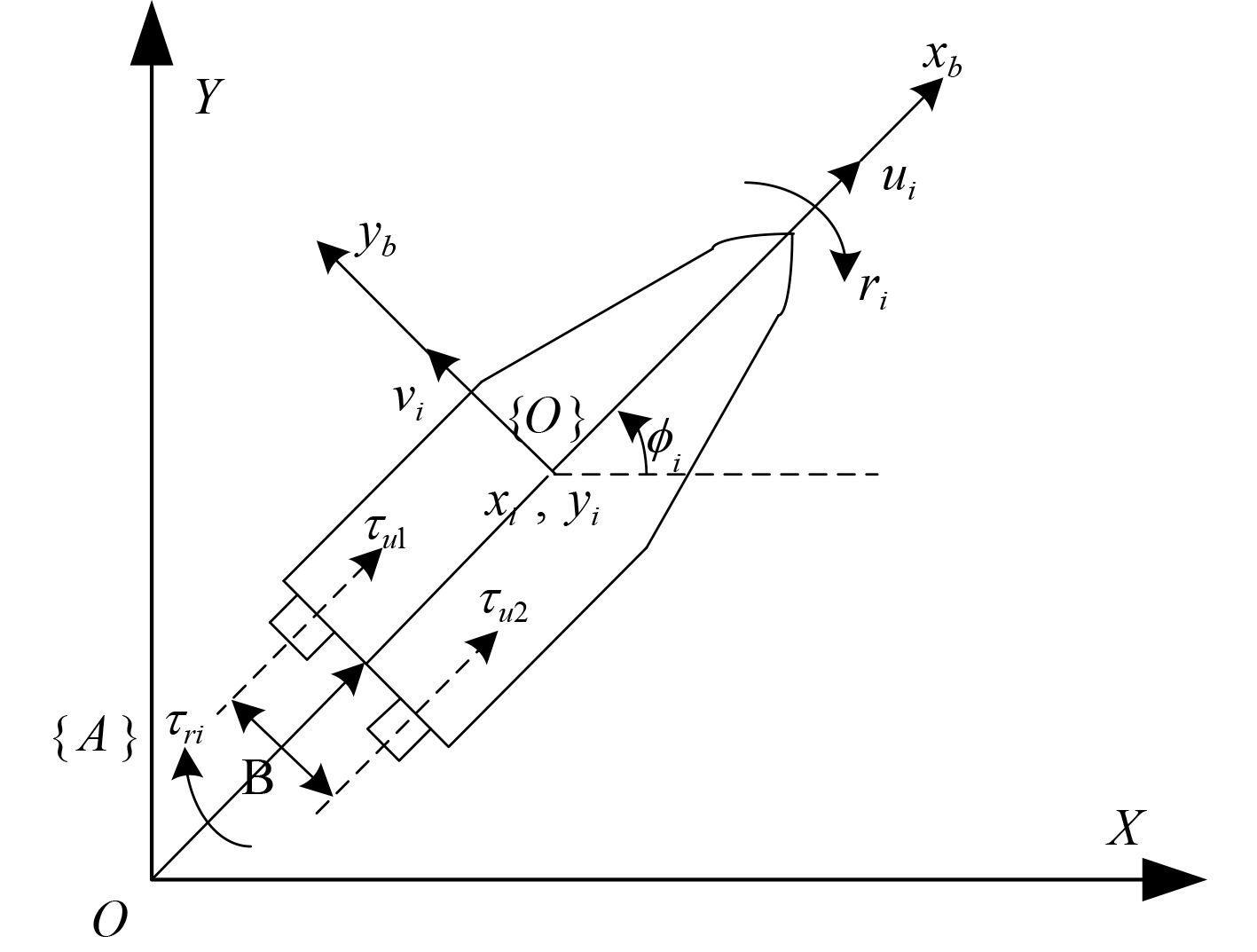
图 1 具有双推进器的无人艇水面运动模型 Fig. 1 Planar model of the ASV with two propellers |
欠驱动无人艇的运动学与动力学模型可描述为[10]
| $\left\{ {\begin{array}{*{20}{l}}{\mathop {{u_i}}\limits^ \cdot = \frac{{{m_{22}}}}{{{m_{11}}}}{v_i}{r_i} - \frac{{{d_{11}}}}{{{m_{11}}}}{u_i} + \frac{1}{{{m_{11}}}}\left( {{\tau _{ui}} + {\tau _1}} \right)}\text{,}\\{\mathop {{v_i}}\limits^ \cdot = - \frac{{{m_{11}}}}{{{m_{22}}}}{u_i}{r_i} - \frac{{{d_{22}}}}{{{m_{22}}}}{v_i} + \frac{{{\tau _2}}}{{{m_{22}}}}}\text{,}\\{\mathop {{r_i}}\limits^ \cdot = \frac{{{m_{11}} - {m_{22}}}}{{{m_{33}}}}{u_i}{v_i} - \frac{{{d_{33}}}}{{{m_{33}}}}{r_i} + \frac{1}{{{m_{33}}}}\left( {{\tau _{ri}} + {\tau _3}} \right)}\text{,}\\{\mathop {{x_i}}\limits^ \cdot = {u_i}\cos {\varphi _i} - {v_i}\sin {\varphi _i}}\text{,}\\{\mathop {{y_i}}\limits^ \cdot = {u_i}\sin {\varphi _i} + {v_i}\cos {\phi _i}}\text{,}\\{\mathop {{\varphi _i}}\limits^ \cdot = {r_i}}\text{。}\end{array}} \right.,i = 1, \ldots ,n + s,$ | (1) |
其中:(
假设
| ${L}= \left[ {\begin{array}{*{20}{c}} {{L_1}} & {{L_2}} \\ {{0_{s \times n}}} & {{0_{s \times s}}} \end{array}} \right]\text{,}$ |
其中:
假设1 领导者的控制输入有界,且对于每一个跟随者,至少存在一个领导者到该跟随者之间有一条有向路径。
引理1 若假设1成立,则上文中定义的
控制目标是为欠驱动无人艇
即
|
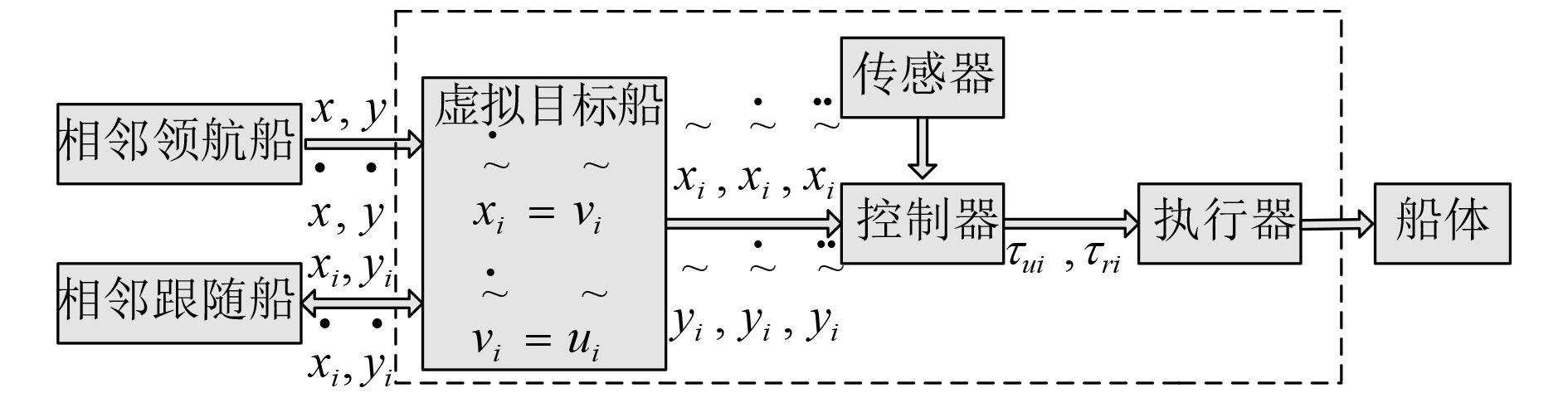
图 2 无人艇包含控制系统 Fig. 2 ASV containment control system |
为了实现包含控制目标,本文设计了无人艇包含控制算法,其结构如图2所示。所有的跟随船都有一个虚拟目标船,用来计算该跟随船的理想位置。虚拟目标船的数学模型为:
| $\begin{array}{l}\mathop {\widetilde {{x_i}}}\limits^ \cdot = \widetilde {{v_i}}\text{,}\\\mathop {\widetilde {{v_i}}}\limits^ \cdot = \widetilde {{u_i}}\text{。}\end{array}$ | (2) |
其中:
无人艇之间的通信内容如下:1)所有的跟随船跟自己的相邻跟随船交换各自虚拟目标船的位置和速度信息;2)跟随船收到其相邻领航船的位置和速度信息。这样,所有跟随船上的虚拟目标船和所有领航船组成了1个虚拟协同控制系统。本文的设计思路是:1)首先为所有的虚拟目标船设计包含控制算法,使得虚拟目标船的位置进入领航船组成的凸包内;2)所有的跟随船以虚拟目标船的位置和速度为控制目标进行跟踪控制。这样,只要控制算法设计合理,就能使所有跟随船进入领航船组成的凸包内。
这样设计的优点是使得每个跟随者都至少有一个领导者到该跟随者有一条有向路径,在通过合理的配置参数,所有的跟随者就能进入领导者组成的凸包内。
2.2 包含控制器设计假设领导者的速度不同,可以采用如下包含控制算法:
| $\begin{array}{l}\widetilde {{u_i}}\left( t \right) = - \left\{ {\sum\limits_{j = 1}^{n + s} {{a_{ij}}\left[ {\widetilde {{x_i}}\left( t \right) - \widetilde {{x_j}}\left( t \right)} \right]} + \alpha \sum\limits_{j = 1}^{n + s} {{a_{ij}}\left[ {\widetilde {{v_i}}\left( t \right) - \widetilde {{v_j}}\left( t \right)} \right]} } \right\} - \\ \beta {\mathop{\rm sgn}} \left\{ {\sum\limits_{j = 1}^{n + s} {{a_{ij}}\left[ {\widetilde {{x_i}}\left( t \right) - \widetilde {{x_j}}\left( t \right)} \right] + \alpha \sum\limits_{j = 1}^{n + s} {{a_{ij}}\left[ {\widetilde {{v_i}}\left( t \right) - \widetilde {{v_j}}\left( t \right)} \right]} } } \right\},\\ i = 1, \ldots ,n\text{。}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\ \ \end{array}$ | (3) |
其中
引理2[11] 假设跟随者之间的通信网络为无向图,且对每一个跟随者都有至少一个领导者到该跟随者有一条有向路径。
令
| $\delta < \min \left\{ {\sqrt {{\lambda _{\min }}\left( M \right)} ,\frac{{4\alpha {\lambda _{\min }}\left( M \right)}}{{4 + {\alpha ^2}{\lambda _{\min }}\left( M \right)}}} \right\},$ |
且
设计控制器之前,首先给出如下定理:
定理1 微分方程
| $\mathop x\limits^ \cdot = - \frac{{ax}}{{\sqrt {{x^2} + c} }}\text{,}$ | (4) |
其中:
定义位置跟踪误差变量
| ${x_{Ai}} = {x_i} - \widetilde {{x_i}},\;{y_{Ai}} = {y_i} - \widetilde {{y_i}},$ | (5) |
其中,
由式(1)可得
| $\left[ {\begin{array}{*{20}{c}} {{u_i}} \\ {{v_i}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos {\varphi _i}} & {\sin {\varphi _i}} \\ { - \sin {\varphi _i}} & {\cos {\varphi _i}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathop {{x_i}}\limits^ \cdot } \\ {\mathop {{y_i}}\limits^ \cdot } \end{array}} \right]\text{。}$ | (6) |
为实现无人艇位置跟踪误差的收敛,设计如下虚拟控制率:
| $\left[ {\begin{array}{*{20}{c}}{{u_{ui}}}\\{{v_{ri}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{\cos {\varphi _i}} & {\sin {\varphi _i}}\\{ - \sin {\varphi _i}} & {\cos {\varphi _i}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{\mathop {\widetilde {{x_i}}}\limits^ \cdot - \frac{{k{x_{Ai}}}}{{\sqrt {x_{Ai}^2 + y_{Ai}^2 + C} }}}\\{\mathop {\widetilde {{y_i}}}\limits^ \cdot - \frac{{k{y_{Ai}}}}{{\sqrt {x_{Ai}^2 + y_{Ai}^2 + C} }}}\end{array}} \right]\text{,}$ | (7) |
其中:
| $\left[ {\begin{array}{*{20}{c}} {\mathop {{x_{Ai}}}\limits^ \cdot } \\ {\mathop {{y_{Ai}}}\limits^ \cdot } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{ - k{x_{Ai}}}}{{\sqrt {x_{Ai}^2 + y_{Ai}^2 + C} }}} \\ {\frac{{ - k{y_{Ai}}}}{{\sqrt {x_{Ai}^2 + y_{Ai}^2 + C} }}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\cos {\varphi _i}} & {\sin {\varphi _i}} \\ { - \sin {\varphi _i}} & {\cos {\varphi _i}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_i} - {u_{ui}}} \\ {{v_i} - {v_{ri}}} \end{array}} \right]\text{,}$ | (8) |
当
| $\left[ {\begin{array}{*{20}{c}} {\mathop {{x_{Ai}}}\limits^ \cdot } \\ {\mathop {{y_{Ai}}}\limits^ \cdot } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{ - k{x_{Ai}}}}{{\sqrt {x_{Ai}^2 + y_{Ai}^2 + C} }}} \\ {\frac{{ - k{y_{Ai}}}}{{\sqrt {x_{Ai}^2 + y_{Ai}^2 + C} }}} \end{array}} \right]\text{,}$ |
由定理1得到
| $\mathop {\lim }\limits_{t \to \infty } {x_{Ai}} = 0,\;\mathop {\lim }\limits_{t \to \infty } {y_{Ai}} = 0\text{。}$ |
令
| $\begin{array}{l}\left[ {\begin{array}{*{20}{c}}{\mathop {{u_{ui}}}\limits^ \cdot }\\{\mathop {{v_{ri}}}\limits^ \cdot }\end{array}} \right] \!=\! \left[ {\begin{array}{*{20}{c}}{ - {r_i}\sin {\varphi _i}} & {{r_i}\cos {\varphi _i}}\\{ - {r_i}\cos {\varphi _i}} & { - {r_i}\sin {\varphi _i}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{\mathop {\widetilde {{x_i}}}\limits^ \cdot - k{w^{ - 1}}{x_{Ai}}}\\{\mathop {\widetilde {{y_i}}}\limits^ \cdot - k{w^{ - 1}}{y_{Ai}}}\end{array}} \right] + \\\left[ {\begin{array}{*{20}{c}}{\mathop {\widetilde {{x_i}}}\limits^{ \cdot \cdot } + k\left( {{w^{ - 1}} - {w^{ - 3}}x_{Ai}^2} \right)\mathop {{x_{Ai}}}\limits^ \cdot - k{w^{ - 3}}{x_{Ai}}{y_{Ai}}\mathop {{y_{Ai}}}\limits^ \cdot }\\{\mathop {\widetilde {{y_i}}}\limits^{ \cdot \cdot } + k\left( {{w^{ - 1}} - {w^{ - 3}}y_{Ai}^2} \right)\mathop {{x_{Ai}}}\limits^ \cdot - k{w^{ - 3}}{x_{Ai}}{y_{Ai}}\mathop {{x_{Ai}}}\limits^ \cdot }\end{array}} \right] \times \\\left[ {\begin{array}{*{20}{c}}{\cos {\varphi _i}} & {\sin {\varphi _i}}\\{ - \sin {\varphi _i}} & {\cos {\varphi _i}}\end{array}} \right] = \\\left[ {\begin{array}{*{20}{c}}{{r_i}\mathop {{v_{ri}}}\limits^ \cdot }\\{ - {r_i}\mathop {{u_{ui}}}\limits^ \cdot }\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}{\cos {\varphi _i}} & {\sin {\varphi _i}}\\{ - \sin {\varphi _i}} & {\cos {\varphi _i}}\end{array}} \right] \times \\\left[ {\begin{array}{*{20}{c}}{\mathop {\widetilde {{x_i}}}\limits^{ \cdot \cdot } + k\left( {{w^{ - 1}} - {w^{ - 3}}x_{Ai}^2} \right)\mathop {{x_{Ai}}}\limits^ \cdot - k{w^{ - 3}}{x_{Ai}}{y_{Ai}}\mathop {{y_{Ai}}}\limits^ \cdot }\\{\mathop {\widetilde {{y_i}}}\limits^{ \cdot \cdot } + k\left( {{w^{ - 1}} - {w^{ - 3}}y_{Ai}^2} \right)\mathop {{x_{Ai}}}\limits^ \cdot - k{w^{ - 3}}{x_{Ai}}{y_{Ai}}\mathop {{x_{Ai}}}\limits^ \cdot }\end{array}} \right]\text{。}\end{array}$ |
下面基于滑模控制理论[10, 12-13],分别设计纵向和横向的轨迹跟踪控制器[10]。
1)纵向控制器设计
定义纵向速度跟踪误差变量
| ${u_{xi}} = {u_i} - {u_{ui}}\text{,}$ | (9) |
纵向滑模面采用一阶的指数镇定面:
| ${S_{1i}} = {u_{xi}} + {\lambda _1}\int_0^t {{u_{xi}}\left( \tau \right){\rm d}\tau } ,\;{\lambda _1} > 0,\;i = 1, \ldots ,n\text{。}$ | (10) |
设计纵向滑模控制器为
| ${\tau _{ui}} = \widehat {{\tau _{ui}}} - {k_1}sat\left( {{S_{1i}}/{\varPhi _1}} \right)\text{,}$ | (11) |
式中:
为了确定
| $\left| {{m_{ii}} - \widehat {{m_{ii}}}} \right| \text{≤} {M_i},\;\left| {{d_{ii}} - \widehat {{d_{ii}}}} \right| \text{≤} {D_i},\;\left| {{\tau _i} - \widehat {{\tau _i}}} \right| \text{≤} {T_i},\;i = 1,2,3\text{。}$ |
定义
| ${V_1} = \frac{1}{2}{m_{11}}S_{1i}^2\text{,}$ |
将
| $\begin{array}{l}\mathop {{V_1}}\limits^ \cdot = {m_{11}}{S_{1i}}\mathop {{S_{1i}}}\limits^ \cdot = \\{S_{1i}}\left[ {\left( {{m_{22}} - \widehat {{m_{22}}}} \right){v_i}{r_i}} \right. + \left( {\widehat {{d_{11}}} - {d_{11}}} \right){u_i} + \left( {{\tau _1} - \widehat {{\tau _1}}} \right) + \\\left( {{m_{11}} - \widehat {{m_{11}}}} \right)\left( { - \mathop {{u_{ui}}}\limits^ \cdot + {\lambda _1}{u_{xi}}} \right) - {k_{1i}}sat\left. {\left( {{S_{1i}}/{\Phi _1}} \right)} \right]\text{,}\end{array}$ |
如将
| $\begin{array}{l}{k_1} = {M_2}\left| {{v_i}{r_i}} \right| + {D_1}\left| {{u_i}} \right| + {T_i} + \\{M_1}\left| { - \mathop {{u_{ui}}}\limits^ \cdot + {\lambda _1}{u_{xi}}} \right| + \widehat {{m_{11}}}{\eta _1}\text{,}\end{array}$ |
其中
| $\mathop {{V_1}}\limits^ \cdot = {m_{11}}{S_{1i}}\mathop {{S_{1i}}}\limits^ \cdot \text{≤} - \widehat {{m_{11}}}{\eta _1}\left| {{S_{1i}}} \right|\text{。}$ |
2)横向控制器设计
定义横向速度跟踪误差变量
| ${v_{xi}} = {v_i} - {v_{ri}}\text{,}$ | (12) |
横向滑模表面定义为二阶的指数镇定面:
| ${S_{2i}} = \mathop {{v_{xi}}}\limits^ \cdot + 2{\lambda _2}{v_{xi}} + \lambda _2^2\int_0^t {{v_{xi}}} \left( \tau \right){\rm d}\tau ,\;{\lambda _2} > 0,\;i = 1, \ldots ,n\text{。}$ | (13) |
将
| ${\mathop S\limits^ \cdot _{2i}} = \left( {\mathop {{v_i}}\limits^{ \cdot \cdot } - \mathop {{v_{ri}}}\limits^{ \cdot \cdot } } \right) + 2{\lambda _{2i}}\left( {\mathop {{v_i}}\limits^ \cdot - {v_{ri}}} \right) + \lambda _2^2{v_{xi}} = 0\text{,}$ | (14) |
将
| $\mathop {{v_i}}\limits^{ \cdot \cdot } = - \frac{{{m_{11}}\left( {\mathop {{u_i}}\limits^ \cdot {r_i} + {u_i}\mathop {{r_i}}\limits^ \cdot } \right) + {d_{22}}\mathop {{v_i}}\limits^ \cdot + \mathop {{\tau _2}}\limits^ \cdot }}{{{m_{22}}}}\text{,}$ | (15) |
| $\mathop {{v_{ri}}}\limits^{ \cdot \cdot } = {v_{0i}} - {u_{ui}}\mathop {{r_i}}\limits^ \cdot\text{,}$ | (16) |
| $\begin{array}{l}{v_{0i}} = \left( {\mathop {\widetilde {{y_i}}}\limits^{ \cdot \cdot } + k\left( {{w^{ - 1}} - {w^{ - 3}}y_{Ai}^2} \right)\mathop {{y_{Ai}}}\limits^ \cdot - k{w^{ - 3}}{x_{Ai}}{y_{Ai}}\mathop {{x_{Ai}}}\limits^ \cdot } \right)\cos {\varphi _i} \;-\\ \left( {\mathop {\widetilde {{x_i}}}\limits^{ \cdot \cdot } + k\left( {{w^{ - 1}} - {w^{ - 3}}x_{Ai}^2} \right)\mathop {{x_{Ai}}}\limits^ \cdot - k{w^{ - 3}}{x_{Ai}}{y_{Ai}}\mathop {{y_{Ai}}}\limits^ \cdot } \right)\sin {\varphi _i}\text{。}\quad\ \ \end{array}$ | (17) |
将式(1),式(15),式(16)代入式(14)可得名义横向控制器
| $\widehat {{\tau _{ri}}} = \widehat {{h_i}}/\widehat {{b_i}}\text{。}$ | (18) |
式中:
| ${b_i} = {m_{22}}{u_{ui}} - {m_{11}}{u_i}\text{,}$ | (19) |
| $\begin{split}{l}{h_i} = {b_i}\left( {\left( {{m_{22}} - {m_{11}}} \right){u_i}{v_i} + {d_{33}}{r_i} - {\tau _3}} \right) - \\ {m_{33}}\left( {2{\lambda _{2i}}{m_{22}}\mathop {{v_{xi}}}\limits^ \cdot + \lambda _{2i}^2{m_{22}}{v_{xi}}} \right) +\\ {m_{33}}\left( {{m_{11}}\mathop {{u_i}}\limits^ \cdot {r_i} + {d_{22}}\mathop {{v_i}}\limits^ \cdot + {m_{22}}{v_{0i}} + \mathop {{\tau _2}}\limits^ \cdot } \right)\text{。}\end{split}$ | (20) |
设计横向滑模控制器为
| ${\tau _{ri}} = \left[ {\widehat {{h_i}} - {k_2}sat\left( {{S_{2i}}/{\varPhi _2}} \right)} \right]/\widehat {{b_i}}\text{。}$ | (21) |
式中:
定义
| ${V_2} = \frac{1}{2}{m_{22}}{m_{33}}S_{2i}^2\text{,}$ |
将
| $\begin{array}{l}\mathop {{V_2}}\limits^ \cdot = {m_{22}}{m_{33}}{S_{2i}}\mathop {{S_{2i}}}\limits^ \cdot \left[ {\frac{{{b_i}{\tau _{ri}} - {h_i}}}{{{m_{22}}{m_{33}}}}} \right] = \\{S_{2i}}\left[ {\left( {{b_i}\widehat {b_i^{ - 1}} - 1} \right)\widehat {{h_i}} + \left( {\widehat {{h_i}} - {h_i}} \right) - {b_i}\widehat {b_i^{ - 1}}{k_2}sat\left( {{S_{2i}}/{\varPhi _2}} \right)} \right]\text{,}\end{array}$ |
如将
| ${k_2} = \gamma \left( {{H_i} + \widehat {{m_{22}}}\widehat {{m_{33}}}{\eta _2}} \right) + \left( {\gamma - 1} \right)\left| {\widehat {{h_i}}} \right|\text{,}$ |
式中
| $\mathop {{V_2}}\limits^ \cdot = {m_{22}}{m_{33}}{S_{2i}}\mathop {{S_{2i}}}\limits^ \cdot \text{≤} - \widehat {{m_{22}}}\widehat {{m_{33}}}{\eta _{2i}}\left| {{S_{2i}}} \right|\text{。}$ |
为验证所提出的包含控制算法和控制器的有效性,下面进行数值仿真试验。船模的具体参数为
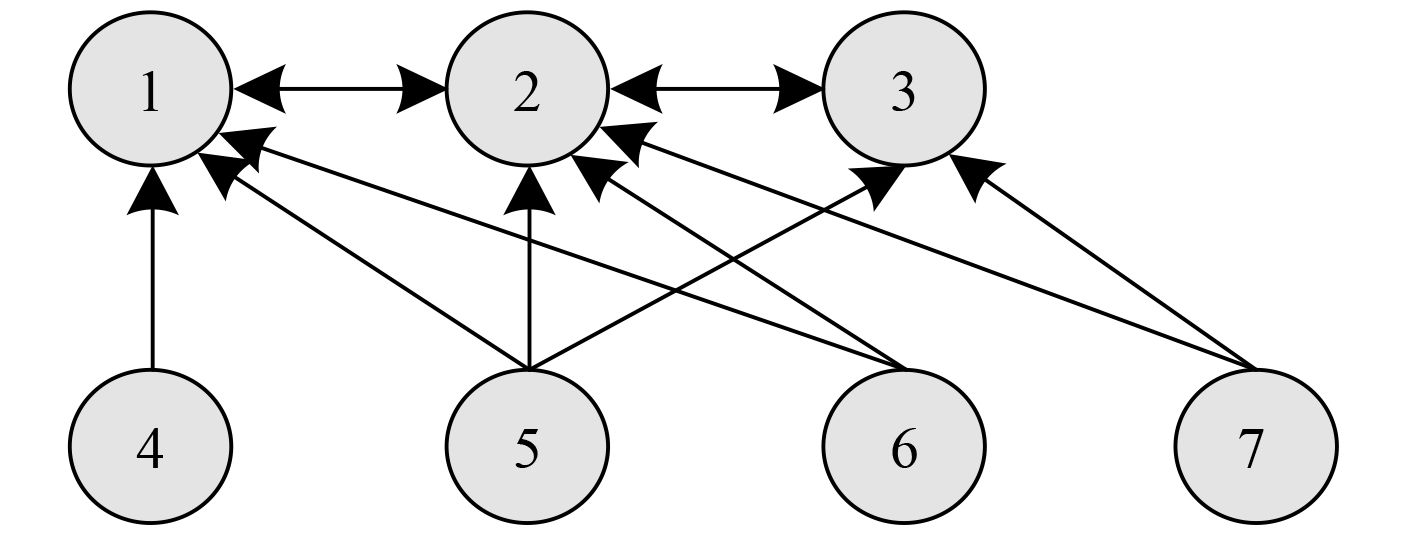
考虑由7个二维空间内的无人艇组成系统。其中无人艇4~7为领导者,无人艇1~3为跟随者。设领导者的动态为
|
图 3 无人艇1~7之间的通信拓扑 Fig. 3 ASV 1~7 communication topology |
|
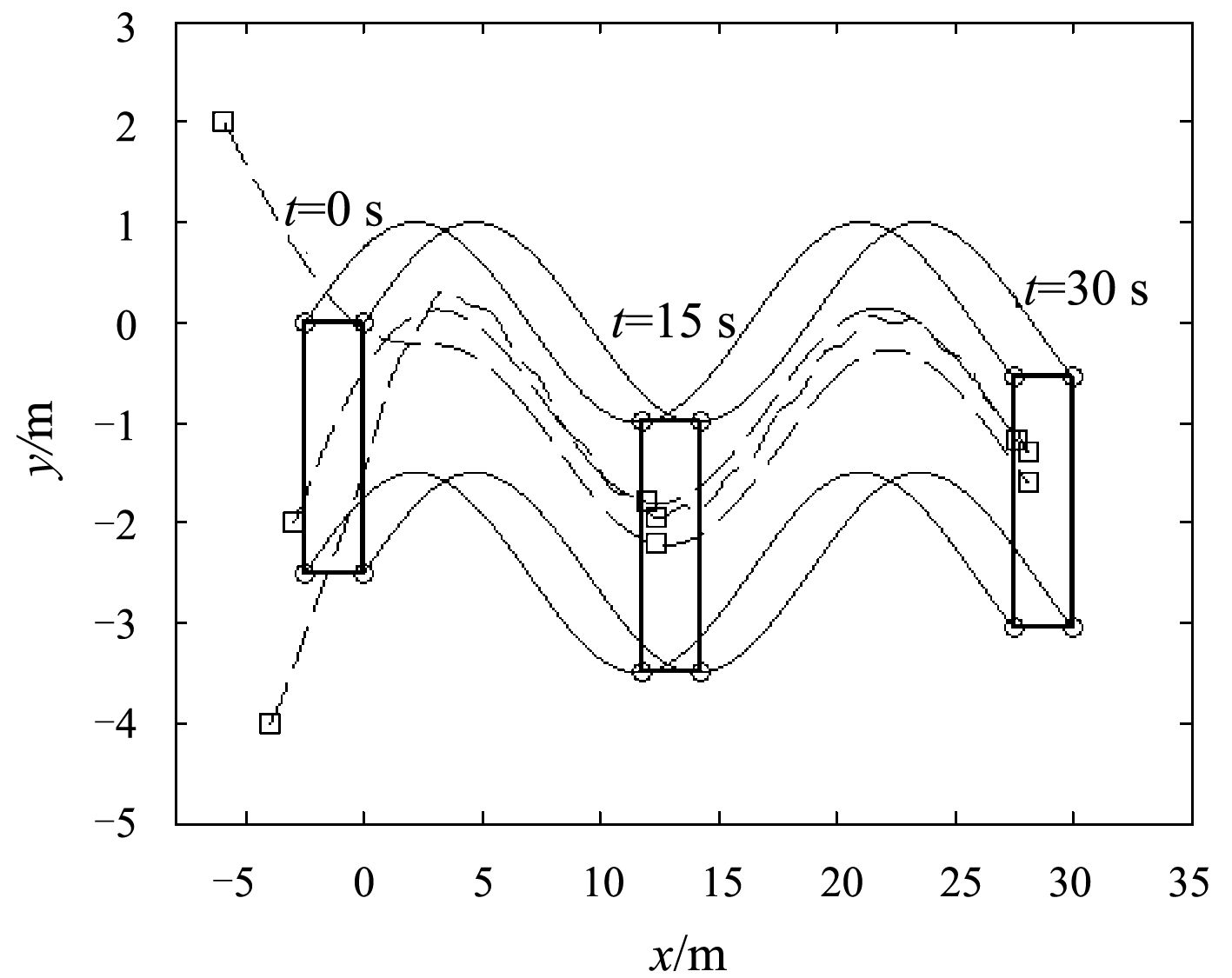
图 4 无人艇1~3跟踪领导者4~7运动轨迹 Fig. 4 ASV 1~3 tracking leader 4~7 motion trajectory |
本文研究了具有多个动态领航船的欠驱动无人艇的包含控制问题,提出了一种基于虚拟领航船的包含控制方法和。然后为虚拟领航船设计了相应的包含控制算法,并基于滑模控制理论为跟随船设计了目标跟踪算法。仿真结果验证了所提出的控制方法的有效性。
| [1] | BURGER M, PAVLOV A, BORHAUG E, et al. Straight line path following for formations of underactuated surface vessels under influence of constant ocean currents[M]. Proceedings of the American Control Conference, 2009: 3065–3070. |
| [2] | Z H PENG, WANG D, LAN W Y, LI X Q, SUN G. Robust adaptive formation control with autonomous surface vehicles[J]. Chinese Control Conference, 2010 : 2115–2120. |
| [3] | BIBULI M, CACCIA M, LAPIERRE L. Path-following algorithms and experiments for an autonomous surface vehicle[C]// Proc. of IFAC Conference on Control Applications in Marine Systems, 2007. |
| [4] | SO-RYEOK O, JING Sn. Path following of underactuated marine surface vessels using line-of-sight based model predictive control[J]. Ocean Engineering, 2010, 37 (2-3): 289–295. DOI: 10.1016/j.oceaneng.2009.10.004 |
| [5] | YU R, ZHU Q, XIA G, et al. Sliding mode tracking control of an underactuated surface vessel[J]. Control Theory and Applications, 2012, 3 : 461–466. |
| [6] | THOMAS G, MATTHIAS S, PETER O. Cooperative line of sight target tracking for heterogeneous unmanned marine vehicle teams: From theory to practice[J]. Robotics and Autonomous Systems, 2014 . |
| [7] | MENG Z, LIN G, REN W. Containment control of networked lagrange systems with group dispersion and cohesion behaviors[C]//Proceedings of the 30th Chinese Control Conference, Yantai, China, 2011: 4639–4644. |
| [8] | PENG Zhou-hua,WANG Dan, WANG Jun. Containment control of networked autonomous underwater vehicles guided by multiple leaders using predictor-based neural DSC approach[R]. Fifth International Conference on Intelligent Control and Information Processing, 2014. |
| [9] | PENG Zhou-hua, WANG Dan. Containment control of networked autonomous underwater vehicles with model uncertainty and ocean disturbances guided by multiple leaders[R]. Information Sciences, 316(2015): 163–179. |
| [10] |
廖煜雷, 庄佳园, 李晔, 等. 欠驱动无人艇轨迹跟踪的滑模控制方法[J]. 应用科学学报, 2011, 29 (4): 428–434.
LIAO Yu-lei, ZHUANG Jia-yuan, LI Ye, et al. Sliding-mode trajectory tacking control for underactuated autonomous surface vehicle[J]. Journal of applied Sciences-Electronics and Information Engineering, 2011, 29 (4): 428–434. |
| [11] | CAO Y, SUART D, REN W, et al. Distributed containment control for multiple autonomous vehicles with double-integrator dynamics: algorithms and experiments[C]// IEEE Transactions on Control Systems Technology, Available online: DOI: 10. 1109/TCST.2010:2053542. |
| [12] |
廖煜雷, 庞永杰. 一类欠驱动机械系统轨迹跟踪的滑模控制方法[J]. 中南大学学报, 2011, 42 (S1): 219–227.
LIAO Yu-lei, PANG Yong-jie. Sliding-mode trajectory tacking control for a class of underactuated mechanical system[J]. Journal of Central South University: Science and Technology, 2011, 42 (S1): 219–227. |
| [13] | ASHRAFIUON H, MUSKE K R, MCNINCH L, et al. Sliding model tracking contol of surface vessels[J]. IEEE Transactions on Industrial Electronics, 2008, 55 (11): 4004–4011. DOI: 10.1109/TIE.2008.2005933 |
| [14] |
李建祯. 多智能体系统一致性若干问题研究[D]. 南京: 南京理工大学, 2011.
LI Jian-zhen. Research on several problems of multi-agent systems consensus[D]. Nanjing: Nanjing University of Science and Technology, 2011. |
 2018, Vol. 40
2018, Vol. 40
