在精确度要求较高和响应速度较快的工程应用领域中,永磁同步电机(PMSM)占有重要位置。时下船用永磁同步电机(PMSM)传统的调速系统,仍然大规模采用常规PI调节器来控制。虽然PI控制容易实现,控制算法简单、稳定,但同样也存在一定的局限性和问题。因为PI算法的本质是一种线性控制,一旦被控对象的模型发生变化或是呈现非线性时,原本的线性PI控制无法满足设计时所要求的性能指标。鲁棒性、精确性都无法合人心意。而参考模型自适应模糊控制,综合了模糊控制和自适应控制优点,在面对不确定模型和非线性系统时,可以实现较好的控制性能。在文献[1] 首次提出用模糊集理论设计MRAC系统和文献[2]对自适应模糊系统进行深入研究之后,国内外学者在这方面做了大量的研究[3–6],并且在某些工程应用中已显示出良好的控制性能。为应对电机模型的不确定性和非线性等问题,本文对系统控制采用间接型自适应模糊控制,通过合理选择模糊规则、模糊基函数和参考模型,实现模型参考自适应。即使被控对象的模型发生变化时,也能够实现很好的控制性能。仿真结果表明:与传统的PI控制相比,基于间接参考模型自适应模糊控制方法的速度控制器具有更快速准确的跟踪能力,同时也降低了调速系统对电机参数变化、负载扰动等因素的敏感性。
1 问题描述有如下形式的n阶非线性系统:
| $\left\{ \begin{array}{l}{{x}^{(n)}} = f\left( {{x},\mathop {x}\limits^ \cdot ,...,{{x}^{(n - 1)}}} \right) + g\left( {{x},\mathop {x}\limits^ \cdot ,...,{{x}^{(n - 1)}}} \right)u\text{。}\\y = {x}\text{。}\end{array} \right.$ | (1) |
式中:f和g为不确定的未知连续函数;
1)变量
2)在满足上述条件下,为使跟踪误差
| ${u^*} = \frac{1}{{g\left( x \right)}}\left[ { - f\left( x \right) + y_m^{(n)} + {k^{\rm T}}e} \right]\text{。}$ | (2) |
代入式(1)得:
| ${e^{(n)}} + {k_1}{e^{(n - 1)}} + \cdot \cdot \cdot + {k_n}e = 0\text{。}$ | (3) |
取合适k值使得
式中:
其中
| ${\xi _l}(x) = \frac{{\prod\limits_{i = 1}^n {{u_{F_i^l}}({x_i})} }}{{\sum\limits_{l = 1}^M {\prod\limits_{i = 1}^n {{u_{F_i^l}}({x_i})} } }}\text{,}$ | (4) |
所以
| ${\hat {f}}(x|{\theta _f}) = \theta _f^{\rm T}\xi (x)\text{,}$ | (5) |
| ${\hat {g}}(x|{\theta _g}) = \theta _g^{\rm T}\xi (x)\text{。}$ | (6) |
式(2)中的
| ${u_I} = \frac{1}{{\mathop g\limits^ \wedge (x|{\theta _g})}}[ - \mathop f\limits^ \wedge (x|{\theta _f}) + y_m^{(n)} + {k^{\rm T}}e]\text{,}$ | (7) |
即为等效控制器的控制律。
将式(7)代入式(1)即得误差方程:
| $\begin{split}&{e^{(n)}} = - {k^{\rm T}}e + [\mathop f\limits^ \wedge (x|{\theta _f}) - f(x)] + \\& [\mathop g\limits^ \wedge (x|{\theta _g} - g(x)]{u_I}\text{。}\end{split}$ | (8) |
上式等价于:
| $\begin{split}\mathop e\limits^ \cdot =& {{A}_c}e + {{b}_c}[(\mathop f\limits^ \wedge (x|{\theta _f}) - f(x)) + \\&(\mathop g\limits^ \wedge (x|{\theta _g}) - g(x)){u_I}]\text{。}\end{split}$ | (9) |
其中:Ac,bc分别为
| $\begin{array}{l}{{\mathit{\boldsymbol{A}}}_c} = \left[ {\begin{array}{*{20}{c}}0&1&0&0&{...}&0&0\\0&0&1&0&{...}&0&0\\{...}&{...}&{...}&{...}&{...}&{...}&{...}\\0&0&0&0&{...}&0&1\\{ - {k_n}}&{ - {k_{n - 1}}}&{...}&{...}&{...}&{ - {k_2}}&{ - {k_1}}\end{array}} \right]\text{,}\\[13pt]{{\mathit{\boldsymbol{b}}}_c} = \left[ {\begin{array}{*{20}{c}}0\\0\\{...}\\0\\1\end{array}} \right]\text{。}\end{array}$ |
因Ac是稳定矩阵,则存在唯一
| ${ {{A}_c}}^{\rm {T}}{P} + {\mathit{\boldsymbol{P{{A}}_c}}} = - {Q}\text{。}$ | (10) |
式中Q为任意
| $\begin{split}& \dot V = \frac{1}{2}{{\dot e}^{\rm T}}{P}e + \frac{1}{2}{e^{\rm T}}{P}\dot e=\\& - \frac{1}{2}{e^{\rm T}}{Q}e + {e^{\rm T}}{P}{b_c}[(\mathop f\limits^ \wedge (x|{\theta _f}) - f(x))+\\& \mathop g\limits^ \wedge (x|{\theta _g}) - g(x)){u_I}]\text{。}\end{split}$ | (11) |
要使
定义
| $\theta _f^* = \arg {\min _{{\theta _f} \in {\Omega _f}}}[{\sup _{x \in {u_I}}}\mathop {|f}\limits^ \wedge (x\left| {{\theta _f}) - f(x)} \right.|]\text{,}$ | (12) |
| $\theta _g^* = \arg {\min _{{\theta _g} \in {\Omega _g}}}[{\sup _{x \in {u_I}}}\mathop {|g}\limits^ \wedge (x\left| {{\theta _g}) - g(x)} \right.|]\text{。}$ | (13) |
其中:
| $\begin{array}{c}{\varOmega _f} = \{ {\theta _f}:\left| {{\theta _f}} \right| \leqslant {M_f}\}\text{,} \\{\varOmega _g} = \{ {\theta _g}:\left| {{\theta _g}} \right| \leqslant {M_g}\} \text{。}\end{array}$ |
Mf和Mg的值为设计者所取。
定义最小逼近误差:
| $\omega = ((\mathop f\limits^ \wedge (x\left| {\theta _f^*)} \right. - f(x)) + (\mathop g\limits^ \wedge (x\left| {\theta _g^*)} \right. - g(x))){u_I}\text{,}$ | (14) |
因此上式可将式(9)变形为下式:
| $\begin{split}& \dot e = {A_c}e + {b_c}[(\mathop f\limits^ \wedge (x\left| {\theta _f^{})} \right. - \mathop f\limits^ \wedge (x\left| {\theta _f^*)} \right.)+\\& (\mathop g\limits^ \wedge (x\left| {\theta _g^{}) - } \right.\mathop g\limits^ \wedge (x\left| {\theta _g^*)} \right.){u_I} + \omega ]\text{,}\end{split}$ | (15) |
将式(5)和式(6)代入式(15)得到如下方程:
| $\begin{split}& \dot e = {A_c}e + {b_c}[{({\theta _f} - \theta _f^*)^{\rm T}}\xi (x)+\\& {({\theta _g} - \theta _g^*)^{\rm T}}\xi (x){u_I} + \omega ]\text{。}\end{split}$ | (16) |
式中:
| $\begin{split}& V = \frac{1}{2}{e^{\rm T}}{P}e + \frac{1}{{2{\gamma _1}}}{({\theta _f} - \theta _f^*)^{\rm T}}({\theta _f} - \theta _f^*)+\\ & \frac{1}{{2{\gamma _2}}}{({\theta _g} - \theta _g^*)^{\rm T}}({\theta _g} - \theta _g^*)\text{,}\end{split}$ | (17) |
其中
| $\begin{split}& V = - \frac{1}{2}{e^{\rm T}}{Q}e + {e^{\rm T}}{P}{b_c}\omega+ \\& \frac{1}{{{\gamma _1}}}{({\theta _f} - \theta _f^*)^{\rm T}}[\mathop {{\theta _f}}\limits^ \cdot + {\gamma _1}{e^{\rm T}}{P}{b_c}\xi (x)]+\\& \frac{1}{{{\gamma _2}}}{({\theta _g} - \theta _g^*)^{\rm T}}[\mathop {{\theta _g}}\limits^ \cdot + {\gamma _2}{e^{\rm T}}{P}{b_c}\xi (x){u_I}]\text{。}\end{split}$ | (18) |
求解参数误差和跟踪误差差距最小的问题转换为使V最小的问题。为此自适应律的选择要使
| $\mathop {{\theta _f}}\limits^ \cdot = - {\gamma _1}{e^{\rm T}}P{b_c}\xi (x)\text{,}$ | (19) |
| $\mathop {{\theta _g}}\limits^ \cdot = - {\gamma _2}{e^{\rm T}}P{b_c}\xi (x){u_I}\text{。}$ | (20) |
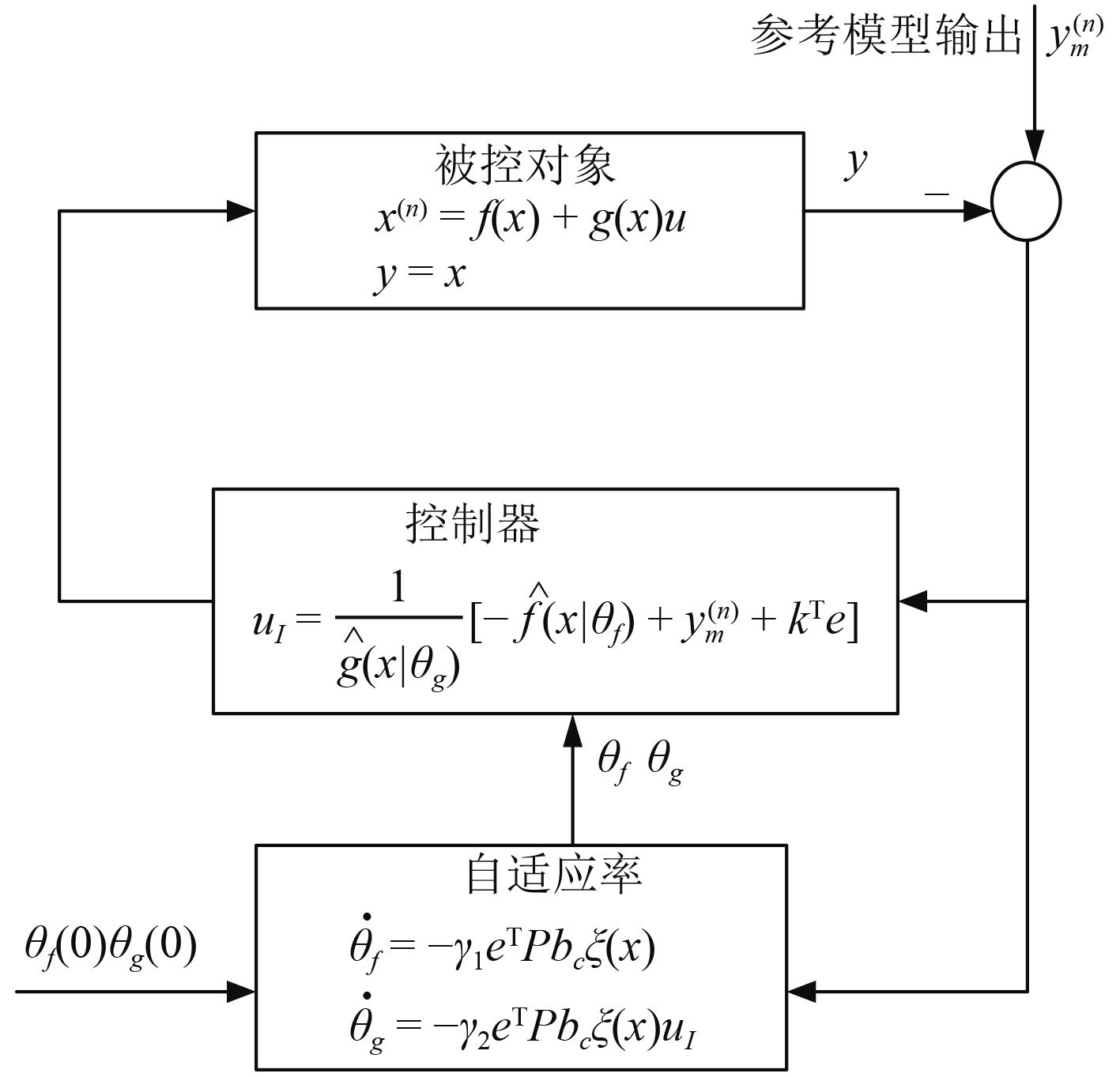
|
图 1 间接自适应模糊控制系统原理图 Fig. 1 Schematic diagram of indirect adaptive fuzzy control system |
1)永磁同步电机机械运动方程
方程为:
| $\left\{ \begin{array}{l}\displaystyle\frac{{{\rm d}{\theta _r}}}{{{\rm d}t}} = {\omega _r}\text{,}\\[10pt]J \displaystyle\frac{{{\rm d}{\omega _r}}}{{{\rm d}t}} = {T_e} - {T_l} - B{\omega _r}\text{。}\end{array} \right.$ | (21) |
设
| $\left\{ \begin{array}{l}\mathop {{x_1}}\limits^ \cdot = {x_2}\text{,}\\\mathop {{x_2}}\limits^ \cdot = \frac{1}{J}({T_e} - {T_l} - B{x_2})\text{。}\end{array} \right.$ | (22) |
其中,
即上式可改写为:
| $\left\{ \begin{array}{l}\mathop {{x_1}}\limits^ \cdot = {x_2}\text{,}\\\mathop {{x_2}}\limits^ \cdot = \frac{{( - {T_l} - B{x_2})}}{J} + (\frac{3}{{2J}}{p_n}{\psi _f}){i_q}\text{,}\\y = {x_1}\text{。}\end{array} \right.$ | (23) |
将式(23)与式(1)相比较,可知此时系统的输出为
式(23)中
| $u = - \frac{{(\mathop f\limits^ \wedge (x|{\theta _f}) + \ddot y + {k^{\rm T}}e)}}{{\mathop g\limits^ \wedge (x|{\theta _g})}}\text{。}$ |
2)构造模糊基函数
以电机转子角
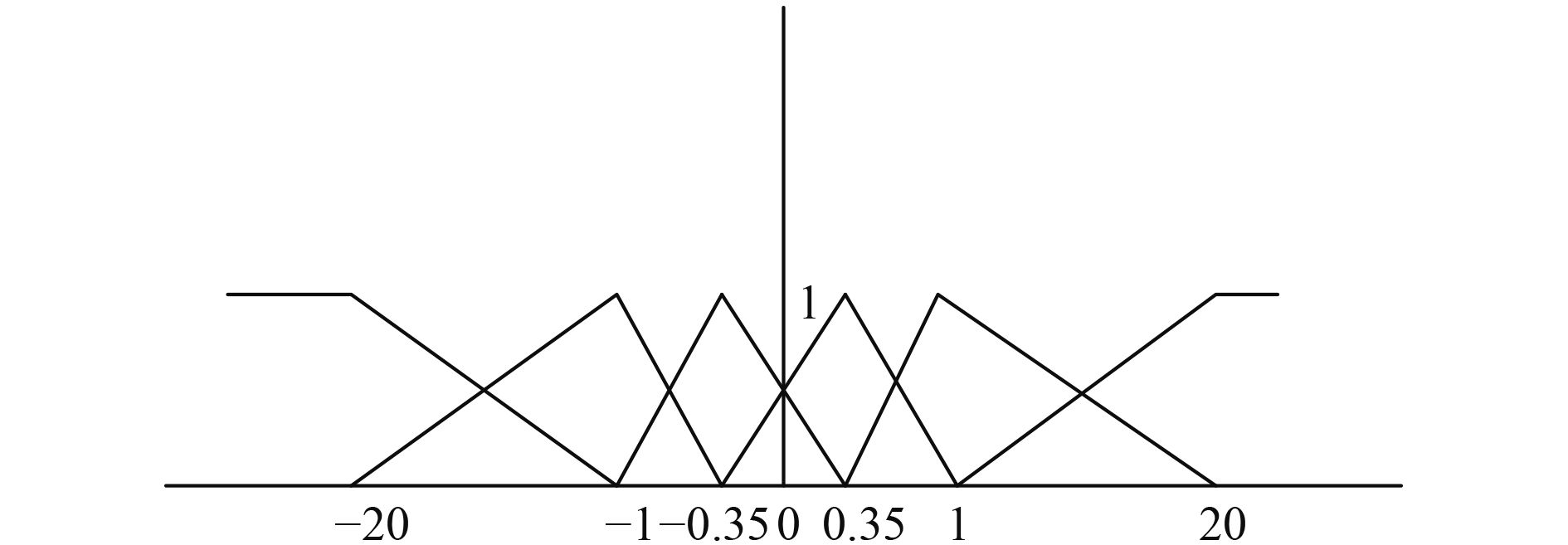
|
图 2
|

|
图 3
|
模糊基函数由Matlab的M文件实现:
M=12,即模糊基函数12维列向量,那么
3)自适应率在线调整
为使问题简化,按上述自适应律设计步骤,设
| $\begin{array}{l}{P} = \left[ {\begin{array}{*{20}{c}}{15}&5\\5&5\end{array}} \right]\text{,}\\[10pt]{{b}_c} = \left[ {\begin{array}{*{20}{c}}0\\1\end{array}} \right]\text{,}\\[10pt]{P}{{b}_c} = \left[ {\begin{array}{*{20}{c}}5\\5\end{array}} \right]\text{。}\end{array}$ |
式(18)中参数
| $\begin{array}{l}{\theta _f}(0) = {(0,0,0,0,0,0,0,0,0,0,0,0)^{\rm T}}\text{,}\\{\theta _g}(0) = {(0,0,0,0,0,0,0,0,0,0,0,0)^{\rm T}}\text{。}\end{array}$ |
取Mg=600与Mf=1 000。
仿真模型如图4所示。
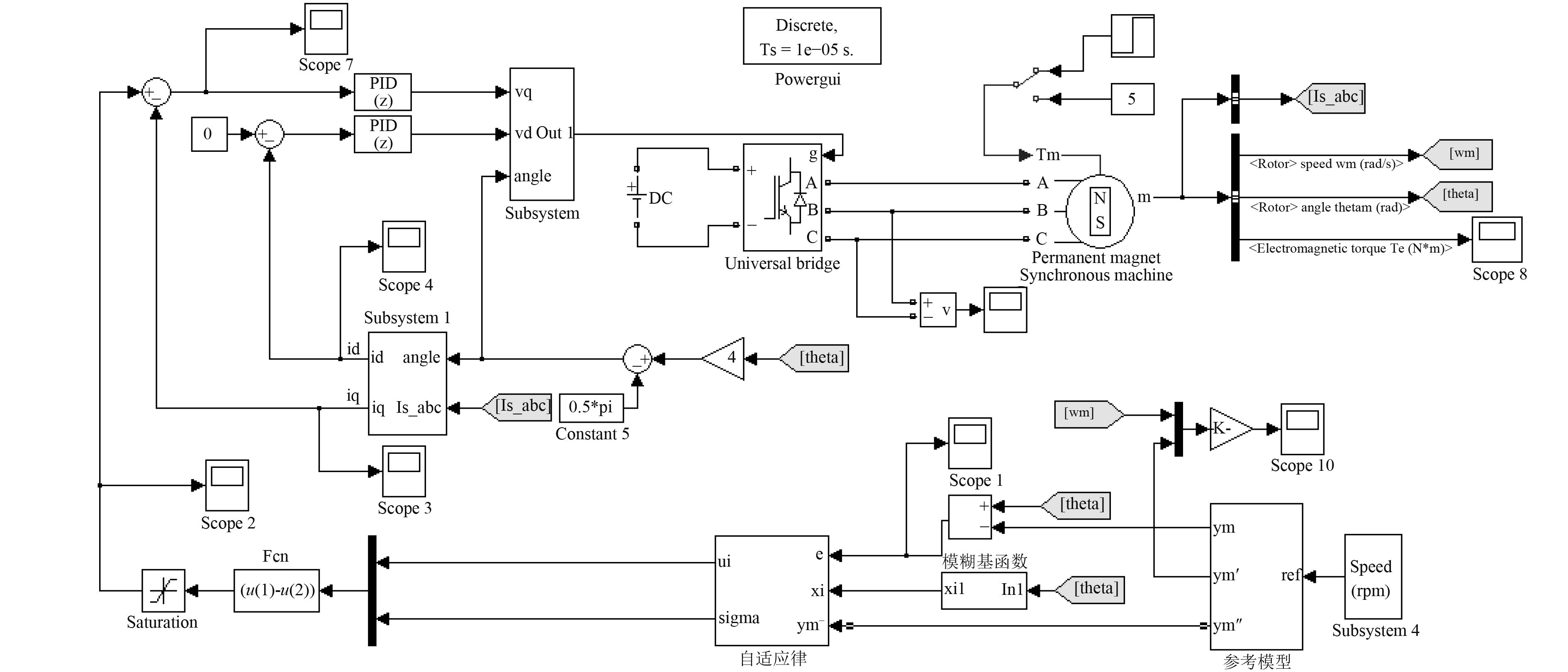
|
图 4 PMSM参考模型自适应模糊控制仿真图 Fig. 4 Reference model adaptive fuzzy control simulation diagram of PMSM |
选择参考模型为2阶系统,则传函标准形式为:
| ${y_m}(s) = \frac{{\omega _n^2}}{{{s^2} + 2\varsigma {\omega _n}s + \omega _n^2}}\text{,}$ |
当
上升时间
超调量
过渡时间
当改变
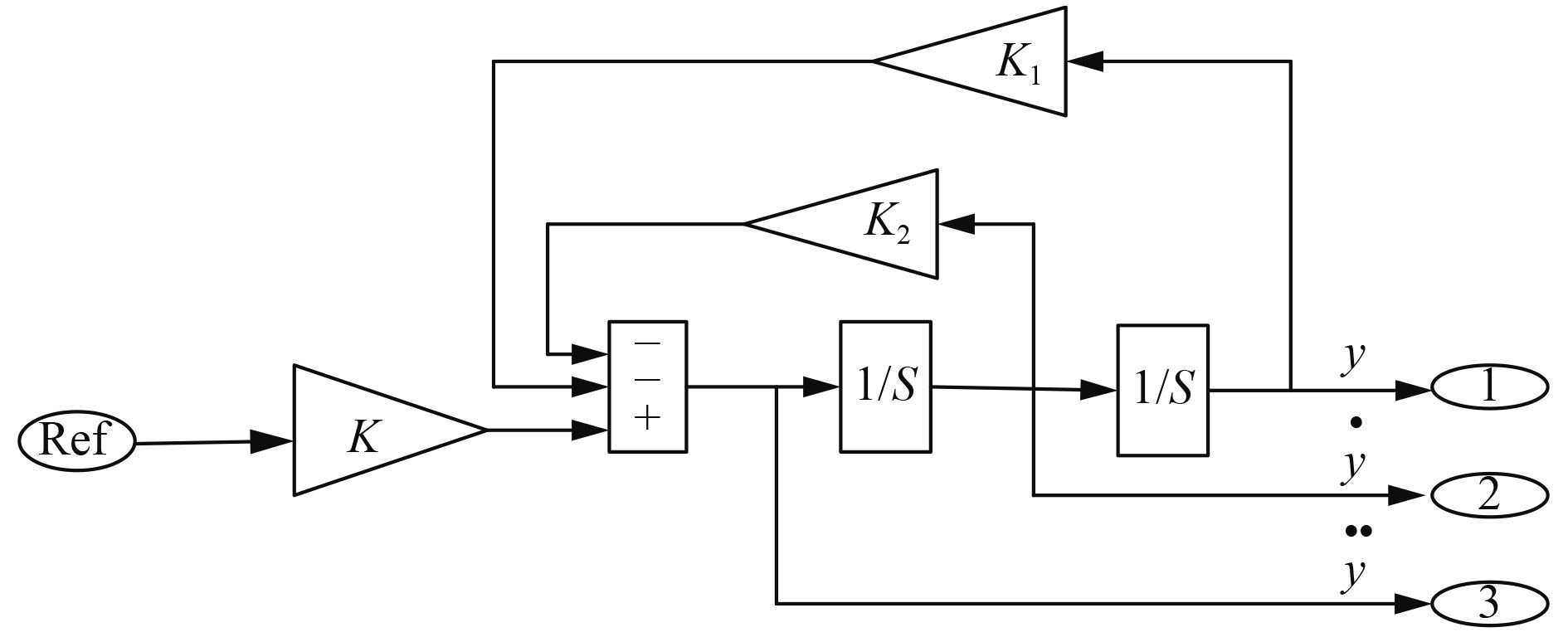
|
图 5 参考模型模块 Fig. 5 Reference model module |
模型参数选择为
条件1:
条件2:
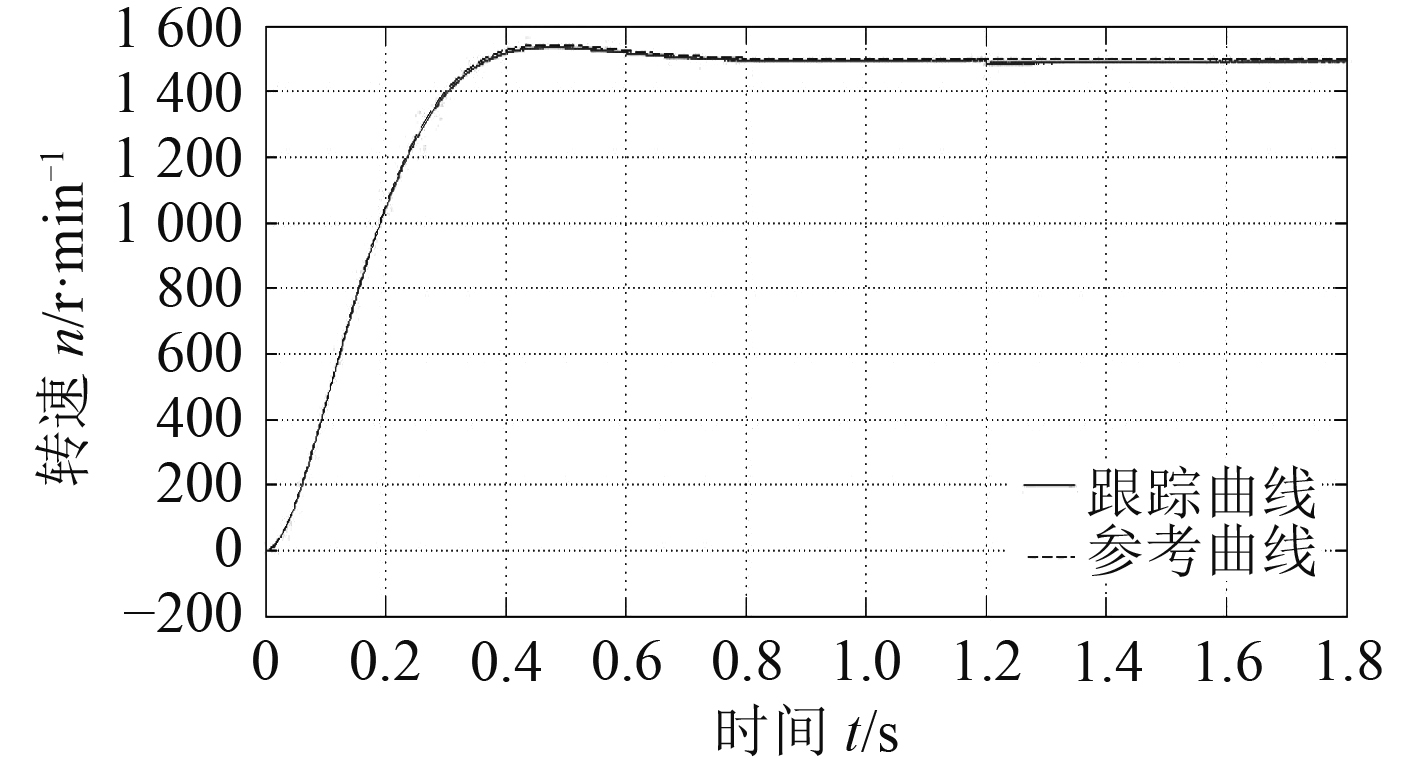
|
图 6 PMSM自适应模糊控制跟踪参考曲线的响应 Fig. 6 Response of PMSM adaptive fuzzy control tracking reference curve |
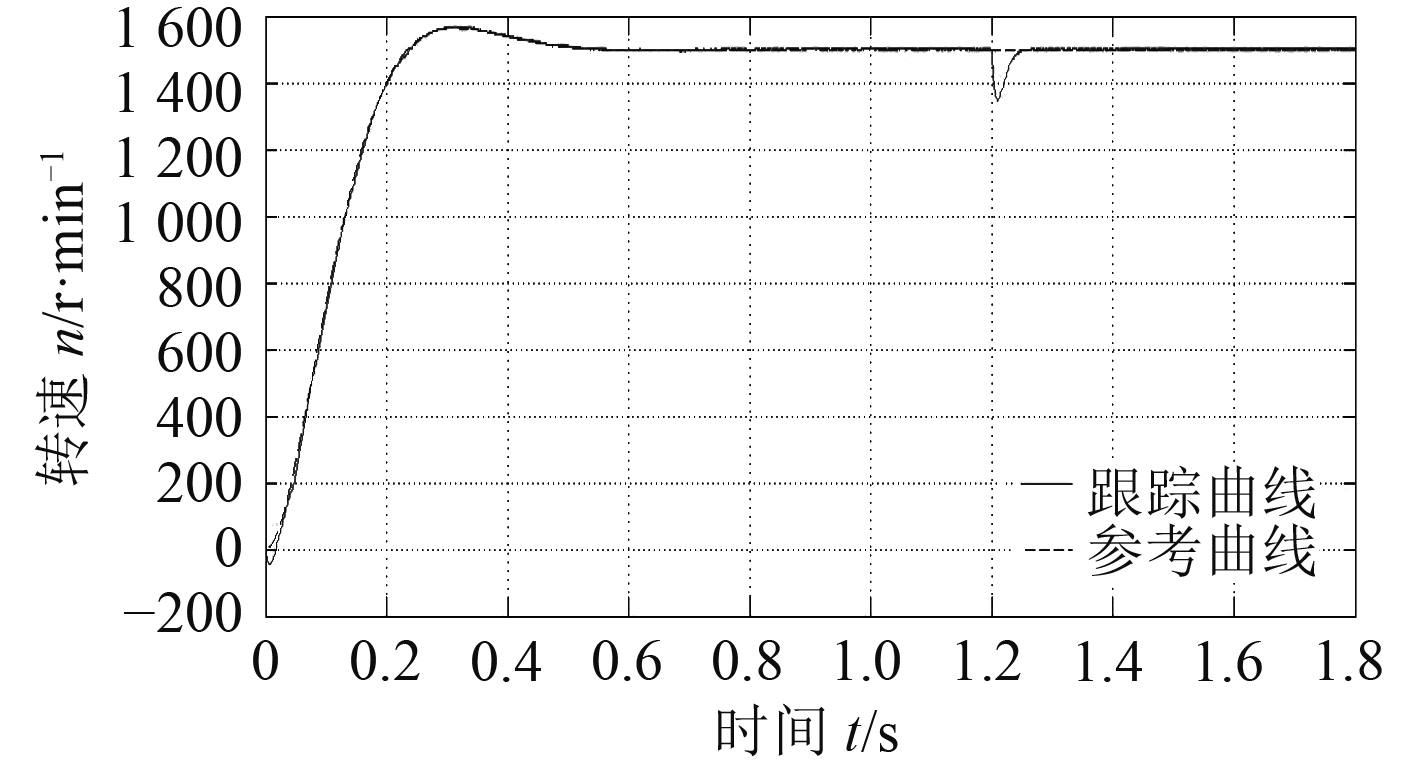
|
图 7 PMSM自适应模糊控制跟踪参考曲线的响应 Fig. 7 Response of PMSM adaptive fuzzy control tracking reference curve |
由仿真结果可以看出:当对永磁同步电机进行间接自适应模糊控制时,可知条件1阻尼系数与角频率不大时,加入扰动时系统跟随参考模型的输出精度较高,即使是条件2时,系统也只是发生较小的振荡后快速稳定并跟踪参考模型输出。由结果可知参考模型参数发生改变,被控系统的输出也能很好的跟随参考曲线,不需要依赖电机的参数与电机自身特性的改变还有就是抗扰动能力强,跟踪精度高。
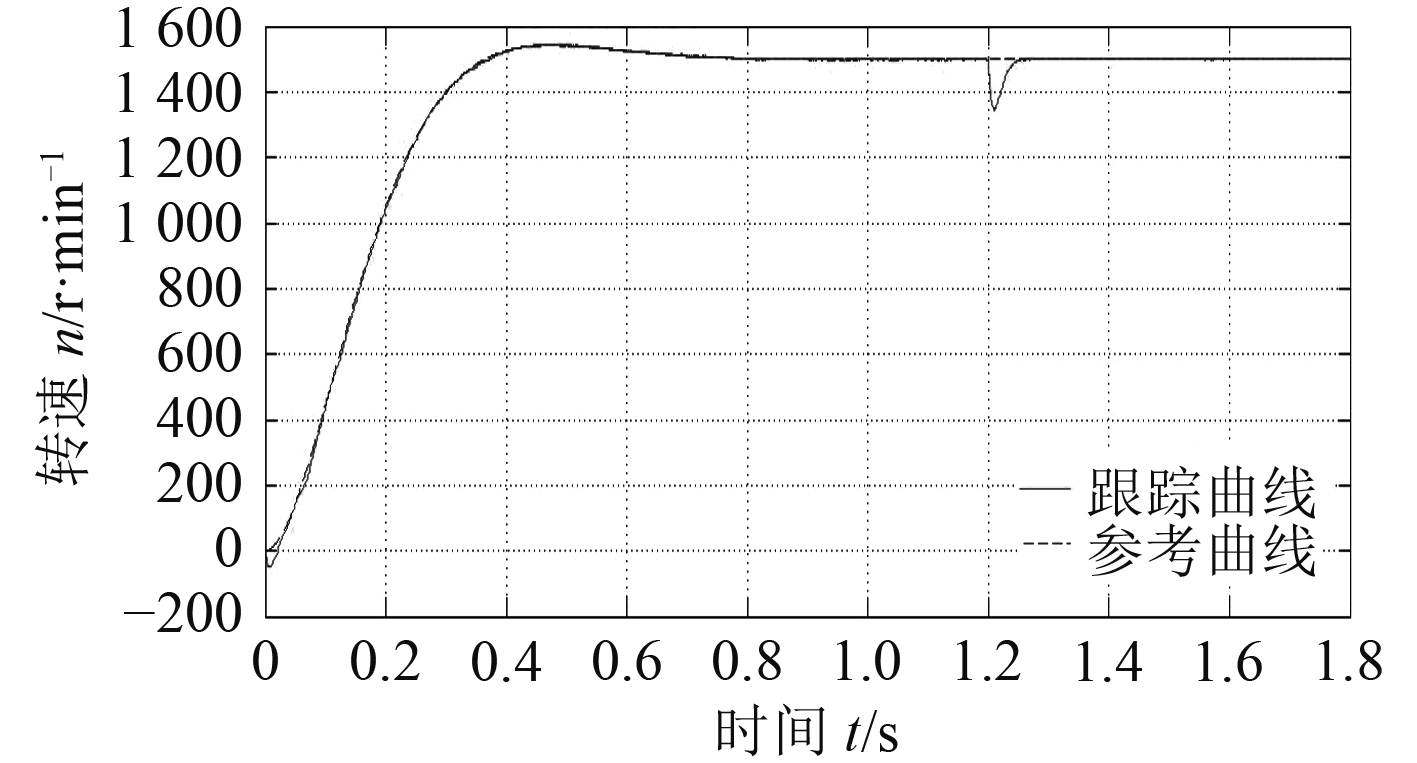
|
图 8 PMSM自适应模糊控制跟踪参考曲线的响应 Fig. 8 Response of PMSM adaptive fuzzy control tracking reference curve |
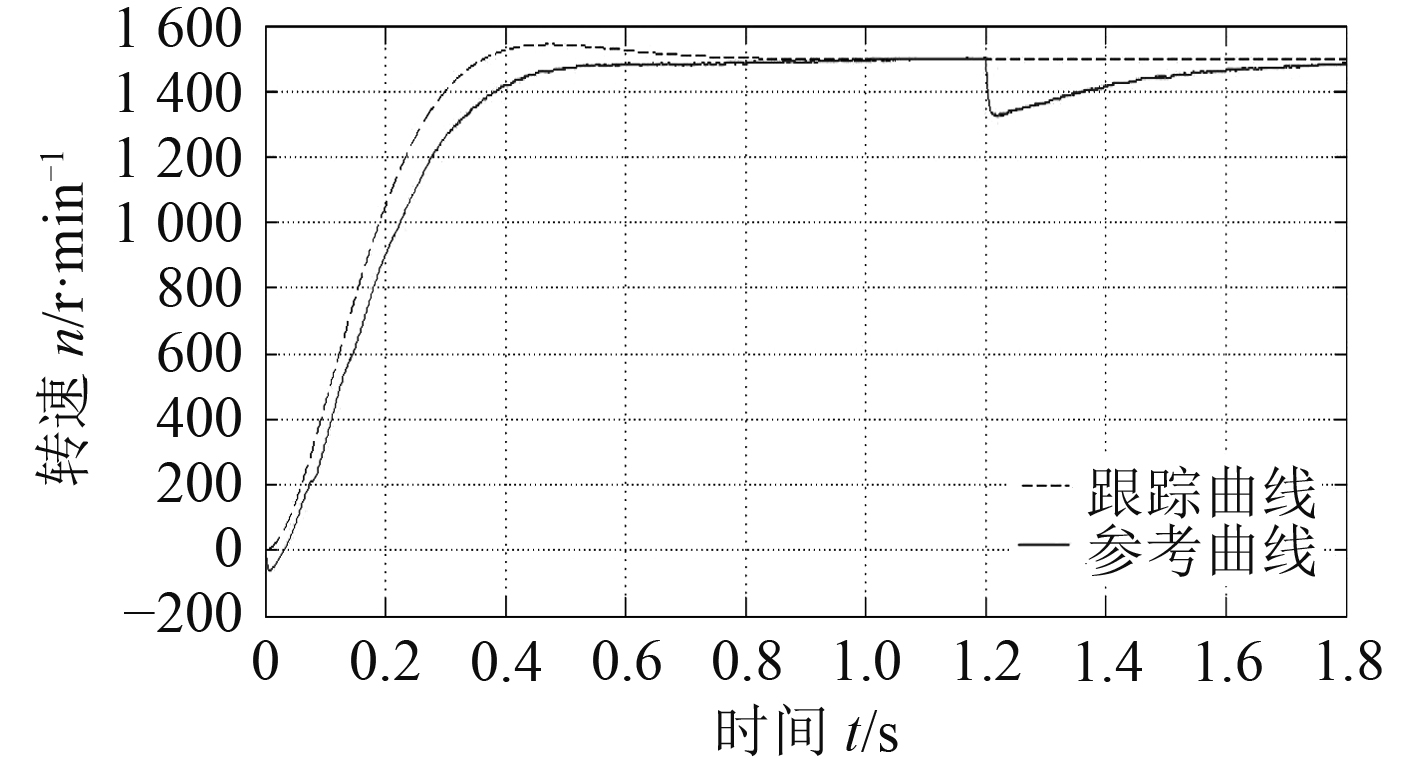
|
图 9 永磁同步电动机PI控制跟踪参考曲线的响应 Fig. 9 Response of permanent magnet synchronous motor PI control tracking reference curve |
从仿真结果可以看出,相同条件下PI控制在跟踪精度上远低于自适应模糊控制,1.2 s对系统施加扰动时也可以看出,自适应模糊控制的抗扰动能力远高于PI控制。所以仿真结果表明:间接自适应模糊控制器通过模糊推理产生模糊基函数并构建等效控制器,使不确定的非线性系统实时在线逼近参考模型,成功实现了模型参考自适应。还可看出,系统的输出响应受电机自身参数影响不敏感,系统参数突变时,系统仍有较好的动、静态性能。自适应模糊控制无论是在跟踪模型精度上,还是在抗扰动能力等方面都有明显的优势。
6 结 语本文针对船用永磁同步电机控制系统中的非线性时变系统,使用模糊系统的模糊基函数逼近永磁同步电机未知参数,并由Lyapunov稳定性理论设计模型参考自适应模糊控制器。根据自适应模糊控制理论,建立Matlab/Simulink系统仿真模型。通过与传统永磁同步电机矢量PI控制对比,由仿真结果证明,参考模型自适应控制在跟踪参考信号的稳定性、跟踪精度等方面远好于传统PI控制,而且对电机参数的改变不敏感,即使给系统加入突变扰动时系统仍具有良好的动静态性能。本文也为永磁同步电机高性能控制及其实用提供了新的研究方法。
| [1] |
郑维敏, 张洪良, 黄圣乐. 用模糊集理论设计模型参考自适应系统[J]. 信息与控制, 1982, 11 (3): 8–14.
ZHEN Wei-min, ZHANG Hong-liang, HUANG Sheng-le. Design model reference adaptive system based on fuzzy set theory[J]. Information and Control, 1982, 11 (3): 8–14. |
| [2] | 王立新. 自适应模糊系统与控制——设计与稳定性分析[M], 北京: 国防工业出版社, 1995 : 120–162. |
| [3] | Noureddine Golea, Amar Golea, Khier Benmahammed. Fuzzy model reference adaptive control[J]. IEEE Transactions on Fuzzy Systems (S1063-6706), 2002, 10 (4): 436–444. DOI: 10.1109/TFUZZ.2002.800694 |
| [4] |
朱嵘嘉, 纪志成. 模糊多参考模型自适应控制及仿真研究[J]. 系统仿真报, 2005, 17 (12): 2997–3003.
ZHU Rongjia, JI Zhicheng. Fuzzy multiple reference model adaptive control and simulation study[J]. Journal of System Simulation, 2005, 17 (12): 2997–3003. |
| [5] |
薛花, 姜建国. 基于EKF永磁同步电机FMRAC方法的仿真研究[J]. 系统仿真学报, 2006, 18 (11): 3324–3327.
XUE Hua, JIANG Jianguo. Investigation to simulation of fuzzy model reference adaptive control strategy of PMSM based on EKF[J]. Journal of System Simulation, 2006, 18 (11): 3324–3327. DOI: 10.3969/j.issn.1004-731X.2006.11.080 |
| [6] |
纪志成, 薛花, 沈艳霞. 永磁同步电机调速系统的模糊PI智能控制新方法[J]. 电工技术学报, 2003, 18 (6): 53–58.
JI Zhicheng, XUE Hua, SHEN Yanxia. Fuzzy PI intelligent control method of permanent magnet synchronous motor speed regulating system[J]. Journal of Electrical Engineering, 2003, 18 (6): 53–58. |
| [7] | 王立新. 模糊系统与模糊控制教程[M], 北京: 清华大学出版社, 2003, 100–118. |
 2018, Vol. 40
2018, Vol. 40
